Study of Heat and Mass Transfer in a Composite Nanofluid Layer

Abstract

A non-linear analysis is done to analyze the heat and mass transport in a composite nanofluid layer confined between two parallel horizontal plates, heated from below. The Nusselt number for temperature and nanoparticle concentrations is obtained as a function of time. It is observed that the suspension of two different nanoparticles in a base fluid significantly affects the heat and mass transport. We observe that the modified diffusivity ratios and the Lewis numbers for the first and second types of nanofluids only affect the mass transportation of the first and second types of nanofluids, respectively.

Nomenclature

Latin Symbols  

$D_{B_1}, D_{B_2}$:

Brownian Diffusion coefficients.

$D_{T_1}, D_{T_2}$:

Thermophoretic diffusion coefficients.

Pr:

Prandtl number.

L:

Dimensional layer depth.

$Le_1, Le_2$:

Lewis numbers.

$N_{A1}, N_{A2}$:

Modified diffusivity ratios.

$N_{B1}, N_{B2}$:

Modified particle-density increments.

p:

Pressure.

$\boldsymbol{g}$:

Gravitational acceleration.

t:

Time.

T:

Temperature.

${\textbf {V}}=(u, v, w)$:

Nanofluid velocity.

 

Greek Symbols  

$\alpha _f = \kappa /\rho c$:

Thermal diffusivity of the nanofluid.

$\kappa$:

Thermal conductivity of the nanofluid.

$\beta _T$:

Thermal volumetric coefficient.

$\mu$:

Dynamic viscosity.

$\rho _{p_1}, \rho _{p_2}$:

Mass densities of nanoparticles.

$\phi _1, \phi _2$:

Nanoparticle volume fractions.

 

1 Introduction

In order to enhance the poor thermal conductivity of liquids, Maxwell, suggested to add solid particles of high thermal conductivity into the liquids, more than a century ago. His idea was implemented with millimeter- or micrometer-sized particles but it was not very fruitful because of such extra-sized particles. The major issues with such particles were settling down under gravity, clogging, and abrasion. So, there was a search for particles smaller than micro-sized particles and this search ultimately ended with the invention of nanofluids (by Choi [1]) which are the fluids comprising a little amount of uniformly dispersed and suspended nanometer-sized particles in a base fluid. Around 15–40% increment in the thermal conductivity (Eastman et al. [2], Das et al. [3]) of the fluid is observed on adding a small amount of nanoparticles into the base fluid. Moreover, the size of nano-particles becomes quite closer to fluid molecules’ size and this prevents nanoparticles to settle down under gravity.

Because of these important properties, nanofluids are widely used in various industries, especially in those processes where cooling is essentially required. Buongiorno [4] was the first to study convective transport in nanofluids in 2006. He noticed that other than base fluid velocity, Brownian diffusion and thermophoresis are mainly responsible for nanoparticles’ absolute velocity in the absence of turbulent motion. Tzou [5, 6] used the Buongiorno model to study the onset of convection in a horizontal nanofluid layer heated from below. Nield and Kuznetsov [7,8,9,10,11] further analyzed the similar problem with porous media. After them, many researchers are still working in this field. Bhadauria et al. [12] described the non-linear study for bi-dimensional convection in a nanofluid-saturated porous medium.

Apart from the direct study of the onset of convection, heat, and mass transfer, various researchers showed their interest in the study of convective flows under the effect of various external modulations like thermal modulation, gravity modulation, magnetic field modulation, etc. These modulations have various practical applications in different industries. Venezian [13] was the first to introduce the effect of modulating the boundary temperatures. Later on, Umavathi [14] studied the thermal modulation in the case of nanofluids. Gresho and Sani [15] were the first to study the consequences of modulating gravitational field on Rayleigh–Bénard Convection. Bhadauria et al. [16] did the non-linear study of thermal instability under temperature/gravity modulation. Bhadauria et al. [17] studied the effect of gravity modulation and internal heating over convection in a nanofluid-saturated porous medium. Thomson [18] and Chandrasekhar [19] were the first to discuss the idea about magneto-convection. This has now become a huge area of research. Kiran et al. [20] recently published an article about magneto-convection under magnetic field modulation. Yadav [21] presented a numerical solution of the onset of buoyancy-driven nanofluid convective motion in an anisotropic porous medium layer with internal heating and variable gravity. Sakshath et al. [22] investigated the effect of horizontal pressure gradient on Rayleigh–Bénard convection of a Newtonian nanoliquid in a high porosity medium using a local thermal non-equilibrium model.

After various kind of modulations, a new type of nanofluid, known as composite nanofluid, has now become an advanced area of interest among the researchers in the recent years. A composite nanofluid is prepared by suspending two or more types of nanoparticles in a base fluid in order to get a stable and homogeneous mixture. The synthesis of such composite materials can be done either by chemical or physical processes (Hanemann and Szabo [23], Zhang et al. [24]). The characteristics of the composite nanofluids lie in between the properties of their constituents. The thermophysical properties of composite nanofluids can be altered to converge to the required heat transfer demands. An extensive review on composite nanofluids and their properties is given by Suleiman et al. [25]. Linear and nonlinear analysis in Hele-Shaw cell in the presence of through-flow and gravity modulation have been done by Bhadauria et al. [26].

The very first study of thermal instability for composite nanofluids is presented by Kumar and Awasthi [27] recently. They concluded that the maximum stability is achieved only when both kinds of nanoparticles are in the same ratio. To the best of our knowledge, no non-linear study on this topic is present in literature till date. This idea motivated us to present this study of heat and mass transfer in a composite nanofluid layer.

2 Mathematical Formulation

An infinitely extended horizontal layer, of composite nanoliquid in which two different types of nanoparticles are suspended homogeneously, restricted between $Z=0$ and $Z=L$ has been considered. The upper plate at $Z=L$ is assumed to be at temperature $T_0$, while the lower plate is at slightly higher temperature $T_0 + \varDelta T$ as shown in Fig. 1. The cartesian coordinate system has been used. Both nanoparticles and the base fluid are assumed to be in local thermal equilibrium. Boundaries are considered to be Free–Free and perfectly insulating. The linearization of equations is done using the Oberbeck–Boussinesq approximation. The governing equations of the system are as follows (Kumar and Awasthi [27]):

Fig. 1

Formal diagram

$$\begin{aligned} \nabla \cdot \textbf{V}=0 \end{aligned}$$

(1)

$$\begin{aligned} \rho \left[ \frac{\partial }{\partial t} + (\textbf{V}\cdot \nabla )\right] \textbf{V}= -\nabla {p} +\mu \nabla ^{2}\textbf{V} +[\phi _1\rho _{p_1} + \phi _2\rho _{p_2} +\rho (1- \phi _1 -\phi _2) \{1-\beta _T (T-T_0)\}]\textbf{g} \end{aligned}$$

(2)

$$\begin{aligned} \rho c \left[ \frac{\partial }{\partial t}+ (\textbf{V}\cdot \nabla )\right] T= \kappa \nabla ^2 T + (\rho c)_{p_1}[D_{B_1} \nabla \phi _1 \nabla T + \frac{D_{T_1}}{T_0} \nabla T \nabla T] + (\rho c)_{p_2}[D_{B_2} \nabla \phi _2 \nabla T + \frac{D_{T_2}}{T_0} \nabla T \nabla T] \end{aligned}$$

(3)

$$\begin{aligned} \left[ \frac{\partial }{\partial t}+ (\textbf{V}\cdot \nabla )\right] \phi _1= D_{B_1} \nabla ^2\phi _1+\left( \frac{D_{T_1}}{T_0}\right) \nabla ^2 T \end{aligned}$$

(4)

$$\begin{aligned} \left[ \frac{\partial }{\partial t}+ (\textbf{V}\cdot \nabla )\right] \phi _2= D_{B_2} \nabla ^2\phi _2+\left( \frac{D_{T_2}}{T_0}\right) \nabla ^2 T \end{aligned}$$

(5)

where $\nabla ^{2}\equiv \frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}+\frac{\partial ^{2}}{\partial z^{2}}$

At the boundaries, the volume fractions of nanoparticles are assumed to be constant. The boundary conditions under consideration are as follows:

$$\begin{aligned} \left. \begin{aligned} w=0,\ \ \frac{\partial w}{\partial z} + \lambda _1 L \frac{\partial ^2 w}{\partial z^2}=0, \ \phi _1=\phi _{10}, \ \phi _2=\phi _{20} \ \ \textrm{at} \ \ z=0 \\ w=0,\ \ \frac{\partial w}{\partial z} - \lambda _2 L \frac{\partial ^2 w}{\partial z^2}=0, \ \phi _1=\phi _{11}, \ \phi _2=\phi _{21} \ \ \textrm{at} \ \ z=L \end{aligned}\right\} \end{aligned}$$

(6)

where $\lambda _1$ and $\lambda _2$ take the value “0” and “$\infty$” for rigid–rigid and free–free boundaries, respectively. Also $\phi _{11}>\phi _{10}$ and $\phi _{21}>\phi _{20}$. In order to non-dimensionalize the equations, we use the following substitutions:

$$\begin{aligned} \left. \begin{aligned}&(x,y,z) = L(x',y',z'),\ \ \ (u,v,w) = (u',v',w')\frac{\alpha _f}{L}, \\&t= \frac{L^2}{\alpha _f} t', \ \ \ p= \frac{\mu \alpha _f}{L^2} p',\\&T'=\frac{T-T_0}{\varDelta T},~~ \phi _{i(=1 or 2)}'=\frac{\phi _i -\phi _{i0}}{\phi _{i1} -\phi _{i0}}. \end{aligned}\right\} \end{aligned}$$

(7)

Making use of (7) into the Eqs. (1)–(6) and leaving the primes for simplicity, we obtain the following non-dimensional equations:

$$\begin{aligned} \nabla \cdot \textbf{V}= 0 \end{aligned}$$

(8)

$$\begin{aligned} \frac{1}{Pr}\left[ \frac{\partial }{\partial t}+(\textbf{V}\cdot \nabla )\right] \textbf{V}= -\nabla p + \nabla ^2 \textbf{V} + \mathbf {e_z} \left[ Ra T - Rn_{1} \phi _1 - Rn_{2} \phi _2 -Rm \right] \end{aligned}$$

(9)

$$\begin{aligned} \left[ \frac{\partial }{\partial t}+(\textbf{V}\cdot \nabla )\right] T= \nabla ^2 T + \left( \frac{N_{B1}}{Le_{1}}\right) \nabla \phi _1 \cdot \nabla T +\left( \frac{N_{A1} N_{B1}}{Le_{1}}\right) \nabla T \cdot \nabla T \nonumber \\ + \left( \frac{N_{B2}}{Le_{2}}\right) \nabla \phi _2 \cdot \nabla T +\left( \frac{N_{A2}N_{B2}}{Le_{2}}\right) \nabla T \cdot \nabla T\qquad \qquad \qquad \end{aligned}$$

(10)

$$\begin{aligned} \left[ \frac{\partial }{\partial t}+(\textbf{V}\cdot \nabla )\right] \phi _1=\left( \frac{1}{Le_1}\right) \nabla ^2\phi _1 +\left( \frac{N_{A1}}{Le_1}\right) \nabla ^2 T \end{aligned}$$

(11)

$$\begin{aligned} \left[ \frac{\partial }{\partial t}+(\textbf{V}\cdot \nabla )\right] \phi _2=\left( \frac{1}{Le_2}\right) \nabla ^2\phi _2 +\left( \frac{N_{A2}}{Le_2}\right) \nabla ^2 T \end{aligned}$$

(12)

The dimensional-less boundary conditions are

$$\begin{aligned} \left. \begin{aligned}&T=1, w=\phi _1=\phi _2=0, \frac{\partial w}{\partial z} + \lambda _1 \frac{\partial ^2 w}{\partial z^2}=0 \ \textrm{at} \ z = 0 ,\\&T=w=0, \phi _1=\phi _2=1, \frac{\partial w}{\partial z} -\lambda _2 \frac{\partial ^2 w}{\partial z^2}=0 \ \textrm{at} \ z = 1, \end{aligned}\right\} \end{aligned}$$

(13)

where

$Ra =\displaystyle \frac{\rho g \beta _T L^3 \varDelta T}{\mu \alpha _f}$ is the thermal Rayleigh number, $Rn_1=\displaystyle \frac{(\rho _{p_1} - \rho )(\phi _{11}-\phi _{10})g d^3}{\mu \alpha _f}$ and $Rn_2=\displaystyle \frac{(\rho _{p_2} - \rho )(\phi _{21}-\phi _{20})g d^3}{\mu \alpha _f}$ are the nanoparticle concentration Rayleigh numbers, $Rm=\displaystyle \frac{\{\rho _{p_1}\phi _{10} + \rho _{p_2}\phi _{20} + \rho (1-\phi _{10}-\phi _{20})\}g d^3}{\mu \alpha _f}$ is the basic density Rayleigh number, $Pr=\displaystyle \frac{\mu }{\rho \alpha _f}$ is Prandtl number, $Le_1 =\displaystyle \frac{\alpha _f}{D_{B_1}}$ and $Le_2 =\displaystyle \frac{\alpha _f}{D_{B_2}}$ are the Lewis numbers, $N_{A1}=\displaystyle \frac{D_{T_1}\varDelta T}{D_{B_1} T_0 (\phi _{11}-\phi _{10})}$ and $N_{A2}=\displaystyle \frac{D_{T_2}\varDelta T}{D_{B_2} T_0 (\phi _{21}-\phi _{20})}$ are the modified diffusivity ratios, and $N_{B1}=\displaystyle (\rho c)_{p_1}\frac{\phi _{11}-\phi _{10}}{\rho c}$ and $N_{B2}=\displaystyle (\rho c)_{p_2}\frac{\phi _{21}-\phi _{20}}{\rho c}$ are the modified particle-density increments.

3 Conduction State

The temperature, pressure, and nanoparticle volume fractions are taken to be the functions of “z” only. The time-independent quiescent solution of Eqs. (8)–(12) is obtained under the following assumptions:

$$\begin{aligned} \textbf{V}=\textbf{0}, \ T=T_b(z), \ p=p_b (z), \ \phi _1=\phi _{1b}(z), \ \phi _2=\phi _{2b}(z). \end{aligned}$$

(14)

The desired conduction state is evaluated (Kumar and Awasthi [27]) as:

$$\begin{aligned} T_b (z) = 1-z, \ \phi _{1b}(z)= z, \ \phi _{2b}(z)= z. \end{aligned}$$

(15)

4 Perturbed State

We impose small perturbations on the conduction state:

$$\begin{aligned} \textbf{V}= \tilde{\textbf{V}},\ \ p=p_b+\tilde{p},\ \ T=T_b+\tilde{T},\ \ \phi _1=\phi _{1b}+ \tilde{\phi _1}, \ \ \phi _2=\phi _{2b}+ \tilde{\phi _2}. \end{aligned}$$

(16)

Using Eq. (16) in Eqs. (8)–(12) and assuming all the physical quantities to be free from “y”, we get the following perturbed equations:

$$\begin{aligned} \nabla \cdot \tilde{\textbf{V}}=0\end{aligned}$$

(17)

$$\begin{aligned} \frac{1}{Pr}\left[ \frac{\partial }{\partial t}+ \left( \tilde{u} \frac{\partial }{\partial x} + \tilde{w} \frac{\partial }{\partial z}\right) \right] \tilde{\textbf{V}}= -\nabla \tilde{p}+ \nabla ^2\tilde{\textbf{V}} + \mathbf {e_z}\left[ Ra \tilde{T} - Rn_1 \tilde{\phi _1}-Rn_2 \tilde{\phi _2} \right] \end{aligned}$$

(18)

$$\begin{aligned} \frac{\partial \tilde{T}}{\partial t} - \tilde{w} + \left( \tilde{u} \frac{\partial }{\partial x} + \tilde{w} \frac{\partial }{\partial z}\right) \tilde{T}= \nabla ^2\tilde{T} + \frac{N_{B1}}{Le_1} \left[ \frac{\partial \tilde{T}}{\partial z}- \frac{\partial \tilde{\phi _1}}{\partial z}\right] + \frac{N_{B2}}{Le_2} \left[ \frac{\partial \tilde{T}}{\partial z}- \frac{\partial \tilde{\phi _2}}{\partial z}\right] \nonumber \\ - \frac{2 N_{A1} N_{B1}}{Le_1} \frac{\partial \tilde{T}}{\partial z}- \frac{2 N_{A2} N_{B2}}{Le_2} \frac{\partial \tilde{T}}{\partial z}\qquad \qquad \qquad \quad \quad \;\;\;\;\;\end{aligned}$$

(19)

$$\begin{aligned} \frac{\partial \tilde{\phi _1}}{\partial t} + \tilde{w} + \left( \tilde{u} \frac{\partial }{\partial x} + \tilde{w} \frac{\partial }{\partial z}\right) \tilde{\phi _1}= \frac{1}{Le_1}\nabla ^2\tilde{\phi _1} + \frac{N_{A1}}{Le_1}\nabla ^2\tilde{T}\end{aligned}$$

(20)

$$\begin{aligned} \frac{\partial \tilde{\phi _2}}{\partial t} + \tilde{w} + \left( \tilde{u} \frac{\partial }{\partial x} + \tilde{w} \frac{\partial }{\partial z}\right) \tilde{\phi _2}= \frac{1}{Le_2}\nabla ^2\tilde{\phi _2} + \frac{N_{A2}}{Le_2}\nabla ^2\tilde{T} \end{aligned}$$

(21)

The corresponding perturbed boundary conditions are

$$\begin{aligned} \left. \begin{aligned}&\tilde{T}=0, \tilde{w}=\tilde{\phi _1}=\tilde{\phi _2}=0, \frac{\partial \tilde{w}}{\partial z} + \lambda _1 \frac{\partial ^2 \tilde{w}}{\partial z^2}=0 \ \textrm{at} \ z = 0 ,\\&\tilde{T}=0, \tilde{w}=\tilde{\phi _1}=\tilde{\phi _2}=0, \frac{\partial \tilde{w}}{\partial z} - \lambda _2 \frac{\partial ^2 \tilde{w}}{\partial z^2}=0 \ \textrm{at} \ z = 1. \end{aligned}\right\} \end{aligned}$$

(22)

where $\displaystyle \tilde{\textbf{V}} = (\tilde{u},\tilde{v},\tilde{w})$.

Now eliminating the pressure term in Eq. (18), introducing the stream function $\psi$ in Eqs. (18)–(21), and removing the tildes, we get the following transformed equations:

$$\begin{aligned} \frac{1}{Pr}\left[ \frac{\partial }{\partial t}(\nabla ^2 \psi )\right] = \nabla ^4 \psi - Ra \frac{\partial T}{\partial x} + Rn_1 \frac{\partial \phi _1}{\partial x}+ Rn_2 \frac{\partial \phi _2}{\partial x}+\frac{1}{Pr}\left[ \frac{\partial (\psi , \nabla ^2 \psi )}{\partial (x,z)}\right] \end{aligned}$$

(23)

$$\begin{aligned} \frac{\partial T}{\partial t} +\frac{\partial \psi }{\partial x}= \nabla ^2 T + \frac{N_{B1}}{Le_1} \left[ \frac{\partial T}{\partial z}- \frac{\partial \phi _1}{\partial z}\right] - \frac{2 N_{A1} N_{B1}}{Le_1} \frac{\partial T}{\partial z} + \frac{N_{B2}}{Le_2} \left[ \frac{\partial T}{\partial z}- \frac{\partial \phi _2}{\partial z}\right] \nonumber \\ - \frac{2 N_{A2} N_{B2}}{Le_2} \frac{\partial T}{\partial z} +\frac{\partial (\psi , T)}{\partial (x,z)}\qquad \qquad \qquad \qquad \qquad \;\;\;\;\end{aligned}$$

(24)

$$\begin{aligned} \frac{\partial \phi _1}{\partial t} - \frac{\partial \psi }{\partial x} = \frac{1}{Le_1}\nabla ^2 \phi _1 + \frac{N_{A1}}{Le_1}\nabla ^2 T + \frac{\partial (\psi , \phi _1)}{\partial (x,z)}\end{aligned}$$

(25)

$$\begin{aligned} \frac{\partial \phi _2}{\partial t} - \frac{\partial \psi }{\partial x} = \frac{1}{Le_2}\nabla ^2 \phi _2 + \frac{N_{A2}}{Le_2}\nabla ^2 T + \frac{\partial (\psi , \phi _2)}{\partial (x,z)} \end{aligned}$$

(26)

where $u = \displaystyle \frac{\partial \psi }{\partial z} \textrm{and} \ w = -\displaystyle \frac{\partial \psi }{\partial x}$.

5 Non-linear Stability Analysis

A non-linear stability analysis is done using the below-mentioned truncated Fourier expressions (Bhadauria et al. [17]):

$$\begin{aligned} \psi = A_{11}(t)\ \textrm{sin}(\textrm{k} x)sin(\pi z) \end{aligned}$$

(27)

$$\begin{aligned} T = B_{11}(t)\ \textrm{cos}( \textrm{k} x)sin(\pi z)+B_{02}(t)sin(2\pi z) \end{aligned}$$

(28)

$$\begin{aligned} \phi _1 = C_{11}(t)\ \textrm{cos}( \textrm{k} x)sin(\pi z)+C_{02}(t)sin(2\pi z) \end{aligned}$$

(29)

$$\begin{aligned} \phi _2 = D_{11}(t)\ \textrm{cos}( \textrm{k} x)sin(\pi z)+D_{02}(t)sin(2\pi z) \end{aligned}$$

(30)

All these expressions are taken in such a way to satisfy the free–free boundary conditions:

$$\begin{aligned} \psi =\nabla ^2 \psi =T=\phi _1=\phi _2=0 \ \textrm{at}\ z=0,1, \end{aligned}$$

(31)

where $A_{11}(t), \ B_{11}(t), \ B_{02}(t), \ C_{11}(t), \ C_{02}(t), \ D_{11}(t) \ \textrm{and} \ D_{02}(t)$ are unknowns and the functions of “t”.

Making use of Eqs. (27)–(30) into the Eqs. (23)–(26) and using the condition of orthogonality with the eigenfunctions, we obtain

$$\begin{aligned} A_{11}'(t) = Pr [-\delta ^2 A_{11}(t)- \frac{\mathrm{{k}}}{\delta ^2}\{Ra B_{11}(t) -Rn_1 C_{11}(t) - Rn_2 D_{11}(t)\}]\end{aligned}$$

(32)

$$\begin{aligned} B_{11}'(t) = - \mathrm{{k}} A_{11}(t) - \mathrm{{k}} \pi A_{11}(t) B_{02}(t) - \delta ^2 B_{11}(t) \end{aligned}$$

(33)

$$\begin{aligned} B_{02}'(t) = - 4 \pi ^2 B_{02}(t)+ \frac{\mathrm{{k}}\pi }{2} A_{11}(t) B_{11}(t) \end{aligned}$$

(34)

$$\begin{aligned} C_{11}'(t) = \mathrm{{k}} [A_{11}(t) - \pi A_{11}(t) C_{02}(t)] -\frac{\delta ^2}{Le_1} [N_{A1} B_{11}(t) + C_{11}(t)]\end{aligned}$$

(35)

$$\begin{aligned} C_{02}'(t) = -\frac{4 \pi ^2}{Le_1}[N_{A1} B_{02}(t) + C_{02}(t)]+ \frac{\mathrm{{k}}\pi }{2} A_{11}(t) C_{11}(t)\end{aligned}$$

(36)

$$\begin{aligned} D_{11}'(t) = \mathrm{{k}} [A_{11}(t) - \pi A_{11}(t) D_{02}(t)] -\frac{\delta ^2}{Le_2} [N_{A2} B_{11}(t) + D_{11}(t)] \end{aligned}$$

(37)

$$\begin{aligned} D_{02}'(t) = -\frac{4 \pi ^2}{Le_2}[N_{A2} B_{02}(t) + D_{02}(t)]+ \frac{\mathrm{{k}}\pi }{2} A_{11}(t) D_{11}(t) \end{aligned}$$

(38)

where $\delta ^2= (\textrm{k}^2 + \pi ^2)$

The above autonomous simultaneous ODEs (32)–(38) are solved numerically using NDSolve of Mathematical under suitably chosen initial conditions.

6 Heat and Mass Transport

The heat transport Nusselt number, $Nu_T(t)$ is defined as

$Nu_T(t)=\displaystyle \frac{{\text {Heat transport by (conduction+convection)}}}{{\text {Heat transport by conduction}}}$

$$\begin{aligned} Nu_T(t)=\displaystyle 1+\left[ \frac{\int \limits _0^{2\pi /\textrm{k}}\left( \frac{\partial T}{\partial z}\right) dx}{\int \limits _0^{2\pi /\textrm{k}}\left( \frac{\partial T_b}{\partial z}\right) dx}\right] _{z=0} \end{aligned}$$

(39)

On putting the values of T and $T_b(z)$ from Eqs. (28) and (15) into the Eq. (39), we have

$$\begin{aligned} Nu_T(t)=1-2\pi B_{02}(t) \end{aligned}$$

(40)

     The nanoparticle concentration Nusselt number for the first type of nanoparticles, $Nu_{\phi 1} (t)$, can be defined as

$$\begin{aligned} Nu_{\phi 1}(t) = 1 + \left[ \displaystyle \frac{\int \limits _0^{2 \pi /\textrm{k}}{(\displaystyle \frac{\partial \phi _1}{\partial z})dx}}{\int \limits _0^{2\pi /\textrm{k}}{(\displaystyle \frac{\partial \phi _{1b}}{\partial z})dx}}\right] _{z=0}+ N_{A1} \left\{ 1 + \left[ \displaystyle \frac{\int \limits _0^{2\pi /\textrm{k}}{(\displaystyle \frac{\partial T}{\partial z})dx}}{\int \limits _0^{2\pi /\textrm{k}}{(\displaystyle \frac{\partial T_b}{\partial z})dx}}\right] _{z=0}\right\} \end{aligned}$$

(41)

     Making use of Eqs. (28), (29) and (15) into the Eq. (41), we get

$$\begin{aligned} Nu_{\phi 1}(t)=(1+2\pi C_{02}(t)) + N_{A1} (1-2\pi B_{02}(t)) \end{aligned}$$

(42)

     Similarly, we can find the nanoparticle concentration Nusselt number for the second type of nanoparticles, $Nu_{\phi 2} (t)$, as follows:

$$\begin{aligned} Nu_{\phi 2}(t)=(1+2\pi D_{02}(t)) + N_{A2} (1-2\pi B_{02}(t)) \end{aligned}$$

(43)

7 Results and Discussion

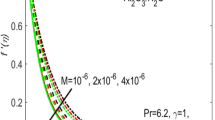
In non-linear analysis, we study heat and mass transport in the system. By thermal Nusselt number and concentration Nusselt number, we study how heat and mass transport, respectively, happens inside the system. Here thermal Nusselt number and concentration Nusselt number are functions of time. The general parametric values are taken as $Le_1=100$, $Le_2=100$, $N_{A1}=2$, $N_{A2}=2$, $Rn_{1}=5$, $Rn_{2}=5$, $R_a=5000$, and $\textrm{k}=2.22144$. We found a common thing in all observations that the graph of thermal Nusselt number and both concentration Nusselt numbers are horizontal for a short time initially which shows a conduction state. After some time, they start increasing which shows a convection state and also oscillate for some time and go to constant which denotes a steady state. In ordinary nanofluid, Bhadauria et al. [17] examined that modified particle density increments and Lewis number have no significant effect on heat transfer. Here we also found the similar result in composite nanofluid which is shown in Figs. 2, 3, 4, and 5. If the value of Prandtl number (Pr) is increased, we observe that heat transfer starts sooner by convection in comparison to the previous Prandtl number which is shown in Fig. 6. In the case of composite nanofluid, we observe that heat transfer by convection is delayed in comparison to ordinary nanofluid which is equivalent to the result of Kumar and Awasthi [27] and shown in Fig. 7. Kumar and Awasthi [27] compared the onset of convection between ordinary and composite nanofluids under the heavy top condition and found a delay in the onset of convection in composite nanofluids. In the case of the first nanoparticle concentration Nusselt number, the effect of $N_{A1}$ enhances the mass transport and has no effect of $N_{A2}$ on mass transport which is shown in Figs. 8, 9. In the case of the second nanoparticle concentration Nusselt number, $N_{A1}$ has no effect and $N_{A2}$ enhances the mass transport which contradicts the result of first nanoparticle concentration Nusselt number and shown in Figs. 16, 17. The above result is similar to the result for ordinary nanofluid, which is compared to the result of Bhadauria et al. [17].

Fig. 2

Plot of $Nu_T$ with t for varying $N_{A1}$

Fig. 3

Plot of $Nu_T$ with t for varying $N_{A2}$

Fig. 4

Plot of $Nu_T$ with t for varying $Le_{1}$

Fig. 5

Plot of $Nu_T$ with t for varying $Le_{2}$

Fig. 6

Plot of $Nu_T$ with t for varying Pr

Fig. 7

Comparison of heat transfer in ordinary and composite nanofluid

Fig. 8

Plot of $Nu_{\phi 1}$ with t for varying $N_{A1}$

Fig. 9

Plot of $Nu_{\phi 1}$ with t for varying $N_{A2}$

If we increase the value of $Le_1$, we observe that the amplitude of oscillations of nanoparticle concentration Nusselt number for the first nanoparticle, i.e., $Nu_{\phi 1}$ slightly increases, while increment in $Le_1$ has no effect on nanoparticle concentration Nusselt number for the second nanoparticle, i.e., $Nu_{\phi 2}$ (Figs. 10, 18). Similarly, if we increase the value of $Le_2$, the amplitude of oscillations of $Nu_{\phi 2}$ is slight increased, while it has no effect over $Nu_{\phi 1}$ (Figs. 11, 19). Let us now discuss the effect of Prandtl number on mass transport in both cases. We found the same effect in both cases which is shown in Figs. 12, 20 and the result is same as the result of Bhadauria et al. [12]. If the ratio of $Rn_{1}$ and $Rn_{2}$ are different in composite nanofluid, then the mass transport by convection takes place sooner in comparison to the same ratio which is shown in Figs. 13, 14, 21 and 22. If nanoparticle concentration is top heavy then we found that there is a delay in the mass transport by convection in comparison to bottom heavy which is shown in Figs. 15, 23.

Fig. 10

Plot of $Nu_{\phi 1}$ with t for varying $Le_{1}$

Fig. 11

Plot of $Nu_{\phi 1}$ with t for varying $Le_{2}$

Fig. 12

Plot of $Nu_{\phi 1}$ with t for varying Pr

Fig. 13

Comparison of $Nu_{\phi 1}$ for same ratio $(Rn_1= Rn_2)$ and different ratio ${(Rn_1 > Rn_2)}$

Fig. 14

Comparison of $Nu_{\phi 1}$ for same ratio $(Rn_1=Rn_2)$ and different ratio $(Rn_1<Rn_2)$

Fig. 15

Comparison of $Nu_{\phi 1}$ for top and bottom heavy configurations

In Fig. 25a, b, the streamlines and isothermals have been shown, respectively, at conduction state for t = 0, 0.025, and 0.050. In Fig. 25a, we observe that the magnitude of streamlines is very weak for t = 0–0.050; therefore, the movement of fluid in the system is almost negligible, which means that heat transfer is only due to conduction. Figure 25b describes that the temperature of all the horizontal fluid layers is almost constant throughout the system, which indicates the conduction state. Figure 26a shows that as time “t” increases from 0.1 to 0.15, the magnitude of streamlines also increases slightly. It means that a small movement of fluid particles has started in the system and, therefore, the heat transfer is due to both conduction and convection, which indicates a transition from conduction to convection state. Figure 26b represents that the isothermals have started deforming from their original horizontal position as “t” increases from 0.1 to 0.15, which shows the very beginning stage of the formation of convection cells. Further, the magnitude of streamlines becomes stronger as time increases and in isothermals, fully developed convective cells can be seen with increasing time as presented in Fig. 27a, b, respectively. In Fig. 28a, b, there is no change in the magnitudes of streamlines and in the position of isothermals with increasing time, which shows that the system has achieved the steady state. In Fig. 29a, it can be noticed that the isohalines are parallel and horizontal, which means that the concentration of nanoparticles is constant with horizontal fluid layers and mass transport is almost negligible in the system for t = 0–0.05. With the passage of time, mass transport starts in the system as depicted by Fig. 29b. Mass transportation also achieves the steady state for higher values of time as shown by Fig. 24.

Fig. 16

Plot of $Nu_{\phi 2}$ with t for varying $N_{A1}$

Fig. 17

Plot of $Nu_{\phi 2}$ with t for varying $N_{A2}$

Fig. 18

Plot of $Nu_{\phi 2}$ with t for varying $Le_{1}$

Fig. 19

Plot of $Nu_{\phi 2}$ with t for varying $Le_{2}$

Fig. 20

Plot of $Nu_{\phi 2}$ with t for varying Pr

Fig. 21

Comparison of $Nu_{\phi 2}$ for same ratio $(Rn_1=Rn_2)$ and different ratio $(Rn_1 < Rn_2)$

Fig. 22

Comparison of $Nu_{\phi 2}$ for same ratio $(Rn_1=Rn_2)$ and different ratio $(Rn_1 > Rn_2)$

Fig. 23

Comparison of $Nu_{\phi 2}$ for top and bottom heavy configurations

Fig. 24

Behavior of mass transport for higher value of time

Fig. 25

Conduction state

Fig. 26

Transition state (conduction to convection)

Fig. 27

Convection state

Fig. 28

Steady state

Fig. 29

Isohalines

8 Conclusions

We have investigated the heat and mass transport in a horizontal composite nanoliquid layer by performing a non-linear analysis. All the results have been presented graphically. These are the major conclusions:

• 1. We found same effect of modified particle density increments in composite nanofluid as compared to the ordinary nanofluid on heat transfer.

• 2. Lewis number has also same effect in composite nanofluid as compared to the ordinary nanofluid on heat and mass transfer.

• 3. We found that heat transfer by convection is delayed in composite nanofluid as compared to ordinary nanofluid.

• 4. Prandtl number has also same effect in composite nanofluid as compared to ordinary nanofluid on heat and mass transfer.

• 5. The effect of modified particle density increments on mass transport depends upon the nanoparticle concentration Nusselt number, i.e., the effect of $N_{A1}$ is only on the first nanoparticle concentration Nusselt number and the effect of $N_{A2}$ is only on the second nanoparticle concentration Nusselt number.

• 6. $Le_1$ has its effect only on the nanoparticle concentration Nusselt number for the first nanoparticle, i.e., $Nu_{\phi 1}$, while $Le_2$ has its effect only on the nanoparticle concentration Nusselt number for the second nanoparticle, i.e., $Nu_{\phi 2}$.