Keywords

1 Introduction

Recently, more and more research attention acts in for semi-supervised classification tasks. On the basis of graph theory, the manifold regularization is becoming a popular technology to extend supervised learners to semi-supervised ones [2, 4, 6]. Considering the structure information provided by unlabeled data, semi-supervised learners outperform related supervised ones and have more applications in reality [1, 3, 12, 15].

Because the performance of semi-supervised learners partly depends on the corresponding supervised ones, we need to choose a good supervised learner to construct a semi-supervised one. Presently, inspired by the idea of non-parallel planes, many supervised algorithms have been designed for dealing with binary classification problems, such as generalized proximal support vector machine (GEPSVM) [9, 16], twin support vector machine (TSVM) [7], least squares twin support vector machine (LSTSVM) [8], multi-weight vector support vector machine (MVSVM) [18], and enhanced multi-weight vector projection support vector machine (EMVSVM) [17]. In these learners with non-parallel planes, each plane is as close as possible to samples from its own class and meanwhile as far as possible from samples belonging to the other class. Owing to the outstanding generalization performance of TSVM and LSTSVM, they have been extended to semi-supervised learning by using the manifold regularization framework [3, 12]. In [12], Laplacian twin support vector machine (LapTSVM) constructs a more reasonable classifier from labeled and unlabeled data by integrating the manifold regularization. Chen et al. [3] proposed Laplacian least squares twin support vector machine (LapLSTSVM) based on LapTSVM and LSTSVM. Different from LapTSVM, LapLSTVM needs to solve only two systems of linear equations with remarkably less computational time. These semi-supervised learners have proved that the manifold regularization is a reasonable and effective technology. On the basis of EMVSVM and manifold regularization, Laplacian pair-weight vector projection (LapPVP) was extended to semi-supervised learning for binary classification problems [14]. LapPVP achieves a pair of projection vectors by maximizing the between-class scatter and minimizing the within-class scatter and manifold regularization.

These performance of semi-supervised learners is partly related to the neighbor graph induced by the manifold regularization. Generally, the neighbor graph is predefined and may be sensitive to noise and outliers [10]. To improve the robustness of LapPVP, we propose a novel semi-supervised learner, named Laplacain pair-weight vector projection with adaptive neighbor graph (ANG-LapPVP). ANG-LapPVP learns a pair of projection vectors by solving the pair-wise optimal formulations, where we maximize the between-class scatter and minimize both the within-class scatter and the adaptive neighbor graph (ANG) regularization. In ANG, the similarity matrix is not fixed but adaptively learned on both labeled and unlabeled data by solving an optimization problem [11, 19, 20]. Moreover, the between- and within-class scatter matrices are computed separably for each class, which can strengthen the discriminant capability of ANG-LapPVP. Therefore, it is easy for ANG-LapPVP to handle binary classification tasks and achieve a good performance.

2 Proposed Method

The propose method ANG-LapPVP is an enhanced version of LapPVP. In ANG-LapPVP, we learn an ANG based on the assumption that the smaller the distance between data points is, the greater the probability of being neighbors is. Likewise, ANG-LapPVP is to find a pair of the projection vectors by maximizing between-class scatter and minimizing both the within-class scatter and the ANG regularization.

Let \(\textbf{X}= [\textbf{X}_\ell ; \textbf{X}_u]\in \mathbb {R}^{n\times m}\) be the training sample matrix, where n and m are the number of total samples and features, respectively; \(\textbf{X}_\ell \in \mathbb {R}^{\ell \times m}\) and \(\textbf{X}_u\in \mathbb {R}^{u\times m}\) are the labeled and unlabeled sample matrices, respectively; \(\ell \) and u are the number of labeled and unlabeled samples, respectively, and \(n=\ell +u\). For convenience, we use \(y_i\) to describe the label situation of sample \(\textbf{x}_i\). If \(y_i=1\), \(\textbf{x}_i\) is a labeled and positive sample; if \(y_i=-1\), \(\textbf{x}_i\) is a labeled and negative sample; if \(y_i=0\), \(\textbf{x}_i\) is unlabeled. Furthermore, the labeled sample matrix \(\textbf{X}_{\ell }\) can be represented as \(\textbf{X}_\ell = [\textbf{X}_1; \textbf{X}_2]\), where \(\textbf{X}_1 = [\textbf{x}_{11}, \textbf{x}_{12}, \dots , \textbf{x}_{1\ell _1}]^T \in \mathbb {R}^{\ell _1 \times m}\) is the positive sample matrix with a label of 1, \(\textbf{X}_2 = [\textbf{x}_{21}, \textbf{x}_{22}, \dots , \textbf{x}_{2\ell _2}]^T \in \mathbb {R}^{\ell _2 \times m}\) is the negative sample matrix with a label of \(-1\), \(\ell =\ell _1+\ell _2\), \(\ell _1\) and \(\ell _2\) are the number of positive and negative samples, respectively.

2.1 Formulations of ANG-LapPVP

For binary classification tasks, the goal of ANG-LapPVP is to find a pair of projection vectors similar to LapPVP. As mentioned above, the proposed ANG-LapPVP is an enhanced version of LapPVP. To better describe our method, we first briefly introduce LapPVP [14]. For the positive class, LapPVP is to solve the following optimization problem:

$$\begin{aligned} \begin{aligned}&\max \limits _{\textbf{v}_1}\quad \textbf{v}_1^T \textbf{B}_1 \textbf{v}_1 - \alpha _1 \textbf{v}_1^T \textbf{W}_1 \textbf{v}_1- \beta _1\textbf{v}_1^T \textbf{X}^T \textbf{L} \textbf{X} \textbf{v}_1 \\&s.t. \quad \textbf{v}_1^T\textbf{v}_1 = 1 \end{aligned} \end{aligned}$$
(1)

where \(\alpha _1 > 0\) and \(\beta _1>0\) are regularization parameters, \(\textbf{L}\) is the Laplacian matrix of all training data, and \(\textbf{B}_1\) is the between-class scatter matrix and \(\textbf{W}_1\) is the within-class scatter matrix of the positive class, which can be calculated by

$$\begin{aligned} \textbf{B}_{1} =\left( \textbf{X}-\textbf{e} \textbf{u}_1^T\right) ^T\left( \textbf{X}-\textbf{e} \textbf{u}_1^T\right) \end{aligned}$$
(2)

and

$$\begin{aligned} \textbf{W}_1 = \left( \textbf{X}_1 -\textbf{e}_1 \textbf{u}_1^T\right) ^T\left( \textbf{X}_1 -\textbf{e}_1 \textbf{u}_1^T\right) \end{aligned}$$
(3)

where \(\textbf{v}_1\in \mathbb {R}^{m}\) is the projection vector of the positive class, \(\textbf{u}_1=\frac{1}{\ell _1}\sum _{i=1}^{\ell _1} \textbf{x}_{1i}\) is the mean vector of the positive samples, \(\textbf{e}_1 \in \mathbb {R}^{\ell _1}\) and \(\textbf{e} \in \mathbb {R}^{\ell }\) are the vectors of all ones with different length.

In the optimization problem (1), the laplacian matrix \(\textbf{L}\) is computed in advance and is independent of the objective function. The concept of ANG was proposed in [11], which has been applied to feature selection for unsupervised multi-view learning [19] and semi-supervised learning [20]. We incorporate this concept into LapPVP and form ANG-LapPVA.

Similarly, the pair of projection vectors of ANG-LapPVP is achieved by a pair-wise optimal formulations. On the basis of (1), the optimal formulation of ANG-LapPVP for the positive class is defined as:

$$\begin{aligned} \begin{aligned}&\max \limits _{\textbf{v}_1,\textbf{S}_1} \quad \textbf{v}_1^T \textbf{B}_1 \textbf{v}_1 - \alpha _1 \textbf{v}_1^T \textbf{W}_1 \textbf{v}_1- \beta _1(\textbf{v}_1^T \textbf{X}^T \textbf{L}_{s_1} \textbf{X} \textbf{v}_1 + \gamma _1 \textbf{S}_1^T \textbf{S}_1) \\&s.t. \quad \textbf{v}_1^T\textbf{v}_1 = 1, \quad \textbf{S}_1 \textbf{e} = \textbf{e}, \quad \textbf{S}_1 > 0 \end{aligned} \end{aligned}$$
(4)

where \(\textbf{S}_1\) is the similarity matrix for the positive class, \(\textbf{L}_{s_1}\) is the Laplacian matrix related to \(\textbf{S}_1\) for the positive class, and \(\gamma _1>0\) is a regularization parameter.

Compared with (1), (4) has a different term, or the third term, which is called the ANG regularization here. \(\textbf{S}_1\) varies with iterations, and then the Laplacian matrix \(\textbf{L}_{s_1} = \textbf{D}_{s_1} - \textbf{S}_1\) is changed, where \(\textbf{D}_{s_1}\) is a diagonal matrix with diagonal elements of \(({D}_{s_1})_{ii} = \sum _j ({S}_{1})_{ij}\). The first and second terms represent the between- and within-class scatters of the positive class, and the regularization parameter \(\alpha _1\) is to make a balance between these two scatters. ANG-LapPVP can keep data points as near as possible in the same class while as far as possible from the other class by maximizing the between-class scatter and minimizing the within-class scatter.

For the negative class, ANG-LapPVP has the following similar problem:

$$\begin{aligned} \begin{aligned}&\max \limits _{\textbf{v}_2, \textbf{S}_2} \textbf{v}_2^T \textbf{B}_2 \textbf{v}_2 - \alpha _2 \textbf{v}_2^T \textbf{W}_2 \textbf{v}_2 - \beta _2 (\textbf{v}_2^T \textbf{X}^T \textbf{L}_{s_2} \textbf{X} \textbf{v}_2 + \gamma _2 \textbf{S}_2^T \textbf{S}_2) \\&s.t. \quad \textbf{v}_2^T\textbf{v}_2 = 1, \quad \textbf{S}_2 \textbf{e} = \textbf{e}, \quad \textbf{S}_2 > 0 \end{aligned} \end{aligned}$$
(5)

where \(\textbf{v}_2\) is the projection vector for the negative class, \(\alpha _2\), \(\beta _2\), and \(\gamma _2\) are positive regularization parameters, \(\textbf{S}_2\) is the similarity matrix for the negative class, \(\textbf{L}_{s_2}\) is the Laplacian matrix related to \(\textbf{S}_2\), \(\textbf{B}_2\) and \(\textbf{W}_2\) are the between- and within-class scatter matrices for the negative class, respectively, which can be written as:

$$\begin{aligned} \textbf{B}_2 = \left( \textbf{X}- \textbf{e} \textbf{u}_2^T\right) ^T\left( \textbf{X}- \textbf{e} \textbf{u}_2^T\right) \end{aligned}$$
(6)

and

$$\begin{aligned} \textbf{W}_2 = \left( \textbf{X}_2-\textbf{e}_2 \textbf{u}_2^T\right) ^T\left( \textbf{X}_2-\textbf{e}_2 \textbf{u}_2^T\right) \end{aligned}$$
(7)

where \(\textbf{u}_2=\frac{1}{\ell _2}\sum _{i=1}^{\ell _2} \textbf{x}_{2i}\) is the mean vector of negative samples, \(\textbf{e}_2 \in \mathbb {R}^{\ell _c}\) is the vector of all ones.

2.2 Optimization of ANG-LapPVP

Problems (4) and (5) form the pair of optimization problems for ANG-LapPVP, where projection vectors \(\textbf{v}_1\) and \(\textbf{v}_2\) and similarity matrices \(\textbf{S}_1\) and \(\textbf{S}_2\) are unknown. It is difficult to find the optimal solution to them at the same time. Thus, we use an alternative optimization approach to solve (4) or (5). During the optimization procedure, we would fix a set of variables and solve the other set of ones.

When \(\textbf{S}_1\) and \(\textbf{S}_2\) are fixed, the optimization formulations of ANG-LapPVP can be reduced to

$$\begin{aligned} \begin{aligned}&\max \limits _{\textbf{v}_1} \quad \textbf{v}_1^T \textbf{B}_1 \textbf{v}_1 - \alpha _1 \textbf{v}_1^T \textbf{W}_1 \textbf{v}_1- \beta _1 \textbf{v}_1^T \textbf{X}^T \textbf{L}_{s_1} \textbf{X} \textbf{v}_1 \\&s.t. \quad \textbf{v}_1^T \textbf{v}_1 = 1 \end{aligned} \end{aligned}$$
(8)

and

$$\begin{aligned} \begin{aligned}&\max \limits _{\textbf{v}_2} \quad \textbf{v}_2^T \textbf{B}_2 \textbf{v}_2 - \alpha _2 \textbf{v}_2^T \textbf{W}_2 \textbf{v}_2 - \beta _2 \textbf{v}_2^T \textbf{X}^T \textbf{L}_{s_2} \textbf{X} \textbf{v}_2 \\&s.t. \quad \textbf{v}_2^T \textbf{v}_2= 1 \end{aligned} \end{aligned}$$
(9)

which are exactly LapPVP.

According to the way in [14], we can find the solutions \(\textbf{v}_1\) and \(\textbf{v}_2\) to (8) and (9), respectively. In [14], (8) and (9) can be respectively converted to the following eigenvalue decomposition problems:

$$\begin{aligned} \begin{aligned}&\textbf{B}_1 \textbf{v}_1 - \alpha _1 \textbf{W}_1 \textbf{v}_1- \beta _1 \textbf{X}^T \textbf{L}_{s_1} \textbf{X} \textbf{v}_1 = \lambda _1 \textbf{v}_1 \\&\textbf{B}_2 \textbf{v}_2 - \alpha _2 \textbf{W}_2 \textbf{v}_2 - \beta _2 \textbf{X}^T \textbf{L}_{s_2} \textbf{X} \textbf{v}_2 = \lambda _2 \textbf{v}_2 \end{aligned} \end{aligned}$$
(10)

where \(\lambda _1\) and \(\lambda _2\) are eigenvalues for the positive and negative classes, respectively. Thus, the optimal solutions here are the eigenvectors corresponding to the largest eigenvalues.

Once we get the projection vectors \(\textbf{v}_1\) and \(\textbf{v}_2\), we take them as fixed variables, then solve \(\textbf{S}_1\) and \(\textbf{S}_2\). In this case, the optimization formulations of ANG-LapPVP are reduced to

$$\begin{aligned} \begin{aligned}&\min \limits _{\textbf{S}_1}~~ \textbf{v}_1^T \textbf{X}^T \textbf{L}_{s_1} \textbf{X} \textbf{v}_1 + \gamma _1 \textbf{S}_1^T \textbf{S}_1 \\&s.t. \quad \textbf{S}_1 \textbf{e} = \textbf{e}, \quad \textbf{S}_1 > 0 \end{aligned} \end{aligned}$$
(11)

and

$$\begin{aligned} \begin{aligned}&\min \limits _{\textbf{S}_2}~~ \textbf{v}_2^T \textbf{X}^T \textbf{L}_{s_2} \textbf{X} \textbf{v}_2 + \gamma _2 \textbf{S}_2^T \textbf{S}_2 \\&s.t. \quad \textbf{S}_2 \textbf{e} = \textbf{e}, \quad \textbf{S}_2 > 0 \end{aligned} \end{aligned}$$
(12)

For simplicity, let \((Z_1)_{ij} = ||\textbf{v}_1^T\textbf{x}_i-\textbf{v}_1^T\textbf{x}_j||^2\) and \((Z_2)_{ij} = ||\textbf{v}_2^T\textbf{x}_i-\textbf{v}_2^T\textbf{x}_j||^2\). Then matrices \(\textbf{Z}_1\) and \(\textbf{Z}_2\) are constant when \(\textbf{v}_1\) and \(\textbf{v}_2\) are fixed. Thus, (11) and (12) can be rewritten as:

$$\begin{aligned} \begin{aligned}&\min \limits _{\textbf{S}_{1}} \quad \frac{1}{2}(\textbf{S}_1 + \frac{1}{2\gamma _1} \textbf{Z}_1)^T(\textbf{S}_1 + \frac{1}{2\gamma _1} \textbf{Z}_1) \\&s.t. \quad \textbf{S}_1 \textbf{e} = \textbf{e}, \quad \textbf{S}_1 > 0 \end{aligned} \end{aligned}$$
(13)

and

$$\begin{aligned} \begin{aligned}&\min \limits _{\textbf{S}_{2}} \quad \frac{1}{2}(\textbf{S}_2 + \frac{1}{2\gamma _2} \textbf{Z}_2)^T(\textbf{S}_2 + \frac{1}{2\gamma _2} \textbf{Z}_2) \\&s.t. \quad \textbf{S}_2 \textbf{e} = \textbf{e}, \quad \textbf{S}_2 > 0 \end{aligned} \end{aligned}$$
(14)

Because (13) and (14) are similar, we describe the optimization procedure only for (13). First, we generate the Lagrangian function of (13) with multipliers \(\delta _1\) and \(\zeta _1\) as follows:

$$\begin{aligned} L(\textbf{S}_1,\delta _1,\zeta _1) = \left( \textbf{S}_1 + \frac{1}{2\gamma _1} \textbf{Z}_1\right) ^T \left( \textbf{S}_1 + \frac{1}{2\gamma _1} \textbf{Z}_1\right) - \delta _1(\mathbf {S_1} \textbf{e}- \textbf{e}) - \zeta _1\textbf{S}_1 \end{aligned}$$
(15)

According to the KKT condition [13], we derive the partial derivative of \(L(\textbf{S}_1,\delta _1,\zeta _1)\) with respect to the primal variables \(\textbf{S}_1\) and make it vanish, which results in

$$\begin{aligned} \textbf{S}_1 = \delta _1 + \zeta _1-\frac{1}{2\gamma _1} \textbf{Z}_1 \end{aligned}$$
(16)

Similarly, the similarity matrix \(\textbf{S}_2\) is achieved by

$$\begin{aligned} \textbf{S}_2 = \delta _2 + \zeta _2 -\frac{1}{2\gamma _2} \textbf{Z}_2 \end{aligned}$$
(17)

where \(\delta _2\) and \(\zeta _2\) are positive Lagrange multipliers.

Since the constraint \(\textbf{S}\textbf{e}=\textbf{e}\), we have

$$\begin{aligned} \delta _1 + \zeta _1 = \frac{1}{n}+\frac{1}{2n\gamma _1} \textbf{Z}_1 \end{aligned}$$
(18)

and

$$\begin{aligned} \delta _2 + \zeta _2 = \frac{1}{n}+\frac{1}{2n\gamma _2} \textbf{Z}_2 \end{aligned}$$
(19)

where the parameters \(\gamma _1\) and \(\gamma _2\) can be computed as follows [11]:

$$\begin{aligned} \gamma _1 = \frac{1}{n} \textbf{e}^T\left( \frac{k}{2} \textbf{Z}_1 \textbf{q}_{k}-\frac{1}{2}\textbf{Z}_1 \widetilde{\textbf{q}}_{k-1}\right) \end{aligned}$$
(20)

and

$$\begin{aligned} \gamma _2 = \frac{1}{n} \textbf{e}^T\left( \frac{k}{2} \textbf{Z}_1 \textbf{q}_{k}-\frac{1}{2}\textbf{Z}_1 \widetilde{\textbf{q}}_{k-1}\right) \end{aligned}$$
(21)

where k is the neighbor number in the graph, \(\textbf{q}_{k}\) and \(\widetilde{\textbf{q}}_{k-1}\) are indicator vectors. We set \(\textbf{q}_k = [0, 0, \cdots , 0, 1, 0, \cdots , 0, 0]^T \in \mathbb {R}^n\) in which the k-th element is one and the others are zero and \(\widetilde{\textbf{q}}_{k-1} = [1,1, \cdots 1, 0, \cdots , 0, 0]^T \in \mathbb {R}^n\) in which the first \((k-1)\) elements are one and the others are zero.

2.3 Strategy of Classification

The pair of projection vectors \((\textbf{v}_1,\textbf{v}_2)\) can project data points into two different subspaces. The distance measurement is a reasonable way to estimate the class label of an unknown data point \(\textbf{x} \in \mathbb {R}^m\). Here, we define the strategy of classification using the minimum distance.

For an unknown point \(\textbf{x}\), we project it into two subspaces induced by \(\textbf{v}_1\) and \(\textbf{v}_2\). In the subspace induced by \(\textbf{v}_1\), the projection distance between \(\textbf{x}\) and positive samples is defined as:

$$\begin{aligned} {d}_1 = \min \limits _{i=1,2,\cdots ,\ell _1} \left( \textbf{v}_1^T \textbf{x} -\textbf{v}_1^T \textbf{x}_{1i}\right) ^2 \end{aligned}$$
(22)

In the subspace induced by \(\textbf{v}_2\), the projection distance between \(\textbf{x}\) and negative samples is computed as:

$$\begin{aligned} {d}_2 = \min \limits _{i=1,2,\cdots ,\ell _2} \left( \textbf{v}_2^T \textbf{x} -\textbf{v}_2^T \textbf{x}_{2i}\right) ^2 \end{aligned}$$
(23)

It is reasonable that \(\textbf{x}\) is taken as the positive point if \(d_1< d_2\), which is the minimum distance strategy. Thus, we assign a label to \(\textbf{x}\) by the following rule:

$$\begin{aligned} \hat{y} = \left\{ \begin{array}{c l} 1, &{} if~~ d_1 \le d_2\\ -1, &{} Otherwise \end{array} \right. \end{aligned}$$
(24)

2.4 Computational Complexity

Here, we analyze the computational complexity of ANG-LapPVP. Problems (4) and (5) are non-convex. The ultimate optimal pair-wise projection vectors are obtained by applying an iterative method. In iterations, the optimization problems of ANG-LapPVP can be decomposed into eigenvalue decomposition ones and quadratic programming ones with constraints.

The computational complexities of an eigenvalue decomposition problem and a quadratic programming one are \(O\left( m^2\right) \) and \(O\left( n^2\right) \), respectively, where m is the number of features and n is the number of samples. Let t be the iteration times. Then, the total computational complexity of ANG-LapPVP is \(O\left( t\left( m^2+n^2\right) \right) \). In the iteration process of ANG-LapPVP, the convergence condition is set as the difference between current and previous projection vectors, i.e., \(||\textbf{v}^t_{1}- \textbf{v}^{t-1}_{1}|| \le 0.001\) or \(||\textbf{v}^t_{2}- \textbf{v}^{t-1}_{2}|| \le 0.001\).

3 Experiments

We conduct experiments in this section. Firstly, we compare ANG-LapPVP with LapPVP on an artificial dataset to illustrate the improvement achieved by the ANG regularization. The comparison with other non-parallel planes algorithms on benchmark datasets is then implemented to analyze the performance of ANG-LapPVP.

3.1 Experiments on Artificial Dataset

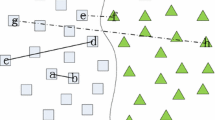
An artificial dataset, called CrossPlane, is generated by perturbing points originally lying on two intersecting planes. CrossPlane contains 400 instances with only 2 labeled and 198 unlabeled ones for each class. The distribution of CrossPlane is shown in Fig. 1. Obviously, some data points belonging to Class \(+1\) are surrounded by the data points of Class \(-1\) and vice versa.

Figure 2 plots the projection vectors learned by LapPVP and ANG-LapPVP. We can see that projection vectors learned by ANG-LapPVP are more suitable than LapPVP. The accuracy of LapPVP is \(91.50\%\), and that of ANG-LapPVP is \(97.00\%\). Clearly, ANG-LapPVP has a better classification performance on the CrossPlane dataset. In other words, ANG-LapPVP is robust to noise and outliers. In to all, the ANG regularization can improve the performance of LapPVP, which makes ANG-LapPVP better.

Fig. 1.
figure 1

Distribution of CrossPlane.

Full size image
Fig. 2.
figure 2

Projection vectors obtained by LapPVP (a) and ANG-LapPVP (b).

Full size image

3.2 Experiments on Benchmark Datasets

In the following experiments, we compare ANG-LapPVP with supervised algorithms, including GEPSVM, MVSVM, EMVSVM, TSVM and LSTSVM to evaluate the effectiveness of ANG-LapPVP, and compare it with semi-supervised algorithms (LapTSVM, LapLSTSVM and LapPVP) to verify the superiority of ANG-LapPVP on ten benchmark datasets. The benchmark datasets are collected from the UCI Machine Learning Repository [5]. We normalize the datasets so that all features range in the interval [0, 1].

Each experiment is run 10 times with random 70% training data and the rest 30% test data. The average classification results are reported as the final ones. The grid search method is applied to finding the optimal hyper-parameters in each trial. Parameters \(\beta _1\) and \(\beta _2\) in both LapPVP and ANG-LapPVP are selected from \(\{2^{-10}, 2^{-9}, \dots , 2^{0}\}\), and other regularization parameters in all methods are selected from the set \(\{2^{-5}, 2^{-4}, \dots , 2^{5}\}\). In semi-supervised methods, the number of nearest neighbors is selected from the set \(\{3, 5, 7, 9\}\).

Table 1. Mean accuracy and standard deviation (%) obtained by supervised algorithms with different scale of labeled data.
Full size table

Comparison with Supervised Algorithms. We first compare ANG-LapPVP with GEPSVM, MVSVM, EMVSVM, TSVM and LSTSVM to investigate the performance of adaptive neighbors graph. Specially, we discuss the impact of the different scale of labeled data on these algorithms. Additionally, ANG-LapPVP has \(50\%\) training samples as unlabeled ones.

Table 1 lists the results of supervised algorithms and ANG-LapPVP with \(10\%\), \(30\%\) and \(50\%\) of training data as labeled samples, where the best results are highlighted. Experimental results in Table 1 show the effectiveness of ANG-LapPVP. With the increasing number of labeled data, the accuracy of ANG-LapPVP on most datasets goes up gradually, which indicates that the labeled data can provide more discriminant information. Moreover, we observe that ANG-LapPVP trained with unlabeled data has the best classification performance on all ten datasets except Breast with \(50\%\) labeled data and German with three situations, which fully demonstrates the significance of the adaptive similarity matrices provided by labeled and unlabeled training data. Generally speaking, semi-supervised algorithms outperform the related supervised ones, and the proposed ANG-LapPVP gains the most promising classification performance.

Comparison with Semi-supervised Algorithms. To validate the superiority of ANG-LapPVP, we further analyze experimental results of LapTSVM, LapLSTSVM, LapPVP and ANG-LapPVP. Tables 2 and 3 list mean accuracy and standard deviation obtained by semi-supervised algorithms on \(30\%\) and \(50\%\) training samples as unlabeled ones, respectively, where the best results are in bold. Additionally, there are \(20\%\) training samples as labeled ones.

Table 2. Mean accuracy and standard deviation (%) obtained by semi-supervised algorithms on \(30\%\) unlabeled data.
Full size table

From the results in Tables 2 and 3, we can see that ANG-LapPVP has a higher accuracy than LapPVP on all ten datasets except Heart with \(30\%\) unlabeled data. The evidence further indicates that ANG-LapPVP with the ANG regularization well preserves the structure of training data and has a better classification performance than LapPVP. Moreover, compared with the other semi-supervised algorithms, ANG-LapPVP has the highest accuracy on eight datasets in Table 2 and on nine datasets in Table 3. That is to say, ANG-LapPVP has substantial advantages over LapTSVM and LapLSTSVM. On the whole, ANG-LapPVP has an excellent ability in binary classification tasks.

Table 3. Mean accuracy and standard deviation (%) obtained by semi-supervised algorithms on \(50\%\) unlabeled data.
Full size table

4 Conclusion

In this paper, we propose ANG-LapPVP for binary classification tasks. As the extension of LapPVP, ANG-LapPVP improves its classification performance by introducing the ANG regularization. The ANG regularization induces an adaptive neighbor graph where the similarity matrix is changed with iterations. Experimental results on the artificial and benchmark datasets validate that the effectiveness and superiority of the proposed algorithm. In a nutshell, ANG-LapPVP has a better classification performance than LapPVP and is a promising semi-supervised algorithm.

Although ANG-LapPVP achieves a good classification performance on datasets used here, the projection vectors obtained by ANG-LapPVP may be not enough when handling with a large scale dataset. In this case, we could consider projection matrices that may provide more discriminant information. Therefore, the dimensionality of projection matrices is a practical problem to be addressed in our following work. In addition, multi-class classification tasks in reality are also in consideration.