Effect of Geometrical Parameters of a Tethered Aerostat on Longitudinal Stability Boundaries

Abstract

Dynamic instabilities often impair the operations of a tethered aerostat (such as supporting antennas and/or aerial platform), especially during the strong wind conditions. Effect of various geometrical parameters on longitudinal stability boundaries of an aerostat tethered in a steady wind is presented in this paper. The mathematical modeling used for stability analysis of the tethered aerostat includes buoyancy forces, apparent mass terms and static forces resulting from the tether cable. The effect of systematic variation of geometrical parameters on longitudinal stability boundaries of the tethered aerostat has been presented graphically. The presented longitudinal stability analysis and a judicious/feasible choice of various geometrical parameters of the tethered aerostat can be utilized to design a new aerostat that can remain longitudinally stable for wide range of wind speeds.

1 Introduction

The paper presents a systematic approach for longitudinal stability analysis and parametric study on longitudinal stability boundaries of an aerostat tethered from an earth-fixed anchor point and flying in steady wind conditions. Pant et al. [1,2,3] have reported good amount of research work on sizing, design and fabrication of Aerostats. Rajani et al. [4, 5] have analyzed dynamic stability of a tethered aerostat. Worth noting work has been reported in the reports available on analytical and experimental determination of stability parameters along with trend study of balloon tethered in wind [6,7,8]. Authors [9, 10] have analyzed stability along with parametric trend study of a tethered aerostat. The contributions in the area of stability analysis of aerostat [11,12,13,14] and tether cable stability and dynamics [15,16,17] have also been reported earlier. Few references [18,19,20] have been used for determining some stability parameters. The paper presents mathematical modeling [8] (Sect. 2), estimation of stability characteristics (Sect. 3) and parametric trend study (Sect. 4) showing the effect of various geometrical parameters on longitudinal stability boundaries of a tethered aerostat.

2 Mathematical Modeling

The stability analysis of an aerostat tethered from an earth-fixed anchor point has been carried out under steady wind conditions. The formulations given by Redd et al. [8] have been used for mathematical modeling of the considered aerostat (Fig. 1) tethered in the steady wind conditions.

Fig. 1

Dimensions of the aerostat and fin

Figure 2 presents the geometrical parameters and various forces and moments acting on tethered aerostat. The use of theoretical formulations [8] based on considered aerostat configuration was made for the calculation of stability derivatives and analysis.

Fig. 2

Geometry of the balloon system [8]

Figure 3 shows the coordinate system along with forces and moments used for the derivation of equations of motion of the tethered aerostat. Figure 3 also shows tether cable forces at the lower and upper end along with related angles.

Fig. 3

Coordinate system and forces acting on tethered aerostat [8]

Table 1 presents the geometric, mass, inertia and aerodynamic characteristics of the considered aerostat used to carry out the stability analysis. Some dimensional parameters were given, while the others were calculated for the given configuration of the tethered aerostat based on the theoretical formulations [8, 19, 20].

Table 1 Characteristics of the considered aerostat

The motion of the tethered aerostat consists of small perturbations about steady flight reference conditions. A linearized analysis similar to that of a rigid airplane has been used during the mathematical modeling while taking into account the following considerations.

• 1. The equations of motion are referred to center of mass of the balloon.

• 2. The balloon is symmetric laterally and has yaw, roll and side slip angles equal to zero in the reference steady-state trimmed condition (ψ_t, φ_t, β_t = 0).

• 3. The balloon and bridle form a rigid system.

• 4. The tether cable is flexible, but inextensible and contributes static forces at the bridle confluence point (BCP).

• 5. The cable weight and drag normal to the cable are needed only for determining the static cable forces, equilibrium shape of the cable and the cable derivatives.

Four different sources of external forces and moments such as aerodynamic, buoyant, tether cable and gravity act on a tethered aerostat. Therefore, the equations of motion of a tethered aerostat can be written as [8].

$$ F_{X,A} + F_{X,C} + F_{X,B} + F_{X,G} = m_{{x,{\text{o}}}} \ddot{x}_{e} $$

(1a)

$$ F_{Z,A} + F_{Z,C} + F_{Z,B} + F_{Z,G} = m_{z,o} \ddot{z}_{e} $$

(1b)

$$ M_{Y,A} + M_{Y,C} + M_{Y,B} + M_{Y,G} = Iy\ddot{\theta } $$

(1c)

The terms m_x,o, m_y,o and m_z,o are total aerostat masses in x-, y- and z-directions, respectively, and can be expressed as:

$$ m_{x,o} = m_{s} + m_{g} + m_{{a{1}}} $$

(2a)

$$ m_{z,o} = m_{s} + m_{g} + m_{{a{3}}} $$

(2b)

The terms m_s, and m_g are the structural mass of aerostat and mass of the gas inside the aerostat. The terms m_a1 and m_a3 are apparent masses associated with accelerations in x- and z-directions, respectively. The apparent masses which depend upon the equilibrium trim angle of attack (α_t) are given by the following equations [8].

$$ m_{{a{1}}} = m_{x,a} {\text{cos}}^{{2}} \alpha_{t} + m_{z,a} {\text{sin}}^{{2}} \alpha_{t} , $$

(3a)

$$ m_{{a{3}}} = m_{x,a} {\text{sin}}^{{2}} \alpha_{t} + m_{z,a} {\text{cos}}^{{2}} \alpha_{t} $$

(3b)

The terms $m_{x,a}$ and $m_{z,a}$ are the apparent masses of the balloon accelerating along the X_b- and Z_b-axes. The mass moments of inertia which depend upon the orientation of the balloon are expressed by the following equations [8].

$$ I_{x} = I_{xx} {\text{cos}}^{{2}} \varepsilon + I_{zz} {\text{sin}}^{{2}} \varepsilon $$

(4a)

$$ I_{y} = I_{yy} $$

(4b)

$$ I_{z} = I_{xx} {\text{sin}}^{{2}} \varepsilon + I_{zz} {\text{cos}}^{{2}} \varepsilon $$

(4c)

$$ I_{xz} = \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \left( {I_{xx} {-}I_{zz} } \right){\text{sin}}^{{2}} \varepsilon $$

(4d)

The terms I_xx, I_yy and I_zz are the mass moments of inertia about the principal axes, and ε is the angle between the principal X-axis and the stability X-axis. In the present analysis, X_b-, Y_b- and Z_b-axes are considered to be principal axes; hence, ε = α_t.

2.1 Aerodynamic Forces and Moments

The aerodynamic forces and moments at trim conditions in non-dimensional form while neglecting higher order perturbation terms are represented by the following relationships [8].

$$ \begin{aligned} F_{X,A} & = - { }\left[ {\left( {\frac{{\rho V_{\infty } S}}{2}} \right)\left( {2C_{D} + C_{{D_{u} }} } \right)\dot{x}_{e} } \right] - \left[ {\left( {\frac{{\rho V_{\infty } S}}{2}} \right)\left( {C_{{D_{\alpha } }} - C_{L} } \right)} \right]\dot{z}_{e} \\ & \quad - \left[ {\left( {\frac{{\rho V_{\infty }^{2} S}}{2}} \right)\left( {C_{{D_{\alpha } }} - C_{L} } \right)} \right]\theta - \left( {\frac{{\rho V_{\infty }^{2} S}}{2}} \right)C_{D} \\ \end{aligned} $$

(5a)

$$ \begin{aligned} F_{{Z,A}} & = - \left[ {\left( {\frac{{\rho V_{\infty } S}}{2}} \right)\left( {2C_{L} + C_{{L_{u} }} } \right)} \right]\dot{x}_{e} - \left[ {\left( {\frac{{\rho S\overline{{c~}} }}{4}} \right)C_{{L_{{\dot{\alpha }}} }} } \right]\ddot{z}_{e} \\ & \quad - {\text{~}}\left[ {\left( {\frac{{\rho V_{\infty } S}}{2}} \right)\left( {C_{{L_{\alpha } }} + C_{D} } \right)} \right]\dot{z}_{e} - \left[ {\frac{{\rho V_{\infty } S\overline{c} }}{4}{\text{~}}\left( {C_{{L_{{\dot{\alpha }}} }} + C_{{L_{q} }} } \right)} \right]\dot{\theta } \\ & \quad - \left[ {\frac{{\rho V_{\infty }^{2} S}}{2}\left( {C_{{L_{\alpha } }} + C_{D} } \right)} \right]\theta + \frac{{\rho V_{\infty }^{2} S}}{2}C_{L} \\ \end{aligned} $$

(5b)

$$ \begin{aligned} M_{Y,A} & = \left[ {\frac{{\rho V_{\infty } S\overline{c} }}{2}\left( {2C_{m} + C_{{m_{u} }} } \right)} \right]\dot{x}_{e} + \left[ {\frac{{\rho S\left( {\overline{c} } \right)^{2} }}{4}C_{{m_{{\dot{\alpha }}} }} } \right]\ddot{z}_{e} + \left( {\frac{{\rho V_{\infty } S\overline{c} }}{2}C_{{m_{\alpha } }} } \right)\dot{z}_{e} \\ & \quad + \frac{{\rho V_{\infty } S\left( {\overline{c} } \right)^{2} }}{4}\left( {C_{{m_{{\dot{\alpha }}} }} + C_{{m_{q} }} } \right)\dot{\theta } + \left( {\frac{{\rho V_{\infty }^{2} S\overline{c} }}{2}C_{{m_{\alpha } }} } \right)\theta + \frac{{\rho V_{\infty }^{2} S\overline{c} }}{2}C_{m} \\ \end{aligned} $$

(5c)

2.2 Tether Cable Forces and Moments

The tether cable forces and moments are expressed as [16]:

$$ F_{X,C} = - k_{xx} x_{e} - k_{xz} z_{e} - \left( {k_{x\theta } + T_{1} \sin \gamma_{1} } \right)\theta + T_{1} \cos \gamma_{1} $$

(6a)

$$ F_{Z,C} = - k_{zx} x_{e} - k_{zz} z_{e} + \left( {T_{1} \cos \gamma_{1} + k_{y\theta } } \right)\theta + T_{1} \sin \gamma_{1} $$

(6b)

$$ M_{Y,C} = - k_{\theta x} x_{e} - k_{\theta z} z_{e} - k_{\theta \theta } \theta - h_{{k_{1} }} T_{1} \sin \gamma_{1} + h_{{k_{2} }} T_{1} \cos \gamma_{1} $$

(6c)

where

$$ h_{{k_{1} }} = \left( {{\text{l}}_{tr} - {\text{l}}_{cg} } \right)\cos \alpha_{t} + \left( {t_{tr} - h_{cg} } \right)\sin \alpha_{t} $$

$$ h_{{k_{2} }} = \left( {t_{tr} - h_{cg} } \right)\cos \alpha_{t} - \left( {{\text{l}}_{tr} - {\text{l}}_{cg} } \right)\sin \alpha_{t} , $$

$$ k_{x\theta } = h_{{k_{2} }} k_{xx} - h_{{k_{1} }} k_{x2} ,\quad \quad k_{z\theta } = h_{{k_{2} }} k_{zx} - h_{{k_{1} }} k_{zz} $$

$$ k_{\theta x} = h_{{k_{2} }} k_{xx} - h_{{k_{1} }} k_{zx} ,\quad \quad {\text{k}}_{{{\theta z}}} = h_{{k_{2} }} k_{xz} - h_{{k_{1} }} k_{zz} $$

$$ k_{\theta \theta } = k_{{\theta \theta_{D} }} + k_{{\theta \theta_{T} }} $$

$$ k_{{\theta \theta_{D} }} = h_{{k_{2} }}^{2} k_{xx} - h_{{k_{2} }} h_{{k_{1} }} \left( {k_{xz} + k_{zx} } \right) + h_{{k_{1} }}^{2} k_{zz} $$

$$ k_{{\theta \theta_{T} }} = h_{{k_{2} }} \left( {T_{1} \sin \gamma_{1} } \right) + h_{{k_{1} }} \left( {T_{1} \cos \gamma_{1} } \right) $$

$$ k_{y\varphi } = - h_{{k_{2} }} k_{yy} ,\quad k_{y\psi } = h_{{k_{1} }} k_{yy} ,\quad k_{\varphi y} = k_{y\varphi } $$

$$ k_{\varphi \varphi } = h_{{k_{2} }}^{2} k_{yy} ,\quad \quad k_{\psi \psi } = h_{{k_{1} }}^{2} k_{yy} $$

$$ k_{\varphi \psi } = - h_{{k_{1} }} h_{{k_{2} }} k_{yy} ,\quad k_{\psi y} = k_{y\psi } ,\quad k_{\psi \varphi } = k_{\varphi \psi } $$

2.3 Buoyancy Forces and Moments

The expressions for the buoyancy forces and moments about the center of mass in the stability axis system can be expressed assuming small perturbation angles as [16]:

$$ F_{X,B} = B\theta $$

(7a)

$$ F_{Z,B} = - B $$

(7b)

$$ \begin{aligned} M_{Y,B} & = B\left[ {\left( {{\text{l}}_{br} - {\text{l}}_{cg} } \right)\cos \alpha_{t} - \left( {h_{cg} - h_{br} } \right)\sin \alpha_{t} } \right] \\ & \quad - B\left[ {\left( {h_{cg} - h_{br} } \right)\cos \alpha_{t} + \left( {{\text{l}}_{br} - {\text{l}}_{cg} } \right)\sin \alpha_{t} } \right]\theta \\ \end{aligned} $$

(7c)

2.4 Gravity Forces and Moments

The component due to structural weight of balloon is considered during the formulation of equations of motion for gravity forces. The effects of apparent mass and lifting gas are already included in the coefficients of the acceleration and buoyancy terms, respectively. The forces and moments due to gravity for small perturbation angles are determined by [8]:

$$ F_{X,G} = - W_{s} \theta $$

(8a)

$$ F_{Z,G} = - W_{s} $$

(8b)

$$ \begin{aligned} M_{Y,G} & = W_{S} \left[ {\left( {{\text{l}}_{sr} + {\text{ l}}_{cg} } \right)\cos \alpha_{t} - \left( {h_{sr} - h_{cg} } \right)\sin \alpha_{t} } \right] \\ & \quad - W_{S} \left[ {\left( {h_{sr} - h_{cg} } \right)\cos \alpha_{t} + \left( {{\text{l}}_{sr} + {\text{l}}_{cg} } \right)\sin \alpha_{t} } \right]\theta \\ \end{aligned} $$

(8c)

3 Estimation of the Stability Characteristics

After the mathematical modeling, the stability characteristics (roots/eigen values) of the considered aerostat can be estimated by executing the following steps:

• 1. Calculate the trim angle of attack.

• 2. Obtain the aerodynamic parameters dependent on trim angle of attack for the steady-state trim condition.

• 3. Calculate the value of tensions in the cable at the upper and lower ends.

• 4. Use the value of tensions to obtain tether cable derivatives.

• 5. Obtain the stability equations by putting the equilibrium part of the balloon’s equations of motion to zero.

• 6. Convert the above stability equations in the matrix form and obtain the roots/eigen values by using the results obtained in the steps 1 to 4.

3.1 Balloon Equations of Motion

After combining all the expressions for each of the external forces and moments (such as aerodynamic, buoyancy, cable-tether and gravity), the following resulting equations of motion (16) about the balloon COM can be obtained.

X -Force

$$ \begin{aligned} m_{x} \ddot{x}_{e} & + \left[ {\frac{{\rho V_{\infty } S}}{2}\left( {2C_{D} + C_{{D_{u} }} } \right)} \right]\dot{x}_{e} { } + k_{xx} x_{e} + \left[ {\frac{{\rho V_{\infty } S}}{2}\left( {C_{{D_{\alpha } }} - C_{L} } \right)} \right]\dot{z}_{e} + k_{xz} z_{e} \\ & \quad + \left[ {k_{x\theta } + \frac{{\rho V_{\infty }^{2} S}}{2}\left( {C_{{D_{\alpha } }} - C_{L} } \right) - \left( {B - W_{s} } \right) + T_{1} \sin \gamma_{1} } \right]\theta + \frac{{\rho V_{\infty }^{2} S}}{2}C_{D} \\ & \quad - T_{1} \cos \gamma_{1} = 0 \\ \end{aligned} $$

(9a)

Z -Force

$$ \begin{aligned} m_{z } \ddot{z}_{e} & + \frac{{\rho V_{\infty } S}}{2}\left( {2C_{L} + C_{{L_{u} }} } \right)\dot{x}_{e} + k_{zx} x_{e} + \frac{{\rho V_{\infty } S}}{2}\left( {C_{{L_{\alpha } }} + C_{D} } \right)\dot{z}_{e} + k_{zz} z_{e} \\ & \quad { + }\frac{{\rho V_{\infty } S\overline{c} }}{4}\left( {C_{{L_{{\dot{\alpha }}} }} + C_{{L_{q} }} } \right)\dot{\theta } + \left( {k_{z\theta } + \frac{{\rho V_{\infty }^{2} S}}{2}\left( {C_{{L_{\alpha } }} + C_{D} } \right) - T_{1} \cos \gamma_{1} } \right)\theta \\ & \quad + \frac{{\rho V_{\infty }^{2} S}}{2}C_{L} + B + W_{S} - T_{1} \sin \gamma_{1} = 0 \\ \end{aligned} $$

(9b)

Pitching Moment

$$ \begin{aligned} & - \left[ {\frac{{\rho V_{\infty } S\overline{c} }}{2}\left( {2C_{m} + C_{{m_{u} }} } \right)} \right]\dot{x}_{e} + k_{{\theta x}} x_{e} - \left[ {\frac{{\rho S\overline{c} ^{2} }}{4}C_{{m_{{\dot{\alpha }}} }} } \right]\ddot{z}_{e} \\ & \quad - \left( {\frac{{\rho V_{\infty } S\overline{c} }}{2}C_{{m_{\alpha } }} } \right)\dot{z}_{e} + k_{{\theta z}} z_{e} + I_{y} \ddot{\theta } - \left[ {\frac{{\rho V_{\infty } S\overline{c} ^{2} }}{4}\left( {C_{{m_{{\dot{\alpha }}} }} + C_{{m_{q} }} } \right)} \right]\dot{\theta } \\ & \quad + \left( {k_{{\theta \theta }} + M_{{s_{1} }} - \frac{{\rho V_{\infty }^{2} S\overline{c} }}{2}C_{{m_{\alpha } }} } \right)\theta - \frac{{\rho V_{\infty }^{2} S\overline{c} }}{2}C_{m} + h_{{k_{1} }} T_{1} \sin \gamma _{1} \\ & \quad - h_{{k_{2} }} T_{1} \cos \gamma _{1} - M_{{s_{2} }} = 0 \\ \end{aligned} $$

(9c)

$$ \begin{aligned} M_{{s_{1} }} & = \left[ {\left( {{\text{l}}_{{br}} - {\text{l}}_{{cg}} } \right)B + \left( {{\text{l}}_{{sr}} + {\text{l}}_{{cg}} } \right)W_{s} } \right]\sin \alpha _{t} \\ & \quad + \left[ {\left( {h_{{cg}} - h_{{br}} } \right)B + \left( {h_{{sr}} - h_{{cg}} } \right)W_{s} } \right]\cos \alpha _{t} \\ M_{{s_{2} }} & = \left[ {\left( {{\text{l}}_{{br}} - {\text{l}}_{{cg}} } \right)B + \left( {{\text{l}}_{{sr}} + {\text{l}}_{{cg}} } \right)W_{s} } \right]\cos \alpha _{t} \\ & \quad - \left[ {\left( {h_{{cg}} - h_{{br}} } \right)B + \left( {h_{{sr}} - h_{{cg}} } \right)W_{s} } \right]\sin \alpha _{t} \\ m_{x} & = m_{{x,o}} \quad {\text{and}}\quad m_{z} = m_{{z,o}} + \frac{{\rho S\overline{c} }}{4}C_{{L_{{\dot{\alpha }}} }} \\ \end{aligned} $$

3.2 Equilibrium Trim Conditions

In the mathematical model used for calculating the stability characteristic, it is seen that all the aerodynamic parameters are dependent on the angle of attack and it is required to calculate the angle of attack at which the steady-state trimmed condition for the balloon is achieved, this angle of attack is called the trim angle of attack. The steady-state trimmed conditions can be obtained by setting the perturbation quantities of Eq. (9a–9c) equal to zero.

$$ \frac{{\rho V_{\infty }^{2} S}}{2}C_{D} - T_{1} \cos \gamma_{1} = 0 $$

(10a)

$$ \frac{{\rho V_{\infty }^{2} S}}{2}C_{L} + B - W_{s} - T_{1} \sin \gamma_{1} = 0 $$

(10b)

$$ - \frac{{\rho V_{\infty }^{2} S\tau }}{2}C_{m} + h_{{k_{1} }} T_{1} \sin \gamma_{1} - h_{{k_{2} }} T_{1} \cos \gamma_{1} - M_{{s_{2} }} = 0 $$

(10c)

Substitute Eq. (10a–10b) into Eq. (10c) to eliminate the cable tension and angle to obtain the following trim equation:

$$ h_{{k_{1} }} \left( {\frac{{\rho V_{\infty }^{2} S}}{2}C_{L} + B - W_{s} } \right) - h_{{k_{2} }} \left( {\frac{{\rho V_{\infty }^{2} S}}{2}C_{D} } \right) - \frac{{\rho V_{\infty }^{2} S\tau }}{2}C_{m} - M_{{s_{2} }} = 0 $$

(11)

Equation (11) can be solved by Newton iterations to find the equilibrium trim angle of attack (α_t) for various wind velocities, provided the aerodynamic coefficients C_L, C_D and C_m are known functions. The calculated α_t can be used to solve the Eq. (10a–10c) to find and followed by the evaluation of α-dependent stability coefficients.

3.3 Formulations for Calculation of Stability Derivatives

The expressions for the longitudinal stability coefficient/derivatives calculated in the previous step are based on the theoretical formulation corresponding to CG location. The derivative based on the aerostat configuration has been calculated for projected horizontal (PHT). Lift curve slope expression given in Eq. (12) uses the values of constants of the respective tail (PHT).

$$ C_{{L_{{\alpha_{t} }} }} = \frac{{\left( {2\pi A} \right)}}{{\left( {2 + \sqrt {4 + \frac{{A^{2} \beta^{2} }}{{\eta^{2} }}\left( {1 + \frac{{\tan^{2} \Lambda }}{{\beta^{2} }}} \right)} } \right)}}{*}\frac{{S_{{{\text{exposed}}}} }}{{S_{{{\text{ref}}}} }} $$

(12)

where $C_{{L_{{\alpha_{t} }} }}$ is the lift curve slope of the tail.

Longitudinal Derivatives (PHT).

$$ C_{L} = 0.0061 + 1.2\alpha + C_{{L_{{\alpha_{t} }} }} \alpha + \eta C_{{D_{c} }} \frac{{S_{P} }}{{S_{{{\text{ref}}}} }}\alpha^{2} $$

$$ C_{{L_{\alpha } }} = 1.2 + C_{{L_{{\alpha_{t} }} }} + 2\eta C_{{D_{c} }} \frac{{S_{P} }}{{S_{{{\text{ref}}}} }}\alpha $$

$$ C_{{L_{{\dot{\alpha }}} }} = C_{{L_{q} }} \frac{{{\text{d}} \in }}{{{\text{d}}\alpha }} $$

$$ C_{{L_{q} }} = 2C_{{L_{{\alpha_{t} }} }} \frac{{L_{{{\text{PHT}}}} }}{D} $$

$$ C_{D} = 0.0396 + \frac{{C_{L}^{2} }}{{\pi e{\rm A}}} $$

$$ C_{{D_{\alpha } }} = 2\frac{{C_{L} }}{\pi eA}C_{{L_{\alpha } }} $$

$$ C_{m} = - 0.02 + 0.04832\alpha + \eta C_{{L_{{\alpha_{t} }} }} \left( {1 - \frac{{{\text{d}}e}}{{{\text{d}}\alpha }}} \right)\frac{{L_{{{\text{PHT}}}} }}{D}\alpha $$

$$ C_{{m_{\alpha } }} = 0.048326 + \eta C_{{L_{{\alpha_{t} }} }} \left( {1 - \frac{{{\text{d}}e}}{{{\text{d}}\alpha }}} \right)\frac{{L_{{{\text{PHT}}}} }}{D}\alpha $$

$$ C_{{m_{q} }} = - 2C_{{L_{{\alpha_{t} }} }} \left( {\frac{{L_{{{\text{PHT}}}} }}{D}} \right)^{2} $$

$$ C_{{m_{{\dot{\alpha }}} }} = C_{{m_{q} }} \tau \frac{{{\text{d}} \in }}{{{\text{d}}\alpha }} $$

where $\tau = \left( {\frac{{V_{t} }}{V}} \right)^{2}$.

3.4 Equilibrium Cable Shape

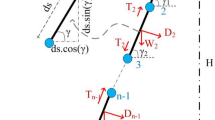
The forces acting on tether cable of length, l (Fig. 4) are the tension, cable weight and drag normal to the cable. Drag along the cable has been neglected. The normal drag force per unit length depends on the component of wind velocity normal to the cable V_n, the drag cable coefficient $C_{{D_{c} }}$ and cable diameter d_c and can be expressed as [8]:

$$ n = C_{{D_{c} }} d_{c} \frac{1}{2}\rho V_{n}^{2} $$

(13)

Fig. 4

Forces acting on the tether cable [8]

Tension (T₁) at upper end of the cable using tension $\left[ {\frac{{{\text{d}}T}}{T} = - \frac{{\overline{p } }}{{{\overline{\text{q}}}}}\left( {\frac{{{\text{d}}f}}{{\overline{q} + \overline{p} - f}} + \frac{{{\text{d}}f}}{{\overline{q} - \overline{p} + f}}} \right)} \right]$ is given by

$$ T_{1} = T_{\tau 1/\tau } $$

(14)

where $\tau \left( \gamma \right) = \left( {\frac{{\overline{q} + \overline{p} - \cos \gamma }}{{\overline{q} - \overline{p} + \cos \gamma }}} \right)^{{\frac{{\overline{p}}}{{\overline{q}}}}}$, $\overline{p} = \frac{{w_{c} }}{2n}$, $\overline{q} = \sqrt {1 + \left( {\overline{p}} \right)^{2} }$, $f = {\text{cos}}\gamma$.

For the known parameters such as l $\left( {{\text{d}}l = \left( {\frac{{T_{1} }}{{n\tau_{1} }}} \right)\frac{\tau }{{\left( {{\text{sin}}^{2} \gamma + 2\overline{p}\cos \gamma } \right)}}{\text{d}}\gamma } \right)$, n, w_c, T₁ and γ₁, the following expressions can be used to determine the coordinates T₁ and γ₁ at upper end and T₀ and γ₀ at the lower end.

$$ \overline{\lambda }_{0} = \overline{\lambda }_{1} - \frac{{n\tau_{1} {\text{l}}}}{{T_{1} }}\quad {\text{and}}\quad T_{0} = T_{1\tau 0/\tau 1} $$

(15)

$$ \tilde{x}_{1} = \frac{{T_{1} }}{{n\tau_{1} }}\mathop \smallint \limits_{{\gamma_{0} }}^{{\gamma_{1} }} \frac{\tau \cos \gamma }{{\left( {{\text{sin}}^{2} \gamma + 2\overline{p}\cos \gamma } \right)}}{\text{d}}\gamma \quad {\text{where}}\quad {\text{d}}\sigma { = }\frac{\tau \cos \gamma }{{\left( {\sin^{2} \gamma + 2\overline{p} \cos \gamma } \right)}}{\text{d}}\gamma $$

(16)

$$ \tilde{z}_{1} = \frac{{T_{1} - T_{0} }}{{w_{c} }}\quad {\text{where}}\quad {\text{d}}\tilde{z} = {\text{d}}l\,{\text{sin}}\,\gamma = \frac{{{\text{d}}T}}{{w_{c} }} $$

(17)

where $\overline{\lambda }\left( \gamma \right) = { }\mathop \smallint \limits_{0}^{\gamma } \frac{\tau \left( \gamma \right)}{{\left( {{\text{sin}}^{2} \gamma + 2\overline{p}\cos \gamma } \right)}}{\text{d}}\gamma$ $\overline{\lambda }_{0} = \overline{\lambda }\left( {\gamma_{0} } \right)$ and $\overline{\lambda }_{1} = \overline{\lambda }\left( {\gamma_{1} } \right)$.

3.5 Cable Force Derivatives

Consider cable in its equilibrium position. If upper end is slowly displaced in the $\tilde{x}\tilde{z}$—plane from its original position $\tilde{x}_{1} , {\tilde{\text{z}}}_{1}$ to a new position the resultant x- and z-force increments are

$$ {\text{d}}F_{x} = k_{xx} {\text{d}}\tilde{x} + k_{xz} {\text{d}}\tilde{z} $$

(18a)

$$ {\text{d}}F_{z} = k_{zx} {\text{d}}\tilde{x} + k_{zz} {\text{d}}\tilde{z} $$

(18b)

The cable derivatives (spring constants) $k_{xx} ,k_{xz} ,k_{zx}$ and $k_{zz}$ for the longitudinal case can be expressed as [8]:

$$ k_{xx} = \frac{1}{\delta }\left[ {T_{1} \cos \gamma_{1} \left( {\sin \gamma_{1} - { }\sin \gamma_{0} } \right) + n\left( {z_{1} - {\text{ l}}\sin \gamma_{0} } \right){\text{sin}}^{3} \gamma_{1} } \right] $$

(19a)

$$ k_{xz} = \frac{1}{\delta }\left[ {T_{1} \cos \gamma_{1} \left( {\cos \gamma_{0} - \cos \gamma_{1} } \right) + n\left( {{\text{l}}\cos \gamma_{0} - \tilde{x}_{1} } \right){\text{sin}}^{3} \gamma_{1} } \right] $$

(19b)

$$ k_{zx} = \frac{1}{\delta }\left[ {T_{1} \sin \gamma_{1} \left( {\sin \gamma_{1} - \sin \gamma_{0} } \right) - \left( {w_{c} + n{\text{sin}}^{2} \gamma_{1} \cos \gamma_{1} } \right)(\tilde{z}_{1} - {\text{lsin}}\gamma_{0} } \right] $$

(19c)

$$ k_{zz} = \frac{1}{\delta }\left[ {T_{1} \sin \gamma_{1} \left( {\cos \gamma_{0} - \cos \gamma_{1} } \right) - \left( {w_{c} + n{\text{sin}}^{2} \gamma_{1} \cos \gamma_{1} } \right)\left( {{\text{l}}\cos \gamma_{0} - \tilde{x}_{1} } \right)} \right] $$

(19d)

where $\delta = x_{1} \left( {\sin \gamma_{1} - \sin \gamma_{0} } \right) + z_{1} \left( {\cos \gamma_{0} - \cos \gamma_{1} } \right) - {\text{l}}\sin \left( {\gamma_{1} - \gamma_{0} } \right)$.

The single lateral cable derivative determined by considering a small force dF_Y to act in the y-direction on the upper end of the cable is given by the following expression.

$$ {\text{d}}F_{Y} = k_{yy} {\text{d}}y $$

(20)

where $k_{yy} = \frac{{n\sqrt {\tau_{1} \left( {{\text{sin}}^{2} \gamma_{1} + 2\overline{p}\cos \gamma_{1} } \right)} }}{{\mathop \smallint \nolimits_{{\gamma_{0} }}^{{\gamma_{1} }} \sqrt {\frac{\tau \left( \gamma \right)}{{\left( {{\text{sin}}^{2} \gamma + 2\overline{p}\cos \gamma } \right)}}} {\text{ d}}\gamma }}$.

3.6 Stability Equations (Longitudinal)

The stability equations are obtained by setting the equilibrium trim portions of the equations of motion (Eq. 10a–10f) equal to zero. The following working forms of the stability equations [3] written about the balloon center of mass are obtained.

X-Force.

$$ \begin{aligned} m_{x} \ddot{x}_{e} & + \left[ {\frac{{\rho V_{\infty } S}}{2}\left( {2C_{D} + C_{{D_{u} }} } \right)} \right]\dot{x}_{e} + k_{xx} x_{e} + \left[ {\frac{{\rho V_{\infty } S}}{2}\left( {C_{{D_{\alpha } }} - C_{L} } \right)} \right]\dot{z}_{e} \\ & \quad + k_{xz} z_{e} + \left[ {k_{x\theta } + \frac{{\rho V_{\infty }^{2} SC_{{D_{\alpha } }} }}{2}} \right]\theta = 0 \\ \end{aligned} $$

(21a)

Z-Force.

$$ \begin{aligned} m_{{z{ }}} \ddot{z}_{e} & + \frac{{\rho V_{\infty } S}}{2}\left( {2C_{L} + C_{{L_{u} }} } \right)\dot{x}_{e} + k_{zx} x_{e} + \frac{{\rho V_{\infty } S}}{2}\left( {C_{{L_{\alpha } }} + C_{D} } \right)\dot{z}_{e} \\ & \quad + k_{zz} z_{e} + \frac{{\rho V_{\infty } S\overline{c} }}{4}\left( {C_{{L_{{\dot{\alpha }}} }} + C_{{L_{q} }} } \right)\dot{\theta } + \left( {k_{z\theta } + \frac{{\rho V_{\infty }^{2} SC_{{L_{\alpha } }} }}{2}} \right)\theta = 0 \\ \end{aligned} $$

(21b)

Pitching Moment.

$$ \begin{aligned} - \left[ {\frac{{\rho V_{\infty } S\overline{c} }}{2}\left( {2C_{m} + C_{{m_{u} }} } \right)} \right]\dot{x}_{e} & + k_{{\theta x}} x_{e} - \left[ {\frac{{\rho S\overline{c} ^{2} }}{4}C_{{m_{{\dot{\alpha }}} }} } \right]\ddot{z}_{e} - \left( {\frac{{\rho V_{\infty } S\overline{c} }}{2}C_{{m_{\alpha } }} } \right)\dot{z}_{e} + k_{{\theta z}} z_{e} \\ & \quad + I_{y} \ddot{\theta } - \left[ {\frac{{\rho V_{\infty } S\overline{c} ^{2} }}{4}\left( {C_{{m_{{\dot{\alpha }}} }} + C_{{m_{q} }} } \right)} \right]\dot{\theta } \\ & \quad + \left( {k_{{\theta \theta }} + M_{{s_{1} }} - \frac{{\rho V_{\infty }^{2} S\overline{c} }}{2}C_{{m_{\alpha } }} } \right)\theta = 0 \\ \end{aligned} $$

(21c)

Using the mathematical model, the stability equations can be written in the state space form as given below:

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = Ax + Bu $$

(22)

where A is the characteristic matrix and B is the input matrix.

Since no control input is being used, the matrix A gives the characteristics of the aerostat system. The equation for longitudinal and lateral stability case can be expressed in the following matrix form, respectively.

$$ \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\dot{u}} \\ {\dot{w}} \\ {\dot{q}} \\ \end{array} } \\ {\dot{\theta }} \\ {\begin{array}{*{20}c} {\dot{x}} \\ {\dot{z}} \\ \end{array} } \\ \end{array} } \right] = A\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} u \\ w \\ \end{array} } \\ {\begin{array}{*{20}c} q \\ {\begin{array}{*{20}c} \theta \\ {\begin{array}{*{20}c} x \\ z \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] $$

(23)

The roots of characteristic equation obtained by computing stability matrix A for longitudinal and lateral case give an insight into the stability of the system.

4 Effect of Geometrical Parameters on Longitudinal Stability Boundaries

The computed values of longitudinal frequencies (ω) and damping rates (η) for the considered aerostat have been plotted as a function of wind velocity in Fig. 5a, b and in root locus form in Fig. 5c. Figure 5a, b indicates that the considered aerostat has three oscillatory modes of motion for the given range of the wind velocities. It can be observed from Fig. 5b that the aerostat was longitudinally stable except below wind velocity of 2 m/s at which one of the roots becomes positive. This fact is also evident from the negative slope of the plot between pitching moment coefficient and angle of attack as shown in Fig. 5d. It could also be observed from Fig. 5b that mode 2 splits into two real non-oscillatory modes above wind velocity of 19 m/s and again merged into one at 35 m/s.

Fig. 5

a Variation of ω with V for longitudinal case. b Variation of η with V for longitudinal case. c ω versus η (Root locus plot for longitudinal case). d C_m versus α for longitudinal case

Next, geometrical parameters were varied to see the effect on longitudinal stability boundaries of the considered aerostat. The results showing the effect of different parameters on the stability boundaries for a range of speed have been presented in the graphical form. Figures 6, 7, 8, 9, 10, 11, 12 and 13 show that the aerostat is unstable below the speed of 2 m/sec and in the region bounded by the two curved/straight boundaries. The unstable region increases or decreases with increase or decrease in the values of most of the dimensional parameters of the considered aerostat. Very little or negligible effect on stability boundaries was observed for some parameters.

Fig. 6

a Effect of L_tr on longitudinal stability boundary b Effect of T_tr on longitudinal stability boundary

Fig. 7

a Effect of L_cg on longitudinal stability boundary b Effect of H_cg on longitudinal stability boundary

Fig. 8

a Effect of L_br on longitudinal stability boundary b Effect of H_br on longitudinal stability boundary

Fig. 9

a Effect of L_sr on longitudinal stability boundary b Effect of H_sr on longitudinal stability boundary

Fig. 10

Effect of cable length (m) on longitudinal stability

Fig. 11

Effect of cable diameter (d_c) on longitudinal stability boundary

Fig. 12

Effect of cable weight (w_c) on longitudinal stability boundary

Fig. 13

Effect of moment arm (PHT) on longitudinal stability boundary

It can be observed from Figs. 6, 7, 8, 9, 10, 11, 12 and 13 that the parameters such as L_tr, T_tr, L_br, L_sr, C.G. (moment arm), l, d_c, w_c affect the stability boundaries strongly while the parameters such as L_cg, H_cg, H_br and H_sr have very little or negligible effect on the stability characteristics/boundaries of the aerostat. It can be observed that the decrease in L_tr (the horizontal component of distance between RP and BCP) decreases the unstable region while decrease in T_tr (the vertical component of distance between RP and BCP) increases the unstable region (Fig. 6a, b). The change in horizontal (L_cg) or vertical (H_cg) component of distance from RP to COM has very little or negligible effect on the stability boundaries (Fig. 7a, b). Increase in the value of horizontal component of distance from RP to COB (L_br) and COM of structure (L_sr) decreases the unstable regions while the vertical components (H_br and H_sr) have negligible effect (Figs. 8a, b and 9a, b).

Reduction in tether cable length (l), cable diameter (d_c) and cable weight (w_c) leads to the reduction in the unstable region (Figs. 10, 11 and 12). Increase in the horizontal tail moment arm reduces the unstable region (Fig. 13).

5 Conclusion

Longitudinal stability analysis and effect of variation of geometrical parameters on longitudinal stability boundaries for a balloon tethered in a steady wind has been presented. Equations of motion of the considered aerostat included aerodynamic, tether cable, buoyancy and gravity forces along with aerodynamic apparent mass and structural mass terms. After mathematical modeling, the roots of the characteristic stability equation were computed and plotted for various steady-wind conditions. It was observed from graphical presentations that the considered aerostat was stable longitudinally. Later on, parametric trend study was carried out to show the influence of various dimensional and aerodynamic parameters of aerostat on longitudinal stability boundaries for a wide range of steady-wind speeds. The study suggests that the judicious and feasible choice of various geometrical parameters can be utilized to design a new tethered aerostat which can remain stable for a wide range of wind speeds. The limitation of the stability analysis carried out was that the downwash has been neglected and provides the basis for the future scope.