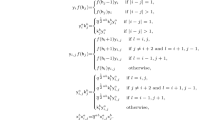3D R From Quantized Coordinate Ring of Type A

Abstract

Let $\mathfrak {g}$ be a classical simple Lie algebra and $U_q(\mathfrak {g})$ be the quantized universal enveloping algebra of $\mathfrak {g}$. There is a Hopf algebra dual to $U_q(\mathfrak {g})$ which corresponds to a q deformation of the algebra of functions on the Lie group of $\mathfrak {g}$. It will be called the quantized coordinate ring and denoted by $A_q(\mathfrak {g})$ in this book. We assume that q is generic throughout. In this chapter, $A_q(\mathfrak {g})$ for $\mathfrak {g}$ of type A is treated based on a concrete realization by generators and relations, deferring a more universal formulation to Sect. 10.2. It turns out that an intertwiner of certain $A_q(\mathfrak {g})$ modules leads to a 3D R, a solution of the tetrahedron equation. It has set-theoretical and birational counterparts which satisfy the tetrahedron equation in the respective setting. The birational case admits bilinearization in terms of tau functions.

3.1 Quantized Coordinate Ring $A_q(A_{n-1})$

Let $n \ge 2$ be an integer. This chapter is devoted to the type A case $\mathfrak {g}= A_{n-1}$.¹ The quantized coordinate ring $A_q(A_{n-1})$ is a Hopf algebra [1] with $n^2$ generators $(t_{ij})_{1\le i,j\le n}$. In terms of the n by n matrix $T = (t_{ij})$, their relations are presented in the so-called $RTT = TTR$ form and the unit quantum determinant condition:

$$\begin{aligned}&\sum _{m,p}R^{ij}_{mp}t_{mk}t_{pl} = \sum _{m,p}t_{jp}t_{im}R^{mp}_{kl},\end{aligned}$$

(3.1)

$$\begin{aligned}&\sum _{\sigma \in \mathfrak {S}_n}(-q)^{l(\sigma )} t_{1\sigma _1}\cdots t_{n\sigma _n} = 1. \end{aligned}$$

(3.2)

The former is called the RTT relation.  The symbol $\mathfrak {S}_n$ denotes the symmetric group of degree n and $l(\sigma )$ is the length of the permutation $\sigma$. The structure constant $R^{ij}_{kl}$ is specified by

$$\begin{aligned} \sum _{i,j,k,l}R^{ij}_{kl}E_{ik}\otimes E_{jl}= q\sum _i E_{ii}\otimes E_{ii} + \sum _{i\ne j}E_{ii}\otimes E_{jj} +(q-q^{-1})\sum _{i>j}E_{ij}\otimes E_{ji}, \end{aligned}$$

(3.3)

where the indices are summed over $\{1,2,\ldots , n\}$, and $E_{ij}$ is a matrix unit. The matrix (3.3) is extracted as

$$\begin{aligned}&\sum _{i,j,m,l}R^{ij}_{ml}E_{im}\otimes E_{jl} = q\lim _{x\rightarrow \infty }x^{-1}R(x)|_{k=q^{-1}} \end{aligned}$$

(3.4)

from the quantum R matrix R(x)  for the vector representation of $U_q(A^{(1)}_{n-1})$ given in [64, Eq. (3.5)].² Explicitly, the relation (3.1) reads as

$$\begin{aligned} \begin{aligned}&[t_{ik}, t_{jl}]={\left\{ \begin{array}{ll}0 &{}(i<j, k>l),\\ (q-q^{-1})t_{jk}t_{il} &{} (i<j, k<l), \end{array}\right. }\\&t_{ik}t_{jk} = q t_{jk}t_{ik}\; (i<j),\quad t_{ki}t_{kj} = q t_{kj}t_{ki}\; (i<j). \end{aligned} \end{aligned}$$

(3.5)

The coproduct or co-multiplication is given by

$$\begin{aligned} \Delta (t_{ij}) = \sum _k t_{ik}\otimes t_{kj}. \end{aligned}$$

(3.6)

We will use the same symbol $\Delta$ flexibly to also mean the multiple coproducts like $(\Delta \otimes 1) \circ \Delta = (1\otimes \Delta ) \circ \Delta$, etc. The antipode S and the counit $\epsilon$ are given by

$$\begin{aligned} S(t_{ij})&= (-q)^{i-j} \sum _{\sigma \in \mathfrak {S}_{n-1}} (-q)^{l(\sigma )}t_{1, \sigma _1}\cdots t_{j-1,\sigma _{j-1}} t_{j+1,\sigma _{j+1}} \cdots t_{n,\sigma _n}, \end{aligned}$$

(3.7)

$$\begin{aligned} \epsilon (t_{ij})&= \delta _{ij}. \end{aligned}$$

(3.8)

The  sum in (3.7) is the quantum minor which extends over permutations of $\{1,\ldots , n \}\setminus \{i\}$.

Example 3.1

The simplest case $n=2$ is $A_q(A_1)$. It is generated by $t_{11}, t_{12}, t_{21}, t_{22}$ with the relations

$$\begin{aligned} \begin{aligned}&t_{11}t_{21} = qt_{21}t_{11},\quad t_{12}t_{22} = qt_{22}t_{12},\quad t_{11}t_{12} = qt_{12}t_{11},\quad t_{21}t_{22} = qt_{22}t_{21},\\&[t_{12},t_{21}]=0,\quad [t_{11},t_{22}]=(q-q^{-1})t_{21}t_{12}, \quad t_{11}t_{22}-qt_{12}t_{21}=1. \end{aligned} \end{aligned}$$

(3.9)

The quantum determinant $t_{11}t_{22}-qt_{12}t_{21}$ appearing in (3.9) is central.  The rule (3.6) implies that the coproduct $\Delta$ is obtained by formally replacing the product in matrix multiplication by $\otimes$ as

$$\begin{aligned} \begin{pmatrix} t_{11} &{} t_{12} \\ t_{21} &{} t_{22} \end{pmatrix}&\overset{\Delta }{\mapsto } \begin{pmatrix} t_{11} \otimes t_{11} + t_{12} \otimes t_{21} &{}\; t_{11} \otimes t_{12} + t_{12} \otimes t_{22} \\ t_{21} \otimes t_{11} + t_{22} \otimes t_{21} &{} \; t_{21} \otimes t_{12} + t_{22} \otimes t_{22} \end{pmatrix}. \end{aligned}$$

(3.10)

The multiple coproduct is similar. It is easy to check that $\Delta$ is an algebra homomorphism, for example, $\Delta (t_{11})\Delta (t_{21}) = q \Delta (t_{21})\Delta (t_{11})$ by using (3.9) and (3.10). A defining axiom $m\circ (1 \otimes S) \circ \Delta = \iota \circ \epsilon$ for example,³ is checked as

$$\begin{aligned} (3.10)&\overset{1 \otimes S}{\mapsto } \begin{pmatrix} t_{11} \otimes t_{22} + t_{12} \otimes (-q t_{21}) &{} \;t_{11} \otimes (-q^{-1} t_{12}) + t_{12} \otimes t_{11} \\ t_{21} \otimes t_{22} + t_{22} \otimes (-q t_{21}) &{} \; t_{21} \otimes (-q^{-1} t_{12}) + t_{22} \otimes t_{11} \end{pmatrix} \nonumber \\&\overset{m}{\mapsto } \begin{pmatrix} t_{11} t_{22} -q t_{12}t_{21} &{} \;-q^{-1} t_{11} t_{12} + t_{12}t_{11} \\ t_{21}t_{22} -qt_{22} t_{21} &{} \; -q^{-1} t_{21}t_{12} + t_{22}t_{11} \end{pmatrix} = \begin{pmatrix} 1 &{} 0 \\ 0&{} 1 \end{pmatrix}. \end{aligned}$$

(3.11)

A sketch of “derivation” of the relations (3.9) from the dual $U_q(sl_2)$ is available in Example 10.2.

Remark 3.2

The map $t_{jk} \mapsto \xi _j^{-1}\xi _kt_{jk}$ with non-zero parameters $\xi _1,\ldots , \xi _{n}$ is a Hopf algebra automorphism.

3.2 Representation Theory

Let $\mathrm {Osc}_q = \langle {{\mathbf{a}}^+ , {\mathbf{a}}^- , {\mathbf{k}}, {\mathbf{k}}^{-1}} \rangle$ be the q-oscillator algebra, i.e. an associative algebra with the relations

$$\begin{aligned} \mathrm{\mathbf{k}} \,\mathrm{\mathbf{a}}^+ = q\,\mathrm{\mathbf{a}}^+\mathrm{\mathbf{k}},\quad \mathrm{\mathbf{k}}\,\mathrm{\mathbf{a}}^- = q^{-1}\mathrm{\mathbf{a}}^-\mathrm{\mathbf{k}},\quad \mathrm{\mathbf{a}}^- \mathrm{\mathbf{a}}^+ = 1-q^2\mathrm{\mathbf{k}}^2,\quad \mathrm{\mathbf{a}}^+\mathrm{\mathbf{a}}^- = 1-\mathrm{\mathbf{k}}^2 \end{aligned}$$

(3.12)

and those following from the obvious ones ${\mathbf{k}}\, {\mathbf{k}}^{-1} = {\mathbf{k}}^{-1} {\mathbf{k}}= 1$.  It has an irreducible representation on the Fock space $\mathcal {F}_q = \bigoplus _{m\ge 0}{\mathbb C}(q)|m\rangle$:

$$\begin{aligned} \mathrm{\mathbf{k}}|m\rangle = q^m |m\rangle ,\quad \mathrm{\mathbf{a}}^+|m\rangle = |m+1\rangle ,\quad \mathrm{\mathbf{a}}^-|m\rangle = (1-q^{2m})|m-1\rangle . \end{aligned}$$

(3.13)

In particular $\mathrm{\mathbf{a}}^-|0\rangle = 0$. The generators $\mathrm{\mathbf{a}}^\pm$ and $\mathbf{k}^{\pm 1}$ will be identified with the elements of $\mathrm {End}(\mathcal {F}_q)$ defined by (3.13) unless otherwise stated. We will also use the diagonal operators $\mathrm{\mathbf{h}}$ and $D_q$ such that

$$\begin{aligned} \mathrm{\mathbf{h}}|m\rangle&= m |m\rangle , \end{aligned}$$

(3.14)

$$\begin{aligned} D_q | m\rangle&= (q^2)_m | m \rangle . \end{aligned}$$

(3.15)

Thus we may identify ${\mathbf{k}}$ as $\mathrm{\mathbf{k}} = q^\mathrm{\mathbf{h}}$. An eigenvalue of $\mathrm{\mathbf{h}}$ will be referred to as a mode of the q-oscillator. For the notation $(q^2)_m=(q^2;q^2)_m$, see (3.65).

We will also be concerned with the dual Fock space $\mathcal {F}^*_q = \bigoplus _{m \ge 0} {\mathbb C}(q)\langle m|$ whose pairing with $\mathcal {F}_q$ is specified by

$$\begin{aligned} \langle m | m'\rangle = (q^2)_m\delta _{m,m'}. \end{aligned}$$

(3.16)

The q-oscillators act on $\mathcal {F}^*_q$ as

$$\begin{aligned} \langle m |\mathrm{\mathbf{k}} = \langle m |q^m,\quad \langle m |\mathrm{\mathbf{a}}^+ = \langle m -1|(1-q^{2m}) ,\quad \langle m |\mathrm{\mathbf{a}}^- = \langle m+1 | \end{aligned}$$

(3.17)

and $\langle m |\mathbf{h} = \langle m |m$. In particular $\langle 0 | {\mathbf{a}}^+ = 0$. They satisfy $(\langle m | X)|m'\rangle = \langle m | (X|m'\rangle )$ and

$$\begin{aligned}&\langle m |X_1\cdots X_j |m'\rangle = \langle m' |\overline{X_j}\cdots \overline{X_1} |m\rangle , \end{aligned}$$

(3.18)

where $\overline{(\cdots )}$ is defined by $\overline{{\mathbf{a}}^{\pm } } = {\mathbf{a}}^{\mp } ,\, \overline{{\mathbf{k}}}={\mathbf{k}}$ and $\overline{\mathbf{h}} = \mathbf{h}$.

The algebra $A_q(A_1)$ in Example 3.1 has the irreducible representation $\pi$ on $\mathcal {F}_q$ depending on a non-zero parameter $\mu$ as follows:

$$\begin{aligned} \pi :&\begin{pmatrix} t_{11} &{} t_{12}\\ t_{21} &{} t_{22} \end{pmatrix} \mapsto \begin{pmatrix} \mathrm{\mathbf{a}}^- &{} \mu \mathrm{\mathbf{k}}\\ -q\mu ^{-1}\mathrm{\mathbf{k}} &{} \mathrm{\mathbf{a}}^+ \end{pmatrix}. \end{aligned}$$

(3.19)

For $A_q(A_{n-1})$, there are similar representations

$$\begin{aligned} \pi _i : A_q(A_{n-1}) \rightarrow \mathrm {End}(\mathcal {F}_q) \qquad (1 \le i \le n-1). \end{aligned}$$

(3.20)

It contains a non-zero parameter $\mu _i$ and factors through (3.19) via the surjective map $A_q(A_{n-1}) \twoheadrightarrow A_{q}(sl_{2,i})$. Here, $sl_{2,i}$ denotes the $A_1=sl_2$-subalgebra of $A_{n-1}$ associated with i. It is given by

$$\begin{aligned} \pi _i: \begin{pmatrix} \!\!\!\!\!\!\!\!\!\!\!\!t_{11} \!\!\!\!\!\!&{} &{} &{} &{} &{}t_{1n}\\ \qquad \ddots &{} &{} &{} &{}&{}\\ &{} \!\!\!\!\!\!\!\!\!\!\!\! t_{i-1,i-1}&{}&{}&{} &{} \\ &{}\qquad \!\! t_{i,i} &{} \!t_{i,i+1} &{}&{}&{}\\ &{}\qquad t_{i+1,i} &{} \!t_{i+1,i+1} &{} &{}&{}\\ &{}&{}&{} \!\!\!\!t_{i+2,i+2}&{}&{}&{}\\ &{}&{}&{}&{} \!\!\!\!\ddots &{} \\ \!\! \!\!\!\!t_{n1} &{}&{}&{}&{}&{} t_{nn} \end{pmatrix} \mapsto \begin{pmatrix} 1&{} &{} &{} &{} &{}&{}&{}\\ &{}\ddots &{} &{} &{} &{} &{}&{}\\ &{} &{} 1 &{}&{}&{} &{} &{} \\ &{}&{}&{}\!\! \!\! \mathrm{\mathbf{a}}^- &{} \mu _i \mathrm{\mathbf{k}} &{}&{}&{}\\ &{}&{}&{} \!\! -q\mu _i^{-1} \mathrm{\mathbf{k}}&{} \;\;\mathrm{\mathbf{a}}^+&{} &{}&{}\\ &{}&{}&{}&{}&{}1&{}&{}\\ &{}&{}&{}&{}&{}&{} \ddots &{} \\ &{}&{}&{}&{}&{}&{}&{} 1 \end{pmatrix} , \end{aligned}$$

(3.21)

where all the blanks on the RHS are to be understood as 0. It is easy to see that $\pi _1, \ldots , \pi _{n-1}$ are all inequivalent and irreducible. Starting from them, one can construct tensor product representations $\pi _{i_1} \otimes \cdots \otimes \pi _{i_l}: A_q(A_{n-1}) \rightarrow \mathrm {End}(\mathcal {F}_q^{\otimes l})$ via $f \mapsto (\pi _{i_1} \otimes \cdots \otimes \pi _{i_l})(\Delta (f))$ using the multiple coproduct $\Delta$ obtained by iterating (3.6) $l-1$ times. A natural question at this stage is, what is the totality of irreducible representations up to equivalence and how they can be realized. The answer has been known for $A_q(\mathfrak {g})$ associated with any classical simple Lie algebra $\mathfrak {g}$.

Theorem 3.3

• (i) For each vertex i of the Dynkin diagram of $\mathfrak {g}$, $A_q(\mathfrak {g})$ has an irreducible representation $\pi _i$ factoring through (3.19) via $A_q(\mathfrak {g}) \twoheadrightarrow A_{q_i}(sl_{2,i})$.

• (ii) Irreducible representations of $A_q(\mathfrak {g})$ up to equivalence are in one-to-one correspondence with the elements of the Weyl group W of $\mathfrak {g}$.

• (iii) Let $w =s_{i_1}\cdots s_{i_l} \in W$ be a reduced expression in terms of the simple reflections. Then the irreducible representation corresponding to w is isomorphic to $\pi _{i_1}\otimes \cdots \otimes \pi _{i_l}$.

In  (i), $q_i= q^{(\alpha _i, \alpha _i)/2}$, where $\alpha _i$ is a simple root.⁴  The assertions (ii) and (iii) actually hold up to the degrees of freedom of the parameters as $\mu _i$ in (3.19). See [138, 139, 146] for the detail. We call $\pi _i\,(i = 1,\ldots , \mathrm {rank\,} \mathfrak {g})$ the fundamental representations.  We will often denote $\pi _{i_1} \otimes \cdots \otimes \pi _{i_l}$ by $\pi _{i_1,\ldots , i_l}$ for short.

Returning to the $\mathfrak {g}=A_{n-1}$ case, the representations $\pi _1, \ldots , \pi _{n-1}$ defined in (3.21) are the fundamental representations of $A_q(A_{n-1})$ in the above sense. The Weyl group $W(A_{n-1}) = \langle s_1,\ldots , s_{n-1}\rangle$ is generated by the simple reflections $s_1,\ldots , s_{n-1}$ obeying the Coxeter relations 

$$\begin{aligned} s^2_i = 1, \quad \;\;s_is_j = s_js_i\; \;(|i-j|\ge 2), \quad \;\; s_is_js_i = s_js_is_j\; \;(|i-j|=1). \end{aligned}$$

(3.22)

From the second relation here and Theorem 3.3 (iii) it follows that $\pi _i \otimes \pi _j \simeq \pi _j \otimes \pi _i$ for $|i-j|\ge 2$. This isomorphism is simply provided as the transposition of components:

$$\begin{aligned} P(x\otimes y) = y\otimes x. \end{aligned}$$

(3.23)

In order to show this, one should check that

$$\begin{aligned} P (\pi _i \otimes \pi _{j})(\Delta (f)) = (\pi _{j} \otimes \pi _{i})(\Delta (f))P\qquad (|i-j| \ge 2) \end{aligned}$$

(3.24)

holds for any $f \in A_q(A_{n-1})$. Since $\Delta$ is an algebra homomorphism, it suffices to consider the $f=t_{km}$ case:

$$\begin{aligned} P\Bigl (\sum _l \pi _i(t_{kl})\otimes \pi _j(t_{lm})\Bigr ) = \Bigl (\sum _l \pi _j(t_{kl})\otimes \pi _i(t_{lm})\Bigr ) P \;\quad \text {for }\; |i-j|\ge 2, \end{aligned}$$

(3.25)

which is equivalent to

$$\begin{aligned} \sum _l \pi _j(t_{lm}) \otimes \pi _i(t_{kl}) = \sum _l \pi _j(t_{kl})\otimes \pi _i(t_{lm}) \;\quad \text {for }\; |i-j|\ge 2. \end{aligned}$$

(3.26)

This indeed holds thanks to the simple and sparse structure of (3.21).

Remark 3.4

Not only for $A_{n-1}$ but for general $\mathfrak {g}$, the equivalence of $\pi _i \otimes \pi _j \simeq \pi _j \otimes \pi _i$ for i, j such that $s_is_j = s_js_i$ is always assured by the transposition P in (3.23).

By virtue of Remark 3.2, all the parameters $\mu _1, \ldots , \mu _{n-1}$ in the fundamental representations $\pi _1,\ldots , \pi _{n-1}$ are removed by the choice $\xi _j = \prod _{k=1}^{j-1}\mu _k$. Henceforth we set $\mu _1= \cdots = \mu _{n-1} =1$ in the rest of the chapter without loss of generality.

3.3 Intertwiner for Cubic Coxeter Relation

The isomorphism of the two irreducible representations will be called the intertwiner.  By Schur’s lemma, it is unique up to the overall normalization. The transposition P in (3.23) is the intertwiner corresponding to the quadratic Coxeter relation.

Let us proceed to the cubic one. In view of the structure (3.21), it suffices to consider $A_q(A_2)$ and the equivalence $\pi _{121} \simeq \pi _{212}$ reflecting the Coxeter relation $s_1s_2s_1 = s_2s_1s_2$. Let

$$\begin{aligned} \Phi : \mathcal {F}_{q} \otimes \mathcal {F}_{q}\otimes \mathcal {F}_{q}\longrightarrow \mathcal {F}_{q} \otimes \mathcal {F}_{q}\otimes \mathcal {F}_{q} \end{aligned}$$

(3.27)

be the associated intertwiner. It is characterized by the relations:

$$\begin{aligned}&\Phi \circ \pi _{121}(\Delta (f)) = \pi _{212}(\Delta (f))\circ \Phi \quad (\forall f \in A_q(A_2)),\end{aligned}$$

(3.28)

$$\begin{aligned}&\Phi (|0\rangle \otimes |0\rangle \otimes |0\rangle ) =|0\rangle \otimes |0\rangle \otimes |0\rangle . \end{aligned}$$

(3.29)

The latter just fixes the normalization. The absence of terms other than $|0\rangle \otimes |0\rangle \otimes |0\rangle$ in its RHS is assured by the weight conservation. See (3.48), (3.47) and (3.30).

It is convenient to work with R defined by

$$\begin{aligned} R = \Phi P_{13} : \; \mathcal {F}_{q} \otimes \mathcal {F}_{q}\otimes \mathcal {F}_{q} \longrightarrow \mathcal {F}_{q} \otimes \mathcal {F}_{q}\otimes \mathcal {F}_{q}. \end{aligned}$$

(3.30)

Here $P_{13}$ is the interchanger of the first and the third components defined before (2.20). We also call R the intertwiner. It will be shown to satisfy the tetrahedron equations of type $RRRR = RRRR$ in Theorem 3.20 (and also $RLLL=LLLR$ in Theorem 3.21), therefore R is a 3D R in the sense of Sect. 2.1. From (3.28) and (3.29), R is characterized by

$$\begin{aligned}&R \circ \pi _{121}(\tilde{\Delta }(f)) = \pi _{212}(\Delta (f))\circ R \quad (\forall f \in A_q(A_2)), \end{aligned}$$

(3.31)

$$\begin{aligned}&R (|0\rangle \otimes |0\rangle \otimes |0\rangle ) =|0\rangle \otimes |0\rangle \otimes |0\rangle , \end{aligned}$$

(3.32)

where $\tilde{\Delta }(f) = P_{13}(\Delta (f))P_{13}$. From (3.6) we have

$$\begin{aligned} \Delta (t_{ij}) = \sum _{1 \le l_1,l_2 \le 3} t_{i l_1} \otimes t_{l_1l_2} \otimes t_{l_2 j}, \quad \tilde{\Delta }(t_{ij})&= \sum _{1 \le l_1,l_2 \le 3} t_{l_2 j} \otimes t_{l_1l_2} \otimes t_{i l_1}. \end{aligned}$$

(3.33)

According to (3.21), the image of the 9 generators $T=(t_{ij})_{1 \le i,j \le 3}$ by the fundamental representations reads as

$$\begin{aligned} \pi _1(T) = \begin{pmatrix} \mathrm{\mathbf{a}}^- &{}\mathrm{\mathbf{k}} &{} 0 \\ -q \mathrm{\mathbf{k}}\; &{} \mathrm{\mathbf{a}}^+ &{} 0\\ 0 &{} 0 &{} 1 \end{pmatrix}, \qquad \pi _2(T) = \begin{pmatrix}1 &{} 0 &{} 0 \\ 0 &{} \mathrm{\mathbf{a}}^- &{} \mathrm{\mathbf{k}} \\ 0 &{} -q \mathrm{\mathbf{k}} &{} \;\mathrm{\mathbf{a}}^+ \end{pmatrix}. \end{aligned}$$

(3.34)

From (3.33), $\pi _{121}(\Delta (T))$ is expressed as

$$\begin{aligned} \begin{pmatrix} \mathrm{\mathbf{a}}^- \otimes 1 \otimes \mathrm{\mathbf{a}}^- - q \mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{k}} &{}{\mathbf{k}}\otimes {\mathbf{a}}^- \otimes {\mathbf{a}}^+ + {\mathbf{a}}^- \otimes 1 \otimes {\mathbf{k}}&{} {\mathbf{k}}\otimes {\mathbf{k}}\otimes 1 \\ -q({\mathbf{a}}^+ \otimes {\mathbf{a}}^- \otimes {\mathbf{k}}+{\mathbf{k}}\otimes 1 \otimes {\mathbf{a}}^- )\;\; &{}\mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{a}}^+ - q \mathrm{\mathbf{k}} \otimes 1 \otimes \mathrm{\mathbf{k}}\;\; &{} {\mathbf{a}}^+ \otimes {\mathbf{k}}\otimes 1 \\ q^2 1 \otimes {\mathbf{k}}\otimes {\mathbf{k}}&{} -q 1 \otimes {\mathbf{k}}\otimes {\mathbf{a}}^+ &{} 1 \otimes \mathrm{\mathbf{a}}^+ \otimes 1 \end{pmatrix}. \end{aligned}$$

(3.35)

$\pi _{121}(\tilde{\Delta }(T))$ is given by reversing the order of the tensor product as

$$\begin{aligned} \begin{pmatrix} \mathrm{\mathbf{a}}^- \otimes 1 \otimes \mathrm{\mathbf{a}}^- - q \mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{k}} &{}\mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{k}} + \mathrm{\mathbf{k}} \otimes 1 \otimes \mathrm{\mathbf{a}}^- &{} 1 \otimes \mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{k}} \\ -q(\mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{a}}^+ + \mathrm{\mathbf{a}}^- \otimes 1 \otimes \mathrm{\mathbf{k}})\;\; &{}\mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{a}}^+ - q \mathrm{\mathbf{k}} \otimes 1 \otimes \mathrm{\mathbf{k}}\;\; &{} 1 \otimes \mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{a}}^+ \\ q^2\mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{k}} \otimes 1 &{} -q\mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{k}} \otimes 1 &{} 1 \otimes \mathrm{\mathbf{a}}^+ \otimes 1 \end{pmatrix}. \end{aligned}$$

(3.36)

$\pi _{212}(\Delta (T))$ takes the form

$$\begin{aligned} \begin{pmatrix} 1 \otimes \mathrm{\mathbf{a}}^- \otimes 1 &{} 1 \otimes \mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{a}}^- &{} 1 \otimes \mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{k}} \\ -q\mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{k}} \otimes 1 \; &{} \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{a}}^- - q \mathrm{\mathbf{k}} \otimes 1 \otimes \mathrm{\mathbf{k}} &{} \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{k}} + \mathrm{\mathbf{k}} \otimes 1 \otimes \mathrm{\mathbf{a}}^+ \\ q^2\mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{k}} \otimes 1 &{} -q(\mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{a}}^- + \mathrm{\mathbf{a}}^+ \otimes 1 \otimes \mathrm{\mathbf{k}})\;\;\; &{} \mathrm{\mathbf{a}}^+ \otimes 1 \otimes \mathrm{\mathbf{a}}^+ - q \mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{k}} \end{pmatrix}. \end{aligned}$$

(3.37)

Thus the intertwining relation (3.31) reads as

$$\begin{aligned} t_{11}\!:&\quad R(\mathrm{\mathbf{a}}^- \otimes 1 \otimes \mathrm{\mathbf{a}}^- - q \mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{k}}) = (1 \otimes \mathrm{\mathbf{a}}^- \otimes 1)R, \end{aligned}$$

(3.38)

$$\begin{aligned} t_{12}\!:&\quad R(\mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{k}} + \mathrm{\mathbf{k}} \otimes 1 \otimes \mathrm{\mathbf{a}}^-) = (1 \otimes \mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{a}}^-)R, \end{aligned}$$

(3.39)

$$\begin{aligned} t_{13}\!:&\quad R (1 \otimes \mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{k}}) = (1 \otimes \mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{k}})R, \end{aligned}$$

(3.40)

$$\begin{aligned} t_{21}\!:&\quad R(\mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{a}}^+ + \mathrm{\mathbf{a}}^- \otimes 1 \otimes \mathrm{\mathbf{k}}) = (\mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{k}} \otimes 1 )R, \end{aligned}$$

(3.41)

$$\begin{aligned} t_{22}\!:&\quad R(\mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{a}}^+ - q \mathrm{\mathbf{k}} \otimes 1 \otimes \mathrm{\mathbf{k}}) =( \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{a}}^- - q \mathrm{\mathbf{k}} \otimes 1 \otimes \mathrm{\mathbf{k}})R, \end{aligned}$$

(3.42)

$$\begin{aligned} t_{23}\!:&\quad R(1 \otimes \mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{a}}^+) = (\mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{k}} + \mathrm{\mathbf{k}} \otimes 1 \otimes \mathrm{\mathbf{a}}^+)R, \end{aligned}$$

(3.43)

$$\begin{aligned} t_{31}\!:&\quad R(\mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{k}} \otimes 1)=(\mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{k}} \otimes 1)R, \end{aligned}$$

(3.44)

$$\begin{aligned} t_{32}\!:&\quad R(\mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{k}} \otimes 1 ) = (\mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{a}}^- + \mathrm{\mathbf{a}}^+ \otimes 1 \otimes \mathrm{\mathbf{k}})R, \end{aligned}$$

(3.45)

$$\begin{aligned} t_{33}\!:&\quad R(1 \otimes \mathrm{\mathbf{a}}^+ \otimes 1) = (\mathrm{\mathbf{a}}^+ \otimes 1 \otimes \mathrm{\mathbf{a}}^+ - q \mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{k}})R, \end{aligned}$$

(3.46)

where the left column specifies the choice of f in (3.31).

The intertwiner R is regarded as a matrix $R = (R^{abc}_{ijk})$ acting on $\mathcal {F}_q^{\otimes 3}$ as

$$\begin{aligned} R(|i\rangle \otimes |j\rangle \otimes |k\rangle ) = \sum _{a,b,c} R^{a b c}_{i j k} |a\rangle \otimes |b\rangle \otimes |c\rangle . \end{aligned}$$

(3.47)

The normalization condition (3.29) becomes $R_{000}^{abc}=\delta _0^a\delta _0^b\delta _0^c$. The simplest equations (3.40) and (3.44) imply

$$\begin{aligned} R^{abc}_{ijk}=0 \;\; \text {unless}\;\, (a+b,b+c) = (i+j,j+k). \end{aligned}$$

(3.48)

This property will be referred to as the weight conservation.  It may also be rephrased as

$$\begin{aligned}{}[R, z^\mathrm{\mathbf{h}}\otimes z^\mathrm{\mathbf{h}}\otimes 1]= [R, 1 \otimes z^\mathrm{\mathbf{h}}\otimes z^\mathrm{\mathbf{h}}]=0, \end{aligned}$$

(3.49)

where $\mathrm{\mathbf{h}}$ is the number operator (3.14) and z is a non-zero parameter. The other equations lead to recursion relations of the matrix elements as follows:

$$\begin{aligned} t_{11}\!:\;&q^{i+k+1} (1\!-\!q^{2 j}) R^{a,b,c}_{i,j-1,k} +(1\!-\!q^{2 b+2}) R^{a,b+1,c}_{i,j,k}= (1\!-\!q^{2 i}) (1\!-\!q^{2 k})R^{a,b,c}_{i-1,j,k-1}, \end{aligned}$$

(3.50)

$$\begin{aligned} t_{12}\!:\;&q^k(1\!-\!q^{2 j}) R^{a,b,c}_{i+1,j-1,k} +q^i (1\!-\!q^{2 k}) R^{a,b,c}_{i,j,k-1} =q^b (1\!-\!q^{2 c+2})R^{a,b,c+1}_{i,j,k}, \end{aligned}$$

(3.51)

$$\begin{aligned} t_{21}\!:\;&q^{i} (1\!-\!q^{2 j})R^{a,b,c}_{i,j-1,k+1} +q^{k}(1\!-\!q^{2 i}) R^{a,b,c}_{i-1,j,k} =q^{b}(1\!-\!q^{2a+2}) R^{a+1,b,c}_{i,j,k}, \end{aligned}$$

(3.52)

$$\begin{aligned} t_{22}\!:\;&q (q^{a+c}\!-\!q^{i+k}) R^{a,b,c}_{i,j,k} +(1\!-\!q^{2j}) R^{a,b,c}_{i+1,j-1,k+1} =(1\!-\!q^{2 a+2}) (1\!-\!q^{2 c+2}) R^{a+1,b-1,c+1}_{i,j,k}, \end{aligned}$$

(3.53)

$$\begin{aligned} t_{23}\!:\;&q^j R^{a,b,c}_{i,j,k+1}-q^aR^{a,b,c-1}_{i,j,k} -q^c (1\!-\!q^{2a+2}) R^{a+1,b-1,c}_{i,j,k}=0, \end{aligned}$$

(3.54)

$$\begin{aligned} t_{32}\!:\;&q^{c}R^{a-1,b,c}_{i,j,k} -q^{j} R^{a,b,c}_{i+1,j,k} +q^{a}(1-q^{2 c+2})R^{a,b-1,c+1}_{i,j,k}=0, \end{aligned}$$

(3.55)

$$\begin{aligned} t_{33}\!:\;&q^{a+c+1} R^{a,b-1,c}_{i,j,k}-R^{a-1,b,c-1}_{i,j,k}+R^{a,b,c}_{i,j+1,k}=0. \end{aligned}$$

(3.56)

The relations (3.54), (3.55) and (3.56) can be used to reduce k, i and j, respectively. Consequently, an arbitrary $R^{abc}_{ijk}$ satisfying (3.48) is attributed to $R^{000}_{000}=1$. Thus R is determined only by these relations. Since the intertwiner exists, compatibility of the reduction procedure and validity of the other relations is guaranteed. The resulting explicit formula will be presented in (3.67).

Lemma 3.5

Set $X_{ij}= (-q)^{i-j} (S(t_{4-j,4-i})|_{q\rightarrow q^{-1}} )'\in A_q(A_2)\, (1 \le i, j \le 3)$, where S is the antipode (3.7) and the prime reverses the order of product of generators. Explicitly we have

$$\begin{aligned} X_{11}&= t_{22}t_{11} - q^{-1}t_{21}t_{12},&\quad X_{12}&= q^{-2}(t_{31}t_{12} - q t_{32}t_{11}), \\ X_{13}&= q^{-3}(-t_{31}t_{22} + q t_{32}t_{21}),&\quad X_{21}&= t_{21}t_{13}-qt_{23}t_{11}, \\ X_{22}&= t_{33}t_{11} - q^{-1}t_{31}t_{13},&\quad X_{23}&= q^{-2}(t_{31}t_{23}-qt_{33}t_{21}), \\ X_{31}&= q(-t_{22}t_{13}+qt_{23}t_{12}),&\quad X_{32}&= t_{32}t_{13}-qt_{33}t_{12}, \\ X_{33}&= t_{33}t_{22}-q^{-1}t_{32}t_{23}. \end{aligned}$$

Then the following relations are valid:

$$\begin{aligned} \pi _{212}(\Delta (X_{ij})) = \pi _{121}(\tilde{\Delta }(t_{ij})), \quad \pi _{212}(\tilde{\Delta }(X_{ij})) = \pi _{121}(\Delta (t_{ij})). \end{aligned}$$

(3.57)

Proof

The two relations are equivalent by the conjugation by $P_{13}$. Let us illustrate a direct check of $\pi _{212}(\Delta (X_{23}) = \pi _{121}(\tilde{\Delta }(t_{23}))$. The LHS is $q^{-2}\pi _{212}(\Delta (t_{31}t_{23}-qt_{33}t_{21}))$. Substituting (3.36) and (3.37), we find that the relation to be shown is given by

$$\begin{aligned}&(\mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{k}} \otimes 1) ( \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{a}}^+ \otimes \mathrm{\mathbf{k}} +\mathrm{\mathbf{k}} \otimes 1 \otimes \mathrm{\mathbf{a}}^+ ) \\&+ (\mathrm{\mathbf{a}}^+ \otimes 1 \otimes \mathrm{\mathbf{a}}^+ - q \mathrm{\mathbf{k}}\otimes \mathrm{\mathbf{a}}^+\otimes \mathrm{\mathbf{k}}) (\mathrm{\mathbf{a}}^-\otimes \mathrm{\mathbf{k}} \otimes 1) = 1 \otimes \mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{a}}^+. \end{aligned}$$

To check this by (3.12) is straightforward. The other cases are similar. $\square$

By definition, the transpose ${}^tY$ of an operator $Y \in \mathrm {End}(\mathcal {F}_q)$ is specified by ${}^tY |m\rangle = \sum _{m'} c^{m}_{m'}|m'\rangle$ for $Y|m\rangle = \sum _{m'} c^{m'}_m|m'\rangle$. Similar notations will be used also for operators on the tensor product of Fock spaces.

Set

$$\begin{aligned} \mathcal {D}_A = D_q\otimes D_q\otimes D_q, \end{aligned}$$

(3.58)

where $D_q$ is defined by (3.15).

Lemma 3.6

The transposed representations are related to the original ones as

$$\begin{aligned} {}^t(\pi _{212}(\Delta (t_{ij})))&= \mathcal {D}_A \pi _{121} (\tilde{\Delta }(t_{j' i'})) \mathcal {D}_A^{-1}, \\ {}^t(\pi _{121}(\tilde{\Delta } (t_{ij})))&= \mathcal {D}_A \pi _{212}(\Delta (t_{j' i'})) \mathcal {D}_A^{-1} \end{aligned}$$

for $i,j \in \{1,2,3\}$, where $i' = 4-i$.

Proof

The two relations are equivalent. See (3.33). From (3.13) and (3.15), we see ${}^t(\mathrm{\mathbf{a}}^{\pm }) = D_q \mathrm{\mathbf{a}}^{\mp } D_q^{-1}$ and ${}^t\mathrm{\mathbf{k}} = D_q \mathrm{\mathbf{k}} D_q^{-1}$. They lead to

$$\begin{aligned} {}^t\pi _1(t_{ij}) = D_q \pi _2(t_{j' i'}) D_q^{-1},\quad {}^t\pi _2(t_{ij}) = D_q \pi _1(t_{j' i'}) D_q^{-1} \end{aligned}$$

for the fundamental representations (3.34). The assertion is a corollary of this property. $\square$

Proposition 3.7

The intertwiner R has the following properties concerning the conjugation by $P_{13}$, the inverse $R^{-1}$ and the transpose ${}^tR$:

$$\begin{aligned}&R = P_{13}RP_{13}, \end{aligned}$$

(3.59)

$$\begin{aligned}&R^{-1} = R, \end{aligned}$$

(3.60)

$$\begin{aligned}&{}^t\!R = \mathcal {D}_A R \mathcal {D}_A^{-1}. \end{aligned}$$

(3.61)

Proof

These properties are proved by invoking the uniqueness of the intertwiner satisfying (3.31) and (3.32). To show (3.59), it suffices to recognize that the set of relations (3.38)–(3.46) are invariant under the conjugation by $P_{13}$.

Next we show (3.60). Comparison of the two choices $f=t_{ij}$ and $f= X_{ij}$ in (3.31) using Lemma 3.5 shows that R and $R^{-1}$ satisfy the same set of intertwining relations. The normalization condition (3.32) is also invariant under the exchange $R \leftrightarrow R^{-1}$, hence (3.60) follows.

Finally, we show (3.61). Take the transpose of (3.31). From Lemma 3.6 we find that $\mathcal {D}_A^{-1}{}^tR\mathcal {D}_A$ again satisfies (3.31). The normalization condition (3.32) is also invariant under the exchange $R \leftrightarrow \mathcal {D}_A^{-1}{}^t\!R\mathcal {D}_A$, hence (3.61) follows. $\square$

In terms of the matrix elements, the properties (3.59) and (3.61) are rephrased as

$$\begin{aligned} R^{abc}_{ijk}&= R^{cba}_{kji}, \end{aligned}$$

(3.62)

$$\begin{aligned} R^{abc}_{ijk}&= \frac{(q^2)_i(q^2)_j(q^2)_k}{(q^2)_a(q^2)_b(q^2)_c}R^{ijk}_{abc}. \end{aligned}$$

(3.63)

Remark 3.8

One may introduce another parameter $\nu$ by replacing the latter two formulas in (3.13) by $\mathrm{\mathbf{a}}^+|m\rangle = \nu |m+1\rangle$, $\mathrm{\mathbf{a}}^-|m\rangle = \nu ^{-1}(1-q^{2m})|m-1\rangle$ keeping (3.12) invariant. It corresponds to changing the normalization of $|m \rangle$ depending on m. The resulting 3D R is $(1 \otimes \nu ^\mathrm{\mathbf{h}} \otimes 1) R (1 \otimes \nu ^{-\mathrm{\mathbf{h}}} \otimes 1)$.

Remark 3.9

If one switches from $\mathbf{k}$ to $\hat{\mathbf{k}}:= q^{1/2}{} \mathbf{k}$ including the zero point energy of the q-oscillator (see (3.13)), all the “non-autonomous” q’s in (3.38)–(3.46) disappear.  It opens an avenue toward another class of 3D R associated with the so-called modular double of q and $\tilde{q}$-oscillators. This topic is not covered in this book. See [97]. The same feature will be observed for the 3D K in Remark 5.5.

Remark 3.10

From (3.16), (3.47) and (3.63), the 3D R acts on the dual Fock space as

$$\begin{aligned} (\langle i | \otimes \langle j| \otimes \langle k | ) R = \sum _{a,b,c} R^{abc}_{ijk}\langle a| \otimes \langle b| \otimes \langle c|. \end{aligned}$$

(3.64)

3.4 Explicit Formula for 3D R

In this section we present explicit formulas of the matrix elements $R^{abc}_{ijk}$ (3.47) of the intertwiner R characterized by (3.31) and (3.32).

We assume that q is generic and use the notation

$$\begin{aligned} \begin{aligned}&(z;q)_m = \prod _{j=1}^m(1-zq^{j-1}),\quad (q)_m=(q;q)_m, \\&\left\{ r_1,\ldots , r_m \atop s_1,\ldots , s_n\right\} _{\!q} = {\left\{ \begin{array}{ll} \frac{\prod _{i=1}^m(q)_{r_i}}{\prod _{i=1}^n(q)_{s_i}} &{} \forall r_i, s_i \in {\mathbb Z}_{\ge 0}, \\ 0 &{} \text {otherwise}, \end{array}\right. } \\&\left( {\begin{array}{c}m\\ n\end{array}}\right) _q = \left( {\begin{array}{c}m\\ m-n\end{array}}\right) _q = \left\{ m \atop n, m-n\right\} _{\!q}. \end{aligned} \end{aligned}$$

(3.65)

Unless stated otherwise, the abbreviation $(q)_m=(q;q)_m$ will be used also for $(q^k)_m$ with $k \in {\mathbb Z}$. Thus $(q^2)_m$ for instance means $(q^2; q^2)_m$. The two-storied symbol in the second line will be used without assuming a “well-poisedness” constraint $\sum _{i=1}^m r_i = \sum _{i=1}^ns_i$. The non-vanishing condition $\forall r_i, s_i \in {\mathbb Z}_{\ge 0}$ is quite important and will impose non-trivial constraints on the summation variables in what follows. The special case $\left\{ j_1+\cdots + j_n \atop j_1,\ldots , j_n\right\} _{\!q}$ is a q-multinomial coefficient belonging to ${\mathbb Z}_{\ge 0}[q]$. In particular the $n=2$ case in the third line is called the q-binomial. 

The Kronecker delta will be written either as $\delta _{ab}$ or $\delta ^a_b$.  We will also use the notation

$$\begin{aligned} (x)_+ = \max (x,0) = x-\min (x,0)\qquad (x \in \mathbb {R}). \end{aligned}$$

(3.66)

Theorem 3.11

$$\begin{aligned} R^{abc}_{ijk}&=\delta _{i+j}^{a+b}\delta _{j+k}^{b+c} \sum _{\lambda +\mu =b}(-1)^\lambda q^{i(c-j)+(k+1)\lambda +\mu (\mu -k)} \frac{(q^2)_{c+\mu }}{(q^2)_c}\left( {\begin{array}{c}i\\ \mu \end{array}}\right) _{q^2}\left( {\begin{array}{c}j\\ \lambda \end{array}}\right) _{q^2}, \end{aligned}$$

(3.67)

where the sum is over $\lambda , \mu \in \mathbb {Z}_{\ge 0}$ such that $\lambda + \mu = b$. (Thus (3.67) is actually a single sum over $(b-i)_+ \le \lambda \le \min (b,j)$ or $(b-j)_+ \le \mu \le \min (b,i)$.)

Proof

The prefactor $\delta _{i+j}^{a+b}\delta _{j+k}^{b+c}$ represents the weight conservation (3.48). The recursion relations (3.55) and (3.56) can be iterated m times to reduce i and j indices as

$$\begin{aligned} R^{abc}_{ijk} = \delta ^{a+b}_{i+j}\delta ^{b+c}_{j+k}\sum _{r=0}^m q^{(m-r)(c-j)+r(a-j-m+r)} \frac{(q^2)_{c+r}}{(q^2)_c}\left( {\begin{array}{c}m\\ r\end{array}}\right) _{q^2} R^{a-m+r,b-r,c+r}_{i-m,j,k},\\ R^{abc}_{ijk} = \delta ^{a+b}_{i+j}\delta ^{b+c}_{j+k}\sum _{r=0}^m(-1)^r q^{r(a+c-2m+2r+1)} \left( {\begin{array}{c}m\\ r\end{array}}\right) _{q^2} R^{a-m+r,b-r,c-m+r}_{i,j-m,k}. \end{aligned}$$

By combining them, general elements are reduced to $R^{00k}_{00k}$. The relation (3.54) shows that $R^{00k}_{00k}=R^{000}_{000}=1$. The result of these reductions is given by (3.67). $\square$

Example 3.12

The following is the list of all the non-zero $R^{abc}_{314}$.

$$\begin{aligned} R^{041}_{314}&= -q^2 (1 - q^4) (1 - q^6) (1 - q^8), \\ R^{132}_{314}&=(1 - q^6) (1 - q^8)(1 - q^4 - q^6 - q^8 - q^{10}),\\ R^{223}_{314}&= q^2 (1 + q^2) (1 + q^4) (1 - q^6) (1 - q^6 - q^{10}), \\ R^{314}_{314}&=q^6(1 + q^2 + q^4 - q^8 - q^{10} - q^{12} - q^{14}),\\ R^{405}_{314}&=q^{12}. \end{aligned}$$

Remark 3.13

From (3.67) we have

$$\begin{aligned} \begin{aligned}&(-1)^b R^{abc}_{ijk}|_{q\rightarrow q^{-1}} \\&=\delta _{i+j}^{a+b}\delta _{j+k}^{b+c} \sum _{\lambda +\mu =b} q^{i(j-c)-(k+1)b+2\lambda (\lambda -j)-2\mu a} \frac{(q^2)_{c+\mu }}{(q^2)_c}\left( {\begin{array}{c}i\\ \mu \end{array}}\right) _{q^2}\left( {\begin{array}{c}j\\ \lambda \end{array}}\right) _{q^2}. \end{aligned} \end{aligned}$$

(3.68)

From $(q^2)_{c+\mu }/(q^2)_c = (q^{2c+2};q^2)_\mu$, it follows that $(-1)^b R^{abc}_{ijk} \ge 0$ in the regime $q>1$.

Remark 3.14

Set $R(x,y) = (1 \otimes x^\mathrm{\mathbf{h}} \otimes 1) R(1 \otimes y^{-\mathrm{\mathbf{h}} }\otimes 1)$, where x, y are non-zero parameters and $\mathrm{\mathbf{h}}$ is defined by (3.14). Thanks to the weight conservation (3.49), R(x, y) also satisfies the tetrahedron equation $R_{124}(x,y)R_{135}(x,y)R_{236}(x,y)R_{456}(x,y) = R_{456}(x,y)R_{236}(x,y)R_{135}(x,y)R_{124}(x,y)$. In particular, $R(-1,1)$ has the elements $(-1)^bR^{abc}_{ijk}$. Thus Remark 3.13 shows that $R(-1,1)$ is a 3D R whose elements are all non-negative for $q \ge 1$.

Example 3.15

$$\begin{aligned} R^{a 0 c}_{i j k}&=q^{ik}\delta ^{a}_{i+j}\delta ^c_{j+k},\quad&R^{a b c}_{i 0 k}&= q^{ac} \frac{(q^2)_i(q^2)_k}{(q^2)_a(q^2)_b(q^2)_c} \delta ^{a+b}_{i}\delta ^{b+c}_{k}, \\ R^{a b c}_{0 j k}&=(-1)^bq^{b(k+1)}\left( {\begin{array}{c}j\\ b\end{array}}\right) _{\!\!\!q^2} \delta ^{a+b}_{j}\delta ^{b+c}_{j+k}, \quad&R^{0 b c}_{i j k}&= (-1)^jq^{j(c+1)}\frac{(q^2)_k}{(q^2)_c} \delta ^{b}_{i+j}\delta ^{b+c}_{j+k}, \\ \quad R^{1 1 k}_{1 1 k}&=1\!-\!(1\!+\!q^2)q^{2k}. \end{aligned}$$

It is an easy exercise to deduce a formula for the operator $R^{ab}_{ij} \in \mathrm {End}(\mathcal {F}_q)$ in the general scheme (2.4) by comparing it with (2.2) and using Theorem 3.11. The result reads as⁵

$$\begin{aligned} R^{ab}_{ij} = \delta ^{a+b}_{i+j}\sum _{\lambda +\mu =b}(-1)^\lambda q^{\lambda +\mu ^2-ib} \left( {\begin{array}{c}i\\ \mu \end{array}}\right) _{q^2}\left( {\begin{array}{c}j\\ \lambda \end{array}}\right) _{q^2} ({\mathbf{a}}^- )^\mu ({\mathbf{a}}^+ )^{j-\lambda } {\mathbf{k}}^{i+\lambda -\mu }, \end{aligned}$$

(3.69)

where the sum extends over $\lambda , \mu \in {\mathbb Z}_{\ge 0}$ such that $\lambda +\mu = b$. As a consequence of the weight conservation (3.49), $R^{ab}_{ij}$ is homogeneous in the sense that

$$\begin{aligned} z^\mathbf{h}R^{ab}_{ij} = R^{ab}_{ij}z^{\mathbf{h}+ j-b}. \end{aligned}$$

(3.70)

Example 3.16

$$\begin{aligned} \begin{pmatrix} R_{0 0}^{0 0} &{} R_{0 1}^{0 0} &{} R_{1 0}^{0 0} &{} R_{1 1}^{0 0} \\ \overset{\phantom {-}}{R_{0 0}^{0 1}} &{} R_{0 1}^{0 1} &{} R_{1 0}^{0 1} &{} R_{1 1}^{0 1} \\ \overset{\phantom {-}}{R_{0 0}^{1 0}} &{} R_{0 1}^{1 0} &{} R_{1 0}^{1 0} &{} R_{1 1}^{1 0} \\ \overset{\phantom {-}}{R_{0 0}^{1 1} }&{} R_{0 1}^{1 1} &{} R_{1 0}^{1 1} &{} R_{1 1}^{1 1} \end{pmatrix} = \begin{pmatrix} 1 &{} 0 &{} 0 &{} 0 \\ \overset{\phantom {-}}{0} &{}\; -q{\mathbf{k}}\;\;&{} \,{\mathbf{a}}^- \;&{} 0\\ \overset{\phantom {-}}{0} &{} \,{\mathbf{a}}^+ &{}{\mathbf{k}}\;&{} 0\\ \overset{\phantom {-}}{0} &{} 0 &{} 0 &{} {\mathbf{a}}^- {\mathbf{a}}^+ -{\mathbf{k}}^2 \end{pmatrix}. \end{aligned}$$

(3.71)

Except for the bottom right element, this coincides with the corresponding matrix from of the 3D L in (11.14)$|_{\alpha =1}$. Its consequence will be mentioned in Example 13.1.

$$\begin{aligned} \begin{pmatrix} R^{02}_{02} &{} R^{02}_{11} &{} R^{02}_{20}\\ \overset{\phantom {-}}{R^{11}_{02}} &{} R^{11}_{11} &{} R^{11}_{20}\\ \overset{\phantom {-}}{R^{20}_{02}} &{} R^{20}_{11} &{} R^{20}_{20} \end{pmatrix}&= \begin{pmatrix} q^2{\mathbf{k}}^2 &{} -{\mathbf{a}}^- {\mathbf{k}}&{} \;({\mathbf{a}}^- )^2 \\ -q(1+q^2)\overset{\phantom {-}}{{\mathbf{a}}^+ } {\mathbf{k}}&{} \;\;{\mathbf{a}}^- {\mathbf{a}}^+ -{\mathbf{k}}^2 &{} \;q^{-1}(1+q^2) {\mathbf{a}}^- {\mathbf{k}}\\ ({\mathbf{a}}^+ )^2 &{} \overset{\phantom {-}}{{\mathbf{a}}^+ } {\mathbf{k}}&{} {\mathbf{k}}^2 \end{pmatrix}. \end{aligned}$$

(3.72)

Reversing the order of the columns of this matrix coincides with the central three-by-three block in (8.8) up to coefficients.

Example 3.17

The following formulas will be used in Example 13.1:

$$\begin{aligned} R^{m,0}_{m,0}&= {\mathbf{k}}^m, \qquad R^{m,1}_{m+1,0} = q^{-m} \left( {\begin{array}{c}m+1\\ 1\end{array}}\right) _{q^2}{\mathbf{a}}^- {\mathbf{k}}^m, \\ R^{m+1,0}_{m,1}&= {\mathbf{a}}^+ {\mathbf{k}}^m, \quad R^{m,1}_{m,1} = q^{1-m}\Bigl ( \left( {\begin{array}{c}m\\ 1\end{array}}\right) _{q^2}{\mathbf{a}}^- {\mathbf{a}}^+ -{\mathbf{k}}^2\Bigr ) {\mathbf{k}}^{m-1}. \end{aligned}$$

Let us present another formula in terms of the q-hypergeometric function [50]: 

$$\begin{aligned} {}_2\phi _1\left( {\alpha , \beta \atop \gamma }; q, w\right) = \sum _{n \ge 0} \frac{(\alpha ;q)_n(\beta ;q)_n }{(\gamma ;q)_n(q;q)_n}w^n. \end{aligned}$$

(3.73)

Theorem 3.18

$$\begin{aligned} R^{abc}_{ijk}&= \delta ^{a+b}_{i+j}\delta ^{b+c}_{j+k}\; \frac{q^{(a-j)(c-j)}}{(q^2)_b}P_b(q^{2i},q^{2j},q^{2k}), \end{aligned}$$

(3.74)

$$\begin{aligned} P_b(x,y,z)&= (q^{2-2b}z;q^2)_b\, {}_2\phi _1\left( {q^{-2b},q^{2-2b}yz \atop q^{2-2b}z}; q^2,q^2x\right) , \end{aligned}$$

(3.75)

$$\begin{aligned} P_b(x,y,z)&= q^{-b(b-1)}(q^2)_b \oint \frac{du}{2\pi {\mathrm i}u^{b+1}} \frac{(-q^{2-2b}xyzu;q^2)_\infty (-u;q^2)_\infty }{(-xu;q^2)_\infty (-zu;q^2)_\infty }, \end{aligned}$$

(3.76)

where the integral encircles $u=0$ anti-clockwise picking up the residue.

Proof

From (3.39) and $R=R^{-1}$ we have $R(1 \otimes \mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{a}}^-) = (\mathrm{\mathbf{k}} \otimes 1 \otimes \mathrm{\mathbf{a}}^- + \mathrm{\mathbf{a}}^+\otimes \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{k}})R$. In terms of matrix elements it reads as

$$\begin{aligned}&q^j (1\!-\!q^{2 k})R^{a,b,c}_{i,j,k-1} = q^a (1\!-\!q^{2 c+2})R^{a,b,c+1}_{i,j,k} + q^c(1\!-\!q^{2 b+2})R^{a-1,b+1,c}_{i,j,k}. \end{aligned}$$

(3.77)

Substituting (3.74) into (3.77) and (3.50), we get the recursion relations

$$\begin{aligned}&(1-z)P_b(x,y,q^{-2}z)=q^{-2b}x(1-q^{-2b}yz)P_b(x,y,z) +P_{b+1}(x,y,z), \end{aligned}$$

(3.78)

$$\begin{aligned}&q^{-2b}xz(1-y)P_b(x,q^{-2}y,z) +P_{b+1}(x,y,z)= (1-x)(1-z)P_b(q^{-2}x,y,q^{-2}z). \end{aligned}$$

(3.79)

The initial condition should be set as $P_0(x,y,z)=1$ since $R^{a0c}_{ijk} = \delta ^{a}_{i+j}\delta ^c_{j+k}q^{ik}$ from (3.67). Obviously, both formulas (3.75) and (3.76) satisfy the initial condition. The remaining task is to show that they satisfy either one of the above recursion relations. It is straightforward to check that (3.75) satisfies (3.78) by comparing coefficients of the powers of x. To show (3.76), substitute it into (3.79) and replace u by $q^2u$ in the RHS. Then the relation to be shown becomes

$$\begin{aligned}&\oint \frac{du(-q^{-2b}xyzu;q^2)_\infty (-q^2u;q^2)_\infty }{u^{b+2}(-xu;q^2)_\infty (-zu;q^2)_\infty }X =0, \\&X= xz(1-y)u(1+u)-(1-x)(1-z)u+(1-q^{2b+2})(1+u). \end{aligned}$$

By setting $f(u) =(-q^{-2-2b}xyzu;q^2)_\infty (-u;q^2)_\infty /((-xu;q^2)_\infty (-zu;q^2)_\infty )$, this is identified with the identity $\oint \frac{du}{u^{b+2}}(f(q^2u)-q^{2b+2}f(u))=0$. $\square$

Note that (3.75) is a terminating series due to the entry $q^{-2b}$. In fact, $P_b(x,y,z)$ is a polynomial belonging to $q^{-2b(b-1)}\mathbb {Z}[q^2,x,y,z]$ with the symmetry $P_b(x,y,z) = P_b(z,y,x)$ reflecting (3.59).

Example 3.19

$$\begin{aligned}&P_0(x,y,z) =1, \quad P_1(x,y,z) = 1-x-z+x y z, \\&q^4P_2(x,y,z) = x^2 y^2 z^2 - (1 + q^2) x y z (-1 + x + z) \\&\qquad \qquad \qquad + q^2 (q^2 - x - q^2 x + x^2 - z - q^2 z + x z + q^2 x z + z^2), \\&R^{405}_{314} = q^{12}P_0(q^6,q^2,q^8), \; R^{314}_{314} = \frac{q^6P_1(q^6,q^2,q^8) }{1-q^2}, \; R^{223}_{314} = \frac{q^2P_2(q^6,q^2,q^8)}{(1-q^2)(1-q^4)}. \end{aligned}$$

This agrees with Example 3.12.

The formula (3.76) is also presented in terms of the generating series:

$$\begin{aligned} \sum _{b \ge 0} \frac{q^{b(b-1)}u^b}{(q^2)_b} P_b(x,q^{2b-2}y,z) = \frac{(-xyzu;q^2)_\infty (-u;q^2)_\infty }{(-xu;q^2)_\infty (-zu;q^2)_\infty }. \end{aligned}$$

(3.80)

Due to (3.76), matrix elements of the 3D R are expressed as

$$\begin{aligned} R^{abc}_{ijk} = \delta ^{a+b}_{i+j}\delta ^{b+c}_{j+k}\,q^{ik+b} \oint \frac{du}{2\pi {\mathrm i}u^{b+1}} \frac{(-q^{2+a+c}u;q^2)_\infty (-q^{-i-k}u;q^2)_\infty }{(-q^{a-c}u;q^2)_\infty (-q^{c-a}u;q^2)_\infty }. \end{aligned}$$

(3.81)

Note that the ratio of the four infinite products equals $(-q^{-i-k}u;q^2)_i/(-q^{c-a}u;q^2)_{a+1}$ because of $a-c=i-k$. By means of the identity

$$\begin{aligned} \frac{(zx;p)_\infty }{(z;p)_\infty } = \sum _{k \ge 0}\frac{(x;p)_k}{(p;p)_k}z^k, \end{aligned}$$

(3.82)

it is expanded as

$$\begin{aligned} \left( \sum _{\lambda \ge 0} \left( {\begin{array}{c}\lambda +a\\ \lambda \end{array}}\right) _{q^2} (-u)^\lambda q^{\lambda (c-a)}\right) \left( \sum _{0 \le \mu \le i}\left( {\begin{array}{c}i\\ \mu \end{array}}\right) _{q^2}q^{\mu (\mu -i-k-1)}u^\mu \right) . \end{aligned}$$

(3.83)

Collecting the coefficients of $u^b$, one gets

$$\begin{aligned} R^{abc}_{ijk} = \delta ^{a+b}_{i+j}\delta ^{b+c}_{j+k} \sum _{\lambda +\mu =b}(-1)^\lambda q^{ik+b+\lambda (c-a)+\mu (\mu -i-k-1)} \left( {\begin{array}{c}\lambda +a\\ a\end{array}}\right) _{q^2}\left( {\begin{array}{c}i\\ \mu \end{array}}\right) _{q^2} \end{aligned}$$

(3.84)

summed over $\lambda , \mu \in \mathbb {Z}_{\ge 0}$ under the constraint $\lambda +\mu =b$. Thus it is actually the single sum over $(b-i)_+ \le \lambda \le b$ or $0 \le \mu \le \min (b,i)$.

Both formulas (3.67) and (3.84) show that $R^{abc}_{ijk}$ is a Laurent polynomial of q with integer coefficients. On the other hand, Example 3.12 suggests that it is actually a polynomial in q. In Lemma 3.29, a stronger claim identifying the constant term of the polynomial will be presented which will lead to further aspects.

One can express (3.84) in terms of the terminating q-hypergeometric as

$$\begin{aligned} R^{abc}_{ijk}&= \delta ^{a+b}_{i+j}\delta ^{b+c}_{j+k}\; (-1)^b q^{ik + b(k-i+1)}\left( {\begin{array}{c}a+b\\ a\end{array}}\right) _{q^2} {}_2\phi _1\left( {q^{-2b},q^{-2i} \atop q^{-2a-2b}}; q^2,q^{-2c}\right) , \end{aligned}$$

(3.85)

which is a different formula from (3.74)–(3.75). It manifests the symmetry

$$\begin{aligned} R^{abc}_{ijk} = (-q)^{b-i}\frac{(q^2)_i(q^2)_j}{(q^2)_a(q^2)_b}R^{jic}_{bak} = (-q)^{b-i}\frac{(q^2)_k}{(q^2)_c}R^{bak}_{jic}, \end{aligned}$$

(3.86)

where the second equality is due to (3.63). In Chap. 13 we will use

$$\begin{aligned} \begin{aligned} R^{abc}_{ijk}&= \delta ^{a+b}_{i+j}\delta ^{b+c}_{j+k}(-1)^jq^{(1-a)j+(a+j)c} \frac{(q^2)_k}{(q^2)_c} \\&\times \sum _{0 \le \mu \le \min (a,j)}(-1)^\mu q^{\mu (\mu -2c-1)} \left( {\begin{array}{c}a+b-\mu \\ b\end{array}}\right) _{q^2}\left( {\begin{array}{c}j\\ \mu \end{array}}\right) _{q^2}, \end{aligned} \end{aligned}$$

(3.87)

which is derived from (3.84) by applying the latter transformation in (3.86).

3.5 Solution to the Tetrahedron Equations

Recall that we have characterized R as the intertwiner of $A_q(A_2)$ modules in (3.31) and (3.32). Various explicit formulas for it are presented in the previous section. Now we proceed to the proof of the tetrahedron equations.

3.5.1 $RRRR=RRRR$ Type

Theorem 3.20

The intertwiner R satisfies the tetrahedron equation of $RRRR=RRRR$ type in (2.6).

Proof

Consider $A_q(A_3)$ and let $\pi _1, \pi _2, \pi _3$ be the fundamental representations given in (3.21). The Weyl group $W(A_3)$ is generated by simple reflections $s_1, s_2, s_3$ with the relations

$$\begin{aligned} s_i^2=1, \quad s_1s_3=s_3s_1, \quad s_1s_2s_1 = s_2s_1s_2,\quad s_2s_3s_2 = s_3s_2s_3. \end{aligned}$$

(3.88)

According to Theorem 3.3, the equivalence of the tensor product representations $\pi _{13} \simeq \pi _{31}$, $\pi _{121} \simeq \pi _{212}$ and $\pi _{232} \simeq \pi _{323}$ are valid. ($\pi _{i_1,\ldots , i_k}$ is a shorthand for $\pi _{i_1} \otimes \cdots \otimes \pi _{i_k}$ as mentioned after Theorem 3.3.) By Remark 3.4, the intertwiner for $\pi _{13} \simeq \pi _{31}$ is just the transposition of the components. Let $\Phi ^{(1)}$ and $\Phi ^{(2)}$ be the intertwiners for the latter two, i.e.

$$\begin{aligned} \begin{aligned}&\Phi ^{(1)}\circ \pi _{121}(\Delta (f)) = \pi _{212}(\Delta (f))\circ \Phi ^{(1)}, \\&\Phi ^{(2)}\circ \pi _{232}(\Delta (f)) =\pi _{323}(\Delta (f))\circ \Phi ^{(2)} \end{aligned} \end{aligned}$$

(3.89)

for any $f \in A_q(A_3)$. By inspection of (3.21), they are both given by the same $\Phi$ as the $A_q(A_2)$ case characterized in (3.27)–(3.29). Therefore from (3.30) we get

$$\begin{aligned} \Phi ^{(1)} = RP_{13},\quad \Phi ^{(2)} = RP_{13}, \end{aligned}$$

(3.90)

which means that they are the copies of the same operator acting on the respective spaces.

Let $w_0 \in W(A_3)$ be the longest element.  We pick two reduced expressions, say,

$$\begin{aligned} w_0 = s_1s_2s_1s_3s_2s_1 = s_3s_2s_1s_3s_2s_3, \end{aligned}$$

(3.91)

where the two sides are interchanged by replacing $s_i$ by $s_{4-i}$ and reversing the order. According to Theorem 3.3, we have the equivalence of the two irreducible representations of $A_q(A_3)$:

$$\begin{aligned} \pi _{121321} \simeq \pi _{321323}. \end{aligned}$$

(3.92)

Let $P_{ij}$ and $\Phi ^{(1)}_{ijk}, \Phi ^{(2)}_{ijk}$ be the transposition P (3.23) and the intertwiners $\Phi ^{(1)}, \Phi ^{(2)}$ that act on the tensor components specified by the indices. These components must be adjacent (i.e. $j-i=k-j=1$) to make the relations (3.25) and (3.89) work. With this guideline, one can construct the intertwiners for (3.92) by following the transformation of the reduced expressions by the Coxeter relations (3.88). There are two ways to achieve this. In terms of the indices, they look as follows:

$$\begin{aligned} \underline{121}321\quad&\Phi ^{(1)}_{123} \qquad \qquad&12\underline{13}21\quad&P_{34} \nonumber \\ 21\underline{232}1 \quad&\Phi ^{(2)}_{345} \qquad \qquad&123\underline{121}\quad&\Phi ^{(1)}_{456} \nonumber \\ 2\underline{13}2\underline{31} \quad&P_{23}P_{56} \qquad \qquad&1\underline{232}12\quad&\Phi ^{(2)}_{234} \nonumber \\ 23\underline{121}3 \quad&\Phi ^{(1)}_{345} \qquad \qquad&\underline{13}2\underline{31}2\quad&P_{12}P_{45} \nonumber \\ \underline{232} 123\quad&\Phi ^{(2)}_{123} \qquad \qquad&3\underline{121}32\quad&\Phi ^{(1)}_{234} \nonumber \\ 32\underline{31}23 \quad&P_{34} \qquad \qquad&321\underline{232} \quad&\Phi ^{(2)}_{456}\nonumber \\ 321323 \quad&\qquad \qquad&321323\quad&\end{aligned}$$

(3.93)

The underlines indicate the components to which the intertwiners given on the right are to be applied. (Note that they are completely parallel with those in (2.22)–(2.23).) Thus the following intertwining relations are valid for any $f \in A_q(A_3)$:

$$\begin{aligned}&P_{34}\Phi ^{(2)}_{123} \Phi ^{(1)}_{345}P_{23}P_{56} \Phi ^{(2)}_{345} \Phi ^{(1)}_{123} \pi _{121321}(\Delta (f)) \nonumber \\&\quad = \pi _{321323}(\Delta (f)) P_{34}\Phi ^{(2)}_{123} \Phi ^{(1)}_{345}P_{23}P_{56} \Phi ^{(2)}_{345} \Phi ^{(1)}_{123}, \end{aligned}$$

(3.94)

$$\begin{aligned}&\Phi ^{(2)}_{456}\Phi ^{(1)}_{234} P_{12}P_{45}\Phi ^{(2)}_{234} \Phi ^{(1)}_{456}P_{34}\pi _{121321}(\Delta (f)) \nonumber \\&\quad = \pi _{321323}(\Delta (f)) \Phi ^{(2)}_{456}\Phi ^{(1)}_{234} P_{12}P_{45}\Phi ^{(2)}_{234} \Phi ^{(1)}_{456}P_{34}. \end{aligned}$$

(3.95)

Since the representation (3.92) is irreducible, the intertwiner is unique up to an overall constant factor. The factor is one because both constructions send $|0\rangle ^{\otimes 6}$ to itself by the normalization (3.29). Therefore we have

$$\begin{aligned} P_{34}\Phi ^{(2)}_{123} \Phi ^{(1)}_{345}P_{23}P_{56} \Phi ^{(2)}_{345} \Phi ^{(1)}_{123} = \Phi ^{(2)}_{456}\Phi ^{(1)}_{234} P_{12}P_{45}\Phi ^{(2)}_{234} \Phi ^{(1)}_{456}P_{34}. \end{aligned}$$

(3.96)

In the current setting, (3.90) implies that both $\Phi ^{(1)}_{ijk}$ and $\Phi ^{(2)}_{ijk}$ are equal to $R_{ijk}P_{ik}$, leading to

$$\begin{aligned} \begin{aligned}&P_{34}R_{123}P_{13}R_{345}P_{35}P_{23}P_{56}R_{345}P_{35}R_{123}P_{13} \\&= R_{456}P_{46}R_{234}P_{24}P_{12}P_{45}R_{234}P_{24}R_{456}P_{46}P_{34}. \end{aligned} \end{aligned}$$

Sending all the $P_{ij}$’s to the right by using $P_{34}R_{123} = R_{124}P_{34}$, etc., we find

$$\begin{aligned} R_{124}R_{135}R_{236}R_{456}\sigma = R_{456}R_{236}R_{135}R_{124}\sigma ', \end{aligned}$$

where $\sigma = P_{34}P_{13}P_{35}P_{23}P_{56}P_{35}P_{13}$ and $\sigma ' = P_{46}P_{24}P_{12}P_{45}P_{24}P_{46}P_{34}$. One can check that $\sigma = \sigma '$, which gives the reverse ordering of the components $|m_1\rangle \otimes \cdots \otimes | m_6\rangle \mapsto |m_6\rangle \otimes \cdots \otimes | m_1\rangle$. Thus they can be canceled, completing the proof of Theorem 3.20. $\square$

In terms of the 3D R, the intertwining relations (3.94) and (3.95) take the form:

$$\begin{aligned} R_{124}R_{135}R_{236}R_{456}\pi _{121321}(\tilde{\Delta }(f)) = \pi _{321323}(\Delta (f))R_{124}R_{135}R_{236}R_{456}, \end{aligned}$$

(3.97)

$$\begin{aligned} R_{456}R_{236}R_{135}R_{124}\pi _{121321}(\tilde{\Delta }(f)) = \pi _{321323}(\Delta (f))R_{456}R_{236}R_{135}R_{124}, \end{aligned}$$

(3.98)

where $\tilde{\Delta }(f) = \sigma \circ \Delta (f) \circ \sigma$. For a generator $f=t_{ij}$ it reads as

$$\begin{aligned} \tilde{\Delta }(t_{ij}) = \sum _{1 \le k_1,\ldots , k_5 \le 4} t_{k_5 j} \otimes t_{k_4 k_5} \otimes t_{k_3 k_4} \otimes t_{k_2 k_3} \otimes t_{k_1 k_2} \otimes t_{i k_1}. \end{aligned}$$

(3.99)

We have started from the two particular reduced expressions of the longest element in (3.91). One can play the same game for any pair of the “most distant” reduced expressions which are related by $s_i \rightarrow s_{4-i}$ and the reverse ordering. The result can always be brought to the form (2.6) by using (3.59) and (3.60).

In general for $A_q(A_{n-1})$ with $n \ge 5$, similar compatibility conditions on the intertwiners can be derived from reduced expressions of the longest element of $W(A_{n-1})$ along the transformation $s_{i_1}\cdots s_{i_l} \rightarrow s_{n-i_l}\cdots s_{n-i_1}$ by the Coxeter relations (3.22), where $l = n(n-1)/2$. Since any reduced expression is transformed to any of the others by the Coxeter relations [119], the compatibility conditions for any $s_{j_1}\cdots s_{j_l} \rightarrow s_{n-j_l}\cdots s_{n-j_1}$ are equivalent to each other by a conjugation.

As an illustration, consider the $n=5$ case. The longest element of $W(A_4)$ has length 10 and the compatibility for $\pi _{1234123121} \simeq \pi _{4342341234}$ leads to

$$\begin{aligned} R_{123}R_{145}R_{246}R_{356} R_{178}R_{279}R_{389}R_{470} R_{580}R_{690} = \text {product in reverse order}. \end{aligned}$$

(3.100)

This can be derived by using the original tetrahedron equation (2.6) five times in addition to the trivial commutativity as

$$\begin{aligned} \begin{aligned}&\quad \underline{R_{123}R_{145}R_{246}R_{356}} R_{178}R_{279}R_{389}R_{470} R_{580}R_{690} \\&= R_{356}R_{246}R_{145}\underline{R_{123}R_{178}R_{279}R_{389}}R_{470} R_{580}R_{690} \\&=R_{356}R_{246}R_{145} R_{389}R_{279}R_{178}R_{123} R_{470}R_{580}R_{690} \\&=R_{356}R_{246} R_{389}R_{279} \underline{R_{145}R_{178}R_{470}R_{580}}R_{690}R_{123} \\&=R_{356}R_{246} R_{389}R_{279} R_{580}R_{470}R_{178}R_{145} R_{690}R_{123} \\&=R_{356}R_{389}R_{580} \underline{R_{246}R_{279}R_{470}R_{690}} R_{178}R_{145}R_{123} \\&=\underline{R_{356}R_{389}R_{580}R_{690}} R_{470}R_{279}R_{246}R_{178} R_{145}R_{123} \\&=R_{690}R_{580}R_{389}R_{356} R_{470}R_{279}R_{246} R_{178}R_{145}R_{123} \\&=R_{690}R_{580}R_{470}R_{389} R_{279}R_{178}R_{356}R_{246} R_{145}R_{123}, \end{aligned} \end{aligned}$$

(3.101)

where the underlines indicate the places to which the tetrahedron equation is applied. The first and the last expressions in (3.101) fit the geometric interpretation as the transformations between the 5-line diagrams in Fig. 3.1 in the same manner as in Fig. 2.2.

Fig. 3.1

The 5-line diagrams connected by (3.101) in the same manner as Fig. 2.2

For general n, the compatibility condition arising from $\pi _{i_1,\ldots , i_l} \simeq \pi _{n-i_l,\ldots , n-i_1}$ allows a similar geometric interpretation in terms of generic positioned n-line diagrams with $n(n-1)/2$ vertices. They are all reducible to the the tetrahedron equation. This last claim follows from [126, Theorem 2.17], which states that any non-trivial loop in a reduced expression (rex) graph (see Sect. 9.2)  is generated from the loops in the one for the longest element in the parabolic subgroups of rank 3, hence $A_3$ in the present case.

3.5.2 $RLLL=LLLR$ Type

Let us introduce the operator L along the scheme (2.12). In (2.11), we choose $V = \mathbb {C} v_0 \oplus \mathbb {C} v_1$ and $\mathcal {F}= \mathcal {F}_q = \bigoplus _{m \ge 0}\mathbb {C}(q)|m\rangle$ which is the Fock space introduced in (3.13) as an irreducible module over the q-oscillator algebra (3.12). Then $L=(L^{ab}_{ij})$ is specified for $a,b,i,j =0,1$ as

$$\begin{aligned}&L^{ab}_{ij}=0 \quad \text {if}\;\; a+b \ne i+j, \end{aligned}$$

(3.102)

$$\begin{aligned}&L^{00}_{00} = L^{11}_{11} = 1, \quad L^{10}_{10} = \mathrm{\mathbf{k}}, \quad L^{01}_{01} = -q \mathrm{\mathbf{k}}, \quad L^{10}_{01} = \mathrm{\mathbf{a}}^+,\quad L^{01}_{10} = \mathrm{\mathbf{a}}^-. \end{aligned}$$

(3.103)

The property

$$\begin{aligned} \mathbf{h}L^{ab}_{ij} = L^{ab}_{ij}(\mathbf{h} + a-i) \end{aligned}$$

(3.104)

is valid, where $\mathbf{h}$ is the number operator (3.14). From (3.13) and (2.13), non-trivial matrix elements $L^{abc}_{ijk}$ read as

$$\begin{aligned} \begin{aligned}&L^{0, 0, c}_{0, 0, k} =L^{1, 1, c}_{1, 1, k}=\delta ^c_k,\quad L^{1, 0, c}_{1, 0, k}=\delta ^c_kq^k, \quad L^{0, 1, c}_{0, 1, k}= -\delta ^c_kq^{k+1}, \\&L^{1, 0, c}_{0, 1, k}=\delta ^c_{k+1}, \quad L^{0, 1, c}_{1, 0, k}=\delta ^c_{k-1}(1-q^{2k}). \end{aligned} \end{aligned}$$

(3.105)

The operator L may be regarded as an $\mathrm {Osc}_{q}$-valued six-vertex model [10, Sect. 8] as in Fig. 3.2.

Fig. 3.2

3D L as an $\mathrm {Osc}_{q}$-valued six-vertex model. The last two relations in (3.12) corresponds to a quantization of the so-called free Fermion condition [10, Fig. 10.1, Eq. (10.16.4)$|_{\omega _7=\omega _8=0}$]

Theorem 3.21

The intertwiner R and the above L satisfy the tetrahedron equation of $RLLL=LLLR$ type in (2.15).

Proof

The equations (2.18) coincide with the intertwining relations (3.38)–(3.46) for R and $R^{-1}=R$. (See (3.60).) This is shown more concretely in Lemma 3.22 below. $\square$

Let us write the quantized Yang–Baxter equation (2.18) as

$$\begin{aligned} R \mathcal {L}^{abc}_{ijk}&= \tilde{\mathcal {L}}^{abc}_{ijk}R, \end{aligned}$$

(3.106)

$$\begin{aligned} \mathcal {L}^{abc}_{ijk}&= \sum _{\alpha , \beta , \gamma }(L^{\alpha \beta }_{ij} \otimes L^{a \gamma }_{\alpha k} \otimes L^{bc}_{\beta \gamma }), \end{aligned}$$

(3.107)

$$\begin{aligned} \tilde{\mathcal {L}}^{abc}_{ijk}&= \sum _{\alpha , \beta , \gamma } (L^{ab}_{\alpha \beta } \otimes L^{\alpha c}_{i\gamma } \otimes L^{\beta \gamma }_{jk}). \end{aligned}$$

(3.108)

The objects $\mathcal {L}^{abc}_{ijk}$ and $\tilde{\mathcal {L}}^{abc}_{ijk}$ are $\mathrm {End}({\mathcal {F}}_q^{\otimes 3})$-valued quantized three-body scattering amplitudes. They are non-vanishing only when $a+b+c=i+j+k$ due to (3.102) and non-trivial only when $a+b+c=i+j+k=1,2$ due to (3.103). For example,

$$\begin{aligned} \mathcal {L}^{001}_{100}&= L^{01}_{10} \otimes L^{00}_{00} \otimes L^{01}_{10} +L^{10}_{10} \otimes L^{01}_{10} \otimes L^{01}_{01} = \mathrm{\mathbf{a}}^- \otimes 1 \otimes \mathrm{\mathbf{a}}^- - q \mathrm{\mathbf{k}} \otimes \mathrm{\mathbf{a}}^- \otimes \mathrm{\mathbf{k}}, \\ \tilde{\mathcal {L}}^{001}_{100}&=L^{00}_{00} \otimes L^{01}_{10} \otimes L^{00}_{00} = 1 \otimes \mathrm{\mathbf{a}}^- \otimes 1. \end{aligned}$$

Observe that these operators are exactly those appearing in the intertwining relation (3.38). This happens generally. One can directly check: 

Lemma 3.22

The quantized three-body scattering amplitudes $\mathcal {L}^{abc}_{ijk}$ and $\tilde{\mathcal {L}}^{abc}_{ijk}$ with $a+b+c=i+j+k=1,2$ coincide with the representations (3.36)–(3.37) of $A_q(A_2)$ as follows:

$$\begin{aligned} \pi _{121}(\tilde{\Delta }(t_{ij}))&= \tilde{\mathcal {L}}^{\bar{\mathbf{e}}_j}_{\bar{\mathbf{e}}_{4-i}} = (-q)^{i-j} \mathcal {L}^{\mathbf{e}_{4-i}}_{\mathbf{e}_j}, \end{aligned}$$

(3.109)

$$\begin{aligned} \pi _{212}(\Delta (t_{ij}) )&= \mathcal {L}^{\bar{\mathbf{e}}_j}_{\bar{\mathbf{e}}_{4-i}} = (-q)^{i-j} \tilde{\mathcal {L}}^{\mathbf{e}_{4-i}}_{\mathbf{e}_j}. \end{aligned}$$

(3.110)

Here $\mathbf{e}_i, \bar{\mathbf{e}}_i$ are arrays of 0, 1 with length three specified by

$$\begin{aligned} \mathbf{e}_i = \overbrace{0,\ldots , 0}^{i-1}, 1, 0, \ldots , 0,\quad \bar{\mathbf{e}}_i = \overbrace{1,\ldots , 1}^{i-1}, 0, 1, \ldots , 1. \end{aligned}$$

(3.111)

From (3.109) and (3.110), the intertwining relation (3.31) and the tetrahedron equation (2.15) are identified.

Remark 3.23

As an equation for R, the tetrahedron equation $RLLL=LLLR$ (3.106) is invariant under the change $L^{ab}_{ij} \rightarrow \alpha ^{a-j}L^{ab}_{ij}$ by a parameter $\alpha$ by virtue of (3.102).

Remark 3.24

Let $L_\alpha = (\alpha ^{a-j}L^{ab}_{ij})$ be the 3D L in Remark 3.23 including a parameter $\alpha$. It is invertible with the inverse

$$\begin{aligned} (L_{\alpha })^{-1} = L_{\alpha ^{-1}}, \end{aligned}$$

(3.112)

This is easily verified by means of (3.12).

As an application of Theorem 3.21, let us present another proof of Theorem 3.20, i.e. $RRRR=RRRR$. We invoke the argument in Sect. 2.5 which establishes $RRRR=RRRR$ by using $RLLL=LLLR$ up to the irreducibility. For the 3D L under consideration, we can make the irreducibility argument precise. Recall the initial and final elements $\overset{6}{L}_{ab}\overset{5}{L}_{ac}\overset{4}{L}_{bc}\overset{3}{L}_{ad} \overset{2}{L}_{bd}\overset{1}{L}_{cd}$ and $\overset{1}{L}_{cd}\overset{2}{L}_{bd}\overset{4}{L}_{bc} \overset{3}{L}_{ad}\overset{5}{L}_{ac}\overset{6}{L}_{ab}$ in (2.22) and (2.23), which are linear operators on

$$\begin{aligned} \overset{a}{V} \otimes \overset{b}{V}\otimes \overset{c}{V}\otimes \overset{d}{V} \otimes \overset{1}{\mathcal {F}}_q \otimes \overset{2}{\mathcal {F}}_q \otimes \overset{3}{\mathcal {F}}_q \otimes \overset{4}{\mathcal {F}}_q \otimes \overset{5}{\mathcal {F}}_q \otimes \overset{6}{\mathcal {F}}_q. \end{aligned}$$

Let us call their matrix elements for the transition $v_{i_1} \otimes v_{j_1} \otimes v_{k_1} \otimes v_{l_1} \mapsto v_{i_4} \otimes v_{j_4} \otimes v_{k_4} \otimes v_{l_4}$ as $\mathcal {L}^{i_4 j_4 k_4l_4}_{i_1 j_1 k_1l_1}$ and $\tilde{\mathcal {L}}^{i_4 j_4 k_4l_4}_{i_1 j_1 k_1l_1}$, respectively. Then (2.22) and (2.23) are the totality of the relations

$$\begin{aligned} R_{124}R_{135}R_{236}R_{456}\mathcal {L}^{i_4 j_4 k_4l_4}_{i_1 j_1 k_1l_1}&= \tilde{\mathcal {L}}^{i_4 j_4 k_4l_4}_{i_1 j_1 k_1l_1} R_{124}R_{135}R_{236}R_{456}, \end{aligned}$$

(3.113)

$$\begin{aligned} R_{456}R_{236}R_{135}R_{124}\mathcal {L}^{i_4 j_4 k_4l_4}_{i_1 j_1 k_1l_1}&=\tilde{\mathcal {L}}^{i_4 j_4 k_4l_4}_{i_1 j_1 k_1l_1}R_{456}R_{236}R_{135}R_{124} \end{aligned}$$

(3.114)

for $i_1,\ldots , l_4 =0,1$. Here we have substituted $S=R$ for our 3D R according to the comment after (2.20). The matrix elements $\mathcal {L}^{i_4 j_4 k_4l_4}_{i_1 j_1 k_1l_1}$ and $\tilde{\mathcal {L}}^{i_4 j_4 k_4l_4}_{i_1 j_1 k_1l_1}$ are $\mathrm {End}(\mathcal {F}^{\otimes 6}_q)$ valued and, from the diagrams (2.21) and (2.14), they are given by

$$\begin{aligned} \mathcal {L}^{i_4 j_4 k_4l_4}_{i_1 j_1 k_1l_1}&= \sum L^{k_2 l_2}_{k_1 l_1}\otimes L^{j_2 l_3}_{j_1 l_2} \otimes L^{i_2 l_4}_{i_1 l_3}\otimes L^{j_3 k_3}_{j_2 k_2} \otimes L^{i_3 k_4}_{i_2 k_3} \otimes L^{i_4 j_4}_{i_3 j_3}, \end{aligned}$$

(3.115)

$$\begin{aligned} \tilde{\mathcal {L}}^{i_4 j_4 k_4l_4}_{i_1 j_1 k_1l_1}&= \sum L^{k_4 l_4}_{k_3 l_3}\otimes L^{j_4 l_3}_{j_3 l_2}\otimes L^{i_4 l_2}_{i_3 l_1}\otimes L^{j_3 k_3}_{j_2 k_2}\otimes L^{i_3 k_2}_{i_2 k_1} \otimes L^{i_2 j_2}_{i_1 j_1}, \end{aligned}$$

(3.116)

where the sums are taken over $i_r, j_r, k_r, l_r=0,1$ for $r=1,2$. These are depicted as follows:

By substituting (3.102), (3.103) and using (3.99), (3.21), one can directly check

$$\begin{aligned} \pi _{121321}(\tilde{\Delta }(t_{ij}))&= (-q)^{i-j}\mathcal {L}^{\bar{\mathbf{e}}_i}_{\bar{\mathbf{e}}_{5-j}}, \quad \pi _{321323}(\Delta (t_{ij})) = (-q)^{i-j}\tilde{\mathcal {L}}^{\bar{\mathbf{e}}_i}_{\bar{\mathbf{e}}_{5-j}} \quad (1 \le i,j \le 4), \end{aligned}$$

(3.117)

where $\bar{\mathbf{e}}_i$ is length four array given by (3.111). Since the representations $\pi _{121321}$ and $\pi _{321323}$ are irreducible by Theorem 3.3, and the relations (3.97)–(3.98) with generators $f=t_{ij}$ are reproduced, the equality $R_{124}R_{135}R_{236}R_{456}=R_{456}R_{236}R_{135}R_{124}$ follows.

3.5.3 $MMLL=LLMM$ Type

Let us present a solution to the tetrahedron equation of type $MMLL=LLMM$ in Sect. 2.6. We take $V = {\mathbb C}v_0 \oplus {\mathbb C}v_1, \mathcal {F}= {\mathcal {F}}_q$ in the setting therein and consider a slight generalization of (2.24)–(2.25) including a spectral parameter: 

$$\begin{aligned} L(z)&= \sum _{a,b,i,j} E_{ai}\otimes E_{bj} \otimes L(z)^{ab}_{ij}, \end{aligned}$$

(3.118)

$$\begin{aligned} M(z)&= \sum _{a,b,i,j} E_{ai}\otimes E_{bj} \otimes M(z)^{ab}_{ij}, \end{aligned}$$

(3.119)

where the sums extend over $\{0,1\}^4$ and both belong to $\mathrm {End}(V \otimes V \otimes {\mathcal {F}}_q)$. The operators $L(z)^{ab}_{ij}, M(z)^{ab}_{ij} \in \mathrm {End}({\mathcal {F}}_q)$, which are nonzero only when $a+b=i+j$, are specified by

(3.120)

Here ${\mathbf{a}}^{\pm } , {\mathbf{k}}$ are q-oscillators in (3.13), and ${\tilde{\mathbf{k}}}$ is ${\mathbf{k}}$ with q replaced by $-q$, i.e.

$$\begin{aligned} {\tilde{\mathbf{k}}}|m\rangle = (-q)^m|m\rangle . \end{aligned}$$

(3.121)

See (3.13). In (3.120), $\mu , \nu$ are fixed parameters and suppressed in the notation. On the other hand, z will play a similar role to the spectral parameter below. We note a simple relation $M(z) = L(z)|_{q\rightarrow -q, \mu \rightarrow \nu }$.

Theorem 3.25

For any $\mu , \nu$, the operators L(z) and M(z) defined in (3.118)–(3.121) satisfy the tetrahedron equation  of type $MMLL=LLMM$ in $\mathrm {End}(V^{\otimes 4} \otimes {\mathcal {F}}_q^{\otimes 2})$ as

$$\begin{aligned} \begin{aligned}&M_{126}(z_{12})M_{346}(z_{34})L_{135}(z_{13})L_{245}(z_{24}) \\&= L_{245}(z_{24})L_{135}(z_{13})M_{346}(z_{34})M_{126}(z_{12}), \end{aligned} \end{aligned}$$

(3.122)

where $z_{ij}=z_i/z_j$.

See Fig. 2.5 for a graphical representation.

Proof

A direct calculation. As an illustration, let us compare $X \in \mathrm {End}(\overset{5}{\mathcal {F}}_q \otimes \overset{6}{\mathcal {F}}_q )$ occurring in $(\text {LHS or RHS})(v_0 \otimes v_0 \otimes v_1 \otimes v_1 \otimes 1 \otimes 1) = v_1 \otimes v_0 \otimes v_0 \otimes v_1 \otimes X + \cdots$. The X is given by

$$\begin{aligned}&L(z_{13})^{01}_{01}L(z_{24})^{10}_{01} \otimes M(z_{12})^{10}_{01}M(z_{34})^{01}_{10} + L(z_{13})^{10}_{01}L(z_{24})^{01}_{01} \otimes M(z_{12})^{10}_{10}M(z_{34})^{01}_{01} \\&= -q\mu ^{-1}z_{13}( {\mathbf{k}}{\mathbf{a}}^+ \otimes {\mathbf{a}}^+ {\mathbf{a}}^- +q {\mathbf{a}}^+ {\mathbf{k}}\otimes {\tilde{\mathbf{k}}}^2) \end{aligned}$$

$$\begin{aligned} L(z_{24})^{01}_{01}L(z_{13})^{10}_{01}\otimes M(z_{34})^{11}_{11}M(z_{12})^{00}_{00} = -q\mu ^{-1}z_{13}{\mathbf{k}}{\mathbf{a}}^+ \otimes 1 \end{aligned}$$

for the RHS. Their difference is proportional to ${\mathbf{k}}{\mathbf{a}}^+ \otimes {\mathbf{a}}^+ {\mathbf{a}}^- +q {\mathbf{a}}^+ {\mathbf{k}}\otimes {\tilde{\mathbf{k}}}^2 - {\mathbf{k}}{\mathbf{a}}^+ \otimes 1$, which is zero due to (3.12), (3.13) and (3.121). $\square$

Theorem 3.25 will be utilized for $A_q(B_n)$ in Chap. 6 and for multispecies TASEP in Chap. 18.

The solution in Theorem 3.25 consists of the 3D L and its slight variant M. There is a parallel solution consisting of the 3D R and its variant, which we write as S below.⁶ Set

$$\begin{aligned} R(z)_{123}=z^{-\mathbf{h}_2}R_{123}z^{\mathbf{h}_2} =z^{\mathbf{h}_1}R_{123}z^{-\mathbf{h}_1}, \quad S(z)_{123}=z^{-\mathbf{h}_2}R_{213}z^{\mathbf{h}_2} =z^{\mathbf{h}_1}R_{213}z^{-\mathbf{h}_1}, \end{aligned}$$

(3.123)

where $\mathbf{h}$ is defined in (3.14), and the second equalities are due to the weight conservation (3.49). The indices 1, 2, 3 specify the components in $\overset{1}{\mathcal {F}}_q\otimes \overset{2}{\mathcal {F}}_q\otimes \overset{3}{\mathcal {F}}_q$. In the notation (3.47), they are described as

$$\begin{aligned} R(z)(|i\rangle \otimes |j\rangle \otimes |k\rangle )&= \sum _{a,b,c} z^{j-b}R^{abc}_{ijk}|a\rangle \otimes |b\rangle \otimes |c\rangle , \end{aligned}$$

(3.124)

$$\begin{aligned} S(z)(|i\rangle \otimes |j\rangle \otimes |k\rangle )&= \sum _{a,b,c}z^{j-b}R^{bac}_{jik}|a\rangle \otimes |b\rangle \otimes |c\rangle . \end{aligned}$$

(3.125)

Theorem 3.26

R(z) and S(z) satisfy the tetrahedron equation  of type $MMLL=LLMM$ in $\mathrm {End}(\mathcal {F}_q^{\otimes 6})$ as

$$\begin{aligned} \begin{aligned}&S(z_{12})_{126}S(z_{34})_{346}R(z_{13})_{135}R(z_{24})_{245} \\&= R(z_{24})_{245}R(z_{13})_{135}S(z_{34})_{346}S(z_{12})_{126}, \end{aligned} \end{aligned}$$

(3.126)

where $z_{ij}=z_i/z_j$.

Proof

By substituting (3.123) into (3.126) and applying (3.49), one finds that the similarity transformation $z_{13}^{-\mathbf{h}_1}z_{23}^{-\mathbf{h}_2}z_{34}^{\mathbf{h}_4}(3.126) z_{13}^{\mathbf{h}_1}z_{23}^{\mathbf{h}_2}z_{34}^{-\mathbf{h}_4}$ removes the z-dependence, completely reducing it to $R_{216}R_{436}R_{135}R_{245} =R_{245}R_{135}R_{436}R_{216}$. Exchanging the indices as $1 \leftrightarrow 5, 2 \leftrightarrow 4$ gives $R_{456}R_{236}R_{531}R_{421} = R_{421}R_{531}R_{236}R_{456}$. From (3.59) this is equivalent to $R_{456}R_{236}R_{135}R_{124} = R_{124}R_{135}R_{236}R_{456}$, which is indeed valid due to Theorem 3.20. $\square$

3.6 Further Aspects of 3D R

Let us quote (3.38)–(3.46) in the form of the adjoint action of the 3D R:

$$\begin{aligned} R^{-1} \mathrm{\mathbf{k}}_2\mathrm{\mathbf{a}}_1^\pm R&= \mathrm{\mathbf{k}}_3 \mathrm{\mathbf{a}}^\pm _1+ \mathrm{\mathbf{k}}_1\mathrm{\mathbf{a}}_2^\pm \mathrm{\mathbf{a}}_3^\mp , \end{aligned}$$

(3.127)

$$\begin{aligned} R^{-1} \mathrm{\mathbf{a}}_2^\pm R&= \mathrm{\mathbf{a}}_1^\pm \mathrm{\mathbf{a}}_3^\pm -q \mathrm{\mathbf{k}}_1\mathrm{\mathbf{k}}_3\mathrm{\mathbf{a}}_2^\pm , \end{aligned}$$

(3.128)

$$\begin{aligned} R^{-1} \mathrm{\mathbf{k}}_2\mathrm{\mathbf{a}}_3^\pm R&= \mathrm{\mathbf{k}}_1 \mathrm{\mathbf{a}}^\pm _3+ \mathrm{\mathbf{k}}_3\mathrm{\mathbf{a}}_1^\mp \mathrm{\mathbf{a}}_2^\pm , \end{aligned}$$

(3.129)

$$\begin{aligned} R^{-1}(\mathrm{\mathbf{a}}_1^\pm \mathrm{\mathbf{a}}_2^\mp \mathrm{\mathbf{a}}_3^\pm -q \mathrm{\mathbf{k}}_1\mathrm{\mathbf{k}}_3 )R&= \mathrm{\mathbf{a}}_1^\mp \mathrm{\mathbf{a}}_2^\pm \mathrm{\mathbf{a}}_3^\mp -q \mathrm{\mathbf{k}}_1\mathrm{\mathbf{k}}_3, \end{aligned}$$

(3.130)

$$\begin{aligned} R^{-1}\mathrm{\mathbf{k}}_1\mathrm{\mathbf{k}}_2 R&= \mathrm{\mathbf{k}}_1\mathrm{\mathbf{k}}_2,\quad R^{-1}\mathrm{\mathbf{k}}_2\mathrm{\mathbf{k}}_3 R = \mathrm{\mathbf{k}}_2\mathrm{\mathbf{k}}_3. \end{aligned}$$

(3.131)

The fact that $R=R^{-1}$ (3.60) has been taken into account. We have written $\mathrm{\mathbf{a}}^+\otimes \mathrm{\mathbf{k}} \otimes 1$ as $\mathrm{\mathbf{k}}_2\mathrm{\mathbf{a}}_1^+$ for example. Thus the q-oscillator operators with different indices are commutative.

3.6.1 Boundary Vector

We define

$$\begin{aligned}&| \eta _1 \rangle = \sum _{m \ge 0}\frac{|m\rangle }{(q)_m}, \qquad | \eta _2 \rangle = \sum _{m \ge 0}\frac{|2m\rangle }{(q^4)_m}, \end{aligned}$$

(3.132)

$$\begin{aligned}&\langle \eta _1 | = \sum _{m\ge 0}\frac{\langle m |}{(q)_m}, \qquad \langle \eta _2 | = \sum _{m\ge 0}\frac{\langle 2m |}{(q^4)_m}, \end{aligned}$$

(3.133)

and call them boundary vectors.  They will play an important role in the reduction procedure in Chaps. 12–17. They actually belong to a completion of $\mathcal {F}_q$ and $\mathcal {F}^*_q$ since infinite sums are involved. Nonetheless, we will refer to them as $|\eta _s\rangle \in \mathcal {F}_q$ and $\langle \eta _s| \in \mathcal {F}^*_q$ for simplicity.

Lemma 3.27

Up to normalization, the boundary vector $|\eta _1\rangle$ is characterized by any one of the following three equivalent conditions:

$$\begin{aligned}&(\mathrm{\mathbf{a}}^+ -1+\mathrm{\mathbf{k}})|\eta _1\rangle = 0, \end{aligned}$$

(3.134)

$$\begin{aligned}&(\mathrm{\mathbf{a}}^--1-q\mathrm{\mathbf{k}})|\eta _1\rangle = 0, \end{aligned}$$

(3.135)

$$\begin{aligned}&(\mathrm{\mathbf{a}}^-+q\mathrm{\mathbf{a}}^+ -1-q)|\eta _1\rangle = 0. \end{aligned}$$

(3.136)

Similarly, the boundary vector $|\eta _2\rangle$ is characterized, up to normalization, by

$$\begin{aligned}&(\mathrm{\mathbf{a}}^+ -\mathrm{\mathbf{a}}^-)|\eta _2\rangle = 0. \end{aligned}$$

(3.137)

Proof

Substituting $|\eta _s\rangle = \sum _m c_m |m\rangle$ into these conditions and using (3.13), one can check that $c_m/c_0$ is determined uniquely as in (3.132). $\square$

A linear combination of (3.134) and (3.135) leads to (3.136). However, the lemma includes a less trivial reverse that (3.136) implies the preceding two.

From (3.17) the dual boundary vectors (3.133) have similar characterizations:

$$\begin{aligned}&\langle \eta _1| ({\mathbf{a}}^- -1 + {\mathbf{k}}) =0, \end{aligned}$$

(3.138)

$$\begin{aligned}&\langle \eta _1| ({\mathbf{a}}^+ -1 -q {\mathbf{k}}) =0, \end{aligned}$$

(3.139)

$$\begin{aligned}&\langle \eta _1| ({\mathbf{a}}^+ + q {\mathbf{a}}^- -1 -q) =0, \end{aligned}$$

(3.140)

$$\begin{aligned}&\langle \eta _2 | ({\mathbf{a}}^- -{\mathbf{a}}^+ ) = 0. \end{aligned}$$

(3.141)

Proposition 3.28

The 3D R and the boundary vectors satisfy the following relations:

$$\begin{aligned}&(\langle \eta _s | \otimes \langle \eta _s | \otimes \langle \eta _s| ) R = \langle \eta _s | \otimes \langle \eta _s | \otimes \langle \eta _s| \qquad (s=1,2), \end{aligned}$$

(3.142)

$$\begin{aligned}&R (|\eta _s\rangle \otimes |\eta _s\rangle \otimes |\eta _s\rangle ) = |\eta _s\rangle \otimes |\eta _s\rangle \otimes |\eta _s\rangle \qquad (s=1,2). \end{aligned}$$

(3.143)

Proof

From Remark 3.10, it suffices to prove (3.143). First we consider the case $s=1$. By Lemma 3.27, it suffices to check

$$\begin{aligned}&(\mathrm{\mathbf{a}}_2^-+q\mathrm{\mathbf{a}}_2^+ -1-q)R|\eta _1\rangle ^{\otimes 3}=0, \end{aligned}$$

(3.144)

$$\begin{aligned}&(\mathrm{\mathbf{a}}_1^+ -1+\mathrm{\mathbf{k}}_1)R|\eta _1\rangle ^{\otimes 3} = (\mathrm{\mathbf{a}}_3^+ -1+\mathrm{\mathbf{k}}_3)R|\eta _1\rangle ^{\otimes 3}=0. \end{aligned}$$

(3.145)

To show (3.144), we multiply $R^{-1}$ from the left and apply (3.128) to convert the LHS into

$$\begin{aligned} \bigl (\mathrm{\mathbf{a}}_1^- \mathrm{\mathbf{a}}_3^- -q \mathrm{\mathbf{k}}_1\mathrm{\mathbf{k}}_3\mathrm{\mathbf{a}}_2^- +q(\mathrm{\mathbf{a}}_1^+ \mathrm{\mathbf{a}}_3^+ -q \mathrm{\mathbf{k}}_1\mathrm{\mathbf{k}}_3\mathrm{\mathbf{a}}_2^+)-1-q\bigr )|\eta _1\rangle ^{\otimes 3}. \end{aligned}$$

(3.146)

From (3.134) and (3.135), one may set $\mathrm{\mathbf{a}}_i^+= 1-\mathrm{\mathbf{k}}_i$ and $\mathrm{\mathbf{a}}_i^-=1+q\mathrm{\mathbf{k}}_i$ here. The resulting polynomial in $\mathrm{\mathbf{k}}_1, \mathrm{\mathbf{k}}_2,\mathrm{\mathbf{k}}_3$ vanishes identically, proving (3.144). By Lemma 3.27, it follows that $(\mathrm{\mathbf{a}}_2^+ -1+\mathrm{\mathbf{k}}_2)R|\eta _1\rangle ^{\otimes 3}=0$ has also been proved. Multiplying $R^{-1}$ again by it and applying (3.128), (3.134), (3.135), we get

$$\begin{aligned} \bigl (-\mathrm{\mathbf{k}}_1- \mathrm{\mathbf{k}}_3+ (1-q)\mathrm{\mathbf{k}}_1\mathrm{\mathbf{k}}_3 +q\mathrm{\mathbf{k}}_1\mathrm{\mathbf{k}}_2\mathrm{\mathbf{k}}_3+ \mathrm{\mathbf{k}}'_2\bigr )|\eta _1\rangle ^{\otimes 3}=0, \end{aligned}$$

(3.147)

where $\mathrm{\mathbf{k}}'_2= R^{-1}\mathrm{\mathbf{k}}_2R$. This enables us to show (3.145). In fact, by multiplying $R^{-1}\mathrm{\mathbf{k}}_2$ by the first relation, its LHS becomes $(\mathrm{\mathbf{k}}_3 \mathrm{\mathbf{a}}^+_1+ \mathrm{\mathbf{k}}_1\mathrm{\mathbf{a}}_2^+\mathrm{\mathbf{a}}_3^- -\mathrm{\mathbf{k}}'_2+\mathrm{\mathbf{k}}_1\mathrm{\mathbf{k}}_2)|\eta _1\rangle ^{\otimes 3}$ owing to (3.127). Substitution of $\mathrm{\mathbf{a}}_i^+= 1-\mathrm{\mathbf{k}}_i$ and $\mathrm{\mathbf{a}}_i^-=1+q\mathrm{\mathbf{k}}_i$ leads to the same expression as (3.147), hence zero. The second relation in (3.145) can be verified in the same manner.

Next we consider the case $s=2$. From Lemma 3.27, it suffices to check $\mathrm{\mathbf{k}}_2(\mathrm{\mathbf{a}}_i^+- \mathrm{\mathbf{a}}_i^-)R|\eta _2\rangle ^{\otimes 3}=0$ $(i=1,3)$ and $(\mathrm{\mathbf{a}}_2^+- \mathrm{\mathbf{a}}_2^-)R|\eta _2\rangle ^{\otimes 3}=0$. The proof is similar to the $s=1$ case and actually simpler in that an intermediate identity like (3.147) need not be prepared. So we demonstrate the last identity only. By multiplying $R^{-1}$ and using (3.128), its LHS becomes

$$\begin{aligned}&\bigl ((\mathrm{\mathbf{a}}_1^+ \mathrm{\mathbf{a}}_3^+ -q \mathrm{\mathbf{k}}_1\mathrm{\mathbf{k}}_3\mathrm{\mathbf{a}}_2^+)- (\mathrm{\mathbf{a}}_1^- \mathrm{\mathbf{a}}_3^- -q \mathrm{\mathbf{k}}_1\mathrm{\mathbf{k}}_3\mathrm{\mathbf{a}}_2^-)\bigr )|\eta _2\rangle ^{\otimes 3}. \end{aligned}$$

From (3.137), we may set $\mathrm{\mathbf{a}}_i^+ = \mathrm{\mathbf{a}}_i^-$ here. $\square$

3.6.2 Combinatorial and Birational Counterparts

As remarked after (3.84), we know $R^{abc}_{ijk} \in \mathbb {Z}[q,q^{-1}]$. Actually a stronger property holds.

Lemma 3.29

$R^{abc}_{ijk}$ is a polynomial in q with the constant term given by

$$\begin{aligned} R^{abc}_{ijk}\left| _{q=0}\right. = R^{ijk}_{abc}\left| _{q=0}\right. = \delta ^a_{j+(i-k)_+}\delta ^b_{\min (i,k)}\delta ^c_{j+(k-i)_+}. \end{aligned}$$

(3.148)

See (3.66) for the definition of the symbol $(x)_+$.

Proof

First we show $R^{abc}_{ijk} \in \mathbb {Z}[q]$. Let A be a ring of rational functions of q regular at $q=0$. In view of $\mathbb {Z}[q,q^{-1}] \cap A = \mathbb {Z}[q]$, it suffices to show $R^{abc}_{ijk} \in A$. From (3.50) we have $R^{abc}_{ijk} \in A R^{a,b-1,c}_{i,j-1,k} + AR^{a,b-1,c}_{i-1,j,k-1}$. By induction on b, this attributes the claim to $R^{a,0,c}_{ijk} \in A$ for arbitrary a, c, i, j, k. But this is obviously true since $R^{a,0,c}_{ijk}= \delta ^{a}_{i+j}\delta ^c_{j+k}q^{ik}$ either from (3.67) or (3.74).

Next we show (3.148). The first equality is due to (3.63). Setting $q=0$ in (3.50) and (3.56), we get

$$\begin{aligned} R^{a,b,c}_{i-1,j,k-1}\left| _{q=0}\right.&= R^{a,b+1,c}_{i,j,k}\left| _{q=0}\right. , \quad R^{a-1,b,c-1}_{i,j,k}\left| _{q=0}\right. = R^{a,b,c}_{i,j+1,k}\left| _{q=0}\right. . \end{aligned}$$

(3.149)

From the symmetry (3.62), it suffices to verify the $i\le k$ case. Then the first relation shows that $R^{abc}_{ijk}\left| _{q=0}\right. =0$ if $b >i$. For $b \le i$, we have $R^{abc}_{ijk}\left| _{q=0}\right. = R^{a,0,c}_{i-b,j,k-b}\left| _{q=0}\right. = \delta ^{a+b}_{i+j}\delta ^{b+c}_{j+k}q^{(i-b)(k-b)}\left| _{q=0}\right.$. This is non-vanishing only if $b=i$ because otherwise $b< i \le k$. Thus we conclude $R^{abc}_{ijk}\left| _{q=0}\right. = \delta ^{a+b}_{i+j}\delta ^{b+c}_{j+k} \delta ^b_i = \delta ^a_{j}\delta ^b_{i}\delta ^c_{j+k-i}$. $\square$

Lemma 3.29 shows that 3D R at $q=0$ maps a monomial to another monomial as $R\left| _{q=0}\right. (|i\rangle \otimes |j\rangle \otimes |k\rangle ) = |j+(i-k)_+\rangle \otimes |\min (i,k)\rangle \otimes |j+(k-i)_+\rangle$. Motivated by this fact, we define the combinatorial 3D R  to be a map on $(\mathbb {Z}_{\ge 0})^3$ given by

$$\begin{aligned} R_\mathrm{combinatorial}: (a,b,c) \mapsto (b+(a-c)_+, \min (a,c), b+(c-a)_+). \end{aligned}$$

(3.150)

Corollary 3.30

The combinatorial 3D R (3.150) is an involution on $({\mathbb Z}_{\ge 0})^3$. It satisfies the tetrahedron equation of type $RRRR=RRRR$ on $({\mathbb Z}_{\ge 0})^6$.

Proof

The assertions follow from (3.60) and Theorem 3.20 by setting $q=0$ and using Lemma 3.29. $\square$

Example 3.31

An example of the tetrahedron equation (2.6) for the combinatorial 3D R. The map R here denotes $R_\mathrm{combinatorial}$ in (3.150). The first SW arrow $R_{124}$ is due to $R_\mathrm{combinatorial}: (3,1,4) \mapsto (1,3,2)$, which can be seen in Example 3.12.

Let us proceed to the third 3D R. Regarding a, b, c as indeterminates, we introduce the map

$$\begin{aligned} R_\mathrm{birational}: (a,b,c) \mapsto (\tilde{a},\tilde{b},\tilde{c})= \left( \frac{ab}{a+c}, \,a+c,\, \frac{bc}{a+c}\right) . \end{aligned}$$

(3.151)

We called it the birational 3D R  in the current context. The combinatorial 3D R (3.150) is reproduced from it by the tropical variable change

$$\begin{aligned} a b \rightarrow a+b, \quad \frac{a}{b} \rightarrow a-b, \quad a+b \rightarrow \min (a,b), \end{aligned}$$

(3.152)

which keeps the distributive law since $a(b+c) = ab + ac$ is replaced by $a+\min (b,c) = \min (a+b, a+c)$. One way to materialize (3.152) is a transformation to logarithmic variables via

$$\begin{aligned} \begin{aligned}&-\lim _{\varepsilon \rightarrow +0}\varepsilon \log (\mathrm {e}^{-\frac{a}{\varepsilon }} \mathrm {e}^{\mp \frac{b}{\varepsilon }}) = a\pm b, \\&-\lim _{\varepsilon \rightarrow +0}\varepsilon \log (\mathrm {e}^{-\frac{a}{\varepsilon }}+ \mathrm {e}^{-\frac{b}{\varepsilon }}) = \min (a,b), \end{aligned} \end{aligned}$$

(3.153)

supposing $a,b \in \mathbb {R}$. In this context, (3.152) is also called the ultradiscretization (UD). 

Set

$$\begin{aligned} Z_i(x)= 1+ x E_{i,i+1}, \end{aligned}$$

(3.154)

where x is a parameter and $E_{i,j}$ is the n-by-n matrix unit whose only non-zero element is 1 at the ith row and the jth column. $Z_i(x)$ is a generator of the unipotent subgroup  of $\mathrm {SL}(n)$. The birational 3D R (3.151) is characterized as the unique solution to the matrix equation

$$\begin{aligned} Z_i(a)Z_j(b)Z_i(c) = Z_j(\tilde{c})Z_i(\tilde{b})Z_j(\tilde{a}) \qquad (|i-j|=1). \end{aligned}$$

(3.155)

It essentially reduces to the $n=3, (i,j)=(1,2)$ case:

$$\begin{aligned} \begin{pmatrix}1 &{} a &{} 0 \\ 0 &{}1 &{} 0 \\ 0 &{}0 &{}1\end{pmatrix} \begin{pmatrix}1 &{} 0 &{} 0 \\ 0 &{}1 &{} b \\ 0 &{}0 &{}1\end{pmatrix} \begin{pmatrix}1 &{} c &{} 0 \\ 0 &{}1 &{} 0 \\ 0 &{}0 &{}1\end{pmatrix} = \begin{pmatrix}1 &{} 0 &{} 0 \\ 0 &{}1 &{} \tilde{c} \\ 0 &{}0 &{}1\end{pmatrix} \begin{pmatrix}1 &{} \tilde{b} &{} 0 \\ 0 &{}1 &{} 0 \\ 0 &{}0 &{}1\end{pmatrix} \begin{pmatrix}1 &{} 0 &{} 0 \\ 0 &{}1 &{} \tilde{a} \\ 0 &{}0 &{}1\end{pmatrix}. \end{aligned}$$

(3.156)

The $R_\mathrm{birational}$ is birational due to $R_\mathrm{birational}^{-1} =R_\mathrm{birational}$. It preserves ab and bc. The intertwining relation (3.28) is a quantization of (3.155) (with $(i,j)=(1,2)$). Note that $Z_i(a)Z_j(b) = Z_j(b)Z_i(a)$ for $|i-j|>1$ also holds analogously to the Coxeter relations.

Given a Weyl group element $w \in W(A_{n-1})$ (not necessarily longest), assign a matrix $M=Z_{i_1}(x_1)\cdots Z_{i_r}(x_r)$ to a reduced expression $w = s_{i_1}\cdots s_{i_r}$. Then to any reduced expression $w = s_{j_1}\cdots s_{j_r}$ one can assign the expression $M=Z_{j_1}(\tilde{x}_1)\cdots Z_{j_r}(\tilde{x}_r)$, where $\tilde{x}_k$ is determined independently of the intermediate steps applying (3.155). This property is the source of the tetrahedron equation for $R_\mathrm{birational}$ and forms a birational counterpart of the previous calculation (3.93). In fact, the uniqueness of the map $(a,b,c,d,e,f) \mapsto (\tilde{a}, \tilde{b}, \tilde{c}, \tilde{d}, \tilde{e}, \tilde{f})$ defined by

$$\begin{aligned} Z_1(a)Z_2(b)Z_1(c)Z_3(d)Z_2(e)Z_1(f) = Z_3(\tilde{f})Z_2(\tilde{e})Z_1(\tilde{d}) Z_3(\tilde{c})Z_2(\tilde{b})Z_3(\tilde{a}) \end{aligned}$$

(3.157)

implies the tetrahedron equation of type $RRRR=RRRR$ for $R_\mathrm{birational}$. To summarize, we have:

Proposition 3.32

The birational 3D R (3.151) is an involutive map on the ring of rational functions of three variables. It satisfies the tetrahedron equation of type $RRRR=RRRR$. 

Let us denote the 3D R detailed in Sects. 3.3 and 3.4 by $R_\mathrm{quantum}$. Then we have the triad of the 3D R’s whose relation is summarized as

$$\begin{aligned} R_\mathrm{quantum} \overset{q\rightarrow 0}{\longrightarrow } R_\mathrm{combinatorial} \overset{\mathrm{UD}}{\longleftarrow } R_\mathrm{birational}. \end{aligned}$$

(3.158)

$R_\mathrm{combinatorial}$ and $R_\mathrm{birational}$ (and $R^\lambda$ below) are typical set-theoretical solutions to the tetrahedron equation. 

Remark 3.33

Define a map $R^\lambda$ involving a parameter $\lambda$ by

$$\begin{aligned} R^\lambda : (a,b,c) \mapsto \left( \frac{ab}{a+c+ \lambda abc}, \,a+c+\lambda abc,\, \frac{bc}{a+c+\lambda abc}\right) \end{aligned}$$

(3.159)

The birational 3D R (3.151) corresponds to $\lambda =0$ or equivalently infinitesimal a, b, c. Then the inversion relation $R^\lambda = (R^\lambda )^{-1}$ and the tetrahedron equation

$$\begin{aligned} R^\lambda _{124}R^\lambda _{135}R^\lambda _{236}R^\lambda _{456} = R^\lambda _{456}R^\lambda _{236}R^\lambda _{135}R^\lambda _{124} \end{aligned}$$

(3.160)

are valid.

3.6.3 Bilinearization and Geometric Interpretation

The map (3.159) is bilinearized in the following sense. Parameterize a, b, c in terms of “tau functions”  as

$$\begin{aligned} a = \frac{\tau \tau _{12}}{\tau _1 \tau _2}, \quad b = \frac{\tau _2 \tau _{123}}{\tau _{12} \tau _{23}}, \quad c = \frac{\tau \tau _{23}}{\tau _2 \tau _3}, \end{aligned}$$

(3.161)

where indices signify the shifts of independent variables of the tau functions in the respective directions., say, $\tau =\tau (\mathbf{x})$, $\tau _{12}=\tau (\mathbf{x}+\mathbf{e}_1+\mathbf{e}_2)$ etc. Suppose the tau function satisfies the bilinear equation

$$\begin{aligned} \tau _1\tau _{23}- \tau _2\tau _{13} + \tau _3\tau _{12} + \lambda \tau \tau _{123} = 0. \end{aligned}$$

(3.162)

Then the image $(a',b',c') = R^\lambda \bigl ((a,b,c)\bigr )$ in the RHS of (3.159) is expressed in the same format as (3.161) as follows:

$$\begin{aligned} a' = \frac{\tau _3 \tau _{123}}{\tau _{13} \tau _{23}}, \quad b' = \frac{\tau \tau _{13}}{\tau _{1} \tau _{3}}, \quad c' = \frac{\tau _1 \tau _{123}}{\tau _{12} \tau _{13}}. \end{aligned}$$

(3.163)

The change $(a,b,c) \mapsto (a',b',c')$ corresponds to the shift $(+3,-2,+1)$ of the argument of the tau functions. It is interpreted as a transformation of the three back faces of a cube to the front ones as in Fig. 3.3.

Fig. 3.3

Birational 3D R corresponds to a transformation generating a cube

The tetrahedron equation (3.160) is bilinearized by using tau functions living on a four-dimensional cube.  We prepare $\tau _I$ with I running over the power set of $\{1,2,3,4\}$. They are supposed to obey

$$\begin{aligned}&\tau _i\tau _{jk} - \tau _j\tau _{ik}+\tau _k\tau _{ij}+\lambda \tau \tau _{ijk}=0, \end{aligned}$$

(3.164)

$$\begin{aligned}&\tau _{il}\tau _{jkl} - \tau _{jl}\tau _{ikl}+\tau _{kl}\tau _{ijl}+\lambda \tau _l\tau _{ijkl}=0, \end{aligned}$$

(3.165)

where $\{i,j,k,l\}=\{1,2,3,4\}$.⁷ The latter is a translation of the former in the l direction.

Now the LHS of the tetrahedron equation (3.160) is described as the successive transformations

$$\begin{aligned} \begin{aligned}&\left( \frac{\tau \tau _{12}}{\tau _1\tau _2}, \frac{\tau _{2}\tau _{123}}{\tau _{12}\tau _{23}}, \frac{\tau _{23}\tau _{1234}}{\tau _{123}\tau _{234}}, \frac{\tau _{}\tau _{23}}{\tau _{2}\tau _{3}}, \frac{\tau _{3}\tau _{234}}{\tau _{23}\tau _{34}}, \frac{\tau _{}\tau _{34}}{\tau _{3}\tau _{4}} \right) \\ \overset{R^\lambda _{456}}{\longmapsto }&\left( \frac{\tau \tau _{12}}{\tau _1\tau _2}, \frac{\tau _{2}\tau _{123}}{\tau _{12}\tau _{23}}, \frac{\tau _{23}\tau _{1234}}{\tau _{123}\tau _{234}}, \frac{\tau _{4}\tau _{234}}{\tau _{24}\tau _{34}}, \frac{\tau _{}\tau _{24}}{\tau _{2}\tau _{4}}, \frac{\tau _{2}\tau _{234}}{\tau _{23}\tau _{24}} \right) \\ \overset{R^\lambda _{236}}{\longmapsto }&\left( \frac{\tau \tau _{12}}{\tau _1\tau _2}, \frac{\tau _{24}\tau _{1234}}{\tau _{124}\tau _{234}}, \frac{\tau _{2}\tau _{124}}{\tau _{12}\tau _{24}}, \frac{\tau _{4}\tau _{234}}{\tau _{24}\tau _{34}}, \frac{\tau _{}\tau _{24}}{\tau _{2}\tau _{4}}, \frac{\tau _{12}\tau _{1234}}{\tau _{123}\tau _{124}} \right) \\ \overset{R^\lambda _{135}}{\longmapsto }&\left( \frac{\tau _{4}\tau _{124}}{\tau _{14}\tau _{24}}, \frac{\tau _{24}\tau _{1234}}{\tau _{124}\tau _{234}}, \frac{\tau _{}\tau _{14}}{\tau _{1}\tau _{4}}, \frac{\tau _{4}\tau _{234}}{\tau _{24}\tau _{34}}, \frac{\tau _{1}\tau _{124}}{\tau _{12}\tau _{14}}, \frac{\tau _{12}\tau _{1234}}{\tau _{123}\tau _{124}} \right) \\ \overset{R^\lambda _{124}}{\longmapsto }&\left( \frac{\tau _{34}\tau _{1234}}{\tau _{134}\tau _{234}}, \frac{\tau _{4}\tau _{134}}{\tau _{14}\tau _{34}}, \frac{\tau _{}\tau _{14}}{\tau _{1}\tau _{4}}, \frac{\tau _{14}\tau _{1234}}{\tau _{124}\tau _{134}}, \frac{\tau _{1}\tau _{124}}{\tau _{12}\tau _{14}}, \frac{\tau _{12}\tau _{1234}}{\tau _{123}\tau _{124}} \right) . \end{aligned} \end{aligned}$$

(3.166)

Similarly, the RHS of (3.160) is realized as

$$\begin{aligned} \begin{aligned}&\left( \frac{\tau \tau _{12}}{\tau _1\tau _2}, \frac{\tau _{2}\tau _{123}}{\tau _{12}\tau _{23}}, \frac{\tau _{23}\tau _{1234}}{\tau _{123}\tau _{234}}, \frac{\tau _{}\tau _{23}}{\tau _{2}\tau _{3}}, \frac{\tau _{3}\tau _{234}}{\tau _{23}\tau _{34}}, \frac{\tau _{}\tau _{34}}{\tau _{3}\tau _{4}} \right) \\ \overset{R^\lambda _{124}}{\longmapsto }&\left( \frac{\tau _{3}\tau _{123}}{\tau _{13}\tau _{23}}, \frac{\tau _{}\tau _{13}}{\tau _{1}\tau _{3}}, \frac{\tau _{23}\tau _{1234}}{\tau _{123}\tau _{234}}, \frac{\tau _{1}\tau _{123}}{\tau _{12}\tau _{13}}, \frac{\tau _{3}\tau _{234}}{\tau _{23}\tau _{34}}, \frac{\tau _{}\tau _{34}}{\tau _{3}\tau _{4}} \right) \\ \overset{R^\lambda _{135}}{\longmapsto }&\left( \frac{\tau _{34}\tau _{1234}}{\tau _{134}\tau _{234}}, \frac{\tau _{}\tau _{13}}{\tau _{1}\tau _{3}}, \frac{\tau _{3}\tau _{134}}{\tau _{13}\tau _{34}}, \frac{\tau _{1}\tau _{123}}{\tau _{12}\tau _{13}}, \frac{\tau _{13}\tau _{1234}}{\tau _{123}\tau _{134}}, \frac{\tau _{}\tau _{34}}{\tau _{3}\tau _{4}} \right) \\ \overset{R^\lambda _{236}}{\longmapsto }&\left( \frac{\tau _{34}\tau _{1234}}{\tau _{134}\tau _{234}}, \frac{\tau _{4}\tau _{134}}{\tau _{14}\tau _{34}}, \frac{\tau _{}\tau _{14}}{\tau _{1}\tau _{4}}, \frac{\tau _{1}\tau _{123}}{\tau _{12}\tau _{13}}, \frac{\tau _{13}\tau _{1234}}{\tau _{123}\tau _{134}}, \frac{\tau _{1}\tau _{134}}{\tau _{13}\tau _{14}} \right) \\ \overset{R^\lambda _{456}}{\longmapsto }&\left( \frac{\tau _{34}\tau _{1234}}{\tau _{134}\tau _{234}}, \frac{\tau _{4}\tau _{134}}{\tau _{14}\tau _{34}}, \frac{\tau _{}\tau _{14}}{\tau _{1}\tau _{4}}, \frac{\tau _{14}\tau _{1234}}{\tau _{124}\tau _{134}}, \frac{\tau _{1}\tau _{124}}{\tau _{12}\tau _{14}}, \frac{\tau _{12}\tau _{1234}}{\tau _{123}\tau _{124}} \right) . \end{aligned} \end{aligned}$$

(3.167)

The initial and the final six components correspond to the faces 12, 13, 14, 23, 24, 34 of the 4D cube up to translation. Their tau functions are simply related by the interchange $\tau _I \leftrightarrow \tau _{\{1,2,3,4\}\setminus I}$. It means that the two sides of the tetrahedron equation represent transformations of the “back” six faces of a 4D cube to the “front” ones as compositions of elementary transformations associated with the 3D cube in Fig. 3.3. This 4D picture is rather transparent. On the other hand, one can also describe it in 3D space as a dissection of a rhombic dodecahedron into four quadrilatelal hexahedra. After all, the 3D R in this chapter provides a quantization of the transformation of the geometric data associated with such objects.

3.7 Bibliographical Notes and Comments

The RTT realization of the quantized coordinate rings has been presented in many publications. See for example [43, 127] and [29, Chap. 7]. The fundamental Theorem 3.3 on the representations of $A_q(\mathfrak {g})$ was obtained in [138, 139, 146]. Its application to the tetrahedron equation was found in [77]. In fact, Sect. 3.3, Theorems 3.11 and 3.5 form an exposition of it along [93, Sect. 2]. In particular, the formula (3.67) is a correction of that for $S^{abc}_{ijk}$ on [77, p. 194] which contained an unfortunate misprint. The solution of the tetrahedron equation of type $RRRR=RRRR$ was derived later also from a quantum geometry consideration [16, 18]. It was shown to coincide with the 3D R in [77] (with the correction of the misprint) at [93, Eq. (2.29)]. The operator version $R^{ab}_{ij}$ (3.69) of the 3D R was introduced in [84, Eq. (8)]. A similar operator with respect to the second component of the 3D R is given in [86, Eqs. (2.68) and (2.70)]. The integral formula (3.76) and Theorem 3.21 are due to [18, 132], respectively. The solution to the tetrahedron equation of type $MMLL=LLMM$ (Theorem 3.25) is due to [90, Theorem 3.4] and [18, Eq. (34)] with some conventional adjustment. Theorem 3.26 is taken from [92, Theorem 3.1]. They have applications to the multispecies totally asymmetric simple exclusion process (Chap. 18) and multispecies totally asymmetric zero rage process. More comments on them are available in Sect. 18.6. Proposition 3.28 for the boundary vector was obtained in [107, Proposition 4.1].

As for the birational and combinatorial 3D R, there are many relevant publications. The map (3.151) is a member of a wider list in [70, 71, 130]. It has also appeared in [112, Proposition 2.5] and [21, Theorem 3.1] for example. It is characterized as the transition map of parameterizations of the totally positive part of the special linear group $\mathrm {SL}(3)$. Such transition maps have been described explicitly for any semisimple Lie groups, and they all admit the combinatorial counterparts via the tropical variable change  [22, 113]. The deformation (3.159) involving a cubic term (see [69]) has been linked to “electrical” Lie groups [110]. Sect. 3.6.3 is an exposition of the classical geometry aspects with an additional perspective concerning tau functions. For related topics, see [16, 24, 69, 78] and the references therein.