Application to Multispecies TASEP

Abstract

This chapter is an exposition of a 3D approach to an integrable Markov process called the n species totally asymmetric simple exclusion process (n-TASEP). The main result is a matrix product formula of the stationary probability involving layer transfer matrices of the $q=0$-oscillator-valued five-vertex model on an $n \times n$ lattice. The stationary condition is translated into their quadratic relations, the so-called Faddeev–Zamolodchikov algebra, which are highly non-local from the viewpoint of the five-vertex model. They are shown to be a far-reaching consequence of the single tetrahedron equation of type $MMLL=LLMM$ in Sect. 2.6 and its solution in Theorem 3.25.

18.1 Introduction

The totally asymmetric simple exclusion process (TASEP) is a continuous-time Markov process of particles obeying a stochastic dynamics governed by a master equation.  We consider the n-TASEP on the 1D periodic lattice ${\mathbb Z}_L$, where each site variable assumes $\{0,1,\ldots , n\}$ (Fig. 18.1).

The first basic problem is the determination of the stationary state, which is analogous to the ground state of quantum spin chains. The probability of finding a given particle configuration in the stationary state is called the stationary probability. It is an analogue of the amplitude of a configuration in the ground state for quantum spin chains. In integrable situations, the amplitude should be obtained by the Bethe ansatz, therefore it is transcendental in general since the Bethe roots are so.  On the other hand, the stationary state is the unique null eigenvector of the Markov matrix, implying that it should be algebraic with respect the parameters of the model. These arguments suggest that stationary probabilities of integrable Markov processes should be something between transcendental and algebraic, and it is the place where the matrix product structure emerges naturally.

The n-TASEP considered in this chapter is indeed integrable, being a special case of a more general partially asymmetric simple exclusion process or the $A^{(1)}_{n}$ vertex model with the standard nested Bethe ansatz solution, e.g. [4]. However, providing a full combinatorial description with the stationary probabilities is another problem, which we are going to address in this chapter by a 3D approach. As we will note in Remark 18.7, it leads to an intriguing duality between $A^{(1)}_{n}$ and $A^{(1)}_{L-1}$ exchanging the role of internal and external spaces. 

Fig. 18.1

A configuration of particles in n-TASEP ($n \ge 4$)

18.2 n-TASEP

18.2.1 Definition of n-TASEP

Consider the periodic 1D chain with L sites ${\mathbb Z}_L$. Each site $i \in {\mathbb Z}_L$ is populated with a local state $\sigma _i \in \{0,1,\ldots , n\}$. It is interpreted as a species of the particle occupying the site i.¹ We assume $1 \le n < L$. Consider a stochastic model on ${\mathbb Z}_L$ such that neighboring pairs of local states $(\sigma _i, \sigma _{i+1})=(\alpha ,\beta )$ are interchanged as $\alpha \, \beta \rightarrow \beta \, \alpha$ if $\alpha >\beta$ with the uniform transition rate. The space of states is given by

$$\begin{aligned} ({\mathbb C}^{n+1})^{\otimes L} \simeq \bigoplus _{(\sigma _1,\ldots , \sigma _L) \in \{0,\ldots , n\}^L} {\mathbb C}|\sigma _1,\ldots , \sigma _L\rangle . \end{aligned}$$

(18.1)

Let ${\mathbb P}(\sigma _1,\ldots , \sigma _L; t)$ be the probability of finding the configuration $(\sigma _1,\ldots , \sigma _L)$ at time t, and set

$$\begin{aligned} |P(t)\rangle = \sum _{(\sigma _1,\ldots , \sigma _L) \in \{0,\ldots , n\}^L} {\mathbb P}(\sigma _1,\ldots , \sigma _L; t)|\sigma _1,\ldots , \sigma _L\rangle . \end{aligned}$$

(18.2)

By n-TASEP we mean the stochastic system governed by the continuous-time master equation

$$\begin{aligned} \frac{d}{dt}|P(t)\rangle = H |P(t)\rangle , \end{aligned}$$

(18.3)

where H is a Markov matrix defined by

$$\begin{aligned} H = \sum _{i \in {\mathbb Z}_L} h_{i,i+1},\qquad h |\alpha , \beta \rangle = \left\{ \begin{array}{ll} |\beta , \alpha \rangle -|\alpha , \beta \rangle &{} \;(\alpha >\beta ),\\ 0 &{} \; (\alpha \le \beta ). \end{array} \right. \end{aligned}$$

(18.4)

Here $h_{i,i+1}$ is the local Markov matrix that acts as h on the ith and the $(i+1)$th components and as the identity elsewhere. The master equation (18.3) preserves the total probability.

The Markov matrix H preserves the subspaces, called sectors, consisting of the configurations with prescribed multiplicity $\textbf{m}=(m_0,\ldots , m_n) \in ({\mathbb Z}_{\ge 0})^{n+1}$ of particles:

$$\begin{aligned} \mathcal {S}(\textbf{m}) = \{{\boldsymbol{\sigma }}=(\sigma _1,\ldots , \sigma _L) \in \{0,\ldots , n\}^L\;|\; \sum _{1 \le j \le L}\delta _{k,\sigma _j}=m_k,\forall k\}. \end{aligned}$$

(18.5)

The space of states (18.1) is decomposed as $\bigoplus _{\textbf{m}} \bigoplus _{{\boldsymbol{\sigma }} \in \mathcal {S}(\textbf{m}) } {\mathbb C}| {\boldsymbol{\sigma }}\rangle$, where the outer sum ranges over $m_i \in {\mathbb Z}_{\ge 0}$ such that $m_0+ \cdots + m_n = L$. A sector $\bigoplus _{{\boldsymbol{\sigma }} \in \mathcal {S}(\textbf{m}) } {\mathbb C}| {\boldsymbol{\sigma }}\rangle$ such that $m_i \ge 1$ for all $0 \le i \le n$ is called basic. Non-basic sectors are equivalent to a basic sector for $n'$-TASEP with some $n'<n$ by a suitable relabeling of species. Thus we shall exclusively deal with basic sectors, therefore $n<L$ is assumed as mentioned before. The spectrum of H is known to exhibit a remarkable duality described by a Hasse diagram [4].

18.2.2 Stationary States

In each sector $\bigoplus _{{\boldsymbol{\sigma }} \in \mathcal {S}(\textbf{m}) } {\mathbb C}| {\boldsymbol{\sigma }}\rangle$ there is a unique vector $|{\bar{P}}(\textbf{m})\rangle$ up to normalization, called the stationary state, satisfying $H|{\bar{P}}(\textbf{m})\rangle = 0$.  The stationary state for 1-TASEP is trivial under the periodic boundary condition in the sense that all the monomials have the same coefficient, i.e. all the configurations are realized with an equal probability.

Example 18.1

Let us present (unnormalized) stationary states in small sectors of 2-TASEP and 3-TASEP in the form

$$\begin{aligned} |{\bar{P}}(\textbf{m})\rangle = |\xi (\textbf{m})\rangle + C|\xi (\textbf{m})\rangle + \cdots + C^{L-1}|\xi (\textbf{m})\rangle \end{aligned}$$

(18.6)

respecting the translational symmetry $HC=CH$ under the ${\mathbb Z}_L$ cyclic shift $C|\sigma _1, \sigma _2,\ldots , \sigma _L\rangle = |\sigma _L, \sigma _1, \ldots , \sigma _{L-1}\rangle$. The choice of the vector $|\xi (\textbf{m})\rangle$ is not unique.

The red underlines are put for convenience for Example 18.3. As these coefficients indicate, stationary states are non-trivial for $n\ge 2$. The theme of this chapter is to elucidate a 3D integrability behind them, which will ultimately be related to the tetrahedron equation.

18.2.3 Matrix Product Formula

Consider a stationary state

$$\begin{aligned} |{\bar{P}}(\textbf{m})\rangle = \sum _{{\boldsymbol{\sigma }} \in \mathcal {S}(\textbf{m})} {\mathbb P}({\boldsymbol{\sigma }}) | {\boldsymbol{\sigma }} \rangle \end{aligned}$$

(18.7)

and postulate that the stationary probability ${\mathbb P}({\boldsymbol{\sigma }})$ is expressed in the matrix product form

$$\begin{aligned} {\mathbb P}(\sigma _1,\ldots , \sigma _L) = \textrm{Tr}(X_{\sigma _1}\cdots X_{\sigma _L}) \end{aligned}$$

(18.8)

in terms of some operators $X_0, \ldots , X_n$. Introduce the notations for the matrix elements of the local Markov matrix (18.4) and the associated product of $X_i$’s as

$$\begin{aligned} h|\alpha , \beta \rangle = \sum _{\gamma ,\delta }h^{\gamma ,\delta }_{\alpha ,\beta } |\gamma , \delta \rangle ,\qquad (hXX)_{\alpha , \beta } := \sum _{\gamma ,\delta }h^{\alpha ,\beta }_{\gamma ,\delta } X_\gamma X_\delta , \end{aligned}$$

(18.9)

where both sums range over $\gamma , \delta \in \{0,1,\ldots , n\}$. Then we have

$$\begin{aligned} H |{\bar{P}}(\textbf{m})\rangle&= \sum _{i \in {\mathbb Z}_L} \sum _{\boldsymbol{\sigma }\in \mathcal {S}(\textbf{m})} {\mathbb P}(\ldots , \sigma _i, \sigma _{i+1},\ldots )h_{i,i+1} |\ldots , \sigma _i, \sigma _{i+1},\ldots \rangle \nonumber \\&= \sum _{i \in {\mathbb Z}_L}\sum _{\boldsymbol{\sigma }\in \mathcal {S}(\textbf{m})} \sum _{\sigma '_i, \sigma '_{i+1}} \textrm{Tr}(\cdots X_{\sigma _i}X_{\sigma _{i+1}}\cdots ) h^{\sigma '_i, \sigma '_{i+1}}_{\sigma _i, \sigma _{i+1}} |\ldots , \sigma '_i, \sigma '_{i+1},\ldots \rangle \nonumber \\&= \sum _{\boldsymbol{\sigma }\in \mathcal {S}(\textbf{m})}\sum _{i \in {\mathbb Z}_L} \textrm{Tr}(\cdots (hXX)_{\sigma _i, \sigma _{i+1}}\cdots ) |\ldots , \sigma _i, \sigma _{i+1},\ldots \rangle . \end{aligned}$$

(18.10)

Therefore if there is another set of operators ${\hat{X}}_0, \ldots , {\hat{X}}_n$ obeying the so-called hat relation 

$$\begin{aligned} (hXX)_{\alpha , \beta } = X_\alpha {\hat{X}}_\beta - {\hat{X}}_\alpha X_\beta , \end{aligned}$$

(18.11)

the stationary condition $H|{\bar{P}}(\textbf{m})\rangle = 0$ holds thanks to the cyclicity of the trace. Then the trace (18.8), if convergent, must coincide with the actual stationary probability up to overall normalization due to the uniqueness of the stationary state in every sector. Note, on the other hand, that ${\hat{X}}_i$ satisfying the hat relation with a given $X_i$ is not unique. For instance, ${\hat{X}}_i \rightarrow {\hat{X}}_i+ c X_i$ leaves (18.11) unchanged.

From (18.4) and (18.9), the hat relation (18.11) is given concretely as

$$\begin{aligned}&[X_i,{\hat{X}}_j]=[{\hat{X}}_i,X_j ]\quad \;\; \qquad (0 \le i,j \le n), \end{aligned}$$

(18.12)

$$\begin{aligned}&X_iX_j={\hat{X}}_iX_j-X_i{\hat{X}}_j \qquad (0 \le j < i \le n). \end{aligned}$$

(18.13)

Suppose we have the operators $X_0(z), \ldots , X_n(z)$ which depend on a spectral parameter z and satisfy

$$\begin{aligned}{}[X_i(x),X_j(y)]&=[X_i(y),X_j(x)]\qquad (0 \le i,j \le n), \end{aligned}$$

(18.14)

$$\begin{aligned} xX_i(y)X_j(x)&=yX_i(x)X_j(y)\qquad \;(0 \le j<i \le n). \end{aligned}$$

(18.15)

Then the hat relations (18.12) and (18.13) are realized by setting

$$\begin{aligned} X_i=X_i(z=1), \qquad {\hat{X}}_i=\frac{d}{dz}X_i(z) |_{z=1} \qquad (0 \le i \le n). \end{aligned}$$

(18.16)

The relations (18.14) and (18.15) are rearranged as

$$\begin{aligned} X_i(x)X_j(y) = \left\{ \begin{array}{lll} X_i(y)X_j(x) + (1-\frac{x}{y})X_j(y)X_i(x) \;\;&{} i<j,\\ X_i(y)X_i(x) &{} i=j,\\ \frac{x}{y}X_i(y)X_j(x) &{} i>j. \end{array} \right. \end{aligned}$$

(18.17)

This exchange rule satisfies the Yang–Baxter relation in the sense that the two ways of rewriting $X_i(x)X_j(y)X_k(z)$ as linear combinations of $X_{k'}(z)X_{j'}(y)X_{i'}(x)$ with $\{i',j',k' \} = \{i,j,k\}$ lead to the identical result. Such a quadratic exchange rule, which is sometimes referred to as Faddeev–Zamolodchikov algebra, is a signal of the integrable structure of the n-TASEP.  In this way, seeking the matrix product formula (18.8) of the stationary probability is transformed to the problem of constructing the operator $X_i(z)$ satisfying (18.17).

18.2.4 Matrix Product Operator $X_i(z)$

We will show that the following operator $X_i(z)$ fulfills (18.17):

(18.18)

It represents a configuration sum, i.e. the partition function of the $\textrm{Osc}_{q=0}$-valued five-vertex model on the size n triangular shape region with a prescribed condition along the SE boundary. The $\textrm{Osc}_{q=0}$-valued five-vertex model has the local “Boltzmann weight” $1, {\textbf{b}}^+ , {\textbf{b}}^- , {\textbf{t}}$ assigned to each vertex as

(18.19)

Each edge of (18.18) takes 0 or 1 and the sum (except those fixed on the SE boundary) extends over all the configurations such that every vertex is one of the above five types.² In (18.19), edges assuming 0 and 1 are colored in black and red respectively. This convention will apply in the rest of the chapter.³ Given such a configuration, the summand is the tensor product of the local Boltzmann weights $1, {\textbf{b}}^+ , {\textbf{b}}^- , {\textbf{t}}$. They are linear operators on the Fock space $\mathcal {F} = \bigoplus _{m \ge 0}{\mathbb C}|m\rangle$⁴ defined by

$$\begin{aligned} {\textbf{b}}^+ {\left| m\right\rangle }={\left| m+1\right\rangle }, \ \ {\textbf{b}}^- {\left| m\right\rangle }={\left| m-1\right\rangle }, \ \ {\textbf{t}}{\left| m\right\rangle }={\delta }_{m,0}{\left| m\right\rangle }, \end{aligned}$$

(18.20)

which obey the relations

$$\begin{aligned} {\textbf{t}}\, {\textbf{b}}^+ =0,\ \ \ \ \ \ {\textbf{b}}^- \,{\textbf{t}}=0,\ \ \ \ \ {\textbf{b}}^+ \, {\textbf{b}}^- =1- {\textbf{t}},\ \ \ \ \ {\textbf{b}}^- \, {\textbf{b}}^+ =1. \end{aligned}$$

(18.21)

The relations (18.20) and (18.21) are identified with the q-oscillator ones (3.13) and (3.12) in the well defined limit

$$\begin{aligned} {\textbf{b}}^{\pm } = \lim _{q\rightarrow 0} \mathrm{\textbf{a}}^{\pm } , \qquad {\textbf{t}}= \lim _{q\rightarrow 0} \mathrm{\textbf{k}}, \end{aligned}$$

(18.22)

where an extra relation ${\textbf{t}}^2 = {\textbf{t}}$ is acquired. The $\textrm{Osc}_{q=0}$ operators ${\textbf{b}}^{\pm } , {\textbf{t}}$ attached to different vertices act on different copies of $\mathcal {F}$. Thus $X_i(z)\in \textrm{End}(\mathcal {F}^{\otimes n(n-1)/2})$.

The trace in (18.8) is taken over $\mathcal {F}^{\otimes n(n-1)/2}$, where each component is calculated by $\textrm{Tr}_{\mathcal {F}}(X) = \sum _{m \ge 0}\langle m | X | m \rangle$ with $\langle m | m'\rangle = \delta _{m,m'}$. See (3.16) and the explanation after Fig. 11.3. Finally, the summands in (18.18) are attached with the overall factor $z^{\alpha _1+\cdots + \alpha _n}$, where $\alpha _i=0,1$ is the variable on the ith vertical edge from the left on the top.

The matrix product operator $X_i(z)$ has the form of a corner transfer matrix [10, Chap. 13] of the $\textrm{Osc}_{q=0}$-valued five-vertex model, although it acts along the perpendicular direction to the layer as opposed to the usual 2D setting. Equivalently, one may view it as a layer transfer matrix of the 3D lattice model where the edges perpendicular to the plane (18.18) are assigned with $\mathcal {F}$. The stationary probability (18.8) is then interpreted as a partition function of the 3D system of prism shape which is periodic along the third direction.

Remark 18.2

The result (18.8) with $X_i$ defined by (18.16) and (18.18) corresponds to the integer normalization

$$\begin{aligned} {\mathbb P}(\sigma _1, \ldots , \sigma _L) = 1\quad \textrm{for}\;\; \sigma _1 \ge \cdots \ge \sigma _L. \end{aligned}$$

In this normalization ${\mathbb P}({\boldsymbol{\sigma }}) \in {\mathbb Z}_{\ge 1}$ holds for all the state ${\boldsymbol{\sigma }} \in \mathcal {S}(\textbf{m})$.

Example 18.3

For $n=2$ the operators $X_0(z), X_1(z), X_2(z)$ are given by

From (18.16) we have ${\hat{X}}_0 = {\textbf{b}}^+ , {\hat{X}}_1 = {\textbf{t}}, {\hat{X}}_2 = {\textbf{b}}^- +2$. For instance,

$$\begin{aligned} {\mathbb P}(00221)&= \textrm{Tr}(X_0X_0X_2X_2X_1) =\textrm{Tr}\bigl ((1+{\textbf{b}}^+ )(1+{\textbf{b}}^+ )(1+{\textbf{b}}^- )(1+{\textbf{b}}^- ){\textbf{t}}\bigl )=1, \\ {\mathbb P}(20201)&= \textrm{Tr}(X_2X_0X_2X_0X_1) =\textrm{Tr}\bigl ((1+{\textbf{b}}^- )(1+{\textbf{b}}^+ )(1+{\textbf{b}}^- )(1+{\textbf{b}}^+ ){\textbf{t}}\bigl )=5, \end{aligned}$$

which reproduce the coefficients in the underlined terms in $|\xi (2,1,2)\rangle$ in Example 18.1. As this example indicates, for the convergence of the trace, it is sufficient to have at least one ${\textbf{t}}$ for every $\mathcal {F}$ component of $\textrm{Tr}_{\mathcal {F}^{\otimes n(n-1)/2}}(X_{\sigma _1}\cdots X_{\sigma _L})$.

Example 18.4

For $n=3$, the operators $X_0(z), \ldots , X_3(z)$ are given by

Here and in what follows, the components of the tensor product will always be ordered so that they correspond, from left to right, to the vertices from the top to the bottom and from the left to the right.

To summarize so far, we are to show:

Theorem 18.5

The operators $X_0(z),\ldots , X_n(z)$ defined by (18.18) satisfy the Faddeev–Zamolodchikov algebra relations (18.14) and (18.15).

 

From the viewpoint of the five-vertex model, this is a highly non-local property. Our goal in the rest of the chapter is to reveal that Theorem 18.5 is a far-reaching consequence of the single local relation which is nothing but the tetrahedron equation.

Remark 18.6

The five vertices in (18.19) are identified with those for the 3D L ${\mathscr {L}}(z=1)^{ab}_{ij}$ in (18.25) at $q=0$. See (18.22). Therefore each Fock space component of the trace (18.8) takes the form $\textrm{Tr}_{\mathcal {F}}({\mathscr {L}}(1)^{a_1,b_1}_{i_1,j_1}\cdots {\mathscr {L}}(1)^{a_L,b_L}_{i_L,j_L})$. It coincides with the matrix product formula (11.26) of a quantum R matrix $S^{\textrm{tr}_3}(z)$ at $z=1,q=0$ up to an overall factor and the conjugation by $(\sigma \otimes \sigma )$.⁵ The coincidence leads to a further reformulation of the stationary probability in terms of a composition of the quantum R matrices at $q=0$ [89]. An important consequence of it is the convergence of the trace. In fact, it assures that at least one ${\textbf{t}}$ is included in ${\mathscr {L}}(1)^{a_1,b_1}_{i_1,j_1},\ldots , {\mathscr {L}}(1)^{a_L,b_L}_{i_L,j_L}$ for every Fock space $\mathcal {F}$ provided that we are in a basic sector defined after (18.5).

Remark 18.7

Another notable feature of the observation in Remark 18.6 is that the relevant quantum affine algebra becomes $U_p(A^{(1)}_{L-1})$ rather than $U_p(A^{(1)}_{n})$. Thus, dealing with n-TASEP on the periodic lattice ${\mathbb Z}_L$ eventually leads to the size n system (18.18) with “symmetry algebra” of rank $L-1$. It is another manifestation of the duality mentioned in the second last paragraph of Sect. 15.6.

18.3 3D L, M Operators and the Tetrahedron Equation

We invoke the results in Sect. 3.5.3. Let $V = {\mathbb C}v_0 \oplus {\mathbb C}v_1$ and $L(z), M(z) \in \textrm{End}(V \otimes V \otimes {\mathcal F}_q)$ be the 3D L and M operators defined in (3.118)–(3.121). They contain the parameters $\mu$ and $\nu$, respectively. In this chapter, for reasons of convention, we will work with

$$\begin{aligned} {\mathscr {L}}(z)&= (\sigma \otimes \sigma \otimes 1 ) L(z)|_{\mu =1} (\sigma \otimes \sigma \otimes 1) = \sum _{a,b,i,j}E_{ai}\otimes E_{bj} \otimes {\mathscr {L}}(z)^{ab}_{i j}, \end{aligned}$$

(18.23)

$$\begin{aligned} {\mathscr {M}}(z)&= (\sigma \otimes \sigma \otimes 1) M(z)|_{\nu =1} (\sigma \otimes \sigma \otimes 1)= \sum _{a,b,i,j}E_{ai}\otimes E_{bj} \otimes {\mathscr {M}}(z)^{ab}_{i j}, \end{aligned}$$

(18.24)

where $\sigma (v_k) = v_{1-k}$ and the other notations are parallel with (3.118) and (3.119). From (3.120), their non-zero matrix elements are given as follows:

(18.25)

Here $\mathrm{\textbf{a}}^{\pm } , \mathrm{\textbf{k}}$ are q-oscillators (3.13) and ${\tilde{\mathrm{\textbf{k}}}}= \mathrm{\textbf{k}}|_{q\rightarrow -q}$ as defined in (3.121). The operators ${\mathscr {L}}(z)$ and ${\mathscr {M}}(z)$ are simply related by ${\mathscr {M}}(z) = {\mathscr {L}}(z)|_{q\rightarrow -q}$. From Theorem 3.25 they also satisfy the tetrahedron equation 

$$\begin{aligned}&{\mathscr {M}}_{126}(z_{12}){\mathscr {M}}_{346}(z_{34}){\mathscr {L}}_{135}(z_{13}){\mathscr {L}}_{245}(z_{24}) \nonumber \\&= {\mathscr {L}}_{245}(z_{24}){\mathscr {L}}_{135}(z_{13}){\mathscr {M}}_{346}(z_{34}){\mathscr {M}}_{126}(z_{12}), \end{aligned}$$

(18.26)

where $z_{ij}=z_i/z_j$. In terms of the 3D diagram representation (cf. Sect. 2.6) as

(18.27)

the tetrahedron equation is expressed as

Let us introduce the dual of V by

$$\begin{aligned} V^* = {\mathbb C}v^*_0 \oplus {\mathbb C}v^*_1,\quad \langle v^*_i,v_j\rangle =\delta _{ij}. \end{aligned}$$

(18.28)

We let ${\mathscr {M}}(z)$ act on $V^*\otimes V^*\otimes \mathcal {F}_q^*$ from the right as

$$\begin{aligned} (v^*_a\otimes v^*_b\otimes \langle \xi |\, ){\mathscr {M}}(z)=\sum _{i,j=0,1}v^*_i\otimes v^*_j{\otimes }{\langle \xi |}{\mathscr {M}}(z)^{ab}_{ij}. \end{aligned}$$

(18.29)

Set

$$\begin{aligned} \left| {\chi }(z) \right\rangle ={\sum _{m \ge 0}\frac{z^m}{(-q;-q)_{m}}{\left| m \right\rangle }}, \qquad \left\langle {\chi }(z) \right| =\sum _{m \ge 0}\frac{z^m}{(-q;-q)_m}\langle m|. \end{aligned}$$

(18.30)

Proposition 18.8

The vectors

$$\begin{aligned}&v_0\otimes v_0{\otimes }{\left| \xi \right\rangle }, \quad v_1\otimes v_1{\otimes }{\left| \xi \right\rangle }, \quad ({\mu }v_1\otimes v_0+{\nu }v_0\otimes v_1){\otimes } |\chi ({\textstyle \frac{\mu z}{\nu }}) \rangle , \end{aligned}$$

(18.31)

$$\begin{aligned}&v^*_0\otimes v^*_0{\otimes }{\left\langle \xi \right| }, \quad v^*_1\otimes v^*_1{\otimes }{\left\langle \xi \right| }, \quad (\mu v^*_1\otimes v^*_0+\nu v^*_0\otimes v^*_1){\otimes }\langle \chi ({\textstyle \frac{\mu }{\nu z}})| \end{aligned}$$

(18.32)

are right and left eigenvectors of ${\mathscr {M}}(z)$ with eigenvalue 1 for any $|\xi \rangle \in \mathcal {F}_q$, $\langle \xi | \in \mathcal {F}_q^*$, and ${\mu },{\nu }(\ne 0)\in {\mathbb C}$.

Proof

The non-trivial cases are verified by directly checking

$$\begin{aligned}&\sum _{i+j=1}\mu ^i\nu ^j{\mathscr {M}}(z)_{i j}^{k l} |\chi ({\textstyle \frac{\mu z}{\nu }})\rangle =\mu ^k\nu ^l|\chi ({\textstyle \frac{\mu z}{\nu }})\rangle , \end{aligned}$$

(18.33)

$$\begin{aligned}&\sum _{i+j=1}\mu ^i\nu ^j \langle \chi ({\textstyle \frac{\mu }{\nu z}})|{\mathscr {M}}(z)^{i j}_{k l} =\mu ^k\nu ^l \langle \chi ({\textstyle \frac{\mu }{\nu z}})|. \end{aligned}$$

(18.34)

One can utilize (3.134), (3.135), (3.138) and (3.139) with $q\rightarrow -q$. $\square$

As a corollary of Proposition 18.8, we have the following equality for any $k,l=0,1$:

$$\begin{aligned} \sum _{i,j}{\mathscr {M}}(z)^{k l}_{i j}|\chi (z)\rangle =|\chi (z)\rangle ,\quad \langle \chi (z^{-1})|\sum _{i,j}{\mathscr {M}}(z)^{i j}_{k l}=\langle \chi (z^{-1})|. \end{aligned}$$

(18.35)

18.4 Layer Transfer Matrices

18.4.1 Layer Transfer Matrices with Mixed Boundary Condition

Fix positive integers m, n. Given the arrays $\textbf{a} = (a_1,\ldots , a_m), \textbf{i} = (i_1,\ldots , i_m) \in \{0,1\}^m$ and $\textbf{b} = (b_1,\ldots , b_n), \textbf{j} = (j_1,\ldots , j_n) \in \{0,1\}^n$, define a linear operator $T(z)^{\textbf{a}, \textbf{b}}_{\textbf{i}, \textbf{j}}$ on $\mathcal {F}_q^{\otimes mn}$ graphically as follows:

It represents the sums over $\{0,1\}$ for all the internal edges under the prescribed boundary condition. Each arrow, either horizontal or vertical, carries V. Each vertex represents ${\mathscr {L}}(z)^{a b}_{i j}$ in (18.25) including the spectral parameter z. Penetrating each vertex from back to front, the Fock space $\mathcal {F}_q$ runs along a blue arrow as in the left diagram in (18.27). When this feature is to be emphasized, we depict $T(z)^{\textbf{a}, \textbf{b}}_{\textbf{i}, \textbf{j}}$, say for $(m,n)=(3,4)$, as

In our working below, the following object plays the central role:

(18.36)

The sum $\sum _{\textbf{i}, \textbf{b}}$ extends over $\textbf{i} \in \{0,1\}^m$ and $\textbf{b} \in \{0,1\}^n$. The operators $T(z)^{\textbf{a}, \textbf{b}}_{\textbf{i}, \textbf{j}}$ and $S(z)^\textbf{a}_\textbf{j}$ are the layer transfer matrices of size $m \times n$ with fixed and mixed (NW-free and SE-fixed) boundary conditions, respectively.

Example 18.9

Consider the simplest case $(m,n)=(1,1)$, where $T(z)^{a b}_{i j} = {\mathscr {L}}(z)^{a b}_{i j}$. Therefore from (18.24) we have

$$\begin{aligned} S(z)^0_0 = 1+z\textbf{a}^+,\quad S(z)^1_1 = 1+z^{-1}{} \textbf{a}^-,\quad S(z)^0_1 = \textbf{k},\quad S(z)^1_0 = -q \textbf{k}. \end{aligned}$$

Example 18.10

Consider the case $(m,n)=(2,2)$. $S(z)^{00}_{00}$ consists of the following 8 terms:

Thus we have

$$\begin{aligned} S(z)^{00}_{00}&= 1\!\otimes \!1 \!\otimes \!1 \!\otimes \!1 + z \textbf{a}^+ \!\otimes \!1 \!\otimes \!1 \!\otimes \!1 + z\textbf{k} \!\otimes \!\textbf{a}^+ \!\otimes \!1 \!\otimes \!1 + z\textbf{a}^- \!\otimes \!\textbf{a}^+\!\otimes \!\textbf{a}^+ \!\otimes \!1 \nonumber \\&+z^2 1 \!\otimes \!\textbf{a}^+ \!\otimes \!\textbf{a}^+ \!\otimes \!1 -qz 1 \!\otimes \!\textbf{k}\!\otimes \!\textbf{k} \!\otimes \!\textbf{a}^+ -qz^2 \textbf{a}^+ \!\otimes \!\textbf{k} \!\otimes \!\textbf{k} \!\otimes \!\textbf{a}^+ -qz \textbf{k}\!\otimes \!1 \!\otimes \!\textbf{a}^+ \!\otimes \!1. \end{aligned}$$

(18.37)

Example 18.11

Consider the case $(m,n)=(2,2)$. $S(z)^{10}_{10}$ consists of the following 8 terms:

Thus we have

$$\begin{aligned} S(z)^{10}_{10}&= z^{-1}1\!\otimes \!\textbf{a}^- \!\otimes \!\textbf{a}^- \!\otimes \!\textbf{a}^+ + \textbf{a}^+ \!\otimes \!\textbf{a}^- \!\otimes \!\textbf{a}^- \!\otimes \!\textbf{a}^+ + \textbf{k} \!\otimes \!1 \!\otimes \!\textbf{a}^- \!\otimes \!\textbf{a}^+ + \textbf{a}^- \!\otimes \!1 \!\otimes \!1 \!\otimes \!\textbf{a}^+ \nonumber \\&+z 1 \!\otimes \!1 \!\otimes \!1 \!\otimes \!\textbf{a}^+ -q 1 \!\otimes \!\textbf{k}\!\otimes \!\textbf{k} \!\otimes \!1 -q \textbf{k} \!\otimes \!\textbf{a}^- \!\otimes \!1 \!\otimes \!\textbf{a}^+ -qz^{-1}{} \textbf{a}^- \!\otimes \!\textbf{k} \!\otimes \!\textbf{k} \!\otimes \!1. \end{aligned}$$

(18.38)

18.4.2 Commutativity

Proposition 18.12

The layer transfer matrices $S(z)^\textbf{a}_\textbf{j}$ with the common SE boundary condition $\textbf{a}, \textbf{j}$ form a commuting family, i.e.

$$\begin{aligned}{}[S(x)^\textbf{a}_\textbf{j},S(y)^\textbf{a}_\textbf{j}]=0. \end{aligned}$$

(18.39)

Proof

This is a consequence of the tetrahedron equation (18.26) and the trivial eigenvectors of ${\mathscr {M}}(z)$ in Proposition 18.8. Consider the following two operators on $\mathcal {F}_q^{\otimes mn}\otimes \mathcal {F}_q$:

$$\begin{aligned} \sum _\mathbf{b,b'} \Bigl ({\mathscr {M}}({\textstyle \frac{x}{x'}})_{a_m,a_m}^{a_m,a_m}\cdots {\mathscr {M}}({\textstyle \frac{x}{x'}})_{a_1,a_1}^{a_1,a_1}\Bigr ) \Bigl ({\mathscr {M}}({\textstyle \frac{y}{y'}})_{b_n,b'_n}^{c_n,c'_n}\cdots {\mathscr {M}}({\textstyle \frac{y}{y'}})_{b_1,b'_1}^{c_1,c'_1}\Bigr ) T({\textstyle \frac{x}{y}})_\textbf{i,j}^\textbf{a,b} T({\textstyle \frac{x'}{y'}})_\mathbf{i',j}^\mathbf{a,b'}, \end{aligned}$$

(18.40)

$$\begin{aligned} \sum _\mathbf{k,k'} T({\textstyle \frac{x'}{y'}})_\mathbf{k',j}^\mathbf{a,c'} T({\textstyle \frac{x}{y}})_\textbf{k,j}^\textbf{a,c} \Bigl ({\mathscr {M}}({\textstyle \frac{y}{y'}})_{j_n,j_n}^{j_n,j_n}\cdots {\mathscr {M}}({\textstyle \frac{y}{y'}})_{j_1,j_1}^{j_1,j_1}\Bigr ) \Bigl ({\mathscr {M}}({\textstyle \frac{x}{x'}})_{i_m,i'_m}^{k_m,k'_m}\cdots {\mathscr {M}}({\textstyle \frac{x}{x'}})_{i_1,i'_1}^{k_1,k'_1}\Bigr ), \end{aligned}$$

(18.41)

where $\textbf{i}=(i_1,\ldots ,i_m)$, etc. The left blocks $({\mathscr {M}}(\cdot )^{\bullet \bullet }_{\bullet \bullet } \cdots {\mathscr {M}}(\cdot )^{\bullet \bullet }_{\bullet \bullet })$ both in (18.40) and (18.41) are actually the identities but it is better to keep them temporarily for the explanation. The operators in (18.40) and (18.41) actually coincide. To see this we depict them as follows.

Fig. 18.2

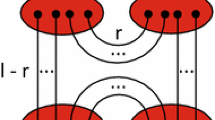
A graphical representation of the tetrahedron equation (18.26). The parameter $z_{ij}$ has been suppressed

Here $T(z)_\textbf{i,j}^\textbf{a,b}$ acts on $\mathcal {F}_q^{\otimes mn}$ (blue arrows) and ${\mathscr {M}}(z)_{i j}^{a b}$ acts on the extra single Fock space $\mathcal {F}_q$ (green arrow). In the upper diagram, the front and the back layers correspond to $T({\textstyle \frac{x}{y}})_\textbf{i,j}^\textbf{a,b}$ and $T({\textstyle \frac{x'}{y'}})_\mathbf{i',j}^\mathbf{a,b'}$ in (18.40), respectively. Similarly, in the lower diagram, the front and the back layers represent $T({\textstyle \frac{x'}{y'}})_\mathbf{k',j}^\mathbf{a,c'}$ and $T({\textstyle \frac{x}{y}})_\textbf{k,j}^\textbf{a,c}$ in (18.41), respectively. Starting from the top right corner of the upper diagram, using the tetrahedron equation (Figure 18.2) repeatedly, one can push the green arrow all the way down to the bottom left. It transforms the upper diagram into the lower, showing that they are equal as operators on $\mathcal {F}_q^{\otimes mn}\otimes \mathcal {F}_q$.

Now we rephrase the equality of (18.40) and (18.41) as

$$\begin{aligned} {\displaystyle \sum _\mathbf{b,b'}} \Bigl ({\mathscr {M}}({\textstyle \frac{y}{y'}})_{b_n,b'_n}^{c_n,c'_n}\cdots {\mathscr {M}}({\textstyle \frac{y}{y'}})_{b_1,b'_1}^{c_1,c'_1}\Bigr ) T({\textstyle \frac{x}{y}})_\textbf{i,j}^\textbf{a,b} T({\textstyle \frac{x'}{y'}})_\mathbf{i',j}^\mathbf{a,b'}\nonumber \\ = {\displaystyle \sum _\mathbf{k,k'}} T({\textstyle \frac{x'}{y'}})_\mathbf{k',j}^\mathbf{a,c'} T({\textstyle \frac{x}{y}})_\textbf{k,j}^\textbf{a,c} \Bigl ({\mathscr {M}}({\textstyle \frac{x}{x'}})_{i_m,i'_m}^{k_m,k'_m}\cdots {\mathscr {M}}({\textstyle \frac{x}{x'}})_{i_1,i'_1}^{k_1,k'_1}\Bigr ) \end{aligned}$$

(18.42)

removing the identity parts. Evaluate (18.42) between $\langle \chi ({\textstyle \frac{y'}{y}})|\in \mathcal {F}_q^*$ and $|\chi ({\textstyle \frac{x}{x'}})\rangle \in \mathcal {F}_q$, where these vectors are on the green arrows on which only the block of ${\mathscr {M}}(z)$’s act. Taking a further sum over $\mathbf{i,i',c,c'}$ on both sides eliminates ${\mathscr {M}}(z)$’s by means of (18.35), leading to

$$\begin{aligned} \langle \chi ({\textstyle \frac{y}{y'}})|\chi ({\textstyle \frac{x}{x'}})\rangle \! \sum _\mathbf{i,i',b,b'}T({\textstyle \frac{x}{y}})_\textbf{i,j}^\textbf{a,b} T({\textstyle \frac{x'}{y'}})_\mathbf{i',j}^\mathbf{a,b'} = \langle \chi ({\textstyle \frac{y}{y'}})|\chi ({\textstyle \frac{x}{x'}})\rangle \! \sum _\mathbf{k,k',c,c'}T({\textstyle \frac{x'}{y'}})_\mathbf{k',j}^\mathbf{a,c'} T({\textstyle \frac{x}{y}})_\textbf{k,j}^\textbf{a,c}. \end{aligned}$$

(18.43)

Since $\langle \chi ({\textstyle \frac{y'}{y}})|\chi ({\textstyle \frac{x}{x'}})\rangle = \sum _{m\ge 0}\frac{(q^2;q^2)_m}{(-q;-q)_m^2}({\textstyle \frac{xy'}{x'y}})^m \ne 0$ by (3.16), it can be removed. From the definition of $S(z)^\textbf{a}_\textbf{j}$ in (18.36), the resulting equality is stated as $S({\textstyle \frac{x}{y}})^\textbf{a}_\textbf{j} S({\textstyle \frac{x'}{y'}})^\textbf{a}_\textbf{j} =S({\textstyle \frac{x'}{y'}})^\textbf{a}_\textbf{j} S({\textstyle \frac{x}{y}})^\textbf{a}_\textbf{j}$. $\square$

One can check the commutativity (18.39) for those $S(z)^\textbf{a}_\textbf{j}$ in Examples 18.9, 18.10 and 18.11. The latter two are already quite non-trivial.

18.4.3 Bilinear Identities of Layer Transfer Matrices

In the proof of Proposition 18.12, we have only used the trivial eigenvectors of ${\mathscr {M}}(z)$ given in Proposition 18.8. A similar argument utilizing the non-trivial eigenvectors (the rightmost ones including $\mu$ and $\nu$) leads to a family of bilinear identities of $S(z)^\textbf{a}_\textbf{j}$ mixing different boundary conditions $\textbf{a}, \textbf{j}$. They include the commutativity (18.39) as the simplest case. To describe the general case we prepare some notation.

Recall that m and n are any positive integers representing the size of the layer as in (18.36). For a subset $I \subseteq \{1,\ldots ,m\}$ with the complement $\overline{I}=\{1,\ldots , m\} \setminus I$ and the sequences $\boldsymbol{\alpha } \in \{0,1\}^{\# I}$, $\boldsymbol{\beta } \in \{0,1\}^{\# \overline{I}}$, let $\boldsymbol{\alpha }_I\boldsymbol{\beta }_{\overline{I}} \in \{0,1\}^m$ be the sequence in which the subsequence with indices from I is $\boldsymbol{\alpha }$ and the rest is $\boldsymbol{\beta }$.⁶ For instance, for $m=5$ and $I=\{1,3,4\}$, we set⁷

$$\begin{aligned} \boldsymbol{\alpha }_I\boldsymbol{\beta }_{\overline{I}} = \boldsymbol{\alpha }_{\{1,3,4\}}\boldsymbol{\beta }_{\{2,5\}} =(\alpha _1,\beta _1,\alpha _2,\alpha _3,\beta _2). \end{aligned}$$

(18.44)

Likewise for $J \sqcup \overline{J} = \{1,\ldots , n\}$ and $\boldsymbol{\gamma } \in \{0,1\}^{\# J}$, $\boldsymbol{\delta } \in \{0,1\}^{\# \overline{J}}$, the array $\boldsymbol{\gamma }_J \boldsymbol{\delta }_{\overline{J}} \in \{0,1\}^n$ denotes a similar sequence. For any sequence $\boldsymbol{\alpha } =(\alpha _1,\ldots ,\alpha _k)\in \{0,1\}^k$, we set $|\boldsymbol{\alpha }|=\alpha _1+\cdots +\alpha _k$ and $\overline{\boldsymbol{\alpha }}=(1-\alpha _1,\ldots ,1-\alpha _k)$. 

Theorem 18.13

For any subsets $I \subseteq \{1,\ldots ,m\}$, $J \subseteq \{1,\ldots ,n\}$ and sequences $\boldsymbol{\alpha }\in \{0,1\}^{\# I}$ and $\boldsymbol{\gamma } \in \{0,1\}^{\# J}$, the bilinear relation⁸

$$\begin{aligned} \sum _{\boldsymbol{\beta ,\delta }} y^{|{\boldsymbol{\beta }}|+|{\boldsymbol{\delta }}|} x^{|\overline{\boldsymbol{\beta }}|+|\overline{\boldsymbol{\delta }}|}\, S(y)^{\boldsymbol{\alpha }_I \boldsymbol{\beta }_{\overline{I}}}_{ \boldsymbol{\gamma }_J \boldsymbol{\delta }_{\overline{J}}}\, S(x)^{\boldsymbol{\alpha }_I \boldsymbol{\overline{\beta }}_{\overline{I}}}_{ \boldsymbol{\gamma }_J \boldsymbol{\overline{\delta }}_{\overline{J}}} =(x \leftrightarrow y) \end{aligned}$$

(18.45)

holds, where the sum runs over $\boldsymbol{\beta } \in \{0,1\}^{\# \overline{I}}$ and $\boldsymbol{\delta } \in \{0,1\}^{\# \overline{J}}$.

The commutativity (Proposition 18.12) is the simplest case of Theorem 18.13 corresponding to $I=\{1,\ldots ,m\},J=\{1,\ldots ,n\}$, where the sum reduces to a single term. As another example, when $(m,n)=(4,3), I=\{1,3\},J=\{2,3\},\boldsymbol{\alpha }=(0,1),\boldsymbol{\gamma }=(1,0)$, the relation (18.45) reads as

$$\begin{aligned}&x^3S(y)^{0010}_{010}S(x)^{0111}_{110} +yx^2S(y)^{0011}_{010}S(x)^{0110}_{110} +yx^2S(y)^{0110}_{010}S(x)^{0011}_{110} \nonumber \\&+y^2xS(y)^{0111}_{010}S(x)^{0010}_{110} +yx^2S(y)^{0010}_{110}S(x)^{0111}_{010} +y^2xS(y)^{0011}_{110}S(x)^{0110}_{010} \nonumber \\&+y^2xS(y)^{0110}_{110}S(x)^{0011}_{010} +y^3S(y)^{0111}_{110}S(x)^{0010}_{010} =(x \leftrightarrow y). \end{aligned}$$

(18.46)

We will present a proof of Theorem 18.13 only for the special case considered in Corollary 18.14 below since the general case is easily inferred from it. It corresponds to the choice $I=\{2,3,\ldots , m\}$, $\boldsymbol{\alpha } = \textbf{a}$, $J = \{2,3,\ldots , n\}$, $\boldsymbol{\gamma } = \textbf{j}$, which will suffice for the proof of Theorem 18.5.

Corollary 18.14

For any sequences $\textbf{a} \in \{0,1\}^{m-1}$ and $\textbf{j} \in \{0,1\}^{n-1}$, we have

$$\begin{aligned}&x^2S(y)^{0\,\textbf{a}}_{0\,\textbf{j}}S(x)^{1\,\textbf{a}}_{1\,\textbf{j}} + yxS(y)^{0\,\textbf{a}}_{1\,\textbf{j}} S(x)^{1\,\textbf{a}}_{0\,\textbf{j}} \nonumber \\&+ yxS(y)^{1\,\textbf{a}}_{0\,\textbf{j}}S(x)^{0\,\textbf{a}}_{1\,\textbf{j}} + y^2S(y)^{1\,\textbf{a}}_{1\,\textbf{j}}S(x)^{0\,\textbf{a}} _{0\,\textbf{j}} =(x \leftrightarrow y). \end{aligned}$$

(18.47)

Proof

The proof is a slight and natural modification of the one for Proposition 18.12. Consider the following equality of operators on $\mathcal {F}_q^{\otimes mn}\otimes \mathcal {F}_q$:

$$\begin{aligned}&{\displaystyle \sum _{\mathbf{b,b'}\atop a''_1+a'''_1=1}} {\mathscr {M}}({\textstyle \frac{x}{x'}})_{a''_1,a'''_1}^{a_1,a'_1} \Bigl ({\mathscr {M}}({\textstyle \frac{y}{y'}})_{b_n,b'_n}^{c_n,c'_n}\cdots {\mathscr {M}}({\textstyle \frac{y}{y'}})_{b_1,b'_1}^{c_1,c'_1}\Bigr ) T({\textstyle \frac{x}{y}})_\textbf{i,j}^\mathbf{a'',b} T({\textstyle \frac{x'}{y'}})_\mathbf{i',j'}^\mathbf{a''',b'} \nonumber \\&={\displaystyle \sum _{\mathbf{k,k'}\atop j''_1+j'''_1=1}} T({\textstyle \frac{x'}{y'}})_\mathbf{k',j'''}^\mathbf{a',c'} T({\textstyle \frac{x}{y}})_\mathbf{k,j''}^\textbf{a,c} {\mathscr {M}}({\textstyle \frac{y}{y'}})_{j_1,j'_1}^{j''_1,j'''_1} \Bigl ({\mathscr {M}}({\textstyle \frac{x}{x'}})_{i_m,i'_m}^{k_m,k'_m}\cdots {\mathscr {M}}({\textstyle \frac{x}{x'}})_{i_1,i'_1}^{k_1,k'_1}\Bigr ), \end{aligned}$$

(18.48)

where $\mathbf{a,a',a'',a'''}$ (resp. $\mathbf{j,j',j'',j'''}$)⁹ differ from each other only in the first components $a_1,a'_1,a''_1,a'''_1$ (resp. $j_1,j'_1,j''_1,j'''_1$). We take $a_1+a'_1=1$ and $j_1+j'_1=1$ and exhibit the constraints $a''_1+a'''_1=1, j''_1+j'''_1=1$ coming from ${\mathscr {M}}(z)^{ab}_{ij}=0$ unless $a+b=i+j$. Unlike the previous (18.40) = (18.41), the identity operators ${\mathscr {M}}(z)^{i,i}_{i,i}=1$ have been omitted already. The diagram for (18.48) is Fig. 18.3 except that the $(a_1,a_1)$ on the end of the top horizontal arrows are replaced by $(a_1,a'_1)$ and $(j_1,j_1)$ at the bottom of the leftmost vertical arrows are changed into $(j_1,j'_1)$.

Fig. 18.3

Diagrams representing (18.40) and (18.41)

Substitution of $\mu =xy',\nu =x'y$ into (18.33) and (18.34) lead to

$$\begin{aligned}&\sum _{i+j=1}\mu ^i\nu ^j {\mathscr {M}}({\textstyle \frac{y}{y'}})_{i j}^{k l}| \chi ({\textstyle \frac{x}{x'}})\rangle =\mu ^k\nu ^l |\chi ({\textstyle \frac{x}{x'}})\rangle , \end{aligned}$$

(18.49)

$$\begin{aligned}&\sum _{i+j=1}\mu ^i\nu ^j\langle \chi ({\textstyle \frac{y'}{y}})|\, {\mathscr {M}}({\textstyle \frac{x}{x'}})^{i j}_{k l}=\mu ^k\nu ^l \langle \chi ({\textstyle \frac{y'}{y}})|. \end{aligned}$$

(18.50)

Multiply (18.48) by $\mu ^{a_1+j_1}\nu ^{a'_1+j'_1}$ and take the sum over $\mathbf{i, i', c, c'}$ and $a_1,a'_1,j_1,j'_1$ with the constraints $a_1+a'_1=1,j_1+j'_1=1$. Sandwich the resulting operator identity by $\langle \chi ({\textstyle \frac{y'}{y}})|(\cdots )|\chi ({\textstyle \frac{x}{x'}})\rangle$. Thanks to the identities (18.35), (18.49) and (18.50), all ${\mathscr {M}}(z)$’s disappear. After canceling $\langle \chi ({\textstyle \frac{y'}{y}})| \chi ({\textstyle \frac{x}{x'}})\rangle \ne 0$ from both sides we are left with

$$\begin{aligned}&\sum _{\mathbf{i,i',b,b'}; a''_1+a'''_1=1,j_1+j'_1=1}\mu ^{a''_1+j_1}\nu ^{a'''_1+j'_1} T({\textstyle \frac{x}{y}})_\textbf{i,j}^\mathbf{a'',b} T({\textstyle \frac{x'}{y'}})_\mathbf{i',j'}^\mathbf{a''',b'}\nonumber \\ =&\sum _{\mathbf{k,k',c,c'}; a_1+a'_1=1,j''_1+j'''_1=1}\mu ^{a_1+j''_1}\nu ^{a'_1+j'''_1} T({\textstyle \frac{x'}{y'}})_\mathbf{k',j'''}^\mathbf{a',c'} T({\textstyle \frac{x}{y}})_\mathbf{k,j''}^\textbf{a,c}. \end{aligned}$$

(18.51)

After dividing by $(yy')^2$, this is identified with

$$\begin{aligned}&\sum _{a''_1+a'''_1=1,j_1+j'_1=1}({\textstyle \frac{x}{y}})^{a''_1+j_1} ({\textstyle \frac{x'}{y'}})^{a'''_1+j'_1}S({\textstyle \frac{x}{y}})_\textbf{j}^\mathbf{a''} S({\textstyle \frac{x'}{y'}})_\mathbf{j'}^\mathbf{a'''}\nonumber \\ =&\sum _{a_1+a'_1=1,j''_1+j'''_1=1}({\textstyle \frac{x}{y}})^{a_1+j''_1} ({\textstyle \frac{x'}{y'}})^{a'_1+j'''_1} S({\textstyle \frac{x'}{y'}})_\mathbf{j'''}^\mathbf{a'} S({\textstyle \frac{x}{y}})_\mathbf{j''}^\textbf{a} \end{aligned}$$

(18.52)

in terms of $S(z)^\textbf{a}_\textbf{j}$ in (18.36), which completes the proof. $\square$

Remark 18.15

The bilinear relation (18.45) can further be generalized by introducing inhomogeneity of the parameters. In (18.36) we consider horizontal arrows as carrying $x_1,\dots ,x_m$ from the top to the bottom and vertical ones do $y_1,\dots ,y_n$ from the left to the right. Set $\textbf{x}=(x_1,\dots ,x_m)$ and $\textbf{y}=(y_1,\dots ,y_n)$. Define $S(\textbf{x};\textbf{y})^\textbf{a}_\textbf{j}$ by putting ${\mathscr {L}}(x_i/y_j)$ on the intersection of the ith horizontal and the jth vertical arrows. As in Theorem 18.13, let I, J be subsets of $\{1,\ldots ,m\},\{1,\ldots ,n\}$ and take $\boldsymbol{\alpha } \in \{0,1\}^{\#I}, \boldsymbol{\gamma } \in \{0,1\}^{\# J}$. Suppose that $(\textbf{x};\textbf{y})$ and $(\mathbf{x'};\mathbf{y'})$ satisfy

$$\begin{aligned} x_1/x'_1=\dots =x_m/x'_m=u,\quad y_1/y'_1=\dots =y_n/y'_n=v. \end{aligned}$$

(18.53)

Then the following relation is valid:

$$\begin{aligned}&\sum _{\boldsymbol{\beta ,\delta }} ({\textstyle \frac{u}{v}})^{|{\boldsymbol{\beta }}|+|{\boldsymbol{\delta }}|}\, S(\textbf{x}; \textbf{y})^{\boldsymbol{\alpha }_I \boldsymbol{\beta }_{\overline{I}}}_{ \boldsymbol{\gamma }_J \boldsymbol{\delta }_{\overline{J}}}\, S(\mathbf{x'}; \mathbf{y'})^{\boldsymbol{\alpha }_I \boldsymbol{\overline{\beta }}_{\overline{I}}}_{ \boldsymbol{\gamma }_J \boldsymbol{\overline{\delta }}_{\overline{J}}} \nonumber \\&=\sum _{\boldsymbol{\beta ,\delta }} ({\textstyle \frac{u}{v}})^{|{\overline{\boldsymbol{\beta }}}| +|{\overline{\boldsymbol{\delta }}}|}\, S(\mathbf{x'}; \mathbf{y'})^{\boldsymbol{\alpha }_I \boldsymbol{\beta }_{\overline{I}}}_{ \boldsymbol{\gamma }_J \boldsymbol{\delta }_{\overline{J}}}\, S(\textbf{x}; \textbf{y})^{\boldsymbol{\alpha }_I \boldsymbol{\overline{\beta }}_{\overline{I}}}_{ \boldsymbol{\gamma }_J \boldsymbol{\overline{\delta }}_{\overline{J}}}, \end{aligned}$$

(18.54)

where the sums are over $\boldsymbol{\beta } \in \{0,1\}^{\# \overline{I}}$ and $\boldsymbol{\delta } \in \{0,1\}^{\# \overline{J}}$ as in (18.45). The derivation is similar and outlined in [90, Remark 5.4].

18.5 Proof of Theorem 18.5

We are ready to prove Theorem 18.5 by using the special case $m=n$ and $q=0$ of the preceding results. Note that the layer transfer matrix $S(z)^\textbf{a}_\textbf{j}$ (18.36) remains well defined at $q=0$. In fact, comparison of (18.25) and (18.19) shows that $q=0$ is achieved just by excluding the rightmost vertex in the former and replacing $\mathrm{\textbf{a}}^{\pm } , \mathrm{\textbf{k}}$ with ${\textbf{b}}^{\pm } , {\textbf{t}}$, respectively. See (18.22). For distinction we prepare the notation of it as

$$\begin{aligned} \mathbb {S}(z)^\textbf{a}_\textbf{j} = \lim _{q\rightarrow 0} S(z)^\textbf{a}_\textbf{j}|_{m=n}. \end{aligned}$$

(18.55)

It is still a non-trivial operator on $\mathcal {F}^{\otimes n^2}$ on which ${\textbf{b}}^{\pm } , {\textbf{t}}$ in each component act as (18.20).

Proposition 18.16

The matrix product operator $X_i(z)$ (18.18) is contained in the layer transfer matrices at $q=0$ as follows:

$$\begin{aligned} \mathbb {S}(z)^{00{\cdots }0}_{00{\cdots }0}&=\sum _{i=0}^nX_i(z){\otimes }\underbrace{\overbrace{{\textbf{b}}^+ \otimes {\cdots }{\otimes } {\textbf{b}}^+ }^{i}{\otimes }\overbrace{1{\otimes }{\cdots }{\otimes }1}^{n-i}}_\textrm{diagonal}{\otimes }1{\otimes }{\cdots }{\otimes }1, \end{aligned}$$

(18.56)

$$\begin{aligned} \mathbb {S}(z)^{10{\cdots }0}_{10{\cdots }0}&=z^{-1}\sum _{i=0}^nX_i(z){\otimes }\underbrace{\overbrace{1{\otimes }{\cdots }{\otimes }1}^{i} \otimes \overbrace{{\textbf{b}}^- {\otimes }{\cdots }{\otimes }{\textbf{b}}^- }^{n-i}}_\textrm{diagonal}\otimes \overbrace{{\textbf{b}}^+ {\otimes }{\cdots }\otimes {\textbf{b}}^+ }^{n-1}{\otimes }1{\otimes }{\cdots }{\otimes }1. \end{aligned}$$

(18.57)

Here “diagonal” signifies the part of the tensor components corresponding to the vertices on the NE–SW diagonal in (18.36)$|_{m=n}$.¹⁰

Proof

We regard the triangular region in (18.18) as embedded into the $n\times n$ square lattice in (18.36)$|_{m=n}$. Since the rightmost vertex of ${\mathscr {L}}(z)$ in (18.25) is absent at $q=0$, the red lines tend to be confined to the upper left region. Also, once an edge on the diagonal boundary in (18.18) becomes black, then the subsequent ones continue to be black in its further NE region. These properties imply the claimed expansion formulas. See the following example from $n=3$, where the dotted ones are to be summed over 0 and 1.¹¹ The four diagrams correspond to $i=0,\ldots , 3$ terms in (18.56) and (18.57) from the left to the right. The general case is similar.

From (18.25), notice that the weight of z for $\mathbb {S}(z)^\textbf{a}_\textbf{j}$ is calculated by #(1 on the top edges) − #(1 on the bottom edges), whereas the one for $X_i(z)$ is just #(1 on the top edges). This explains the extra overall factor $z^0$ and $z^{-1}$ in (18.56) and (18.57). $\square$

Example 18.17

Consider the case $n=2$. Setting $q=0$ in Example 18.10, we have

$$\begin{aligned} \mathbb {S}(z)^{00}_{00}&= (1+z {\textbf{b}}^+ )\!\otimes \!1 \!\otimes \!1 \!\otimes \!1+ z{\textbf{t}}\!\otimes \!{\textbf{b}}^+ \!\otimes \!1 \!\otimes \!1+ (z{\textbf{b}}^- +z^21)\!\otimes \!{\textbf{b}}^+ \!\otimes \!{\textbf{b}}^+ \!\otimes \!1 \\&= X_0(z)\!\otimes \!1 \!\otimes \!1 \!\otimes \!1 + X_1(z)\!\otimes \!{\textbf{b}}^+ \!\otimes \!1 \!\otimes \!1+ X_2(z) \!\otimes \!{\textbf{b}}^+ \!\otimes \!{\textbf{b}}^+ \!\otimes \!1 \end{aligned}$$

by Example 18.3 in agreement with (18.56). Similarly, Example 18.11 leads to

$$\begin{aligned} z\mathbb {S}(z)^{10}_{10}&= (1+z {\textbf{b}}^+ )\!\otimes \!{\textbf{b}}^- \!\otimes \!{\textbf{b}}^- \!\otimes \!{\textbf{b}}^+ + z{\textbf{t}}\!\otimes \!1 \!\otimes \!{\textbf{b}}^- \!\otimes \!{\textbf{b}}^+ + (z{\textbf{b}}^- +z^21)\!\otimes \!1 \!\otimes \!1 \!\otimes \!{\textbf{b}}^+ \\&=X_0(z) \!\otimes \!{\textbf{b}}^- \!\otimes \!{\textbf{b}}^- \!\otimes \!{\textbf{b}}^+ + X_1(z)\!\otimes \!1 \!\otimes \!{\textbf{b}}^- \!\otimes \!{\textbf{b}}^+ + X_2(z)\!\otimes \!1 \!\otimes \!1 \!\otimes \!{\textbf{b}}^+ \end{aligned}$$

in agreement with (18.57).

Proof of Theorem 18.5. Substituting (18.56) into the commutativity (18.39) and collecting the coefficient of

$$\begin{aligned} \overbrace{({\textbf{b}}^+ )^2{\otimes }{\cdots }{\otimes }({\textbf{b}}^+ )^2}^{j}{\otimes } \overbrace{{\textbf{b}}^+ {\otimes }{\cdots }{\otimes }{\textbf{b}}^+ }^{i-j} {\otimes }1{\otimes }{\cdots }{\otimes }1\qquad (0 \le j \le i \le n), \end{aligned}$$

(18.58)

we get (18.14).

Next we show (18.15). Set $\textbf{a}=(0,{\ldots },0)$, $\textbf{j}=(0,{\ldots },0)$ in Corollary 18.14 and use the obvious property $S(z)^{10\cdots 0}_{00{\cdots }0}=0$ to derive

$$\begin{aligned}&x^2\mathbb {S}(y)^{00{\cdots }0}_{00{\cdots }0}\mathbb {S}(x)^{10{\cdots }0}_{10{\cdots }0} +y^2\mathbb {S}(y)^{10{\cdots }0}_{10{\cdots }0} \mathbb {S}(x)^{00{\cdots }0}_{00{\cdots }0} \nonumber \\&-y^2\mathbb {S}(x)^{00{\cdots }0}_{00{\cdots }0}\mathbb {S}(y)^{10{\cdots }0}_{10{\cdots }0} -x^2\mathbb {S}(x)^{10{\cdots }0}_{10{\cdots }0} \mathbb {S}(y)^{00{\cdots }0}_{00{\cdots }0}=0. \end{aligned}$$

(18.59)

Write the diagonal parts in (18.56) and (18.57) as $Y_i$ and $W_i$, i.e. we set

$$\begin{aligned} \mathbb {S}(z)^{00\cdots 0}_{00\cdots 0}&= \sum _{i=0}^nX_i(z) \otimes Y_i \otimes 1 \otimes \cdots \otimes 1, \quad Y_i = ({\textbf{b}}^+ )^{\otimes i}\otimes 1^{\otimes n-i}, \end{aligned}$$

(18.60)

$$\begin{aligned} z\mathbb {S}(z)^{10\cdots 0}_{10\cdots 0}&= \sum _{i=0}^nX_i(z) \otimes W_i \otimes ({\textbf{b}}^+ )^{\otimes n-1} \otimes 1 \otimes \cdots \otimes 1, \quad W_i =1^{\otimes i} \otimes ({\textbf{b}}^- )^{\otimes n-i}. \end{aligned}$$

(18.61)

Substitution of them into (18.59) generates the terms all having the common off-diagonal tail $({\textbf{b}}^+ )^{\otimes n-1} \otimes 1 \otimes \cdots \otimes 1$. It therefore reduces to the identity without the tail. Explicitly it is given by

$$\begin{aligned} \sum _{0 \le i,j \le n} \Bigl (&xX_i(y)X_j(x) \otimes Y_iW_j + y X_i(y)X_j(x) \otimes W_iY_j \nonumber \\&- yX_i(x)X_j(y) \otimes Y_iW_j - x X_i(x)X_j(y) \otimes W_i Y_j \Bigr ) = 0, \end{aligned}$$

(18.62)

where $Y_k, W_k$ correspond to the diagonal part in Proposition 18.16. Now let us pick the coefficients of the terms whose diagonal part is

$$\begin{aligned} \overbrace{{\textbf{b}}^+ {\otimes }{\cdots }{\otimes }{\textbf{b}}^+ }^{j} {\otimes }\overbrace{{\textbf{t}}{\otimes }{\cdots }{\otimes }{\textbf{t}}}^{i-j} {\otimes }\overbrace{{\textbf{b}}^- {\otimes }{\cdots }{\otimes }{\textbf{b}}^- }^{n-i} \qquad (0 \le j < i \le n). \end{aligned}$$

(18.63)

In view of (18.21), such a term does not arise from $W_iY_j$ but only comes from the expansion of

$$\begin{aligned} Y_i W_j&= (\overbrace{{\textbf{b}}^+ \otimes \cdots \otimes {\textbf{b}}^+ }^{i}{\otimes }\overbrace{1 \otimes \cdots \otimes 1}^{n-i}) (\overbrace{1{\otimes }{\cdots }{\otimes }1}^{j}\otimes \overbrace{{\textbf{b}}^- \otimes \cdots \otimes {\textbf{b}}^- }^{n-j}) \nonumber \\&= \overbrace{{\textbf{b}}^+ \otimes \cdots \otimes {\textbf{b}}^+ }^{j} \otimes \overbrace{(1-{\textbf{t}})\!\otimes \!\cdots \!\otimes \!(1-{\textbf{t}})}^{i-j} \otimes \overbrace{{\textbf{b}}^- \otimes \cdots \otimes {\textbf{b}}^- }^{n-i} \end{aligned}$$

(18.64)

with a fixed coefficient $(-1)^{i-j}$. Thus (18.62) gives $xX_i(y)X_j(x) = yX_i(y)X_j(x)$ for $0 \le j < i \le n$, which is (18.15). This completes the proof of Theorem 18.5. $\square$

18.6 Bibliographical Notes and Comments

Matrix product construction of the stationary probability was initiated in [39] for the single species TASEP subject to non-trivial boundary reservoirs. For a general introduction to the subject, see for example [23, 32, 140] and the references therein. As mentioned in the main text, the stationary probabilities become non-trivial even under the periodic boundary condition for the n-TASEP with $n \ge 2$. The first systematic result about it was obtained in [47], where the combinatorial construction, called the Ferrari–Martin (FM) algorithm, was put forward.  Many works followed it, seeking an operator formulation and/or generalization to multispecies partially asymmetric simple exclusion processes, e.g. [45, 124].

This chapter, which is mainly based on [90], presents a unique approach from the 3D integrability. It identifies the tetrahedron equation of type $MMLL=LLMM$ (Sects. 2.6 and 3.5.3) as the ultimate structure validating the matrix product formula based on $X_i(z)$ in (18.18). As noted in Remark 18.6, the quantum group theoretical origin of the FM algorithm is a composition of the quantum R matrices (11.26) at $q=0$ [89].

There is another class of stochastic models known as the totally asymmetric zero range process (TAZRP).  See for instance [46] for a general background. Among them, there is a special example, n-TAZRP, which admits results quite parallel to this chapter [91, 92].  A contrasting feature of the n-TAZRP is that it allows occupancy of more than one particle at a site with some combinatorial constraint on their hopping rule. The n-TASEP and the n-TAZRP are sister models. The quantum R matrices relevant to the FM-like algorithms are those associated with the anti-symmetric tensor representations (11.26) and the symmetric tensor representations (13.10), respectively. The solutions to the tetrahedron equation relevant to the layer transfer matrices (matrix product operators) are those consisting of the 3D L (Theorem 3.25) and the 3D R (Theorem 3.26), respectively. The n-TAZRP [91, 92] is a special limit of the integrable Markov process associated with the stochastic R matrix [87] quoted in Sect. 13.7. The latter contains numerous models which have been studied extensively. A bird’s eye view of their degeneration scheme is given in [81, Figs. 1 and 2]. A survey from the 3D viewpoint is available in [100].