Seismic Induced Pounding of Structures and Its Mitigation

Abstract

Limited availability of land resources and increasing population have led to closely spaced buildings in cities, in which the stipulated separation distance is most often not available between the buildings. When subjected to an external excitation, such as from wind or earthquake, the differences in the dynamic characteristics of these adjacent buildings cause phase differences in their responses, leading to chances of structural collision or pounding. Pounding between closely spaced buildings under earthquake excitation has been identified as a serious hazard, due to falling of building material, as well as a major cause of structural damage, that may range from minor, affecting non-structural components only, to heavy. There have been reports of significant pounding damage during several past earthquakes in not only buildings but between decks and abutments and at expansion joints of bridges as well. There is, thus, a necessity of mitigating the effects of pounding at the design stage, or in existing structures, through construction details or by the installation of vibration control devices. In this chapter, first, the various situations in which structural pounding can arise under seismic excitation are presented, followed by the types of pounding, such as one-sided pounding and two-sided pounding. A summary of the pounding damage that has been reported in past earthquakes is provided. The different pounding models developed by researchers are examined, and the effects of varying dynamic properties and separation distance on pounding are studied. Codal specifications on the minimum separation distance are highlighted and a discussion is made on the various mitigation strategies for seismic pounding.

4.1 Introduction

Structural pounding refers to the lateral collision between adjacent buildings. In high-density metropolitan cities, the stipulated separation distance is often not available between buildings. This is chiefly because in the past, building codes did not specify any definite recommendations or guidelines to counteract pounding effects. This was taken to advantage and to maximize land usage as well as to avoid having large expansion joints, buildings that are adjacent to each other or within the same facility have been built very close to each other. In such closely spaced buildings, structural pounding under earthquake excitation has been identified as a serious hazard due to falling of building material as well as a major cause of structural damage that may range from minor, affecting non-structural components only, to heavy. It can lead to infill wall damage, plastic deformation, column shear failure, local crushing and possible collapse of the structure. In fact, pounding between adjacent buildings can sometimes be more dangerous than the effect of the earthquake on a single building. The damage from structural pounding can be categorized into four types, namely major structural damage, failure and falling of building scraps creating a life safety hazard, loss of building functions due to failure of mechanical, electrical or fire protection systems and architectural, non-structural and minor structural damage. An example of the effect of pounding between two closely spaced buildings is illustrated in Fig. 4.1.

Fig. 4.1

Pounding damage observed in Christchurch CBD, 2011 [1]

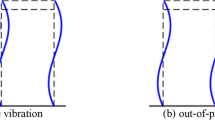
When an earthquake occurs, due to the differences in the dynamic characteristics of buildings, adjacent buildings will vibrate out of phase and pounding will occur if sufficient separation distance is not provided between them (see Fig. 4.2). For neighbouring buildings with similar heights and structural properties, the effects of pounding will be limited to some local damage, mostly non-structural and light structural damage, and structural acceleration response will be higher in the form of short duration peaks. But the damage is severe when the colliding buildings have considerably different masses, periods and heights. Understandably, the pounding effect is more dangerous if the floor heights of the two adjacent buildings are different. If the floor heights of the two buildings are the same, then during the earthquake, the slab of one building hits the slab of the next building. But if the floor heights are different, then during the earthquake, the slab of one building acts like a battering ram into the column of the adjacent building and causes massive damage (Fig. 4.3). In this case, the column of one building may sustain repeated impacts along its height from the slab of the adjacent building, resulting in localized damage to the column and possibly partial collapse of the storey. Further, structures with different periods of vibration may sustain different levels of damage under identical pounding conditions during the same earthquake. Pounding may also occur because of structural irregularities that result in torsion.

Fig. 4.2

a Similar seismic behavior. b Different seismic behaviour [2]

Fig. 4.3

Pounding effects: buildings with different floor heights [3]

There have been reports of significant pounding damage during several past earthquakes in not only buildings, but between decks and abutments, and at expansion joints of bridges as well. For the longer bridge structures, it is often the seismic wave propagation effect that is considered to be a dominant factor leading to the pounding of neighbouring superstructure segments (Fig. 4.4). This effect, due to time lag and spatial variation of seismic waves, results in different seismic inputs acting at the supports along the structure. Pedestrian bridges may also pose a potential pounding risk as they may collide against the structures to which they connect.

Fig. 4.4

a Horizontal pounding at expansion joints in bridges. b Lateral pounding at bridge piers [4]

There is, thus, a necessity of mitigating the effects of pounding at the design stage, or in existing structures, through construction details or by the installation of vibration control devices. In this chapter, first, the various situations in which structural pounding can arise under seismic excitation are presented, followed by the types of pounding, such as one-sided pounding and two-sided pounding. A concise summary of the pounding damage that has been reported in past earthquakes is included. Next, the phenomenon of structural pounding is investigated in detail and the treatment of the contact problem between two pounding structures made by researchers elaborated upon. The effects of varying structural dynamic properties and separation distance on the pounding forces generated are presented next. Lastly, various mitigation strategies for seismic pounding, along with codal specifications on the minimum seismic separation gap are highlighted.

4.2 Conditions and Types of Structural Pounding

It is clear from the foregoing discussion that structural pounding can arise under various conditions. These are enumerated below.

• (a) Adjacent buildings with equal building height and equal floor height (Fig. 4.5a). This would be caused due to insufficient separation gap as well as differences in structural time periods and structural damping. This would mostly arise when the adjoining buildings are of different structural materials, e.g. one is a steel building and the other is a reinforced concrete building.

  Fig. 4.5

  

  Representation of different situations where pounding occurs [5]

• (b) Adjacent buildings with the same floor levels but different heights (Fig. 4.5b). Here, apart from the close proximity of the buildings, the marked difference in dynamic properties between the taller and more flexible building and the shorter and stiffer building would cause pronounced pounding.

• (c) Adjacent structures with different total height and floor levels (Fig. 4.5c). The damage in this condition is expected to be severe due to the collision of the floor slab of one building with the column of the adjacent building at its mid-height.

• (d) Structures are situated in a row (Fig. 4.5d). In this situation, two cases may arise, namely one-sided and two-sided pounding. This has been elaborated upon subsequently.

• (e) Buildings having irregular lateral load resisting systems in ‘plan’ rotate during an ‘earthquake’ and due to the torsional rotations, pounding occurs near the building periphery against the adjacent buildings (Fig. 4.5e).

• (f) Adjacent units of the same building, which are connected by one or more bridges, or through expansion joints, may undergo pounding if the gaps are not designed to account for the possibility of collision between the units.

• (g) Possible settlement and rocking of structures located on soft soils may also lead to unanticipated pounding.

One-sided and two-sided pounding

Anagnostopoulos [6] carried out a study on the seismic pounding of several adjacent buildings in a row and considered the effect of several parameters, such as building mass, time period and gap size, and reported that the end building structures experience substantial increment in response as compared to the interior one. This occurs because the building at the end of a row suffers one-sided pounding as it is free to move in the other direction.

On the other hand, if a building is situated between two other buildings, it will suffer pounding from both sides at the same time and it cannot move freely in either direction (see Fig. 4.6). For this reason, one-sided pounding is generally more hazardous than two-sided pounding.

Fig. 4.6

Pounding between buildings in a row (two-sided pounding) [7]

4.3 Pounding Damage in Past Earthquakes

Some of the more notable worldwide observations on structural damage due to pounding are now discussed.

In the Alaska earthquake of 1964, the tower of the Anchorage Westward Hotel was damaged by pounding with an adjoining three-storied ballroom portion of the hotel [8] (Fig. 4.7).

Fig. 4.7

Anchorage Westward hotel damaged by pounding in the Alaska earthquake of 1964 [9]

Pounding damage was also observed in Caracas during the Venezuela earthquake of 1967 (Fig. 4.8).

Fig. 4.8

Pounding damage in Caracas during the Venezuela earthquake of 1967 [8]

In the San Fernando earthquake of 1971, the second storey of the Olive View Hospital struck the outside stairway. In addition, the first floor of the hospital hit against a neighbouring warehouse. The pounding of the main building against the stairway tower during the earthquake caused considerable damage at the contact points and caused permanent tilting of the tower [10] (Fig. 4.9). In subsequent years, in the 1972 Managua earthquake [11], the 1977 Romania earthquake [12], the 1977 Thessaloniki earthquake [13] and the 1981 Central Greece earthquake [14], many buildings were damaged because of structural pounding.

Fig. 4.9

Pounding damage of Olive View hospital. a View of Olive View hospital. b Permanent tilting of a stairway tower during the San Fernando earthquake, 1971 [15]

Mexico City, being a very congested city, recorded very significant pounding damages in the 1985 earthquake [16], so much so that structural pounding was assigned to be a leading cause of building collapse. More than 20% of the 114 affected structures were damaged because of pounding. To cite an instance, a 14-storey reinforced concrete residential building Nuevo León, located in the Nonoalco Tlatelolco apartment complex, consisted of three structurally independent units that were connected with non-structural expansion joints. After the earthquake, these joints were found to be destroyed, so it was supposed that pounding between the units had occurred and a significant impact load had been applied to the building structures.

In the Loma Prieta earthquake of 1989 [17], over 200 pounding occurrences involving more than 500 buildings took place at sites located over 90 km from the epicenter. Many old buildings with separation distances of barely 1.0–1.5 inches suffered. Structural pounding damage was observed in the form of large diagonal shear cracks in the masonry columns of a ten-storied building.

In the 1994 Northridge earthquake, the 4-inch wide seismic joint used to separate interstate 5 and state road 14 interchange of the Santa Clara River Bridge, located approximately 12 km from the epicenter, was insufficient to accommodate the relative displacements that were developed during the ground motion. This resulted in substantial pounding damage [8] (Fig. 4.10).

Fig. 4.10

Pounding damage in the Santa Clara River Bridge during the 1994 Northridge earthquake [19]

Poundings between adjacent decks or between a deck and an abutment occurred in the 1995 Hyogo-ken Nanbu earthquake [18], in which the expansion joints, contact faces of decks as well as the elastomeric bearings and columns were affected.

In 1999, in the Chi-Chi earthquake in central Taiwan, structural pounding was observed in several school buildings that had undergone expansion [20] (Fig. 4.11). These structures had older and newer portions with different fundamental vibration periods as well as insufficient gaps between them.

Fig. 4.11

Pounding occurrence between newer and older portions of a school building in the 1999 Chi-Chi earthquake, Taiwan [20]

During the 2007 Niigata Chuetsu-Oki Japan earthquake too, pounding damage was observed in school buildings [20]. This type of damage occurred when the adjacent structures had floor slabs located at different elevations and insufficient separation distance between them (Fig. 4.12).

Fig. 4.12

Pounding damage due to unequal slab levels during the 2007 Niigata Chuetsu-Oki Japan earthquake [21]

Other prominent observations of pounding in both building and bridge structures have been made in the 1988 Saguenay earthquake, 1992 Cairo earthquake, 1995 Kobe earthquake, 1999 Kocaeli earthquake, 2008 Wenchuan earthquake and 2011 Tohoku earthquake.

There have been several instances of structural pounding in Indian earthquakes as well. In the 2001 Bhuj earthquake [22], pounding of adjacent structures was evident in the Ayodhya apartment buildings in Ahmedabad with significant damages. In the following year, the Diglipur harbour sustained pounding damage at the intersection of the approach segment and the main berthing structure during the 2002 Diglipur earthquake (Fig. 4.13). During the Sumatra earthquake of 2004, pounding damage at junctions was noticed at the top ends of piles of the approach jetty [23]. In the 2006 Sikkim earthquake [24], pounding damages were observed between two long wings in the building and corridors connecting the wings of a nine-storey masonry infill reinforced concrete framed hostel building at the Sikkim Manipal Institute of Medical Sciences (SMIMS) Tadong, Gangtok, which caused severe damages in the walls and columns.

Fig. 4.13

Pounding damage at the intersection of approach to main jetty at Diglipur harbour during the 2002 Diglipur earthquake [25]

4.4 Pounding Models

Structural pounding is a complex phenomenon involving plastic deformations at contact points, local cracking or crushing, fracturing due to impact, friction, etc. The process of energy transfer during impact is highly complicated, which makes the mathematical analysis of this type of problem difficult. Forces created by collisions are applied and removed during a short interval of time, initiating stress waves which travel away from the region of contact. The collisions between adjacent buildings are simulated by means of contact elements that are activated when the bodies come in contact and deactivated if they are separated.

To facilitate an estimation of the structural responses under pounding, a simplified treatment of the contact problem between two pounding structures has been made by researchers. Anagnostopoulos [6] simulated the pounding of buildings through the use of linear, viscoelastic impact elements, and the same model was used by Jankowski et al. [26] while examining the pounding of superstructure segments in bridges. The linear, viscoelastic pounding model, though simple, assumes uniform energy dissipation during the entire pounding action, which is not a realistic one. Moreover, the contact problem is intrinsically non-linear, and this characteristic was considered by Davis [27] who modelled the interaction between two colliding structures by a Hertz contact force. The Hertzian impact model was also adopted by Pantelides and Ma [8] and Chau and Wei [28].

Though this model does not consider the energy dissipation at contact, it is a suitable model for cases where the coefficient of restitution is high, as may be assumed in colliding structures. The Hertzian impact stiffness parameter values are available for different structural materials such as concrete and steel, as well as for different contact surface geometries [29]. A more accurate non-linear viscoelastic impact element model that accounts for the energy dissipation that takes place during the approach period of the pounding was developed by Jankowski [30]. However, the impact stiffness and damping ratio parameters have to be evaluated iteratively, and their values for different material and surface geometry characteristics are needed for greater applicability of this model. An overview of the various modelling techniques is presented below.

The stereo-mechanical theory of impact is the classical formulation of the problem of impacting bodies. The stereo-mechanical approach assumes instantaneous impact and uses momentum balance and the coefficient of restitution to modify the velocities of the colliding bodies after impact. The original theory considered the impacting bodies as rigid; later, a correction factor to account for energy losses was introduced. The theory concentrates on determining the final velocities of two impacting bodies depending on their initial velocities and a coefficient of restitution to account for plasticity during impact. The final velocities of the bodies are determined from the following equations:

$${{\varvec{V}}}_{1}^{\prime}={{\varvec{V}}}_{1}-\left(1+{\varvec{e}}\right)\frac{{{\varvec{m}}}_{2}\left({{\varvec{V}}}_{1}-{{\varvec{V}}}_{2}\right)}{{{{\varvec{m}}}_{1}+{\varvec{m}}}_{2}}$$

(4.1)

$${{\varvec{V}}}_{2}^{\prime}={{\varvec{V}}}_{2}+\left(1+{\varvec{e}}\right)\frac{{{\varvec{m}}}_{1}\left({{\varvec{V}}}_{1}-{{\varvec{V}}}_{2}\right)}{{{{\varvec{m}}}_{1}+{\varvec{m}}}_{2}}$$

(4.2)

where ${V}_{1}^{\prime}$ and ${V}_{2}^{\prime}$ are final velocities, ${V}_{1}$ and ${V}_{1}$ are initial velocities of the colliding bodies, e is the coefficient of restitution and ${m}_{1}$ and ${m}_{2}$ denote the masses of the bodies.

Amongst the various contact force-based models, the simplest contact element consists of a linear elastic element (Fig. 4.14). The spring is assumed to have restoring force characteristics such that only when the relative distance between the masses becomes smaller than the initial distance, the spring contracts and generates forces which enable us to consider the phenomenon of pounding. This collision spring is assumed to be the axial stiffness of the floors and the beams in each storey.

Fig. 4.14

Linear spring model

The force in the contact element can be expressed according to the equations given below.

$${{\varvec{F}}}_{{\varvec{c}}}={{\varvec{K}}}_{{\varvec{l}}}\left({{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}}\right) ; {{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}}>0$$

(4.3)

$${{\varvec{F}}}_{{\varvec{c}}}=0 ; {{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}}\le 0$$

(4.4)

Here, ${u}_{1}$ and ${u}_{2}$ are the displacements of the impacting bodies, ${K}_{l}$ is the spring constant of the element and ${g}_{p}$(= δ in Fig. 4.14) is the separation distance between the structures.

However, in this, the energy loss during impact cannot be modelled. Whenever two mechanical systems collide, there is an exchange of momentum and also energy is dissipated in the high stress region of contact. The energy loss is taken into account by the Kelvin–Voight element model.

The Kelvin–Voight element is represented by a linear spring in parallel with a damper. This impact model is thus capable of modelling the energy dissipation during impact and the impact force is represented by the equations given below.

$${{\varvec{F}}}_{{\varvec{c}}}={{\varvec{K}}}_{{\varvec{k}}}\left({{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}}\right)+{{\varvec{C}}}_{{\varvec{k}}}({{{\varvec{u}}}}_{1}-{{{\varvec{u}}}}_{2}) ; {{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}}>0$$

(4.5)

$${{\varvec{F}}}_{{\varvec{c}}}=0 ; {{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}}\le 0$$

(4.6)

where ${u}_{1}$, ${u}_{2}$ and their derivatives are the displacements and velocities of the impacting bodies, ${K}_{k}$ is the spring constant of the element and ${g}_{p}$ (= δ in Fig. 4.15) is the separation distance between the structures. The damping coefficient ${C}_{k}$ can be related to the coefficient of restitution (e), by equating the energy losses during impact.

Fig. 4.15

Kelvin–Voight model

$${{\varvec{C}}}_{{\varvec{K}}}=2{\varvec{\zeta}}\sqrt{{{\varvec{K}}}_{{\varvec{k}}}\frac{{{\varvec{m}}}_{1}{{\varvec{m}}}_{2}}{{{\varvec{m}}}_{1}+{{\varvec{m}}}_{2}}}$$

(4.7)

$${\varvec{\zeta}}={\varvec{ln}}{\varvec{e}}/\sqrt{{{\varvec{\pi}}}^{2}+{({\varvec{ln}}{\varvec{e}})}^{2}}$$

(4.8)

Here, ${m}_{1}$ and ${m}_{2}$ are the masses of the colliding bodies and ζ is the damping coefficient.

The disadvantage of the Kelvin model is that its viscous component is active with the same damping coefficient during the entire time of the collision. The damping forces cause negative impact forces that pull the colliding bodies together, during the unloading phase, instead of pushing them apart. Ye et al. [31] re-examined and modified the Kelvin model and the theoretical derivation has been verified with numerical experiment. The corrected damping ratio value can be expressed as

$${{\varvec{\zeta}}}_{{\varvec{k}}}=3{{\varvec{K}}}_{{\varvec{k}}}\frac{\left(1+{\varvec{e}}\right)}{2{\varvec{e}}\left({\mathbf{v}}_{1}-{\mathbf{v}}_{2}\right)}$$

(4.9)

where ${\mathrm{v}}_{1}$ and ${\mathrm{v}}_{2}$ are the initial velocities of colliding bodies.

One of the most popular models for representing pounding is the Hertz model, which uses a non-linear spring of stiffness (${K}_{h}$). The impact force is represented by the following equations:

$${{\varvec{F}}}_{{\varvec{c}}}={{\varvec{K}}}_{{\varvec{h}}}{\left({{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}}\right)}^{{\varvec{n}}} ; {{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}}>0$$

(4.10)

$${{\varvec{F}}}_{{\varvec{c}}}=0 ; {{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}} \le 0$$

(4.11)

The use of the Hertz contact law has a distinct advantage in modelling pounding, since one would expect the contact area between the colliding structures to increase as the contact force increases, leading to a non-linear stiffness described by the Hertz coefficient (n). The impact stiffness parameter, ${K}_{h},$ depends on the material properties of the colliding structures and the contact surface geometry. The Hertz coefficient, n, is typically taken as 1.5. Studies have shown that the system displacement response is relatively insensitive to the exponent, n, in the contact law. The contact force–displacement relationship for the various impact models is shown in Fig. 4.16.

Fig. 4.16

Contact force–displacement relationship for various impact models: a Linear spring element; b Kelvin model; c Hertz non-linear spring; and (d) Hertz damp model [32]

The Hertz model suffers from the limitation that it cannot represent the energy dissipated during contact. Hence, an improved version of the Hertz model is considered, whereby a non-linear damper is used in conjunction with the Hertz spring. Similar models have been used in other areas such as robotics, and multi-body systems. However, its efficiency in structural engineering has not been considered.

In the Hertz damp model, the contact force can be expressed as

$${{\varvec{F}}}_{{\varvec{c}}}={{\varvec{K}}}_{{\varvec{h}}}{\left({{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}}\right)}^{{\varvec{n}}}+{{\varvec{C}}}_{{\varvec{h}}} \left({{{\varvec{u}}}}_{1}-{{{\varvec{u}}}}_{2}\right) ; {{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}}>0$$

(4.12)

$${{\varvec{F}}}_{{\varvec{c}}}=0 ; {{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}} \le 0$$

(4.13)

where ${C}_{h}$ is the damping coefficient, (${u}_{1}-{u}_{2}$−${g}_{p}$) is the relative penetration and ${{(u}}_{1}-{{u}}_{2})$ is the penetration velocity. A non-linear damping coefficient is proposed so that the expected hysteresis loop during impact matches the one shown in Fig. 4.16d.

The damping coefficient is taken as follows:

$${{\varvec{C}}}_{{\varvec{h}}}={\varvec{\zeta}}{{\varvec{\delta}}}^{{\varvec{n}}}$$

(4.14)

where ζ is the damping constant, and δ is the relative penetration (${u}_{1}-{u}_{2}$−${g}_{p}$).

Equating the energy loss during the stereo-mechanical impact to the energy dissipated by the damper, an expression for the damping constant () can be found in terms of the spring stiffness ${K}_{h}$, the coefficient of restitution (e) and the relative approaching velocity (${\mathrm{v}}_{1}-{\mathrm{v}}_{2}$), as follows:

$${\varvec{\delta}}=\frac{3{{\varvec{K}}}_{{\varvec{h}}}\left(1-{{\varvec{e}}}^{2}\right)}{4\left({{\varvec{v}}}_{1}-{{\varvec{v}}}_{2}\right)}$$

(4.15)

Hence, the force during contact can be expressed as

$${{\varvec{F}}}_{{\varvec{c}}}={{\varvec{K}}}_{{\varvec{h}}}{\left({{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}}\right)}^{{\varvec{n}}}\left[1+\frac{3\left(1-{{\varvec{e}}}^{2}\right)}{4\left({\mathbf{v}}_{1}-{\mathbf{v}}_{2}\right)}\left({{{\varvec{u}}}}_{1}-{{{\varvec{u}}}}_{2}\right)\right] ;{{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}}>0$$

(4.16)

$${{\varvec{F}}}_{{\varvec{c}}}=0 ; {{\varvec{u}}}_{1}-{{\varvec{u}}}_{2}-{{\varvec{g}}}_{{\varvec{p}}} \le 0$$

(4.17)

4.5 Effect of Varying Structural Dynamic Properties and Separation Distance on Pounding

The pounding behaviour of structures is largely dependent on the predominant excitation frequencies, compared to the natural frequencies of the structure. It is seen that for structures with different natural periods, the same earthquake excitation can produce different magnitudes of pounding force and resulting structural responses. Again, pounding results in modification of the responses of the colliding structures. Papadrakakis et al. [33] performed shake table tests on pounding between two-storey reinforced concrete buildings, subject to sinusoidal excitation. The results indicated that pounding amplified the displacement responses of the stiffer structure and reduced the responses of the flexible structure. Anagnostopoulos et al. [34] extended their studies from a series of SDOF systems to MDOF. They idealized the buildings as lumped mass, shear beam type and found that if there are large differences in the masses of the colliding buildings, then pounding can cause more damage to the building with the smaller mass. Goltabar et al. [35] considered pounding between buildings of different heights and pointed out that the impact causes an increment in responses of taller buildings but the reverse in shorter ones. Adjacent multi-storied buildings subjected to seismic pounding were also considered by Abdel-Mooty et al. [36], and the results indicated that pounding force increases when the difference in dynamic properties of adjacent buildings increases. They also observed that the top colliding floors are subjected to maximum pounding force and that the number of pounding decreases as separation distance increases.

A systematic study was carried out by Pantelides and Ma [8] to examine the behaviour of a damped SDOF structural system with one-sided pounding during an earthquake. Their findings, which serve to illustrate the effect of the dynamic properties of a structure as well as that of the seismic separation distance on the pounding behaviour, are discussed in some detail now. The model proposed by Davis [27] was used. In Fig. 4.17, a simplified SDOF idealization of the damped elastic structural system undergoing one-sided structural pounding is made. The barrier in Fig. 4.17 is assumed to be rigid, and both the structure and the barrier are subjected to the same ground motion. The rigid barrier can be justified by considering the adjoining structural system to be a very stiff block of squat buildings.

Fig. 4.17

Structural SDOF system model with adjacent barrier [8]

$x\left(t\right)$ is the lateral displacement of the flexible structure relative to ground, $a$ is the separation distance between the flexible and rigid structure and ${xg}$ is the earthquake ground acceleration. Here, the pounding force is denoted by $F(t)$ which is the impact force between the SDOF system and the neighbouring rigid structural model through a Hertz non-linear spring.

The impact force is expressed as (Pantelides et al. (1989)) [8]

$$F\left(t\right)=R{[x\left(t\right)-a]}^{3/2}, \quad x(t)a$$

(4.18)

$$F\left(t\right)=0, \quad x(t)<a$$

(4.19)

where R is the impact stiffness parameter which depends on the material of the two structures that come in contact and also on the contact surface geometry. The value of the impact stiffness parameter is $80$ kN mm^−3/2 for concrete structures.

The equation of motion for the mass of the flexible structure subjected to one-sided pounding is

$$m{\ddot{x}}\left(t\right)+c{\dot{x}}\left(t\right)+kx\left(t\right)+F(t)=-m{{\ddot{x}}_{g}}(t)$$

(4.20)

where $m$, $k,c$ denote the mass, damping and elastic stiffness of the SDOF model of the structure.

Substituting Eqs. (4.18) and (4.19) in Eq. (4.20), the equation of motion considering pounding is

$$m{\ddot{x}}+c{\dot{x}}\left(t\right)+kx\left(t\right)+R{[x\left(t\right)-a]}^\frac{3}{2}=-m{{\ddot{x}}_{g}}$$

(4.21)

When pounding does not occur, the equation of motion is

$$m{\ddot{x}}+c{\dot{x}}\left(t\right)+kx\left(t\right)=-m{{\ddot{x}}_{g}}$$

(4.22)

Here, to examine the effect of the earthquake excitation’s predominant frequency on the response of pounding of an elastic structural system, a sinusoidal base motion with a magnitude of 0.1 g and duration of 30 s is first considered, with two cases of excitation frequency, namely f₁ = 2 Hz and f₂ = 0.67 Hz. In addition, the effects of the separation gap and damping ratio of the elastic structure on the magnitude of the pounding force are investigated. The properties of the example SDOF elastic structure considered are mass $m=350$ Mg, elastic stiffness $Ke=10.5$ kN/mm and damping ratio ζ = 2%. The period of the structural system is 1.15 s (0.87 Hz). The separation distance is assumed to be $a=25$ mm.

Figure 4.18a and b indicates the displacement and acceleration time history of the SDOF structure for the two excitations. Figure 4.18c shows the pounding force in the case of excitation f₂. The value of the peak pounding force is obtained as about 4.5 MN. As shown in Fig. 4.18a, when the excitation frequency is equal to f₁, the displacement never exceeds 25 mm and no pounding occurs. When the excitation has a frequency equal to f₂, both displacement and acceleration responses are significantly large and pounding occurs many times. This happens because in this case, the excitation frequency f₂ is closer to the natural frequency of the structural system than the frequency f₁. The maximum displacement for f₂ is 53 mm and the maximum acceleration is 1.29 g. The displacement and acceleration responses of the structure for no pounding case are given in Fig. 4.18d and e, respectively. The maximum displacement and peak acceleration for the no pounding case are 125.2 mm and 0.28 g, respectively. The maximum displacement of structure in the pounding case is much lower than that of the no pounding case, while the peak acceleration increases several times in the pounding case as compared to the no pounding case. This happens because, due to the rigid obstruction, the displacement response is reduced in the pounding case but the acceleration response is highly increased due to several collisions with the obstruction.

Fig. 4.18

Response of SDOF elastic structure during artificial sinusoidal earthquake when pounding occurs: a Displacement response, b Acceleration response, c Pounding force, d Displacement response when pounding does not occur e Acceleration Response when pounding does not occur

Next, in order to examine the effect of the separation gap on the maximum pounding force and number of impacts, a series of separation distances are studied from 12.5 mm to where pounding does not occur, at an interval of 12.5 mm. The results are given in Fig. 4.19a and b.

Fig. 4.19

Effect of seismic gap on maximum level of pounding force and number of impact

In Fig. 4.19a, at 12.5 mm separation distance, maximum pounding force occurs (7.5MN) and the number of pounding is also maximum (215 times). As the gap increases, the number of impacts decreases (Fig. 4.19b). But in Fig. 4.19a, as the separation gap increases up to 35 mm, the maximum pounding force decreases, but again increases giving a peak (6.8MN) when the gap is 75 mm and then it decreases gradually. The interesting observation from Fig. 4.19b is that there is a sharp decrease in the number of impacts with an initial increase in the separation gap, beyond which the number of poundings remains almost constant for a wide range of the value of the separation gap.

Next, pounding under a recorded earthquake is studied. Two different structural time periods, T = 1 s and 3 s, are subjected to the El Centro earthquake data of 18 May 1940. Figure 4.20a–c indicates the displacement response, the acceleration response and the pounding force generated, respectively.

Fig. 4.20

Response of SDOF elastic structure during 1940 El Centro earthquake: a Displacement, b Acceleration and c Pounding force

Though pounding occurs in both cases, the peak displacement of the more flexible structure with period 3 s is approximately 2.46 times that of the structure with period 1 s, while the peak acceleration of the structure with period 1 s is approximately 1.34 times that of the structure with period 3 s. Further, the peak pounding force of the structure with period 1 s is approximately 1.3 times that of the structure with period 3 s. These results indicate that structures with different periods of vibration may sustain different levels of damage under identical pounding conditions during the same earthquake.

The pounding response of the structure is also dependent on the damping ratio of the structure. The SDOF example structural system with period T = 1 s is considered. Two damping ratios are considered, namely 2 and 8%. Figure 4.21a–c indicates the displacement response, acceleration response and pounding force, respectively.

Fig. 4.21

Effect of damping on pounding of elastic structure: a Displacement, b Acceleration and c Pounding force

For the case of increased damping, peak displacement is reduced by 52.11%, peak acceleration is reduced by 65.12% and peak pounding force is reduced by 65.7%. In addition, the number of pounding occurrences is reduced by 65.3%. Hence, it is clear that supplemental damping in the structure can mitigate the pounding response very effectively.

In order to examine the effect of damping on the separation distance required to prevent pounding, a series of separation distances are studied from a = 25 mm to where pounding does not occur, at an interval of 12.5 mm. Three damping ratios are considered, namely 2, 8 and 20%. The results are shown in Fig. 4.22a and b. The input excitation is the 1940 El Centro earthquake. In Fig. 4.22a, the pounding force is not always reduced with an increase in the separation gap when the damping ratio is low. Even for structural damping as high as 8%, the pounding force remains constant over a large range of the separation gap. Only for very high damping, say 20%, the pounding force decreases linearly with an increase in separation gap. In Fig. 4.22b, it is observed that for lower structural damping, the number of poundings also does not decrease all the time with an increase in separation gap. Even for a high damping ratio, say 8%, it remains almost constant over a large range of separation gap. Only for a very high damping ratio, say 20%, does the number of poundings decrease linearly with an increase in separation gap.

Fig. 4.22

Effect of damping on separation distance, maximum level of pounding force and number of impacts: a Effect of separation distance on maximum pounding force generated, b Effect of separation distance on number of pounding occurred

4.6 Mitigation Measures and Codal Provisions for Pounding

It is clear from the foregoing sections that there is an utmost necessity of mitigating the effects of pounding both at the design stage as well as in existing structures. It is of course worth mentioning that buildings having simple regular geometry, uniformly distributed mass and stiffness in the plan as well as in elevation would perform better under pounding conditions than buildings with irregular configurations. Anagnostopoulos et al. [34] observed that the effects of pounding were reduced as the separation distance increases, and many building codes also suggest this method. Goltabar et al. [35] concluded that by maintaining proper distance between adjacent structures and by hardening buildings, the effect of impact could be reduced. The use of special ‘bumper’ shear walls has been suggested as a good alternative to the separation distance requirement, especially for situations where a new building is to be built next to an existing building with practically no gap in between the two. Bumper damper elements are link elements that are activated when the gap is closed. Such elements reduce energy transfer during pounding and high-frequency pulses. These bumper elements have already been incorporated in the Greek code and in Euro code-08 for earthquake-resistant design.

Different techniques to control pounding in existing structures have been proposed, ranging from simple retrofitting schemes to the provision of supplemental energy dissipation systems in the pounding structures. Westermo [37] recommended a simple reconstruction technique to avoid pounding by connecting building structures through a link and beam system which transmits the connection forces to the floors of the structures (see Fig. 4.23).

Fig. 4.23

Connecting buildings by a link and beam element [37]

The mitigation of pounding response in bridges can be achieved by the use of restrainers, as in Fig. 4.24, and by variable dampers.

Fig. 4.24

Restrainers in bridges [38]

The use of crushable devices and shock transmission units to control pounding in elevated bridges has also been considered. Jankowski et al. [26] confirmed that the pounding in elevated bridges could be avoided by inserting hard rubber bumpers between segments and by linking them to one another. The results of their experiment indicate that for the workable application of such links, shock transmission units can be used. The bumper layer was also used by Cheng et al. [39] to mitigate the effect of pounding on concrete, liquid storage structures.

Structural pounding can be mitigated by the incorporation of some passive control device, such as friction/metallic/fluid/viscoelastic dampers or active control systems into the buildings. A theoretical study on the control of seismic pounding by connecting the adjacent structures with friction dampers was conducted by Dutta and Ghosh [40]. Friction dampers are popular due to their low capital and maintenance costs and ready commercial availability. The model in their study is shown in Fig. 4.25. They concluded that linking adjacent buildings with friction dampers could be a good option to control pounding.

Fig. 4.25

a Two base-excited adjacent structures connected by friction damper and b its mechanical model [40]

In another study on the use of passive energy dissipation devices to control pounding, Das and Ghosh [41] studied tuned mass dampers (TMDs) and concluded that the TMD is equally effective in reducing both structural responses as well as pounding force. However, the TMD effectiveness is largely dependent on the mass ratio and the selection of the proper tuning ratio of the damper.

Codal provisions

The codes of Argentina, Australia, Canada, France, India, Indonesia, Mexico, Taiwan and the USA account for the pounding phenomenon by the specification of a minimum separation distance between the neighbouring buildings. It is to be noted that, apart from the structural displacement responses, the appropriate separation distance is guided by several other factors, such as the importance factor and deflection amplification factor. The values of the separation distance depend on the type of soil and the seismic action as well.

Chenna and Ramancharla [42] have presented a review and comparison of the different worldwide codal provisions on the separation distance between adjacent buildings. It is observed that the procedure to determine the separation distance in the codes of these countries is not the same. For example, in Canada and Israel, the sum of the displacements of each building is specified as the separation distance to be maintained by the code. In France, it is a quadratic combination of the maximum displacements. In Taiwan, it depends on the building height and in Argentina, the minimum separation gap is 2.5 cm. According to UBC-1997 [43], the building separation distance for adjacent buildings located on the same property line is given by the square root of the sum of the squares of the maximum building displacements. FEMA 273-1997 [44] specifies the minimum separation distance as 4% of the building height to avoid pounding.

The New Zealand Loading Code NZS 4203:1992 [45] states the separation of adjacent structures as a distance equal to the sum of their maximum design lateral displacement for the ultimate limit state and 24 mm is the minimum separation gap requirement. According to IBC-2009 [46] and ASCE:7-2010 [47], the separation distance between two adjacent buildings is computed from

$${{\varvec{\delta}}}_{{\varvec{M}}}=\frac{{{\varvec{C}}}_{{\varvec{d}}}{{\varvec{\delta}}}_{{\varvec{m}}{\varvec{a}}{\varvec{x}}}}{{\varvec{I}}}$$

(4.23)

where ${\delta }_{{\text{max}}}$ is the maximum elastic displacement that occurs anywhere in a floor from the application of the design base shear to the structure.${C}_{d}$ is the deflection amplification factor and I is the importance factor for seismic loading.

Further, IBC-2009 stipulates that adjacent buildings on the same property shall be separated by a distance not less than ${\delta }_{MT}$, determined by Eq. 4.24

$$\delta_{MT} = \sqrt {(\delta_{M1} )^2 + (\delta_{M2} )^2 }$$

(4.24)

where ${\delta }_{M1}$, ${\delta }_{M2}$ denote the maximum inelastic response displacements of the adjacent buildings.

The Indian code for seismic resistant design, IS-1893-Part1-2016 [48], stipulates that two adjacent buildings or two adjacent units of the same building with separation joint between them shall be separated by a distance equal to R times the sum of storey displacements of the two buildings or units, where R is the response reduction factor. However, when floors are at the same level, the separation is given by (${\mathrm{R}}_{1}{\Delta }_{1}$+${\mathrm{R}}_{2}{\Delta }_{2}$). Here, ${\mathrm{R}}_{1}$ and ${\mathrm{R}}_{2}$ are the response reduction factors and ${\Delta }_{1}$ and ${\Delta }_{2}$ are displacements corresponding to buildings 1 and 2, respectively.

Overall, it is gauged that the current separation distances are rather ad-hoc and at times found to be oversimplified or over-conservative. More in-depth studies are required to be dedicated to the evaluation of the separation distance between adjacent buildings to prevent the possibility of structural pounding at the design stage. Further research is also required to be directed to the mitigation of structural pounding, especially in existing closely spaced structures, through construction details and by the incorporation of structural vibration control systems.