Pressure Transient Characteristics of Highly Deviated Wells in Fractured-Vuggy Carbonate Gas Reservoirs

Abstract

More and more attention has been paid to the study of flow properties in fractured-vuggy reservoirs because lots of such reservoirs have been found worldwide with significant gas production and reserves. In order to improve carbonate gas reservoir production, highly deviated wells (HDW) are widely used in the field. However, it is very difficult to consider the complex pore structure of fractured-vuggy reservoirs and evaluate the pressure transient behaviors of HDW. This paper presents a semi-analytical model that analyzed the pressure behavior of HDW in fractured-vuggy carbonate gas reservoirs which consist of fractures, vugs and matrix. Introducing pseudo-pressure; Fourier transformation, Laplace transformation, and Stehfest numerical inversion were employed to establish a point source and line source solutions. Furthermore, the validity of the proposed model was verified by comparing with two existing pressure transient models. Then the flow characteristics were analyzed thoroughly by examining the pressure derivative curve which can be divided into five flow stages. The physical meanings of the model parameters were analyzed through sensitivity analysis. Finally, a field case was successfully used to show the application of the proposed semi-analytical model. The study contributes to the highly efficient evaluation of the pressure transient behaviors for HDW in fractured-vuggy carbonate gas reservoirs.

1 Introduction

Fractured-vuggy carbonate gas reservoirs are an extremely complex porous structure which are composed of different combinations of matrix, fracture and vug systems and thus have fluid transport behavior of triple-porosity system [1]. In order to improve gas reservoir development and production, highly deviated wells (HDW) are widely used [2]. A new difficulty that arises from the application of this technology to improve reservoir development is the challenge in evaluating the pressure transient behaviors of HDW in this special gas reservoirs.

Triple-porosity models for carbonate reservoirs have been proposed through analytical, semi-analytical and numerical methods by different authors as extensions to the double-porosity model of Warren and Root [3]. In order to better describe fractured reservoirs, Abdassah and Ershaghi introduced the concept of triple-porosity system and established a triple-porosity and single-permeability pressure model, which is considered an unsteady interporosity flow model between the fractures and the other two systems, namely matrix and vug [4]. Later, another dual-permeability model was proposed to characterize vuggy, matrix and natural fractures in carbonate reservoirs by Camacho-Velázquez et al. [5]. Gulbransen et al. proposed a multiscale mixed finite element method for detailed modeling of fractured-vuggy reservoirs as a first step toward a uniform multiscale, multiphysics framework [6]. Jia et al. presented the first study of flow issues within a porous-vuggy carbonate reservoir that does not consider a fracture system and established a model of well testing, rate decline analysis for this reservoir [7]. Zhang et al. established a new numerical model that considered the effect of geomechannics on fractures and vugs [8]. In order to estimate the volume of vugs by well test analysis, Du et al. introduced a new well test model considering the coupling between oil flow and wave propagation [9].

A substantial amount of research has focused on the pressure behavior and production performance of deviated wells. Cinco et al. first presented a study of unsteady- state performance of a deviated well by point source function and methods of images and superposition principle [10]. The authors proposed an approximate solution of skin factor for deviated wells (less than 75°). Besson and Aquitaine built a practical equation to analyze the productivity of a deviated well with respect to any angle of slant and degree of anisotropy [11]. Based on their study, they found that a deviated well is less affected by anisotropy than a horizontal well in terms of productivity. Abbaszadeh first proposed analytical solution for the pressure drawdown behavior of a deviated limited-entry well, which is used the method of source and Green’s functions to derive these solutions [12]. Ozkan and Raghavan presented a solution for a deviated limited-entry well with closed top and bottom boundaries by employing the integral transformation [13]. Meng et al. introduced a semi-analytical model of HDW for analyzing the pressure behavior which considered the non-darcy performance in triple-porosity medium [14]. Dong et al. presented a new skin factor model for limited-entry slant wells in anisotropic reservoirs by the approximation treatment of large-time pressure solution [15]. Wang et al. proposed a new model for analyzing production behavior of HDW in fractured-vuggy gas reservoirs by semi-analytical method and presented the effects of relevant parameters on production performance [16].

Currently, not much study has been conducted on the pressure transient behavior of HDW in fractured-vuggy gas reservoirs. In this paper, a semi-analytical model was presented by employing Laplace transformation, Fourier transformation, Stehfest numerical inversion algorithm and point source function.

2 Physical Model

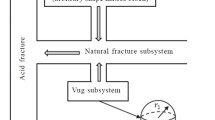
A schematic for a HDW in a fractured-vuggy carbonate gas reservoir is presented in Fig. 1. The gas reservoirs are characterized by vugs system, matrix system and fractures system. Figure 2 is a representation of the physical modeling scheme of a fractured-vuggy carbonate medium. The assumptions employed to define the pressure behavior mathematically are listed as follows:

Fig. 1.

A HDW in a fractured-vuggy carbonate gas reservoir.

Fig. 2.

Flow sketch for a cell [17].

• (1) A laterally infinite gas reservoir contains a HDW.

• (2) A horizontal gas reservoir with equal thickness and two impermeable boundaries at the top and bottom.

• (3) Gas flows only through the fracture system into the wellbore while interporosity flow occurs from the vugs and the matrix systems to the fracture system during well production.

• (4) Isothermal single phase flow which follows Darcy's law. Meanwhile, the effects of gravity and capillary forces are negligible.

• (5) The initial pressure is uniform throughout the reservoir and is equal to $p_{i}$.

• (6) The HDW produces at a constant rate $q_{g}$ or at constant pressure $p_{wf}$.

• (7) The horizontal permeability $k_{h}$ and $k_{v}$ the vertical permeability are not the same.

3 Mathematical Model

3.1 Establishment of Mathematical Model

The interporosity flow from vugs and matrix to fractures is assumed to be in a pseudo-steady state in this study. Combining transport equation as well as the equation of state with the continuity equation and the introduction of pseudo-pressure [18] (the detailed procedure for pseudo-pressure is documented in Appendix A), the governing equation for the triple-porosity system in radial cylindrical coordinate is given as follows:

$$ \frac{1}{r}\frac{\partial }{\partial r}(r\frac{{\partial m_{f} }}{\partial r}) + \frac{{k_{fv} }}{{k_{fh} }}\frac{{\partial^{2} m_{f} }}{{\partial z^{2} }} = \frac{1}{0.0864}\frac{{\phi_{f} \mu_{g} C_{tf} }}{{k_{fh} }}\frac{{\partial m_{f} }}{\partial t} - \alpha_{m} \frac{{k_{m} }}{{k_{fh} }}(m_{m} - m_{f} ) - \alpha_{c} \frac{{k_{c} }}{{k_{fh} }}(m_{c} - m_{f} ) $$

(1)

The matrix system could be represented by the following equation:

$$ \frac{{\phi_{m} \mu_{g} C_{tm} }}{0.0864}\frac{{\partial m_{m} }}{\partial t} = \alpha_{m} k_{m} (m_{f} - m_{m} ) $$

(2)

The equation representing the vugs system is given as:

$$ \frac{{\phi_{c} \mu_{g} C_{tc} }}{0.0864}\frac{{\partial m_{c} }}{\partial t} = \alpha_{c} k_{c} (m_{f} - m_{c} ) $$

(3)

It is assumed that the initial pseudo-pressure $m_{i}$ is uniform in the triple-porosity system:

$$ m_{j} (r,t = 0) = m_{i} ,\;\;(j = f,m,c) $$

(4)

The outer boundary is closed:

$$ \left. {\frac{{\partial m_{j} }}{\partial r}} \right|_{{r = r_{e} }} = 0,\;\;(j = f,m,c) $$

(5)

A continuous point source ($x_{w} ,y_{w} ,z_{w}$) with a constant gas rate $\widetilde{q}$ is present at the inner boundary, which could be represented as:

$$ \begin{gathered} \begin{array}{*{20}l} {\widetilde{q}B_{gi} = \left\{ {\begin{array}{*{20}l} {\mathop {\lim }\limits_{\varepsilon \to 0} \left( {\mathop {\lim }\limits_{r \to 0} \frac{{k_{hf} }}{{\alpha_{p} \mu_{g} \varepsilon }}\int_{{z_{w} - {\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{z_{w} + {\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-\nulldelimiterspace} 2}}} {r\frac{{\partial m_{f} }}{\partial r}dz} } \right)\;} \hfill \\ 0 \hfill \\ \end{array} } \right.} \hfill & \begin{gathered} \left| {z - z_{w} } \right| \le {\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-\nulldelimiterspace} 2} \hfill \\ \left| {z - z_{w} } \right|{{ > \varepsilon } \mathord{\left/ {\vphantom {{ > \varepsilon } 2}} \right. \kern-\nulldelimiterspace} 2} \hfill \\ \end{gathered} \hfill \\ \end{array} \hfill \\ \hfill \\ \end{gathered} $$

(6)

The boundaries are impermeable at the bottom and top of the reservoir:

$$ \left. {\frac{{\partial m_{f} }}{\partial z}} \right|_{z = 0} = \left. {\frac{{\partial m_{f} }}{\partial z}} \right|_{z = h} = 0 $$

(7)

The governing equations and the initial and boundary conditions (Eq. (1)–(7)) are transformed into dimensionless terms (Eq. (8)–(14)) based on the definitions of dimensionless variables in Table 1.

Table 1. Definitions of dimensionless variables.

The dimensionless governing equations for the fracture, matrix and vugs systems are:

$$ \frac{1}{{r_{D} }}\frac{\partial }{{\partial r_{D} }}(r_{D} \frac{{\partial m_{fD} }}{{\partial r_{D} }}) + \frac{{\partial^{2} m_{fD} }}{{\partial z_{D}^{2} }} = \omega_{f} \frac{{\partial m_{fD} }}{{\partial t_{D} }} - \lambda_{m} (m_{mD} - m_{fD} ) - \lambda_{c} (m_{cD} - m_{fD} ) $$

(8)

$$ \omega_{m} \frac{{\partial m_{mD} }}{{\partial t_{D} }} = \lambda_{m} (m_{fD} - m_{mD} ) $$

(9)

$$ \omega_{c} \frac{{\partial m_{cD} }}{{\partial t_{D} }} = \lambda_{c} (m_{fD} - m_{cD} ) $$

(10)

The transformed initial condition is given as:

$$ m_{jD} (r_{D} ,t_{D} = 0) = 0,\;\;(j = f,m,c) $$

(11)

Similarly, the transformed outer boundary condition is:

$$ \left. {\frac{{\partial m_{jD} }}{{\partial r_{D} }}} \right|_{{r_{D} = r_{eD} }} = 0,\;\;(j = f,m,c) $$

(12)

Furthermore, the transformed inner boundary condition is:

$$ \begin{array}{*{20}l} {\mathop {\lim }\limits_{{\varepsilon_{D} \to 0}} \left( {\mathop {\lim }\limits_{{r_{D} \to 0}} \int_{{z_{wD} - {{\varepsilon_{D} } \mathord{\left/ {\vphantom {{\varepsilon_{D} } 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{z_{{w_{D} }} + {{\varepsilon_{D} } \mathord{\left/ {\vphantom {{\varepsilon_{D} } 2}} \right. \kern-\nulldelimiterspace} 2}}} {r_{D} \frac{{\partial m_{fD} }}{{\partial r_{D} }}dz_{D} } } \right) = \left\{ \begin{gathered} - h_{D} \hfill \\ 0 \hfill \\ \end{gathered} \right.\;\;\;} \hfill & \begin{gathered} \left| {z_{D} - z_{wD} } \right| \le {{\varepsilon_{D} } \mathord{\left/ {\vphantom {{\varepsilon_{D} } 2}} \right. \kern-\nulldelimiterspace} 2} \hfill \\ \left| {z_{D} - z_{wD} } \right|{{ > \varepsilon_{D} } \mathord{\left/ {\vphantom {{ > \varepsilon_{D} } 2}} \right. \kern-\nulldelimiterspace} 2} \hfill \\ \end{gathered} \hfill \\ \end{array} $$

(13)

Finally, the transformed top and bottom boundaries is:

$$ \left. {\frac{{\partial m_{fD} }}{{\partial z_{D} }}} \right|_{{z_{D} = 0}} = \left. {\frac{{\partial m_{fD} }}{{\partial z_{D} }}} \right|_{{z_{D} = h_{D} }} = 0 $$

(14)

3.2 Solution of Mathematical Model

3.2.1 Basic Continuous Point Source Solution

The Laplace transformation as well as the Fourier transformation and inversion were used to solve the dimensionless models (Eq. (8)–(14)). The solution in Laplace space is as follows (the detailed procedure for the solution is documented in Appendix B).

$$ \begin{aligned} \overline{m} _{{fD}} = & \frac{1}{s}\left[ {\frac{{K_{1} (r_{{eD}} \sqrt {sf(s)} )}}{{I_{1} (r_{{eD}} \sqrt {sf(s)} )}}I_{0} (r_{D} \sqrt {sf(s)} ) + K_{0} (r_{D} \sqrt {sf(s)} )} \right] \\ & + \,\frac{2}{s}\sum\limits_{{n = 1}}^{\infty } {\left[ {\frac{{K_{1} (r_{{eD}} \sqrt {u_{n}^{2} + sf(s)} )}}{{I_{1} (r_{{eD}} \sqrt {u_{n}^{2} + sf(s)} )}}I_{0} (r_{D} \sqrt {u_{n}^{2} + sf(s)} )} \right.} \\ & \left. {\;\; + \,K_{0} (r_{D} \sqrt {u_{n}^{2} + sf(s)} )} \right]\cos (\mu _{n} z_{{wD}} )\cos (\mu _{n} z_{D} ) \\ \end{aligned} $$

(15)

Where

$$ u_{n} = \frac{n\pi }{{h_{D} }} $$

(16)

$$ f(s) = w_{f} + \frac{{\lambda_{c} \omega_{c} }}{{\lambda_{c} + \omega_{c} s}} + \frac{{\lambda_{m} \omega_{m} }}{{\lambda_{m} + \omega_{m} s}} $$

(17)

In Eq. (15) $k_{0}$ is modified Bessel function of zero order of the second kind; $k_{1}$ is modified Bessel function of order one of the second kind; $I_{0}$ is modified Bessel function of order zero of the first kind; $I_{1}$ is modified Bessel function of order one of the first kind.

3.2.2 Pressure Distribution of a HDW

The wellbore was treated as a uniform flux line source in order to obtain the pressure solution of HDWs. It was also assumed that there was an infinitesimal point on the HDW. Integration was carried out along the deviated line for the line source solution based on the principle of superposition for a point source. The dimensionless pressure distribution of HDW in Laplace domain is thus given as:

$$ \begin{aligned} \overline{m} _{{fD}} = & \frac{1}{{sL_{{wD}} }}\int_{{ - \frac{{L_{{wD}} }}{2}}}^{{\frac{{L_{{wD}} }}{2}}} {\left[ {\frac{{K_{1} (r_{{eD}} \sqrt {sf(s)} )}}{{I_{1} (r_{{eD}} \sqrt {sf(s)} )}}I_{0} (\widetilde{{r_{D} }}\sqrt {sf(s)} ) + K_{0} (\widetilde{{r_{D} }}\sqrt {sf(s)} )} \right]} d\eta \\ & + \,\frac{2}{{sL_{{wD}} }}\int_{{ - \frac{{L_{{wD}} }}{2}}}^{{\frac{{L_{{wD}} }}{2}}} {\left\{ {\sum\limits_{{n = 1}}^{\infty } {\left[ {\frac{{K_{1} (r_{{eD}} \sqrt {u_{n}^{2} + sf(s)} )}}{{I_{1} (r_{{eD}} \sqrt {u_{n}^{2} + sf(s)} )}}I_{0} (\widetilde{{r_{D} }}\sqrt {u_{n}^{2} + sf(s)} )} \right.} } \right.} \\ & \left. {\;\; + K_{0} (\widetilde{{r_{D} }}\sqrt {u_{n}^{2} + sf(s)} )} \right]\left\{ {\cos (\mu _{n} \widetilde{z}_{{wD}} )\cos (\mu _{n} z_{D} )} \right\}d\eta \\ \end{aligned} $$

(18)

In Eq. (18)

$$ \widetilde{r}_{D} = \sqrt {(x_{D} - x_{wD} - \eta \sin \theta_{w} )^{2} + (y_{D} - y_{wD} )^{2} } $$

(19)

$$ \widetilde{z}_{wD} = z_{wD} + \eta \cos \theta_{w} $$

(20)

$$ \theta_{w} = \tan^{ - 1} \left( {\sqrt {\frac{{k_{vf} }}{{k_{hf} }}} \tan \theta } \right) $$

(21)

$$ L_{wD} = \frac{{L_{w} }}{{r_{w} }}\sqrt {\frac{{k_{f} }}{{k_{hf} }}\sin^{2} \theta + \frac{{k_{f} }}{{k_{vf} }}\cos^{2} \theta } $$

(22)

The pressure solution with wellbore storage and skin effect in Laplace domain is obtained based on the principle of superposition as:

$$ \overline{m}_{wD} = \frac{{s\overline{m}_{fD} + S}}{{s + C_{D} s^{2} (s\overline{m}_{fD} + S)}} $$

(23)

$$ C_{D} = \frac{C}{{6.28\left( {\phi C_{t} } \right)_{f + c + m} hr_{w}^{2} }} $$

(24)

Equation (23) can then be inverted to obtain $m_{wD}$ in real space using suitable numerical inversion algorithms such as Stehfest's inversion algorithm [19].

4 Results and Discussion

4.1 Model Validation

To the best of our knowledge, there are no existing models for highly deviated wells in triple-porosity gas reservoir media. In this section, two specific models, i.e., a vertical well in triple-porosity gas reservoir medium and a deviated well in homogeneous gas reservoir medium were used to verify the proposed model.

Comparison with a Vertical Well in Triple-Porosity gas Reservoir Medium.

It is obvious that when the inclination angle of highly deviated well approaches 0°, the deviated well is simplified as a vertical well. Furthermore when the outer boundary condition is neglected in the model, the well is in an infinite boundary reservoir. Based on the specific situation, this model could be compared with a vertical well in triple-porosity medium that is proposed by Abdassah and Ershaghi in a real domain (Fig. 3) [4]. The details of relevant parameters needed for the model validation are listed in Table 2.

Comparison with a Deviated well in Homogeneous Reservoir Medium.

Cinco et al. first presented the study of unsteady- state performance of a deviated well, but there is a restriction that has been criticized because of their inability to incorporate the high-angle wells (more than 75°). After that, Ozkan and Raghavan presented a new efficient solution that can remove the restriction. When the triple-porosity media and the outer boundary condition are not taken into account in the model, it just presents a deviated well in an infinite boundary homogeneous reservoir. Based on the specific situation, this model could be compared with the model that is presented by Ozkan and Raghavan (Fig. 4) [13]. The details of relevant parameters needed for the model validation are also listed in Table 2.

Fig. 3.

Comparison of pressure curves between the model of Abdassah and Ershaghi [4] and the proposed model with an approximate 0° angle of inclination in an infinite reservoir boundary

Fig. 4.

Comparison of pressure curves between the model of Ozkan and Raghavan [13] and the proposed model with an infinite boundary homogeneous reservoir medium

As shown in Fig. 3 and Fig. 4, the proposed models in this paper had very good matches with the aforementioned conditions of the models of Abdassah et al. [4] and the model of Ozkan and Raghavan [13]. Therefore, our presented model is a general model, which could analyze the pressure-transient behavior of HDW in naturally fractured vuggy gas reservoirs.

Table 2. The values of relevant parameters for verification and sensitivity analysis.

4.2 Analyses of Transient Pressure Behavior with Triple-Porosity Flows

Different flow regime analysis was conducted to study the effects of various flow mechanisms on the overall pressure behavior, in order to understand the pressure behavior with triple-porosity flows. Figure 5 shows the complete transient pressure behavior of a HDW in a fractured-vuggy carbonate gas reservoir under closed circular boundary which can be divided into five flow stages. The first stage was dominated by wellbore storage and skin effect and the dimensionless pseudo pressure and pseudo pressure derivative curves showed a straight line with a slope of 1. Next, skin factor affected the shape of the derivative curve which looked like a “hump”. The second stage of the pressure behavior of a HDW was dominated by the inclination angle ($\theta$). When the inclination angle approached 0°, the HDW was treated as a vertical well and the second stage would not be obvious or would completely disappear on the curve. The third flow regime which showed a “dip” on the pressure derivative curve was dominated by interporosity flow between fractures and vugs. The interporosity flow between fractures and vugs appeared first when the wellbore pressure began to deplete because the gas flow in the vugs was relatively smoother than in the matrix. Therefore, wellbore pressure depletion was slowed down due to gas supplement from vugs to the fracture system. The penultimate stage which also showed a “dip” on the pressure derivative curve was dominated by interporosity flow between fractures and matrix. It is worth noting that the third and fourth stages could interfere with each other, depending on the value of $\lambda_{c}$ and $\lambda_{m}$. The fifth stage was dominated by closed circular boundary, which showed on the derivative curve with a slope of 1.

Fig. 5.

Pressure curves for HDW in fractured-vuggy carbonate gas reservoir under closed circular boundary.

4.3 Model Sensitivity Analyses

Based on Table 2 data, a detailed sensitivity analysis was carried out to examine the influences of certain parameters on the pressure transient of the benchmark model of the HDW in triple-porosity media under closed circular boundary. These parameters included the inclination angle of the HDW, fracture storativity ratio, interporosity flow coefficient between fractures and vugs, interporosity flow coefficient between fractures and matrix. The values used in the sensitivity analysis of a specific parameter were different from what was used in the aforementioned benchmark model. The influences of these parameters and their estimates are vital for future transient analysis and forecasting.

Inclination Angle.

Figure 6 shows the effects of inclination angle on pressure performance of a HDW in a triple-porosity media. It was seen that the inclination angle of a HDW just affects the second stage in the log-log pressure curve, and the other parts of the curve had no obvious changes In Fig. 6, while the change of dimensionless pseudo pressure curves was insensitive in the second stage, dimensionless pseudo pressure derivative curves obviously changed with inclination angle. With increase in inclination angle, the “dip” becomes deeper, the slope of the tail of the “dip” becomes more severe. The tail of the “dip” expresses linear flow that parallels with top and bottom boundary along the HDW as in Fig. 7. When inclination angle is higher than 83°, the well can be considered as a horizontal well [20]. In this situation, the slope of the tail of the “dip” was approximately 0.5.

Fig. 6.

Effect of inclination angle on pressure curves and their derivative curves.

Fig. 7.

Schematics of linear flow of a HDW.

Fracture Storativity Ratio.

The fractures storativity ratio is the reflection of the relative gas-storage capacity of fracture a gas reservoir. Different fracture storativity ratios ($\omega_{f}$ = 0.001, 0.01, 0.1) were examined to explore their influence on the pressure response of a HDW in triple-porosity medium under closed circular boundary. The pressure drops and pressure derivatives at different fracture storativity ratio which were calculated with the proposed model are presented in Fig. 8. From the pressure drop and pressure derivative curves, the fracture storativity ratio primarily influenced the third stage. Meanwhile, the influences of the third stage also brought about the changes in the second stage which was more obvious in the pressure derivative curves. The “dip of the third stage tends to be shallower as the fracture storativity ratio was increased on the pressure derivative curve. On the contrary, at the third stage, the pressure derivative was decreased with increase in fracture storativity ratio.

Fig. 8.

Effect of fracture storativity ratio on the pressure curves and their derivative curves.

Fig. 9.

Effect of interporosity flow coefficient between fractures and vugs on the pressure curves and their derivative curves.

Interporosity Flow Coefficient.

Figure 9 and Fig. 10 show the effects of $\lambda_{c}$ and $\lambda_{m}$ on pressure performance of the HDW in a triple-porosity medium. From the pressure derivative curves, $\lambda_{c}$ and $\lambda_{m}$ primarily influenced the third stage and the fourth stage. These two parameters had similar changes. Thus, the position of “dip” inclined to left or right was only affected by the interporosity flow coefficient. The larger the interporosity flow coefficient, the earlier the time of interporosity and the “dip” was more inclined to the left. In addition, because the interporosity flow between fractures and vugs is more likely to happen than the interporosity flow between fractures and matrix, the third stage always appeared before the fourth stage.

Fig. 10.

Effect of interporosity flow coefficient between fractures and matrix on the pressure curves and their derivative curves.

4.4 Application of a Real Field Case

The most striking aspect of the proposed model is that it can be applied to obtain more parameters which reflect comprehensive flow characteristics by using history matching procedure, i.e. fractures storativity ratio, interporosity flow coefficient between fractures and vugs, interporosity flow coefficient between fractures and matrix. If those parameters are unknown, the determination of these unknown parameters is in fact a subject of inverse problems. Determination of these unknown parameters could combine the solution of the present model with an auto history matching algorithm [21].

In this section, a pressure buildup test from a well in the Arum River Basin in Turkmenistan was used to demonstrate the practical application of the proposed model. Arum River Basin is a large scale sedimentary basin, which is located between the border of Turkmenistan and Uzbekistan. The carbonate rock reservoir bed is formed by post-depositional diagenesis processes, including dissolution and dolomitization. Vugs, fractures and dissolution pores are highly dispersed in the reservoir.

The well testing time was conducted in June, 2013. The wellbore radius is 0.0899 m, inclination angle of HDW is 72°, length of HDW is 534 m, the effective thickness of formation is 48.5 m, the effective porosity (matrix + fractures + vugs) is 0.112 and specific gas gravity is 0.60. The production rate of the gas well was 87.4 × 10⁴ m³/d. The pressure and pressure derivative curves presented in Fig. 11 were constructed from the well test data. The pressure derivative curve showed the second and the third stages, which was dominated by inclination angle of the HDW and interporosity flow between fractures and vugs. However, the fourth stage was missing which is attributed to an insufficient testing time. Furthermore, the unknown parameters could be determined by combining the present solution with an auto history matching algorithm. Figure 11 shows that the proposed model had a good fitting with actual well test data. The final matching results are given as: Fracture permeability in the horizontal direction ($k_{hf}$) is 10.2 mD; fracture permeability in the vertical direction ($k_{vf}$) is 1.1 mD; the fracture storativity ratio ($\omega_{f}$) is 0.0042; the vug storativity ratio ($\omega_{c}$) is 0.039; the matrix storativity ratio ($\omega_{m}$) is 0.9586; the interporosity flow between fractures and vugs ($\lambda_{c}$) is 1.85 × 10 ⁻⁶; the initial pressure ($p_{i}$) is 53.31MPa. In summary, the matching effect is desirable and the interpretation results are credible.

Fig. 11.

Matching of well test data using the presented model.

5 Conclusions

This research investigated the pressure-transient behavior of highly deviated well (HDW) in naturally fractured-vuggy carbonate gas reservoir. Based on this work, several important conclusions could be drawn as follows:

• (1) Firstly a semi-analytical solution for a HDW in naturally fractured-vuggy carbonate gas reservoir with a closed circular boundary is presented.

• (2) Pressure type curves for a HDW in naturally fractured-vuggy carbonate gas reservoir were divided into five flow stages. Among these, the second stage was dominated by the inclination angle ($\theta$) of the HDW. The third stage was dominated by interporosity flow between fractures and vugs. The fourth stage was dominated by interporosity flow between fractures and matrix. Each parameter had a different influence on type curves.

• (3) Successful well test data interpretation validated the presented model and several reservoir parameters were obtained. It is further demonstrated that this model could be applied to real case studies.

Appendices

Appendix A. Calculation of Pseudo-pressure

In Eqs. (1)–(7), $m_{f}$, $m_{m}$, $m_{c}$ is the pseudo-pressure of the fracture system, matrix system and vugs system, respectively, $MPa/s$. The pseudo-pressure can be given as follows:

$$ m = \int_{0}^{p} {\frac{2p}{{\mu_{g} Z}}} dp $$

(A.1)

Appendix B. Calculation of Continuous Point Source Solution

Equations (8)–(14) can be transformed into Laplace domain by the Laplace transformation.

The dimensionless governing equations of fractures, matrix and vugs systems in the Laplace domain are as follows:

$$ \frac{1}{{r_{D} }}\frac{\partial }{{\partial r_{D} }}(r_{D} \frac{{\partial \overline{m}_{fD} }}{{\partial r_{D} }}) + \frac{{\partial^{2} \overline{m}_{fD} }}{{\partial z_{D}^{2} }} = \omega_{f} s\overline{m}_{fD} - \lambda_{m} (\overline{m}_{mD} - \overline{m}_{fD} ) - \lambda_{c} (\overline{m}_{cD} - \overline{m}_{fD} ) $$

(B.1)

$$ \omega_{m} s\overline{m}_{mD} = \lambda_{m} (\overline{m}_{fD} - \overline{m}_{mD} ) $$

(B.2)

$$ \omega_{c} s\overline{m}_{cD} = \lambda_{c} (\overline{m}_{fD} - \overline{m}_{cD} ) $$

(B.3)

The outer boundary condition is transformed as:

$$ \left. {\frac{{\partial \overline{m}_{jD} }}{{\partial r_{D} }}} \right|_{{r_{D} = r_{eD} }} = 0,\;\;\;(j = f,m,c) $$

(B.4)

The inner boundary condition is transformed as:

$$ \begin{array}{*{20}l} {\mathop {\lim }\limits_{{\varepsilon_{D} \to 0}} \left( {\mathop {\lim }\limits_{{r_{D} \to 0}} \int_{{z_{wD} - {{\varepsilon_{D} } \mathord{\left/ {\vphantom {{\varepsilon_{D} } 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{z_{{w_{D} }} + {{\varepsilon_{D} } \mathord{\left/ {\vphantom {{\varepsilon_{D} } 2}} \right. \kern-\nulldelimiterspace} 2}}} {r_{D} \frac{{\partial \overline{m}_{fD} }}{{\partial r_{D} }}dz_{D} } } \right) = \left\{ \begin{gathered} - \frac{{h_{D} }}{s} \hfill \\ 0 \hfill \\ \end{gathered} \right.\;\;\;} \hfill & \begin{gathered} \left| {z_{D} - z_{wD} } \right| \le {{\varepsilon_{D} } \mathord{\left/ {\vphantom {{\varepsilon_{D} } 2}} \right. \kern-\nulldelimiterspace} 2} \hfill \\ \left| {z_{D} - z_{wD} } \right|{{ > \varepsilon_{D} } \mathord{\left/ {\vphantom {{ > \varepsilon_{D} } 2}} \right. \kern-\nulldelimiterspace} 2} \hfill \\ \end{gathered} \hfill \\ \end{array} $$

(B.5)

The top and bottom boundaries are transformed as:

$$ \left. {\frac{{\partial \overline{m}_{fD} }}{{\partial z_{D} }}} \right|_{{z_{D} = 0}} = \left. {\frac{{\partial \overline{m}_{fD} }}{{\partial z_{D} }}} \right|_{{z_{D} = h_{D} }} = 0 $$

(B.6)

Where

$$ \overline{m}_{jD} = \int_{0}^{\infty } {e^{{ - st_{D} }} m_{jD} (t_{D} } )dt_{D} ,\;\;\;(j = f,m,c) $$

(B.7)

To eliminate the variable $z_{D}$ in the governing equation, Eqs. (B.1)–(B.5) can be transformed by Fourier cosine transform. The Fourier cosine transform and inverse Fourier cosine transform are given as follows:

$$ \widehat{m}_{jD} = \int_{0}^{{h_{D} }} {m_{jD} \cos \left( {\frac{{n\pi z_{D} }}{{h_{D} }}} \right)} dh_{D} ,\;\;\;(j = f,m,c) $$

(B.8)

$$ m_{jD} = \sum\limits_{n} {\widehat{m}_{jD} \frac{{\cos \left( {\frac{{n\pi z_{D} }}{{h_{D} }}} \right)}}{N(n)}} ,\;\;\;(j = f,m,c) $$

(B.9)

Where

$$ \begin{gathered} \begin{array}{*{20}l} {N(n) = \int_{0}^{{h_{D} }} {\cos^{2} \left( {\frac{{n\pi z_{D} }}{{h{}_{D}}}} \right)dz_{D} } = \left\{ \begin{gathered} h_{D} \hfill \\ \frac{{h_{D} }}{2} \hfill \\ \end{gathered} \right.} \hfill & \begin{aligned} & n = 0 \\ & n = 1,2,3 \ldots \\ \end{aligned} \hfill \\ \end{array} \hfill \\ \hfill \\ \end{gathered} $$

(B.10)

By employing the Fourier cosine transform (Eq. (B8)), Eqs. (B.1)–(B.5) can be transformed as follows:

$$ \frac{{d^{2} \widehat{{\overline{m} }}_{fD} }}{{dr_{D}^{2} }} + \frac{1}{{r_{D} }}\frac{{d\widehat{{\overline{m} }}_{fD} }}{{dr_{D} }} - \left[ {u_{n}^{2} + sf(s)} \right]\widehat{{\overline{m} }}_{fD} = 0 $$

(B.11)

Where

$$ u_{n} = \frac{n\pi }{{h_{D} }} $$

(B.12)

$$ f(s) = w_{f} + \frac{{\lambda_{c} \omega_{c} }}{{\lambda_{c} + \omega_{c} s}} + \frac{{\lambda_{m} \omega_{m} }}{{\lambda_{m} + \omega_{m} s}} $$

(B.13)

The outer boundary condition is transformed as:

$$ \left. {\frac{{\partial \widehat{{\overline{m} }}_{jD} }}{{\partial r_{D} }}} \right|_{{r_{D} = r_{eD} }} = 0,\;\;\;(j = f,m,c) $$

(B.14)

The inner boundary condition is transformed as:

$$ \mathop {\lim }\limits_{{r_{D} \to 0}} r_{D} \frac{{\partial \widehat{{\overline{m} }}_{fD} }}{{\partial r_{D} }} = - \frac{{h_{D} }}{s}\cos (u_{n} z_{wD} ) $$

(B.15)

Then Eq. (B.11) can be transformed to a modified Bessel function of zero order, like this:

$$ \begin{aligned} & \left( {r_{D} \sqrt {u_{n}^{2} + sf(s)} } \right)^{2} \frac{{d^{2} \widehat{{\overline{m} }}_{fD} }}{{d\left( {r_{D} \sqrt {u_{n}^{2} + sf(s)} } \right)^{2} }} \\ & + \,r_{D} \sqrt {u_{n}^{2} + sf(s)} \frac{{d\widehat{{\overline{m} }}_{fD} }}{{d\left( {r_{D} \sqrt {u_{n}^{2} + sf(s)} } \right)}} - r_{D}^{2} \left( {u_{n}^{2} + sf(s)} \right)\widehat{{\overline{m} }}_{fD} = 0 \\ \end{aligned} $$

(B.16)

The general solution of Eq. (B.16) is given as follows:

$$ \widehat{{\overline{m} }}_{fD} = A_{0} I_{0} \left[ {r_{D} \sqrt {u_{n}^{2} + sf(s)} } \right] + B_{0} K_{0} \left[ {r_{D} \sqrt {u_{n}^{2} + sf(s)} } \right] $$

(B.17)

Based on the outer and inner boundary conditions (Eq. (B14)–(B.15)), the solution in Laplace domain can be obtained by inverse Fourier cosine transform as follows:

$$ \begin{aligned} \overline{m} _{{fD}} = & \;\frac{1}{s}\left[ {\frac{{K_{1} (r_{{eD}} \sqrt {sf(s)} )}}{{I_{1} (r_{{eD}} \sqrt {sf(s)} )}}I_{0} (r_{D} \sqrt {sf(s)} ) + K_{0} (r_{D} \sqrt {sf(s)} )} \right] \\ & + \,\frac{2}{s}\sum\limits_{{n = 1}}^{\infty } {\left[ {\frac{{K_{1} (r_{{eD}} \sqrt {u_{n}^{2} + sf(s)} )}}{{I_{1} (r_{{eD}} \sqrt {u_{n}^{2} + sf(s)} )}}I_{0} (r_{D} \sqrt {u_{n}^{2} + sf(s)} )} \right.} \\ & \left. { + \;\;K_{0} (r_{D} \sqrt {u_{n}^{2} + sf(s)} )} \right]\cos (\mu _{n} z_{{wD}} )\cos (\mu _{n} z_{D} ) \\ \end{aligned} $$

(B.18)