1 Introduction

Surge waves form due to sudden changes in flow conditions. Positive surge waves commonly occur in the natural system and hydraulic conveyance structures. Closure of sluice gates in water management and hydropower plants induce an abrupt change in velocity leading to the formation of a pressure wave. Tsunami waves and tidal bores also exhibit the characteristics of flow discontinuity with respect to pressure and velocity profiles. Such phenomena exhibit high turbulence, which contributes to air entrainment, sediment gathering, and induces contaminant and debris transport [14]. Turbulent structures located under the front of the tidal bore may lead to bed erosion [5] and the adjacent community’s flooding damage [22]. Bed erosion results in river channel expansion, adverse effect on water safety and habitat environment, and jeopardizes bridges over the river [7]. Like tidal bores, the dam-break waves cause sediment movement and channel bed erosion and can cause swift changes in the bed formation across the channel downstream. Consequently, the flow will be altered, and the estimation of factors such as peak water depth and time to reach the residence area for alert purposes will become difficult [24]. The related studies of dam-break waves date back to [19], who applied equations of motion to the dam-break case. Reference [8] presented laboratory studies for dam-break waves over various roughness of flume beds and verified its outcomes with the theoretical solutions. Although the experimental studies of dam-break waves are getting more attention, the overall number of experimental studies is still limited (e.g., [6, 18, 20]). In recent years, several studies have been carried out to investigate the air entrainment and turbulent patterns of moving and stationary surge waves experimentally (e.g., [11, 12]). Most of the existing experimental studies are based on single point measurements and the overall turbulent characteristics cannot be obtained. Reference [15] are among the first to numerically simulate surge waves, where they have presented the turbulent behaviour within the waves.

In the 2000s, the air entrainment nature of the dam-break waves, also known as “white water”, has been focused on. Several experimental studies of dam-break waves were conducted over the stepped channel and using conductivity probes have determined the air entrainment over the vertical axis and bubble dimensions (e.g., [4, 2]). As for the numerical simulation, the widely used volume of fluid (VOF) method for interface capture was proposed by Reference [9]. For aeration near the interface due to the turbulence, Hirt and Souders [10] firstly introduced for FLOW-3D® to calculate the air fraction based on the comparison between “stabilizing forces” and “destabilizing forces” near the interface. More recently, [23] have developed a calibration approach to determine the ideal magnitude for adjustable parameters in the same model. Lubin and Glockner [16] also demonstrated the numerical work of aeration in plunging waves. Advanced numerical methods allow us to address mixing and air entrainment in dam-break waves and surge waves. Furthermore, this allows a detailed description of complex features of flow [10]. Based on the literature review, there are several numerical and experimental approaches to study the turbulent structure and the air entrainment properties of the surge waves individually. However, few studies have connected two aspects at different Froude numbers numerically. Therefore, within the positive surge waves, the research project studies the interconnection between the turbulence and aeration characteristics numerically and improves compliance with the experimental data available.

2 Methodology

2.1 Governing Equations and Numerical Solutions

In order to resolve the turbulent motion at the surge front, Large Eddy Simulation (LES) is employed. The governing equations for LES are obtained by filtering the Navier–Stokes equation:

$$\rho \frac{{\partial \overline{{{\text{u}}_{{\text{i}}} }} }}{{\partial {\text{t}}}} + \rho \frac{{\partial \overline{{{\text{u}}_{{\text{i}}} }} \overline{{{\text{u}}_{{\text{j}}} }} }}{{\partial {\text{x}}_{{\text{j}}} }} = - \frac{{\partial \overline{p}}}{{\partial {\text{x}}_{{\text{i}}} }} + \frac{\partial }{{\partial {\text{x}}_{{\text{j}}} }}\left( {\mu \left( {\frac{{\partial \overline{{{\text{u}}_{{\text{i}}} }} }}{{\partial {\text{x}}_{{\text{j}}} }} + \frac{{\partial \overline{{{\text{u}}_{{\text{i}}} }} }}{{\partial {\text{x}}_{{\text{i}}} }}} \right)} \right) + \frac{{\partial \tau_{{{\text{ij}}}}^{{{\text{SGS}}}} }}{{\partial {\text{x}}_{{\text{j}}} }}$$
(1)

where \(\overline{{{\text{u}}_{{\text{i}}} }}\) and \({\overline{\text{p}}}\) are the filtered velocity and pressure, respectively. Equation 1 is presented in the suffix notation and \({\text{i or j = 1}}\) in this notation corresponds to the x-direction, \({\text{i or j = 2}}\) corresponds to the y-direction, and \({\text{i or j = 3}}\) to the z-direction. The sub-grid scale (SGS) turbulent shear stress is expressed as:

$$\tau_{{{\text{ij}}}}^{{{\text{SGS}}}} = \rho \overline{{{\text{u}}_{{\text{i}}} {\text{u}}_{{\text{j}}} }} - \rho \overline{{{\text{u}}_{{\text{i}}} }} \overline{{{\text{u}}_{{\text{j}}} }}$$
(2)

The SGS turbulence model defines this filtered turbulent shear stress:

$${\uptau }_{{{\text{ij}}}}^{{{\text{SGS}}}} { = } - {{2\mu }}_{{\text{t}}} {\text{S}}_{{{\text{ij}}}}$$
(3)

where \({\text{S}}_{{{\text{ij}}}}\) is the strain rate and defined as:

$${\text{S}}_{{{\text{ij}}}} { = }\frac{{1}}{{2}}\left( {\frac{{\partial \overline{{{\text{u}}_{{\text{i}}} }} }}{{\partial {\text{x}}_{{\text{j}}} }}{ + }\frac{{\partial \overline{{{\text{u}}_{{\text{j}}} }} }}{{\partial {\text{x}}_{{\text{i}}} }}} \right)$$
(4)

The eddy viscosity of the SGS motion is constructed based on the Smagorisnky-Lilly model [21]:

$${\upmu }_{{\text{t}}} {{ = \rho }}\left( {{\text{C}}_{{\text{s}}} {\Delta }} \right)^{{2}} \sqrt {{\text{2S}}_{{{\text{ij}}}} {\text{S}}_{{{\text{ij}}}} }$$
(5)

where \(\Delta\) is the filter size of the sub-grid scale model, represented as the size of the mesh, and \({\text{C}}_{{\text{s}}}\) is the Smagorinsky constant.

The air–water interface model is based on the volume of fluid (VOF) method for identifying the boundary between water and air. In this method, the interface can be determined by introducing the water volume fraction, \({\upalpha }_{{\text{w}}}\) [1]:

$$\frac{{\partial {\upalpha }_{{\text{w}}} }}{{\partial {\text{t}}}} + \nabla \cdot \left( {{\upalpha }_{{\text{w}}} {\text{u}}} \right) + \nabla \cdot \left[ {{\text{u}}_{{\text{c}}} {\upalpha }_{{\text{w}}} \left( {{1} - {\upalpha }_{{\text{w}}} } \right)} \right]{ = 0}$$
(6)

In Eq. 6 \({\text{u}}_{{\text{c}}}\) represents the “relative velocity” for water and air. \(\alpha_{{\text{w}}} = 1\) demonstrates the cells filled with water, and \(\alpha_{{\text{w}}} = 0\) for the cells filled with air only. The interface, surge front, and in-depth where air entrainment is expected, the water volume fraction is \(0 < \alpha_{{\text{w}}} < 1\).

2.2 Implementation in OpenFOAM

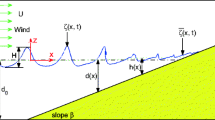
The computational domain is shown in Fig. 1. The gate is located at \({\text{x = 0}}\). The computational domain is extended from \({\text{x = }} - {\text{L}}_{{{\text{xu}}}}\) upstream to \({\text{x}} = {\text{L}}_{{{\text{xd}}}}\) downstream of the gate. With the removal of the gate, a surge wave propagates downstream with a celerity of \({\text{c}}\) and depth of \({\text{d}}_{{2}}\). The initial water depth before the gate is \({\text{d}}_{{0}}\) and the downstream water depth is \({\text{d}}_{{1}}\). The domain is surrounded by rigid walls on three sides with the upper face open to the atmosphere. The boundary conditions for velocity and pressure are coupled as no-slip and fixed flux pressure, respectively. Surge Froude number is defined based on the unperturbed water depth and velocity downstream of the surge wave:

$${\text{Fr}}_{{1}} { = }\frac{{{\text{c + U}}_{{1}} }}{{\sqrt {{\text{gd}}_{{1}} } }}$$
(7)
Fig. 1
figure 1

Sketch of the moving surge wave in the computational domain

Full size image

Here, the initial velocity \({\text{U}}_{{1}} { = 0}.\) References [13] and [25] have reported undular waves at surge Froude numbers up to \({\text{Fr}}_{{1}} { } \approx { 1}{\text{.5}}\). This paper, therefore, covers surge Froude numbers beyond this range as it aims to investigate the turbulent properties across the surge breaking front. The initial water depths, \({\text{d}}_{{0}}\) and \({\text{d}}_{{1}}\), and the domain dimensions, \({\text{L}}_{{{\text{xd}}}}\) and \({\text{L}}_{{{\text{xu}}}}\), are determined based on the Method of Characteristics (MOC). According to the MOC, the \({\text{d}}_{{0}}\) and \({\text{d}}_{{1}}\) ratio dominates the expecting \({\text{Fr}}_{{1}}\) [2]:

$${\text{Fr}}_{{1}} { = }\frac{{\text{c}}}{{\sqrt {{\text{gd}}_{{1}} } }}{ = }\frac{{{0}{\text{.63545 + 0}}{.3286}\left( {\frac{{{\text{d}}_{{1}} }}{{{\text{d}}_{{0}} }}} \right)^{{{0}{\text{.65167}}}} }}{{{0}{\text{.00251 + }}\left( {\frac{{{\text{d}}_{{1}} }}{{{\text{d}}_{{0}} }}} \right)^{{{0}{\text{.65167}}}} }}$$
(8)

Using the theoretical celerity of positive surge (c), obtained from Eq. 8, and the celerity of negative surge (\({\text{c}}_{{0}} { = }\sqrt {{\text{gd}}_{{0}} }\)), the length of the computational domain before and after the gate, \({\text{L}}_{{{\text{xu}}}} {\text{ and L}}_{{{\text{xd}}}}\), are selected. The uniform square mesh of the size of \(\Delta {\text{x}} = \Delta {\text{y}}\) is implemented. Figure 1 illustrates the Area of Interest (AI), where local mesh refinement of the size of \({\text{dx = dy}}\) is implemented. This provided increased resolution around the surge front and behind the surge. Table 1 summarizes the flow conditions for 3 surge Froude numbers \({\text{Fr}}_{{1}} { = }\) 1.60, 2.13, and 2.49.

Table 1 Computational domain and flow conditions of the simulated cases
Full size table

3 Results and Discussion

3.1 Mixing and Vorticity Profile

The simulations are conducted for 3 surge Froude numbers. VOF provides one velocity for water and air combined. To distinguish between water and air in Fig. 2, the product of vorticity, \({\upzeta }\), and water volume fraction, \({\upalpha }_{{\text{w}}}\), is plotted as \(\zeta_{{\text{w}}} = \alpha_{{\text{w}}} \zeta\). Figure 2a, b and c illustrate the \(\zeta_{{\text{w}}}\) profiles at 3 time steps for \({\text{Fr}}_{{1}}\) = 1.60, 2.13, and 2.49, respectively. As seen in Fig. 2a, the mixing at \({\text{Fr}}_{{1}}\) = 1.60 over the length of the surge is confined to the surface. Behind the surge, the advected vortices induce mixing in depth. However, this in-depth mixing behind the surge is mainly confined to \({\text{y}} > {\text{d}}_{{1}}\). For \({\text{Fr}}_{{1}}\) = 2.49, on the other hand, the mixing in the surge front induces more in-depth mixing. The surge wave is often characterized by the recirculating flow at the air–water interface and a shear layer that is induced at the surge toe [3]. The deeper reach of vortices behind the surge can be explained by the extension of the mixing cone in the shear layer. At lower surge Froude numbers, the velocity gradient is smaller, which leads to a weaker shear layer. This, in turn, results in limited mixing at the surge front.

Fig. 2
figure 2

Contour lines of the \({\zeta}_{\text{w}}\) at t = 4.0, 4.5, and 5.0 s for a \({\text{F}}{\text{r}}_{1}\) = 1.60; b \({\text{F}}{\text{r}}_{1}\) = 2.13; and c \({\text{F}}{\text{r}}_{1}\) = 2.49, with surge length \({\text{L}}_{{\text{s}}}\) (m) labelled, as estimated in Fig. 5

Full size image
Fig. 3
figure 3

Contour lines of the \(\alpha_{{\text{w}}}\) at t = 4.0, 4.5, and 5.0 s for a \({\text{Fr}}_{{1}}\) = 1.60; b \({\text{Fr}}_{{1}}\) = 2.13; and c \({\text{ Fr}}_{{1}}\) = 2.49

Full size image

The corresponding air concentration profiles for Fig. 2 are given in Fig. 3. In Fig. 3a, the air entrainment is confined to behind the surge at all three instances. Furthermore, the size of the air pockets (shown in white) for \({\text{Fr}}_{{1}}\) = 1.60 is small. On the other hand, as shown in Fig. 3c, air entrainment induced by the coherent structures across the surge front reaches the full depth. The air pockets also entail larger envelopes, visible by large white patches in this figure. This is similar to observations made by Reference [17]. For stationary hydraulic jumps, with Froude numbers ranging from 5.1 to 8.3, they reported that bubble size increases with the Froude number.

3.2 Water Depth Profiles and Perturbation

In order to investigate the water depth and phase change with time, the profiles of surge waves have to be translated. All the obtained profiles at different times, t, are shifted by a length of \({\text{L}}_{{{\text{lag}}}} {\text{ = ct}},\) where c is the theoretical surge wave celerity. This space lag has translated the moving surge wave at different instances to a standing wave, where the approximate positions of the surge front at different instances coincide. Water depth profiles are selected at \(\alpha_{{\text{w}}} = {0}{\text{.5}}\).

The average space lag profiles are presented in Fig. 4(a1) and (b1) for \({\text{Fr}}_{{1}}\) = 1.60 and 2.49, respectively. The average profile for each Froude number is obtained using the instantaneous profiles at about 60 instances after a fully developed turbulent surge wave was observed. Similarly, the water depth perturbations are estimated based on average and instantaneous profiles. These perturbations are plotted in Fig. 4(a2) and (b2). Water depth perturbation envelopes, marking the minimum and maximum levels of water depth perturbations, are also plotted in these figures. In both surge Froude numbers one distinct peak can be identified close to the surge toe. Across the length of the surge, the normal water depth perturbation, \({\text{h}}^{^{\prime}} /{\overline{\text{h}}}\), is generally lower. However, the perturbation peaks again around the surge heel. This is clear, specially at higher surge Froude number of \({\text{Fr}}_{{1}}\) = 2.49. Figure 4(a3) and (b3) demonstrate the magnitude of water depth perturbation, where the primary peak at the toe and the secondary peak at the heel are visible.

Fig. 4
figure 4

Plots of normalized parameters (1) \({\text{h/d}}_{{2}}\), (2) \(\text{h}^{\prime} / {\overline{\text{h}}}\), and (3) \(\overline{{{\text{h}}^{{{\prime}2}} }} /{\overline{\text{h}}}^{{2}}\) for (a) \({\text{Fr}}_{{1}}\) = 1.60 and b \({\text{Fr}}_{{1}}\) = 2.49, where \({\text{h}}\) is the instantaneous water depth, \({\overline{\text{h}}}\) is the average water depth, and \({\text{h}}^{^{\prime}} = {\text{h}} - {\overline{\text{h}}}\) is the water depth perturbation

Full size image

Based on the observation from water depth and magnitude of water depth perturbation plots in Figs. 4(a3) and (b3), surge length, \({\text{L}}_{{\text{s}}} ,\) at different \({\text{Fr}}_{{1}}\) can be estimated. The surge lengths plotted in Fig. 5 are the distance between two peaks observed in the magnitude of water depth perturbation. The estimated \({\text{L}}_{{\text{s}}}\)/\({\text{d}}_{{1}}\) and \({\text{L}}_{{\text{s}}}\)/\({\text{d}}_{{2}}\) are plotted against \({\text{Fr}}_{{1}}\) in Fig. 5. As shown in this figure, both normalized surge lengths, \({\text{L}}_{{\text{s}}}\)/\({\text{d}}_{{1}}\) and \({\text{L}}_{{\text{s}}}\)/\({\text{d}}_{{2}}\), increase with surge Froude number, \({\text{Fr}}_{{1}}\). Along with our observations from Figs. 2 and 3, this indicated that both the mixing length and strength of the recirculating flow near the air–water interface change with the surge Froude number.

Fig. 5
figure 5

Plots of \({\text{L}}_{{\text{s}}}\)/\({\text{d}}_{{1}}\) and \({\text{L}}_{{\text{s}}}\)/\({\text{d}}_{{2}}\) with \({\text{ Fr}}_{{1}} { = 1}{\text{.60, 2}}{.13, 2}{\text{.49}}\)

Full size image

3.3 Air Concentration Near Surge Toe and Heel

For air entrainment profiles, we have also applied the space-lag approach. All the profiles are translated with a distance of \({\text{L}}_{{{\text{lag}}}} {\text{ = ct}}{.}\) Fig. 6 illustrates 10, 50, and 90 percentiles of air concentration in depth, as well as the average air concentration profile. Figure 6a and c demonstrate such profiles close to heel and toe, respectively. The depth between the 10 and 90 percentiles in the profile closer to the toe is smaller than the analogous depth for a profile closer to the heel. This trend demonstrates lower air entrainment depth closer to the toe, which is attributed to this profile's vicinity to the tip of the mixing cone.

Fig. 6
figure 6

Plots of y direction distribution of air volume fraction, \({\upalpha }_{{\text{a}}}\) and \({\upzeta }_{{\text{w}}}\) for \({\text{Fr}}_{{1}} { = 2}{\text{.13}}\) at a, b x = 12.4 m (close to surge heel) and c, d 12.8 m (close to surge toe) at t = 4 s

Full size image

4 Conclusion

Positive surge waves generated from a sudden opening of the sluice gate are simulated in this study. Various breaking surge Froude numbers in the range of \({\text{Fr}}_{{1}}\) = 1.60–2.49 are studied. We have employed the combination of Large Eddy Simulation and Volume of Fluid to capture the detailed structures of the turbulent flow and patterns of air entrainment behind the surge wave. At low Froude numbers, the mixing induced by vortices is limited to the vicinity of the air–water interface. These vortices reach a greater depth at higher Froude numbers, leading to higher levels of air entrainment both near the surface and in-depth. Average water depth profiles, perturbation envelope and magnitude, are also generated by shifting and averaging the instantaneous water depth profiles. Two perturbation peaks are observed in the vicinity of the surge heel and surge toe. These peaks are used to define the surge length, which then is plotted against the surge Froude number. Furthermore, for \({\text{Fr}}_{{1}}\) = 2.13, a smaller aeration depth is observed at the surge toe compared to the heel. Our numerical simulations shed light on the detailed structures of a transient surge wave. Validation with existing experimental studies and further detailed analysis will be reported in a future publication.