Keywords

1 Introduction

The increasing implementation of photovoltaic systems makes the modeling of these systems a great requirement, in order to be able to predict their performances and the parameters influencing them. For this purpose, various equivalent circuits were used in the literature to model a photovoltaic generator. But, thanks to its high simplicity-precision ratio, the single-diode equivalent model of the five parameters (The photo-generated current Iph, the reverse saturation Is, the series resistance Rs, the parallel resistance Rp, and the ideality factor n) modeling the physical effects inside the PV generator remains the most used [1–3].

According to the literature, several methods have been utilized for the estimation of the single-diode model’s five parameters allowing the prediction of the maximum power that a PV generator can provide, under varying levels of illumination (E) and temperature (T). Therefore, the used methods can be divided into three kinds of parameters’ extraction. In the first group, we have the works using analytical formulas, which rely on the values of the key-points available on the PV panel’s datasheet [2–4]. In the second group, we find all numerical methods exploiting the measured characteristics and trying to minimize the errors between the experimental and calculated I–V curves [5–11]. As a third group, we cite the methods based on the meta-heuristic algorithms corresponding to natural phenomena to estimate the five parameters and predict the maximum power point [12, 13].

Villalva’s method [8] stay one of the most cited works in this area, it is based on a three remarkable-points curve adjustment technique and uses an iterative process to estimate the series resistance’s value. Therefore, it can be concluded that this method ensures an accurate prediction only in the vicinity of the maximum power point and not for the whole I–V curve. In addition, the iterative process may increase the calculation cost as well. Unlike Villalva’s method which fixes the value of the ideality factor in advance, Benahmida et al. [6] propose an iterative method for which the calculation of this value is done using the available values of the three remarkable points on the generator's datasheet. The mean inconvenient of both methods is the use of the iterative process that may increase the needed time for the identification, and also the use of the error minimization only for the maximum power point which can lead to the loss of accuracy for the estimation of the rest of the I–V curve. Maouhoub [11] introduces an analytical approach based on the least-squares technic for characterizing the PV panels. But this method necessitates the calculation of the slope in the vicinity of the short-circuit point to calculate the value of Rs. Then, the value of Rs will be very influenced by the precision of the measurement of this slope. Nassar-eddine et al. [9] compare two different extraction methods, the first is an analytical approach, and the second is iterative, also based on the minimization of the absolute error only for the maximum power point.

With the aim of identifying PV generators’ parameters with high precision under different weather conditions, a new numerical method is introduced in this work. The extraction starts first by calculating the values of n and Rs solving a two nonlinear equations’ system, instead using an iterative process which can increase the calculation time and lead to the loss of precision. The three values of the other remaining parameters (Rp, Is, and Iph) are directly calculated using three analytical equations which do not rely on any kind of approximations. Furthermore, in order to be able to model a photovoltaic generator working at external conditions using its identification already done for standard test conditions, a new contribution has been made in the current paper.

2 Single-Diode Modelling

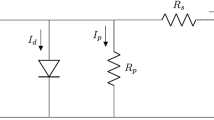
The current method uses the single-diode circuit shown in Fig. 1 as a basic model for the identification. In this equivalent circuit, Iph is the photo-generated current, Is and n are respectively the reverse saturation current and the ideality factor, of the diode modeling the semi-conductor material that the solar cell contains, and Rp and Rs are respectively the shunt resistance and the series resistance.

Fig. 1
figure 1

Single-diode electrical model of a solar cell

Full size image

The equation linking the current between the two surfaces of the PV module to its output voltage is given as a function of the five parameters as follow [2–9]:

$${\text{I}} = {\text{I}}_{{{\text{ph}}}} - {\text{I}}_{{\text{s}}} \left( {{\text{exp}}\left( {\frac{{{\text{V}} + {\text{IR}}_{{\text{s}}} }}{{{\text{nC}}_{1} }}} \right) - 1} \right) - \frac{{{\text{V}} + {\text{IR}}_{{\text{s}}} }}{{{\text{R}}_{{\text{p}}} }}$$
(1)

\(C_{1} = N_{s} V_{th}\), where Ns is the number of cells connected in series, forming the PV generator. Vth correspond to the thermal voltage giving by: \(V_{th} = \frac{{K_{B} T}}{q}\). KB is the constant of Boltzmann equals to 1.38064852.10 − 23 J/K, and q is the electron charge equals to 1. 60217646.10 − 19 C.

Using the Lambert W function, the implicit Eq. (1) can have an analytical solution given by the following formula [14, 15]:

$$\begin{aligned} {\text{I}} & = \frac{{{\text{I}}_{{\text{s}}} + {\text{I}}_{{{\text{ph}}}} }}{{1 + {\text{R}}_{{\text{s}}} {\text{G}}_{{\text{p}}} }} - \frac{{{\text{G}}_{{\text{p}}} }}{{1 + {\text{R}}_{{\text{s}}} {\text{G}}_{{\text{p}}} }}{\text{V}} - \frac{{{\text{nC}}_{1} }}{{{\text{R}}_{{\text{s}}} }} \\ & \quad \times {\text{W}}\left( {\frac{{{\text{I}}_{{\text{s}}} {\text{R}}_{{\text{s}}} }}{{{\text{nC}}_{1} \left( {1 + {\text{R}}_{{\text{s}}} {\text{G}}_{{\text{p}}} } \right)}}{\text{exp}}\left( {\frac{{{\text{V}} + {\text{R}}_{{\text{s}}} \left( {{\text{I}}_{{\text{s}}} + {\text{I}}_{{{\text{ph}}}} } \right)}}{{{\text{nC}}_{1} \left( {1 + {\text{R}}_{{\text{s}}} {\text{G}}_{{\text{p}}} } \right)}}} \right)} \right) \\ \end{aligned}$$
(2)

where \({\text{G}}_{{\text{p}}} = \frac{1}{{{\text{R}}_{{\text{p}}} }}\).

3 Method’s Theory

With the aim of extracting the expressions that will allow the calculation of the five parameters’ values exploiting the four values corresponding to the key-points of the I-V curve at STC, the application of the Eq. (1) to the remarkable points will be requested [3, 6, 9, 11]:

  • Short-circuit point (I = Isc, V = 0)

    $$I_{sc} + I_{s} \left( {E_{sc} - 1} \right) + \frac{{I_{sc} R_{s} }}{{R_{p} }} - I_{ph} = 0$$
    (3)

  • Maximum power point (I = Imp, V = Vmp)

    $$ {\text{I}}_{{{\text{mp}}}} - {\text{I}}_{{{\text{ph}}}} + {\text{I}}_{{\text{s}}} \left( {{\text{E}}_{{{\text{mp}}}} - 1} \right) + \frac{{{\text{V}}_{{{\text{mp}}}} + {\text{I}}_{{{\text{mp}}}} {\text{R}}_{{\text{s}}} }}{{{\text{R}}_{{\text{p}}} }} = 0$$
    (4)

  • Open-circuit point (I = 0, V = Voc)

    $$ {\text{I}}_{{{\text{ph}}}} = {\text{I}}_{{\text{s}}} \left( {{\text{E}}_{{{\text{oc}}}} - 1} \right) + \frac{{{\text{V}}_{{{\text{oc}}}} }}{{{\text{R}}_{{\text{p}}} }}$$
    (5)

where:

$$ {\text{E}}_{{{\text{sc}}}} = {\text{exp}}\left( {\frac{{{\text{I}}_{{{\text{sc}}}} {\text{R}}_{{\text{s}}} }}{{{\text{nC}}_{1} }}} \right),{\text{E}}_{{{\text{mp}}}} = {\text{exp}}\left( {\frac{{{\text{V}}_{{{\text{mp}}}} + {\text{I}}_{{{\text{mp}}}} {\text{R}}_{{\text{s}}} }}{{{\text{nC}}_{1} }}} \right)\,{\text{and}}\,{\text{E}}_{{{\text{oc}}}} = {\text{exp}}\left( {\frac{{{\text{V}}_{{{\text{oc}}}} }}{{{\text{nC}}_{1} }}} \right)$$
(6)

The series resistance and the ideality factor’s estimation require two equations containing just Rs and n as parameters to be determined. To this end, we use as a first equation the expression giving the fill-factor FF as a function of the four parameters: Rs, n, Is, and Rp, given by the following formula [16, 17]:

$$ {\text{FF}} = \frac{{{\text{I}}_{{{\text{mp}}}}^{2} }}{{{\text{V}}_{{{\text{oc}}}} {\text{I}}_{{{\text{sc}}}} }}\left( {{\text{R}}_{{\text{s}}} + \frac{{{\text{R}}_{{\text{p}}} }}{{\frac{{{\text{I}}_{{\text{s}}} {\text{R}}_{{\text{p}}} }}{{{\text{nC}}_{1} }}{\text{E}}_{{{\text{mp}}}} + 1}}} \right)$$
(7)

Otherwise, given that FF measures the I–V characteristic’s squareness, it is also given as the ratio of the maximum power provided by a real PV generator to the maximum power of an ideal generator, and it can be calculated also as:

$$FF = \frac{{V_{mp} I_{mp} }}{{V_{oc} I_{sc} }}$$

To reduce the number of unknown parameters in the Eq. (7), we replace Iph in Eq. (4) by its expression of the Eq. (5), and finally, we get the reverse saturation current Is only as a function of the three parameters Rs, n, and Rp as:

$$I_{s} = \frac{{\frac{{V_{oc} - V_{mp} - I_{mp} R_{s} }}{{R_{p} }} - I_{mp} }}{{E_{mp} - E_{oc} }}$$
(8)

To get rid of Is from Eq. (7), we replace (8) in (7), so that (7) becomes an expression linking only the three parameters Rs, n, and Rp from which we can get Rp as a function of n and Rs:

$$ {\text{R}}_{{\text{p}}} = \frac{{{\text{C}}_{2} - {\text{exp}}\left( {{\text{C}}_{2} } \right) + 1}}{{\frac{{{\text{I}}_{{{\text{mp}}}} }}{{{\text{nC}}_{1} }} + \frac{{{\text{I}}_{{{\text{mp}}}}^{2} }}{{\left( {{\text{FFV}}_{{{\text{oc}}}} - {\text{R}}_{{\text{s}}} {\text{I}}_{{{\text{mp}}}}^{2} } \right)}}\left( {1 - {\text{exp}}\left( {{\text{C}}_{2} } \right)} \right)}}$$
(9)

where:

$$C_{2} = \frac{{V_{oc} - V_{mp} - I_{mp} R_{s} }}{{nC_{1} }}$$
(10)

Finally, to use the “fsolve” function of MATLAB, which solves nonlinear equations’ systems, Eq. (7) is considered as the first equation of the two equations’ system, which will be used for the numerical extraction of n and Rs. The second equation can be extracted by replacing Iph in Eq. (3) with its expression of the Eq. (5):

$$I_{sc} - I_{s} \left( {E_{oc} - E_{sc} } \right) - \frac{{V_{oc} - I_{sc} R_{s} }}{{R_{p} }} = 0$$
(11)

In which Is and Rp are given respectively in Eqs. (8) and (9) only as function of n and Rs.

To guarantee the rapid convergence of the system’s resolution towards the accurate solutions, the right choice of their initial guesses is necessary. To this end, the approximate analytical expression of Rs proposed by Kumar et al. [3], and the formula of n used by Nassar-eddine et al. [9] and Maouhoub [11], given in the system below, are used for the initialization.

$$ \left\{ {\begin{array}{*{20}l} {{\text{n}}_{0} = \frac{{{\text{K}}_{{\text{v}}} - \frac{{{\text{V}}_{{{\text{oc}}}} }}{{{\text{T}}_{{{\text{STC}}}} }}}}{{{\text{C}}_{1} \left( {\frac{{{\text{K}}_{{\text{i}}} }}{{{\text{I}}_{{{\text{sc}}}} }} - \frac{3}{{{\text{T}}_{{{\text{STC}}}} }} - \frac{{{\text{E}}_{{\text{g}}} }}{{{\text{K}}_{{\text{B}}} {\text{T}}_{{{\text{STC}}}}^{2} }}} \right)}}} \\ {{\text{R}}_{{{\text{s}}0}} = \frac{{{\text{V}}_{{{\text{mp}}}} }}{{{\text{I}}_{{{\text{mp}}}} }} - \frac{{2{\text{V}}_{{{\text{mp}}}} - {\text{V}}_{{{\text{oc}}}} }}{{\left( {{\text{I}}_{{{\text{sc}}}} - {\text{I}}_{{{\text{mp}}}} } \right) \times {\text{ln}}\left( {1 - \frac{{{\text{I}}_{{{\text{mp}}}} }}{{{\text{I}}_{{{\text{sc}}}} }}} \right) + \frac{{{\text{I}}_{{{\text{mp}}}} }}{{{\text{I}}_{{{\text{sc}}}} - {\text{I}}_{{{\text{mp}}}} }}}}} \\ \end{array} } \right.$$
(12)

Ki (A/°C) and Kv (V/°C) are respectively the temperature coefficient of short-circuit current, and the temperature coefficient of open-circuit voltage. Eg is the band gap energy.

After the numerical prediction of the values of n and Rs, the values of Rp, Is, and Iph are calculated respectively using the analytical Eqs. (9), (8), and (5).

4 Results and Discussion

To confirm the accuracy of the current reduced form, the photovoltaic generator Kyocera KC200GT operating under STC (E = 1000 W/m2 and T = 25 °C) is chosen to apply the method [18]. The measured parameters from the I-V characteristics of the KC200GT PV module working under STC are (Isc = 8.21A; Vmp = 26.89 V; Imp = 7.66A; Voc = 33.07 V). As the first task, we calculate the five parameters of the PV generator for STC. Then, we estimate its I-V characteristics for non-STC. The precision of the method can be judged by using several statistical indicators. For this work, we select the Normalized Root Mean Square Error (NRMSE), and the absolute error (AE) [6, 11, 12, 17]:

$$ {\text{NRMSE}} = \frac{{\sqrt {\frac{1}{{\text{N}}} \times \mathop \sum \nolimits_{{{\text{i}} = 1}}^{{\text{N}}} \left( {{\text{I}}_{{{\text{i}},{\text{Measured}}}} - {\text{I}}_{{{\text{i}},{\text{Predicted}}}} } \right)^{2} } }}{{\frac{1}{{\text{N}}}\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{\text{N}}} {\text{I}}_{{{\text{i}},{\text{Measured}}}} }}$$
(13)
$$ {\text{AE}} = \left| {{\text{X}}_{{{\text{i}},{\text{Measured}}}} - {\text{X}}_{{{\text{i}},{\text{Predicted}}}} } \right|$$
(14)

where N represents the number of measured data points, and X symbolizes current I or voltage V.

4.1 Results for KC200GT Under STC

Table 1 regroups the predicted values of the five parameters using the new method, compared to four other selected methods from literature. The table contains as well the values of the provided NRMSE for the multi-crystalline KC200GT by different methods. Based on the results, it can be observed that the value of NRMSE supplied by the new approach is the lowest compared to the other estimating technics.

Table 1 Predicted parameters for the multi-crystalline KC200GT operating under STC
Full size table

4.2 Results for KC200GT Under Non-STC

In order to estimate the values of the five parameters in external conditions and then calculate the I–V characteristics of the PV generator, equations below are employed to make the transfer of Iph and Is from STC to Non-STC [6, 9, 11]:

$$ {\text{I}}_{{{\text{ph}}}} \left( {{\text{E}},{\text{T}}} \right) = \left( {{\text{I}}_{{{\text{ph}},{\text{STC}}}} + {\text{K}}_{{\text{i}}} \left( {{\text{T}} - {\text{T}}_{{{\text{STC}}}} } \right)} \right) \times \frac{{\text{E}}}{{{\text{E}}_{{{\text{STC}}}} }}$$
(15)
$$ {\text{I}}_{{\text{s}}} \left( {{\text{E}},{\text{T}}} \right) = \frac{{{\text{I}}_{{{\text{ph}}}} \left( {{\text{E}},{\text{T}}} \right) - \frac{{{\text{V}}_{{{\text{oc}}}} \left( {{\text{E}},{\text{T}}} \right)}}{{{\text{R}}_{{\text{p}}} \left( {{\text{E}},{\text{T}}} \right)}}}}{{{\text{exp}}\left( {\frac{{{\text{V}}_{{{\text{oc}}}} \left( {{\text{E}},{\text{T}}} \right)}}{{{\text{N}}_{{\text{s}}} {\text{V}}_{{{\text{th}}}} {\text{n}}\left( {{\text{E}},{\text{T}}} \right)}}} \right) - 1}}$$
(16)

To extract the other three parameters, we use the expressions used by Petrone, where it is assumed that the three parameters are independent of temperature variations. They only depend on irradiance levels, as the following equations show [19]:

$$ {\text{R}}_{{\text{s}}} \left( {{\text{E}},{\text{T}}} \right) = {\text{R}}_{{{\text{s}},{\text{STC}}}} \left( {\frac{{{\text{I}}_{{{\text{sc}},{\text{STC}}}} {\text{V}}_{{{\text{oc}}}} \left( {{\text{E}},{\text{T}}_{{{\text{STC}}}} } \right)}}{{{\text{V}}_{{{\text{oc}},{\text{STC}}}} {\text{I}}_{{{\text{sc}}}} \left( {{\text{E}},{\text{T}}_{{{\text{STC}}}} } \right)}}} \right)$$
(17)
$$ {\text{R}}_{{\text{p}}} \left( {{\text{E}},{\text{T}}} \right) = {\text{R}}_{{{\text{p}},{\text{STC}}}} \left( {\frac{{{\text{I}}_{{{\text{sc}},{\text{STC}}}} {\text{V}}_{{{\text{oc}}}} \left( {{\text{E}},{\text{T}}_{{{\text{STC}}}} } \right)}}{{{\text{V}}_{{{\text{oc}},{\text{STC}}}} {\text{I}}_{{{\text{sc}}}} \left( {{\text{E}},{\text{T}}_{{{\text{STC}}}} } \right)}}} \right)$$
(18)
$$ {\text{n}}\left( {{\text{E}},{\text{T}}} \right) = {\text{n}}_{{{\text{STC}}}} \left( {\frac{{{\text{V}}_{{{\text{oc}}}} \left( {{\text{E}},{\text{T}}_{{{\text{STC}}}} } \right)}}{{{\text{V}}_{{{\text{oc}},{\text{STC}}}} }}} \right)$$
(19)

where Isc (E,T) is given as [20]:

$$ {\text{I}}_{{{\text{sc}}}} \left( {{\text{E}},{\text{T}}} \right) = {\text{I}}_{{{\text{sc}},{\text{STC}}}} \times \left( {\frac{{\text{E}}}{{{\text{E}}_{{{\text{STC}}}} }}} \right)^{\beta } \left( {1 + {\text{K}}_{{\text{i}}} \left( {{\text{T}} - {\text{T}}_{{{\text{STC}}}} } \right)} \right)$$
(20)

The use of all five equations requires as well a prior knowledge of short-circuit current and open-circuit voltage values in the external conditions. For this purpose, a modified expression of Voc is used to calculate the value of this parameter under non-standard test conditions [2, 17].

$$ {\text{V}}_{{{\text{oc}}}} \left( {{\text{E}},{\text{T}}} \right) = \left( {{\text{V}}_{{{\text{oc}},{\text{STC}}}} + {\text{K}}_{{\text{v}}} \left( {{\text{T}} - {\text{T}}_{{{\text{STC}}}} } \right)} \right) \times \left( {\frac{{\text{E}}}{{{\text{E}}_{{{\text{STC}}}} }}} \right)^{\alpha }$$
(21)

To demonstrate the suggested model's accuracy, it is compared to two additional models from literature, which are listed below as:

  • Model 1 [2, 6]:

    $$ {\text{V}}_{{{\text{oc}}}} \left( {{\text{E}},{\text{T}}} \right) = {\text{V}}_{{{\text{oc}},{\text{STC}}}} + {\text{K}}_{{\text{v}}} \left( {{\text{T}} - {\text{T}}_{{{\text{STC}}}} } \right) + {\text{N}}_{{\text{s}}} {\text{nV}}_{{{\text{th}},{\text{STC}}}} {\text{ln}}\left( {\frac{{\text{E}}}{{{\text{E}}_{{{\text{STC}}}} }}} \right)$$
    (22)

  • Model 2 [2]:

    $$ {\text{V}}_{{{\text{oc}}}} \left( {{\text{E}},{\text{T}}} \right) = {\text{V}}_{{{\text{oc}},{\text{STC}}}} + {\text{K}}_{{\text{v}}} \left( {{\text{T}} - {\text{T}}_{{{\text{STC}}}} } \right) + {\upgamma }\left( {{\text{E}} - {\text{E}}_{{{\text{STC}}}} } \right)$$
    (23)

Voc,STC is the open-circuit voltage at STC. α, β and γ are three adjustment coefficients. Table 2 shows the values of the used coefficients for KC200GT.

Table 2 Required parameters for switching to non-STC for the multi-crystalline Kyocera KC200GT
Full size table

Figure 2a presents the measured values of the open-circuit voltage and the calculated values using the introduced modified model and compares them to two other models from the literature for the PV generator KC200GT working under 25 °C and various levels of irradiance. As it is observed, when compared to other models, the new model gives the highest accuracy. The thing that can also be seen from Fig. 2b, which presents the absolute errors between the measured data points and the calculated ones using different models, where the new model gives the lowest values of absolute error for the whole levels of irradiance.

Fig. 2
figure 2

a Measured and calculated open-circuit voltages using the three models for various levels of irradiance. b The absolute errors corresponding

Full size image

Figure 3a presents measured I-V curves and the calculated ones based on the predicted five parameters’ values at STC and using the transfer equations from STC to non-STC. As it can be seen from Fig. 3b showing the calculated values of NRMSE using the new model of Voc and the other two models of literature, the new method provides the best accuracy giving the lowest values of NRMSE for all levels of irradiance and which does not exceed 2.5% in the worst case (Fig. 3b). On the first hand, Fig. 4a presents the predicted I-V curves using the current method as well as the measured curves for the PV panel KC200GT under 1000 W/m² and different levels of temperature. On the other hand, Fig. 4b gives the values of NRMSE for various levels of temperature and which do not exceed 3%.

Fig. 3
figure 3

a Measured data and predicted I-V curves at different levels of irradiance. b Normalized root mean square errors obtained using the three models of the open-circuit voltage

Full size image
Fig. 4
figure 4

a Predicted I–V curves and measured data at various levels of temperature for the PV generator Kyocera KC200GT. b The corresponding normalized root mean square errors

Full size image

5 Conclusion

This paper proposes an accurate reduced form for estimating the values of the single-diode model's five parameters. The introduced method uses only the provided information about the remarkable-points in the datasheet, and it does not rely on any approximations or iterative processes. That makes the proposed method efficient, simple, and fast. The approach has been tested for the multi-crystalline Kyocera KC200GT and found to be the most accurate compared to the other selected methods from literature. In this paper, a new contribution to predict the values of the open-circuit voltage for external conditions with high precision has been done as well. Then, the I-V characteristics for non-STC are estimated.