Magnetic Shape Memory Alloys: Phenomenological Constitutive Modeling and Analysis

Abstract

Increasing demand for a lighter and more durable material with sensing and actuation functionality, Magnetic Shape Memory Alloys (MSMA) are promising members, among many other smart materials. This study investigates the Magneto-Thermo-Mechanical (MTM) behavior of MSMA through a 3D phenomenological constitutive modeling thermodynamically consistent way. A specific Helmholtz free energy function is considered after identifying the external and internal state variables. The evolution equations of the internal state variables are defined by proposing a transformation function. The model parameters are calibrated through different MTM loading conditions. Selective model simulations demonstrate the magnetic field coupling with the actuation strain.

1 Introduction

Magnetic shape memory alloys (MSMA) are one of the most emerging classes of multi-functional materials which respond to the magnetic field, temperature, and external load [1,2,3,4]. It has the potential to produce large Magnetic-Field-Induced Strain (MFIS) through microstructural changes at least one order of higher magnitude than those of available magnetostrictive materials [5,6,7,8,9]. MSMAs also exhibit conventional pseudo-elastic and shape memory behavior. However, MSMAs have advantages on actuation frequency (1KHz) over conventional SMAs due to the availability of high frequency applied magnetic field [10].

The macroscopic responses of MSMAs are the manifestations of four fundamental microscopic mechanisms: the motion of magnetic domain walls, the rotation of magnetization vector, field-induced variant reorientation, and field induced phase transformation [11, 12]. Ni-Mn-Ga alloys are the most widely investigated MSMAs for variant reorientation. Martensitic transformation in Ni₂MnGa alloys was firstly reported by Webster et al. [13]. The detailed studies on the crystal structure of MSMAs were done by Zasimchuk et al. [14]. Ullako et al. [15] reported the first magnetic controlled shape memory effect in MSMAs. They observed 0.2% magnetic-field-induced strain (MFIS) in a stress-free experiment. NiCoMnIn alloys also exhibit MFIS under applied magnetic field. Such type of MFIS is caused by Field Induced Phase Transformation (FIPT) [16,17,18].

In this work, we develop a coupled constitutive equation of MSMAs for FIPT. The microstructure dependence is approximated phenomenologically by the evolution equations of the selected internal state variables. The model parameters are calibrated from the experimental data. Finally, MTM responses are simulated for FIPT.

2 Mechanism of Field-Induced Phase Transformation

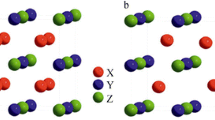
FIPT mechanism is similar to the temperature-induced phase transformation in conventional Shape Memory Alloys (SMAs). The Zeeman Energy (ZE)¹, which depends on the difference between saturation magnetizations of austenitic and martensitic phase, is converted to mechanical energy through FIPT [19,20,21]. The higher symmetric austenitic phase is ferromagnetic [22,23,24]. The anti-ferromagnetic martensitic phase has three possible variants of the tetragonal crystalline structure, which is depicted in Fig.1. The specimen is in the austenitic phase at room temperature and at a high magnetic field. After removing the applied field, the phase is transformed into the martensitic phase.

3 Constitutive Modeling

A multiplicative decomposition of deformation gradient $\boldsymbol{F}$ into lattice $\boldsymbol{F}_l$ and inelastic part $\boldsymbol{F}_\iota$ is considered [25, 26] such that

$$\begin{aligned} \boldsymbol{F} = \boldsymbol{F}_l \boldsymbol{F}_\iota \nonumber . \end{aligned}$$

The selection of an appropriate free energy function is one of the significant challenges for modeling multi-functional material. The function should be proposed in such a way so that the constitutive responses should be able to capture all the significant features of MSMA like phase transformation, and its temperature dependence. We propose a Helmholtz free energy density $\tilde{\psi }$ per reference volume, containing a lattice energy $\tilde{\psi }_l$, an inelastic energy $\tilde{\psi }_\iota$, and a mixing energy $\tilde{\psi }_{mix}$ as [27,28,29,30]

$$\begin{aligned} \tilde{\psi }(\boldsymbol{C}_l, \boldsymbol{C}_\iota ,\boldsymbol{H}, \xi , \theta )=\tilde{\psi }_l(\boldsymbol{C}_l, \boldsymbol{H}, \theta , \xi )+\tilde{\psi }_\iota (\boldsymbol{C}_\iota )+ \tilde{\psi }_{mix}(\xi ) \end{aligned}$$

(1)

and we obtain the constitutive equations using Coleman-Noll [31] procedure :

$$\begin{aligned} \boldsymbol{S}=2\rho _0\boldsymbol{F}_\iota ^{-1}\frac{\partial \tilde{ \psi _l}}{\partial \boldsymbol{C}_l}\boldsymbol{F}_\iota ^{-T}\nonumber ,\quad \eta = -\frac{\partial \tilde{\psi _l}}{\partial \theta }\nonumber ,\quad \mu _0\boldsymbol{M} = -\rho _0\frac{\partial \tilde{ \psi _l}}{\partial \boldsymbol{H}}, \quad -\rho _0\frac{\partial \tilde{\psi }}{\partial \xi }\cdot \dot{\xi }\ge 0. \end{aligned}$$

The lattice right Cauchy green tensor $\boldsymbol{C}_l = \boldsymbol{F}^T_l\boldsymbol{F}_l$, magnetic field strength $\boldsymbol{H}$, and temperature $\theta$ are the physical or external state variables for the constitutive equations. Further, $\boldsymbol{C}_\iota$ and the martensitic volume fraction $\xi$ are the internal state variables. Moreover, $\boldsymbol{S}$ is the Second Piola-Kirchhoff stress, $\eta$ is the entropy, and $\boldsymbol{M}$ is the magnetization.

Fig. 1

Crystalline structure of austenitic phase (A) and martensitic phase (M). M₁ is variant-1, M₂ is variant-2, and M₃ is variant-3

4 Numerical Implementation and Model Calibration

For the small strain assumption, multiplicative decomposition becomes additive decomposition of strain with a lattice and an inelastic part

$$\begin{aligned} \boldsymbol{E} = \boldsymbol{\varepsilon }:= & {} \frac{1}{2}\left( \boldsymbol{C}- \boldsymbol{I}\right) \nonumber \\= & {} \frac{1}{2}\left( \boldsymbol{F}^T\boldsymbol{F}- \boldsymbol{I}\right) \nonumber \\= & {} \frac{1}{2}\left( \left( \boldsymbol{F}_l\boldsymbol{F}_\iota \right) ^T \left( \boldsymbol{F}_l\boldsymbol{F}_\iota \right) - \boldsymbol{I}\right) \nonumber \\= & {} \frac{1}{2}\left( \left( \boldsymbol{I}+\nabla u^T_\iota + \nabla u^T_l\right) \left( \boldsymbol{I}+\nabla u_\iota + \nabla u_l\right) -\boldsymbol{I}\right) \nonumber \\= & {} \frac{1}{2}\left( \nabla u_l + \nabla u^T_l \right) + \frac{1}{2}\left( \nabla u_\iota + \nabla u^T_\iota \right) + h.o.t\nonumber \\= & {} \boldsymbol{\varepsilon }_l + \boldsymbol{\varepsilon }_\iota . \end{aligned}$$

(2)

The lattice strain could further be decomposed into an elastic and a thermal strain, i.e., $\boldsymbol{\varepsilon }_l = \boldsymbol{\varepsilon }_e + \boldsymbol{\varepsilon }_\theta$. We discard the thermal expansion and write $\boldsymbol{\varepsilon }_l = \boldsymbol{\varepsilon }_e$. Moreover, for FIPT, the inelastic strain becomes transformation strain, i.e., $\boldsymbol{\varepsilon }_\iota = \boldsymbol{\varepsilon }_t$. After identifying the internal state variable $\left( \xi , \boldsymbol{\varepsilon }_t \right)$ and external state variables $\left( \boldsymbol{\varepsilon }_e, \theta , \boldsymbol{H}\right)$, the explicit form of Helmholtz free energy function [32] is given by

$$\begin{aligned} \psi \left( \boldsymbol{\varepsilon }_e, \theta , \boldsymbol{H},\boldsymbol{\varepsilon }_t, \xi \right) = -\frac{1}{2\rho } \boldsymbol{\varepsilon }_e : \boldsymbol{L}:\boldsymbol{\varepsilon }_e -\boldsymbol{\sigma }:\boldsymbol{\varepsilon }_t + u_0 - \frac{\mu _0}{\rho }\boldsymbol{H}\cdot \boldsymbol{M} -\theta \eta _0 + \frac{1}{\rho }f\left( \xi \right) , \end{aligned}$$

(3)

where, $\boldsymbol{L}$, $u_0$, $\eta _0$, c, and $\boldsymbol{M}$ are the stiffness tensor, internal energy, entropy, specific heat, and saturation magnetization, respectively. The effective material properties are determined by using the rule of mixture. $f\left( \xi \right)$ is the hardening function during forward and reverse phase transformation. We used the polynomial type hardening function [33],

$$\begin{aligned} f\left( \xi \right) = {\left\{ \begin{array}{ll} \frac{1}{2}A \left( \xi +\frac{\xi ^{n_1+1}}{n_1+1}+\frac{\left( 1-\xi \right) ^{n_2+1}}{n_2+1}\right) +C\xi ;\, \dot{\xi }>0\\ \frac{1}{2}B \left( \xi +\frac{\xi ^{n_3+1}}{n_3+1}+\frac{\left( 1-\xi \right) ^{n_4+1}}{n_4+1}\right) +D\xi ; \,\dot{\xi }<0 \end{array}\right. }. \end{aligned}$$

(4)

where A, B, C, D represent model parameters. Moreover, $n_1, n_2, n_3$ and $n_4$ are hardening exponents for phase transformation. Considering the explicit form of (3), we write by using Coleman-Noll procedure

$$\begin{aligned} \left( \boldsymbol{\sigma }- \rho \frac{\partial \psi }{\partial \boldsymbol{\varepsilon }_e}\right) :\dot{\boldsymbol{\varepsilon }_e}-\rho \left( \frac{\partial \psi }{\partial \theta }+\eta \right) \dot{\theta }+\left( \mu _0\boldsymbol{M}+\rho \frac{\partial \psi }{\partial \boldsymbol{H}}\right) \cdot \dot{\boldsymbol{H}}+\boldsymbol{\sigma }:\dot{\boldsymbol{\varepsilon }_t}-\rho \frac{\partial \psi }{\partial \xi }\dot{\xi }\ge 0 \nonumber . \end{aligned}$$

The constitutive equations then take the following forms:

$$\begin{aligned} \boldsymbol{\sigma } = \rho \frac{\partial \psi }{\partial \boldsymbol{\varepsilon _e}} =\boldsymbol{L}:\boldsymbol{\varepsilon }_e \nonumber \quad \eta = - \frac{\partial \psi }{\partial \theta }, \quad \mu _0\boldsymbol{M} = -\rho \frac{\partial \psi }{\partial \boldsymbol{H}}\nonumber , \end{aligned}$$

and the residual inequality reads

$$\begin{aligned} \boldsymbol{\sigma }:\dot{\boldsymbol{\varepsilon }_t}-\rho \frac{\partial \psi }{\partial \xi }\dot{\xi }\ge 0. \end{aligned}$$

(5)

We further consider the flow rule of the transformation strain

$$\begin{aligned} \dot{\boldsymbol{\varepsilon }_t} = \boldsymbol{\varLambda }\dot{\xi }. \end{aligned}$$

(6)

Expanding the entropy inequality equation (5), we finally obtain

$$\begin{aligned} \pi \dot{\xi }\ge 0 \end{aligned}$$

(7)

where, $\pi = \boldsymbol{\sigma }:\boldsymbol{\varLambda } -\rho \frac{\partial \psi }{\partial \xi }\dot{\xi }\ge 0$ is the thermodynamics driving force.

4.1 1-D Reduction of the Model

We represent the 1-D result by assuming the uniaxial loading in a prismatic bar along its longitudinal axis. The stress tensor has only one non-zero component, that is

$$\begin{aligned} \sigma _{11} = \sigma \ne 0\nonumber . \end{aligned}$$

The one dimensional form of thermodynamic driving force reduces to

$$\begin{aligned} \pi = E_{max}|\sigma | + \frac{1}{2}L^{-1}\sigma \cdot \varDelta {L} \cdot L^{-1}\sigma + \rho \varDelta {\eta _0}\theta + \mu _0\varDelta {M}\cdot H - \rho \varDelta {u}- \frac{\partial f}{\partial \xi }. \end{aligned}$$

(8)

We now introduce the following transformation function

$$\begin{aligned} \phi := {\left\{ \begin{array}{ll} \pi - Y, \; \dot{\xi }> 0\\ \pi + Y, \; \dot{\xi }< 0\nonumber \end{array}\right. }, \end{aligned}$$

where Y is a positive scalar associated with the internal dissipation during the microstructure evolution [33]. The constraint on the evolution of the martensitic volume fraction can be expressed in terms of so-called Kuhn-Tucker conditions for both forward and reverse phase transformations as [34]

$$\begin{aligned} \phi \le 0, \quad \phi \dot{\xi }= 0. \end{aligned}$$

(9)

Table 1 Material parameters for smooth transformation hardening model [20]

The material parameters required for model calibration can be found out directly from the experiments, and the values are given in Table 1. The hardening parameters, A, B, C, D, and Y are calibrated from the following end conditions

$$\begin{aligned} \pi \left( \boldsymbol{\sigma }, \boldsymbol{H}_{Ms}\right) = Y \implies \dot{\xi }> 0;\qquad \xi = 0\nonumber \\ \pi \left( \boldsymbol{\sigma }, \boldsymbol{H}_{Mf}\right) = Y \implies \dot{\xi }> 0; \qquad \xi = 1\nonumber \\ \pi \left( \boldsymbol{\sigma }, \boldsymbol{H}_{As}\right) = -Y \implies \dot{\xi }< 0; \xi = 1\nonumber \\ \pi \left( \boldsymbol{\sigma }, \boldsymbol{H}_{Af}\right) = -Y \implies \dot{\xi }< 0; \xi = 0\nonumber \\ f\left( \xi = 1\right) |_{\dot{\xi } > 0} = f\left( \xi = 1\right) |_{\dot{\xi } < 0}\nonumber . \end{aligned}$$

Figure 2a represents the phase transformation between stress and magnetic field plane at a specified temperature. The red curve demonstrates the forward phase transformation, and the blue curve is for the reverse phase transformation. The transformation magnetic field increases with an increase in applied load. With a uniaxial tensile load at stress level ($\sigma = 100$ MPa), the new transformation magnetic fields are represented as $M_{Hf}, M_{Hs}, A_{Hs}$, and $A_{Hf}$ as the martensitic finish, martensitic start, austenitic start, and austenitic finish magnetic field, respectively. On the other hand, Fig. 2b represents the phase transformation in the stress and temperature field plane at the specified magnetic field.

Figure 3a represents the model simulation of the magnetic field induced strain at constant stress ($\sigma = -1$ MPa) in an isothermal environment. The material is initially in the martensitic phase. The initial strain and magnetic field are zero. When we increase the magnetic field up to $A_{Hs}$, there is negligible change in the strain. As the magnetic field increases from $A_{Hs}$ to $A_{Hf}$, strain increases due to the magnetic-field-induced phase transformation. The anti-ferromagnetic martensite is transformed into the ferromagnetic austenite in this regime. Similarly, the austenite transforms to martensite during the unloading process. The phase transformation starts at magnetic flux $M_{Hs}$ and ends when it reaches $M_{Hf}$. The hysteresis effects are captured both in mechanical as well as magnetization constitutive response. Figure 3b represents the model prediction of magnetization response at constant stress ($\sigma = -1$ MPa).

Fig. 2

a Phase transformation diagram in $\sigma _{11}-\mu _0 H$ plane at ($\theta = 200$ K). b Phase Transformation diagram in the $\sigma _{11}-\theta$ plane at ($\mu _0 H = 13$ T)

Fig. 3

a Model response for strain-field response at $(\sigma = -1$ MPa). b Model prediction of magnetization response at $(\sigma = -1$ MPa)

5 Conclusion

This work proposes the magneto-thermo-mechanical coupled model for MSMAs. The magneto-thermo-mechanical constitutive equations are derived from a proposed Helmholtz free energy function in a consistent thermodynamic way. The hysteretic behaviors of such materials are taking into account through evolution equations of internal variables. We did not verify our results to any experimental data yet. However, our main objective is to capture qualitatively memory effect of such material system. Model predictions capture the hysteresis effects, both for the mechanical and magnetic responses.