Keywords

1 Introduction

SARS-CoV was first detected in humans in 2002 and then the strains of the coronavirus family emerged at various times such as H1N1 followed by H5N1 and H5N7 during 2009. After a few years, MERS-CoV emerged in the Middle East in 2015 which was again a respiratory syndrome, whereas now, from the same family of a novel coronavirus, COVID-19 has emerged as the most contagious of all [1, 2]. COVID-19 has been stated pandemic, and the virus which causes it has been found to have profound variations in its arrangement and epidemiology. They have zoonotically enclosed RNA respiratory viruses that barely spread in their original form among humans, but they replicate to permit effective human transmission. Similar properties were shown by SARS in 2002–2003 and H1N1 influenza in 2009 [3, 4].

Common and recognized routes of transmission were identified as droplet transmission and airborne transmission. In droplet transmission, the droplet diameter is greater than 5 μm and travelling distance is less than 1 m. Droplets act as a viable virus carrier, and on encountering facial parts such as nose, lips, or eyes, the virus enters the upper respiratory tract. Accordingly, in airborne transmission, the droplets with diameter ≤5 μm can travel a distance more than 1 m and enter through the nasal passage of individuals [4, 5]. The two different modes (i) absolute contact transmission (contaminated surface not involved) and (ii) indirect contact transmission (contaminated surface involved) in the transmission of pandemic potential viruses have been provocative [5,6,7]. Nevertheless, a range of studies and models has proposed that indirect contact transmission would be the primary mode of transmission for certain respiratory viruses, in certain situations [8].

Furthermore, some reports show that coronavirus like SARS, MERS, and influenza (H1N1) are capable of survival on dry surfaces for long duration that allows further spread [9,10,11]. SARS-CoV and influenza virus can also live for prolonged periods in the environmental reservoirs such as soil, food, and sewage [12,13,14,15,16,17]. The significance of transmission of such viruses can be seen in the study of influenza and human coronavirus experiments, which were conducted on dry surfaces, field investigations, and surface sampling for viruses.

Several studies, involving viruses from CoV family on dry surfaces, have highlighted the role of infected surfaces in the spread of viruses, and consideration of the role of dry surfaces in the spread of the virus may further improve findings in this area [1]. Comparing transmission paths, droplets and airborne routes are a significant source of direct contact, whereas transmission source of indirect contact is still unknown. Influenza virus, SARS-CoV, and possibly MERS-CoV when released into the atmosphere in amounts well above the contagious dosage, they could live on surfaces for long periods, and several authorities or studies have reported contamination of hospital surfaces [18]. The infected surface may further contaminate hands or instruments, thereby causing inoculation by interaction with facial parts such as eyes, nose, and mouth. Pandemic potential viruses like influenza, MERS-CoV, and SARS-CoV could live on dry surfaces for prolonged periods, causing contamination in open locations which requires improved disinfection ensuring prevention and successful control of infection [1]. Research is done to validate empirical mathematical model, various models have been developed to estimate the rate of virus suppression, etc., and majorly, it was implemented on coronavirus family viruses like Middle East respiratory syndrome (MERS) and severe acute respiratory syndrome (SARS) [1, 18].

Mathematical modelling can be used as an appropriate tool in these types of virus susceptibility and rate of transmission effecting, susceptible-infected-recovered (S-I-R) is a basic infection dynamic approach for mathematical modelling, and it has been implemented in SARS, MERS, Hong Kong flu, etc. Advance approach such as susceptible-infected-recovered-susceptible (S-I-R-S), susceptible-exposed- infected-recovered (S-E-I-R), and bats-hosts-reservoir-people (B-H-R-P) transmission network model can be implemented in COVID-19 computational research. Resulting data can be used to validate the concepts of social distancing, quarantine, lockdown, etc. with a realistic scenario.

The outbreak caused by COVID-19 has challenged the researchers and health officials due to the exponential increase in the number of infected cases along with significant escalation in the number of deaths. Detail analysis is still undergoing, but the scientific data are yet to be revealed, whereas the public is interested in the duration of the outbreak and the expected number of infected cases to be reached at its highest level. Since the outbreak, various mathematical models have been proposed by various researchers to predict the number using calculation [19]. In this paper, we have reviewed models that can be used to predict the spread of this novel coronavirus (COVID-19) and the effect of mitigate measures to contain its spread.

2 COVID-19

The novel coronavirus (COVD-19) has affected approximately 213 countries including small territories also. Given the magnitude and the extent of its spread, the WHO has declared it a pandemic, and globally, it has been treated as a notified disaster. Apart from human suffering, it is also causing major economic disruptions. As per WHO, coronavirus (COVID-19) belongs to the coronavirus family such as the Middle East respiratory syndrome coronavirus (MERS-CoV) and severe acute respiratory syndrome coronavirus (SARS-CoV) which causes illness ranging from the common cold to respiratory infections [19, 20]. It has been predicted that the emergence of this virus has been from bats which were primarily from the Wuhan market, China [19, 20]. Symptoms of COVID-19 show from common cold further leading to respiratory disease, which is being spread after people, encounter the symptomatic person [18,19,20]. Figure 1 represents some common transmission modes of COVID-19.

Fig. 1
figure 1

Common transmission modes of COVID-19 [1, 18,19,20]

Full size image

As on 10 September 2020, 28,238,792 cases of novel coronavirus have been detected globally resulting in 911,500 deaths, and 20,238,900 have recovered. The active number of cases remains 7,027,675, and 60,717 patients are reported to be in critical condition. United States of America, India, Brazil, Russia, and Peru are five major impacted countries combined having approximately 61% of global coronavirus cases [20]. Table 1 represents the top 10 countries with their COVID-19 data.

Table 1 Top 10 countries COVID-19 data till 27th November 2020 [20]
Full size table

3 Mathematical Modelling Methodology

Modelling is considered as an important tool to study epidemics worldwide, and it is useful for studying of infection dynamics approach in world emerging problems like COVID-19 nowadays. In Fig. 2, we can signify the route map of the mathematical approach, and it is implementing connectivity with the real scenario.

Fig. 2
figure 2

Approach and connectivity of mathematical modelling [21]

Full size image

Mathematical modelling can be utilized to study the contribution of the diverse elements to the empirical observations. This relation can be stated with ease not containing any mathematical equation when the presence of a variable represents linearity to various variables. In these types of modelling, variables raising the rate of infection are not adding up; therefore, these models play an important role in the identification of disease/virus [21]. The following are some major utilized infectious dynamics and advanced models which can be implemented in predicting future situations.

3.1 Susceptible-Infected-Recovered (S-I-R) Modelling

S-I-R model proposed by William Ogilvy Kermack can be used to detect the spread of disease and is based on a simplified approach that supposes that spread of the virus is mainly due to person-to-person transmission [21, 22]. In S-I-R type of modelling, very few infected individuals were considered that can pass the virus/disease to many people. Three groups are mainly categorized here passing through stages of check-ups, etc. Firstly, they are susceptible, then they become infectious, and finally, they recover [23]. This type of methodology is applied in a situation that occurs for a short period, and it takes the form of a disease that infects or kills a major part of the society before it vanishes [24].

$${\text{S}}\, \to \,{\text{I}}\, \to \,{\text{R}}$$

Modelling starts with the identification of independent and dependent variables. t = independent variable, i.e., period in days.

As each variable is a function of time, S-I-R variables are stated as:

$$\begin{gathered} {\text{S}}\, = \,{\text{S}}\left( {\text{t}} \right), \hfill \\ {\text{I}}\, = \,{\text{I }}\left( {\text{t}} \right), \hfill \\ {\text{R}}\, = \,{\text{R }}({\text{t}}) \hfill \\ \end{gathered}$$

If P is the total population in a specific area, the fraction of the total population concerning all three variables can be represented as

$$\begin{gathered} {\text{s}}({\text{t}})\, = \,{\text{S}}({\text{t}})/{\text{P}}, \hfill \\ {\text{i}}({\text{d}})\, = \,{\text{I}}({\text{t}})/{\text{P}}, \hfill \\ {\text{r}}({\text{t}})\, = \,{\text{R}}({\text{t}})/{\text{P}} \hfill \\ \end{gathered}$$

Using fractions makes interpretation easy as each of the variables susceptible, infected, and recovered is reported as a fraction of the total population. The following are some assumptions to be considered while defining this differential equation model approach.

  1. I.

    At each time, s(t) + i(t) + r(t) = 1 and S + I + R = P

  2. II.

    Here, new born and immigrants are ignored; therefore, no addition to the susceptible category.

  3. III.

    A person leaves the susceptible group by entering the infected category.

  4. IV.

    If every infected person contacts a specified range of people (i.e., b) per day that is a sufficient number for virus supersession.

  5. V.

    On average, an infected person infects several new people every day is represented by bs(t).

  6. VI.

    Fixed fraction (i.e., k) number of infected persons recovers on a specific given day (“infected” is “infectious” that can transmit the virus to a susceptible individual. A “recovered” individual can still feel miserable and might even die later from virus. With these assumptions, the authors arrived at the following differential equations.

  1. (a)

    The susceptible equation:

    $$\frac{ds}{dt}=-bs\left(t\right)I(t)$$

    This equation leads to the following differential equation for s(t).

    $$\frac{ds}{dt}=-bs\left(t\right)i(t)$$
  2. (b)

    The recovered equation:

    $$\frac{dr}{dt}=ki(t)$$
  3. (c)

    The infected equation:

    $$\frac{ds}{dt}+\frac{di}{dt}+\frac{dr}{dt}=U$$

    Therefore,

    $$\frac{di}{dt}=bs\left(t\right)i\left(t\right)-ki(t)$$

Figure 3 represents the trajectory of the epidemic in the I-S graph, and it is clear that threshold effect can be observed from the existent curve.

Fig. 3
figure 3

Graphical representation of epidemic [21,22,23,24]

Full size image
$${R}_{0}=\frac{Pb}{K}>1$$

The equation states that the number of infected will increase until the susceptible is reduced to k/b and will decrease thereafter.

Here, R0 = basic reproductive ratio represents the threshold for an epidemic to occur. It also represents the average value of susceptible contaminated by an infected person. Now, dividing the infected equation by the susceptible equation,

$$\frac{di}{ds}=-\frac{bs\left(t\right)i\left(t\right)-ki(t)}{bs\left(t\right)i(t)}$$

Therefore,

$$\frac{di}{ds}=-\left(1+\frac{ki\left(t\right)}{bs\left(t\right)i\left(t\right)}\right)=\frac{k}{bs\left(t\right)}-1$$

Integrating the above equation,

$$i=\frac{k}{b}\mathrm{log}s\left(t\right)-s(t)+c$$

Here, the approximation calculation for the value of constant, i.e., c as

$$c\approx P-\frac{k}{b}\mathrm{log}P$$

From this integrated equation, the maximum number of the infections can be computed as

$${I}_{max}=P\left(1-\frac{1+\mathrm{log}{R}_{0}}{{R}_{0}}\right)$$

The above equation states that infection (I) must disappear somewhere near the positive value of susceptible (s). This implies that the epidemic disappears. Therefore, the epidemic terminates before the condition where all susceptible moves to the infected category and few infected recovers completely.

3.2 Susceptible-Infected-Recovered (S-I-R) Modelling Considering Demographic Effects

Basic susceptible-infected-recovered (S-I-R) modelling is elaborated in this section with the addition of demography, i.e., new-born babies, immigrants, and deaths taking place are considered here [23, 25]. This model closely represents the real scenario. The model is represented with the help of a block diagram in Fig. 4. Here, births (or immigrants) addition is represented at the rate “m” and deaths/emigrants at the rate “d”.

Fig. 4
figure 4

Representation of S-I-R modelling with demography [23, 25]

Full size image
  1. (d)

    The susceptible equation with demography:

    $$\frac{ds}{dt}=mP-bs\left(t\right)i\left(t\right)-ds(t)$$
  2. (e)

    The recovered equation with demography:

    $$\frac{dr}{dt}=ki\left(t\right)-dr(t)$$
  3. (f)

    The infected equation with demography:

    $$\frac{di}{dt}=bs\left(t\right)i\left(t\right)-ki\left(t\right)-di(t)$$

Total population, P = S + I + R (and dP/dt = 0).

Here, an assumption on birth rate and death rate is the same, i.e., m = d. There exist two equilibrium stages, i.e., no disease (represented by superscript *) and endemic (represented by superscript **). This endemic scenario exists with the assumption that the basic reproductive ratio remains positive (i.e., R0 > 1).

$${\text{S}}^{*} \, = \,{\text{P}},{\text{ I}}^{*} \, = \,0,{\text{ R}}^{*} \, = \,0$$

And,

$${S}^{**}=\frac{k+d}{b}$$

Dividing both sides by P,

$$\frac{{S}^{**}}{P}=\frac{k+d}{Pb}=\frac{1}{{R}_{0}} ,$$
$${I}^{**}=\frac{d(P-{S}^{**})}{b{S}^{**}}=\frac{d({R}_{0}-1)}{b}$$

Endemic equilibrium exists only if S** < P and I** > 0 which means R0 > 1. Here, \({R}_{0}=\frac{Pb}{k+d}\)

3.3 Susceptible-Exposed-Infected-Recovered (S-E-I-R) Modelling

Susceptible-exposed-infected-recovered (S-E-I-R) modelling approach is a modified S-I-R modelling approach that includes the category of people who are exposed to the virus but cannot transfer it to possible contacts. This type of occurrence delays and minimizes the chances of virus transmission via contact, etc. [21, 24]. Mainly, when a virus carrier is infectious without symptoms, there is a possibility that he/she cannot transmit it to another person. Here, term h is introduced that specifies the latent period in an exposed individual. The latent period specifies a period of virus/disease, where a person is exposed to infection, but he/she is not yet infectious [26]. In simple words, the rate at which an exposed person becomes infective, i.e., period of transmission from E to I.

As each variable is a function of time, exposed variable E is stated as E = E (t).

P is the total population in a specific area, and the fraction of the total population concerning exposed term can be represented as e(t) = E(t)/P (Fig. 5).

Fig. 5
figure 5

Compartmental diagram representing of S-E-I-R modelling [21, 24, 26]

Full size image

Total population, P = S + E + I + R.

And, basic reproductive ratio (R0) can be calculated here assuming m = d and represented as

$${R}_{0}=\frac{Pb}{k+d} \frac{h}{h+d}$$
  1. (a)

    The susceptible equation in S-E-I-R model:

    $$\frac{ds}{dt}=m(P-s\left(t\right))-b\frac{s\left(t\right)i\left(t\right)}{P}-ds(t)$$
  2. (b)

    The exposed equation in S-E-I-R model:

    $$\frac{de}{dt}=\frac{bs\left(t\right)i(t)}{P}-\left(m+h\right). e(t)$$
  3. (c)

    The recovered equation in S-E-I-R model:

    $$\frac{dr}{dt}=ki\left(t\right)-dr\left(t\right)+ms(t)$$
  4. (d)

    The infected equation in S-E-I-R model:

    $$\frac{di}{dt}=he\left(t\right)-\left(m+k\right).i(t)$$

3.4 Susceptible-Infected-Recovered-Susceptible (S-I-R-S) Modelling

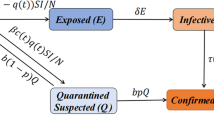
S-I-R-S modelling is mainly considered where immunity exists for a short period and the recovered person re-enters the susceptible categorized group. Therefore, it is known as an epidemic model having the existence of temporary immunity [26, 27]. A term z is considered here to specify the immunity losing rate. Mathematical modelling of S-I-R-S is represented as follows (Fig. 6).

Fig. 6
figure 6

S-I-R-S compartmental representation (it supposes source is saved from re-entering of infection temporally after recovery) [26, 27]

Full size image

Three main differential equations represented as

$$\frac{ds}{dt}=-bs\left(t\right)i\left(t\right)+zr\left(t\right),$$
$$\frac{di}{dt}=bs\left(t\right)i\left(t\right)-ki\left(t\right),$$
$$and \frac{dr}{dt}=ki\left(t\right)-zr(t)$$

Total population, P = S + I + R and dP/dt = 0.

In this system, there exist two equilibrium stages, i.e., no disease (represented by superscript *) and endemic (represented by superscript **). This endemic scenario exists with the assumption that the basic reproductive ratio remains positive (i.e., Pb/k > 1).

$${\text{S}}^{*} \, = \,{\text{P}},{\text{ I}}^{*} \, = \,0,{\text{ R}}^{*} \, = \,0$$

And,

$${S}^{**}=\frac{k}{b}, { I}^{**}=\frac{P-\left(\frac{k}{b}\right)}{1+\left(\frac{k}{z}\right)}, {R}^{**}=\frac{P-\left(\frac{k}{b}\right)}{1+\left(\frac{z}{k}\right)}$$
(1)

Three main differential equations represented as

$$\frac{ds}{dt}=-bs\left(t\right)i\left(t\right)+zr\left(t\right),$$
$$\frac{di}{dt}=bs\left(t\right)i\left(t\right)-ki\left(t\right),$$
$$and \frac{dr}{dt}=ki\left(t\right)-zr(t)$$

Total population, P = S + I + R and dP/dt = 0.

In this system, there exist two equilibrium stages, i.e., no disease (represented by superscript *) and endemic (represented by superscript **). This endemic scenario exists with the assumption that the basic reproductive ratio remains positive (i.e., Pb/k > 1).

$${\text{S}}^{*} \, = \,{\text{P}},{\text{ I}}^{*} \, = \,0,{\text{ R}}^{*} \, = \,0$$

And,

$${S}^{**}=\frac{k}{b}, { I}^{**}=\frac{P-\left(\frac{k}{b}\right)}{1+\left(\frac{k}{z}\right)}, {R}^{**}=\frac{P-\left(\frac{k}{b}\right)}{1+\left(\frac{z}{k}\right)}$$
(2)

3.5 Bats-Hosts-Reservoir-People Transmission Network Model

B-H-R-P transmission network model is a newly developed mathematical model that was proposed by bioRxiv on 19 January 2020 [25]. It is specified on COVID-19 occurrence, developed using some known sources/parameters of transmission. Here, it is stated that the virus transverses between the main sources, i.e., bats, and then it enters into unknown hosts, i.e., wild animals, fishes. The hosts were sent to market in the form of seafood, and other sources were stated as the reservoir of the novel coronavirus. People get exposure through buying these products in the market, and thus, virus is further transmitted. Calculation of basic reproduction number (R0) is mainly from the reservoir-people model for accessibility of COVID-19 transmission [25].

B-H-R-P transmission network model is developed by networking connectivity between four sources of transmission, i.e., bats, hosts, reservoir, and people. S-E-I-R modelling is approached in bats and hosts. Infected bats are transmitting the virus hosts susceptible group, and further infected hosts transfer it to reservoirs (i.e., seafood). Reservoirs are categorized in a single group, i.e., do not follow any modelling approach because they are haunted form of hosts and remain infected. Further, people caught this virus via reservoirs and people which are categorized into five groups, i.e., susceptible, exposed, symptomatic infected people, asymptomatic infected people, and removed. Therefore, S-E-I-R model is applied in people transmission part with the addition of an extra group as asymptomatic infected people.

4 Validation of Mathematical Modelling

Day to day data are required to validate any type of infectious mathematical modelling for certain virus/disease. S-E-I-R is having exposed parameter; that is why, it requires data of people who are exposed to the virus but not infected. S-I-R-S requires people data who are recovered and again suspected. So, a simple approach to validate it is via S-I-R modelling requiring only three parameters, i.e., number of suspected individuals from the total population, infectious, and recovered (including deaths also).

Suppose, we have an area having a total population of 5000. Out of the total population, 2500 are suspected individuals, 2000 are confirmed with infection, and 500 are recovered (i.e., recovered from infection or dead).

Here, First condition is implemented, i.e., P = S + I + R.

Suppose, average period of infectiousness at thirteen days, i.e., k = 1/13 = 0.077.

And, if each infected would make possibility infecting contact every four days, then b = 1/4 = 0.25. Then, R0 = 0.25/0.077 = 3.25.

R0 > 1, therefore, it is epidemic-type situation.

Suppose, we want to report the situation for the next five days implementing source data. Initially, S (0) = 2500

I (0) = 2000

R (0) = 500

Calculating the rate of susceptibility,

$${\text{dS}}/{\text{dt}}\, = \, - {\text{bs}}({\text{t}}){\text{I}}({\text{t}})\, = \, - 0.25 \, \times \, \left( {2500/5000} \right)\, \times \,2000\, = \, - 250$$

Similarly, \({\text{dI}}/{\text{dt}}\, = \,{\text{bs}}({\text{t}}){\text{I}}({\text{t}}){-}{\text{kI}}({\text{t}})\, = \,250{-}\left( {0.077\, \times \,2000} \right)\, = \,96\) and \({\text{dR}}/{\text{dt}}\, = \,{\text{kI}}({\text{t}})\, = \,154\)

Therefore, for t = 1 (first-day data) (Fig. 7):

$$\begin{aligned} {\text{S}}\left( 1 \right)\, & = \,2500 - 250\, = \,2250 \\ {\text{I}}\left( 1 \right)\, & = \,2000\, + \,96\, = \,2096 \\ {\text{R}}\left( 1 \right)\, & = \,500\, + \,154\, = \,654 \\ \end{aligned}$$
Fig. 7
figure 7

Graphical representation of the example

Full size image

For second day,

$$\begin{aligned} {\text{S}}\left( 2 \right)\, & = \,2250 - \left( {0.25\, \times \,0.45\, \times \,2096} \right)\, = \,2250{-}235.8\, = \,2014.2 \\ {\text{I}}\left( 2 \right)\, & = \,2096\, + \,\left( {235.8 - 161.392} \right)\, = \,2170.408 \\ {\text{R}}\left( 2 \right)\, & = \,654\, + \,161.392\, = \,815.392 \\ \end{aligned}$$

For third day,

$$\begin{aligned} {\text{S}}\left( 3 \right)\, & = \,2014.2 - \left( {0.25\, \times \,0.4028\, \times \,2170.408} \right)\, = \,1795.64 \\ {\text{I}}\left( 3 \right)\, & = \,2170.408\, + \,\left( {218.56 - 167.1214} \right)\, = \,2221.85 \\ {\text{R}}\left( 3 \right)\, & = \,815.392\, + \,167.1214\, = \,982.5134 \\ \end{aligned}$$

For fourth day,

$$\begin{aligned} {\text{S}}\left( 4 \right)\, & = \,1795.64 - \left( {0.25\, \times \,0.3591\, \times \,2221.85} \right)\, = \,1596.1835 \\ {\text{I}}\left( 4 \right)\, & = \,2221.85\, + \,\left( {199.4665{-}171.0824} \right)\, = \,2250.23 \\ {\text{R}}\left( 4 \right)\, & = \,982.5134\, + \,171.0824\, = \,1153.6 \\ \end{aligned}$$

For fifth day,

$$\begin{aligned} {\text{S}}\left( 5 \right)\, & = \,1596.1835 - \left( {0.25\, \times \,0.3192\, \times \,2250.23} \right)\, = \,1416.6 \\ {\text{I}}\left( 5 \right)\, & = \,2250.23\, + \,\left( {179.57 - 173.27} \right)\, = \,2256.53 \\ {\text{R}}\left( 5 \right)\, & = \,1153.6\, + \,173.27\, = \,1326.87 \\ \end{aligned}$$

4.1 Implementation of Mathematical Modelling to Forecast the Importance of Social Factors (Lockdown, Social Distancing, and Quarantine)

An analysis was performed by Kucharski et al. [28] to determine the dynamics of initial transmission of disease and to evaluate the effectiveness of prevention and control in new areas which was critical to assess the ability for sustaining the transmission. The analysis was performed by combining COVID-19 transmission with the mathematical model where four datasets were taken between December 2019 and February 2020 within the outside and inside Wuhan. If more cases were introduced from outside Wuhan, then the observed estimation will be observed to assess the potential for sustained human-to-human transmission. It was observed that one week before the travel restriction, the median daily reproduction number (Rt) from 2.35 (1.15–4.77) started to decline after one week of restriction on 23 Jan 2020 to 1.05 (0.41–2.39). Based on the observation for Rt, the transmission potential was calculated in various locations in Wuhan for SARS-like variation. Understanding the model if at least four independent cases are introduced in an area than there are 50% of symptoms of this disease will establish within that population. The results predict that the transmission of COVID-19 would decline in later weeks in January 2020 after the introduction of control measures. With the invasion of more numbers in China from international borders with identical symptoms of disease before the implementation of protective measures, initially, the transmission chain might not establish but eventually, it will outbreak [28].

A data-driven susceptible-exposed-infectious-quarantine-recovered (SEIQR) model was developed by Yuzhen Zhang et al. which can simulate the epidemic with interventions of social distancing and epicentre lockdown. To estimate the model parameters, the officially reported data were combined with the population migration data by estimating the daily infected ration and daily susceptible population size. On 1st January 2020, the estimated latent infected individual initially was 380.1 (379.8–381.0), and after inclusion of thirty days of social distancing, the number of infected people was reduced from 2.2 to 1.58, whereas in other provinces, it reduced from 2.56 to 1.65, and with the implementation of social distancing, it could reduce the impact of the pandemic in China with an estimated reduction of 98.9% of infected people and 99.3% of many deaths by 23rd February 2020. However, with the lockdown of point source or epicentre, it would partially reduce the effect and would lead to the improvement in the scenario. To make it more effective and minimize the impact, social distancing should be implemented stepwise where the epicentre should be targeted first followed by province and later the whole nation to minimize the economic loss [29].

Benjamin Ivorra and Angel M defined BE-CoDids (between countries disease spread) epidemiological model to study the transmission of COVID-19 between humans and within countries. It is a combination of the individual-based model (where countries are considered as an individual) which is simulated between different countries with compartment model (a system of ordinary differential equations), simulating the rate of spread of disease within countries. When the simulation completes, BE-CoDids produces an output of outbreak characteristics (the risk of disease introduces or spreads per country, the magnitude of epicentre, etc.) of COVID-19 of referring countries [30, 31] (Fig. 8).

Fig. 8
figure 8

Role of basic reproductive ratio in virus transmission [30,31,32,33]

Full size image

5 Conclusion

The transmission of COVID-19 is modelled using different types of mathematical models. The S-I-R modelling is a basic approach that does not include births, migrants, deaths emigrants, and it can be used for a small community where variation is negligible, and S-I-R modelling can be updated concerning demography consideration, and it validates a realistic situation scenario in major areas. While S-E-I-R model explains epidemic situations, it can be implemented well in presently COVID-19 emerging situations. It includes an extra term, i.e., exposed that is infected with the virus but cannot transfer further to possible contacts. The S-I-R-S modelling is approached where recovered people are having temporary immunity, and again, it enters in the susceptible category. Immunity and medication factors play an important factor in S-E-I-R and S-I-R-S modelling. All mentioned mathematical modelling approaches can be arranged in a network model, and predictive results can be calculated for COVID-19 situation. B-H-R-P transmission network model is well-implemented and well-defined model using initial reported conditions of COVID-19. Using and updating these models, we can calculate and predict many parameters required as precautions that can be used for the welfare of society. The requirement of emergencies situations like social distancing, quarantine, and lockdown can be well determined using calculations from this mathematical approach. Further, it can also be used in computational tools for simulating epidemic or pandemic conditions.