Probabilistic Supply Chain Models with Partial Backlogging for Deteriorating Items

Abstract

A supply chain (SC) is a network comprising suppliers, producers, manufacturers, distributors and retailers. Generally, it is represented as single tier, two tier and multi-tier according to its various independent nodes, i.e., entities in the SC. For smooth flow of SC, an inventory is maintained and optimized. At supplier, the raw material inventory is required to dispatch at various producers. The finished product inventory with the help of raw material received from suppliers is produced at producer level. An assembled inventory from finished product is produced at manufacturer level. Various distributors transport this assembled inventory using various modes of transportation to retailers. At final node of SC, the customer will purchase the product. Thus, inventory management is a crucial task in a SC. In probabilistic inventory models, using suitable probability distribution for demand rate, an inventory can be optimized. Here, we develop the inventory models by assuming various probability distributions for demand and deterioration rate under shortages. For modeling, we consider probabilistic demand per unit time as well as the probabilistic deterioration rates. Under these assumptions, probabilistic economic order quantity (EOQ) models are developed under partial backlogging. Classical methods are unable to solve these situations by these assumptions. Therefore, the proposed genetic algorithm is useful to solve the EOQ models. Numerical case study is presented and solved by using non-traditional method, i.e., genetic algorithm. Sensitivity analysis of various parameters is also presented.

1 Introduction

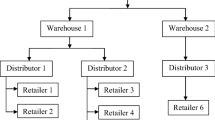
Supply chain (SC) consists of several stakeholders like suppliers of raw materials, producers of unique product, manufacturers for assembling the produced product, warehouse for storage purpose, retailers for distribution purpose and transporters for shipping the manufactured product from each node of SC to other node. Each stakeholder in the SC has a role to optimize the SC. The major objective of SC is to satisfy or to meet the customer demand in such a way that the profit or cost of maintaining the SC would be maximum or minimum, respectively. All the above stakeholders in the SC operate independently for generating their profits. The SC connects each stakeholder to the end customer. It consists of suppliers, manufacturers, transporters, warehouses and customers. Every entity in the SC has to satisfy the customer demand and to generate profit for itself, whereas customers are the integral part of it. The term SC conjures up supply of product moving from suppliers to manufacturers, manufactures to distributors, distributors to retailers and retailers to customers in a SC. The detailed working procedure of SC network as, producers receive raw materials from various outside suppliers which produces number of units of the perishable product. After production of units of perishable item, it transports to the manufacturers site for packaging or assembling the final product, then manufacturer transports the final product to several independent warehouses for storage purpose. Lastly, produced perishable product transports to various independent retailers for distributing to customers. Here, we have developed the new probabilistic economic order quantity (EOQ) inventory models for multi-tier SC; see Fig. 1. In the literature, several authors developed EOQ inventory models with stock-dependent, replenishment-dependent, ramp-type function of demand, etc. Here, we assumed that the market demand is uncertain and follow a certain probability distribution. The answers of basic questions in inventory like how much to store and optimum order quantity can be obtained from the developed models. Also, a new solution methodology based on evolutionary algorithm is developed. This solution methodology can be applicable to all types of optimization problems involved in inventory management.

Fig. 1

Supply chain network (SCN)

Beamon (1998) highlighted the two basic random processes occurring in the SC: (i) production planning and inventory process and (ii) distribution (i.e., transportation) and logistics process. The inventory process deals with the manufacturing and storage problems in SC, whereas production planning deals with the cooperation between each and every manufacturing process. The distribution process deals with how products are transported from suppliers to producers, from producers to manufacturers, from manufacturers to retailers. This process includes procurement of inventory and transportation of raw material as well as finished product. Each stage of SC is connected through the flow of products, information and funds. These flows are in both ways. For effectively managing the SC, a manager has to decide the location, capacity and type of plants, warehouses and retailers to establish the SCN. The SCN problem covers wide range of formulations such as simple single product type to complex multi-product one and from linear deterministic models to complex nonlinear ones. SC connects each stakeholder to the end customer.

EOQ inventory model was firstly introduced by Ghare and Schrader (1963) with constant deterioration; i.e., it follows an exponential distribution $g(t)=\theta >0$ where $g(t)$ is the rate of deterioration. Later, this model was extended by Covert and Philip (1973), under which they assumed variable deterioration and it follows the Weibull distribution $g(t)=\gamma \beta \,t^{\beta -1}, \quad {} 0\le t \le T$ where $T$ is the cycle time and $\alpha >0$ and $\beta >0$. Afterward, Philip (1974) formulated more general EOQ inventory model with Weibull distributed deterioration. Padmanabhan and Vrat (1995) developed three EOQ inventory models by assuming no, complete and partial backlogging. Under continuous review policy, the inventory models were proposed in which stock-dependent demand rate, i.e., $D(t)=\alpha +\beta \,I(t), \alpha , \beta >0$ per unit time $t$, was assumed.

Wee (1995) developed the replenishment strategy for a perishable product under complete as well as partial backlogging with different backlog rates. Bose et al. (1995) formulated an EOQ inventory model for deteriorating items with linear time-dependent demand rate per unit time $D(t)=a+b\cdot t, a>0, b>0$. Such model can be applicable to highly deteriorated products like fruits, milk products, etc. Bhunia and Maiti (1997) formulated two deterministic EOQ inventory models under variable production. They modeled the level of inventory at time $t$ during the production period at a finite replenishment rate, i.e., $R(t)=\alpha -\beta \, I(t)$ and $R(t)=\alpha +\beta \, D(t)$. In both the models, demand rate was assumed to be a linearly increasing function of time $t$. Later, Bhunia and Maiti (1998) extended earlier developed EOQ inventory models under complete backlogging by considering finite rate of replenishment.

Wu (2001) developed an EOQ inventory model by considering ramp-type demand and stochastic deterioration rate. Shortages were allowed in the developed model, and they were partially backlogged with backlogging rate $1/[1+\delta (T-t)]$ per unit time where $\delta >0$ is the backlogging parameter. The necessary and sufficient conditions for the existence of unique optimal solution were provided. For representing ramp-type behavior of demand rate, a well-known Heaviside’s function was used. Later, such ramp-type function demand was used by Skouri et al. (2009) and they developed an inventory model for general demand rate as any function of time up to stabilization. They assumed shortages were completely backlogged during the waiting time of further replenishments at a rate $\delta (t)\in (0, 1)$ which satisfies backlog rate $=(\delta (t)+T\, \delta ^{'}(t)) \ge 0.$ Thus, a monotonically decreasing function $\delta ^{'}(t)\le 0$ of waiting time was used for shortages. A ramp-type function for representing demand rate was considered, i.e., $D(t)=f(t), t<\mu$ and $D(t)=f(\mu ), \text {otherwise}$ where f(t) is any positive, continuous function of time and $\mu$ is the specific time during the scheduling period.

Dye et al. (2005) developed an EOQ inventory model. Shortages were allowed and partially backlogged for perishable items in a SC. The time-dependent backlog rate was assumed in the developed model, i.e., $\text {backlog rate}=1/(1+\delta [T-t]), \delta >0.$ Later, Eroglu and Ozdemir (2007) presented a deterministic EOQ inventory model for a manufacturer with few defective products in a lot. The proposed model can be applicable to a SC consisting of only a manufacturer and a retailer under shortages. Uniform defective rate of products was considered in the developed model, i.e., $f(p)\sim U(0, 0.1)$ where p is the proportion of defectives in the lot. Raosaheb and Bajaj (2011) formulated transportation and inventory model with retailer storage under uncertain environment. In the same year, Latpate and Bajaj (2011) developed multi-objective production distribution SC model for manufacturer storage under uncertain environment. Later, Kurade and Latpate (2021) proposed different EOQ inventory models under no, complete and partial backlogging. The time-dependent demand and deterioration rates were assumed in the developed model. In the same year, Latpate and Bhosale (2020) proposed SC coordination model with stochastic market demand. Bhosale and Latpate (2019) formulated a fuzzy SC model with Weibull distributed demand for dairy product.

Remainder of the chapter is organized as follows: In Sect. 2, preliminary concepts of demand and deterioration variation of the inventory model are stated. Also, this section is dedicated to the formulation of probabilistic inventory model with assumptions. Subsequently, Sect. 3 develops binary coded genetic algorithm approach to solve the formulated probabilistic inventory model under various demand distributions. The developed probabilistic EOQ inventory model is illustrated with the hypothetical data for various demand distributions in Sect. 4 with results discussed in the same section. Finally, sensitivity analysis of various parameters is discussed in Sect. 5. The managerial implications are added in Sect. 6. Concluding remarks with future scope are given in Sect. 7. Last, an exhaustive list of references is provided.

2 Mathematical Model

The main working behavior of the SC is displayed in Fig. 1. This figure shows the general network of SC, in which product flows from suppliers to retailers through various stages. Thus, from supplier, producer, manufacturer and warehouses the finished product will reach to the customer. The customer is always an integral part of a SC network. In supply chain network (SCN), generally information and funds flow from customers to suppliers and units of product flow from suppliers to customers. Multi-echelon SCN provides an unique optimal way for efficiently and effectively managing SC. It manages product and information flows both in and between several linked but independent stakeholders.

Here, we consider a SCN in Fig. 1 in which the inventory is stored at different independent nodes of SC. At supplier, the inventory of a raw material is stored for the purpose of production of a finished product at several producers. The finished product inventory is stored at producer level. The assembly of a finished product is done at manufacturer level. Thus, the inventory of finished product is stored at manufacturer level. At warehouses, the transported finished product is stored for the purpose of distribution to several retailers. Thus, at each point of a SC different kinds of inventory are stored. For managing this inventory, we have proposed a probabilistic inventory model, in which the demand of a product from the market is assumed to be probabilistic. The goal is to determine an EOQ of the product in the scheduling period, $t\in [0, T]$.

2.1 Preliminaries

2.1.1 Demand Variation

EOQ inventory models are developed by maximizing profit in which demand follows a probability distribution per unit time with known parameters. Demand rate follows an uniform and normal distribution.

Uniform Distribution

An uniform distribution with parameters a and b is denoted by U(a, b), and its probability density function is

$$\begin{aligned} f(t)=\dfrac{1}{b-a}; \quad {} \quad {} a<t<b, \qquad {} a,b\in \mathbf {R}. \end{aligned}$$

(1)

Normal Distribution

A normal distribution with mean $\mu$ and variance $\sigma ^2$ is denoted by $N(\mu , \sigma ^2)$, and its probability density function is

$$\begin{aligned} f(t)=\dfrac{1}{\sigma \sqrt{2\pi }}e^{ -\left( t-\mu \right) ^2 /2 \sigma ^2 }; \qquad {} t\in \mathbf {R},\qquad {} \sigma >0, \qquad {} \mu \in \mathbf {R}. \end{aligned}$$

(2)

2.1.2 Deterioration Variation

During the normal storage period, the deterioration may occur in several perishable products. Deterioration includes vaporization, drying, decay, damage or spoilage such that the product cannot be used for its intended application. For representing the deterioration of perishable product, we use Weibull distribution.

Weibull Distribution: It includes all types of deterioration such as constant, increasing and decreasing. It is defined as

$$\begin{aligned}&g(t)=\gamma \beta t^{\beta -1}; \quad {}\quad {} t>0, \quad {}\quad {} \gamma>0, \quad {} \quad {} \beta >0.&\end{aligned}$$

(3)

Note: If $\beta >1$, it shows increasing deterioration; if $\beta <1$, it shows decreasing deterioration; and if $\beta =1$, it shows constant deterioration.

Fig. 2

Graphical representation of inventory system in partial backlogging

During the period $t \in [t_1, T]$ (see Fig. 2), it is generally assumed that customers are impatient in nature and do not wish to wait for replenishment. Thus, only a fraction of backlogged demand is considered and backlogging rate is taken to be variable. Backlogging rate depends on the length of time, for the customer waits before receiving the product. Here, backlogging rate is considered as a decreasing exponential function of waiting time (Abad, 2001; Chang & Dye, Chang and Dye (1999); Dye et al., 2007).

$$\therefore \text {Backlogging rate} = \dfrac{1}{1+\delta (T-t)};\quad t_1 \le t \le T.$$

Here, we consider the expected demand per unit time of a product which is obtained as:

$$\begin{aligned} \text {Expected demand in }(t,\ t+\Delta t)= & {} D_0 \cdot P[\text {demand of a product in interval} \,\,\,(t,\ t+\Delta t)]\nonumber \\= & {} D_0\cdot \lim _{\Delta t \rightarrow 0 } \left[ \frac{F(t+\Delta t)-F(t)}{\Delta t}\right] \nonumber \\= & {} D_0\cdot f(t). \nonumber \end{aligned}$$

Assumptions: The assumptions considered in the problem are:

• 1. Replenishment rate is infinite with negligible lead time.

• 2. Time periods between two successive demands of an unique perishable product are independent and identically distributed random variables.

• 3. Continuous review policy of inventory model for single perishable product is considered.

• 4. The demand and deterioration rate are probabilistic in nature.

• 5. Storage facility is available at each node of SC.

Notations: These are listed below:

• $I_1(t)=$ positive inventory in a cycle of length T.

• $I_2(t)=$ negative inventory in a cycle of length T.

• $D_0=$ total demand in the inventory cycle.

• $D(t)=$ demand rate.

• $Q =$ order quantity (per cycle).

• $B =$ maximum inventory level (per cycle).

• $g(t)=$ deterioration rate.

• $\gamma$ and $\beta =$ deterioration parameters.

• $\delta =$ backlogging parameter in the backlogging period.

• $f(t)=$ probability density function.

• $F(t)=$ cumulative distribution function.

• $P(T, t_1)=$ profit per unit time for partial backlogging model.

Costs:

The notations of various costs involved in the inventory model are listed below:

• $C=$ the purchase cost (per unit).

• $C_2=$ a finite shortage cost (per unit).

• $S=$ the selling price (per unit), where $S > C$.

• $A=$ the ordering cost (per order).

• $R=$ the cost of lost sales (i.e., opportunity cost) (per unit).

• $r=$ the inventory carrying cost as a fraction (per unit per unit time).

Decision Variables:

The notations of various decision variables involved in the problem are listed below:

• $t_1=$ length of the duration over which inventory level is positive in a cycle.

• $T=$ length of the scheduling period.

The inventory level decreases in satisfying the market demand as well as due to the deterioration during the period $[0, t_1]$ (see Fig. 2). Thus, the differential equations considering the partial backlogging during the cycle [0, T] are given as:

$$\begin{aligned}&\frac{d I_1(t)}{dt}+g(t) I(t)=-D(t), \qquad {} 0 \le t \le t_1. \end{aligned}$$

(4)

$$\begin{aligned}&\frac{d I_2(t)}{dt}=\frac{-D(t)}{[1+\delta (T-t)]}, \qquad {} t_1 \le t \le T. \end{aligned}$$

(5)

The solutions of Eqs. (4) and (5), for the boundary condition $I(t_1)=0$, are

$$\begin{aligned}&I_1(t)=D_0 e^{-\int g(t) dt} \int _{t}^{t_1} f(x) e^{\int g(x) dx} dx,\qquad {} 0 \le t \le t_1.\end{aligned}$$

(6)

$$\begin{aligned}&I_2(t)=-D_0 \int _{t_1}^{t} f(x) \left[ \frac{1}{[1+\delta (T-t)]}\right] dx,\qquad {} t_1 \le t \le T. \end{aligned}$$

(7)

$\therefore$ inventory level at the beginning of the cycle (maximum inventory level) is

$$\begin{aligned} B=D_0\ \int _{0}^{t_1} f(x) e^{\int g(x) dx} dx. \end{aligned}$$

(8)

Thus,

$$\begin{aligned} \text{ Sales } \text{ revenue }&= S\left\{ \int _{0}^{t_1}D(x) dx-I_2(t) \right\} \nonumber \\&=S\left\{ \int _{0}^{t_1}D_0f(x) dx+ \int _{t_1}^{T} D_0f(x) \left[ \frac{1}{[1+\delta (T-x)]}\right] dx \right\} \nonumber \\&= S D_0\left\{ F(t_1)+\int _{t_1}^{T} f(x) \left[ \frac{1}{[1+\delta (T-x)]}\right] dx\right\} . \end{aligned}$$

(9)

$$\begin{aligned} \text{ Carrying } \text{ cost } =r C\int _{0}^{t_1} I_1(x) dx = r C D_0\int _{0}^{t_1} e^{-\int g(t) dt} \left\{ \int _{t}^{t_1} f(x) e^{\int g(x) dx} dx \right\} dt. \end{aligned}$$

(10)

$$\begin{aligned} \text{ Shortage } \text{ cost }&= C_2\left\{ \int _{t_1}^{T}[-I_2(x)] dx \right\} \nonumber \\&= -C_2\left\{ \int _{t_1}^{T} \left[ -D_0\int _{t_1}^{t} f(x) \left[ \frac{1}{[1+\delta (T-x)]}\right] dx\right] dt \right\} \nonumber \\&= C_2D_0\left\{ \int _{t_1}^{T} \left[ \int _{t_1}^{t} f(x) \left[ \frac{1}{[1+\delta (T-x)]}\right] dx\right] dt\right\} . \end{aligned}$$

(11)

$$\begin{aligned} \text{ Material } \text{ cost }&=C \left\{ \int _{0}^{t_1} I_1(x) dx- \int _{t_1}^{T} I_2(x) dx\right\} \nonumber \\&=\left\{ C D_0\int _{0}^{t_1} f(x) e^{\int g(x) dx} dx\right\} +\left\{ \int _{t_1}^{T} \left[ \frac{C D_0f(x) }{[1+\delta (T-x)] }\right] dx \right\} . \end{aligned}$$

(12)

$$\begin{aligned} \text{ Opportunity } \text{ cost }&= R \int _{t_1}^{T} D(x) \left[ 1-\frac{1}{[1+\delta (T-x)] }\right] dx \nonumber \\&= R \,\,D_0 \int _{t_1}^{T}f(x) \left[ 1-\frac{1}{[1+\delta (T-x)] }\right] dx \nonumber \\&= R \,\,D_0 \int _{t_1}^{T}f(x) \left[ \frac{\delta (T-x)}{[1+\delta (T-x)] }\right] dx. \end{aligned}$$

(13)

Therefore from above defined expressions, the profit per unit time is

$$\begin{aligned}\text {Profit}&=\dfrac{1}{T}(\text {Sales revenue}-\text {order cost}-\text {carrying cost}-\text {shortage cost}\\ \qquad&-\,\text {material cost}-\text {opportunity cost)}\end{aligned}$$

$$\begin{aligned} \therefore P(T,\ t_1)&= \frac{1}{T}\left( S D_0\left\{ F(t_1)+\int _{t_1}^{T} \left[ \frac{f(x)}{[1+\delta (T-x)]}\right] dx\right\} -C D_0\int _{0}^{t_1} f(x) e^{\int g(x) dx} dx\right. \nonumber \\&\quad \left. {}- r C D_0\int _{0}^{t_1} e^{-\int g(t) dt} \left\{ \int _{t}^{t_1} f(x) e^{\int g(x) dx} dx \right\} dt\right. \nonumber \\&\quad \left. {}-C_2D_0\left\{ \int _{t_1}^{T} \left[ \int _{t_1}^{t} f(x) \left[ \frac{1}{[1+\delta (T-x)]}\right] dx\right] dt\right\} - A\right. \nonumber \\&\quad \left. {}-\int _{t_1}^{T} \left[ \frac{C D_0f(x) }{[1+\delta (T-x)] }\right] dx -R \,\,D_0 \int _{t_1}^{T}f(x) \left[ \frac{\delta (T-x)}{[1+\delta (T-x)] }\right] dx\right) . \end{aligned}$$

(14)

The optimum values of T and $t_1$ can be obtained by solving the above nonlinear expression using GA. From this, the optimum order quantity is

$$\begin{aligned} Q = I_1(0)-I_2(T)=D_0 \left[ \int _{0}^{t_1} f(x) e^{\int g(x) dx} dx + \int _{t_1}^{T} f(x) \left[ \frac{1}{[1+\delta (T-t)]}\right] dx \right] .\nonumber \\ \end{aligned}$$

(15)

Particular cases: Case 1: Demand rate follows an uniform distribution (Eq. 1) and deterioration rate follows a Weibull distribution (Eq. 3), i.e., $f(t)\sim U(a, b)$ and $g(t)\sim W(\gamma , \beta )$.

Thus Equation 14 becomes,

$$\begin{aligned} P(T, t_1)&= \frac{1}{T}\left( S D_0\left\{ \frac{t_1-a}{b-a}+\int _{t_1}^{T} \frac{1}{b-a} \left[ \frac{1}{[1+\delta (T-x)]}\right] dx\right\} \right. \nonumber \\&\quad \left. -C D_0\int _{0}^{t_1} \frac{e^{\gamma x^\beta }}{b-a} dx {}- r C D_0\int _{0}^{t_1} e^{-\gamma t^\beta } \left\{ \int _{t}^{t_1} \frac{e^{\gamma x^\beta }}{b-a} dx \right\} dt\right. \nonumber \\&\quad \left. {}-C_2D_0\left\{ \int _{t_1}^{T} \left[ \int _{t_1}^{t} \frac{1}{b-a} \left[ \frac{1}{[1+\delta (T-x)]}\right] dx\right] dt\right\} - A\right. \nonumber \\&\quad \left. {}-\int _{t_1}^{T} \frac{1}{b-a} \left[ \frac{C D_0 }{[1+\delta (T-x)] }\right] dx -R \,\,D_0 \int _{t_1}^{T} \frac{1}{b-a} \left[ \frac{\delta (T-x)}{[1+\delta (T-x)] }\right] dx\right) . \end{aligned}$$

(16)

Case 2: Demand rate follows a normal distribution (Eq. 2) and deterioration rate follows a Weibull distribution (Eq. 3), i.e., $f(t)\sim N(\mu , \sigma ^2)$ and $g(t)\sim W(\gamma , \beta )$. Thus Equation 14 becomes,

$$\begin{aligned} P(T, t_1)&= \frac{1}{T}\left( S D_0\left\{ \int _{-\infty }^{t_1}\frac{e^{-\frac{(x-\mu )^2}{2 \sigma ^2}}}{\sigma \sqrt{2 \pi }}+\int _{t_1}^{T} \frac{e^{-\frac{(x-\mu )^2}{2 \sigma ^2}}}{\sigma \sqrt{2 \pi }} \left[ \frac{1}{[1+\delta (T-x)]}\right] dx\right\} \right. \nonumber \\&\quad \left. {}-C D_0\int _{0}^{t_1} \frac{e^{-\frac{(x-\mu )^2}{2 \sigma ^2}}}{\sigma \sqrt{2 \pi }}e^{\gamma x^\beta } dx- r C D_0\int _{0}^{t_1} e^{-\gamma t^\beta } \left\{ \int _{t}^{t_1} \frac{e^{-\frac{(x-\mu )^2}{2 \sigma ^2}}}{\sigma \sqrt{2 \pi }} e^{\gamma x^\beta } dx \right\} dt\right. \nonumber \\&\quad \left. {}-C_2D_0\left\{ \int _{t_1}^{T} \left[ \int _{t_1}^{t} \frac{e^{-\frac{(x-\mu )^2}{2 \sigma ^2}}}{\sigma \sqrt{2 \pi }} \left[ \frac{1}{[1+\delta (T-x)]}\right] dx\right] dt\right\} - A\right. \nonumber \\&\quad \left. {}-\int _{t_1}^{T} \frac{e^{-\frac{(x-\mu )^2}{2 \sigma ^2}}}{\sigma \sqrt{2 \pi }} \left[ \frac{C D_0 }{[1+\delta (T-x)] }\right] dx -R \,\,D_0 \int _{t_1}^{T} \frac{e^{-\frac{(x-\mu )^2}{2 \sigma ^2}}}{\sigma \sqrt{2 \pi }} \left[ \frac{\delta (T-x)}{[1+\delta (T-x)] }\right] dx\right) . \end{aligned}$$

(17)

3 Genetic Algorithm

Genetic algorithm (GA) is an optimization technique, which achieves better optimization of the problem through random search. It is a population-based random search algorithm. Holland (1992) was the main founder of GA. Initially, he introduced this for solving the problems of natural system. Later, it has been widely applied by several researchers for solving their optimization problems. During those days, his Schema theorem was gained much attention by several researchers.

At initial stage, the research work about GA was found in proceedings of international conferences. It is a biologically inspired search and stochastic algorithm which works using genetic operators Deb (2005), namely reproduction/selection, crossover and mutation. Mainly, it is inspired by Darwin’s theory of evolution which is one of the competitive intelligent algorithms used for optimization. Its advantage is that researchers require minimum problem information about various parameters of GA. Its main parameters are population size N, crossover probability $P_{Cross}$ and mutation probability $P_{Mut}$. According to the initialization of population, there are two types of GA, binary coded (BCGA) and real coded (RCGA). If initial population is generated using binary number, then the resultant GA is called as BCGA; otherwise, it is called as RCGA.

It always deals with the coding of the problem, and it requires only information about objective functions for computing fitness function. In single objective optimization problem, fitness function is nothing but simply the value of objective function. But in case of multi-objective optimization problems, it is a suitably well-defined function by considering all objectives. The solutions obtained from GA are always efficient and robust since it works with a set of feasible points instead of single point in the search space. Generally, multi-objective optimization problems are handled by two different techniques. One is to concatenate all the objectives to get the single objective with feasible constraints. The second one is to determine the Pareto optimal solution set. Pareto optimal solutions are the non-dominated solutions. Generally, if solution of the problem is strictly better than at least in one objective function, then it is considered as a non-dominated solution.

Several researchers contributed for the development of GAs like Latpate and Kurade (2017) formulated a fuzzy multiple objective genetic algorithm (fuzzy–MOGA). The performance of this algorithm was analyzed using hypothetical case study for a SC network. In this network, a manufacturing company having multiple plants in different geographical regions was assumed. It consists of five raw material suppliers and four manufacturing plants which produce single type of product, for distributing six warehouses and eight retailers. Pareto decision space for various uncertainty levels in demand and cost parameters was provided. Later, Latpate and Kurade (2020) developed new fuzzy non-dominated sorting GA (fuzzy–NSGA II) for optimizing crude oil SC of India. The formulated transportation model was suitable for deciding optimum routes and modes of shipping. The hybridization of ant colony optimization (ACO) and GA was proposed by Maiti (2020). In this hybridization, the initial population of candidate solutions was generated by ACO. Efficiency of the algorithm was tested for different test functions. Maity et al. (2017) used MOGA for solving their proposed multi−item inventory model in which demand was stock dependent. GA has a major drawback like it requires more computational complexity and its convergence performance. For convergence, it requires more simulation runs. To overcome this, a compound mutation strategy in intelligent bionic genetic algorithm (IB−GA) and multi-stage composite genetic algorithm (MSC−GA) was proposed by Li et al. (2011). The latter one has better convergence with high accuracy. Using Markov chain theory, they studied the global convergence under the elitist preserving strategy.

Here, we have proposed binary coded GA (BCGA) for solving the formulated probabilistic EOQ inventory models with roulette wheel selection, single-point crossover and bitwise mutation for development of solution methodology; see Algorithm 1.

Genetic Operators

• (1) Roulette wheel selection: There are various types of selection techniques like roulette wheel selection, tournament selection, crowded tournament selection, etc. The roulette wheel selection obtains duplicate copies of best chromosomes and eliminates worst from the population, keeping its size fixed. In the proposed BCGA, initial population is randomly generated from a continuous uniform distribution. Each randomly generated individual chromosome in the initial population is a candidate solution to the problem. In this selection mechanism, chromosomes are assigned a probability of being selected, based on their fitness values.

• (2) Single-point crossover: It is used for exchanging information between randomly selected parent chromosomes by recombining parts of their genetic materials. This operation performed probabilistically combines parts of two parent chromosomes to generate offspring. Its step-by-step procedure is explained below:

  • (a) It works using crossover probability say $P_{cross}$. Thus, only ($M\cdot P_{cross}$) chromosomes in the population go for crossover where $M$ is the population size.

  • (b) Randomly select any two parent chromosomes from the population of mating pool. It is generated, when a selection operator is applied on the population. Mating pool has size $M$. Let $X_{1}=\{X_{11},X_{12},\cdots ,X_{1(k-1)},X_{1k},X_{1(k+1)},\cdots ,X_{1N}\}$ and $X_{2}=\{X_{21},X_{22},\cdots ,X_{2(k-1)},X_{2k},X_{2(k+1)},\cdots ,X_{2N}\}$ be the two parent chromosomes selected for crossover operation.

  • (c) Draw a random number in continuous uniform distribution from $1$ to $N$, i.e., $U(1, N)$. Let it be $k\in [1, N]$.

  • (d) Then, the resulting offspring becomes $X_{1}^{}{'}=\{X_{11},X_{12},\cdots ,X_{1(k-1)},X_{2k},X_{2(k+1)},\cdots ,X_{2N}\}$ and $X_{2}^{}{'}=\{X_{21},X_{22},\cdots ,X_{2(k-1)},X_{1k},X_{1(k+1)},\cdots ,X_{1N}\}$.

• (3) Bitwise mutation: It is applied to forbid the premature convergence, and it has the ability to explore the new solution space. Mutation is the process in which the genetic structure of a chromosome is randomly altered. It leads to genetic diversity in a population. It is a step-by-step working procedure explained below.

  • (a) It works using mutation probability say $P_{mut}$. Thus, only ($M\cdot P_{mut}$) genes in the population go for mutation.

  • (b) Draw a random number from continuous uniform distribution, i.e., $j\in [1, M]$.

  • (c) Let a chromosome $X_{j}=\{X_{j1},X_{j2},\cdots ,X_{j(k-1)},X_{jk},X_{j(k+1)},\cdots ,X_{jN}\}$ of length $N$ be randomly selected for mutation.

  • (d) Again draw two points from continuous uniform distribution, i.e., $r_1, r_2\in [1, N]$.

  • (e) Let $r_1=1$ and $r_2=k$. Then, 1st and kth genes are selected for the mutation, i.e., $X_{j1}$ and $X_{jk}$.

  • (f) Let $X_{j1}=1$ and $X_{jk}=0$, then the new chromosome becomes

    $X_{j}^{}{'}=\{X_{j1}^{}{'},X_{j2},\ldots ,X_{j(k-1)},X_{jk}^{}{'},X_{j(k+1)},\ldots ,X_{jN}\}$ where $X_{j1}^{}{'}=0$ and $X_{jk}^{}{'}=1$.

4 Numerical Example

The SC described in earlier section is demonstrated using a hypothetical example. Let demand per unit time follow uniform distribution, i.e., $f(t)\sim U(a=0, b=1)$, and normal distribution, i.e., $f(t)\sim N(\mu =1, \sigma ^2=0.04)$. Other parameter values for the model are: $D_0 = 100$, $A = 10$, $r = 0.15$, $C = 3$, $S = 10$, $\beta =1.5$ and $\delta =2$. We have used GA with roulette wheel selection, single-point crossover, bitwise mutation, number of iterations 100, crossover probability 0.8, mutation probability 0.2, string length 40 and population size 20. Our aim is to determine the values of $t_1$ and T which maximize $P(T,\ t_1)$. Using Algorithm 1, EOQ (Q) and profit (P) are evaluated by using Eqs. 16 and 17. The effect of parameter $\gamma$ with respect to carrying charge (r) is shown in Tables 1 and 2.

Table 1 Optimum solutions for uniform distributed demand

Table 2 Optimum solutions for normal distributed demand

From Table 1, we conclude that as r increases with fixed $\gamma$ the optimum profit and EOQ both decrease for uniform distributed demand. Similar results are seen for normal distributed demand; see Table 2. Also, as $\gamma$ increases with fixed r, EOQ and optimum profit both decrease. From Tables 1 and 2, we see that the profit in uniform distribution is more than normal distribution. The codes are written by R software and run on i3–3110M, CPU @ 2.40 GHz and 4 GB RAM.

5 Sensitivity Analysis

The effect of various parameters, viz., total order quantity $D_0$, order cost A, per unit purchase cost C and selling cost S on the optimality of solution, is studied through the sensitivity analysis. For fixed $\gamma =0.2$ and $\beta =1.5$, the effect of $50\%$ over- and under-estimation of these parameters on EOQ (Q) and optimum profit (P) has been examined. That means the sensitivity analysis is performed by changing each of the parameters by ${-}50\%$, ${-}30\%$, ${+}20\%$ and ${+}50\%$ taking one parameter at a time and keeping the remaining parameters unchanged. The obtained results for uniform and normal distributed demand rate are shown in Table 3.

Table 3 Effect of changes in the parameters of the probabilistic demand inventory model

On the basis of the results of Table 3, the following observation can be made:

• (1) All parameters except order cost effects equally on P.

• (2) Total demand during the scheduling period, purchase cost and selling cost for uniform distribution effects mostly on P.

• (3) Order cost has low effect on P for uniform distributed demand rate.

• (4) Effect of almost all parameters except order cost for normal distribution is much high.

• (5) The parameters except selling cost affects high on backlogging time for uniform distribution.

• (6) For normal distribution, all parameters have low effect on backlogging and cycle time.

6 Managerial Implications

According to the demand of deteriorated item, the manager of a company finds the suitable probability distribution for the deteriorated item. Also, by comparing various probability distributions manager can decide the unique probability distribution which maximizes the profit of a company. The proposed models help the manager to understand the uncertainty in the market. Also, these models can assist the manager in accurately determining the optimal order quantity and profit. Before applying the model and proposed algorithm, manager has to collect necessary information about SC of the company. Such types of probabilistic EOQ inventory models can be useful in manufacturing and distributing industries. Moreover, these models can be used in inventory control of certain deteriorating items such as food items, electronic components, fashionable commodities and others.

7 Conclusions

In this study, EOQ inventory models under probabilistic market demand for a multi-echelon SC have been proposed for items with Weibull distributed deterioration. In the developed EOQ inventory models, shortages were allowed and they were partial backlogged. The backlogging rate is a variable, and it depends on the length of time for the customer waits before receiving the item. Thus, it is considered as a decreasing exponential function of waiting time. In the literature, deterministic inventory models were developed by several researchers by assuming market demand of a deteriorating item depends on stock, on time, on replenishment, etc. But here, we have developed probabilistic EOQ inventory models, which can be helpful where demand of the deteriorating item is uncertain in nature. Also, we are providing a novel solution methodology for solving proposed inventory models using binary coded GA. This methodology can be helpful for solving deterministic as well as probabilistic inventory models.

In a future study, it is hoped to further incorporate the proposed model into more realistic assumptions, such as lead time as a decision variable and a finite rate of replenishment. Also, formulated models can be solved by using particle swarm optimization, ant colony optimization, etc.