The Relative (de-)Perfectoidification Functor and Motivic p-Adic Cohomologies

Abstract

We motivate the study of the categories of non-archimedean analytic motives with a survey on their different p-adic realizations, and we show that rigid analytic and perfectoid motives are equivalent over a base of characteristic p.

The author is partially supported by the Agence Nationale de la Recherche (ANR), projects ANR-14-CE25-0002 and ANR-18-CE40-0017

1 Introduction

The categories of (derived, abelian) motives arise naturally by imposing homotopy-invariance onto the (infinity) category of sheaves of $\Lambda$-vector spaces on the category of smooth spaces over a base S. Depending on the choice of the topology (typically: the Nisnevich topology or the étale topology), the choice of S (a scheme, a rigid analytic variety [1]...) the choice of the interval over which homotopies are defined (typically the affine line, but there are log-variants [2]) and the choice of the coefficient ring $\Lambda$ (which may even be omitted [3] or replaced with a ring spectrum [4]) such categories may enjoy different properties and may be useful for the inspection of the various invariants and constructions related to Weil cohomology theories such as periods, Chow groups, the six functor formalism, nearby cycles or even automorphic forms, etc.

The aim of this paper is to make a quick survey on some particular applications of the formalism of motives in the realm of p-adic Hodge theory. More specifically, we consider perfectoid ${\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}(S)={\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}(S,\mathbb {Q})$ and rigid analytic étale motives ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S)={\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S,\mathbb {Q})$. That is, we consider the homotopy invariant infinity-étale sheaves of $\mathbb {Q}$-vector spaces on smooth perfectoid resp. rigid analytic varieties over an adic space S, where homotopies are defined over the perfectoid (closed) ball resp. the rigid analytic (closed) ball.

In particular, we focus on the equivalence between the two categories introduced above:

$$\begin{aligned} {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S)\cong {\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}(S) \end{aligned}$$

($\clubsuit $)

that is shown in [5]. Such an equivalence can be considered as a method to “(de-)perfectoidify” functorially and canonically an adic space over a base, up to homotopy. We remark that whenever S is perfectoid, there is a canonical equivalence ${\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}(S)\cong {\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}(S^\flat )$ induced by the classic tilting functor of perfectoid spaces, which preserves homotopies and the étale sites. This leads to an equivalence

$$\begin{aligned} {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S)\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S^\flat ) \end{aligned}$$

($\spadesuit $)

that can be interpreted as a way to “(un-)tilt” canonically and functorially even rigid analytic spaces, up to homotopy. It is expected (see [5]) to give the following generalization of ($\spadesuit$) which should hold for an arbitrary adic space S over $\mathbb {Q}_p$, using the language of diamonds:

$$\begin{aligned} {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S)\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S^\diamond ). \end{aligned}$$

(♢)

In this paper, we give a full proof of ($\clubsuit$) in the case of a perfectoid base S in characteristic p, generalizing the statement of [6] that only deals with the case of a perfectoid field $S={{\,\mathrm{Spa}\,}}(K,K^\circ )$.

Moreover, we make a survey on how the language of motives can be used to define and prove some fundamental properties of de Rham-like p-adic cohomologies on adic spaces and algebraic variety in characteristic p (that is, Große-Klönne’s overconvergent de Rham cohomology, and Berthelot’s rigid cohomology). We then recall how to merge such constructions with the (un-)tilting and (de-)perfection procedures of ($\clubsuit$)-($\spadesuit$)-(♢) and obtain new de Rham like cohomology theories for perfectoid varieties and rigid spaces in positive characteristic. Finally, we cite further cohomology theories that have been introduced using rigid motives by other authors (such as Ayoub and Le Bras) and a Betti-like cohomology in the spirit of Berkovich. We insist on the fact that, in all these procedures, the role of homotopies is crucial, and that consequently, motivic categories provide a natural framework where such definitions and proofs can be made.

2 Definitions and Main Properties of Adic Motives

Once and for all, we fix a cardinal $\kappa$ and we consider only adic spaces that have a $\kappa$-small covering by affinoid subspaces. The categories of motives that we will introduce are easily seen not to depend on $\kappa$, but this choice allows one to prove that they are compactly generated, under suitable hypotheses (see [7, Proposition 2.4.20]).

Definition 2.1

Let K be a non-archimedean field, and S be a stably uniform adic space over it.

• (1) We let $\mathbb {B}^1_K$ be the rigid analytic variety ${{\,\mathrm{Spa}\,}}(K\langle T\rangle , \mathcal {O}_K\langle T\rangle )$ and $\mathbb {B}^1_S$ be the fiber product $S\times _K\mathbb {B}^1_K$, for any adic space S over K.

• (2) If K is perfectoid, we let $\widehat{\mathbb {B}}^1_K$ be the perfectoid space ${{\,\mathrm{Spa}\,}}(K\langle T^{1/p^{\infty }}\rangle , \mathcal {O}_K\langle T^{1/p^\infty }\rangle )$ and $\widehat{\mathbb {B}}^1_S$ be the fiber product $S\times _K\widehat{\mathbb {B}}^1_K$, for any perfectoid space S over K.

• (3) We also let $\mathbb {T}^1_S$ [resp. $\widehat{\mathbb {T}}^1_S$] be the rational open U(1/T) of $\mathbb {B}^1_K$ [resp. of $\widehat{\mathbb {B}}^1_K$].

• (4) We let ${{\,\mathrm{\mathrm{{RigSm}}}\,}}/S$ be the full subcategory of adic spaces over S whose objects are locally étale over a poly-disc $\mathbb {B}^N_S$ (in case S is a rigid analytic variety, this recovers the usual notion of smooth rigid analytic varieties over S) and equip it with the étale topology.

• (5) In case K is a perfectoid field and S is perfectoid, we also consider the full subcategory ${{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S$ of adic spaces over S whose objects are locally étale over the perfectoid poly-disc $\widehat{\mathbb {B}}^N_S$, and equip it with the étale topology.

Definition 2.2

Let K and S be as above, and $\Lambda$ be a (commutative, unital) $\mathbb {Q}$-algebra.

• (1) We let $\mathrm{{Sh}}_{{\acute{\text {e}}{\mathrm{{t}}}}}({{\,\mathrm{\mathrm{{RigSm}}}\,}}/S,\Lambda )$ [resp. $\mathrm{{Sh}}_{{\acute{\text {e}}{\mathrm{{t}}}}}({{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S,\Lambda )$] be the monoidal DG-category of complexes of étale sheaves of $\Lambda$-vector spaces on ${{\,\mathrm{\mathrm{{RigSm}}}\,}}/S$ [resp. ${{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S$].

• (2) We let $\mathrm {RigDA}^{{{\,\mathrm{eff}\,}}}_{{\acute{\text {e}}{\mathrm{{t}}}},\mathbb {B}^1}(S,\Lambda )$ (or ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S)$ for short) be the monoidal DG-subcategory of $\mathrm{{Sh}}_{{\acute{\text {e}}{\mathrm{{t}}}}}({{\,\mathrm{\mathrm{{RigSm}}}\,}}/S,\Lambda )$ spanned by those objects $\mathcal {F}$ that are $\mathbb {B}^1$-local, meaning that the natural map $\mathcal {F}(\mathbb {B}^1_X)\rightarrow \mathcal {F}(X)$ is an equivalence, for all $X\in {{\,\mathrm{\mathrm{{RigSm}}}\,}}/S$. We recall that there is a left adjoint $\mathrm{{Sh}}_{{\acute{\text {e}}{\mathrm{{t}}}}}({{\,\mathrm{\mathrm{{RigSm}}}\,}}/S,\Lambda )\rightarrow {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S)$ to the natural inclusion.

• (3) Similarly, we let $\mathrm {PerfDA}^{{{\,\mathrm{eff}\,}}}_{{\acute{\text {e}}{\mathrm{{t}}}},\widehat{\mathbb {B}}^1}(S,\Lambda )$ (or ${\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(S)$ for short) be the DG-subcategory of $\mathrm{{Sh}}_{{\acute{\text {e}}{\mathrm{{t}}}}}({{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S,\Lambda )$ spanned by those objects $\mathcal {F}$ that are $\widehat{\mathbb {B}}^1$-local.

• (4) We will use the same notation ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S)$, ${\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(S)$ for the associated monoidal stable infinity-categories.

We remark that Yoneda defines a functor

$$h:{{\,\mathrm{\mathrm{{RigSm}}}\,}}/S\rightarrow {{\,\mathrm{{Psh}}\,}}({{\,\mathrm{\mathrm{{RigSm}}}\,}}/S)\rightarrow {{\,\mathrm{{Psh}}\,}}({{\,\mathrm{\mathrm{{RigSm}}}\,}}/S,\Lambda )\rightarrow {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S)$$

and for any X we will let $\Lambda _S(X)$ be the image of X under h. We use the same notation for perfectoid spaces and ${\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(S)$.

Definition 2.3

We let K, S and $\Lambda$ be as above.

• (1) We let $T_S$ be the quotient of the split inclusion $\Lambda _S(S)\rightarrow \Lambda _S(\mathbb {T}^1)$ given by the unit.

• (2) Similarly, if S is perfectoid, we define an object $\widehat{T}_S$ in ${\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(S)$ as the quotient of the split inclusion $\Lambda _S(S)\rightarrow \Lambda _S(\widehat{\mathbb {T}}^1)$ given by the unit.

• (3) We introduce ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S)$ and ${\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}(S)$ as the targets of the universal left adjoint DG-functors

  $$ {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S)\rightarrow {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S)\quad {\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(S)\rightarrow {\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}(S) $$

  to DG-categories in which the endofunctor $-\otimes T_S$ [resp. $-\otimes \widehat{T}_S$] becomes invertible. They are endowed with a monoidal structure for which the functors above are monoidal.

• (4) We use the notation ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S)$ and ${\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}(S)$ also for the associated monoidal stable infinity-categories.

• (5) When we write ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(S)$ we mean that one can consider either the category ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S)$ (${{\,\mathrm{eff}\,}}$ standing for effective motives) or the category ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S)$, and similarly for ${\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{({{\,\mathrm{eff}\,}})}(S)$.

All in all, in the category ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S)$ one can find objects of the form $\Lambda _S(X)$ where X is any smooth rigid analytic variety over S coming from the Yoneda functor, as well as any complex of sheaves $\Omega$ that represents a Weil cohomology theory (with $\Lambda$-coefficients, in our situation). The homology of the mapping complexes ${{\,\mathrm{Map}\,}}(\Lambda _S(X),\Omega )$ coincide with the cohomology theory associated to $\Omega$. Almost by construction, we point out that the objects $\Lambda _S(X)$ are isomorphic to $\Lambda _S(\mathbb {B}^1_X)$ and coincide with the homotopy colimit of any diagram of the form $\Lambda _S(U^\bullet )$ with $U^\bullet$ being an étale hypercover of X. This translates in terms of cohomology theories into $\mathbb {B}^1$-invariance, and the existence of some exact sequences à la Mayer-Vietoris.

By means of the six-functor formalism (see [8]) it is possible to define motives $\Lambda _S(X)$ attached to any rigid analytic variety X over S (not necessarily smooth). In particular, the definition of a well-behaved cohomology theory on smooth varieties extends automatically to all varieties.

It is also possible to consider (co-)homology theories which are equipped with a richer structure than the one of a mere $\Lambda$-module: as soon as one has a functor $H:{{\,\mathrm{\mathrm{{RigSm}}}\,}}/S\rightarrow \mathbf {C}$ with $\mathbf {C}$ being a $\Lambda$-linear DG-category such that H satisfies étale descent and is homotopy invariant [and for which the Tate twist is invertible] then by construction one can (Kan) extend it to motives

obtaining a so-called realization functor $\mathcal {R}_H$. In Sect. 5 we will try to convince the reader that it is sometimes easier to define a motivic realization $\mathcal {R}_H$ and hence deduce an interesting (co-)homology theory H on ${{\,\mathrm{\mathrm{{RigSm}}}\,}}/S$.

Remark 2.4

One is free to replace the sites, the interval objects, and the rings of coefficients with any other choice and define corresponding categories of motives. Classically, the categories of étale motives over a scheme S are denoted by ${{\,\mathrm{{DA}}\,}}^{({{\,\mathrm{eff}\,}})}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S,\Lambda )$ (here, ${{\,\mathrm{{DA}}\,}}^{({{\,\mathrm{eff}\,}})}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S)$ for short). One may also consider non-commutative variants where the category of $\Lambda$-modules is replaced by the infinity-category of spectra, or the category of modules of any commutative ring spectrum.

Remark 2.5

For the categories of algebraic motives ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S)$ the realizations functors induced by Betti, de Rham and $\ell$-adic cohomologies have been widely studied in different articles: see [9,10,11].

Rather than making a full recollection of all the formal properties of motives and their variants, for which there are already staple references such as [9, 10, 12, 13], we focus on two peculiar properties of the categories of rigid motives which are proved in [7].

The first property is the so-called (effective) semi-separatedness.

Theorem 2.6

([7, Corollary 2.9.10]) Let $S'\rightarrow S$ be a universal homeomorphism. The base change functor induces an equivalence of categories

$$ {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(S)\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(S') $$

Remark 2.7

As noted in [7], the effective part of the statement is not known for the usual algebraic motives ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S)$.

Corollary 2.8

Let $X'\rightarrow X$ be a universal homeomorphism between smooth rigid analytic varieties over a base S. The induced map of motives $\Lambda _S(X')\rightarrow \Lambda _S(X)$ is invertible in ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(S)$.

Proof

The motive $\Lambda (X)$ is the image of $\Lambda _X(X)=\Lambda$ under the functor $p_\sharp$ which is the left adjoint to the functor ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S)\rightarrow {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(X)$ induced by the pullback $p^*$ along the map $p:X\rightarrow S$. By the previous theorem, we deduce $p_\sharp \Lambda _X(X)\cong p'_\sharp \Lambda _{X'}(X')$ as wanted. $\square$

The second property is referred to as “continuity” in [7].

Theorem 2.9

([7, Theorem 2.8.14]) Let $\{S_i\}$ be a cofiltered system of stably uniform adic spaces over a non-archimedean field K with qcqs transition maps and let S be a uniform adic space such that $S\sim \varprojlim S_i$ in the sense of Huber [14, (2.4.1)]. Then the base change functors induce an equivalence of categories

$$ {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(S)\cong \varinjlim {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(S_i) $$

where the homotopy colimit is computed in the category of presentable infinity-categories, and colimit-preserving functors.

Remark 2.10

The analogous statement for algebraic motives also holds: in case S is the limit of a diagram of schemes $\{S_i\}$ with affine transition maps, then ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(S)\cong \varinjlim {{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^ {({{\,\mathrm{eff}\,}})}(S_i)$. However, the proof of the analytic version is much more involved, and uses homotopies in a crucial way: this is related to the fact that (in case all spaces $S, S_i$ are affinoid) the ring $\varinjlim \mathcal {O}(S_i)$ does not coincide with $\mathcal {O}(S)$, but it is only dense in it. In particular, the “continuity” statement for étale sheaves (on the big sites), before performing the $\mathbb {B}^1$-localization, is false.

A special case of continuity gives the following computation of “stalks” for ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(-)$.

Corollary 2.11

Let $s={{\,\mathrm{Spa}\,}}(C,C^+)\rightarrow S$ be an étale point of a stably uniform adic space S. Let $U\rightarrow S$ vary among étale neighborhoods of s in S. The base-change functors induce an equivalence in the category of presentable infinity-categories and colimit-preserving functors:

$$ {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}({{\,\mathrm{Spa}\,}}(C,C^+))\cong \varinjlim _\mathrm{s\in U\rightarrow S}{\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(U). $$

3 De-Perfectoidification

The aim of this section is to prove the following.

Theorem 3.1

Let S be a rigid space over a non-archimedean field K of characteristic p. Then the base change along $S^{{{\,\mathrm{Perf}\,}}}\rightarrow S$ and the relative perfection functor define equivalences:

$${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(\mathrm{{S}})\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(\mathrm{{S}}^{{{\,\mathrm{Perf}\,}}})\cong {\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{({{\,\mathrm{eff}\,}})}(\mathrm{{S}}^{{{\,\mathrm{Perf}\,}}}).$$

The first half of the statement follows from the “separatedness” and the “continuity” properties of ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}$.

Proposition 3.2

Let S be a rigid space over a non-archimedean field K of characteristic p. Then the base change along $S^{{{\,\mathrm{Perf}\,}}}\rightarrow S$ defines an equivalence:

$${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(S)\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(S^{{{\,\mathrm{Perf}\,}}}).$$

Proof

The space $S^{{{\,\mathrm{Perf}\,}}}$ is a weak projective limit of the diagram $\cdots \rightarrow S{\mathop {\rightarrow }\limits ^{\varphi }} S{\mathop {\rightarrow }\limits ^{\varphi }}S$ with $\varphi$ being the Frobenius. We note that by Theorem 2.6 the motivic functor $\varphi ^*$ is an equivalence, and the claim then follows from Theorem 2.9. $\square$

We now move to the second part of the statement. From now on, we will therefore assume that $S=S^{{{\,\mathrm{Perf}\,}}}$ is a perfectoid space of characteristic $p>0$. The second half is a refinement of [6, Theorem 6.9] in two different directions: on the one hand we get rid of the Frob$\acute{\mathrm{e}}$t-localization (or, equivalently, of correspondences see [15]) proving an effective claim that holds for ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}$; on the other hand, we promote the equivalence from the case of a base field of height one ${{\,\mathrm{Spa}\,}}(K^\flat ,K^{\flat \circ })$ to a general (perfectoid) base S.

It is worth noting that, because of the computation of stalks for ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(-)$ (which can be generalized easily to ${\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{({{\,\mathrm{eff}\,}})}(-)$) the missing crucial case is the one of a base $S={{\,\mathrm{Spa}\,}}(C,C^+)$ which is a complete algebraically closed valued field, with a valuation of height $n\in \mathbb {N}_{\ge 2}$. As this case is not essentially easier than the one of a general base S we do not restrict to this case in what follows.

In order to extend the result of [6], we follow the blueprint given by the proof of loc. cit., and we simplify it at the same time. We try to highlight here the main differences with respect to the original approach. We first introduce some notation.

Definition 3.3

Let $\mathcal {F}$ be in ${{\,\mathrm{{Psh}}\,}}({{\,\mathrm{\mathrm{{RigSm}}}\,}}/S,\Lambda )$.

• (1) We let $\mathbb {L}_\varphi \mathcal {F}$ be the presheaf $X\mapsto \varinjlim _n\mathcal {F}(X^{(p^{-n})})$ where we let $X^{(p^{-n})}$ be $X\times _{S,\varphi ^{-n}}S$ and $X^{(p^{-n-1})}\rightarrow X^{(p^{-n})}$ be the map induced by Frobenius.

• (2) We let $\mathbb {L}_{\mathbb {B}^1}\mathcal {F}$ be the normalized complex associated to the cubical presheaf of complexes of abelian groups $\underline{{\text {Hom}}}(\mathbb {B}^{\bullet },\mathcal {F})$ where $\underline{{\text {Hom}}}(\mathbb {B}^r,\mathcal {F})(-)= \mathcal {F}((-)$ $\langle u_1,\ldots , u_r\rangle )$.

Proposition 3.4

Let $\mathcal {F}$ be in ${{\,\mathrm{{Psh}}\,}}({{\,\mathrm{\mathrm{{RigSm}}}\,}}/S,\Lambda )$. The natural map $\mathcal {F}\rightarrow \mathbb {L}_{\mathbb {B}^1}\mathbb {L}_\varphi \mathcal {F}$ is an equivalence in ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S,\Lambda )$.

Proof

It is well known that the maps $\mathcal {F}\rightarrow \mathbb {L}_{\mathbb {B}^1}\mathcal {F}$ are $\mathbb {B}^1$-equivalences, see [16]. By construction, the complex $\mathbb {L}_{\varphi }\mathcal {F}$ is local with respect to the relative Frobenius maps $\Lambda _S(X^{(p^{-1})})\rightarrow \Lambda _S(X)$ (we will refer to this property as “being ${{\,\mathrm{Frob}\,}}$-local”) and doesn’t alter those which are already ${{\,\mathrm{Frob}\,}}$-local. We deduce that the map $\mathcal {F}\rightarrow \mathbb {L}_{\varphi }\mathcal {F}$ is a ${{\,\mathrm{Frob}\,}}$-local equivalence, that is an equivalence with respect to the localization over relative Frobenius maps. In particular, the map of the statement is a $(\mathbb {B}^1,{{\,\mathrm{Frob}\,}})$-local equivalence hence a $(\mathbb {B}^1,{{\,\mathrm{Frob}\,}},{\acute{\text {e}}{\mathrm{{t}}}})$-local equivalence, but the latter are simply $(\mathbb {B}^1,{\acute{\text {e}}{\mathrm{{t}}}})$-local equivalences as shown in Corollary 2.8. $\square$

Proposition 3.5

Locally with respect to the analytic topology, any space $X\in {{\,\mathrm{\mathrm{{RigSm}}}\,}}/S$ [resp. ${{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S$] is given by ${{\,\mathrm{Spa}\,}}(R,R^+)$ with $(R,R^+)$ given by [the completed perfection of] the following adic pair

$$\begin{aligned} \left( \mathcal {O}(U)\langle \underline{x},\underline{y}\rangle /(P_1,\ldots ,P_m),\mathcal {O}(U)\langle \underline{x},\underline{y}\rangle /(P_1,\ldots ,P_m)^+\rangle \right) \end{aligned}$$

(⋆)

where $U\subset S$ is an affinoid subspace, $\underline{x}:=(x_1,\ldots ,x_n)$ is a n-tuple of variables with $n\in \mathbb {N}$, $\underline{y}:=(y_1,\ldots ,y_m)$ is a m-tuple of variables with $m\in \mathbb {N}$, and $\underline{P}:=(P_1,\ldots ,P_m)$ is a m-tuple of polynomials in $\mathcal {O}(U)[\underline{x},\underline{y}]$ such that $\det (\frac{\partial P_i}{\partial y_j})$ is invertible in $\mathcal {O}(U)\langle \underline{x},\underline{y}\rangle /(P_1,\ldots ,P_m)$.

Proof

Any étale space over the perfectoid relative poly-disc $\mathbb {B}^n_S\sim \varprojlim _{\varphi }\mathbb {B}^n_S$ is locally defined over $\mathbb {B}^n_S$ so the claim on ${{\,\mathrm{\mathrm{{RigSm}}}\,}}/S$, which follows from [14, Proposition 1.7.1(iii)] immediately implies the claim on ${{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S$. $\square$

Proposition 3.6

Let $X={{\,\mathrm{Spa}\,}}(R,R^+)$ and $X'={{\,\mathrm{Spa}\,}}(R',R'^+)$ be spaces in ${{\,\mathrm{\mathrm{{RigSm}}}\,}}/S$ of the form $(\star )$ and let $f:X'^{{{\,\mathrm{Perf}\,}}}\rightarrow X$ be a morphism. There exists a homotopy $H:X'^{{{\,\mathrm{Perf}\,}}}\times \widehat{\mathbb {B}}^1\rightarrow X$ such that $H_0=f$ and $H_1$ has a (unique) model $X'^{(p^{-n})}\rightarrow X$ for some $n\gg 0$.

Proof

We let $R'^+_n$ be the image in $\widehat{R}'^+:=\mathcal {O}^+(X'^{{{\,\mathrm{Perf}\,}}})$ of the injective map $\mathcal {O}^+(X'^{(p^{-n})})\rightarrow \mathcal {O}^+(X'^{{{\,\mathrm{Perf}\,}}})$ (we recall that $X'$ is reduced as it is smooth over the reduced space S which is perfectoid) and we remark that $\widehat{R}'^+$ is the $\pi$-adic completion of $R'^+_\infty :=\bigcup R'^+_n$. The morphism f is determined by some mapping $x_i\mapsto s_i\in \widehat{R}'^+$ and $y_j\mapsto t_j\in \widehat{R}'^+$. By means of [6, Corollary A.2] we may find a unique array of power series $F_1,\ldots ,F_m\in \widehat{R}'[\![\underline{\sigma }-\underline{s}]\!]$ such that $P(\sigma ,F(\sigma ))=0$, $F(\underline{s})=\underline{t}$. Moreover, they are in $\widehat{R}'^+[\![\pi ^{-N}(\underline{\sigma }-\underline{s})]\!]$ for a sufficiently big $N\gg 0$. For any $\tilde{\underline{s}}\in R'^+_\infty$ which is sufficiently close to $\underline{s}$ we may then define a homotopy H as the map determined by

$$ (\underline{x},\underline{y})\mapsto (\underline{s}+(\underline{s}-\tilde{\underline{s}})\cdot \tau , \underline{F}((\underline{s}-\tilde{\underline{s}})\cdot \tau )) $$

and remark that, by definition, we have $H_0=f$. In order to show that $H_1$ factors (uniquely, as the maps $R'_n\rightarrow \widehat{R}'$ are injective) over some $X'^{(p^{-n})}$, we are left to show that the elements $\tilde{\underline{t}}:=\underline{F}(\underline{s}-\tilde{\underline{s}})$ lie in $R'_\infty$.

Suppose without loss of generality that $\tilde{\underline{s}}$ lie in $R'=R'_{0}$. We consider the $R'$-algebra E defined as $E=R'\langle \underline{y}\rangle /(\underline{P}(\tilde{\underline{s}},\underline{y}))$ which is étale over $R'$, and over which the map $R' \rightarrow \widehat{R}'$ factors. In particular, the étale morphism ${{\,\mathrm{Spa}\,}}( E,E^+)\times _{X'}X'^{{{\,\mathrm{Perf}\,}}}\rightarrow X'^{{{\,\mathrm{Perf}\,}}}$ splits. In light of the equivalence between the étale topos of $X'^{{{\,\mathrm{Perf}\,}}}$ and $X_0$ we conclude that ${{{\,\mathrm{Spa}\,}}( E,E^+)}\rightarrow X'$ splits proving that $\tilde{t}$ is a m-tuple in $R'_0$ as wanted. $\square$

Proposition 3.7

Let $X={{\,\mathrm{Spa}\,}}(R,R^+)$ and $X'={{\,\mathrm{Spa}\,}}(R',R'^+)$ be spaces in ${{\,\mathrm{\mathrm{{RigSm}}}\,}}/S$ of the form $(\star )$. The canonical map

$$ (\mathbb {L}_{\mathbb {B}^1}\mathbb {L}_\varphi \Lambda (X))(X')\rightarrow ( \mathbb {L}_{\mathbb {B}^1}\mathbb {L}_\varphi {{\,\mathrm{Perf}\,}}_*{{\,\mathrm{Perf}\,}}^*\Lambda (X))(X') $$

is a quasi-isomorphism.

Proof

By direct inspection, we may rewrite the two complexes above as follows:

$$ \varinjlim _{n} N\Lambda ((X'\times \mathbb {B}^\bullet )^{(p^{-n})},X)\rightarrow N\Lambda (X'^{{{\,\mathrm{Perf}\,}}}\times \widehat{\mathbb {B}}^\bullet ,X) $$

with N denoting the normalized complex associated to the cubical complex of abelian groups. The claim then follows from (the proof of) Proposition 3.6 by arguing as in [6, Proposition 4.2]. $\square$

Proof of Theorem 3.1

The effective part of the theorem easily implies the stable version, so we stick to it for simplicity. By means of Proposition 3.5 and the equivalence fo the étale site of $X^{{{\,\mathrm{Perf}\,}}}$ and of X we see that ${{\,\mathrm{Perf}\,}}^*$ sends a class of compact generators to a class of compact generators, and that ${{\,\mathrm{Perf}\,}}_*$ commutes with ${\acute{\text {e}}{\mathrm{{t}}}}$-sheafification, preserving then the ${\acute{\text {e}}{\mathrm{{t}}}}$-local equivalences. The multiplication $\mu$ on $\widehat{\mathbb {B}}^1$ defines a morphism

$$ {{\,\mathrm{Perf}\,}}^*({{\,\mathrm{Perf}\,}}_*\Lambda _S(\widehat{\mathbb {B}}^1_X)\otimes \Lambda _S({\mathbb {B}}^1_S))\cong {{\,\mathrm{Perf}\,}}^*{{\,\mathrm{Perf}\,}}_*\Lambda _S(\widehat{\mathbb {B}}^1_X)\otimes \Lambda _S(\widehat{\mathbb {B}}^1_S)\rightarrow \Lambda _S(\widehat{\mathbb {B}}^1_X)\otimes \widehat{\mathbb {B}}^1_S{\mathop {\rightarrow }\limits ^{\mu }}\Lambda _S(\widehat{\mathbb {B}}^1_X) $$

which induces a homotopy between the identity and the zero-map on ${{\,\mathrm{Perf}\,}}_*(\Lambda (\widehat{\mathbb {B}}^1_X))$, showing that ${{\,\mathrm{Perf}\,}}_*$ sends $\widehat{\mathbb {B}}^1$-local equivalences to $\mathbb {B}^1$-local equivalences.

We deduce that in order to prove the claim, it suffices to show that $\mathcal {F}\rightarrow {{\,\mathrm{Perf}\,}}_*{{\,\mathrm{Perf}\,}}^*\mathcal {F}$ is a $(\mathbb {B}^1,{\acute{\text {e}}{\mathrm{{t}}}})$-local equivalence for any $\mathcal {F}$ and we may actually restrict to the case where $\mathcal {F}$ is $\Lambda _S(X)$ with X as in $(\star )$ as such motives are a class of compact generators (by Proposition 3.5). Using Proposition 3.4 we may alternatively prove that $\mathbb {L}_{\mathbb {B}^1}\mathbb {L}_\varphi \Lambda _S(X)\rightarrow \mathbb {L}_{\mathbb {B}^1}\mathbb {L}_\varphi {{\,\mathrm{Perf}\,}}_*{{\,\mathrm{Perf}\,}}^*\Lambda _S(X)$ is a weak-equivalence, and this follows from Proposition 3.7. $\square$

When trying to generalize the second half of Theorem 3.1 to the case of a perfectoid S in characteristic 0, one is immediately stopped by the lack of a canonical map ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(S)\rightarrow {\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}(S)$ which is as “geometric” as the one given by the perfection in positive characteristic. As in [6] we now give an alternative route to constructing such a map, in a compatible way with the characteristic p case.

Definition 3.8

We let $s{{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S$ be the full subcategory of ${{\,\mathrm{Rig}\,}}/S$ whose objects are spaces X that are locally étale over $\mathbb {B}^N_S\times _S\widehat{\mathbb {B}}^M_S$ for some $M,N\in \mathbb {N}$. This category obviously contains ${{\,\mathrm{Sm}\,}}/S$ (by taking $M=0$) and ${{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S$ (by taking $N=0$). We let $s{\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(S)$ be the category of $\widehat{\mathbb {B}}^1$-invariant étale (hyper)sheaves on $s{{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S$ with values in $\Lambda$-modules. The continuous inclusions $\alpha :{{\,\mathrm{Sm}\,}}/S\rightarrow s{{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S$ and $\beta :{{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S\rightarrow s{{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S$ induce adjoint pairs

$$ \alpha ^*\negmedspace : {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S)\rightleftarrows s{\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(S):\negmedspace \alpha _* $$

and

$$ \beta ^*\negmedspace : {\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(S)\rightleftarrows s{\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(S):\negmedspace \beta _*. $$

In particular, there is a functor $\beta _*\alpha ^*:{\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S)\rightarrow {\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(S)$.

We remark that the functor above is the same as the one of Theorem 3.1 in case ${{\,\mathrm{char}\,}}S=p$. Indeed, under this hypothesis, we may consider the relative perfection functor also at the level of semi-perfectoid spaces $s{{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S\rightarrow {{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S$, $X\mapsto X^{{{\,\mathrm{Perf}\,}}}$. It induces an adjoint pair

$$ {{\,\mathrm{Perf}\,}}'^*\negmedspace : {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(S)\rightleftarrows s{\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(S):\negmedspace {{\,\mathrm{Perf}\,}}'_* $$

and we note that the functor ${{\,\mathrm{Perf}\,}}^*$ is nothing more than the composition ${{\,\mathrm{Perf}\,}}'^*\alpha ^*$. Our claim then follows from the following:

Proposition 3.9

Suppose that S has characteristic p. The functor $\beta ^*$ is a left adjoint to ${{\,\mathrm{Perf}\,}}'^*$. In particular, $\beta _*\alpha ^*\cong {{\,\mathrm{Perf}\,}}^*$.

Proof

We remark that $\beta :{{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S\rightarrow s{{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S$ is a left adjoint to ${{\,\mathrm{Perf}\,}}':s{{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S\rightarrow {{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S$. By the Yoneda lemma, we deduce that they extend to an adjoint pair

$$\beta ^*,:{{\,\mathrm{{Psh}}\,}}({{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S,\Lambda )\rightleftarrows {{\,\mathrm{{Psh}}\,}}(s{{\,\mathrm{\mathrm{{PerfSm}}}\,}}/S,\Lambda ):{{\,\mathrm{Perf}\,}}'^*$$

between the (infinity) categories of (complexes of) presheaves. Both functors preserve étale (hyper)covers, fiber products and the object $\widehat{\mathbb {B}}^1_S$ so they both preserve $({\acute{\text {e}}{\mathrm{{t}}}},\widehat{\mathbb {B}}^1_S)$-equivalences. As ${{\,\mathrm{Perf}\,}}'^*$ has a left adjoint that preserves these equivalences, we deduce that it also preserves $({\acute{\text {e}}{\mathrm{{t}}}},\widehat{\mathbb {B}}^1_S)$-local objects. We then conclude that the adjunction $(\beta ^*,{{\,\mathrm{Perf}\,}}'^*)$ extends to an adjunction on the motivic categories, as wanted. $\square$

It is a non-trivial endeavor to prove the following generalization of Theorem 3.1 whose proof we won’t comment here.

Theorem 3.10

([5]) Let S be a perfectoid space over some field. The functor $\beta _*\alpha ^*$ defines an equivalence ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(S)\cong {\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{({{\,\mathrm{eff}\,}})}(S)$.

By putting together Theorem 3.1 and the previous result, we obtain the following:

Corollary 3.11

Let S be a perfectoid space. There is an equivalence ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(S)\cong {\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{({{\,\mathrm{eff}\,}})}(S)\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(S^\flat )$.

Proof

The tilting equivalence translates motivically into an equivalence ${\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{({{\,\mathrm{eff}\,}})}(S)\cong {\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{({{\,\mathrm{eff}\,}})}(S^\flat )$. The equivalence of the statement is then obtained by putting together Theorems 3.1 and 3.10. $\square$

4 Classic De Rham-Like Cohomologies via Motives

In this section, we make a survey on the “classic” de Rham-like cohomology theories for rigid analytic varieties and perfectoid spaces, revisited in the language of motives, based on [17] and [18] which is further expanded by [5].

Remark 4.1

Though we won’t comment on them in the present article, also $\ell$-adic realizations for analytic motives have been defined in [19] and [7, Sect. 2.10].

We start by a recollection of standard facts on the rigid and the overconvergent de Rham cohomologies, that will be necessarily imprecise and incomplete. All the details can be found in [20,21,22,23].

Let’s fix a field k of characteristic $p>0$ that we will assume to be perfect (for simplicity). The approach of Berthelot [24] and Monsky-Washnitzer [25] for the definition of a de Rham-like p-adic cohomology for varieties over k can be summarized (somehow a posteriori, following Große-Klönne) as follows: a smooth variety $\bar{X}$ over k can be lifted locally as a smooth variety $\mathcal {X}$ over W(k) (the DVR given by the Witt ring). The choice of such lifts is unique, étale-locally on the special fiber, “up to homotopy”, and even canonical “up to automorphisms” if we consider smooth formal lifts $\mathfrak {X}$ over W(k). A precise statement can be found in [26, Théorèmes 2.2.2, 3.3.2]. It is therefore possible, “somehow canonically” to associate locally a smooth rigid analytic variety (the generic fiber X of $\mathfrak {X}$) to the smooth variety $\bar{X}$.

This way, we have changed the base field: from k (of positive characteristic) to $K={{\,\mathrm{Frac}\,}}W(k)$ which has characteristic 0, but with a major drawback: we now have to consider rigid analytic varieties rather than algebraic varieties. Without further structure, a (non-proper) smooth rigid analytic variety doesn’t give rise to a well-behaved de Rham-like cohomology theory. One needs to do a choice of a “thickening” (what we will call an overconvergent structure following [27]) $X^\dagger :=(X\Subset X')$ of X into a strictly larger (i.e., containing the absolute compactification over K) smooth rigid analytic variety $X'$ and consider the subcomplex $\Omega _{X^\dagger /K}$ of $\Omega _{X/K}$ of those differential forms that extend to a strict neighborhood of X inside $X'$. Once again, such local choices are sufficiently canonical, “up to homotopy” (see [22]). It is therefore possible “somehow canonically” to associate locally to the smooth variety X a smooth overconvergent variety $X^\dagger$ and a de Rham-like complex $\Omega _{X^\dagger /K}$ which is used to define a cohomology theory for X, and a posteriori for $\bar{X}$ by combining the two procedures above. It is a non-trivial task to prove that these cohomology theories are well-defined and functorial, and enjoy the expected properties of a de Rham-like cohomology theory (for example, being finite dimensional on qcqs varieties): see [23, 28,29,30] etc.

We now give an alternative way to describe the above phenomena. Since the eventual aim is to define a Weil cohomology theory for varieties over k [resp. analytic varieties over K] it is quite natural to consider the motivic categories associated to these objects. As expected, they form a convenient setting where to state and study lifts and thickenings “up to homotopy”. We collect the principal motivic facts in the following statement.

Theorem 4.2

Let K be a complete non-archimedean field of characteristic 0 with valuation ring $\mathcal {O}_K$ and a perfect residue field k, and let $\Lambda$ be a $\mathbb {Q}$-subalgebra of K. We also let $\mathbb {B}^{1\dagger }_K$ be the overconvergent variety given by the strict embedding $\mathbb {B}^1_K\Subset \mathbb {P}^{1{{\,\mathrm{an}\,}}}_K$ and ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{\dagger ({{\,\mathrm{eff}\,}})}(K)$ be the (effective) DG-category of $\mathbb {B}^{1\dagger }$-invariant étale sheaves of $\Lambda$-vector spaces on smooth overconvergent varieties over K.

• (1) The complex of presheaves $\Omega ^\dagger :X^\dagger \mapsto \Omega _{X^\dagger /K}$ is a $(\mathbb {B}^{1\dagger },{\acute{\text {e}}{\mathrm{{t}}}})$-local object of ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{\dagger {{\,\mathrm{eff}\,}}}(K)$. In particular, for any overconvergent smooth rigid variety $X^\dagger$ one has

  $${{\,\mathrm{Map}\,}}(\Lambda _K(X^\dagger ),\Omega ^\dagger )\cong \Omega ^\dagger _{X^\dagger /K}.$$

• (2) The forgetful functor $l:X^\dagger =(X\Subset X')\mapsto X$ induces an equivalence of monoidal compactly generated stable infinity categories ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{\dagger ({{\,\mathrm{eff}\,}})}(K)$ $\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(K)$.

• (3) The analytification functor $\tilde{X}\mapsto \tilde{X}^{{{\,\mathrm{an}\,}}}$ induces a compact-preserving, colimit-preserving map of monoidal compactly generated stable infinity categories ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(K)\rightarrow {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(K)$.

• (4) The special fiber functor induces an equivalence of monoidal compactly generated stable infinity categories ${{\,\mathrm{{FDA}}\,}}^{({{\,\mathrm{eff}\,}})}_{{\acute{\text {e}}{\mathrm{{t}}}}}(\mathcal {O}_K)\cong {{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(k)$ where ${{\,\mathrm{{FDA}}\,}}^{({{\,\mathrm{eff}\,}})}_{{\acute{\text {e}}{\mathrm{{t}}}}}(\mathcal {O}_K)$ is the category of (effective, étale, with $\Lambda$-coefficients) motives of formal schemes over $\mathcal {O}_K$ (see [7, Remark 3.1.5(2)]).

• (5) The generic fiber functor induces a compact-preserving, colimit-preserving map of monoidal compactly generated stable infinity categories ${{\,\mathrm{{FDA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(\mathcal {O}_K)\rightarrow {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(K)$.

• (6) In particular, we obtain the following compact-preserving, colimit-preserving, monoidal functor:

  $$ {{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k)\cong {{\,\mathrm{{FDA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(\mathcal {O}_K)\rightarrow {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^\dagger (K) $$

  and a monoidal contravariant realization functor on the last category, with values in K-modules:

  $$ \mathcal {R}^\dagger _{dR}:{\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^\dagger (\mathrm{{K}})\rightarrow \mathrm{{D(K)}}^{{{\,\mathrm{{op}}\,}}} $$

  induced by $M\mapsto {{\,\mathrm{Map}\,}}(M,\Omega ^\dagger )$. The associated cohomology theory on ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k)$ coincides with Berthelot’s rigid cohomology $H_{{{\,\mathrm{rig}\,}}}^*$, the one on ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)$ coincides with Große-Klönne’s overcovergent de Rham cohomology $H_{{{\,\mathrm{dR}\,}}^\dagger }^*$ and the one on ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)$ (via analytification) coincides with the usual algebraic de Rham cohomology $H_{{{\,\mathrm{dR}\,}}}^*$.

• (7) In case K is perfectoid, for any fixed embedding $k\rightarrow K^\flat$ we can define, in light of $(\spadesuit )$ a functor

  $$ {{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k)\rightarrow {{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K^\flat )\rightarrow {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K^\flat )\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^\dagger (K). $$

  which is equivalent to the one in Point (6).

• (8) Compact motives of $\,{\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)$ are fully dualizable. In particular, the overconvergent de Rham cohomology is finite dimensional on any compact motive in ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)$ such as motives of smooth quasi-compact rigid varieties over K, or analytifications of quasi-projective (not necessarily smooth) varieties over K.

• (9) Compact motives of ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k)$ are fully dualizable. In particular, rigid cohomology is finite dimensional on any compact motive in ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k)$ such as motives of any quasi-projective (not necessarily smooth) variety $\bar{X}$ over k.

Proof

Points (1) and (6) are shown in [17, Proposition 5.12], point (2) is [17, Theorem 4.23] and point (4) is [1, Corollaire 1.4.29]. Point (7) is the content of [18]. The functors of points (3) and (5) are left adjoint functors, hence colimit-preserving. As they preserve direct products, they induce monoidal functors on motives. Moreover, they send affine smooth varieties to affinoid smooth varieties. Motives of such spaces are a class of compact generators (by [1, Proposition 1.2.34]) so the functors are also compact-preserving. The fact that compact motives in ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k)$ and ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)$ are dualizable follows from [31] and the same is true for ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)$ by [1, Théorème 2.5.35]. Points (8) and (9) then follows from the classic description of compact objects (perfect complexes) in D(K). $\square$

Remark 4.3

The content of Theorem 4.2(4) is the most precise way to state the following: it is possible to associate canonically a smooth rigid analytic motive over K to any variety $\bar{X}$ over k. Similarly, the content of Theorem 4.2(2) can be rephrased by saying that it is possible to associate canonically an overconvergent rigid analytic motive over to any rigid analytic variety X over K.

Remark 4.4

Let $\mathcal {X}$ be an algebraic variety over $\mathcal {O}_K$. The special fiber of its $\pi$-adic completion is just the special fiber $\mathcal {X}_k$ of $\mathcal {X}$. In light of Theorem 4.2(4) we conclude that cohomologically speaking, the act of $\pi$-adically completing $\mathcal {X}$ gives the same information as the act of taking its special fiber. More precisely: the following triangle commutes.

Remark 4.5

Following [32, Sects. 0.2–0.3] there are two possible ways to “analitify” a smooth algebraic variety $\mathcal {X}$ over $\mathcal {O}_K$: on the one hand one can consider the formal scheme given by its $\pi$-adic completion $\mathfrak {X}$ and then the generic fiber $\mathfrak {X}_\eta$ of it; on the other hand one can first take the generic fiber $\mathcal {X}_K$ (an algebraic variety over K) and then its analytification $\mathcal {X}_K^{{{\,\mathrm{an}\,}}}$. It is well-known (see [32, Proposition 0.3.5]) that the first rigid analytic space is canonically embedded as an open subvariety of the second, and that they coincide whenever $\mathcal {X}$ is smooth and proper (they differ in general: for example whenever $\mathcal {X}$ is lives on the generic fiber ${{\,\mathrm{Spec}\,}}K$ of ${{\,\mathrm{Spec}\,}}\mathcal {O}_K$, the first space is empty). It is easy to see that such functors preserve étale covers and homotopies, therefore defining the following (non-commutative) square of monoidal colimit-preserving maps:

where the natural transformation $\alpha$ is induced by the functorial open immersion $\mathfrak {X}_\eta \subset \mathcal {X}_K^{{{\,\mathrm{an}\,}}}$ and $\mathcal {R}_{dR}$ is the (overconvergent) de Rham realization. We then obtain two monoidal realizations . When applied to some motive $\Lambda _{\mathcal {O}_K}(\mathcal {X})$, one gives the rigid cohomology of the special fiber $\mathcal {X}_k$ and the other gives the de Rham cohomology of the generic fiber $\mathcal {X}_K$, respectively. Moreover, $\alpha$ defines a canonical natural transformation between the two which is invertible on the full monoidal subcategory with sums generated by (the motives of) smooth and proper varieties.

Remark 4.6

Even though the motivic categories are defined as sheaves on smooth varieties (or smooth formal schemes, or smooth rigid varieties etc.) it is possible to define motives attached to an arbitrary quasi-projective variety (or arbitrary rigid varieties) using the 6 functor formalism: the (homological) motive $\Lambda (X)$ attached to such a variety X is given by $f_!f^!\Lambda$ with $f:X\rightarrow {{\,\mathrm{Spa}\,}}K$ being the structural morphism. This formalism is fully developed in [8, 33] (in the algebraic case) and in [7] (in the analytic case).

5 New De Rham-Like Cohomologies via Motives

In this section, we make a survey on the “new” de Rham-like cohomology theories for rigid analytic varieties and perfectoid spaces whose construction is based on the properties of motivic categories.

We start by a de Rham cohomology for perfectoid spaces introduced in [17, 18, 34], which is further expanded by [5]. Simply by combining Theorems 3.1 and 4.2 we deduce the following.

Theorem 5.1

Let K be a perfectoid field.

• (1) Suppose that ${{\,\mathrm{char}\,}}K=0$. Let $\widehat{X}\sim \varprojlim X_h$ be a smooth perfectoid space obtained by relative perfection of an étale map $X_0\rightarrow \mathbb {B}^N_K$. For any i, the system $H^i_{dR^\dagger }(X_h)$ is eventually constant, and the association $\widehat{X}\mapsto H^i_{dR}(X_h)$, $h\gg 0$ induces a well-defined functorial cohomology theory $H^*_{{{\,\mathrm{dR}\,}}}(\widehat{X},K)$ on smooth perfectoid motives over K. It has étale descent, a Künneth formula, and finite dimension whenever X is quasi-compact.

• (2) Suppose that ${{\,\mathrm{char}\,}}K=p>0$. For any fixed un-tilt $K^\sharp$ of K the association $\widehat{X}\mapsto H^i_{dR}(\widehat{X}^\sharp ,K^\sharp )$ is a well-defined functorial cohomology theory $H^i_{dR^\dagger }(\widehat{X},K^\sharp )$ on smooth perfectoid motives over K. It has étale descent, a Künneth formula, and finite dimension whenever X is quasi-compact.

• (3) Suppose that ${{\,\mathrm{char}\,}}K=p>0$. For any fixed un-tilt $K^\sharp$ of K the association ${X}\mapsto H^i_{dR}({X}^{{{\,\mathrm{Perf}\,}}},K^\sharp )$ is a well-defined functorial cohomology theory on smooth rigid analytic varieties over K which extends to arbitrary rigid analytic varieties and is compatible with rigid cohomology with coefficients is $K^\sharp$ whenever X is of good reduction. Moreover, it has étale descent, a Künneth formula, and finite dimension whenever X is smooth and quasi-compact or the analytification of a quasi-projective algebraic variety.

Remark 5.2

In [5] also a relative version of the (overconvergent) de Rham cohomology for rigid analytic spaces is introduced. It is also shown that it enjoys many properties which are common to the archimedean/algebraic analogue, such as the fact that $H^*_{dR}(X/S)$ is a vector bundle on the base whenever $X\rightarrow S$ is smooth and proper.

Suppose that K is a perfectoid field of characteristic $p>0$. The need of choosing an un-tilt of K in order to define a de Rham-like cohomology theory for (rigid analytic) varieties over K can be considered unnatural and unsatisfactory for some purposes. To remedy this, in [5] the various cohomology theories $X\mapsto H^*_{dR}(X,K^\sharp )$ are “pasted together” into a vector bundle over the Fargues-Fontaine curve of K by means of the following

Theorem 5.3

([5]) Let K be a perfectoid field of characteristic $p>0$. We let $\mathcal {X}_K$ be the analytic space given by the adic Fargues-Fontaine curve associated to it. There is a monoidal realization functor

$$ \mathcal {R}_{dRFF}:{\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)\rightarrow \mathrm {QCoh}({\mathcal {X}_K})^{{{\,\mathrm{{op}}\,}}} $$

giving rise to a cohomology theory $H^*_{dR}(-,\mathcal {X}_K)$ with values in quasi-coherent ${\mathcal {X}_K}$-modules (defined as in [35]). Moreover, whenever M is compact (eg. M is the motive of a quasi-compact smooth rigid variety, or the analytification of a quasi-projective algebraic variety) then the modules $H^*_{dR}(M,\mathcal {X}_K)$ are vector bundles, and equal to zero if $|i|\gg 0$.

Remark 5.4

The previous result gives a canonical analytic de Rham cohomology in positive characteristic, and answers positively to a conjecture of Fargues [36, Conjecture 1.13] and Scholze [37, Conjecture 6.4].

Remark 5.5

In [5] also a relative version of the previous theorem is shown, building on Remark 5.2.

The cohomology $H_{dR}^*(-,\mathcal {X}_K)$ above is not the only motivic cohomology theory with values on vector bundles on a Fargues-Fontaine curve. Fix an algebraically closed complete valued field C over $\mathbb {Q}_p$. In [34], Le Bras gives a motivic, overconvergent and rational version of the $\mathbb {A}_{\inf }$-cohomology introduced for smooth and proper formal schemes over $\mathcal {O}_C$ defined as follows: consider the pro-étale sheaf $\mathbb {A}_{\inf ,X}$ defined on affinoid perfectoid spaces over $X:=\mathfrak {X}_C$ as ${{\,\mathrm{Spa}\,}}(P,P^+)\mapsto W(P^{\flat +})$ and its pull-back $R\nu _*\mathbb {A}_{\inf }$ to the Zariski site of $\mathfrak {X}$. Take the complex obtained by décalage $L\eta _\mu R\nu _*\mathbb {A}_{\inf }$ ($\mu$ being $[\varepsilon ]-1$) and, finally, the complex $R\Gamma _{{{\,\mathrm{{Zar}}\,}}}(\mathfrak {X},L\eta _\mu R\nu _*\mathbb {A}_{\inf })$. This complex is known to be related to the various p-adic integral cohomologies defined on $\mathcal {X}$ (see [38]).

Theorem 5.6

([34]) Let C be an algebraically closed complete valued field over $\mathbb {Q}_p$.

• (1) Let X be a smooth rigid analytic variety over C endowed with a dugger structure $X^\dagger =(X\Subset X')$. Consider the association

  $$ X\mapsto \varinjlim _{X\Subset X_h\subset X'} R\Gamma _{{\acute{\text {e}}{\mathrm{{t}}}}}(X_h, L\eta _t R\nu _*\mathbb {B}) $$

  where $R\nu _*\mathbb {B}$ is the pull-back to the étale topos of $X_h$ of the pro-étale sheaf $\mathbb {B}$ defined on affinoid perfectoid spaces over $X_h$ as ${{\,\mathrm{Spa}\,}}(P,P^+)\mapsto \mathcal {O}(\mathcal {Y}_{(P,P^+)})$ and $L\eta _t$ is the décalage functor with respect to a generator t of $\ker (\theta :W(P^{\flat +})\rightarrow P^+)$. It gives rise to a well-defined functor

  $$ \mathcal {R}_{\mathcal {F}\mathcal {F}}:{\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(C)\rightarrow \mathrm {QCoh}(\mathcal {X}_{C^\flat })^{{{\,\mathrm{{op}}\,}}} $$

• (2) If $C=\mathbb {C}_p$ and $M\in {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(C)$ is compact (for example, it is the motive of a quasi-compact smooth rigid variety, or the analytification of a quasi-projective algebraic variety) then the cohomology groups $H^i(\mathcal {R}_{\mathcal {F}\mathcal {F}}M)$ are vector bundles on the curve $\mathcal {X}_{C^\flat }$ and equal to 0 for $|i|\gg 0$.

Remark 5.7

It is not hard to see that $\mathcal {R}_{\mathcal {F}\mathcal {F}}$ is the rational, overconvergent analogue of the $\mathbb {A}_{\inf }$-cohomology, and it is also possible to relate it to the de Rham cohomology, see [34].

Finally, we sketch briefly the construction of Ayoub of a “new motivic Weil cohomology” for varieties over a field k of positive characteristic. The aim of this construction is somehow different from the previous ones: we have mentioned that the $\mathbb {A}_{\inf }$-cohomology specializes to the various p-adic cohomology theories, and is therefore intimately linked to p-adic Hodge theory and p-adic periods. The constructions above are aimed to generalizations and extensions of this idea.

On a different direction, one can try to build a realization which specializes to the various $\ell$-adic realizations (including $\ell =p$): such an approach would be interesting, for example, to inspect the independence on $\ell$ for $\ell$-adic cohomologies. Choose a (non necessarily complete!) valued field K of mixed characteristic, with k as residue field and let $\widehat{K}$ be its completion. We already considered the following two adjoint pairs

$$ \xi :{{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k)\rightleftarrows {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(\widehat{K}):\chi $$

$$ {{\,\mathrm{Rig}\,}}^*:{{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)\rightleftarrows {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(\widehat{K}):{{\,\mathrm{Rig}\,}}_* $$

The fact that $\xi$ and ${{\,\mathrm{Rig}\,}}^*$ are monoidal induces formally a decomposition of the functors above:

where the category ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k,\chi )$ [resp. ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K,{{\,\mathrm{Rig}\,}}_*1)$] in the middle denotes the category of modules over the motive $\chi 1$ [resp. ${{\,\mathrm{Rig}\,}}_*1$]. This object inherits a natural algebra structure deduced from the monoidality of $\xi$ [resp. ${{\,\mathrm{Rig}\,}}^*$]. The adjunction on the left is simply given by the free module structure/forgetful pair, while the adjunction on the right is built out of the natural $\chi 1$-module structure [resp. ${{\,\mathrm{Rig}\,}}_*1$-module structure] which can be given to the objects of the form $\chi M$ [resp. ${{\,\mathrm{Rig}\,}}_*M$].

The main theorem of [39] is then the following.

Theorem 5.8

([39]) Let K be a subfield of $\mathbb {C}$ equipped with a rank-1 valuation with residue field k of characteristic $p>0$ and completion $\widehat{K}$.

• (1) The functor ${{{\,\mathrm{Rig}\,}}'^*}$ of (B) gives an equivalence of monoidal $\infty$-categories

  $${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K,{{\,\mathrm{Rig}\,}}_*1)\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(\widehat{K}).$$

• (2) The (homological) algebraic de Rham realization

  $$ \mathcal {R}_{dR}:{{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)\rightarrow D(K) $$

  induces a monoidal functor

  $$ \mathcal {R}'_{dR}:{\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(\widehat{K})\cong {{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K,{{\,\mathrm{Rig}\,}}_*1)\rightarrow D(K,\mathcal {A}_K) $$

  where the category on the right denotes the category of modules over the object $\mathcal {A}_K:=\mathcal {R}_{dR}{{\,\mathrm{Rig}\,}}_*1$ equipped with its natural DG-algebra structure.

• (3) The complex $\mathcal {A}_K$ is in $D_{\ge 0}(K)$. In particular $A_K:=H_0(\mathcal {A}_K)$ has a K-algebra structure, there exists a map of DG-algebras $\mathcal {A}_K\rightarrow A_K$ and one can define a realization for ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k)$ as follows:

  $$ \mathcal {R}_{new}:{{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k){\mathop {\rightarrow }\limits ^{\xi }}{\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(\widehat{K})\cong {{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K,{{\,\mathrm{Rig}\,}}_*1){\mathop {\longrightarrow }\limits ^{\mathcal {R}'_{dR}}} D(K,\mathcal {A}_K)\rightarrow D(A_K). $$

• (4) The algebra $A_K$ can be explicitly computed in terms of generators and relations.

• (5) There are ring maps $A_K\rightarrow \widehat{K}$ and $A_K\rightarrow \overline{\mathbb {Q}}_\ell$ for any $\ell \ne p$ (depending on a choice of isomorphism $\overline{\mathbb {Q}}_\ell \cong \mathbb {C}$) such that the realizations obtained by base change

  $$ {{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k){\mathop {\longrightarrow }\limits ^{\mathcal {R}_{new}}} D(A_K)\rightarrow D(\widehat{K})\qquad {{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k){\mathop {\longrightarrow }\limits ^{\mathcal {R}_{new}}} D(A_K)\rightarrow D(\overline{\mathbb {Q}}_\ell ) $$

  are equivalent to the rigid realization, and the $\ell$-adic realization, respectively.

Remark 5.9

One of the main results of [39] is actually the explicit computation of the algebra $A_K$ that we only vaguely mentioned in the theorem above. It turns out that the description of the ring $A_K$ is the non-archimedean analogue of the construction of the ring of complex periods considered in [40]. In spite of this explicit presentation, a full understanding of the algebraic properties of $A_K$ (eg. being an integral domain) seem to be out of reach, and any progress in this direction would be of much interest as explained in [39].

The construction above is based on the equivalence ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(\widehat{K})\cong$ ${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K,{{\,\mathrm{Rig}\,}}_*1)$ arising from the monoidal left adjoint functor ${{\,\mathrm{Rig}\,}}^*$. In [7] the other monoidal functor $\xi$ is analyzed, obtaining the following analogue of Theorem 5.8((1)).

Theorem 5.10

([7, Theorem 3.3.3]) Suppose that $\widehat{K}$ is algebraically closed. The functor ${\xi '}$ of (A) defines an equivalence of monoidal $\infty$-categories

$${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k,\chi 1)\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(\widehat{K}).$$

Remark 5.11

In [7] a more general statement is shown: one can extend the equivalence above even in the case of a higher rank valuation, defined by some valuation subring $\widehat{K}^+\subset \widehat{K}$, obtaining an equivalence

$${{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}({{\,\mathrm{Spec}\,}}(\widehat{K}^+/\pi ),\chi 1)\cong {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}({{\,\mathrm{Spa}\,}}(\widehat{K},\widehat{K}^+))$$

where $\pi \in \widehat{K}^+$ is a non-zero topologically nilpotent element.

6 A Betti-Like Cohomology via Motives

The aim of this section is to define another motivic cohomology theory for rigid analytic varieties and perfectoid spaces. Contrarily to the de Rham version considered above, this won’t be a Weil cohomology and can’t be expected to compare to $\ell$-adic cohomologies. Nonetheless, Berkovich showed ([41]) that it contains some interesting information, and the motivic language can be used to extend his results. The main theorems of this section are taken from [42].

We recall that the Berkovich topological space $|X|_{{{\,\mathrm{Berk}\,}}}$ underlying a rigid analytic variety X is the maximal Hausdorff quotient of the (locally spectral) topological space |X| It coincides with the topological space defined by the partially proper topology on X, or equivalently, to the topological space introduced by Berkovich.

Theorem 6.1

([42]) Let K be a complete non-archimedean valued field, and let $\ell$ be a prime which is invertible in the residue field k. Let also C be a fixed complete algebraic closure of K.

• (1) Put $\Lambda =\mathbb {Q}$. There is an $\ell$-adic realization functor

  $$ \mathcal {R}_\ell :{\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{({{\,\mathrm{eff}\,}})}(K)\rightarrow {\mathrm{{Sh}}}_{\mathrm{pro}\acute{\mathrm{e}}\mathrm{t}}\,(K,\mathbb {Q}_\ell ) $$

  which is monoidal, and which sends compact objects to constructible complexes. For any smooth variety X over K, the homology groups $H_*(\mathcal {R}_{\ell }\Lambda (X))$ compute the $\ell$-adic homology of X.

• (2) The canonical functor

  $$ \iota ^*:\mathrm{{Sh}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K,\Lambda )\rightarrow {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(K) $$

  induced by the inclusion of the small étale site into the big one, has a left adjoint

  $$\mathcal {R}_B:{\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(K)\rightarrow \mathrm{{Sh}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K,\Lambda )$$

  that can be described explicitly as the functor induced by mapping a variety X to the singular complex $\Lambda [{{\,\mathrm{Sing}\,}}(|X_C|_{{{\,\mathrm{Berk}\,}}})]$ of the topological space $|X_C|_{{{\,\mathrm{Berk}\,}}}$ with coefficients in $\Lambda$.

• (3) Suppose that K is a finite extension of $\mathbb {Q}_p$ and let $F:{{\,\mathrm{Gal}\,}}(k)\rightarrow {{\,\mathrm{Gal}\,}}(K)$ be a fixed lift of Frobenius. The following diagram

  

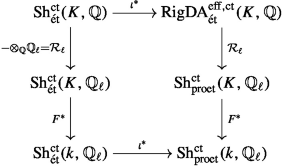
  is commutative and left adjointable, in the sense that there are left adjoint functors $\mathcal {R}_B$ to the functors $\iota ^*$ and the canonical natural transformation $\mathcal {R}_BF^*\mathcal {R}_\ell \Rightarrow F^*\mathcal {R}_\ell \mathcal {R}_B$ is invertible.

Proof

Only the last point does not appear as stated in [42], but it is easily seen to be equivalent to [42, Corollary 5.5]. $\square$

Remark 6.2

In [42] we showed that the theorem above can be used to have a concrete generalization of a result of Berkovich [41] for which whenever K is a local field, the Betti cohomology of the underlying Berkovich space with $\mathbb {Q}_\ell$-coefficients of a variety X coincides with the smooth part of the Galois $\ell$-adic representation given by the associated étale cohomology.

As we focus in this paper on the role of motivic tilting and de-perfectoidification, we point out that the Berkovich realization given above can be equivalently defined for perfectoid motives, in a compatible way with the equivalences of Theorem 3.1.

Proposition 6.3

([42]) Let K be a perfectoid field and C be a complete algebraic closure of it.

• (1) The functor $X\mapsto \Lambda [{{\,\mathrm{Sing}\,}}(|X_C|_{{{\,\mathrm{Berk}\,}}})]$, where $\Lambda [{{\,\mathrm{Sing}\,}}(T)]$ is the singular complex of a topological space T with coefficients in $\Lambda$, induces a colimit-preserving monoidal functor

  $$\mathcal {R}_B:{\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(K)\rightarrow \mathrm{{Sh}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K,\Lambda ).$$

• (2) The following diagram is commutative.

  

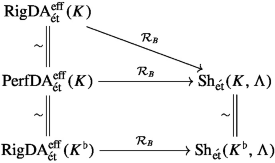
Proof

In light of [42, Sect. 4] only the formula for the perfectoid version of $\mathcal {R}_B$ needs to be justified. As the tilting equivalence gives rise to homeomorphisms on the Berkovich spaces attached to perfectoid spaces, we may assume ${{\,\mathrm{char}\,}}C=p$. By the equivalence ${{\,\mathrm{Perf}\,}}^*:{\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}^{{{\,\mathrm{eff}\,}}}(C)\cong {\mathrm{{PerfDA}}}_{\acute{\text {e}}{\mathrm{{t}}}}^{{{\,\mathrm{eff}\,}}}(C)$ the formula then follows from the analogous formula for rigid analytic varieties and the homeomorphism $|X^{{{\,\mathrm{Perf}\,}}}|\cong |X|$. $\square$

As previously anticipated, this cohomology theory is not a Weil cohomology. It does not even extend to the stable categories of motives as indeed it “kills” Tate twists (this is compatible with Remark 6.2).

Remark 6.4

If X is a geometrically connected rigid variety of good reduction over K, then $\mathcal {R}_B\Lambda (X)\cong \Lambda [0]$. In particular, we have $\mathcal {R}_B(T_K)\cong 0$.

As a matter of fact, because of the functor $\xi :{{\,\mathrm{{DA}}\,}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(k)\rightarrow {\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)$ that we introduced above, it is impossible to define any Weil realization functor from ${\mathrm{{RigDA}}}_{{\acute{\text {e}}{\mathrm{{t}}}}}(K)$ with values in $\mathbb {Q}$-vector spaces, whenever K is a local field of mixed characteristic. Any such realization would otherwise violate Serre’s counterexample to the existence of a rational Weil cohomology theory for varieties over a finite field ([43, Page 315]).