Advanced Neutron Imaging

Abstract

Advances in neutron optics and availability of new brilliant neutron sources have opened up new opportunities in the field of neutron imaging. This chapter deals with the concept of phase contrast and polarized neutron imaging. According to quantum mechanics, the sub-atomic particles exhibit both wave and particle nature, and therefore, one can describe the interaction of neutron with matter from the wave optics perspective as well. Therefore, the concept of phase and amplitude of neutron wave can be used to describe neutron interaction and scattering and extend them to neutron imaging. We discuss different modalities of phase-contrast imaging, both in near-field and far-field conditions and illustrate their applications using few examples. In particular, we discuss various imaging modalities utilizing optics-free propagation, crystal optics-based analyser and grating-based neutron optics. Moreover, neutrons carry spin, which is defined by an internal angular momentum with a quantum number. In analogy with the electromagnetic waves, therefore, polarization of this wave is defined by the quantum mechanical property of neutron spin. Polarized neutron techniques take advantage of the coupling that exists between the neutron spin and nuclear and the magnetic interactions due to neutron spin-dependent scattering properties. The spin rotation analysis of polarized neutron beam in combination with an imaging setup can be used to obtain the magnetic field distributions. This chapter discusses the concept of polarized neutron imaging and its different experimental realizations in detail.

6.1 Introduction

In traditional neutron radiography, we are primarily concerned with the intensity variations caused by inhomogeneous attenuation of the neutron beam in the object. This inhomogeneous neutron attenuation causes an intensity modulation in the transmitted beam, which is referred to as absorption contrast. It is worthwhile to point out that this absorption imaging includes both attenuation and scattering out of the beam, mostly due to incoherent scattering. This concept of attenuation-based imaging has been widely used since the discovery of X-ray by Rontgen, and later on, the same principles were adopted by the neutron imaging community. However, this approach fails to work with materials of high transmittance or when one is interested in probing the magnetic or electric field distribution inside a bulk. In order to overcome the limitations of conventional neutron imaging techniques, the concept of wave particle duality of neutrons, as defined through quantum mechanics, can be invoked. In terms of wave picture, neutron–matter interaction can then be treated on par with wave matter interaction, and hence, the concept of “phase of wave” can be implemented to improve the capabilities of existing neutron imaging techniques. The development of the neutron phase-contrast imaging technique is, therefore, an important advancement in improving the contrast and sensitivity of the existing transmission-based neutron imaging techniques [1,2,3,4].

Because phase information is often lost in traditional transmission imaging, many approaches have been developed to convert the unseen “phase” to intensity modulation. The concept of phase-contrast imaging was discovered in 1942 by Zernike, and he invented optical Zernike phase-contrast (ZPC) microscope to visualize phase undulations [5]. Zernike was awarded the Nobel Prize in Physics in 1953 for this invention. Following it, Nomarski then devised differential interference contrast (DIC) microscopy in 1952, based on beam-splitting and shear interferometry concepts [6]. The disadvantage of these proposed techniques was that quantitative image analysis was not possible. In 1972, Gerchberg and Saxton [7] proposed Gerchberg-Saxton (GS) algorithm, the first iterative phase-retrieval algorithm for quantitative phase measurement, and the ideas have been successfully demonstrated in the fields of optical and X-ray microscopy. In contrast to iterative methods, Teague first proposed the idea of free-space propagation to recover phase quantitatively, in a non-iterative manner, using the transport of intensity equation (TIE) in 1982 [8, 9].

However, the widespread adoption of phase-based techniques for neutrons started only in early 2000. This long delay could be attributed to multiple reasons such as difficulties in fabrication of neutron optics, need for high mechanical stability in optical alignment and low neutron source coherence combined with low neutron flux at neutron imaging facilities. During the previous decade, new developments in fabrication technologies of neutron optics along with the availability of high brightness neutron sources have contributed towards the adoption of various phase-sensing techniques for neutrons.

On a different note, neutron spin-based imaging with polarized neutrons combines absorption (attenuation) and phase-based interactions and has become an important visualization probe for magnetic fields, domains and quantum effects such as the Meissner effect and flux trapping among others. It is achieved by obtaining the change in polarization of the neutron beam due to Larmor precession as it passes through a region of magnetic field. The neutron’s deep penetration capability in most of the materials makes it a unique probe for non-destructive study of magnetic fields inside objects.

This chapter describes the basic principles of neutron phase-sensitive imaging and polarized neutron imaging, and presents an overview of the progress in this emerging field of neutron imaging in the last decade.

6.2 Basic of Phase-Contrast Imaging

The neutron–matter interaction (nuclear interaction, for simplicity) through the wave model can be best described through the complex refractive index of the matter, expressed as:

$$n = \sqrt {1 - \frac{{\overline{V} }}{E}} = 1 - \frac{{\lambda^{2} N}}{2\pi }\sqrt {b_{{\text{c}}}^{2} - \left( {\frac{{\sigma_{{\text{r}}} }}{2\lambda }} \right)^{2} } + i\frac{{\sigma_{{\text{r}}} N\lambda }}{4\pi } = n_{{\text{r}}} + in_{{\text{i}}}$$

(6.1)

where λ is neutron wavelength, N is the mean number of scattering nuclei per unit volume and $b_{{\text{c}}} = \left\langle b \right\rangle$ is the mean coherent scattering length. The complex refraction index counts for absorption (σ_a) and incoherent scattering (σ_{s, incoh}) processes. (σ_r) = (σ_a) + (σ_{s, incoh}) is the total reaction cross section per atom. One can express the complex refractive index simply as follows:

$$n({\mathbf{r}},\lambda ) = 1 - \delta ({\mathbf{r}},\lambda ) - i\beta ({\mathbf{r}},\lambda )$$

(6.2)

Real part δ corresponds to the phase of the propagating wave and β represents the absorption in the medium. Furthermore, if the neutron absorption within the object is negligible, the imaginary component in the above relation may be ignored, and the complex refractive index of the object for monochromatic neutron of wavelength λ can be compactly described through the following relation:

$$n = 1 - \frac{{\lambda^{2} Nb_{{\text{c}}} }}{2\pi }$$

(6.3)

Consider a plane wave with amplitude $A_{0}$, and initial wave-vector k, incident on a material with thickness d and refractive index (Fig. 6.1). Let the amplitude of the unperturbed wave after the material be $\psi = A_{0} {\text{e}}^{{{\text{i}}(kd - \omega t)}}$; where $k = \omega /c$, and amplitude of the perturbed wave after the object is given by

$$\psi = A_{0} {\text{e}}^{{{\text{i}}(k^{\prime}d - \omega t)}} = A_{0} {\text{e}}^{{ - {\text{i}}\frac{\omega }{c}\delta d}} {\text{e}}^{{ - \frac{\omega }{c}\beta d}} {\text{e}}^{{{\text{i}}(kd - \omega t)}}$$

(6.4)

Fig. 6.1

Example of phase shift and wave attenuation as the wave passes through the object

where $k^{\prime} = {{n\omega } /c}$. It may be noted that this equation contains a phase factor $\exp ( - {\text{i}}\phi (d))$ with $\phi (z) = {{\omega \delta d} /c}$, which represents the phase difference between matter and vacuum (in terms of wave picture). Similarly, the amplitude attenuation of the wave is given by ${\text{exp}}({{ - \omega \beta d} /c})$. Hence, the intensity in the exit plane of the object is $I = \left| \psi \right|^{2} = I_{0} {\text{e}}^{ - 2k\beta d} = I_{0} {\text{e}}^{ - \mu d}$, which is nothing but Lambert–Beer’s law where $I_{0} = \left| {A_{0} } \right|^{2}$ and attenuation coefficient μ is defined as $\mu = 2k\beta = {{4\pi \beta } /\lambda }$. This is the basic principle of conventional neutron radiography where the information based on differential attenuation or absorption is recorded. However, it can be observed that any information contained in the phase of the wave has been completely lost. The phase-contrast technique aims to detect this component of the wave by using suitable optical elements.

Therefore, it can be stated that phase-contrast imaging additionally takes advantage of the real portion of the refractive index (1 − δ), whereas traditional neutron radiography takes advantage of the imaginary part (β). In contrast to X-rays, which have a refractive index of slightly less than unity, neutrons have a refractive index that can be larger than or less than unity. This is due to the fact that neutrons’ coherent scattering length can be either positive or negative. The phase shift due to nuclear coherent scattering for an object of uniform thickness D for the neutrons can be expressed as $\Delta \phi = - Nb_{{\text{c}}} \lambda D$.

In order to further illustrate these conclusions and evaluate the advantage of phase-based approach over conventional absorption-based neutron imaging, consider a simulated phantom consisting of a carbon tube enclosed in a lead cylinder. Figure 6.2a shows the absorption and (b) the phase map of the simulated phantom. As observed in Fig. 6.1a, absorption map of the item is mostly attributable to lead and the carbon tube is totally hidden. These are common circumstances in which traditional radiography fails to probe the materials. The phase map is presented in Fig. 6.2b, and the phase contributions of both the lead and carbon sinkers are apparent.

Fig. 6.2

a Absorption and b phase shift distribution of a carbon tube enclosed in the lead cylinder

Similarly, phase shift due to magnetic interaction, for a uniform length of thickness D can be expressed as

$$\Delta \phi_{{{\text{mag}}}} = \pm \frac{\mu Bm\lambda D}{{2\pi \hbar^{2} }}$$

(6.5)

where μ is the neutron dipole moment, B the applied magnetic field, m the neutron mass and λ is neutron wavelength.

It may be noted that phase shifts can appear in the presence of different varieties of scalar and vector electromagnetic potentials. Although not discussed here, phase shift effects can also occur due to gravitational [10], Coriolis [11], Aharonov–Cashire [12], Aharonov–Bohm [13], magnetic Josephson [14], Fizeau [15] and geometric (Berry) [16] interactions, and have been verified experimentally using neutron interferometry techniques, and the same has been briefly presented in Table 6.1.

Table 6.1 Type of interaction and different types of phase shift due to these potentials [10,11,12,13,14,15,16]

To expand on the concepts, we examine the most fundamental type of phase-contrast imaging, which involves free-space propagation of a coherent wave-field through a transparent object and then measuring the intensity modulation with a spatially resolved detector after propagating the exit wavefront over a distance z behind the object. This is the classical way of observing the diffraction effects using more coherent laser sources. In the absence of the object in the beam path, a constant intensity would be recorded on the detector. If we place the object in the beam path, make the beam propagation distance zero after the object, we have a contact image that shows only absorption-contrast. It is worth noting that a contact image of a perfectly transparent object just shows the intensity distribution in the detector plane. Nonetheless, the object shifts the phase of the wavefield, but the wave amplitude remains constant, and thus, the intensity remains constant. Refraction and diffraction create amplitude fluctuations in the propagating wavefield due to interference of wavefields, which leads to variations in the recorded intensity when the detector is moved further away from the object. Figure 6.3 shows the different regimes of the phase-contrast imaging where the detector can be placed, and the data can be recorded. This completely depends upon the object-related information that one wants to retrieve from these measurements. The advantage of the near-field regime is that there is a direct correlation between the data recorded on the detector and the phase-contrast effect. Sometimes, one need not retrieve the phase difference, and the projection image itself can be used for further analysis. However, in the far-field regime, one records the interference pattern (in reciprocal space), and hence, suitable phase retrieval algorithms need to be employed before any meaningful conclusion can be drawn from the recorded pattern. Near-field regimes are easy to implement experimentally; however, sensitivity in terms of phase difference would be higher in the far-field regime.

Fig. 6.3

Different regimes in the X-ray/neutron phase-contrast imaging

Figure 6.4 shows schematics of various phase-sensing techniques, which have been implemented using thermal and cold neutron sources. In what follows, we discuss in detail the basic ideas behind different phase-contrast imaging techniques and present some experimental findings using these techniques.

Fig. 6.4

a Crystal-based interferometer, b analyser-based setup, c grating-based setup, d propagation-based setup for neutron-based phase-contrast imaging [17]

6.3 Neutron Interferometry

6.3.1 Single-Crystal Neutron Interferometers

Interferometry is the most obvious choice when one is interested in measuring the phase shifts. Maier-Leibnitz made the first attempts to build a neutron interferometer in 1962 with coherent neutron beams. Maier-Leibnitz and Springer [18] using a pair of prisms, and up to 60 µm path separation was reported. However, the first successful X-ray interferometer, equivalent to Mach–Zehnder optical interferometers, was reported by Bonse and Hart in 1965 [19] using perfect single crystals, and later, the same technique was also adopted for neutron interferometry [20]. The interferometer is made up of three crystal slices that are carved from a single big, nearly flawless monolithic silicon crystal (Fig. 6.5). The first crystal slice serves as a beam splitter, dividing the monochromatic and well-collimated entering beam into two coherent neutron beams.

Fig. 6.5

A neutron interferometer made of a single piece of perfect silicon crystal. a A diagram of the interferometer: at the first plate, an incident beam is split into two beam paths, which are then recombined at the last plate. The intensity modulation of two beams leaving the interferometer is typical and depends on the relative phase of the two beams in the interferometer [21]. b Photographs of a variety of neutron interferometers [22]

The second slice serves as a mirror, allowing the two beams in the third slice, the analyser, to recombine. To compensate for the interferometer’s built-in phase patterns, a compensator is frequently used in one of the coherent beams. The sample is placed between the mirror and the analyser in one of the two beams.

Neutron interferometry can be considered as a method of measuring the phase difference induced by a sample (in the direction of the illuminating wave’s propagation) across spatial locations perpendicular to the wave’s propagation, modulo 2π. The intensity $I(x,y)$ recorded in the detector plane can be given as follows:

$$I(x,y) = I_{0} (x,y) + a(x,y)\cos \left[ {\Phi (x,y) + \phi_{{\text{r}}} (x,y)} \right]$$

(6.6)

where $I_{0} (x,y)$ is the background illumination intensity, a(x, y) is the amplitude of the beam, $\Phi (x,y)$ is the phase of the object and $\phi_{{\text{r}}} (x,y)$ is the reference phase. There are various techniques such as Fourier transform, fringe skeletonization, phase-stepping, phase-shifting, temporal and spatial heterodyning which can be used for phase extraction from the recorded interferogram. In practice, techniques of “phase unwrapping” need to be employed to produce a phase image in the range [−π, π] from the interferogram.

Furthermore, it is also possible to do tomographic measurement by collecting projection images at multiple rotation angles and local distribution of the refractive index decrement can then be reconstructed using conventional filtered back-projection algorithms [4, 23]. Figure 6.6 shows the first reconstructed 3D phase tomography images of the aluminium screw [4].

Fig. 6.6

Neutron phase tomography of aluminium screw from the phase shifts using neutron interferometry [24]

6.3.2 Moire Interferometry

Although perfect crystal neutron interferometry is very sensitive to small phase shifts for thermal or cold neutrons, however, these interferometers are not only difficult to fabricate, but have narrow wavelength acceptance and also require very stringent conditions in terms of vibration isolation and incident beam collimation. In order to overcome the limitations of existing single-crystal interferometers, research has been carried out to develop grating-based interferometers. Recent advances in far-field phase grating-based Moiré interferometry have allowed neutron interferometry to be extended to medium-intensity thermal neutron sources, demonstrating the potential for neutron interferometry studies to be extensively employed. Figure 6.7 shows the schematic of the experimental technique [25]. The first grating (G₁) diffracts a neutron beam into three rays: one transmitted and two deflected. The second grating (G₂) is placed between phase grating G₁ and analyser grating G₃. This grating’s principal function is to refocus diffracted waves from G₁ into a sequence of Fourier image in a specified plane downstream. The G₃ grating is positioned close to this plane in order to induce phase Moiré effects between itself and the Fourier images. The three grating setup has the advantage that large sample size (~cm²) can be accommodated due to large possible separation between the second and third grating. Therefore, by detecting changes in the interference pattern, as compared with the empty interferometer, the microstructures within the material can be detected.

Fig. 6.7

Three PGMI schematic diagram where the third grating is offset from the echo plane to produce the Moire pattern [25]

It should be noted that, unlike the near-field gratings discussed later in this chapter, phase-based Moire gratings are effective in the far-field region, producing interference fringes (~mm scale) that are orders of magnitude greater than the grating’s period (~µm scale), allowing direct detection with an neutron imaging detector [26].

6.4 Near-Field Phase-Contrast Imaging

As discussed previously, there is a simple linear relation between phase shifts and intensity recorded by the detector in the near-field regime as given by the transport of intensity equation. The transport of the intensity equation (TIE), which Teague had undeniably first derived in 1982, is simply an alternative statement of the energy conservation law and sets out a quantitative relationship between the variation of the longitudinal intensity I(x) and the phase of the coherent beam ϕ(x). In the compact form, the can be expressed as follows:

$$\nabla \cdot \left[ {I({\mathbf{x}})\nabla \phi ({\mathbf{x}})} \right] = - \frac{2\pi }{\lambda }\frac{\partial }{\partial z}I({\mathbf{x}})$$

(6.7)

where z represents longitudinal displacement along the beam. Expanding the left hand side of the above equation, one can then rewrite the above as follows:

$$\nabla I({\mathbf{x}}) \cdot \nabla \phi ({\mathbf{x}}) + I({\mathbf{x}})\nabla^{2} \phi ({\mathbf{x}}) = - \frac{2\pi }{\lambda }\frac{\partial }{\partial z}I({\mathbf{x}})$$

(6.8)

where the two terms on the LHS can be identified as the phase gradient (the first derivative) and phase curvature (the second derivative), respectively. Therefore, both phase gradient and phase curvature determine the longitudinal fluctuation of the intensity. Like a prism, the phase gradient causes intensity translation and constitutes a prism-like effect that transversely displaces optical energy. The transverse displacement is directly proportional to the local deflection angles (refraction).

Similarly, like a lens, phase curvatures cause intensity convergence or divergence and measures the Laplacian of the phase (Fresnel diffraction). This interpretation of the transport of intensity equation has therefore opened the door for the development of new non-interferometric phase-contrast techniques. In the following section, we describe phase-contrast techniques that measure the first derivative of phase (analyser and grating-based neutron imaging) and second derivative of phase (propagation-based phase-contrast imaging) and discuss some experimental results.

6.4.1 Analyser-Based Neutron Imaging

Analyser-based imaging is a form of imaging that utilizes the properties of a single crystal to bring out the phase gradients as per the refractive index variation in the sample [27]. This modality corresponds to Schlieren imaging in classical optics [28] and was adopted for neutron imaging using a combination of diffractive neutron optics [29, 30]. The angular deviation due to refraction of neutron beam as it transverses the object, gives rise to local phase gradient, lending the name differential phase to this contrast modality. Due to the weak nature of neutron–matter interaction, angular deviations due to local phase gradients are within a few arcsec or microradians. This matches with the angular acceptance or the Darwin width of perfect single crystals (as an example, for Si(111) the Darwin width is ~8 arcsec for thermal neutrons). This implies that only the neutrons travelling within this narrow angular width will be transmitted or reflected by the crystal analyser, and that too with variable degree of reflectivity. Usually, a monochromatic neutron beam, selected by using a neutron monochromator, is incident upon a sample, and the transmitted beam is then reflected by an analyser single crystal. The intensity recorded by the detector after transmission through the analyser in each position can be expressed as follows

$$I = I_{0} R\left( {\theta_{{\text{a}}} + \alpha (x,y)} \right)$$

(6.9)

where $\alpha (x,y)$ is the refraction angle, $I_{0}$ is the apparent absorption intensity, and $R(\theta )$ is the reflectivity of the analyser crystal at the angle θ. The analyser is aligned at the Bragg angle as that of the monochromator, and by rotating the crystal analyser around the Bragg angle, data at multiple points on the rocking curve is collected. This data can be subsequently processed to separate both absorption and refraction contribution from the object. Furthermore, one can repeat the measurement steps at different sample orientation and three-dimensional tomography can be carried out. A tomographic reconstruction based on the standard filtered back projection method (FBP) and utilising the linear filter function (Ram-Lak filter) would, however, not result in a proper reconstruction of the real component of the refractive index. Using the Fourier derivative theorem, a new filter function defined as follows can be derived [2].

$$F(k(\nu )) = \left\{ {\begin{array}{*{20}l} { - i\,{\text{sign}}(\nu ),} \hfill & {\left| \nu \right| \le 1/2\Delta y^{\prime } } \hfill \\ {0,} \hfill & {\left| \nu \right| \ge 1/2\Delta y^{\prime } } \hfill \\ \end{array} } \right.$$

(6.10)

where ν is represents spatial frequency component and sign(ν) is the sign function.

Spatially unresolved, disorderly or partially arranged sample microstructures may lead to the small angle neutron scattering around the refracted ray. The unresolved microstructure may broaden the refracted neutron beam, and the same can be recorded in the transmitted direct beam. The method, therefore, can be used to obtain signatures of small-angle scattering contrast because the relevant angular range of refraction matches well with small-angle scattering from structures in the micrometre and sub-micrometre range (100 nm–10 µm). The following line integral may be used to quantify and approximate the small-angle scattering-induced width of the refracted beams or their angular distribution [31]

$$\Delta \theta^{2} = \int {\frac{\sigma (x,y)N(x,y)}{{R^{2} (x,y)}}} {\text{d}}l$$

(6.11)

where σ is the scattering cross-section, N the particle density and R is a parameter with the dimension of a length specifying an average size or correlation length in the scattering object. In contrast to the phase shift, with this definition of small-angle scatter signal, one can reconstruct slices using the conventional linear filter. Using double single-crystal setup, the first attempts to probe the spatial distribution of small-angle scattering signal using a spatially resolved neutron imaging detector have been reported [31]. Figure 6.8 shows three-dimensional phase tomographic reconstruction of the aluminium cylinder with asymmetric hole along with different cut-away sections using analyser-based phase-contrast imaging. Figure 6.9 shows ultrasmall angle X-ray contrast tomography slice images of different concentrations of β-carotene in D₂O inside various holes in a square Al matrix.

Fig. 6.8

Reproduced from [30] with permission from © Elsevier 2004

Three-dimensional refraction contrast reconstruction of the sample volume (aluminium cylinder with asymmetric hole drilled); cut-open (a, b); view from top (c); sagittal cut (d); frontal cut (e).

Fig. 6.9

Reproduced from [31] with permission from Copyright © 2004 American Institute of Physics

Reconstructed sample cross section of Al matrix filled with different concentrations of β-carotene in D₂O: (1) 23.0 (5) wt%, (2) 11.6 (5) wt%, (3) 5.8 (5) wt%, (4) 3.8 (5) wt%; a refraction contrast; b absorption contrast; c USANS contrast.

6.4.2 Near-Field Grating-Based Neutron Imaging

When a plane wave illuminates a periodic transmission mask, coherent wave propagation in the near-field causes a periodic self-image of the transmission mask. If the plane wave and the diffraction mask were both infinitely long, these recurrences would continue indefinitely. This phenomenon, known as the Talbot effect, was first observed in 1836 by Talbot and is a natural consequence of Fresnel diffraction. The Talbot effect is used in neutron grating interferometer imaging, which requires a phase grating to create a near-field Talbot diffraction pattern and an analyser grating to analyse the interference pattern [2]. Simply put, it is a multi-collimator that converts local angular deviations into variation in locally transmitted intensity that can be easily detected with a neutron imaging detector [32].

Typically, an absorbing mask with transmitting slits, also known as a source grating, is placed near the neutron source (pin-hole) to create an array of line sources, with each line source meeting the differential phase-contrast image process coherence requirements. The need for the periodic absorption mask arises, as usually, the neutron sources are highly incoherent, and therefore, there is a need to generate a coherent source for generating near-field diffraction pattern. The period and distances are chosen so that at the chosen Talbot distance, the interference patterns due to different individual beams from the source grating are superimposed constructively. The relationship between the different relevant parameters can be expressed as: p_s = p_aD₁/D₂, where p_s is the source grating period and D₁ is the distance between source grating and phase grating, D₂ is the distance between phase and analyser grating, and p_a is period of analyser grating. To separate the phase information from the recorded Moire pattern, a phase stepping approach or Fourier transform approach can be used. Just like the analyser-based imaging, both the phase gradient and the attenuation image can be reconstructed using a set of the recorded interferogram.

Similar to the analyser-based imaging, another application of grating-based imaging setup is to detect dark-field image contrast, through analysis of the decrement visibility of interference pattern. The visibility is defined as V = (I_max − I_min)/(I_max + I_min), where I_max and I_min are the maximum and the minimum intensity of a modulation period across the beam. The loss of visibility can be either due to small-angle scattering from sub-microscopic structures or when magnetic features affect spin-up and spin-down components of the neutron [32]. Likewise as in the analyser-based imaging, one can carry out three-dimension tomographic reconstruction of the real part of the refractive index using Hilbert filter followed by back projection [2].

The dark-field contrast, which is caused by local convolution of the small-angle scattering function with the amplitude of the interference pattern, has a logarithmic dependence on the sample thickness, allowing for tomographic reconstruction similar to conventional tomography algorithm [33]. This differs from dark-field contrast in an analyser-based setup, which is quantified as a broadening of the angular intensity distribution. Although the functionality of grating interferometers is quite similar to that of analyser-based imaging, the key advantage is that it can accept a significantly higher neutron wavelength spread and input divergence.

Figure 6.10 shows a tomographic reconstruction of a piece of aluminium with several drilled holes, displaying the refractive index distribution, dark-field contrast and three-dimensional rendering of a sediment found in the dark-field tomogram [33].

Fig. 6.10

Reproduced from [33] with permission from Copyright © 2008 American Institute of Physics

A tomographic reconstruction of a piece of aluminium with 4 mm drilled holes a the refractive index distribution (from differential phase contrast data), b dark-field contrast (displaying image contrast due to sediments) and c a three-dimensional rendering of a sediment found in the dark-field tomogram.

Figure 6.11a shows a (110)-oriented iron silicon (FeSi) single-crystal disc using dark-field neutron imaging technique. The structures in the dark-field image arise due to strongly degraded neutron wave-front on account of multiple refraction at the domain walls, leading to enhanced scattering of neutron wave. Figure 6.12b shows 3D neutron dark-field imaging of morphology of vortex lattice domain structure in the Type-II superconductor (ultra-pure niobium) as a function of magnetic field [34]. Thus, the neutron phase-contrast imaging provides a powerful non-destructive method in direct visualization and better understanding the magnetic domains within the bulk of a magnetic material as first postulated by Weiss.

Fig. 6.11

a Dark-field image of a 1 mm monocrystalline FeSi plate. Reproduced with permission from [35] Copyright © 2008 American Institute of Physics. b Neutron transmission and dark-field images of ultra-pure niobium as a function of magnetic field showing the flux line lattice within the vortex domains and the vortex lattice domain formation [34]

Fig. 6.12

Neutron radiograph of iron spring within an aluminium matrix a absorption image, b phase-contrast image

6.4.3 Free-Space Propagation-Based Neutron Imaging

If the analyser crystal in the analyser-based phase-contrast imaging setup is removed from the beam path, the neutron beam originating from the sample at various angles will propagate through free space until they reach the detector. A traditional absorption image can be obtained by placing the detector directly behind the sample. However, if the detector is moved away from a well collimated coherent neutron beam, Fresnel or near-field diffraction occurs [36]. To elaborate, the rays that do not pass by the edges of the object remains undeflected. Those that go through it are slightly deflected, and become out of phase when compared to the undeflected ones. The various sets of wavefronts superimpose and interfere at some distance behind the sample because they originate from a single coherent source. The “image” is formed due to the superposition of the distorted wavefront with the undistorted incident wavefront. This superposition gives rise to interference fringes at the edges or feature boundaries as there is a discontinuity in phase at these edges. These fringes improve edge visibility (contrast). In practice, the blurring of the image caused by the divergence of the neutron beam limits the maximum sample-to-detector distance [37]. Figure 6.12 depicts an iron spring encased in an aluminium matrix. It may be noted that thermal neutrons have an extremely small absorption cross-section in aluminium. Even for springs constructed of iron, the absorption image (Fig. 6.12a) shows very weak contrast. The phase contrast image (Fig. 6.12b) on the other hand, even for the aluminium matrix, displays substantially improved contrast, and the structure within the matrix is obvious due to the edge enhancement [38].

The edge-enhancement effect at the edges is illustrated in Figs. 6.13 and 6.14 using a conical piece of lead and iron syringe. Lead is high-Z element but has low neutron attenuation cross-section and high coherent scattering cross-section. The profile map across the drilled hole in the lead is shown in Fig. 6.13. In the plotted profile, the enhancement of intensity across the edges, owing to the phase effects is obvious. A similar enhancement effect across the edge of the iron syringe is also clearly visible in Fig. 6.14. These results conclusively demonstrate that this approach of phase-contrast imaging clearly produces superior images as compared to conventional neutron radiographs. One of the critical demands of this technique is that one need to have very coherent beam of neutrons. This demand increases data collection time as effective coherence property of the neutron source is achieved using a small aperture (~1 mm). Similarly, high-resolution detectors are needed to record the increased visibility at the edges or across the discontinuities within the sample.

Fig. 6.13

Left Neutron phase radiograph of lead sample with conical hole and Right edge profile across highlighted area

Fig. 6.14

Left Neutron phase radiograph of iron syringe and Right edge profile across the highlighted area

The neutron beam must have a high degree of transverse spatial coherence, as characterized by the cross-correlation between two points in the wave (at all times), in order to obtain the phase-induced intensity variation in the image. The coherence area, whose width is given by the transverse coherence length, characterizes the extent of spatial coherence (l_c = $\frac{\lambda R}{a}$). It is dependent on the neutron wavelength $\lambda$, neutron source dimension $a$ and the distance between source and object $R$. To improve phase effects in phase-contrast neutron imaging, the following must be achieved: (a) maximization of the ${R/a}$ of the system and (b) maximization of the neutron beam effective wavelength. These goals must be achieved while meeting the accompanying design restrictions, such as a sufficient neutron flux on the image plane and an appropriate SNR for neutron radiography.

Like the previous phase-contrasting approaches, computed tomography can be performed again in order to re-build quantitatively the 3D distribution of the of the object refractive index. As discussed previously, phase tomography reconstruction algorithms can be divided into two classes. In the first case, one retrieves the phase using earlier described approaches and then uses the conventional filtered back projection (FBP) algorithm to reconstruct the real part of the refractive index. This is a two-step methodology and the process of phase retrieval and reconstruction are decoupled with each other. If the projections or the recorded images contain information about the second derivative of the some function g(x, y, z), or more specifically, the Laplacian of the phase shift generated by the object, then the same (line-integral) can be expressed as:

$$L(y^{\prime},z,\theta ) = \int\limits_{ - \infty }^{\infty } {\left( {\frac{{\partial^{2} g(x^{\prime},y^{\prime},z)}}{{\partial^{2} y^{\prime}}} + \frac{{\partial^{2} g(x^{\prime},y^{\prime},z)}}{{\partial^{2} z}}} \right)} {\text{d}}x^{\prime}$$

(6.12)

Therefore, the tomographical reconstruction utilizing the traditional FBP will not lead to an appropriate reconstruction of the original object function. Using the Fourier derivative theorem, a new filter function defined as follows can be derived [39]

$$F(k(\nu )) = \left\{ {\begin{array}{*{20}l} {\frac{\left| \nu \right|}{{\nu^{2} + \omega^{2} }},} \hfill & {\left| \nu \right| \le 1/2\Delta y^{\prime } } \hfill \\ {0,} \hfill & {\left| \nu \right| \le 1/2\Delta y^{\prime } } \hfill \\ \end{array} } \right.$$

(6.13)

where ν and ω are frequency components in two orthogonal direction in the Fourier space. This one-step approach, although less accurate than the earlier discussed two-step method, is easy to implement computationally. This algorithm was first derived by Bronikov in the context of X-ray phase-contrast tomography. We illustrate the same using an example of a carbon tube inside the lead cylinder, as discussed previously.

Bronikov version of back-projection technique was used for tomographic reconstruction of the lead (Pb)-containing carbon sinker sample in phase-contrast mode. We have generated radiography data over 180° in the step of 1°, and it was used as input to the reconstruction algorithm. Figure 6.15b shows the reconstructed image at the midplane of Fig. 6.15a, which is nothing but the phase radiograph of the object. The edge-enhancement effects in the phase-contrast mode help to increase contrast and makes it possible to image these materials using neutrons. Figure 6.15b brings out the spatial distribution of the carbon sinker enclosed within lead cylinder. It may be noted that this technique is able to provide the distribution of coherent scattering length density without any need of neutron optics.

Fig. 6.15

a Phase contrast image of carbon sinker enclosed in lead matrix, b tomographically reconstructed slice image

6.5 Polarized Neutron Imaging

It may be recalled that neutrons can interact with a magnetic field by the virtue of spin, and hence, are an excellent probe for studying magnetic field distributions. Therefore, the distribution of magnetic fields, and even electric fields within solid samples can be examined and visualized in three-dimensions, which is not possible with any other available experimental technique. Over the last decade, a number of experimental techniques utilising polarized neutron beam have been developed, allowing for the spatially resolved investigation of magnetic field distribution [40,41,42,43,44,45,46,47]. The most common methods for polarizing neutrons are as follows:

• (i) Total external reflection from polarizing magnetic multi-layer-based super-mirrors such as Fe/Si-based polarizing supermirror. This technique is most suitable to obtain the polarized neutron in cold energy region.

• (ii) It is preferred to use Bragg reflection by single crystals such as Cu₂MnAl (Heusler crystals), to obtain polarized neutrons in thermal neutrons.

• (iii) Polarized He-3 filters, which rely on the spin-dependent absorption of neutrons by ³He; anti-parallel spins have a significant absorption cross-section, whereas all neutrons with parallel spins pass through the filter cell. The benefit of the filter is that it works well over a wide range of neutron energies.

It is worth recalling that the neutron’s spin, which is oriented anti-parallel to its magnetic moment, will experience Larmor precession around the field, as it transverses region of magnetic field of intensity B. Polarized neutron imaging is based on measuring the precession angles of a spins of polarized monochromatic neutron beam that is transmitted through a magnetic field in combination of neutron imaging detector. The use of an area detector allows for the measurement of a spatially resolved magnetic field distribution. When working with a beam of neutrons, which is an ensemble of many neutrons, it is more convenient to deal with the polarization vector rather than individual spins. Precession of the polarization vector can thus be used instead of neutron spin (S). The polarization vector (P) may be thought of as the normalized average spin orientation of the whole beam and defined as expectation values of the Pauli spin matrices (σ) as $P = \left\langle \sigma \right\rangle = \frac{2}{\hbar }\left\langle S \right\rangle$.

That precession of the polarization vector as the neutron transverse through a region of stationary magnetic field (B) can be described by Bloch-equation as follows:

$$\frac{{\text{d}\vec{P}}}{\text{d}t} = \gamma_{n} [\vec{P}(t) \times \vec{B}(t)]$$

(6.14)

where γ_n is neutron’s gyromagnetic ratio. As the polarization vector precesses around the magnetic field B(t), its instantaneous angular velocity of the precession is given by:

$$\omega (t) = \gamma_{n} \left| {\vec{B}(t)} \right|\sin \theta$$

(6.15)

where the angle θ is the angle between the vectors P(t) and B(t) and is independent of orientation of the magnetic field vector. It is important to note that if there are magnet field components perpendicular to the original polarization direction, neutron spins will fluctuate between the two spin-states, and consequently, the polarization vector will oscillate as well. The following formula may be used to calculate the rotation angle of the polarization vector around the magnetic field B(t):

$${\text{d}}\phi = \omega (t){\text{d}}t$$

(6.16)

Substituting the neutron path variable ds (dt = ds/v) for the time variable dt, one can obtain following relation:

$${\text{d}}\phi (s) = \omega \frac{{{\text{d}}s}}{v} = \left( {\frac{\lambda m}{h}} \right)\omega {\text{d}}s = \gamma_{n} \frac{\lambda m}{h}\left| {\vec{B}(s)} \right|\sin \theta {\text{d}}s$$

(6.17)

where v and λ are the neutron velocity and wavelength, respectively, m is the mass of neutron, h is the Planck constant and ds is a short section of neutron path. Therefore, total angle of spin precession around the vector B can be easily obtained by integrating Eq. (6.17) across the neutron path:

$$\phi = \int {\gamma_{n} \frac{\lambda m}{h}\left| {\vec{B}(s)} \right|\sin \theta {\text{d}}s}$$

(6.18)

The spin precession is dependent on the magnitude and direction of the magnetic field, as well as the neutron wavelength, as can be seen from the preceding equation. As a result, a monochromatic neutron beam with a longer wavelength (cold neutrons) is preferred to precisely investigate the magnetic field. It is worth noting that the precession angle can be linked to the integrated field along the neutrons path through the magnetic field, provided monochromatic neutron beam is used for carrying out the experiments. However, it is also possible to utilize polychromatic neutron beam, if the energy of neutron can be measured, and therefore, its wavelength distribution is known or can be precisely measured. Multiple observations with all conceivable combinations of neutron beam polarization vectors and in combination with polarization analyser are required for a complete three-dimensional reconstruction of the magnetic field vector B. A typical experimental arrangement for carrying out polarized neutron imaging experiments is shown in Fig. 6.16.

Fig. 6.16

Reproduced from [48] with permission from © 2009 Elsevier

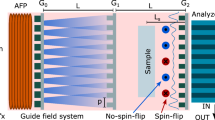
Experimental setup for polarized neutron imaging.

As seen from Fig. 6.16, the signal recorded by the two-dimensional neutron detector placed after the neutron analyser is nothing but a two-dimensional inhomogeneous intensity distribution (projection image), and the same can be expressed as a product of the contrast due to polarization vector rotation, I_p(x, y), and the traditional attenuation image, I_abs(x, y), as follows:

$$I(x,y) = I_{{\text{a}}} (x,y) \times I_{{\text{p}}} (x,y) = I_{{\text{a}}} (x,y)\frac{1}{2}\left( {1 + \cos \alpha (x,y)} \right)$$

(6.19)

where

$$I_{{\text{a}}} (x,y) = I_{0} (x,y){\text{e}}^{{ - \int {\mu (x,y,z){\text{d}}z} }}$$

(6.20)

where μ(x, y, z) is the sample’s linear attenuation coefficient as a function of spatial coordinates (x, y, z), I₀(x, y) is the incident beam’s intensity, and α is the angle the analyser maximum direction of transmission and neutron polarization vector. It should be emphasized that, as can be shown from Eq. (6.19), the measured intensity is only dictated by the sample attenuation if there are no magnet field components perpendicular to the initial polarization direction (ϕ = 0 because no rotational precession is present for θ = 0). Alternatively, if the magnetic field of the sample can be turned off (e.g. magnetic field created by a current), the impact of sample attenuation may be evaluated first and subsequently utilized for normalization and to isolate the magnetic field component from Eq. (6.19). Another option is to rotate the polarizer 180° and repeat the measurement for two spin components separately. The degree of beam depolarization can be reconstructed precisely [8] using spin up and down measurements for both with the sample and without sample, and the attenuation attributable to the sample can be easily isolated.

The other directions of magnetic field components can be studied by realigning the spin polarizer and analyser along the other axes. By varying the orientations of the spin polarizer and analyser, a series of nine measurements may be acquired, allowing the complete three-dimensional magnetic field distribution to be reconstructed. Figure 6.17a shows an example of distribution of trapped magnetic field in a Niobium superconducting radio-frequency cavity, and influence of AC external magnetic field on flux trapping behaviour by varying their amplitude, frequency and offset was investigated. The spatially resolved magnetic field distribution within the cavity shows that in contrast to type-I superconductor, the trapped flux seems to be homogeneously distributed. Similarly Fig. 6.17b shows three-dimensional distribution of magnetic field within the type-I superconductor lea at 4.3 K. This shows that polarized neutron imaging can be used to visualize and quantify an arbitrary magnetic vector; fields within bulk materials can be visualized and quantified in 3D using a set of nine spin-polarized neutron imaging measurements and using novel tensorial multiplicative algebraic reconstruction techniques [49].

Fig. 6.17

a Nb_oxid sample (orientation 90°), B_offset = 0 mT … 5 mT (horizontal images) and increasing AC-frequency f = 0.1, 0.25 and 0.5 Hz (vertical images), blue ~0.5 and red ~0.9 normalized intensity [50]. b Tensorial neutron tomography measurement of the three-dimensional distribution of the y-component of the magnetic vector field inside the bulk of the superconductor at 4.3 K. a 3D visualization of the magnetic flux density, b colour-coded magnetic flux density (y-component) in the vertical cross section (yz-plane) and c magnetic flux distribution in selected horizontal planes as marked by the arrows [49]

Another approach enabling polarized neutron imaging is to use Ramsey’s technique of separated oscillating fields in conjunction with a neutron imaging detector, which is comparable to other spin-echo techniques like pulsed nuclear magnetic resonance or neutron spin-echo (Fig. 6.18). A neutron Ramsey apparatus consists of a region homogeneous steady magnetic field through use of permanent magnets or coils, and the spins of the (monoenergetic) polarized neutron beam is non-adiabatically flipped twice by 90° by a combination of two phase-locked fields oscillating perpendicularly the direction of steady magnetic field. A spin analyser is positioned between the neutron imaging detector and the second spin flipper, and by successively scanning the oscillating field around the Larmor frequency, quantitative distribution of the magnetic fields may be obtained through careful analysis of obtained Ramsey pattern.

Fig. 6.18

a Photograph of the Ramsey apparatus. Reproduced from [51] with permission from Copyright © 2009 Elsevier. b A radiography image of 9 mm-long cylindrical ferromagnetic rod obtained using Ramsey technique showing magnetic field lines and corresponding phase shifts. Reproduced from [52] with permission from Copyright © 2009 American Physical Society

6.6 Neutron Spin-Echo Imaging

As discussed in previous section, one can use different types of neutron optical elements to introduce modulation in the neutron beam. These structured modulations of the neutron beam intensity in presence and absence of the object helps to retrieve phase gradients that can be related to the real part of the neutron scattering length. The basic idea of neutron spin-echo imaging technique is to manipulate the polarization state of beam, and generate controlled spatial modulation of the neutron beam intensity by creating Larmor precession phase differences. Such modulations have been already used in small-angle scattering experiments.

Figure 6.19 shows the fundamental concept of the experimental setup. The setup is realized by two triangular magnetic field sectors with equal apex angles, in which the spins of a polarized neutron beam precesses around the external magnetic field. Magnetic fields within these triangular sectors are of opposing sign and strength, and these values are modified based on the distances between these devices and the detector. The precession of neutron spin in the first magnetic field is fully compensated by the second magnetic field for those neutrons that arrive at the detector plane along the optical axis of the triangle magnetic field areas, fulfilling the requirement of a spin-echo of the precession in each device [47].

Fig. 6.19

Schematic illustration of experimental setup for carrying out neutron spin-echo imaging [53]

The precession of the neutron spin, along a path parallel to the optical axis, is proportionally to the relative distance from the optical axis. The precession of neutron spin in the triangular region of magnetic field B, as shown in Fig. 6.19, is dependent only on the height of the neutron path, say y, and be expressed as follows:

$$\phi = \frac{{2\lambda m\gamma_{n} B}}{{h\tan \theta_{0} }}y$$

(6.21)

where θ₀ is the inclination of the precession field surfaces to the beam, λ the wavelength and γ_n and m the gyromagnetic ratio and the mass of the neutron and the h is the Planck constant. For the neutron travelling along another path and arriving at the same height from the optical axis will likewise have a spin-echo, if L₁B₁ = L₂B₂, where B₁ and B₂ are the magnetic fields in the precession devices and L₁ and L₂ are the distances to the detector. The resultant spin precession is only dependent on the location of the neutron (y-coordinate) at the detector which can be simply written as

$$\phi = \frac{{2\lambda m\gamma_{n} }}{{h\tan \theta_{0} }}(B_{1} - B_{2} )y$$

(6.22)

This precession results at the lateral modulation in the neutron beam intensity are recorded at detector with a period:

$$p = \frac{{\pi h\lambda \tan \theta_{0} }}{{2m\gamma_{n} (B_{1} - B_{2} )}}$$

(6.23)

The period of the modulation is determined by the wavelength employed, the magnetic field settings and the field inclination. Figure 6.20 depicts an example of neutron spin-echo-based imaging. The object consist of two cuvettes kept on top of each other, while the top cuvette contained a magnetic metal powder of few micron grain size, and the lower cuvette was filled monodispersed polystyrene nanoparticles of 136 nm diameter suspended in D₂O solution. The pixel-by-pixel analysis of data showed good agreement with the complimentary SESANS measurements and theory curves describing the structural features of 1 µm and 136 nm for the metallic powder and the PS dispersion, respectively [53].

Fig. 6.20

a Sample setup photo with the exposed area highlighted. b Attenuation contrast image of exposed region. c Dark-field SEMSANS image displaying the visibility of the spin-echo modulation at a certain spin-echo length. Three areas of interest are highlighted in b, c: powder sample (i), empty beam area (j) and PS dispersion (k) [53]

The data was analysed pixel by pixel and found to be in good agreement with complementary SESANS measurements and generated theoretical curves. The data could be modelled and explain properly with dimensions of 1 µm and 136 nm metallic powder, thereby validating the proposed approach.

6.7 Summary

We have outlined various advanced phase neutron imaging techniques, which can be easily implemented in a conventional neutron imaging facility. The phase-contrast imaging extends the use of neutrons for new class of materials like metal composites, metal foams, where the contrast in the attenuation-based imaging is expected to be quite weak. We believe that the phase-based neutron imaging will be useful in increasing utilization of neutron imaging for industrial problems. In parallel, neutron spin-dependent interaction with the matter can be used to map the electric and magnetic field within the bulk of the materials. Due to high penetration depth of neutrons in most of the materials, the polarized neutron imaging is uniquely placed. One can even combine the phase-sensitive interaction with polarized neutrons to obtain anisotropic distributions in magnetic fields.