A Six-Node Triangular Shell Based on the Local Frame of Lie Group

Abstract

Most of the previous shell elements based on the classic geometrically exact shell theory focused on the quadrilateral meshes. However, shell elements with quadrilateral meshes are difficult to model shell structures with arbitrary geometry. In this paper, a novel six-node triangular shell with five degrees of freedom per node based on the local frame approach is presented on the special Euclidean group SE(3), which is an extension of our recent work [1]. Considering the classic Mindlin–Ressiner hypothesis, the total Lagrangian method and Green–Lagrange strain tensor are employed for shells with large displacements and large rotations. To ensure the objectivity of the discretized strain measures, the rigid-body motion of the reference point within an element is removed and the relative motion is interpolated. To improve element solution accuracy, the strain interpolation schemes based on the assumed strain method are used to eliminate membrane and shear locking. The effectiveness of the presented novel triangular shell is demonstrated by several popular geometrically nonlinear benchmark examples.

1 Introduction

Geometrically nonlinear behaviors of plates and shells are widely involved in the fields of aerospace and civil engineering. As reported in our recent work [1, 2], shell and beam elements based on the geometrically exact theory on SE(3) exhibit good properties. The Jacobian matrices corresponding to the inertial and elastic forces are invariant under the rigid-body motion, which results in the reduction of the geometric nonlinearity of rigid-body motion. For the geometrically nonlinear problems, the number of the update times required for the Jacobian matrices declines sharply, which improves the computational efficiency in dynamic analysis. However, this related study of the geometrically exact shell on SE(3) only focused on quadrilateral elements. In practice, the modeling complex engineering structures such as a spinning solar sail with a hexagonal membrane [3] frequently requires the combination of quadrilateral and triangular elements or integral triangular elements. Moreover, triangular shell elements are relatively efficient for automatic mesh generation and perform well in dealing with shell structures with complicate geometry.

Usually, to develop shell elements with good performance, the membrane and shear locking are difficult to circumvent. Because the locking phenomena affect the computational accuracy for shells dominated by bending or membrane-bending mixed problems [4, 5]. Fortunately, numerous and effective locking alleviation techniques for membrane and shear locking have been investigated over the past decades. As one of the most commonly used techniques, the uniform or selective reduced integration techniques, originally reported in Ref. [6, 7], were successfully used to alleviate locking [8,9,10,11,12,13]. However, the use of the technique of reduced integration is often accompanied with the appearance of spurious zero energy modes [14]. As an alternative, the assumed natural strain (ANS) approach shows better accuracy and robust [15,16,17]. This approach was originally applied to four-node quadrilateral plate elements [18] by Hughes and Tezduyar, and then to shell elements by Dvorkin and Bathe [19]. Later, the ANS approach was widely employed for the locking alleviation of in a family of shell elements based on the Mixed Interpolation of Tensorial Components (MITC) approach and other shell elements [20,21,22,23,24,25,26,27]. In our recent study [1], the ANS approach was also used to eliminate shear locking of a geometrically exact shell formulated on SE(3) and good solution accuracy was observed.

On basis of the Simo’s shell theory [28], Flores et al. [29] proposed a group of triangular shell elements for linear and nonlinear analysis. As a matter of fact, the work done by Flores et al. was an extension of the triangular shell elements proposed by Oñate et al. [30, 31]. Lee and Bathe [20] presented several three-node and six-node MITC shell elements and corresponding assumed strain interpolation schemes to avoid membrane and transverse locking. Kim and Bathe [21] proposed a triangular six-node shell element that represented a significant improvement over the previous six-node shell element [20]. Recently, MRezaiee–Pajand et al. [24] extended the six-node shell element proposed by Kim and Bathe to geometrically nonlinear analysis. However, a six-node triangular shell based on geometrically exact shell theory in the SE(3) framework has not been reported so far.

The unique feature of the Local Frame of Lie Group (LFLG) [1] can eliminate the geometrically nonlinear of the overall rigid motion for flexible components. Therefore, the generalized inertial forces and internal forces as well as their Jacobian matrices are invariable under the arbitrary rigid body motion. However, our recent work has been limited to quadrilateral shell meshes [1], and there are difficulties in modeling finite elements of shell structures containing arbitrary geometries. The contribution of this paper is to develop a six-node triangular shell with 5-DoF per node based on the local frame, which is helpful to promote the development of the next-generation software of multibody system dynamics [1]. Besides, to improve solution accuracy, the strain interpolation schemes presented in [20, 21] are used to alleviate membrane and shear locking. The versatility of the presented triangular shell was validated by several popular geometrically nonlinear benchmarks.

2 Deformation Description

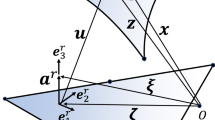
$\mathcal{B}_{0} \;{\text{and}}\;\mathcal{B}$ refer to the reference and current configurations of a six-node shell element in Fig. 1. The configuration space of a geometrically exact shell [28] can be represented by a position on the mid-surface and a unit direction vector. e = {e₁, e₂, e₃}, an inertial coordinate system, is regarded as a reference system. Additionally, A₁, A₂, and A₃ denote the areas of the triangles P12, P23, and P31, respectively.

The position of any point P in the current configuration can be written as

$$ {\mathbf{x}}_{P} (\xi_{1} ,\xi_{2} ,\xi_{3} ) = {\mathbf{x}}(\xi_{1} ,\xi_{2} ) + \xi_{3} {\mathbf{t}}(\xi_{1} ,\xi_{2} ) = {\mathbf{x}}(\xi_{1} ,\xi_{2} ) + {\mathbf{R}}(\xi_{1} ,\xi_{2} ){\mathbf{y}}_{P} (\xi_{3} ), $$

(1)

where x ∈ ${\mathbb{R}}^{3}$ and t ∈ S² (a unit sphere) denote the position vector and the unit direction vector under global coordinate system. In addition, R, an element of the special orthogonal group SO(3), represents the rotation of the director vector, y_P(ξ₃) = ξ₃e₃, and ξ₃ ∈ [−h/2, h/2] is the coordinate spanning the shell’s thickness. Note that according to [28], the variation δt of the direction vector belongs to the tangent space of S² and has only two independent components. As a matter of fact, per node of the classical geometrically exact shell has 5-DoF.

Fig. 1.

General motion of a six-node shell element.

The current configuration on SE(3) can be expressed as

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{x}}_{P} {(}\xi_{1} {,}\xi_{2} {,}\xi_{3} {)}} \\ 1 \\ \end{array} } \right] = {\mathbf{H}}(\xi_{1} ,\xi_{2} )\left[ {\begin{array}{*{20}c} {{\mathbf{y}}_{P} (\xi_{3} )} \\ 1 \\ \end{array} } \right], $$

(2)

where H ∈ SE(3), including the translational and rotational information of a shell, can be obtained as follows

$$ {\mathbf{H}} = \mathcal{H}({\mathbf{R}},{\mathbf{x}}) = \left[ {\begin{array}{*{20}c} {\mathbf{R}} & {\mathbf{x}} \\ {{\mathbf{0}}_{1 \times 3} } & 1 \\ \end{array} } \right] $$

(3)

Taking the variation and derivative of H to a parameter s, the following expressions can be obtained

$$ \updelta {\mathbf{H}} = {\mathbf{H}}(\updelta {\mathbf{h}})^{\sim } ,\quad \quad \frac{{{\text{d}}{\mathbf{H}}}}{{{\text{d}}s}} = {\mathbf{H}}\tilde{\mathbf{f}}, $$

(4)

with

$$ \updelta {\mathbf{h}} = \left[ {\begin{array}{*{20}c} {\updelta {\mathbf{h}}_{u} } \\ {\updelta {\mathbf{h}}_{\omega } } \\ \end{array} } \right] \in {\mathbb{R}}^{6} ,\quad \quad (\updelta {\mathbf{h}})^{\sim } = \left[ {\begin{array}{*{20}c} {(\updelta {\mathbf{h}}_{\omega } )^{\sim } } & {\updelta {\mathbf{h}}_{u} } \\ {{\mathbf{0}}_{1 \times 3} } & 0 \\ \end{array} } \right] \in se(3), $$

(5)

where ${\mathbf{h}} = [{\mathbf{h}}_{u}^{{\text{T}}} {, }{\mathbf{h}}_{\omega }^{{\text{T}}} ]^{{\text{T}}}$ and ${\mathbf{f}} = \left[ {\begin{array}{*{20}c} {{\mathbf{f}}_{u}^{{\text{T}}} } & {{\mathbf{f}}_{\omega }^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}}$ consist of two 3 × 1 vectors. The notations $( \bullet )^{\sim }$ and $\tilde{ \bullet }$ represent that there is an invertible linear map from ${\mathbb{R}}^{k}$ to the Lie algebra, the expression of which depends on the dimension k. se(3) indicates the Lie algebra space of SE(3). In addition, δh_u = R^Tδx is the position variable, and (δh_ω)^~  = R^TδR.

According to continuum mechanics, the strain tensor E(ξ₁, ξ₂, ξ₃) can be obtained as

$$ E_{ij} = \frac{1}{2}\left( {F_{ik}^{{\text{T}}} F_{kj} - \delta_{ij} } \right) = \frac{1}{2}\left( {\frac{{\partial {\mathbf{x}}_{P}^{{\text{T}}} }}{{\partial \xi_{i} }}\frac{{\partial {\mathbf{x}}_{P} }}{{\partial \xi_{j} }} - \frac{{\partial {\mathbf{x}}_{P}^{{{\text{0T}}}} }}{{\partial \xi_{i} }}\frac{{\partial {\mathbf{x}}_{P}^{0} }}{{\partial \xi_{j} }} \, } \right), $$

(6)

with

$$ \left\{ {\begin{array}{*{20}c} {\frac{{\partial {\mathbf{x}}_{P} {(}\xi_{1} {,}\xi_{2} {,}\xi_{3} {)}}}{{\partial \xi_{1} }} = {\mathbf{RNf}}_{1} } \\ {\frac{{\partial {\mathbf{x}}_{P} {(}\xi_{1} {,}\xi_{2} {,}\xi_{3} {)}}}{{\partial \xi_{2} }}{ = }{\kern 1pt} {\kern 1pt} {\mathbf{RNf}}_{2} } \\ {\frac{{\partial {\mathbf{x}}_{P} {(}\xi_{1} {,}\xi_{2} {,}\xi_{3} {)}}}{{\partial \xi_{3} }}{ = }{\kern 1pt} {\kern 1pt} {\mathbf{Re}}_{3} } \\ \end{array} } \right., $$

(7)

where F_kj and δ_ij in Eq. (6) indicate the deformation gradient and the Kronecker delta, i, j, k = 1, 2, 3. ${\mathbf{N}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{3 \times 3} } & { - {\tilde{\mathbf{y}}}_{P} } \\ \end{array} } \right]$, ${\mathbf{f}}_{i} = \left[ {\begin{array}{*{20}c} {{\mathbf{f}}_{iu}^{{\text{T}}} } & {{\mathbf{f}}_{i\omega }^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}} \in {\mathbb{R}}^{6}$, i = 1, 2. Assuming a curved initial configuration, the deformation measures can be decomposed into

$$ {\mathbf{f}}_{i} (\xi_{1} ,\xi_{2} ) = {\mathbf{f}}_{i}^{0} (\xi_{1} ,\xi_{2} ) + {{\varvec{\upvarepsilon}}}_{i} (\xi_{1} ,\xi_{2} ), $$

(8)

where ${\mathbf{f}}_{i}^{0}$ and ε_i are the deformation measures of the reference configuration and the deformation of the current configuration with respect to the reference configuration, respectively. Then, ε_i can be obtained as

$$ {{\varvec{\upvarepsilon}}}_{i} = \left[ {\begin{array}{*{20}c} {{\mathbf{f}}_{iu} - {\mathbf{f}}_{iu}^{0} } \\ {{\mathbf{f}}_{i\omega } - {\mathbf{f}}_{i\omega }^{0} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{R}}^{{\text{T}}} {\mathbf{x}} - {\mathbf{R}}^{{\text{T}}} {\mathbf{x}}^{0} } \\ {axi({\mathbf{R}}^{{\text{T}}} {\mathbf{R^{\prime}}}) - axi({\mathbf{R}}^{{0{\text{T}}}} {\mathbf{R}}^{0^{\prime}} )} \\ \end{array} } \right], $$

(9)

where $( \bullet )_{,i} = \partial ( \bullet )/\partial \xi_{i}$, and $axi( \bullet )$ refers to the axial vector of the antisymmetric matrix $\bullet$. The tangent operator T_SO(3) and its inverse are introduced as

$$ \left\{ \begin{aligned} & {\mathbf{T}}_{SO(3)} ({{\varvec{\Theta}}}) = {\mathbf{I}}_{3 \times 3} - a_{2} ({{\varvec{\Theta}}}){\tilde{\varvec{\Theta }}} + a_{3} ({{\varvec{\Theta}}}){\varvec{\tilde{\Theta }\tilde{\Theta }}} \\ & {\mathbf{T}}_{SO(3)}^{ - 1} ({{\varvec{\Theta}}}) = {\mathbf{I}}_{3 \times 3} + \frac{1}{2}{\tilde{\mathbf{\Theta }}} + a_{4} ({{\varvec{\Theta}}}){\varvec{\tilde{\Theta }\tilde{\Theta }}} \\ \end{aligned} \right., $$

(10)

where $a_{3} ({{\varvec{\Theta}}}) = (\left\| {{\varvec{\Theta}}} \right\| - \sin (\left\| {{\varvec{\Theta}}} \right\|))/\left\| {{\varvec{\Theta}}} \right\|^{3}$, $a_{4} ({{\varvec{\Theta}}}) = (1 - \frac{{\left\| {{\varvec{\Theta}}} \right\|}}{2}\cot (\frac{{\left\| {{\varvec{\Theta}}} \right\|}}{2}))/\left\| {{\varvec{\Theta}}} \right\|^{2}$.

The expressions of $E_{ij}$ in Eq. (6) can be written as

$$ \left\{ \begin{aligned} & E_{11} = - {\mathbf{f}}_{1u}^{{\text{T}}} \xi_{3} {\tilde{\mathbf{e}}}_{3} {\mathbf{f}}_{1\omega } + {\mathbf{f}}_{1u}^{{0{\text{T}}}} \xi_{3} {\tilde{\mathbf{e}}}_{3} {\mathbf{f}}_{1\omega }^{0} + \frac{1}{2}({\mathbf{f}}_{1u}^{{\text{T}}} {\mathbf{f}}_{1u} - {\mathbf{f}}_{1u}^{{0{\text{T}}}} {\mathbf{f}}_{1u}^{0} ) \\ & E_{12} = E_{21} = - {\mathbf{f}}_{1u}^{{\text{T}}} \xi_{3} {\tilde{\mathbf{e}}}_{3} {\mathbf{f}}_{2\omega } + {\mathbf{f}}_{1u}^{{0{\text{T}}}} \xi_{3} {\tilde{\mathbf{e}}}_{3} {\mathbf{f}}_{2\omega }^{0} + \frac{1}{2}({\mathbf{f}}_{1u}^{{\text{T}}} {\mathbf{f}}_{2u} - {\mathbf{f}}_{1u}^{{0{\text{T}}}} {\mathbf{f}}_{2u}^{0} ) \\ & E_{13} = E_{31} = \frac{1}{2}({\mathbf{f}}_{1u} - {\mathbf{f}}_{1u}^{0} )^{{\text{T}}} {\mathbf{e}}_{3} \\ & E_{22} = - {\mathbf{f}}_{2u}^{{\text{T}}} \xi_{3} {\tilde{\mathbf{e}}}_{3} {\mathbf{f}}_{2\omega } + {\mathbf{f}}_{2u}^{{0{\text{T}}}} \xi_{3} {\tilde{\mathbf{e}}}_{3} {\mathbf{f}}_{2\omega }^{0} + \frac{1}{2}({\mathbf{f}}_{2u}^{{\text{T}}} {\mathbf{f}}_{2u} - {\mathbf{f}}_{2u}^{{0{\text{T}}}} {\mathbf{f}}_{2u}^{0} ) \\ & \begin{array}{*{20}c} {E_{23} = E_{32} = \frac{1}{2}({\mathbf{f}}_{2u} - {\mathbf{f}}_{2u}^{0} )^{{\text{T}}} {\mathbf{e}}_{3} } & {E_{33} = 0} \\ \end{array} \\ \end{aligned} \right.. $$

(11)

The membrane strain χ, bending strain δ, and shear strain ρ are given by

$$ \begin{array}{*{20}l} {\chi_{ij} = \frac{1}{2}({\mathbf{f}}_{iu}^{{\text{T}}} {\mathbf{f}}_{ju} - {\mathbf{f}}_{iu}^{{0{\text{T}}}} {\mathbf{f}}_{ju}^{0} )} \hfill \\ {\delta_{ij} = - \xi_{3} ({\mathbf{f}}_{iu}^{{\text{T}}} {\tilde{\mathbf{e}}}_{3} {\mathbf{f}}_{j\omega } - {\mathbf{f}}_{iu}^{{0{\text{T}}}} {\tilde{\mathbf{e}}}_{3} {\mathbf{f}}_{j\omega }^{0} )} \hfill \\ {\rho_{i} = ({\mathbf{f}}_{iu} - {\mathbf{f}}_{iu}^{0} )^{{\text{T}}} {\mathbf{e}}_{3} } \hfill \\ \end{array} . $$

(12)

3 Equilibrium Equations

The virtual work of static equilibrium equations can be expressed as

$$ \delta \mathcal{W}_{{{\text{int}}}} - \delta \mathcal{W}_{{{\text{ext}}}} = 0 , $$

(13)

where δ$\mathcal{W}_{{{\text{int}}}}$ and δ$\mathcal{W}_{{{\text{ext}}}}$ indicate the virtual work done by the internal and external forces.

Considering the isotropic linear elastic material, the internal virtual work reads

$$ \updelta \mathcal{W}_{{{\text{int}}}} = \int_{S} {(\updelta {{\varvec{\upchi}}}^{{\text{T}}} {\mathbb{C}}_{m} {{\varvec{\upchi}}} + \updelta {{\varvec{\updelta}}}^{{\text{T}}} {\mathbb{C}}_{b} {{\varvec{\updelta}}} + \updelta {{\varvec{\uprho}}}^{{\text{T}}} {\mathbb{C}}_{s} {{\varvec{\uprho}}}){\text{d}}S} , $$

(14)

where S is the reference surface area, the matrices ${\mathbb{C}}_{m}$, ${\mathbb{C}}_{s}$ and ${\mathbb{C}}_{b}$ are the corresponding constitutive matrices of the membrane, bending and shear strain, respectively.

The virtual work done by the external forces is obtained as

$$ \delta \mathcal{W}_{{{\text{ext}}}} = \int_{V} {\updelta {\mathbf{x}}_{P}^{{\text{T}}} \,{\mathbf{p}}_{{\text{e}}} } {\text{d}}V = \int_{S} {\updelta {\mathbf{h}}^{{\text{T}}} {\mathbf{p}}_{{{\text{ext}}}} } {\text{d}}S, $$

(15)

where

$$ {\mathbf{p}}_{{{\text{ext}}}} = \int {\left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{3 \times 3} } \\ {{\tilde{\mathbf{y}}}_{P} (\xi_{3} )} \\ \end{array} } \right]{\mathbf{R}}^{{\text{T}}} {\mathbf{p}}_{{\text{e}}} {\text{d}}\xi_{3} } , $$

(16)

where p_e and p_ext are both 3 × 1 vectors of applied external forces expressed in the reference frame and the local frame, and I_3×3 is a 3 × 3 unit matrix.

4 Finite Element Discretization

For the discretization of the virtual work of the internal force, the core is the variations of the deformation measures ε_i. According to Eq. (9), the variations of ε_i can be evaluated as

$$ \updelta {\varvec{\upvarepsilon}}_{i} = \left[ {\begin{array}{*{20}c} {\updelta {\mathbf{f}}_{iu} } \\ {\updelta {\mathbf{f}}_{i\omega } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{G}}_{iu} \updelta {\mathbf{h}}_{{\text{N}}} } \\ {{\mathbf{G}}_{i\omega } \updelta {\mathbf{h}}_{{\text{N}}} } \\ \end{array} } \right],\;\updelta {\mathbf{h}}_{{\text{N}}} = \left[ {\begin{array}{*{20}c} {{\varvec{\updelta}} {\mathbf{u}}^{{\text{N}}} } \\ { {{\varvec{\updelta \Theta}}}^{{\text{N}}} } \\ \end{array} } \right], $$

(17)

where u^N and Θ^N denote the local displacement and rotation vectors of nodes, and the detailed expressions of G_iu and G_iω can be obtained according to the Appendix.

The discretization form of the virtual work of the internal force can be expressed as

$$ \updelta \mathcal{W}_{{\text{int}}} = \updelta {\mathbf{h}}_{{\text{N}}}^{{\text{T}}} \int_{S} {(B_{m}^{{\text{T}}} \,{\mathbb{C}}_{m} {\varvec{\chi}} + {\mathbf{B}}_{b}^{{\text{T}}} \,{\mathbb{C}}_{b} {\varvec{\updelta}} + {\mathbf{B}}_{s}^{{\text{T}}} \,{\mathbb{C}}_{s} {\varvec{\uprho}} ){\text{d}}S} , $$

(18)

where

$$ {\mathbf{B}}_{m} = \left[ {\begin{array}{*{20}c} {{\mathbf{f}}_{1u}^{{\text{T}}} {\mathbf{G}}_{1u} } \\ {{\mathbf{f}}_{2u}^{{\text{T}}} {\mathbf{G}}_{2u} } \\ {{\mathbf{f}}_{1u}^{{\text{T}}} {\mathbf{G}}_{2u} + {\mathbf{f}}_{2u}^{{\text{T}}} {\mathbf{G}}_{1u} } \\ \end{array} } \right], $$

(19)

$$ {\mathbf{B}}_{s} = \left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{3}^{{\text{T}}} {\mathbf{G}}_{1u} } \\ {{\mathbf{e}}_{3}^{{\text{T}}} {\mathbf{G}}_{2u} } \\ \end{array} } \right], $$

(20)

$$ {\mathbf{B}}_{b} = \left[ {\begin{array}{*{20}c} { - {\mathbf{f}}_{1u}^{{\text{T}}} {\tilde{\mathbf{e}}}_{3} {\mathbf{G}}_{1\omega } + {\mathbf{f}}_{1\omega }^{{\text{T}}} {\tilde{\mathbf{e}}}_{3} {\mathbf{G}}_{1u} } \\ { - {\mathbf{f}}_{2u}^{{\text{T}}} {\tilde{\mathbf{e}}}_{3} {\mathbf{G}}_{2\omega } + {\mathbf{f}}_{2\omega }^{{\text{T}}} {\tilde{\mathbf{e}}}_{3} {\mathbf{G}}_{2u} } \\ { - {\mathbf{f}}_{1u}^{{\text{T}}} {\tilde{\mathbf{e}}}_{3} {\mathbf{G}}_{2\omega } + {\mathbf{f}}_{2\omega }^{{\text{T}}} {\tilde{\mathbf{e}}}_{3} {\mathbf{G}}_{1u} - {\mathbf{f}}_{2u}^{{\text{T}}} {\tilde{\mathbf{e}}}_{3} {\mathbf{G}}_{1\omega } + {\mathbf{f}}_{1\omega }^{{\text{T}}} {\tilde{\mathbf{e}}}_{3} {\mathbf{G}}_{2u} } \\ \end{array} } \right]. $$

(21)

The linearization of the virtual work done by the internal forces can be computed as

$$ \Delta (\updelta \mathcal{W}_{{\text{int}}} ) = \updelta {\mathbf{h}}_{{\text{N}}}^{{\text{T}}} {\mathbf{K}}_{{{\text{mat}}}} \Delta {\mathbf{h}}_{{\text{N}}} + \updelta {\mathbf{h}}_{{\text{N}}}^{{\text{T}}} {\mathbf{K}}_{{{\text{geo}}}} \Delta {\mathbf{h}}_{{\text{N}}} , $$

(22)

the expressions of the material and geometric stiffness matrices K_mat and K_geo are expressed as follows

$$ {\mathbf{K}}_{{{\text{mat}}}} = \int_{S} {{(}{\mathbf{B}}_{m}^{{\text{T}}} {\mathbb{C}}_{m} {\mathbf{B}}_{m} + {\mathbf{B}}_{s}^{{\text{T}}} {\mathbb{C}}_{s} {\mathbf{B}}_{s} + {\mathbf{B}}_{b}^{{\text{T}}} {\mathbb{C}}_{b} {\mathbf{B}}_{b} ){\text{d}}S} , $$

(23)

$$ {\mathbf{K}}_{{{\text{geo}}}} = \int_{S} {{(}\Delta {\mathbf{B}}_{m}^{{\text{T}}} {\mathbb{C}}_{m} {{\varvec{\upchi}}} + \Delta {\mathbf{B}}_{s}^{{\text{T}}} {\mathbb{C}}_{s} {{\varvec{\uprho}}} + \Delta {\mathbf{B}}_{b}^{{\text{T}}} {\mathbb{C}}_{b} {{\varvec{\updelta}}}){\text{d}}S} , $$

(24)

where the expressions of ΔB_m ΔB_s and ΔB_b can be obtained from the Appendix.

The discretized virtual work of the external forces can be presented as

$$ \updelta \mathcal{W}_{{{\text{ext}}}} = \updelta {\mathbf{h}}_{{\text{N}}}^{{\text{T}}} \int_{S} {{\mathbf{N}}_{u}^{{*{\text{T}}}} } \int {\left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{3 \times 3} } \\ {{\tilde{\mathbf{y}}}_{p} (\xi_{3} )} \\ \end{array} } \right]({\mathbf{R}}^{{\text{T}}} {\mathbf{p}}_{e} ){\text{d}}\xi_{3} {\text{d}}S} , $$

(25)

then, the following expression can be obtained after performing the linearization

$$ \Delta (\updelta \mathcal{W}_{{{\text{ext}}}} ) = \updelta {\mathbf{h}}_{{\text{N}}}^{{\text{T}}} \int_{S} {{\mathbf{N}}_{u}^{{*{\text{T}}}} \int {\left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{3 \times 3} } \\ {{\tilde{\mathbf{y}}}_{p} (\xi_{3} )} \\ \end{array} } \right]\widetilde{{({\mathbf{R}}^{{\text{T}}} {\mathbf{p}}_{e} )}}\;{\mathbf{N}}_{\omega }^{*} {\text{d}}\xi_{3} {\text{d}}S\Delta {{\varvec{\Theta}}}^{{\text{N}}} } } , $$

(26)

where ${\mathbf{N}}^{*} (\xi_{1} ,\xi_{2} ) = \left[ {\begin{array}{*{20}c} {{\mathbf{N}}_{u}^{{*{\text{T}}}} } & {{\mathbf{N}}_{\omega }^{{*{\text{T}}}} } \\ \end{array} } \right]^{{\text{T}}}$ is the standard shape function of the six-node triangular element.

5 Strain Interpolation Schemes

The strain interpolation schemes for membrane and shear strains reported in [20] performs well for problems dominated by both bending and membrane and results in an effective MITC6 shell element. Since successful applications of the schemes, the strain interpolation schemes are also employed to alleviate membrane and shear locking in this study.

Figures 2 and 3 exhibit the interpolation schemes for membrane and shear strains, respectively. Note that for membrane strains, to obtain the in-plane shear strain $\overline{\chi }_{12}$, the following equation is used

$$ \overline{\chi }_{12} = \frac{1}{2}(\overline{\chi }_{11} + \overline{\chi }_{22} ) - \overline{\chi }_{33} , $$

(27)

$$ \xi_{1}^{1} = \xi_{2}^{1} = \frac{1}{2} - \frac{1}{2\sqrt 3 },\;\xi_{1}^{2} = \xi_{2}^{2} = \frac{1}{2} + \frac{1}{2\sqrt 3 },\;\xi_{1}^{3} = \xi_{2}^{3} = \frac{1}{2} + \frac{1}{2\sqrt 3 }, $$

(28)

For details on how to obtain the coefficients a₁, b₁, c₁, …, f₁, f₂, see Ref. [20].

Fig. 2.

The interpolation and tying points used for membrane strain.

Fig. 3.

The interpolation and tying points used for shear strain.

Fig. 4.

Cantilever plate subjected to end moment.

Fig. 5.

Load–displacement curves of free end.

Fig. 6.

Deformation configurations.

6 Numerical Examples

6.1 Cantilever Plate Subjected to End Moment

Figure 4 illustrates a cantilever bending plate with a distributed moment acting on its free end. This is a typical example to test the large rotation capability of the proposed shell elements [23, 24, 32]. The geometry property of this cantilever plate are set to l = 12, w = 1, and thickness h = 0.01, respectively. The Young’s modulus and Poisson’s ration are set to E = 1.2 × 10⁶ and v = 0. When using the end moment M_max = 2M₀, the plate rolls up into a complete circle, where M₀ = EI/l. The cantilever plate is modeled using a 2 × 16 × 1 shell elements.

In fact, the analytical solution of this example can be obtained from the formula 1/ρ = M/EI, ρ is the curvature radius. The displacements of the free end x or z can be expressed as

$$ \left\{ \begin{aligned} & \frac{x}{l} = \frac{{M_{0} }}{M}\sin (\frac{{M_{0} }}{M}) - 1 \\ & \frac{z}{l} = \frac{{M_{0} }}{M}(1 - \cos (\frac{{M_{0} }}{M})) \\ \end{aligned} \right.. $$

(29)

The variation of displacements versus load steps is illustrated in Fig. 5 and the result obtained by the novel shell element is coincide with the analytical solution. Figure 6 displays the deformed configurations at various load stages and a perfect complete circle is obtained when M = M_max.

6.2 Slit Annular Plate Under Transverse Line Load

A slit annular plate with z-direction distributed transverse forces is exhibited in Fig. 7. This numerical example considered in previous study [23, 24, 32] is to validate the effectiveness of the novel triangular shell element for the thin-walled shell structures. The inner diameter R_i, outer diameter R_e, and thickness h are set to 6, 10, and 0.03, respectively. The Young’s modulus and Poisson’s ration of this annular plate are set to E = 21 × 10⁶ and v = 0.0. As shown in Fig. 7, the AB edge of the slit annular plate is subjected to a uniformly distributed load, and the other edge is fixed to the ground. As reported in [23, 24], the converged result computed by Sze et al. [32] is considered as a reference solution. As shown in Fig. 8, the six-node triangular shell obtains the converged result using a 2 × 10 × 30 element mesh. Figure 9 exhibits the final deformed configuration relative to the initial configuration.

6.3 Pinched Cylinder with Free Edges

Figure 10 exhibits a cylinder shell with concentrated forces and this classical example was considered in our recent work [1]. The geometry property of this shell are set to L = 10.35 mm, R = 4.953 mm, and thickness h = 0.094 mm, respectively. The load applied F to the shell of the shell are set to 40000 N. The material constants of this shell are set to E = 10.5 × 10⁶ N/mm² and v = 0.3125, respectively. In this example, only one-eighth of the shell was modeled due to the geometric symmetry. To demonstrate the correctness of the presented triangular shell element, the obtained results are compared with the converged results in [1]. The variations of the magnitudes of displacements at nodes A, B, and C under different meshes are shown in Fig. 11. It can be clearly seen that the converged result obtained using the navel triangular shell with 2 × 12 × 8 elements is coincide with the reference solution computed by the geometrically exact shell with quadrilateral meshes. Figure 12 depicts the deformed configurations of pinched cylinder under different pulling forces.

Fig. 7.

Problem description of the slit annular plate.

Fig. 8.

Load–displacement curves of slit annular plate.

6.4 Spherical Shell with an 18° Hole

To verify the large deformation capabilities of the novel triangular shell, a spherical shell with thicknesses of h = 0.04(R/h = 250) mm that was previously considered in Ref. [23, 24] is studied in this example. The radius R, Young’s modulus E, and Poisson’s ration v of this spherical shell are set to 10 mm, 6.825 × 10⁷ N/mm² and 0.3, respectively. Figure 13 exhibits the spherical shell with concentrated forces F = 2λF₀, where F₀ = 1 N. The factor λ is set to 200, and only one-quarter of the shell structure was modeled in this example due to the geometric symmetry. The AM and BN planes are symmetric, and the equator indicates a free edge. The converged results obtained using [24] are taken as the reference solutions. It can be seen from Fig. 14 that the results obtained using the novel triangular shell converge at 2 × 20 × 20 meshes, which demonstrates the correctness of the novel triangular shell. Therefore, the novel triangular shell on SE(3) performs well for shell structures with large deformation.

The deformed configurations of the shell under different concentrated forces are exhibited in Figs. 15 and 16.

Fig. 9.

Deformed and initial meshes of slit annular plate.

Fig. 10.

Reference configuration of the pinched cylinder.

7 Conclusions

In this study, based on the local frame approach, a 5-DoF triangular shell with six nodes on SE(3) is presented allowing for large displacements and rotations. To improve the computational accuracy, strain interpolation strategies are used to eliminate the membrane and shearing locking, which is different from the locking alleviation techniques employed by the quadrilateral shell elements in our previous study [1]. According to the excellent performance of the above geometrically nonlinear problems, we can conclude that the proposed triangular shell element is an attractive element for shell structures with curved sides.

Obviously, only the static part of the triangular shell is exhibited in this paper. As reported by [1], the most attractive advantages of the local frame approach are the improvement of the computational efficient and the elimination of the geometric nonlinearity caused by rigid-body motion during the dynamic analysis. However, the geometric nonlinearity of rigid-body motion cannot be completely eliminated due to the absence of drilling DoFs. In fact, the relationship between the drilling DoF and the mid-surface motion can be further established by the polar decomposition of the mid-plane deformation gradient tensor [33], a 6-DoF shell including drilling rotations based on the local frame can be derived. If using this 6-DoF triangular shell in the dynamic analysis, the geometric nonlinearity of rigid-body motion will be eliminated, which results in the reduction of the times of the iterative matrix and the improvement of the computation efficient. This related part is exactly what we are going to study.

Fig. 11.

Magnitudes of displacements.

Fig. 12.

Deformed configurations of the cylinder shell under pulling forces.

Fig. 13.

Pinched hemisphere with an 18° hole

Fig. 14.

Load–displacement curves of a hemispherical shell.

Fig. 15.

Deformed configuration of the hemispherical shell (P = 0.5P_max).

Fig. 16.

Deformed configuration of the hemispherical shell (P = P_max).

Appendix

To observe the objective of the strain measures [34], the relative rotation is interpolated, which is consistent with Ref. [2]. The formula is expressed as

$$ {{\varvec{\Theta}}}_{{\text{I}}}^{{\text{r}}} = N_{{\text{I}}}^{ * } {\mathbf{d}}_{{\text{I}}}^{{\text{r}}} ,\quad {\mathbf{d}}_{{\text{I}}}^{{\text{r}}} = \log ({\mathbf{R}}_{{\text{r}}}^{ - 1} {\mathbf{R}}_{{\text{I}}} ), $$

(30)

where the notation ${{\varvec{\Theta}}}_{{\text{I}}}^{{\text{r}}}$ denotes the relative rotation between nodes r and I, and Rr is the rotation matrix at the reference node, which is typically chosen as the first node within an element [2]. The variations of the relative configuration vector ${\mathbf{d}}_{{\text{k}}}^{{\text{r}}}$ and the strain measures can be given by

$$ \updelta {\mathbf{d}}_{{\text{k}}}^{{\text{r}}} = \left[ {\begin{array}{*{20}c} { - {\mathbf{T}}_{SO(3)}^{ - 1} ( - {\mathbf{d}}_{{\text{k}}}^{{\text{r}}} )} & {{\mathbf{T}}_{SO(3)}^{ - 1} ({\mathbf{d}}_{{\text{k}}}^{{\text{r}}} )} \\ \end{array} } \right]\updelta {{\varvec{\Theta}}}_{{{\text{rk}}}} ,\;\updelta {{\varvec{\Theta}}}_{{{\text{rk}}}} = \left[ {\begin{array}{*{20}c} {\updelta {{\varvec{\Theta}}}_{{\text{r}}} } \\ {\updelta {{\varvec{\Theta}}}_{{\text{k}}} } \\ \end{array} } \right], $$

(31)

$$ \left\{ {\begin{array}{*{20}l} {\updelta {\mathbf{f}}_{\alpha u} = {\mathbf{R}}^{{\text{T}}} {\mathbf{N}}_{u,\alpha }^{ * } {\mathbf{R}}^{ * } {\updelta }{\mathbf{u}}^{{\text{N}}} + \exp ({\tilde{\mathbf{d}}})^{{\text{T}}} \widetilde{{{\mathbf{R}}_{{\text{r}}}^{{\text{T}}} {\mathbf{x}}_{,\alpha } }}\;\updelta {{\varvec{\Theta}}}_{{\text{r}}} + \widetilde{{{\mathbf{R}}^{{\text{T}}} {\mathbf{x}}_{,\alpha } }}\;{\mathbf{T}}({\mathbf{d}}){\updelta }{\mathbf{d}}} \hfill \\ {\updelta {\mathbf{f}}_{\alpha \omega } = {\mathbf{T}}_{u\omega + } (\updelta {\mathbf{h}}_{\omega } ,{\mathbf{h}}_{\omega } )\updelta {\mathbf{d}} + {\mathbf{T}}({\mathbf{d}})\updelta {\mathbf{d}}_{,\alpha } = {{\varvec{\Xi}}}_{{{\mathbf{T}}_{SO(3)}^{{\text{T}}} }} ({\mathbf{d}}_{,\alpha } )\;({\updelta }{\mathbf{d}}) + {\mathbf{T}}({\mathbf{d}})\;\updelta {\mathbf{d}}_{,\alpha } } \hfill \\ \end{array} } \right., $$

(32)

where the symbols exp and T denote the exponential mapping and tangent operations on SO(3), ${\mathbf{d}} = \sum\limits_{k = 1}^{{{\text{N}} - 1}} {N_{{\text{I}}}^{ * } {\mathbf{d}}_{{\text{I}}}^{{\text{r}}} }$ denotes the relative configuration vector on the gauss points, N is the number of nodes. The expressions of G_iu and G_iω are easy to obtain from Eq. (32), and the linearization of δf_α can be derived with the help of an arbitrary 3 × 1 vector a

$$ \begin{array}{*{20}c} {\Delta \updelta {\mathbf{f}}_{\alpha u}^{{\text{T}}} {\mathbf{a}} = {(}\updelta {\mathbf{u}}^{{\text{N}}} )^{{\text{T}}} {\mathbf{M}}^{ * } \Delta {{\varvec{\Theta}}}^{{\text{N}}} { + (}\updelta {\mathbf{u}}^{{\text{N}}} )^{{\text{T}}} {\mathbf{R}}^{{ * {\text{T}}}} {\mathbf{N}}_{,\alpha }^{{ * {\text{T}}}} ({\mathbf{R}}_{{\text{r}}} \widetilde{{\exp ({\tilde{\mathbf{d}}}) \cdot {\mathbf{a}}}}\;\Delta {{\varvec{\Theta}}}_{{\text{r}}} + {\mathbf{R}}\tilde{\mathbf{a}} {\kern 1pt} \Delta {\mathbf{d}})\quad \quad \quad } \\ {{ + }\,\updelta {{\varvec{\Theta}}}_{{\text{r}}}^{{\text{T}}} \widetilde{{{\mathbf{R}}_{{\text{r}}}^{{\text{T}}} {\mathbf{x}}_{,\alpha } }}{\kern 1pt} {\kern 1pt} \exp ({\tilde{\mathbf{d}}}){\tilde{\mathbf{a}}\mathbf{T}}({\mathbf{d}})\Delta {\mathbf{d}} + \updelta {{\varvec{\Theta}}}_{{\text{r}}}^{{\text{T}}} (\widetilde{{\exp ({\tilde{\mathbf{d}}}){\mathbf{a}}}}{\kern 1pt} )\widetilde{{{\mathbf{R}}_{{\text{r}}}^{{\text{T}}} {\mathbf{x}}_{,\alpha } }}\Delta {{\varvec{\Theta}}}_{{\text{r}}} \quad \quad } \\ {\quad \quad \quad + \,(\widetilde{{\exp ({\tilde{\mathbf{d}}}){\mathbf{a}}}}){\kern 1pt} {\mathbf{R}}_{{\text{r}}}^{{\text{T}}} {\mathbf{N}}_{u,\alpha }^{ * } {\mathbf{R}}^{ * } \Delta {\mathbf{u}} - \Delta \updelta {\mathbf{d}}^{{\text{T}}} {\mathbf{T}}({\mathbf{d}})^{{\text{T}}} \widetilde{{{\mathbf{R}}^{{\text{T}}} {\mathbf{x}}_{,\alpha } }}{\kern 1pt} {\mathbf{a}} - (\Delta {\mathbf{T}}({\mathbf{d}})\updelta {\mathbf{d}})^{{\text{T}}} \widetilde{{{\mathbf{R}}^{{\text{T}}} {\mathbf{x}}_{,\alpha } }}{\kern 1pt} {\mathbf{a}}} \\ {\quad \quad \updelta {\mathbf{d}}^{{\text{T}}} {\mathbf{T}}({\mathbf{d}})^{{\text{T}}} {\tilde{\mathbf{a}}}({\mathbf{R}}^{{\text{T}}} {\mathbf{N}}_{u,\alpha }^{ * } {\mathbf{R}}^{ * } \Delta {\mathbf{u}} + \exp ({\tilde{\mathbf{d}}})^{{\text{T}}} \widetilde{{{\mathbf{R}}_{{\text{r}}}^{{\text{T}}} {\mathbf{x}}_{,\alpha } }}{\kern 1pt} {\kern 1pt} \Delta {{\varvec{\Theta}}}_{{\text{r}}} + \widetilde{{{\mathbf{R}}^{{\text{T}}} {\mathbf{x}}_{,\alpha } }}\;{\mathbf{T}}({\mathbf{d}})\Delta {\mathbf{d}})} \\ \end{array} , $$

(33)

$$ \begin{array}{*{20}c} {\Delta \updelta {\mathbf{f}}_{\alpha \omega }^{{\text{T}}} {\mathbf{a}} = \Delta \updelta {\mathbf{d}}^{{\text{T}}} {{\varvec{\Xi}}}_{{{\mathbf{T}}^{{\text{T}}}_{SO(3)} }} ({\mathbf{d}}_{,\alpha } )^{{\text{T}}} {\mathbf{a}}{\kern 1pt} + (\Delta \updelta {\mathbf{T}}_{SO(3)} ({\mathbf{d}}){\mathbf{d}}_{,\alpha } )^{{\text{T}}} {\mathbf{a}} + (\updelta {\mathbf{T}}_{SO(3)} ({\mathbf{d}})\Delta {\mathbf{d}}_{,\alpha } )^{{\text{T}}} {\mathbf{a}}} \\ { + \,\Delta \updelta {\mathbf{d}}^{{\text{T}}} {\mathbf{T}}_{SO(3)} ({\mathbf{d}})^{{\text{T}}} {\mathbf{a}} + \updelta {\mathbf{d}}^{{\text{T}}} \Delta {\mathbf{T}}_{SO(3)} ({\mathbf{d}})^{{\text{T}}} {\mathbf{a}}\quad \quad \quad \quad \quad \quad \quad } \\ \end{array} , $$

(34)

$$ {\mathbf{M}}^{ * } = \left[ {\begin{array}{*{20}c} {\widetilde{{{\mathbf{R}}_{1}^{{\text{T}}} {\mathbf{M}}_{1} }}} & {} & {} & {} \\ {} & {\widetilde{{{\mathbf{R}}_{2}^{{\text{T}}} {\mathbf{M}}_{2} }}} & {} & {} \\ {} & {} & \ddots & {} \\ {} & {} & {} & {\widetilde{{{\mathbf{R}}_{{\text{N}}}^{{\text{T}}} {\mathbf{M}}_{{\text{N}}} }}} \\ \end{array} } \right],\;\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{1} } \\ {{\mathbf{M}}_{2} } \\ \vdots \\ {{\mathbf{M}}_{{\text{N}}} } \\ \end{array} } \right] = {\mathbf{N}}_{u,\alpha }^{ * T} {\mathbf{Ra}}, $$

(35)

R^* represents the rotation transformation between δx^N and δu^N. The core of the first and second derivatives for d is to compute the first and second derivatives of T_SO(3) and its inverse, which can be found in Ref. [2] and [35] and will not be repeated here. The expressions of B_i and ΔB_i can be easily obtained using the Eqs. (32), (33) and (34).