1 Introduction

Thin-walled structures constitute a rather broad class of engineering structures. Roughly speaking, some 80% of structures of diverse scales and applications belong to this group. They are the result of engineering tendency to optimize the structures by reducing their weight while keeping high capacity. Such a confronting set of objectives led to the thinness of the walls (dead-load reduction) combined with the curved geometry that allows the use of high membrane stiffness to carry transverse loading. With such preferable properties, thin-walled structures are nowadays widely utilized in automotive, aerospace, transportation, defense industries, to name but a few.

The research on thin-walled structures (referred to as shells from this point on) is rather broad and diverse in scope, so that an exhaustive overview would be prohibitively long. But it would be worthwhile to mention certain research directions, particularly those that represent the contemporary trend of development in the field. Beside classical structural materials (primarily metals), the use of modern fiber-reinforced composites (FRC) gained in importance in the past couple of decades as it opens up further opportunities for weight reduction and use of directionally dependant material properties. The susceptibility to hidden failures and delamination of these structures resulted in efforts to provide models for interlaminar damage and failure of FRC structures [44] and development of various methods for non-destructive damage detection [20, 39]. Another possibility of improving structural properties of shells is seen in the use of functionally graded materials, as they enable even higher efficiency of material utilization [9, 25, 28, 37]. Furthermore, the recognition of high adaptability intrinsic for natural systems led to biomimetics in structural engineering. The resulting active/adaptive structures comprise actuators and sensors and can actively influence their mechanical behavior. Of particular interest are active elements with high integrability into/onto the shell structures. Piezoelectric elements as a common choice have been the subject of interest of numerous researchers, who provided numerical tools for their modeling and simulation already in the 90s as given in the survey by Benjeddou [4]. The authors of the article at hand have also been active in this enticing research field lately [32, 40,41,42].

A successful research and development in all the above-mentioned fields rely on the fundamental engineering activities—modeling and simulation. The finite element method (FEM) has established itself as the prime numerical tool in the field of structural analysis. Surely, different fields and problems demand models of different levels of complexity. The majority of workhorse shell elements in commercial FEM software packages are based on a first-order 2D theory. The foundation of the classical first-order 2D theory is the Kirchhoff–Love model. The triangular and quadrilateral semiloof elements by Irons [21] should be mentioned as ones of the most successful shell elements that implement the discrete Kirchhoff–Love kinematical assumptions. Though the Kirchhoff–Love model is a rather simple one and often sufficient, the attention was early shifted to the Reissner–Mindlin model in the shell formulations for FEM. The latter one is the basis of the first-order shear deformation 2D theory. Hence, it involves the transverse shear effects (not included in the Kirchhoff–Love model) and is therewith applicable to both thin and moderately thick shells. However, the reason for the early shift is not to be sought in the indisputably greater generality of the model, but it is more of a pragmatic nature—namely the reduced continuity requirements from the FE shape functions (\(C^0\) continuity for the Reissner–Mindlin model vs. \(C^1\) continuity needed for the Kirchhoff–Love model). A rather large group of elements belonging to the family of degenerate (referring to degenerated solid) shell elements have been developed based on the Reissner–Mindlin kinematics (e.g., [1, 14, 22, 31]). These elements are applicable over a wide range of shell curvatures and thickness, but handling rotational degrees of freedom proved to be somewhat challenging in geometrically nonlinear cases. Hence, some researchers turned their attention to the so-called solid–shell element formulations that use only translational displacements as nodal degrees of freedom [23, 26]. Furthermore, for better accuracy of strain and stress recovery, particularly when composite laminates are considered, layer-wise theories have been developed [19, 27]. A rather interesting approach has been lately proposed in articles by Carrera et al. [10] and Valvano and Carrera [47], in which finite elements with node-dependant kinematics are applied to combine the equivalent single-layer approach with a layer-wise approach and thus increase the accuracy locally, i.e., in the sub-domains where the problem at hand demands higher accuracy. Another interesting approach that aims at a seamless integration of design (CAD) and analysis (FEM) is denoted as isogeometric FE analysis. Isogeometric FE developments for shells have been based on both Kirchhoff–Love and Reissner–Mindlin kinematics [5, 15, 34].

The list of finite element formulations developed for shells could be continued almost indefinitely as this is one of a few topics in structural mechanics that have attracted so much interest and work. The above-given rather short extract of the work in the field only serves as a proof of that. This paper aims at a novel, numerically very efficient, three-node shell element based on the Reissner–Mindlin kinematics. The authors are aware of the recent developments based on the edge-based smoothing techniques [13, 45] which, in this manner, practically account for curved geometry up to certain degree despite the faceted FE representation of the geometry. The present development is based on observation of an ’isolated element’, meaning that the element properties are not influenced by the surrounding elements. Although the advantages of the edge-based smoothing techniques are obvious, one of the reasons for this choice is the possibility of efficient direct implementation into the simplified corotational FE formulation as proposed by Marinkovic et al. [33] and Nguyen et al. [35]. It will be shown that the present element offers good performance and successfully resolves benchmark problems that are well-known as challenging for shell finite elements.

2 Element formulation

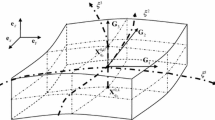
The developed shell element is a three-node element that implements six degrees of freedom per node (three translations and three rotations). Besides the global coordinate system, the element local coordinate system (\(x',y',z'\)) is of particular importance for the formulation. The local coordinate system is defined so that the \(x'\)-axis is oriented from node 1 toward node 2, while the \(z'\)-axis is perpendicular to the element surface. The \(y'\)-axis is determined in a straightforward manner by the cross-product of the \(z'\)- and \(x'\)-axis unit vectors. The element implements the Mindlin–Reissner kinematics, so that the displacement field is interpolated by means of the mid-surface displacements u', v' and w' along the local \(x', y'\) and \(z'\)-axes, respectively, and the rotations \(\theta _{x'i}\) and \(\theta _{y'i}\) around the local \(x'\) and \(y'\)-axes, respectively, thus:

$$\begin{aligned} \begin{Bmatrix} u' \\ v' \\ w' \end{Bmatrix} =\sum ^3_{i=1} \left( N_i \begin{Bmatrix} u'_i \\ v'_i \\ w'_i \end{Bmatrix}+ \frac{h}{2}N_i t \begin{Bmatrix} \theta _{y'i} \\ -\theta _{x'i} \\ 0 \end{Bmatrix} \right) \end{aligned}$$
(1)

where h denotes the constant shell thickness, \(t\in [-1,1]\) and \(N_i\) are the linear shape functions:

$$\begin{aligned} N_1(x',y')&= \frac{1}{2A}\left( x'_2 y'_3-x'_3 y'_2 + y'_{23}x' + x'_{32}y'\right) \nonumber \\ N_2(x',y')&= \frac{1}{2A}\left( x'_3 y'_1-x'_1 y'_3 + y'_{31}x' + x'_{13}y'\right) \nonumber \\ N_3(x',y')&= \frac{1}{2A}\left( x'_1 y'_2-x'_2 y'_1 + y'_{12}x' + x'_{21}y'\right) \end{aligned}$$
(2)

In Eq. (2) A is the element area, and \(x'_i\) and \(y'_i, i = 1,2,3\) are the local coordinates of the element nodes, while \(x'_{ij}\) and \(y'_{ij}\) denote the abbreviated coordinate differences, i.e., \(x'_{ij} = x'_i-x'_j\) and \(y'_{ij} = y'_i-y'_j\). The element area A is given by:

$$\begin{aligned} A=\frac{1}{2}\left( x'_{21}y'_{31} - x'_{31}y'_{21}\right) \end{aligned}$$
(3)

One may note that the original element kinematics demands only five degrees of freedom. The drilling degree of freedom, namely the rotation around the local \(z'\)-axis, \(\theta _{z'}\), will be introduced later, when the membrane behavior of the element is considered. Due to the flat shape, the elastic behavior of the element can be represented as a superposition of a plate and membrane element (Fig. 1). For such an approach, it is rather convenient to separate the degrees of freedom (dofs) with respect to the element local coordinate system into plate-related and membrane-related dofs. As Fig. 1 shows, the plate-related dofs are the transverse deflection \(w'\) and the rotations around the in-plane axes, \(\theta _{x'}\) and \(\theta _{y'}\). On the other hand, the membrane-related dofs are the in-plane displacements \(u'\) and \(v'\), and the rotation around the \(z'\)-axis, \(\theta _{z'}\). Hence, they can be sorted as follows:

$$\begin{aligned} \{u_{\mathrm{mem}}\}&= \begin{Bmatrix} u'_1&\quad v'_1&\quad \theta _{z'1}&\quad u'_2&\quad v'_2&\quad \theta _{z'2}&\quad u'_3&\quad v'_3&\quad \theta _{z'3} \end{Bmatrix}^{\mathrm{T}} \nonumber \\ \{u_{\mathrm{p}}\}&= \begin{Bmatrix} w'_1&\quad \theta _{x'1}&\quad \theta _{y'1}&\quad w'_2&\quad \theta _{x'2}&\quad \theta _{y'2}&\quad w'_3&\quad \theta _{x'3}&\quad \theta _{y'3} \end{Bmatrix}^{\mathrm{T}} \end{aligned}$$
(4)

where the index in the subscript of each degree of freedom represents the node number. Correspondingly, the element stiffness matrix is separated into the plate, \([K_{\mathrm{p}}]\), and membrane part, \([K_{\mathrm{mem}}]\), leading to the following form of the static finite element relation:

$$\begin{aligned} \begin{bmatrix} K_{\mathrm{s}} \end{bmatrix} \begin{Bmatrix} u_{\mathrm{e}} \end{Bmatrix} = \begin{bmatrix} [K_{\mathrm{mem}}]&\quad [0]\\ [0]&\quad [K_{\mathrm{p}}] \end{bmatrix} \begin{Bmatrix} \{u_{\mathrm{mem}}\} \\ \{u_{\mathrm{p}}\} \end{Bmatrix} = \begin{Bmatrix} f_\mathrm{e} \end{Bmatrix} \end{aligned}$$
(5)

where \([K_\mathrm{s}]\) is the resulting element stiffness matrix, \(\{u_\mathrm{e}\}\) is the vector of nodal degrees of freedom and \(\{f_\mathrm{e}\}\) is the element load vector (both forces and moments). For the membrane part, the assumed natural deviatoric strain (ANDES) formulation [16] is used, while the plate part of the element is based on the discrete shear gap (DSG) approach [8].

Fig. 1
figure 1

Shell element; local element coordinate system

Full size image

2.1 Plate element (modified DSG3 formulation)

The plate stiffness \([K_{\mathrm{p}}]\) can be expressed as the sum of bending stiffness \([K_{\mathrm{pb}}]\) and shear stiffness \([K_{\mathrm{ps}}]\):

$$\begin{aligned}{}[K_{\mathrm{p}}] = [K_{\mathrm{pb}}]+[K_{\mathrm{ps}}] \end{aligned}$$
(6)

Once the corresponding strain–displacement matrices \([B_{\mathrm{pb}}]\), \([B_{\mathrm{ps}}]\), respectively, are determined with respect to the local coordinate system, the stiffness matrices are simply computed:

$$\begin{aligned}{}[K_{\mathrm{pb}}] = \int _{(A)}[B_{\mathrm{pb}}]^{\mathrm{T}}[D][B_{\mathrm{pb}}]\mathrm{d}A \end{aligned}$$
(7)

and

$$\begin{aligned}{}[K_{\mathrm{ps}}] = \int _{(A)}[B_{\mathrm{ps}}]^{\mathrm{T}}[F][B_{\mathrm{ps}}]\mathrm{d}A \end{aligned}$$
(8)

where [D] and [F] are the material matrices related to bending and transverse shear deformation, respectively. They are obtained by integrating the corresponding material constants through the thickness [7]. Since the plate strain–displacement matrices are constant over the element domain, the in-plane integration comes down to the multiplication with the element area A.

2.1.1 Bending strain–displacement matrix \([B_{\mathrm{pb}}]\)

The strain–displacement matrix due to bending, \([B_{\mathrm{pb}}]\), is derived directly from the discretized displacement field (Eq. 1):

$$\begin{aligned} \begin{Bmatrix} \varepsilon ^b_{x'x'} \\ \varepsilon ^b_{y'y'} \\ \gamma ^b_{x'y'} \end{Bmatrix}&= z'\begin{Bmatrix} \frac{\partial \theta _{y'}}{\partial x'} \\ -\frac{\partial \theta _{x'}}{\partial y'} \\ \frac{\partial \theta _{y'}}{\partial y'}-\frac{\partial \theta _{x'}}{\partial x'} \end{Bmatrix} \nonumber \\&= z'\sum _{i=1}^3 \begin{bmatrix} 0&\quad 0&\quad N_{i,x'}\\ 0&\quad -N_{i,y'}&\quad 0 \\ 0&\quad -N_{i,x'}&\quad N_{i,y'} \end{bmatrix} \begin{Bmatrix} w'_i \\ \theta _{x'i} \\ \theta _{y'i} \end{Bmatrix} \end{aligned}$$
(9)

which yields \([B_{\mathrm{pb}}]\) in the closed form:

$$\begin{aligned}{}[B_{\mathrm{pb}}]=\frac{1}{2A} \begin{bmatrix} 0&\quad 0&\quad y'_{23}&\quad 0&\quad 0&\quad y'_{31}&\quad 0&\quad 0&\quad y'_{12} \\ 0&\quad -x'_{32}&\quad 0&\quad 0&\quad -x'_{13}&\quad 0&\quad 0&\quad -x'_{21}&\quad 0 \\ 0&\quad -y'_{23}&\quad x'_{32}&\quad 0 &\quad -y'_{31}&\quad x'_{13}&\quad 0 &\quad -y'_{12}&\quad x'_{21}\end{bmatrix} \end{aligned}$$
(10)

2.1.2 Shear strain–displacement matrix \([B_{\mathrm{ps}}]\)

For treatment of the notorious transverse shear locking effect, the present element implies the discrete shear gap technique as proposed by Bletzinger et al. [8] and the cell strain smoothing technique proposed by Nguyen-Thoi et al. [36]. The idea behind the discrete shear gap approach is the separation of deformation into a part due to transverse shear and a part due to bending. The shear gap represents the difference between the total deformation and the deformation due to bending. It is obtained by integration of the kinematical equation for the transverse shears along the natural coordinates \(\xi _2\) and \(\xi _3\) (see Fig. 2). As a consequence of different order of interpolations for the part due to the transverse deflection and the part due to rotations within the kinematically derived discretized transverse shear, the obtained shear gap cannot be identically equal to zero in the physical regimes which impose this condition (bending of rather thin structures). The resulting parasitic transverse shear makes the model too stiff, and the effect is well-known as shear locking.

Fig. 2
figure 2

Triangular coordinates \(\xi _1, \xi _2\), \(\xi _3\)

Full size image

The DSG approach starts by evaluating the shear gaps at the nodes, using the nodal rotations and displacements:

$$\begin{aligned}&\Delta {w^1}_{\gamma {\xi _2}} = \Delta {w^3}_{\gamma {\xi _2}} =\Delta {w^1}_{\gamma {\xi _3}} = \Delta {w^2}_{\gamma {\xi _3}}=0 \nonumber \\&\Delta {w^2}_{\gamma {\xi _2}} = w'_2-w'_1+\frac{1}{2}\left( x'_{21}\left( \theta _{y'1}+\theta _{y'2} \right) -y'_{21}\left( \theta _{x'1}+\theta _{x'2}\right) \right) \nonumber \\&\Delta {w^3}_{\gamma {\xi _3}} = w'_3-w'_1+\frac{1}{2}\left( x'_{31}\left( \theta _{y'1}+ \theta _{y'3}\right) -y'_{31}\left( \theta _{x'1}+\theta _{x'3}\right) \right) . \end{aligned}$$
(11)

Furthermore, the obtained nodal shear gaps are interpolated using the linear shape functions (2) and subsequently differentiated in order to obtain the DSG-based transverse shear field:

$$\begin{aligned} \gamma _{x'z'}= & {} \frac{\partial w^*_{\gamma }}{\partial x'} =\frac{\partial N_2}{\partial x'} \Delta {w^2}_{\gamma {\xi _2}}+\frac{\partial N_3}{\partial x'}\Delta {w^3}_{\gamma {\xi _3}} \end{aligned}$$
(12)
$$\begin{aligned} \gamma _{y'z'}= & {} \frac{\partial w^*_{\gamma }}{\partial y'}=\frac{\partial N_2}{\partial y'} \Delta {w^2}_{\gamma {\xi _2}}+\frac{\partial N_3}{\partial y'}\Delta {w^3}_{\gamma {\xi _3}} \end{aligned}$$
(13)

In a compact matrix form, it reads:

$$\begin{aligned} \{\gamma ^*\} = \begin{Bmatrix} \gamma _{y'z'} \\ \gamma _{x'z'} \end{Bmatrix} = [B_{\mathrm{s}}]\{u_{\mathrm{p}}\} \end{aligned}$$
(14)

where \([B_{\mathrm{s}}]\) is the strain–displacement matrix yielding the transverse shears. For the present element, it is given in the closed form as:

$$\begin{aligned} \begin{bmatrix}B_{\mathrm{s}}\end{bmatrix} =\frac{1}{2A} \begin{bmatrix} x'_{32}&\quad A&\quad 0&\quad x'_{13}&\quad a_1&\quad a_3&\quad x'_{21}&\quad -\,a_2&\quad -\,a_3 \\ y'_{23}&\quad 0&\quad -\,A&\quad y'_{31}&\quad a_4&\quad a_2&\quad y'_{12}&\quad -\,a_4&\quad -\,a_1 \end{bmatrix} \end{aligned}$$
(15)

with:

$$\begin{aligned} a_1= & {} \frac{1}{2}y'_{12}x'_{13} \quad a_2 = \frac{1}{2}y'_{31}x'_{21}\nonumber \\ a_3= & {} \frac{1}{2}x'_{21}x'_{13} \quad a_4 = \frac{1}{2}y'_{12}y'_{31} \end{aligned}$$
(16)

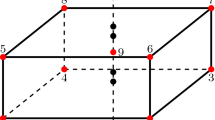
The transverse shear stiffness is further modified by applying the strain smoothing technique [29]. Using the element centroid as an additional node, the element is divided into three sub-triangles (see Fig. 3). The transverse shear strain–displacement matrices are computed for each sub-triangle and then averaged by implementing the assumption that the displacement of the centroid is the average of the nodal displacements:

$$\begin{aligned} {[}B^{\vartriangle _1}_{\mathrm{s}}]= & \begin{bmatrix}{}{[} \frac{1}{3}B^{\vartriangle _1}_{{\mathrm{s}}1}+B^{\vartriangle _1}_{{\mathrm{s}}3}{]} & {[}\frac{1}{3}B^{\vartriangle _1}_{{\mathrm{s}}1}{]}& {[}\frac{1}{3}B^{\vartriangle _1}_{{\mathrm{s}}1}+B^{\vartriangle _1}_{{\mathrm{s}}2}{]}\end{bmatrix} \nonumber\\ {[}B^{\vartriangle _2}_s]= & \begin{bmatrix}{} {[}\frac{1}{3}B^{\vartriangle _2}_{{\mathrm{s}}1}{]}&{[} \frac{1}{3}B^{\vartriangle _2}_{{\mathrm{s}}1}+B^{\vartriangle _2}_{{\mathrm{s}}2}{}{]}&{[} \frac{1}{3}B^{\vartriangle _2}_{{\mathrm{s}}1}+B^{\vartriangle _2}_{{\mathrm{s}}3}{]}\end{bmatrix} \\ {[}B^{\vartriangle _3}_s]= & \begin{bmatrix}{} {[}\frac{1}{3}B^{\vartriangle _3}_{{\mathrm{s}}1}+B^{\vartriangle _3}_{{\mathrm{s}}2}{]}&{[} \frac{1}{3}B^{\vartriangle _3}_{{\mathrm{s}}1}+B^{\vartriangle _3}_{{\mathrm{s}}3} {]}&{[}\frac{1}{3}B^{\vartriangle _3}_{{\mathrm{s}}1}{]}\end{bmatrix} \nonumber \end{aligned}$$
(17)

where \([B^{\vartriangle _j}_s]\) is the nodal transverse shear strain–displacement matrix of the jth sub-triangle. Finally, the averaged transverse shear strain–displacement matrix is determined in a straightforward manner :

$$\begin{aligned}{}[B_{\mathrm{ps}}]=\frac{1}{3}\sum _{i=1}^3[B^{\vartriangle _i}_{{\mathrm{s}}}]. \end{aligned}$$
(18)
Fig. 3
figure 3

Sub-triangles \(\vartriangle _1, \vartriangle _2\), \(\vartriangle _3\)

Full size image

2.2 Membrane element

For the membrane part, the ANDES membrane formulation by Felippa and Militello [16] is implemented. This formulation combines the free formulation (FF) by Bergan and Nygård [6] and a modified version of the assumed natural strain (ANS) formulation by Park and Stanley [38]. Only the fundamental ideas of the approach and selected basic equations are given here. The interested reader should address references [2, 16, 18] for the detailed formulation and reasoning behind certain steps of the formulation.

The basic idea behind the FF is representation of the displacement field by a chosen set of modes and modal coefficients. This actually implies that, regarding the displacements involved in the membrane part \(\{u_{\mathrm{mem}}\}\), the discretized displacement field given in Eq. (1) is abandoned. The mode set includes basic modes consisting of a complete set of linearly independent rigid-body and constant strain modes, and higher-order modes, which are in this case linear strain modes. According to the FF, the overall number of modes corresponds to the overall number of nodal degrees of freedom involved in the membrane part, so that the relation between the modal coefficients and nodal dofs is defined by an invertible square transformation matrix. This is also important for the rank sufficiency of the stiffness matrix. Modifications of the FF allow for a larger number of modes in the group of higher-order modes, provided a sufficient number of additional kinematic constraints between the modes are defined, thus retaining the invertibility of the transformation matrix between the modal and nodal dofs. To ensure variational correctness, another important requirement from the higher-order modes is that they are energy orthogonal with respect to the constant strain modes.

Since the modes are grouped into the basic and higher-order modes, the membrane stiffness matrix, \([K_{\mathrm{mem}}]\), is correspondingly decomposed into the basic, \([K_{\mathrm{b}}]\), and higher-order stiffness, \([K_{\mathrm{h}}]\).

$$\begin{aligned}{}[K_{\mathrm{mem}}]=[K_{\mathrm{b}}]+[K_\mathrm{h}]. \end{aligned}$$
(19)

2.2.1 Basic stiffness

In the ANDES formulation, the basic stiffness is computed in exactly the same manner as in the FF [6]:

$$\begin{aligned}{}[K_{\mathrm{b}}]=V^{-1}[L][C][L]^\mathrm{T} \end{aligned}$$
(20)

where V is the element volume (\(V=Ah\)), [C] is the Hooks matrix and [L] is the \(3\times 9\) force-lumping matrix that consistently maps an arbitrary constant stress field into the element nodal forces. In order to derive the lumping matrix, the virtual work along element sides is expressed for the constant stress state, whereby the beam-type shape functions are used along the element sides. The resulting lumping matrix has the following closed form:

$$\begin{aligned} \begin{aligned}&[L] \\&\quad =\frac{h}{2}\begin{bmatrix} y'_{23}&\quad 0&\quad x'_{32} \\ 0&\quad x'_{32}&\quad y'_{23} \\ \frac{\alpha }{6}y'_{23}\left( y'_{32}-y'_{12}\right)&\quad \frac{\alpha }{6}x'_{32} \left( x'_{31}-x'_{12}\right)&\quad \frac{\alpha }{3}\left( x'_{31} y'_{13}-x'_{12}y'_{21}\right) \\ y'_{31}&\quad 0&\quad x'_{13} \\ 0&\quad x'_{13}&\quad y'_{31} \\ \frac{\alpha }{6}y'_{31}\left( y'_{32}-y'_{12}\right)&\quad \frac{\alpha }{6}x'_{13} \left( x'_{12}-x'_{23}\right)&\quad \frac{\alpha }{3}\left( x'_{12} y'_{21}-x'_{23}y'_{32}\right) \\ y'_{12}&\quad 0&\quad x'_{21} \\ 0&\quad x'_{21}&\quad y'_{12} \\ \frac{\alpha }{6}y'_{12}\left( y'_{32}-y'_{12}\right)&\quad \frac{\alpha }{6}x'_{21} \left( x'_{23}-x'_{31}\right)&\quad \frac{\alpha }{3}\left( x'_{23} y'_{32}-x'_{31}y'_{13}\right) \\ \end{bmatrix} \end{aligned} \end{aligned}$$
(21)

where \(\alpha\) is a free parameter that will be addressed later. If \(\alpha\) is equal to zero, the basic stiffness comes down to the stiffness matrix of the constant strain triangular (CST) element. In this case, the rows and columns associated with the drilling degree of freedom vanish.

2.2.2 Higher-order stiffness

The objective of the higher-order modes is to provide adequate coverage of the in-plane bending. Hence the choice in the ANDES formulation is to use three (in-plane) bending modes which produce linear natural strains along the element sides (Fig. 4). They are also referred to as ’deviatoric’ strains (strains that deviate from the constant strain state). The drilling degrees of freedom are essential in their description.

Fig. 4
figure 4

Natural strain components

Full size image

For this purpose, the ANDES formulation makes use of the so-called hierarchical rotations, \(\overline{\theta }_i\), extracted by subtracting the mean rotation (the rotation yielded by the constant strain element), \(\theta _0\), from the nodal drilling rotations (see Fig. 5):

$$\begin{aligned} \overline{\theta }_i={\theta }_i-\theta _0. \end{aligned}$$
(22)
Fig. 5
figure 5

CST deformation and hierarchical rotations

Full size image

Since \(\theta _0\) can be determined by:

$$\begin{aligned} \begin{aligned} \theta _0=\frac{1}{4A}\left( x'_{23}u'_{1}+x'_{31}u'_{2}+x'_{12}u'_{3}+y'_{23} v'_{1}+y'_{31}v'_{2}+y'_{12}v'_{3}\right) \end{aligned} \end{aligned}$$
(23)

the hierarchical rotations are finally obtained by means of the following relation:

$$\begin{aligned} \begin{Bmatrix} \overline{\theta }_1 \\ \overline{\theta }_2 \\ \overline{\theta }_3 \end{Bmatrix}=\underbrace{ \frac{1}{4A}\begin{bmatrix} x'_{32}&\quad y'_{32}&\quad 4A&\quad x'_{13}&\quad y'_{13}&\quad 0&\quad x'_{21}&\quad y'_{21}&\quad 0 \\ x'_{32}&\quad y'_{32}&\quad 0&\quad x'_{13}&\quad y'_{13}&\quad 4A&\quad x'_{21}&\quad y'_{21}&\quad 0 \\ x'_{32}&\quad y'_{32}&\quad 0&\quad x'_{13}&\quad y'_{13}&\quad 0&\quad x'_{21}&\quad y'_{21}&\quad 4A \end{bmatrix}}_{[T_{\theta u}]} \{u_{\mathrm{mem}}\} \end{aligned}$$
(24)

The form of the three in-plane bending modes together with the sets of hierarchical rotations defining them is depicted in Fig. 6. However, those three modes are linearly dependent (obviously, their sum vanishes) and, hence, a fourth, torsion mode is added to the set (Fig. 6).

Fig. 6
figure 6

Deformation modes—higher stiffness

Full size image

Another important aspect, before proceeding to the stiffness matrix, is the transformation of the natural strains to the Cartesian strain components. One can think of the natural strains as a measurement result obtained by means of a strain gage rosette, with the three strain gages oriented along the element sides. Thus, the transformation is given by the classical strain gage rosette transformation:

$$\begin{aligned}{}[T_{\mathrm{nat}}] =\frac{1}{4A^2} \begin{bmatrix} y'_{23}y'_{13} l^2_{21}&\quad x'_{23}x'_{13} l^2_{21}&\quad \left( y'_{23}x'_{31} + x'_{32}y'_{13}\right) l^2_{21} \\ y'_{31}y'_{21}l^2_{32}&\quad x'_{31}x'_{21}l^2_{32}&\quad \left( y'_{31}x'_{12} + x'_{13}y'_{21}\right) l^2_{32} \\ y'_{12}y'_{32} l^2_{13}&\quad x'_{12}x'_{32} l^2_{13}&\quad \left( y'_{12}x'_{23} + x'_{21}y'_{32}\right) l^2_{13} \end{bmatrix}^{\mathrm{{T}}} \end{aligned}$$
(25)

where \(l_{21}\),\(l_{32}\),\(l_{13}\) are the lengths of the element sides. Now, the higher-order stiffness is computed by:

$$\begin{aligned}{}[K_{\mathrm{h}}]=\beta _0\frac{9}{4}[T_{\theta u}]^{\mathrm{{T}}}[K_{\theta }][T_{\theta u}] \end{aligned}$$
(26)

where \(\beta _0\) is one of the free dimensionless parameters, while \([K_{\theta }]\) is the higher-order stiffness in terms of hierarchical rotations:

$$\begin{aligned}{}[K_{\theta }]=\frac{h}{3}\left( [Q_4]^{\mathrm{{T}}}[C_{\mathrm{nat}}][Q_4]+[Q_5]^{\mathrm{{T}}}[C_{\mathrm{nat}}][Q_5]+ [Q_6]^{\mathrm{{T}}}[C_{\mathrm{nat}}][Q_6]\right) \end{aligned}$$
(27)

with:

$$\begin{aligned} {[}C_{nat}]=[T_{nat}]^{\mathrm{{T}}}[C][T_{nat}] \end{aligned}$$
(28)

where

$$\begin{aligned} {[}Q_4]= & {} \frac{1}{2}\left( [Q_1]+[Q_2]\right) \nonumber \\ {[}Q_5]= & {} \frac{1}{2}\left( [Q_2]+[Q_3]\right) \nonumber \\ {[}Q_6]= & {} \frac{1}{2}\left( [Q_1]+[Q_3]\right) \end{aligned}$$
(29)

Finally, the matrices \([Q_1], [Q_2]\) and \([Q_3]\) are given in terms of additional nine dimensionless parameters \(\beta _1\) - \(\beta _9\):

$$\begin{aligned} {[}Q_1]= & {} \frac{2A}{3} \begin{bmatrix} \frac{\beta _1}{l^2_{21}}&\quad \frac{\beta _2}{l^2_{21}}&\quad \frac{\beta _3}{l^2_{21}} \\ \frac{\beta _4}{l^2_{32}}&\quad \frac{\beta _5}{l^2_{32}}&\quad \frac{\beta _6}{l^2_{32}} \\ \frac{\beta _7}{l^2_{13}}&\quad \frac{\beta _8}{l^2_{13}}&\quad \frac{\beta _9}{l^2_{13}} \end{bmatrix} \nonumber \\ {[}Q_2]= & {} \frac{2A}{3} \begin{bmatrix} \frac{\beta _9}{l^2_{21}}&\quad \frac{\beta _7}{l^2_{21}}&\quad \frac{\beta _8}{l^2_{21}} \\ \frac{\beta _3}{l^2_{32}}&\quad \frac{\beta _1}{l^2_{32}}&\quad \frac{\beta _2}{l^2_{32}} \\ \frac{\beta _6}{l^2_{13}}&\quad \frac{\beta _4}{l^2_{13}}&\quad \frac{\beta _5}{l^2_{13}} \end{bmatrix} \nonumber \\ {[Q}_3]= & {} \frac{2A}{3} \begin{bmatrix} \frac{\beta _5}{l^2_{21}}&\quad \frac{\beta _6}{l^2_{21}}&\quad \frac{\beta _4}{l^2_{21}} \\ \frac{\beta _8}{l^2_{32}}&\quad \frac{\beta _9}{l^2_{32}}&\quad \frac{\beta _7}{l^2_{32}} \\ \frac{\beta _2}{l^2_{13}}&\quad \frac{\beta _3}{l^2_{13}}&\quad \frac{\beta _1}{l^2_{13}} \end{bmatrix} \end{aligned}$$
(30)

Considering purely membrane ANDES element, Fellipa [17] provided the optimal values of \(\alpha\) and \(\beta\)-parameters, together with the complete reasoning and justification for those values. However, Shin and Lee [45] argued that a shell element requires modified values of the free parameters, due to the physical regimes that involve membrane-bending coupling. In those cases, the higher-order stiffness as defined in the ANDES formulation would give rise to drill rotation locking. On the other hand, if the higher-order stiffness is decreased too much with respect to the entire element stiffness, a problem referred to as “free-corner” problem by Cook [11] appears. Hence, Shin and Lee [45] performed a parameter study showing that the values \(\alpha =1/8\) and \(\beta _0=\alpha ^2/4\) represent a reasonable choice for the three-node shell element. They also offered a slightly modified version that accounts for the inter-planar angle between adjacent elements and the ratio of the in-plane element maximal dimension to the thickness. This actually means that, in the modified approach, parameter \(\beta _0\) differs from element to element and, with the mesh refinement, it converges to \(\beta _0=\alpha ^2/4\). However, we remain consistent in our “isolated element”-based approach and adopt the above-given constant values for \(\alpha\) and \(\beta _0\). The remaining \(\beta\)-parameters are as defined by the original ANDES formulation: \(\beta _1=1, \beta _2=2, \beta _3=1, \beta _4=0, \beta _5=1, \beta _6=-1\), \(\beta _7=-1, \beta _8=-1, \beta _9=-2\).

3 Element validation

In what follows, a set of examples is considered in order to demonstrate properties of the developed shell element. The examples include basic patch tests and several popular benchmark tests. The benchmark tests are proposed by various authors and have proven to represent a challenge for shell elements. Those examples are computed using the present element and the linear triangular shell element from ABAQUS (Abaqus S3). The ability of the element to yield the correct (reference) solution and the convergence rate are studied. As certain authors used non-SI units (e.g., inch, pound-force), whereas in the remaining examples SI units were used, only numerical values will be given in the considered examples. Any set of units for length and force may be associated with those values (e.g., N for force and m for length, or pound-force for force and inch for length) in any of the considered examples, as long as they are consistently used and kept throughout the whole example.

3.1 Patch tests

Patch tests are generally used as an indicator of the element quality. They are set up as simple examples with the known exact solutions, which have to be reproduced by the developed element with distorted FE meshes. This is a necessary condition for convergence.

In the patch tests briefly described below, the developed element was evaluated with respect to the ability to exactly reproduce the constant stress state. The considered patch tests are force patch tests, meaning that the FE assemblage is exposed to external forces giving rise to constant stress states. Furthermore, the tests were designed so as to isolate and check specific behavior of the element—first the membrane and then bending behavior was in focus. This required adequate load cases used with the very same geometry and FE mesh, both shown in Fig. 7. The thickness of the structure is 0.001, and the isotropic material is characterized by the Young’s modulus of \(1.0\times 10^6\) and the Poisson’s ratio of 0.3.

Fig. 7
figure 7

Geometry patch test

Full size image

3.1.1 Membrane patch test

In order to test the membrane behavior of the element, the considered structure was exposed to four different load cases.

In the first two cases, two opposite edges were exposed to a constant line load. In the first case, the edges aligned with the y axis were loaded, while in the second case the loaded edges were those aligned with the x axis. The load was selected so that the structure was exposed to a tensile normal stress. A constant line load \(q_n = 1\), normal to the element edge, was applied. This resulted in nodal forces of the magnitude 0.06 and drilling moments of the magnitude 0.012 (given by \(\alpha q_n l^2/12\), where l is the edge length), see Fig. 8. Such a load gives rise to the constant normal stress of 1000, which was exactly reproduced by all elements in the FE assemblage.

In the remaining two cases, the only difference was that the line loads were linear along the edges taking values between \(+\,1\) and \(-\,1\). The resulting nodal forces are represented in Fig. 8. In these two cases, the resulting stress is the constant in-plane shear stress of the magnitude 1224.7. Again, the correct stress state was exactly reproduced in all shell elements in each case.

Fig. 8
figure 8

Load cases membrane patch test

Full size image

3.1.2 Plate patch tests

Similarly to the membrane patch tests, the plate patch tests included four load cases with the constant or linear line bending moments. In each plate patch test, the line bending moments were defined completely analogously to the line forces used in the corresponding membrane patch test. Hence, in the first two cases, those were constant line moments and in the latter two, linear line moments. The resulting nodal moments are graphically represented in Fig. 9. The resulting stresses on the outer surfaces of the structure are same as in the analogous cases with the line forces. Those values were also exactly reproduced in all elements.

Fig. 9
figure 9

Load cases plate patch test

Full size image

3.2 Raasch problem

The Raasch challenge was originally proposed by Ingo Raasch, who reported non-converging results in 1991 when he used the shell elements available in the commercial finite element software MSC/NASTRAN [24]. Furthermore, Knight [24] reported that the shell elements without the transverse shear flexibility (Kirchhoff–Love kinematics) converged to the correct value in contrast to the shell elements with the transverse shear flexibility (Reissner–Mindlin kinematics) available at that time.

The geometry of the Raasch test is a hook-like curved strip consisting of two different arc segments that are tangent at their point of intersection. The radius \(R_1\) of the first segment is 14, while the radius \(R_2\) of the second segment is 46 (Fig. 10). The thickness of the structure is 2 and the width is 20. The end of the structure placed at the origin of the coordinate system (first segment) in Fig. 10 is clamped. The free end of the structure (second segment) is exposed to the uniformly distributed load f of 8.7563 acting in the width direction (z-direction). The structure is considered to be made of an isotropic material with the Young’s modulus of \(22.77\times 10^6\) and the Poisson’s ratio of 0.35.

Fig. 10
figure 10

Geometry Raasch hook

Full size image

The geometry, kinematic boundary conditions and loading lead to a complex deformation state that involves bending, twisting and in-plane shearing. This is the reason why the example turned out to be rather challenging for various shell element formulations. MacNeal et al. [30] concluded that the transfer of twisting moment from element to element produced spurious transverse shear deformation and inferred from this that a proper treatment of the shell normal and drilling degrees of freedom within the element formulation was necessary to obtain the correct, i.e., reference solution.

In order to check the ability of reproducing the reference solution and evaluate the rate of convergence, several FE meshes are considered (18, 216, 896 and 1072 elements). The obtained results are further normalized by the reference solution that reads \(w_{\mathrm{ref}} = 0.12535\) [24]. The comparative results by the presented element and Abaqus S3 element are summarized in Table 1. Obviously, in this example both elements show a similar convergence rate and converge to the correct result.

Table 1 Normalized tip displacements in z-direction—Raasch hook problem
Full size table

3.3 Twisted beam

The twisted beam test is a widely used benchmark problem to check the accuracy and performance of developed elements. The beam geometry is twisted at an angle of \(90^{\circ }\) between the two ends. The warped geometry gives rise to rather complex deformations for any load acting at the free end perpendicularly to the beam axis. The cantilevered beam, with the length of \(L=12\) and the width of \(W=1.1\), is presented in Fig. 11. It is made of a material characterized by the Young’s modulus of 29.0 and the Poisson’s ratio of 0.22. In order to test the present element for thin and thick shell structures, two different thicknesses are considered—0.05 and 0.32.

Fig. 11
figure 11

Geometry twisted beam

Full size image

For each thickness, two load cases are studied with the point load of \(f=1.0\) acting at the center of the free end. In the first case, the load acts in the y-direction, while in the second case it acts in the z-direction (see Fig. 11). The obtained results for four different meshes, containing 48, 96, 384 and 1280 elements, are normalized by the reference solution provided by Simo et al. [46] for the thin structure (\(w_{\mathrm{ref}} = 0.3431, v_{\mathrm{ref}} = 1.390\)) and MacNeal and Harder [30] for the thick twisted beam (\(w_{\mathrm{ref}} = 1.754\times 10^{-3}, v_{\mathrm{ref}} = 5.424\times 10^{-3}\)). Table 2 shows a good convergence rate of the results by the presented element for any combination of the considered load cases and thickness. It is slightly better than the convergence rate by the Abaqus S3 element.

Table 2 Normalized displacements twisted beam problem
Full size table

3.4 Pinched hemispherical shell with \(18^{\circ }\) hole

The next test case involves a doubly curved structure. It is a hemispherical shell with an \(18^\circ\) hole at the top, exposed to two pairs of forces. The pair of forces (\(f=1\)) aligned with the z axis acts inward the hemisphere, i.e., toward the hemisphere center. On the other hand, the pair of forces along the x-axis acts outward the hemisphere. The double symmetry allows to model only one quarter of the structure with symmetry conditions applied, see Fig. 12. The hemisphere has a radius of 10 and thickness of 0.04, Young’s modulus is \(68.25\times 10^6\) and Poisson’s ratio is 0.3. Three FE meshes, with 128, 512 and 2048 elements, are used, the finest of which is depicted in Fig. 12. Following the same procedure as in the previous examples, Table 3 gives the normalized displacements of points A and B, at which the external forces act, in the x- and y-direction, respectively, computed with the present element and Abaqus S3 element. The normalization is done with respect to the reference solution by Simo et al. [46], which reads \(u_{\mathrm{ref}}= w_{\mathrm{ref}} = 0.093\).

Fig. 12
figure 12

Geometry pinched hemisphere

Full size image
Table 3 Normalized displacements (\(w_A, u_B\)) of the pinched hemisphere of point A and B
Full size table

3.5 Pinched cylinder with end diaphragm

The next test case studied is a cylindrical shell with rigid diaphragms at both ends and subjected to two oppositely oriented forces acting at the middle of the length and toward the cylinder axis (see Fig. 13). This is also one of the standard test cases used to evaluate the performance of shell element formulations. The symmetry of the considered case allows consideration of only one-eight of the model with symmetry conditions, as seen in Fig. 13, below. The geometry of one-eight of the cylinder is defined by the radius \(R = 300\), the length \(L = 300\) and the thickness \(t = 3\). The material is considered to be isotropic with the Young’s modulus \(Y = 3\times 10^6\) and the Poisson’s ratio of 0.3. The concentrated force acting upon the reduced model (one-eight) at point A is \(f = 0.25\) (Fig. 13). Again, the convergence analysis reveals slightly better convergence of the results by the present element compared to Abaqus S3. Table 4 gives the vertical displacement \(w_A\) (at point A) for several meshes, whereby the results are normalized by the reference solution \(w_{\mathrm{ref}} =-1.8248\times 10^{-2}\) provided by Belytschko [3].

Fig. 13
figure 13

Geometry pinched cylinder

Full size image
Table 4 Normalized vertical displacements of the pinched cylinder of point A
Full size table

3.6 Cooks membrane

Finally, the popular benchmark problem named after Cook et al. [12], the Cooks membrane problem, is addressed. The considered structure has a trapezoidal form (see Fig. 14) in the x–y plane. It is clamped along the longer edge aligned with the x axis and subjected to a line force acting along the shorter x axis-oriented edge. The magnitude of the line force is 1/16 which amounts to a total force of 1. The isotropic material is described by the Young’s modulus \(Y = 1\) and Poisson’s ratio of 1/3. In this example, the acting load gives rise to in-plane bending and extensive shear deformation.

Fig. 14
figure 14

Geometry Cooks membrane

Full size image
Table 5 Normalized displacements (u) of the cooks membrane of point A
Full size table

The solutions for the vertical displacement at the point A (\(u_A\)) are normalized with the reference solution \(u_{\mathrm{ref}} = 23.91\) provided by Winkler and Plakomytis [43] and listed in Table 5. Obviously, the present element performs better than the Abaqus S3 element in this test case.

4 Conclusions

Thin-walled structures grow in number and diversity every day. This growth is driven by many factors including cost and weight economy, novel materials and production techniques, possibility of converting them into adaptive systems by means of active elements. The peculiarities in their mechanical behavior have always been an impetus for researchers to develop adequate mechanical models. And with the appearance of FEM, this transferred to the development of reliable, accurate and efficient shell-type finite elements.

The three-node shell element proposed in this paper implements the Reissner–Mindlin kinematics. Just as any other three-node element, it is a flat element and the shell behavior is recovered by directly combining the plate and membrane behavior. The formulation implements the already existing solutions for plate and membrane elements, but, to the best of the authors knowledge, it represents a novel combination. The membrane part is based on the assumed natural deviatoric strain (ANDES) formulation with the appropriate modification of the free parameters to accommodate for bending-membrane coupling present in shell elements. The plate part relies on the discrete shear gap (DSG) formulation to resolve the shear locking, and the cell smoothing technique is used to improve the accuracy. The cell smoothing is applied only to the part defining the transverse shears. Besides the typical five degrees of freedom per node (three translations and two rotations about the in-plane axes), the drilling degree of freedom (rotation about the normal) is also included in the element formulation. The examples have demonstrated that the element successfully passes the patch test and resolves the challenging benchmark cases offering therewith a good convergence rate. Those properties of the element combined with the high meshing ability intrinsic for triangular elements render the proposed shell element a powerful numerical tool when simulating the global behavior of shell structures.

In further work, the element formulation is to be extended to cover geometrically nonlinear cases, laminated structures with directionally dependent material properties and inclusion of multifunctional materials such as piezoelectric ceramics, which implies coupled-field effects. These developments are currently in progress.