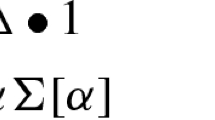Keywords

1 Introduction

Church introduced a Lambda operator λ in 1941 and it is a vital tool used in syntax and semantics. Since Montague’s times, a typed formation of lambda abstraction has been popular in linguistics [1].Footnote 1 Sometimes, a lambda operator can be defined under lambda expressions to focus on a specific property in a context. It appears such as (a term = property) and fetching the predicate expressions in a second order logic and first order logic, respectively [2].Footnote 2 On the other hand, a lambda calculus is a set of expressions and rules that produce certain new expressions. In general, a single typed and monotyped lambda calculus is discussed many times in a literature [3].

However, it is a fact that the first order logic in contrast to a simple typed lambda calculus allows infinite types of expressions that fundamentally enumerate from the finite forms.Footnote 3 Secondly, typed lambda notations are standard in mathematics and computer science. At the same time, a single term calculus in itself has denoted a formal representation of syntactic structures that are somehow different from the first order and high order logic.  On the other hand, we find three schemes when we seeing the axiomatic nature of a simple typed lambda calculus [4]. The following schemes are as

figure a

In the context of a natural language (i.e. English), lambda operator λ resolves passive and other cases within the propositional functions. It transforms such a function into one place predicate situation and binds the variables (x, y) in abstraction to define the expressions in the following way.Footnote 4

figure b

Here (d) shows that variable (x) is bound by the lambda operator and it is a well-formed expression for <e, t> type [5, p. 116].

The paper has a total of five sections. The first section begins with the basic introduction of lambda calculus. The second section discusses the syntactic and semantic background of lambda calculus. The third section deals with the aims/objectives of the study. The fourth section analyzes the natural language expressions concerning lambda abstraction and application. The fifth section concludes the results and the future research.

2 Related Works

As already has been pointed out lambda abstraction finds significant during Montague, and later many semanticists incorporated this into linguistics. It became a powerful tool to establish formal semantics. The following Fig. 1 shows the grammatical nature of a lambda expression.

Fig. 1
figure 1

Lambda expression λ with grammar

Full size image

Figure 1 interprets how lambda expression applies in relative clause, predicates and many other cases in a natural language. However, a classic instance of the lambda abstraction usually defines under ‘the proper treatment of quantifiers in English’. See the Table 1.

Table 1 Syntax (rules and interpretations) 
Full size table

Table 1 specifies that syntactic rules on the left handside translate into parallel with lambda symbol λ that directly controls the NP and VP constitutes [1, 6, p. 350].

In fact, lambda operator/abstraction operator λ is a kind of binder which denotes the infinite set of individuals in L1. In that case, it shows the characteristic function of the set and sometimes, it shows the value description with the notation φ. On the other hand, when both lambda operator and value notation removes from the set, the left part is called β-reduction. Based on such function, almost many predicates like love, like, kill, eat, see, meet, etc., defines effortlessly [7, pp. 94–95].

Table 2 demonstrates that a predicate ‘like’ can be expressed with various names (i.e. Mary, John, Bill, Keat, etc.) bind with λ operator. It has a wide range here and may cover set of individual those who like m = Mary. Secondly, the value notation φ characterizes the set of individuals. And at last, both lambda operator λ and value notation φ can be removed from the set of individuals to form a β-reduction situation.

Table 2 Syntax (categories and λ operator)
Full size table

3 Aims and Objectives

  • To present a general survey on lambda operator λ

  • To analysis natural language expressions in syntax and semantics through typed lambda calculus λ

  • To compute results when typed lambda calculus switches from one natural language to another

  • To propose an algorithm based on semantics of typed lambda calculus λ.

4 Analysis with Typed Lambda Calculus λ

We know that all objects around us identify with certain names, symbols, and terms, etc. Moreover, they are significant for a natural language considered English, Hindi, Punjabi, Marathi, Malayalam, etc. It is fascinating and challenging for us to develop any logical system for such languages. We take English as a formal language to understand the logical system for its expressions through typed lambda calculus. We begin with the following proposition.

figure d

It is a combination of Subject/NP and Predicate/VP where an individual constant Bill and Elysha respectively around the verb ‘loves’. Here V denotes a verb that has binary relations and it is called a binary predicate. The ‘loves’ predicate attracts both arguments, but the first argument is an empty slot intituitvely. The following way defines this  in L1.

figure e

We can compare the empty situation of ‘loves’ predicate with an abstraction that requires the formal representation to fill it up. See Table 3.

Table 3 Propositions with Lambda λ
Full size table

Table 3 shows that a proposition ‘Bill loves Elysha’ has a binary predicate where the empty slot (_____) is equal to abstraction. It fills up with a lambda operator λ under the name of  a variable x.Footnote 5

4.1 Lambda Abstraction (Syntax and Semantics)

Furthermore, we must discuss both syntax and semantics-based lambda abstraction rules.

Table 4, suggests that the input type goes to set of individuals and [λu. α] is the output expression. At the same time, the semantics rule gives [[λu. α]]M,g expression if there is an α and the domain of type must be under truth values.

Table 4  Lambda abstraction
Full size table

4.2 Lambda Operator λ in Syntax

In syntax, individuals and their truth values and statements with conjunctions, disjunctions, quantifiers and formulas are TYPE only according to simply-typed lambda calculus. Thus, each expression carries at least one type of expression. Table 5 induces such expressions formally as.

Table 5  Lambda and syntax
Full size table

Of these seven categories, the first is the basic level information about variables such as x, y, z in a constant form. The second application part deals with α and β; those also type expressions. The third part shows that α and β both represent similarity if they are terms. The negation part tells us that if φ is a formula then it can appear with ¬ also. Binary connectives mean that if any formula comes with φ ψ then it can be combined with ˅, ˄, ¬, ↔ like connectives. In quantification, a  universal quantifier ∀ and existential quantifier ∃  exist  with variables in a formula. On the other hand,  in the lambda abstraction, any t expression binds  with a lambda operator λ.

4.3 Lambda Operator λ in Semantics

Model and assignment function determine the natural language expressions by mapping the semantic values in Lλ. Further, we say that  <D, I> both are necessary for M as a model that assigns the semantic values.Footnote 6 The following way describes this in  L1.

figure f

Table 6 shows that the first slot is for basic expressions with a non-logical constant and a variable. The second one is about the application of α and β expressions in the context of type. The third ‘equality slot’ discusses the truth value of α and β if they belong to the same type. The fourth ‘negation slot' tell us  that the φ formula translates into a ¬φ form. The fifth slot is the (negative, conjunctive, junction, etc.) binary connectives formed by wffs. The sixth ‘quantification slot' deals with universal and existential quantifiers, and the last seventh slot shows the lambda λ as a binder for types [7, 8, pp. 170–88].

Table 6 Lambda and semantics
Full size table

5 Discussions and Results

Based on the above lambda abstraction λ in Tables 5 and 6, we take as input to compare two different languages to see the actual output. The first abstraction rule in syntax begins with usual expressions and ends with the lambda λ. It is sufficient to generalize the formal syntactic representations in both languages here. Secondly, abstraction rule in semantics has similar categorization and it computes such languages.

We see Tables 7 and 8 where both languages (English and Punjabi) have 1:1 correspondance in syntax and semantics of lambda calculus λ. Moreover, two natural languages are going to map in the same way. In other words, we argue that any ‘y’ kind of a natural language gets generated by formal language  ‘xs’ . However, double complex and compound predicates, reduplicated forms and mainly addressing notes are typical instances that will discuss by following intention and intuition-based research and applications [8, 9].

Table 7 Syntactic representations in English and Punjabi
Full size table
Table 8 Semantic representations in English and Punjabi
Full size table
figure g
figure h

Step 1: Objects with < e , t / et >

figure i
figure j

Under step 1 we take two sets of common nouns (CNs) and proper nouns (PNs) with a single predicate ‘loves’. AGR refers to another name such as arguments of both CNs and PNs that represent either e type or t type in a discourse [10, 11].

Step 2: Slots (______)

figure k

According to step 2, it shows that an external or a front AGR place must be an empty slot in a predicate ‘loves’. Such slot finds with CNs and PNs sets.

Step 3: Slots with lambda operator λ

figure l

Step 3 determines that the empty slots in CNs and PNs are abstraction places that fills up with a lambda operator λ. We add this operator in front of each empty slot.

Step 4: Lambda operator λ as binder for variables x

figure m

In step 4, we argue that a lambda operator λ binds x variable in the same slot. Because it is difficult to select each name separately for the same function here.

Step 5: Model and assignment functions

figure n

The step 5 defines the formal representation with a model (M) that contains (D) and (I) function assignment as g. Any set of individuals, as appears in step 1, is a part of e, t/et domain which directly links with truth values (1, 0).

6 Conclusion

We understand that a language like English has a formal representation. Small and simple statements in any natural language are expressions that are nothing but a set of finite or infinite types. We find that a lambda operator λ describes such infinite sets better because it takes all types of expressions (equality-based, negation-based, and so on) in the form of a type and binds them to avoid repeating any name. It also frames syntax and semantics of a natural language. Following such observations, a proposed algorithm helps us to analyze small CNs and PNs individual sets.