Keywords

1 Introduction

The performance of a structural building in a seismic event is affected by the distribution of its mass, stiffness, and strength both in lateral and vertical directions [1]. IS 1893 (Part 1): 2016 classifies irregularity into two types, viz., plan irregularity and vertical irregularity. Mass irregularity is considered to exist in structural buildings when the seismic weight of any floor is more than 150% than that of the floor below [2]. How does mass irregularity influence the performance of a framed structure has been studied in this research. Al-Ali and Krawinkler [3] investigated the effect of mass irregularity on inelastic response parameters of a shear building frame like storey drift, ductility demand, or energy dissipation. Mass irregularity was introduced through mass modification factors varying from 0.25 to 4. Small variation in mass has insignificant effect on these inelastic response parameters. Valmundson and Nau [4] considered 5, 10, and 20-storey shear buildings and varied mass of one of their floors and kept mass of remaining floors constant. For 1.5 mass ratio, they observed an increase of up to 20% in ductility demand. Irregularity in lower floors proved more critical. Michalis et al. [5] performed incremental dynamic analysis on buildings with mass of some floors twice the mass of the corresponding floors in reference regular frame and found that the effect of mass irregularity is more on inter storey drift. Vinod et al. [6] through their study on irregularity concluded that both its extent and location had an effect on storey drift as well as floor displacements of a structural building. The effect is more when the mass of the lower and upper storeys increases as compared with increase in mass of middle storeys. Poncet and Trembler [7] considered eight-storey concentrically braced steel frame with setbacks to study its performance due to mass irregularity. Two mass ratios and three locations of mass irregularity were considered. These irregular structures showed lower performance than the regular reference frame. Magliulo et al. [8] studied the behaviour of a structure having mass, stiffness, and strength irregularities and subjected to earthquake loading. They found that the plastic demand is affected by strength irregularity and not by mass irregularity. The strength irregularity had no impact on seismic demand of columns, however; it increased the seismic demand in beams. Yael Daniel and Oen Lavan [9] used multi-tuned mass damper in irregular structures for seismic control. They presented a method to optimize the location and size of these dampers. Total mass of the damper was considered as an objective function and minimized while floor accelerations were used as constraints. The method proved effective in seismic response control of the irregular structures and was found applicable to all types of irregularities. Nazarimofrad and Mehdi [10] controlled the response of an irregular multi-storey building subjected to seismic load using an active tendon system. Soil structure interaction effect was also considered and control forces were generated through linear quadratic regulator control algorithm. The results indicated that the method is less efficient in reducing the responses of the buildings located in soft soils.

The optimal location of actuators had been found applying different optimization methods in seismic control of both regular and irregular buildings by researchers. Nazarimofrad et al. [11] used multi-objective genetic algorithm to obtain the optimum number and location of active tendons in 3D irregular buildings with plan irregularity. The method proved effective in reducing actuator requirement by 50%. Rao and Sivasubramanian [12] used multiple start-guided neighbourhood search algorithm and proposed a method to get the optimal actuator location in active seismic control. Rao et al. [13] did research on optimal placement of actuators in tall buildings applying the genetic algorithm. For the same purpose, Liu et al. [14] used a discrete nonlinear optimization method and genetic algorithm. Askari et al. [15] used multi-objective genetic algorithm in active control and magnetorheological dampers in semi-active control simultaneously.

In this research, the relative performance of a regular and an irregular deficient shear building frame having mass irregularities at different floors is first investigated, compared and then an optimized active tendon system operated through LQR control algorithm is used to control its response to an earthquake using multi-objective genetic algorithm. The two objectives minimized in Pareto optimization are the ratio of the controlled and uncontrolled base shear and the number of tendons/actuators (cost of control system).

2 Problem Formulation

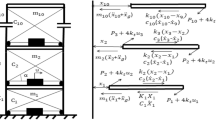
A model of the deficient frame that is regular having active tendons in each storey with the bay width and height 4 m and 3 m, respectively, is shown in Fig. 1. The mass of each floor and stiffness of each storey are 17,100 kg and 2.68 × 107 N/m, respectively. The tendons are inclined at 36.870 with the floors and have stiffness equal to 2.30 × 106 N/m. The size of both beams and columns is the same, i.e. 300 mm × 300 mm and 5% damping has been assumed. The free body diagrams have also been shown with the frame. In matrix form, the equation of motion is:

$${\text{M}}\mathop {\text{X}}\limits^{{..}} {\mkern 1mu} {\text{ + }}{\mkern 1mu} {\text{C}}\mathop {\text{X}}\limits^{.} {\mkern 1mu} {\text{ + }}{\mkern 1mu} {\text{KX}}{\mkern 1mu} {\text{ = }}{\mkern 1mu} \delta \mathop {\text{X}}\limits^{..} {\text{g}}{\mkern 1mu} {\text{ + }}{\mkern 1mu} \gamma {\text{U}}$$
(1)

where

$$ \begin{aligned} {\text{M}} & = \left[ {\begin{array}{*{20}c} {{\text{m}}_{1} } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {{\text{m}}_{10} } \\ \end{array} } \right],{\text{C}} = \left[ {\begin{array}{*{20}c} {{\text{c}}_{1} + {\text{c}}_{2} } & { - {\text{c}}_{2} } & \cdots & 0 \\ { - {\text{c}}_{2} } & \ddots & \ldots & \vdots \\ \vdots & \vdots & \ddots & { - {\text{c}}_{10} } \\ 0 & \ldots & { - {\text{c}}_{10} } & {{\text{c}}_{10} } \\ \end{array} } \right] \\ {\text{K}} & = \left[ {\begin{array}{*{20}c} {{\text{k}}_{1} + {\text{k}}_{2} } & { - {\text{k}}_{2} } & \cdots & 0 \\ { - {\text{k}}_{2} } & \ddots & \ldots & \vdots \\ \vdots & \vdots & \ddots & { - {\text{k}}_{10} } \\ 0 & \ldots & { - {\text{k}}_{10} } & {{\text{k}}_{10} } \\ \end{array} } \right] \\ \end{aligned} $$
Fig. 1
figure 1

Ten-storey shear building frame and its free body diagram

Full size image

In the above equation, mi, ki, and ci denote, respectively, the mass, stiffness, and damping of the ith storey where i = 1, 2, 3, …, 10. X(t), and U(t) are floor displacements and control forces, respectively. [γ] denotes the location of the tendons and {δ} is coefficient vector for ground acceleration. P, \(\mathrm{\alpha }\), and \({\mathrm{k}}_{\mathrm{c}}\) are the prestressing force, inclination, and stiffness of tendons, respectively.

$$\left\{\updelta \right\}=-\mathrm{M}*\mathrm{I}={\left[-{\mathrm{m}}_{1},-{\mathrm{m}}_{2}\ldots {\mathrm{m}}_{10}\right]}^{\mathrm{T}}$$
$$\mathrm{U}\left(\mathrm{t}\right)={[{\mathrm{u}}_{1},{\mathrm{u}}_{2},\dots {\mathrm{u}}_{\mathrm{r}}]}^{\mathrm{T}} ,\mathrm{ X}\left(\mathrm{t}\right)={[{\mathrm{x}}_{1},{\mathrm{x}}_{2},\dots ,{\mathrm{x}}_{10}]}^{\mathrm{T}} ,\upgamma =\overline{\upgamma }{\theta}$$
$$\overline{\upgamma }=4{\mathrm{k}}_{\mathrm{c}}\mathrm{cos\alpha }\left[\begin{array}{cccc}-1& 1& \dots & 0\\ 0& \ddots & \dots & \vdots \\ \vdots & \dots & -1& 1\\ 0& \dots & 0& -1\end{array}\right],{ \theta}=\left[\begin{array}{ccc}1& \cdots & 0\\ \vdots & \ddots & \vdots \\ 0& \cdots & 1\end{array}\right]$$

I represents the influence coefficient vector.

In state-space Eq. 1 is written as:

$$\dot{\mathrm{Z}}=\mathrm{AZ}+{\mathrm{B}}_{\mathrm{r}}{\ddot{\mathrm{X}}}_{\mathrm{g}}+{\mathrm{B}}_{\mathrm{u}}\mathrm{U}$$
(2)

where \(\mathrm{A}={\left[\begin{array}{cc}{[0]}_{10 \times10}& {[1]}_{10 \times10}\\ \left[\frac{-\mathrm{K}}{\mathrm{M}}\right]& \left[\frac{-\mathrm{C}}{\mathrm{M}}\right]\end{array}\right]}_{20\times20},{\mathrm{B}}_{\mathrm{r}}=\left\{\begin{array}{c}\left\{0\right\}\\ \left\{\frac{\updelta }{\mathrm{M}}\right\}\end{array}\right\}, {\mathrm{B}}_{\mathrm{u}}={\left\{\begin{array}{c}\left\{0\right\}\\ \left\{\frac{\upgamma }{\mathrm{M}}\right\}\end{array}\right\}}_{20 \times \mathrm{r}}\)

Mass irregularity has been introduced in the above frame using six modification factors 1.5, 2, 2.5, 3, 3.5, and 4 in the first, second, and third storeys separately under different cases and sub-cases as shown in Table 1.

Table 1 Mass modification factors
Full size table

3 Linear Quadratic Regulator (LQR)

In LQR, a quadratic performance index shown in Eq. (3) is minimized to obtain the control force ‘U’.

$$\mathrm{J}={\int }_{0}^{{\mathrm{t}}_{\mathrm{f}}}\left({\mathrm{Z}}^{\mathrm{T}}\left(\mathrm{t}\right)\mathrm{QZ}\left(\mathrm{t}\right)+{\mathrm{U}}^{\mathrm{T}}\left(\mathrm{t}\right)\mathrm{RU}\left(\mathrm{t}\right)\right)\mathrm{dt }$$
(3)

In the above equation, \({\mathrm{t}}_{\mathrm{f}}\) is the duration of an earthquake. Z is given by Eq. (2). Q is a 2n × 2n positive semi-definite matrix, and R is an n × r positive definite matrix, n is the degrees of freedom, and r is number of actuators employed. In the present optimization, Eq. (2) is used as a constraint and control force is obtained as given in Eq. (4).

$$\mathrm{U}\left(\mathrm{t}\right)=\left(\frac{-1}{2}\right){\mathrm{R}}^{-1}{\mathrm{B}}^{\mathrm{T}}\mathrm{PZ}\left(\mathrm{t}\right)=-\mathrm{GZ}\left(\mathrm{t}\right)$$
(4)

Equation (5) given below is called matrix Riccati equation provides the value of P

$$\left[\mathrm{PA}-\left[\frac{1}{2}\right]{\mathrm{PBR}}^{-1}{\mathrm{B}}^{\mathrm{T}}\mathrm{P}+{\mathrm{A}}^{\mathrm{T}}\mathrm{P}+2\mathrm{Q}\right]=0$$
(5)

4 Multi-objective Genetic Algorithm

Genetic algorithm is a method of optimization that works on the principles of genetics and natural selection. This method can handle large number of variables and is also suitable for non-differentiable objective functions. The three main operations in genetic algorithm are selection of chromosomes, crossover, and mutation. Multi-objective genetic algorithm is a type of optimization where more than one conflicting objective functions are optimized simultaneously using genetic algorithm. It gives a set of optimal solutions termed as pareto front. In this research, multi-objective genetic algorithm is used to minimize the ratio of controlled to uncontrolled base shear of the frame (J1) and number of tendons/actuators to be installed (J2). Maximum storey drift and maximum floor displacement are used as constraints and the design variables (X) are the position of tendons.

$$ {\text{Minimize }}{:}\,\,\,\,{\text{ J}}_{1} \left( {\text{X}} \right),{\text{J}}_{2} ({\text{X}}) $$
(6)
$$ {\text{Subjected to constraints}}{:}\,\,\,{\text{CSD(X)}} \le {\text{SD}}_{{\text{P}}} ,\,{\text{CFD(X)}} \le {\text{FD}}_{{\text{P}}} $$
(7)

\({\mathrm{SD}}_{\mathrm{p}}\) and \({\mathrm{FD}}_{\mathrm{p}}\) are the permissible limits of maximum storey drift and maximum floor displacement.

5 Results and Discussion

The simulation of the deficient shear building frame with and without mass irregularities has been done in Mat Lab 2019 in this study. The comparisons of uncontrolled responses, viz., floor displacements and storey drifts with mass irregularities at different floors of the cases 2–7 with that of the regular frame of case 1 are presented in Fig. 2. Uncontrolled peak displacements, in most of the cases, of modification factors have decreased when the mass irregularity is present in the second storey and third storey. The maximum reduction is 7% and has occurred in case 4c. Mass irregularity in the first storey leads to increase peak floor displacement for all modification factors. The maximum increase of peak floor displacement occurs in case 7b and is about 4% as shown in Fig. 2. Drift in first, second, and third storeys has increased in almost all cases of mass irregularity as compared with reference regular frame. The maximum increase in peak storey drift is 36.31% and has occurred in case 7a (mass irregularity in first storey with modification factor of 4) as shown in Fig. 2.

Fig. 2
figure 2figure 2

Comparison of the uncontrolled floor displacement and storey drift of irregular frames with regular one

Full size image

The base shear in almost all cases with mass irregularity has increased as compared with reference regular frame as shown in Fig. 3. The maximum increase of base shear has taken place in case 7a (mass irregularity in first storey with MF 4) and is equal to 37%.

Fig. 3
figure 3

Uncontrolled base shear of the irregular frames

Full size image

In all the cases discussed, it is found that the maximum floor displacement and maximum storey drift of both, i.e. regular and irregular frames are beyond their prescribed permissible limits, i.e. 60 mm and 12 mm, respectively, and thus need to be controlled. For this purpose, linear quadratic regulator (LQR) control algorithm is used in this study to obtain control force required for active tendon system present in some storeys of the frame. This active tendon system is a combination of active tendons and actuators. The optimal location of these tendons is obtained through multi-objective genetic algorithm. The two conflicting objectives minimized for all cases are the controlled to uncontrolled base shear ratio of the frame and the number of tendons (cost of control system) against maximum floor displacement and storey drift as constraints. All the possible combinations of the two conflicting objectives known as Pareto curves are obtained and presented in Fig. 4. In this study, the selected combination in each case having base shear reduction of 70% with corresponding optimal position of the tendons is given in Table 2. In the table, ‘X’ and ‘✓’ denote the absence and presence of tendon in a storey, respectively. The table indicates that MF greater than or equal to 2 especially at the second floor requires an extra tendon for the same reduction of responses as that of the reference regular frame. There is no need to place tendons in the upper three storeys in almost all the cases of irregularities considered and placement of tendon in the first storey is indispensable.

Table 2 Optimal position of tendons in different cases
Full size table
Fig. 4
figure 4

Pareto curves

Full size image

The controlled and uncontrolled responses in all cases with tendons placed optimally as per Table 2 are compared in Fig. 5. In the figure, UC, C, and P stand for uncontrolled, controlled, and permissible, respectively. As can be seen in the figures, the optimal control system keeps the responses within the permissible limits in all the cases of mass irregularity. Also, the base shear in each and every case has reduced by at least 70% (Fig. 6).

Fig. 5
figure 5figure 5

Comparison of controlled and uncontrolled responses

Full size image
Fig. 6
figure 6

Comparison of controlled and uncontrolled base shear of the frame for different cases

Full size image

The control forces in each of the optimally placed tendons for the considered seven cases of mass irregularity with modification factors up to 4 are shown in Table 3.

Table 3 Control force in tendons under different cases
Full size table

6 Conclusion

This study is done on active seismic control of structural buildings with mass irregularities. For this purpose, an active tendon system with tendons/actuators placed optimally using multi-objective genetic algorithm is employed through linear quadratic regulator. The numerical analysis is done on a 10-storey deficient shear frame with mass irregularity in the first, second, and third storeys introduced with modification factors (MF) 1.5, 2, 2.5, 3, 3.5, and 4 as seven different cases. Controlled to uncontrolled base shear ratio and the number of tendons are minimized with constrained peak floor displacement and storey drift. The results are presented below:

  1. (1)

    Mass irregularity has influenced both uncontrolled floor displacements and storey drift of the deficient frame subjected to El Centro earthquake. The maximum increase in peak values of floor displacement and storey drift due to the mass irregularity considered are 4% and 36%, respectively. In few cases, peak floor displacement has decreased with maximum reduction being 7%.

  2. (2)

    Top three storeys do not require any tendon, however, placement of tendon in the first storey is indispensable as per the optimization results.

  3. (3)

    An extra tendon is required in case of mass irregularity in the second and third storeys of the frame with modification factor greater than 2 for the same reduction of responses as compared with that of the regular frame.

  4. (4)

    Even deficient frames with mass irregularity can be made safe without retrofitting using active control system.

  5. (5)

    The maximum force in a tendon under any case is 49.03 kN. The maximum total control force is 140.79 kN and is generated when the mass irregularity is present in the third storey with modification factor equal to 3.