Dynamic Analysis of a Functionally Greded Sandwich Beam Traversed by a Moving Mass Based on a Refined Third-Order Theory

Abstract

Dynamic analysis of a functionally graded sandwich (FGSW) beam traversed by a moving mass is presented in the basis of a refined third-order shear deformation theory. The beam consists of three layers, a homogeneous core and two functionally graded skin layers with material properties varying in the thickness direction by a power gradation law. Both Voigt and Mori-Tanaka micromechanical models are employed to evaluate the effective properties of the beam. A finite element formulation, taking into account the effect of inertial, Coriolis and centrifugal forces, is derived and used in combination with Newmark method to compute dynamic response of the beam. The accuracy and efficiency of the derived formulation are confirmed by comparing obtained results with the data of Refs. [3, 4, 6, 11]. The effects of the material gradation, the moving mass speed and the beam geometry on the dynamic behavior of the beam are studied in detail and highlighted. The influence of the micromechanical model on the dynamic response of the beam is also examined and discussed.

1 Introduction

Sandwich structures are extensively used in different engineering applications such as automotive, aerospace and defense industries because of their light weight and high stiffness-to-weight ratio. With the development of manufacturing methods [1], functionally graded materials (FGMs), a new type of advanced composites initiated by Japanese researchers in mid-1980 [2], can be incorporated in the sandwich construction to improve the performance of structural components. Functionally graded sandwich (FGSW) structures can be designed to have a smooth variation of material properties between layers, which helps to eliminate the interface separation as often seen in the conventional sandwich structures. Many investigations on vibration analysis of FGSW structures have been reported in the literature, contributions that are most relevant to the present work are briefly discussed below.

Based on the modified Fourier series method, Su et al. [3] studied free vibration of FGSW beams resting on a Pasternak foundation. Both Voigt and Mori-Tanaka micromechanical models were used by the authors to evaluate the effective properties of the beams. Vo et al. [4] presented free vibration and buckling analyses of FGSW beams using a finite element formulatiion. The effect of thickness stretching was takien into acount by Vo et al. [5] in bibration and buckling analyses of FGSW beams. Regarding dynamic analysis of FGM beams under moving loads, the topic discussed herein, Khalili et al. [6] employed the differential quadrature method to compute dynamic response of Euler-Bernoulli beams under a moving mass. The Ritz method was used by Songsuwan et al. [7] to investigate the effect of thickness gradation of material properties on vibration of sandwich beams subjected a moving harmonic load. The influence of elastic foundation on the dynamic behavior of the sandwich beams was taken into consideration by the authors. Based on different shear deformation theories, Şimşek [8] studied vibration of a FGM beam due to a moving mass. Şimşek and Kocaturk [9] used polynomials to approximate the displacement field in dynamic analysis of FGM beams under a moving force. The effect of longitudinal variation of the material properties on the dynamic behaviour of FGM beams under two successive moving harmonic loads was considered in [10]. The finite element method was used in [11, 12] to study dynamic response of FGM under moving loads. Nonlinear dynamic analysis of a cracked beam on elastic foundation subjected to a moving mass has been studied using the finite element method [13].

In this paper, dynamic analysis of a functionally graded sandwich beam traversed by a moving mass is presented on the basis of a third-order shear deformable finite element formulation. The core of the beam is pure ceramic while its two skin layers are power-law FGM. Equation of motion in term of the finite element analysis is derived and solved by the Newmark method. Both Voigt and Mori-Tanaka micromechanical models are employed to evaluate the effective properties of the beam. The effects of material gradation, the moving mass speed and the beam geometry on the dynamic behavior of the beam are examined in detail and highlighted.

2 Theoretical Formulations

2.1 The FGSW Beam Model

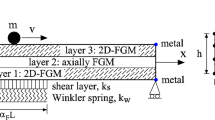
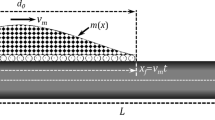
A simply supported FGSW beam with length L, rectangular cross-section (b × h), under a mass m_c, moving with a constant speed v from left to right as shown in Fig. 1 is considered. It is assumed that the mass m_c is always in contact with the beam. The beam consists of three layers, namely a ceramic core and two FGM layers. Denoting $z_{0} ,\,z_{1} ,\,\,z_{2} ,\,z_{3}$, in which $z_{0} = - h/2,\,\,z_{3} = h/2$, are the vertical coordinates of the bottom surface, interfaces and top face, respectively.

Fig. 1.

The FGSW beam under a moving mass

The beam is formed from ceramic and metal whose volume fraction varies in the thickness direction according to [4]

$$ V_{c} = \left\{ {\begin{array}{*{20}l} {\left( {\frac{{z - z_{0} }}{{z_{1} - z_{0} }}} \right)^{n} } \hfill & {{\text{for}}\quad z \in \left[ {z_{0} ,z_{1} } \right]} \hfill \\ 1 \hfill & {{\text{for}}\quad z \in \left[ {z_{1} ,z_{2} } \right]} \hfill \\ {\left( {\frac{{z - z_{3} }}{{z_{2} - z_{3} }}} \right)^{n} } \hfill & {{\text{for}}\quad z \in \left[ {z_{2} ,z_{3} } \right]} \hfill \\ \end{array} } \right. $$

(1)

and

$$ V_{m} + V_{c} = 1, $$

(2)

where V_c, V_m, respectively, are the volume fraction of ceramic and metal; n is the power-law index, defining the variation of the constituents in the thickness direction.

Both Voigt and Mori-Tanaka micromechanical models are used herein in to evaluate the effective properties of the beam. The effective property $P_{f} (z)$ based on the Voigt’s model resulted from Eqs. (1) and (2) is of the form

$$ P_{f} (z) = \left\{ {\begin{array}{*{20}l} {\left( {P_{c} - P_{m} } \right)\left( {\frac{{z - z_{0} }}{{z_{1} - z_{0} }}} \right)^{n} + P_{m} } \hfill & {{\text{for}}\quad z \in \left[ {z_{0} ,z_{1} } \right]} \hfill \\ {P_{c} } \hfill & {{\text{for}}\quad z \in \left[ {z_{1} ,z_{2} } \right]} \hfill \\ {\left( {P_{c} - P_{m} } \right)\left( {\frac{{z - z_{3} }}{{z_{2} - z_{3} }}} \right)^{n} + P_{m} } \hfill & {{\text{for}}\quad z \in \left[ {z_{2} ,z_{3} } \right]} \hfill \\ \end{array} } \right. $$

(3)

where, $P_{c} \,$ and $P_{m}$ are the properties of ceramic and metal, respectively.

According to the Mori–Tanaka scheme, the effective Young’s modulus $\left( {E_{f} } \right)$ and Poisson’s ratio $\left( {v_{f} } \right)$ can be expressed as

$$ E_{f} = \frac{{9K_{f} G_{f} }}{{3K_{f} + G_{f} }},\quad v_{f} = \frac{{3K_{f} - 2G_{f} }}{{6K_{f} + 2G_{f} }} $$

(4)

where $K_{f}$ and $G_{f}$ are, respectively, the effective local bulk modulus and shear modulus, which can be calculated from the moduli and volume fraction of the constituent materials as

$$ \begin{aligned} & \frac{{K_{f} - K_{m} }}{{K_{c} - K_{m} }} = \frac{{V_{c}^{{}} }}{{1 + V_{m} (K_{c} - K_{m} )/(K_{m} + 4G_{m} /3)}}, \\ & \frac{{G_{f} - G_{m} }}{{G_{c} - G_{m} }} = \frac{{V_{c} }}{{1 + V_{m} \left( {G_{c} - G_{m} } \right)/\left\{ {G_{m} + G_{m} \left( {9K_{m} + 8G_{m} } \right)/\left[ {6\left( {K_{m} + 2G_{m} } \right)} \right]} \right\}}} \\ \end{aligned} $$

(5)

in which $K_{c}$, $G_{c}$ and $K_{m}$, $G_{m}$, respectively, are the local bulk modulus and the shear modulus of the ceramic and metal and defined by following form

$$ K_{c} = \frac{{E_{c} }}{{3(1 - 2\mu _{c} )}},\quad G_{c} = \frac{{E_{c} }}{{2\left( {1 + \mu _{c} } \right)}},\quad K_{m} = \frac{{E_{m} }}{{3(1 - 2\mu _{m} )}},\quad G_{m} = \frac{{E_{m} }}{{2\left( {1 + \mu _{m} } \right)}}, $$

(6)

Noting that the effective mass density $\left( {\rho _{f} } \right)$ is defined by Voigt model [3].

2.2 Mathematical Model

Based on a refined third-order shear deformation recently proposed by Shimpi [14], the displacements in the x- and z-directions, respectively, are given by

$$ \begin{aligned} & u(x,z,t) = u_{0} (x,t) - zw_{{b,x}} + f(z)w_{{s,x}} , \\ & w(x,z,t) = w_{b} (x,t) + \,w_{s} (x,t) \\ \end{aligned} $$

(7)

where

$$ f(z) = z\left[ {\frac{1}{4} - \frac{5}{3}\left( {\frac{z}{h}} \right)^{2} } \right]\, $$

(8)

In Eq. (7) $u_{0} \left( {x,t} \right)\,$ is the axial displacement of a point on the x-axis, $w_{b} (x,t)$ and $\,w_{s} (x,t)$ are, respectively, bending and shear components of the transverse displacement; t is the time variable.

The axial strain and shear strain resulted from Eq. (7) are of the form

$$ \begin{aligned} & \varepsilon _{{xx}} = u_{{0,x}} - zw_{{b,xx}} + f(z)w_{{s,xx}} , \\ & \gamma _{{zx}} = g(z)w_{{s,x}} \\ \end{aligned} $$

(9)

$$ {\text{with}}\;g(z) = 5\left[ {\frac{1}{4} - \left( {\frac{z}{h}} \right)^{2} } \right] $$

(10)

Based on the Hooke’s law, the constitutive relation for the FGSW is as follows

$$ \sigma _{{xx}} = E(z)\varepsilon _{{xx}} ,\quad \tau _{{xz}} = G(z)\gamma _{{xz}} $$

(11)

Where E(z) and G(z) are, respectively, the elastic modulus and shear modulus, $\sigma _{{xx}} ,\,\tau _{{xz}}$ are the axial stress and shear stress, respectively.

The strain energy of the beam $(U)$ is then given by

$$ U = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A} {\left( {\sigma _{{xx}} \varepsilon _{{xx}} + \gamma _{{zx}} \tau _{{xz}} } \right)} } \,dAdx, $$

(12)

where A = bh is the cross-sectional area.

From Eqs. (9) and (11), the strain energy can be written as

$$ \begin{array}{*{20}c} {U = \frac{1}{2}\int\limits_{0}^{L} {\left[ {A_{{11}} u_{{0,x}}^{2} - 2A_{{12}} u_{{0,x}} w_{{b,xx}} + A_{{22}} w_{{b,xx}} ^{2} } \right.} + 2A_{{us}} u_{{0,x}} w_{{s,xx}} } \\ {\left. { - 2A_{{bs}} w_{{b,xx}} w_{{s,xx}} + A_{{ss}} w_{{s,xx}}^{2} + A_{{sh}} w_{{s,x}}^{2} } \right]dx} \\ \end{array} $$

(13)

In the Eq. (13) $A_{{ij}}$ are the beam rigidities, defined as

$$ \begin{array}{*{20}c} {\left( {A_{{11}} ,A_{{12}} ,A_{{22}} } \right) = \int_{A} {E_{f} \left( {1,z,z^{2} } \right)} \;dA = b\sum\limits_{{i = 1}}^{3} {\int\limits_{{z_{{i - 1}} }}^{{z_{i} }} {E_{f} \left( {1,z,z^{2} } \right)dz} } } \\ {\left( {A_{{us}} ,A_{{bs}} ,A_{{ss}} } \right) = \int\limits_{A} {E_{f} \left[ {f(z),zf(z),f^{2} (z)} \right]} \;dA = b\sum\limits_{{i = 1}}^{3} {\int\limits_{{z_{{i - 1}} }}^{{z_{i} }} {E_{f} \left[ {f(z),zf(z),f^{2} (z)} \right]dz} } } \\ {A_{{sh}} = \int\limits_{A} {G(z)g} (z)\;dA = b\sum\limits_{{i = 1}}^{3} {\int\limits_{{z_{{i - 1}} }}^{{z_{i} }} {G(z)g(z)dz} } } \\ \end{array} $$

(14)

where $E(z),\,\,G(z),$ are, respectively, the elastic modulus and shear modulus. With the Mori-Tanaka scheme adopted for the effective moduli herein, the above rigidities can be evaluated numerically.

The kinetic energy $\left( T \right)$ of the FGSW beam are then given by

$$ \begin{aligned} T & = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{V}^{{}} {\rho (z)\left( {\dot{u}^{2} + \dot{w}^{2} } \right)} } \;dAdx \\ & = \frac{1}{2}\int\limits_{0}^{L} {\left\{ {I_{{11}} [\dot{u}_{0}^{2} + (\dot{w}_{b}^{{}} + \dot{w}_{s} )^{2} ] - 2I_{{12}} \dot{u}_{0} \dot{w}_{{b,x}} + I_{{22}} \dot{w}_{{b,x}}^{2} + 2I_{{us}} \dot{u}_{0} \dot{w}_{{s,x}} } \right.} \\ & - 2I_{{bs}} \dot{w}_{{b,x}} \dot{w}_{{s,x}} + \left. {I_{{ss}} \dot{w}_{{s,x}}^{2} } \right\}dx \\ \end{aligned} $$

(15)

with $I_{{ij}}$ are the mass moments, defined as

$$ \begin{aligned} & (I_{{11}} ,I_{{12}} ,I_{{22}} ) = \int_{A} {\rho _{f} \left( {1,z,z^{2} } \right)\,} dA = b\sum\limits_{{i = 1}}^{3} {\int\limits_{{z_{{i - 1}} }}^{{z_{i} }} {\rho _{f} \left( {1,z,z^{2} } \right)dz} } \\ & \left( {I_{{us}} ,I_{{bs}} ,I_{{ss}} } \right) = \int_{A} {\rho _{f} \left[ {f(z),zf(z),f^{2} (z)} \right]} \;dA = b\sum\limits_{{i = 1}}^{3} {\int\limits_{{z_{{i - 1}} }}^{{z_{i} }} {\rho _{f} \left[ {f(z),zf(z),f^{2} (z)} \right]dz} } \\ \end{aligned} $$

(16)

where $\rho _{f}$, is mass density. With the Voigt model used for $\rho _{f}$, explicit expressions for the above mass moments can be easily obtained.

Finally, the potential energy due to the moving mass is given by [11]

$$ \,V = - \int\limits_{0}^{L} {\left[ {\left( {m_{c} g - m_{c} \ddot{w} - 2m_{c} v\dot{w}_{{,x}} - m_{c} v^{2} w_{{,xx}} } \right)w - m_{c} \ddot{u}_{0} u_{0} (x,t)} \right]} \,\delta \left( {x - vt} \right)dx $$

(17)

where v is the velocity of the moving mass, $g = 9,81\left( {m/s^{2} } \right)$ is the gravity acceleration; $m_{c} \ddot{u}_{0}$ and $\,m_{c} \ddot{w}$ are, respectively, the axial and transverse inertia forces; $2m_{c} v\dot{w}_{{,x}}$ and $2m_{c} v^{2} w_{{,xx}}$ are the Coriolis and centrifugal forces, respectively; δ(.) is the Dirac delta function; x is the abscissa of the moving mass measured from the left end of the beam.

3 Finite Element for Mulation

Assuming the beam is divided into NE elements with length of l. The vector of nodal displacements for a standard two-node beam element with ten degrees of freedom is given by

$$ {\mathbf{d}} = \left\{ {{\mathbf{d}}_{{u0}} ,{\mathbf{d}}_{{wb}} ,{\mathbf{d}}_{{ws}} } \right\}^{T} $$

(18)

where

$$ \begin{aligned} & {\mathbf{d}}_{{u0}} = \left\{ {\begin{array}{*{20}c} {u_{{01}} } & {u_{{02}} } \\ \end{array} } \right\}^{T} ,\,\,{\mathbf{d}}_{{wb}} = \left\{ {\begin{array}{*{20}c} {w_{{b1}} } & {w_{{b,x1}} } & {w_{{b2}} } & {w_{{b,x2}} } \\ \end{array} } \right\}^{T} , \\ & {\mathbf{d}}_{{ws}} = \left\{ {\begin{array}{*{20}c} {w_{{s1}} } & {w_{{s,x1}} } & {w_{{s2}} } & {w_{{s,x2}} } \\ \end{array} } \right\}^{T} \\ \end{aligned} $$

(19)

are, respectively, the vectors of the nodal axial, bending, and shear component of the transverse displacements. A superscript “T’ in Eq. (19) and hereafter is used to denote the transpose of a vector or a matrix.

The axial displacement $u_{0} (x,t)$, bending component $w_{b} (x,t)$, and shear component $w_{s} (x,t)$ of the transverse displacement are interpolated from their nodal values according to

$$ u_{0} = {\mathbf{N}}_{u} {\mathbf{d}}_{{u0}} ,\quad w_{b} = {\mathbf{H}}_{{wb}} {\mathbf{d}}_{{wb}} ,\quad w_{s} = {\mathbf{H}}_{{ws}} {\mathbf{d}}_{{ws}} , $$

(20)

where ${\mathbf{N}}_{u}$, ${\mathbf{H}}_{{wb}}$ and ${\mathbf{H}}_{{ws}}$ are matrices of shape functions with the following form

$$ {\mathbf{N}}_{u} = \left[ {N_{1} \quad N_{2} } \right],\quad {\mathbf{H}}_{{wb}} = \left[ {\begin{array}{*{20}c} {H_{1} } & {H_{2} } & {H_{3} } & {H_{4} } \\ \end{array} } \right],\quad {\mathbf{H}}_{{ws}} = \left[ {\begin{array}{*{20}c} {H_{1} } & {H_{2} } & {H_{3} } & {H_{4} } \\ \end{array} } \right] $$

(21)

with N_i (i = 1, 2) and H_i (i = 1…4) is linear and Hermite functions, respectively. Based on the interpolation scheme, one can write the strain energy in Eq. (13) in the forms

$$ U = \frac{1}{2}\sum\limits_{{i = 1}}^{{{\text{NE}}}} {{\mathbf{d}}^{T} {\mathbf{k}}\;{\mathbf{d}}} $$

(22)

where k is the element stiffness matrix, which can be written in the sub-matrices as

$$ {\mathbf{k}} = \left[ {\begin{array}{*{20}c} {{\mathbf{k}}_{{u_{0} u_{0} }} } & {{\mathbf{k}}_{{u_{0} w_{b} }} } & {{\mathbf{k}}_{{u_{0} w_{s} }} } \\ {{\mathbf{k}}_{{w_{b} u_{0} }} } & {{\mathbf{k}}_{{w_{b} w_{b} }} } & {{\mathbf{k}}_{{w_{b} w_{s} }} } \\ {{\mathbf{k}}_{{w_{s} u_{0} }} } & {{\mathbf{k}}_{{w_{s} w_{b} }} } & {{\mathbf{k}}_{{w_{s} w_{s} }} } \\ \end{array} } \right] $$

(23)

In the above equation, ${\mathbf{k}}_{{u_{0} u_{0} }}$, ${\mathbf{k}}_{{w_{b} w_{b} }}$ and ${\mathbf{k}}_{{w_{s} w_{s} }}$ are, respectively, the element stiffness matrices stemming from the axial stretching, bending, shear deformation, and they have the forms

$$ \begin{aligned} & {\mathbf{k}}_{{u_{0} u_{0} }} = \int\limits_{0}^{l} {{\mathbf{N}}_{{u,x}}^{T} A_{{11}} {\mathbf{N}}_{{u,x}} dx} ;\quad {\mathbf{k}}_{{w_{b} w_{b} }} = \int\limits_{0}^{l} {{\mathbf{H}}_{{w_{b} ,xx}}^{T} A_{{22}} } {\mathbf{H}}_{{w_{b} ,xx}} dx; \\ & {\mathbf{k}}_{{w_{s} w_{s} }} = \int\limits_{0}^{l} {\left[ {\mathbf{H}} \right._{{w_{s} ,xx}}^{T} A_{{ss}} } {\mathbf{H}}_{{w_{b} ,xx}} + A_{{sh}} {\mathbf{H}}_{{w_{b} ,x}}^{T} \left. {{\mathbf{H}}_{{w_{b} ,x}} } \right]dx \\ \end{aligned} $$

(24)

and ${\mathbf{k}}_{{u_{0} w_{b} }}$, ${\mathbf{k}}_{{u_{0} w_{s} }}$, and ${\mathbf{k}}_{{w_{b} w_{s} }}$ are, respectively, the axial-bending, axial-shear, and bending-shear coupling matrices with the following forms

$$ \begin{aligned} & {\mathbf{k}}_{{u_{0} w_{b} }} = - \int\limits_{0}^{l} {{\mathbf{N}}_{{u,x}}^{T} A_{{12}} {\mathbf{H}}_{{w_{b} ,xx}} dx} ,\quad {\mathbf{k}}_{{u_{0} w_{s} }} = \int\limits_{0}^{l} {{\mathbf{N}}_{{u,x}}^{T} A_{{us}} {\mathbf{H}}_{{w_{s} ,xx}} dx} , \\ & {\mathbf{k}}_{{w_{b} w_{s} }} = - \int\limits_{0}^{l} {{\mathbf{H}}_{{b,xx}}^{T} A_{{bs}} {\mathbf{H}}_{{w_{s} ,xx}} dx} \\ \end{aligned} $$

(25)

Similarly, the kinetic energy (15) can be written in the form

$$ T = \frac{1}{2}\sum\limits_{{i = 1}}^{{{\text{NE}}}} {{\dot{\boldsymbol{dhb}}}^{T} {\mathbf{m}}} \;{\dot{\boldsymbol{d}}} $$

(26)

with the element mass matrix m can be written in sub-matricies as

$$ {\mathbf{m}} = \left[ {\begin{array}{*{20}c} {{\mathbf{m}}_{{u_{0} u_{0} }} } & {{\mathbf{m}}_{{u_{0} w_{b} }} } & {{\mathbf{m}}_{{u_{0} w_{s} }} } \\ {{\mathbf{m}}_{{w_{b} u_{0} }} } & {{\mathbf{m}}_{{w_{b} w_{b} }} } & {{\mathbf{m}}_{{w_{b} w_{s} }} } \\ {{\mathbf{m}}_{{w_{s} u_{0} }} } & {{\mathbf{m}}_{{w_{s} w_{b} }} } & {{\mathbf{m}}_{{w_{s} w_{s} }} } \\ \end{array} } \right] $$

(27)

where

$$ \begin{aligned} & {\mathbf{m}}_{{u_{0} u_{0} }} = \int\limits_{0}^{l} {{\mathbf{N}}_{{u,x}}^{T} I_{{11}} {\mathbf{N}}_{{u,x}} dx} ;\quad {\mathbf{m}}_{{w_{b} w_{b} }} = \int\limits_{0}^{l} {\left( {{\mathbf{H}}_{{w_{b} }}^{T} I_{{11}} {\mathbf{H}}_{{w_{b} }} + {\mathbf{H}}_{{w_{b} ,x}}^{T} I_{{22}} {\mathbf{H}}_{{w_{b} ,x}} } \right)} dx; \\ & {\mathbf{m}}_{{w_{s} w_{s} }} = \int\limits_{0}^{l} {\left( {{\mathbf{H}}_{{w_{s} }}^{T} I_{{11}} {\mathbf{H}}_{{w_{s} }} + {\mathbf{H}}_{{w_{b} ,x}}^{T} I_{{ss}} {\mathbf{H}}_{{w_{b} ,x}} } \right)} dx \\ & {\mathbf{m}}_{{u_{0} w_{b} }} = - \int\limits_{0}^{l} {{\mathbf{N}}_{u}^{T} I_{{12}} {\mathbf{H}}_{{w_{b} ,x}} dx} ,\quad {\mathbf{m}}_{{u_{0} w_{s} }} = \int\limits_{0}^{l} {{\mathbf{N}}_{u}^{T} I_{{us}} {\mathbf{H}}_{{w_{s} ,x}} dx} , \\ & {\mathbf{m}}_{{w_{b} w_{s} }} = - \int\limits_{0}^{l} {\left( {{\mathbf{H}}_{{w_{b} }}^{T} I_{{11}} {\mathbf{H}}_{{w_{s} }} + {\mathbf{H}}_{{b,x}}^{T} I_{{bs}} {\mathbf{H}}_{{w_{s} ,x}} } \right)dx} \\ \end{aligned} $$

(28)

Finally, the potential energy in Eq. (17) can be writen as

$$ V = \sum\limits_{{}}^{{NE}} {\left( {{\ddot{\boldsymbol{d}}}^{T} {\mathbf{m}}_{c} {\ddot{\boldsymbol{d}}} + {\dot{\boldsymbol{d}}}^{T} {\mathbf{c}}_{c} {\dot{\boldsymbol{d}}} + {\mathbf{d}}^{T} {\mathbf{k}}_{c} {\mathbf{d}} - {\mathbf{d}}^{T} {\mathbf{f}}_{c} } \right)} $$

(29)

where ${\mathbf{m}}_{c} ,\,\,{\mathbf{c}}_{c}$ and ${\mathbf{k}}_{c}$ are, respectively, the element mass, damping and stiffness matrices due to the effects of the inertia, Coriolis and the centrifugal forces of the moving mass; ${\mathbf{f}}_{c}$ is the time-dependent element nodal load vector generated by the moving mass. The expressions for these matrices and vector are as follows

$$ \mathop {{\mathbf{m}}_{c} }\limits_{{10 \times 10}} = m_{c} \left[ {\begin{array}{*{20}c} {{\mathbf{N}}^{T} {\mathbf{N}}} & 0 & 0 \\ 0 & {{\mathbf{H}}_{{wb}}^{T} {\mathbf{H}}_{{wb}} } & {{\mathbf{H}}_{{wb}}^{T} {\mathbf{H}}_{{ws}} } \\ 0 & {{\mathbf{H}}_{{ws}}^{T} {\mathbf{H}}_{{wb}} } & {{\mathbf{H}}_{{ws}}^{T} {\mathbf{H}}_{{ws}} } \\ \end{array} } \right]_{{x_{e} }} $$

(30)

$$ \mathop {{\mathbf{c}}_{c} }\limits_{{10 \times 10}} = 2m_{c} v\left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {{\mathbf{H}}_{{wb}}^{T} {\mathbf{H}}_{{wb,x}} } & {{\mathbf{H}}_{{ws}}^{T} {\mathbf{H}}_{{wb,x}} } \\ 0 & {{\mathbf{H}}_{{ws}}^{T} {\mathbf{H}}_{{wb,x}} } & {{\mathbf{H}}_{{ws}}^{T} {\mathbf{H}}_{{ws,x}} } \\ \end{array} } \right]_{{x_{e} }} $$

(31)

$$ \mathop {{\mathbf{k}}_{c} }\limits_{{10 \times {\text{10}}}} = m_{c} v^{2} \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {{\mathbf{H}}_{{wb}}^{T} {\mathbf{H}}_{{wb,xx}} } & {{\mathbf{H}}_{{ws}}^{T} {\mathbf{H}}_{{wb,xx}} } \\ 0 & {{\mathbf{H}}_{{ws}}^{T} {\mathbf{H}}_{{wb,xx}} } & {{\mathbf{H}}_{{ws}}^{T} {\mathbf{H}}_{{ws,xx}} } \\ \end{array} } \right]_{{x_{e} }} $$

(32)

and

$$ \mathop {{\mathbf{f}}_{c} }\limits_{{10 \times 1}} = m_{c} g\left[ {\begin{array}{*{20}c} 0 & {{\mathbf{{\rm H}}}_{{wb}}^{T} } & {{\mathbf{{\rm H}}}_{{ws}}^{T} } \\ \end{array} } \right]_{{x_{e} }}^{T} $$

(33)

The notation $\left[ . \right]_{{x_{e} }}$ in Eqs. (30) to (33) mean that $\left[ . \right]$ is evaluated at $x_{e}$ - the current abscissa of the moving mass with respect to the left node of the element. Noting that except for the element under the moving mass, the element matrices ${\mathbf{m}}_{c} ,\,{\mathbf{c}}_{c}$, and the the force vector ${\mathbf{f}}_{c}$ are zeros for all other elements.

The finite element equation for the dynamic analysis of the beam can be written in the form

$$ \left( {{\mathbf{M}} + {\mathbf{M}}_{c} } \right){\ddot{\boldsymbol{D}}} + {\mathbf{C}}_{c} {\dot{\boldsymbol{D}}} + \left( {{\mathbf{K}} + {\mathbf{K}}_{c} } \right){\mathbf{D}} = {\mathbf{F}}_{{}} $$

(34)

where ${\ddot{\boldsymbol{D}}},\,{\dot{\boldsymbol{D}}},\,$ and ${\mathbf{D}}$ are, respectively, accelerations, velocities, and the vectors of nodal displacements. ${\mathbf{M}},\,\,{\mathbf{M}}_{c} ,\,\,{\mathbf{C}}_{c} ,\,\,{\mathbf{K}},\,\,{\mathbf{K}}_{c} ,\,$ and ${\mathbf{F}}$ are the global matrices and vector obtained by respectively assembling the matrices ${\mathbf{m}},\,{\mathbf{m}}_{c} ,\,{\mathbf{c}}_{c} ,\,{\mathbf{k}},\,{\mathbf{k}}_{c}$ and ${\mathbf{f}}_{c}$ over the elements. Equation (34) can be solved by the direct integration Newmark method. The average acceleration method which ensures the numerical instability method is adopted herein.

4 Numerical Results

Dynamic behaviour of the simply supported FGSW beam under a moving mass is numerically investigated in this section. To this end, a beam with with (b × h) = (1 × 1) m, made from alumina (Al₂O₃) and aluminum (Al) with the following properties is considered

• E_c = 380 GPA, ρ_c = 3960 kg/m³, ν_c = 0.3 for alumina (Al₂O₃).

• E_m = 70 GPA, ρ_m = 2702 kg/m³, ν_m = 0.3 for aluminum (Al).

The following dimensionless parameters are used for dynamic magnification factor (D_d), mass ratio (r_m), normal stress ($\sigma _{{xx}}^{*}$), shear stress $\left( {\tau _{{xz}}^{*} } \right)$ as [6, 7]

$$ D_{d} = {\text{max}}\left( {\frac{{w(L/2,t)}}{{w_{{st}} }}} \right);\quad r_{m} = \frac{m}{{\rho _{c} AL}};\quad \sigma _{{xx}}^{*} = \frac{{\sigma _{{xx}} }}{{\sigma _{0} }},\quad \tau _{{xz}}^{*} = \frac{{\tau _{{xz}} }}{{\sigma _{0} }} $$

(35)

where w_st = mgL³/48E_cI is the static deflection of a simply supported alumina beam under a load mg acting at the mid-span; A = bh is the cross-sectional area of the beam; and σ₀ = mg/A. A uniform time step ∆t = ∆T/400 with ∆T is the total time necessary for the mass to cross the beam, is used for the Newmark procedure.

4.1 Accuracy and Convergence Studies

Before computing the dynamic response of the beam, the accuracy of the derived formulation is needed to verify. To this end, Table 1 compares the fundamental frequency $\mu = \omega L^{2} /h\sqrt {\rho _{m} /E_{m} }$ of the FGSW beam with L/h = 10 obtained in the present work with that of Ref. [3] for various layer thickness ratios. Both Voigt model and Mori–Tanaka scheme are considered. Very good agreement between the result of the present work with that of Ref. [3] is noted from Table 1.

Table 1. Comparison of fundamental frequency parameter of FGSW beam with L/h = 10.

Figure 2 compares the time histories for mid-span deflection of the FGSW beam under a moving point force with v = 50 m/s of the present work with the result of Songsuwan et al. [7]. Regardless of the layer thickness ration, the good agreement between the present result with that of Ref. [7] is seen from Fig. 2. Noting that the Timoshenko beam theory was used in combination with Ritz method was used in Ref. [7] in computing the dynamic response of the beam.

Table 2 shows the convergence of the derived formulation in evaluating dynamic magnification factor of FGM beam under a moving mass, where the result of Ref. [6] using the differential quadrature method is also given. As seen from table the convergence of the present formulation is achieved by using 18 elements. The factor D_d of the beam obtained in the present work is in good agreement with that of Ref. [6]. Noting that the result in Table 2 was obtained for the beam made from alumina and steel with the geometrical and material data given in [6]. Because of the above convergence, a mesh of 18 elements is used in all computations reported below.

Fig. 2.

Comparison of time histories for mid-span deflection of FGSW beam under a moving force (L/h = 10, n = 0.5, v = 50 m/s)

Table 2. Convergence of the formulation in evaluating dynamic magnification factor of a FGM beam.

4.2 Parametric Study

In Fig. 3, the time histories for mid-span deflection of the (2-1-2) beam are depicted for L/h = 20, n = 0.5, r_m = 0.5 and various values of the moving mass speed. The result is shown in the figure for both the Voigt model and Mori-Tanaka scheme. The maximum midspan deflection in Fig. 3 is seen to be affected by the moving mass speed (v), and it is larger when the beam under a higher moving mass speed. The dynamic deflection obtained by the Voigt model is smaller than that using the Mori-Tanaka scheme.

Fig. 3.

Time histories for mid-span deflection of (2-1-2) beam for L/h = 20, n = 0.5, r_m = 0.5.

Table 3. Dymanic magnification factor of FGSW beam for L/h = 10, r_m = 0.5.

To investigate the effect of the power-law index (n) and moving mass speed (v) on the dynamic behavior of the beam, the dynamic magnification factor of symmetric and non-symmetric beams are considered. Table 3 lists the values of the factor D_d of the beam for various values of the speed v and the power-law index n. Table 3 shows that the factor D_d increases with the increase of both the power-law index (n) and moving mass speed (v). At a given moving mass speed v and index n, the factor D_d obtained from Mori-Tanaka scheme is higher than that obtained from Voigt model. The effect of the material parameter (n) can be seen more clearly from Fig. 4, where the variation of the factor D_d of (2-1-2) beam with the the power-law index (n) is shown for L/h = 20, r_m = 0.5 and various values of moving mass speed (v).

Figure 5 illustrates the variation of the factor D_d of (2-1-2) beam with the moving mass speed (v) for L/h = 20, r_m = 0.5. The influence of the moving mass speed on the factor D_d is clearly seen from the figures, and the factor D_d increases to a maximum value after it undergoes a period of repeatedly increasing and decreasing.

Fig. 4.

Variation of dynamic magnification factor D_d of (2-1-2) beam with power-law index n for L/h = 20 and r_m = 0.5.

Fig. 5.

Variation of dynamic magnification factor D_d of (2-1-2) beam with moving mass speed v for L/h = 20 and r_m = 0.5.

Fig. 6.

Thickness distribution of normal stress of FGSW beam for L/h = 20, r_m = 0.5 and v = 50 m/s.

Fig. 7.

Thickness distribution of shear stress of FGSW beam for L/h = 20, r_m = 0.5 and v = 50 m/s.

Figures 6 and 7 depict the thickness distribution of the normal and shear stresses of the symmetric (1-1-1) and non-symmetric (2-2-1) beams for L/h = 20, r_m = 0.5, and v = 50 m/s, respectively. The stresses are are computed at the time when the moving mass arrives at the mid-span. The increase of the power-index n leads to the increase of the maximum tensile and compressive normal stresses of the symmetric beam (Fig. 6). Some difference between the stresses of symmetric and non-symmetric beams can be seen from the figures. The shear stress of both the symmetric and non-symmetric beams increases by the increase of the power-index (n) as seen from Fig. 7.

5 Conclusions

The dynamic analysis of a FGSW beam has been carried out in the basis of the refined third-order shear deformabale finite element formulation. The beam consists of three layers, a homogeneous core and two functionally graded skin layers with material properties varying in the thickness direction by a power gradation law. Both the Voigt and Mori-Tanaka micromechanical models are employed to evaluate the effective properties. The effect of material gradation, the moving mass speed, the beam layer thickness ratio on the dynamic displacements and the stresses of the beam are discussed in detail. The results show that the above-mentioned effects play a very important role on the dynamic responses of the beam and it is believed that new results presented for dynamics of FGSW beams under moving loads are of interest to the scientific and engineering community in the area of FGM structures.