Keywords

1 Introduction

In a couple of years, Non-Orthogonal Multiple Access (NOMA) being the center of attraction for the researcher to facilitate multiple users in powdered form on the same time/frequency bands to improve the spectral efficiency of 5G communication over orthodox Orthogonal Multiple Access (OMA) in CRNs [4, 6, 8, 13].

Usually, the signal received at the destination through direct and indirect path is combined with the utilization of space diversity to mitigate various impairment [9, 11] of channel. Relays are used to create an indirect route. These relays are dedicated and user-oriented. The relays which standalone and not been selected by among users are known as dedicated relays. Outage probability of two users and relay selection by two-stage techniques are examined through a dedicated relays Cooperative NOMA (CNOMA) [2, 7, 14]. However, in the ad hoc network, installation of dedicated relays is robust and sophisticated. The user-oriented relays are utilized among users. In this case, users are being used as relays to improve the reliability of transmission for weaker channel gains user because more energetic gain users decode the other users signal through Successive Interference Cancellation (SIC) [3, 12]. Moreover, in relay processing, all available users can participate and enhanced processing complexity on SIC and through the grouping of (far and near) users with near user act as a relay for away user [1, 5].

The left of the paper is sorted as Sect. 2 presents a CNOMA-based CRNs system model. The examination of performance is to be done in Sect. 3. Sections 4 and 5 illustrate the discussion of results and conclusion, respectively.

2 System Model

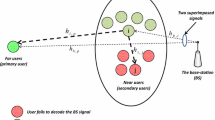
Taking a downlink underlay, NOMA-based CRNs with a base station (BS) which unicast/multicast the multiplexed signal to a primary user (PU) and a bunch of (N) secondary users (SUs) in the first slot, respectively. During the second slot of time, all SUs have decoded their signals utilizing Successive Interference Cancellation (SIC). Best SU \((n^{*})\) is being selected which further act as a relay to retransmits the remaining signal to PU. Both the signal is reached to PU (from BS as well as best SU), and the best signal is to be selected through selection combining techniques (Fig. 1).

Fig. 1
figure 1

System model

Full size image

In first slot of time, the multiplexed signal at BS is defined as \({x_b ={{a}_{p}}{{x}_{p}}+{{a}_{s_n}}{{x}_{s_n}}}\) aired to PU and multiple SUs with unit power, where \({x}_{p}\) and \({x}_{s_n}\) are signal of PU and N SUs, respectively. \({a}_{p}\) and \({a}_{s_n}\) are the corresponding power coefficient with \({a}_{s_n}<{a}_{p}\) and \({{a}^{2}_{s_n}} + {{a}^{2}_{p}}=1\), i.e. \(n\in (1,2,\ldots N)\). Thus, the signal observed at PU and n SUs is expressed as

$$\begin{aligned} {{y}_{b,p}}=\sqrt{{{P}_{\mathrm {BS}}}}{x_b}{{h}_{b,p}}+{{w}_{b,p}}\end{aligned}$$
(1)
$$\begin{aligned} {{y}_{b,s_n}}=\sqrt{{{P}_{\mathrm {BS}}}}{x_b}{{h}_{b,{s_n}}}+{{w}_{b,{s_n}}} \end{aligned}$$
(2)

where \({P_{\mathrm {BS}}}\) mentions the BS power, \({h_{b,i}}\) and \({w_{b,i}}\) interprets the channel coefficients and Gaussian noise [10, 15] between a BS and node i, i.e. \(i\in (p,s_n)\), respectively.

Therefore, the received Signal-to-Interference-plus-Noise-Ratio (SINR) at PU is written as

$$\begin{aligned} {{\gamma }_{b,p}}=\frac{\rho a_{p}^{2}{{\left| {{h}_{b,p}} \right| }^{2}}}{\rho a_{s_n}^{2}{{\left| {{h}_{b,p}} \right| }^{2}}+1}. \end{aligned}$$
(3)

Meanwhile, SUs are decoding the high priority, i.e. PU signal first with integration of SIC at n SUs to detect PU signal is expressed as

$$\begin{aligned} {{\gamma }_{b,p\rightarrow s_n}}=\frac{\rho a_{p}^{2}{{\left| {{h}_{b,s_n}} \right| }^{2}}}{\rho a_{s_n}^{2}{{\left| {{h}_{b,s_n}} \right| }^{2}}+1}, \end{aligned}$$
(4)

and the SINR at n SUs can be derived as

$$\begin{aligned} {{\gamma }_{b,s_n}}=\rho {{{a}^{2}_{s_n}}} {{\left| {{h}_{b,s_n}} \right| }^{2}}. \end{aligned}$$
(5)

where \(\rho \simeq \frac{{{P}_{\mathrm {BS}}}}{{{N}_{0}}} \simeq \frac{{{P}_{S_n}}}{{{N}_{0}}}\) is assumed without loss of generality.

In second phase, after decoding all SUs signal, then the best SU, i.e. \((s_{n^{*}})\) reencode and retransmit the remaining signal, i.e. \({x_{s_{n^{*}}} ={{a}_{p}}{{x}_{p}}}\) to PU. Thus, the signal observed at PU comprised as

$$\begin{aligned} {{y}_{s_{n^{*}},p}}=\sqrt{{{P}_{S_n}}}{{h}_{s_{n^{*}},p}}{x_{s_{n^{*}}}}+{{w}_{s_{n^{*}},p}} \end{aligned}$$
(6)

and the corresponding SINR is represented as

$$\begin{aligned} {{\gamma }_{s_{n^{*}},p}}=\rho {{{a}^{2}_{p}}} {{\left| {{h}_{s_{n^{*}},p}} \right| }^{2}}. \end{aligned}$$
(7)

The best relay or SU selection is to be completed by

$$\begin{aligned} s_{n^{*}}=\arg \max ({{\gamma }_{b,s_n}}) \end{aligned}$$
(8)

3 Performance Evalution

3.1 Outage Probability of SUs

The SUs outage probability mathematically expressed as

$$\begin{aligned} {P}_{\mathrm {out},{s}} = P\left( \gamma _{b,p\rightarrow s_n}<\tau _{p}\right) +P\left( \gamma _{b,p\rightarrow s_n}\ge \tau _p , \gamma _{b,s_n}<\tau _{s_n} \right) \end{aligned}$$
(9)

where \(\tau _p = 2^{2C_{\mathrm {out},p}}-1\) and \(\tau _{s_n} = 2^{C_{\mathrm {out},{s_n}} }-1\) denote threshold SINR correspondingly associated with \(2C_{\mathrm {out},p}\) and \(C_{\mathrm {out},{s_n}}\) outage capacities of PU and n SUs, respectively.

Substituting all given values into (9) and rearranged as

$$\begin{aligned} {P}_{\mathrm {out},{s}}= & {} P\left( \frac{\rho a_{p}^{2}{{\left| {{h}_{b,s_n}} \right| }^{2}}}{\rho a_{s}^{2}{{\left| {{h}_{b,s_n}} \right| }^{2}}+1}<\tau _p\right) \\&\quad + P\left( \frac{\rho a_{p}^{2}{{\left| {{h}_{b,s_n}} \right| }^{2}}}{\rho a_{s}^{2}{{\left| {{h}_{b,s_n}} \right| }^{2}}+1}\ge \tau _p,\ \rho {{{a}^{2}_{s}}} {{\left| {{h}_{b,s_n}} \right| }^{2}}<\tau _{s_n} \right) \end{aligned}$$

After simplification, the expression is rearranged as

$$\begin{aligned} = P\left( {{\left| {{h}_{b,s_n}} \right| }^{2}}<\frac{\theta }{\rho } \right) + P\left( {{\left| {{h}_{b,s_n}} \right| }^{2}}\ge \frac{\theta }{\rho } ,\ {{\left| {{h}_{b,s_n}} \right| }^{2}}<\frac{\phi }{\rho }\right) \end{aligned}$$

where \(\theta = \frac{\tau _p}{a_p^2 - \tau _p a_{s_n}^2}\) and \(\phi = \frac{\tau _{s_n}}{ a_{s_n}^2}\).

The above expression is concluded as

$$\begin{aligned} {P}_{\mathrm {out},{s_n}}= P\left( {{\left| {{h}_{b,s_n}} \right| }^{2}}<\frac{\eta }{\rho } \right) \end{aligned}$$
(10)

where \(\eta = \max \left( \theta ,\ \phi \right) \).

The pdf of \(f_{\left| h_{b,{s_{n}}} \right| ^2} \) due to order statistics can be given as

$$\begin{aligned} f_{\left| h_{b,{s_{n}}} \right| ^2} \left( x\right)= & {} \frac{ N!}{(N-n)!(n-1)!} f_{\left| h_{b,{s}} \right| ^2} \left( x\right) \times \left( F_{\left| h_{b,{s}} \right| ^2} \left( x\right) \right) ^{n-1}\\&\quad \times \left( 1-F_{\left| h_{b,{s}} \right| ^2} \left( x\right) \right) ^{N-n} \end{aligned}$$

Further it can be simplified as

$$\begin{aligned} f_{\left| h_{b,{s_{n}}} \right| ^2} \left( x\right) = \frac{ N!}{(N-n)!(n-1)!} \frac{1}{\lambda _{b,{s}}} \sum _{k=0}^{n-1}{\left( \begin{matrix} n-1 \\ k \\ \end{matrix} \right) } \left( -1 \right) ^k \mathrm {e}^\frac{-x\left( N-n+k+1\right) }{\lambda _{b,{s}}} \end{aligned}$$
(11)

From (10) and (11) provides

$$\begin{aligned} {P}_{\mathrm {out},{s}} = \frac{ N!}{(N-n)!(n-1)!} \frac{1}{\lambda _{b,{s}}} \sum _{k=0}^{n-1}{\left( \begin{matrix} n-1 \\ k \\ \end{matrix} \right) } \left( -1 \right) ^k \int \limits _{0}^{\frac{\eta }{\rho }} \mathrm {e}^\frac{-x\left( N-n+k+1\right) }{\lambda _{b,{s}}} \mathrm {d}x \end{aligned}$$

After solving above expression gives outage probability of SUs as

$$\begin{aligned} {P}_{\mathrm {out},{s}} = \frac{ N!}{(N-n)!(n-1)!} \sum _{k=0}^{n-1}{\left( \begin{matrix} n-1 \\ k \\ \end{matrix} \right) } \left( -1 \right) ^k \left( \frac{ 1-\mathrm {e}^\frac{-\eta \left( N-n+k+1\right) }{\rho \lambda _{b,{s}}}}{N-n+k+1}\right) \end{aligned}$$
(12)

3.2 Outage Probability of PU

The outage probability of a PU is being calculated through

$$\begin{aligned} P_{\mathrm {out},p} = P_{\mathrm {out},\mathrm {dir}} \times P_{\mathrm {out},\mathrm {indir}} \end{aligned}$$
(13)

Taking

$$\begin{aligned} {P_{{\mathrm {out},\mathrm {dir}}}}= & {} P\left( \gamma _{b,p}<\tau _p\right) \\= & {} P\left( \frac{\rho a_{p}^{2}{{\left| {{h}_{b,p}} \right| }^{2}}}{\rho a_{s_n}^{2}{{\left| {{h}_{b,p}} \right| }^{2}}+1}<\tau _p\right) \\= & {} P\left( {{\left| {{h}_{b,p}} \right| }^{2}}<\frac{\theta }{\rho } \right) \end{aligned}$$
$$\begin{aligned} P_{\mathrm {out},\mathrm {dir}}=1-\mathrm {e}^{\frac{-\theta }{\rho }} \end{aligned}$$
(14)

now taking

$$\begin{aligned} P_{\mathrm {out},\mathrm {indir}} = P\left\{ \min \left( \gamma _{b,p\rightarrow {s_{n^{*}}}},\ \gamma _{{s_{n^{*}},p}} \right) <\tau _p\right\} \end{aligned}$$

Generally, it can be written as

$$\begin{aligned}= & {} \prod _{n=1}^{N} P\left\{ \min \left( \gamma _{b,p\rightarrow {s_{n}}},\ \gamma _{{s_{n},p}} \right)<\tau _p\right\} \\= & {} \prod _{n=1}^{N} \left[ 1- P\left\{ \min \left( \gamma _{b,p\rightarrow {s_{n}}},\ \gamma _{{s_{n},p}} \right) <\tau _p\right\} \right] \\ \end{aligned}$$
$$\begin{aligned} = \prod _{n=1}^{N} \left[ 1- P \left( \gamma _{b,p\rightarrow {s_{n}}} \ge \tau _p\right) P\left( \gamma _{{s_{n},p}}\ge \tau _p\right) \right] \end{aligned}$$
(15)

Substituting provided values into (15), gets

$$\begin{aligned}= & {} \prod _{n=1}^{N} \left[ 1- P \left( \frac{\rho a_{p}^{2}{{\left| {{h}_{b,s_n}} \right| }^{2}}}{\rho a_{s_n}^{2}{{\left| {{h}_{b,s_n}} \right| }^{2}}+1} \ge \tau _p\right) P\left( \rho {{{a}^{2}_{p}}} {{\left| {{h}_{s_{n^{*}},p}} \right| }^{2}}\ge \tau _p\right) \right] \\= & {} \prod _{n=1}^{N} \left[ 1- P\left( {{\left| {{h}_{b,s_n}} \right| }^{2}}<\frac{\theta _n}{\rho } \right) P\left( {{\left| {{h}_{s_n,{p}}} \right| }^{2}}<\frac{\Phi _n}{\rho } \right) \right] \end{aligned}$$

Therefore,

$$\begin{aligned} P_{\mathrm {out},\mathrm {indir}} = \prod _{n=1}^{N} \left[ 1- \mathrm {e}^{\frac{-\theta _n}{\rho }} \times \mathrm {e}^{\frac{-\Phi _n}{\rho }}\right] \end{aligned}$$
(16)

where \(\Phi _n = \frac{\tau _p}{a_p^{2}}\), pdf of \(P\left( {{\left| {{h}_{b,s_n}} \right| }^{2}}<\frac{\theta _n}{\rho } \right) = \mathrm {e}^{\frac{-\theta _n}{\rho }} \) and \(P\left( {{\left| {{h}_{s_n,{p}}} \right| }^{2}}<\frac{\Phi _n}{\rho } \right) = \mathrm {e}^{\frac{-\Phi _n}{\rho }}\), respectively.

Substituting (14) and (16) into (13), gets outage probability of a PU as

$$\begin{aligned} P_{\mathrm {out},p} = \prod _{n=1}^{N} \left[ 1- \mathrm {e}^{\frac{-\left( \theta _n + \Phi _n\right) }{\rho }} \right] \times \left[ 1- \mathrm {e}^{\frac{- \theta }{\rho }} \right] \end{aligned}$$
(17)

3.3 Outage Capacity of SUs

From (12) can be simplified for an SU is to be expressed as

$$\begin{aligned} P_{\mathrm {out},s} = 1-\mathrm {e}^{\frac{-\eta }{\rho \lambda _{b,s}}} \end{aligned}$$
(18)

At high \(\rho \), assumed \(\mathrm {e}^{x} = 1+x\) the expression can be modified as

$$\begin{aligned} P_{\mathrm {out},s} = {\frac{\eta }{\rho \lambda _{b,s}}} \end{aligned}$$

The outage capacity of SUs depends on the value of \(\tau _{s_n}\), so that

$$\begin{aligned} P_{\mathrm {out},s}= & {} {\frac{\frac{\tau _{s_n}}{a_{s_n}^{2}}}{\rho \lambda _{b,s}}}\\ P_{\mathrm {out},s}\times {\rho \lambda _{b,s}}= & {} {{\frac{\tau _{s_n}}{a_{s_n}^{2}}}} \\ P_{\mathrm {out},s}\times {\rho \lambda _{b,s}}{a_{s_n}^{2}}= & {} 2^{C_{\mathrm {out},{s_n}} }-1 \end{aligned}$$

Therefore, outage capacity of SUs is written as

$$\begin{aligned} {C_{\mathrm {out},{s_n}}}=\log _2\left( 1+P_{\mathrm {out},s} {\rho \lambda _{b,s}}{a_{s_n}^{2}}\right) \end{aligned}$$
(19)

3.4 Outage Capacity of PU

Similarly, from (17), expression can be rewritten as

$$\begin{aligned} P_{\mathrm {out},p} = \prod _{n=1}^{N} \frac{ \theta _n }{\rho } \end{aligned}$$
(20)

where letting \(\left[ 1- \mathrm {e}^{\frac{- \theta }{\rho }} \right] =1\), \(\mathrm {e}^x = 1+x\) and \(\theta _n \gg \Phi _n\) at high \(\rho \).

For simplicity taking \(n=1\), the expression can be defined as

$$\begin{aligned} P_{\mathrm {out},p} = \frac{\tau _p}{\left( a_p^2 - \tau _p a_{s_n}^2\right) \rho } \end{aligned}$$

where \(\theta _n = \frac{\tau _p}{a_p^2 - \tau _p a_{s_n}^2}\).

$$\begin{aligned} \rho a_p^2 P_{\mathrm {out},p}= & {} \tau _p\left( 1+ \rho a_{s_n}^2 P_{\mathrm {out},p}\right) \\ \frac{\rho a_p^2 P_{\mathrm {out},p}}{1+ \rho a_{s_n}^2 P_{\mathrm {out},p}}= & {} 2^{2C_{\mathrm {out},p}}-1 \end{aligned}$$

Thus, the outage capacity of a PU for \(n=1\) is to be illustrated as

$$\begin{aligned} C_{\mathrm {out},p} = \frac{1}{2} \log _2\left( 1+\frac{\rho a_p^2 P_{\mathrm {out},p}}{1+ \rho a_{s_n}^2 P_{\mathrm {out},p}}\right) \end{aligned}$$
(21)

Now, outage sum capacity of given system is to be represented as

$$\begin{aligned} C_{\mathrm {out},\mathrm {sum}} = C_{\mathrm {out},p}+C_{\mathrm {out},s_n} \end{aligned}$$
(22)

4 Results and Discussion

BS and PU lie at center (0, 0) and edge (1, 1) of the cell simultaneously, and N SUs are distributed in between them. The channel gain \(\lambda _{j,k} = d_{j,k}^{-\xi }\) with \(\xi = 3\) and \(d_{j,k}\) defines the path loss factor for urban areas and normalized distance between (j, k) nodes, respectively. Taking \(C_{\mathrm {out},p}= C_{\mathrm {out},{s_n}} = 0.5\) bps/Hz along with associated \(a_{p}^2 = 0.86\) and \(a_{s_n}^2 = 0.14\) coefficients.

Fig. 2
figure 2

Impact of outage on the proposed CNOMA and OMA in DF technique with power allocation coefficients, \(a_{p}^2 = 0.86\) and \(a_{s_n}^2 = 0.14\) and target rates, \(C_{\mathrm {out},p}= C_{\mathrm {out},{s_n}} = 0.5\) bps/Hz for PE and SE, respectively

Full size image

Figure 2 shows the comparison between proposed CNOMA and orthodox OMA through DF technique of relaying in given CRNs. The related figure depicts the analyses results which are equal to the simulated solutions. Simultaneously, the proposed CNOMA provides outstanding behavior over OMA which is being offered in Fig. 2. Outage behavior of PU and SUs is continuously enhanced and reduced with the rising value of \(\rho \), respectively. The intersection point on outage probabilities curves of SUs and PU represents the approximate assignment powers to SUs (14%) and PU (86%) at (\(\rho = 10\,\mathrm {dB}\)) of the total system power, respectively. Therefore, PU behaves well than SU and OMA also, as given in Fig. 2.

Fig. 3
figure 3

Comparing impact on outage capacities of CNOMA and OMA with \(a_{p}^2 = 0.86\), \(a_{s_n}^2 = 0.14\) and \(C_{\mathrm {out},p}= C_{\mathrm {out},{s_n}} = 0.5\) bps/Hz for PE and SE, respectively

Full size image

The outage sum capacity of CNOMA and OMA has been depicted through Fig. 3 w.r.t. different values of \(\rho \). Moreover, outage capacity of PU under CNOMA is gradually enhanced initially then becomes constant along \(\rho \) due to presence of noise in the denominator as compared to OMA. The outage capacities of both PU and SUs increase along \(\rho \) under CNOMA but behaves much better than the existing orthodox OMA technique, as shown in Fig. 3. Thus, the outage sum capacity of CNOMA shows outstanding behavior over OMA.

5 Conclusion

This paper concludes that the outage probabilities and capacities of SUs, as well as a PU for the given CNOMA, outperform over orthodox OMA with implementing DF relaying technique in CRNs, respectively. The closed-form solutions of outage capacity and probabilities are also discussed along with the comparison of sum capacity of the system as mentioned earlier to OMA technique through simulation results.