Photorefractive Waveguides

Abstract

A general theory for the existence of bright solitons is studied in a photorefractive waveguide under the paraxial and Wentzel-Kramers-Brillouin-Jefferys approximation. The planar waveguide structure increases the self-focussing while decreasing the minimum or threshold power required for self trapping. The waveguide structure lowers the power required to form a soliton. The power required to just self trap a soliton keeps on reducing as the strength of the waveguide increases. Distinct regions of power are identified in which the characteristics of the self trapping are discussed in detail. The propagation of the solitons is visualized with and without the presence of the waveguide structure. This theory can be applied to waveguides embedded in photorefractive crystals exhibiting the linear and quadratic electro-optic effect simultaneously, which then reduces to centrosymmetric photorefractive waveguides and conventional photorefractive waveguides. The interesting case of pyroelectric photorefractive waveguides is also discussed while photovoltaic waveguides are briefly commented upon.

7.1 Introduction

We have seen previously that a spatial soliton traversing in a photorefractive crystal induces a waveguide which then guides the soliton beam itself [1, 2]. An interesting case arises if we embed a planar waveguide inside a photorefractive crystal. The diffraction effect will be counteracted due to the waveguiding of the planar waveguide. So, in a photorefractive waveguide, the minimum power required for soliton formation or the threshold power is much lower as compared to that in conventional photorefractive media. There has been a recent upsurge in interest in such photorefractive waveguides because of the potential important implications for practical applications [3,4,5,6,7]. Optical spatial solitons have important uses in various applications such as optical switching, routing, waveguiding and navigations etc. Also, in contrast to temporal solitons, the threshold power required is quite large for spatial solitons. This difficulty can be overcome simply if the spatial solitons are created in a waveguide. The self defocusing is partly eliminated due to the self focusing effect of the waveguide and the formation of optical spatial solitons takes place with relatively lower powers.

In this chapter, we shall study the propagation characteristics of bright spatial solitons in a biased planar photorefractive waveguide having both the linear and quadratic electro-optic effect under the WKBJ approximation. We shall use the paraxial wave equation incorporating the waveguiding effect through a waveguide parameter. Then we shall assume a variational solution of a quasi-soliton and proceed towards determining the variational parameters. Finally, we assign a physical interpretation to each parameter and analyze the quasi-soliton characteristics and the effect of the waveguide parameter on the self trapping.

7.2 Mathematical Formulation

We shall consider an optical beam propagating along the z direction in a photorefractive crystal. In addition, a waveguide has been embedded in the photorefractive crystal. The photorefractive crystal exhibits the linear electro-optic effect, the quadratic electro-optic effect or both the linear and quadratic electro-optic effect simultaneously. The optical c-axis of the photorefractive waveguide is considered to be along the x-axis. The beam is polarized along the x-direction we consider the diffraction along the same axis. The external bias is along the x-direction and hence a space charge field $\overrightarrow {E}_{sc} = \hat{x}E_{sc}$ is set up in the photorefractive waveguide.

The electric field $\overrightarrow {E}$ of the incident beam propagating through the photorefractive waveguide satisfies the following wave equation [5, 6],

$$\nabla^{2} \overrightarrow {E} + (k_{0} n_{e}^{\prime } )^{2} \overrightarrow {E} - gx^{2} \overrightarrow {E} = 0$$

(7.1)

where $n_{e}^{\prime }$ is the perturbed extraordinary index of refraction,$k_{0}$ is the wave number in free space. Since, ${\Delta }n = n_{e}^{\prime } - n_{e} = - \frac{1}{2}an_{e}^{3} r_{eff} E_{sc} - \frac{1}{2}bn_{e}^{3} g_{eff} \varepsilon_{0}^{2} (\varepsilon_{r} - 1)^{2} E_{sc}^{2}$, $n_{e}^{\prime }$ can be expressed in first order approximation as [8],

$$n_{e}^{\prime 2} = n_{e}^{2} - an_{e}^{4} r_{eff} E_{sc} - bn_{e}^{4} g_{eff} \in_{0}^{2} ( \in_{r} - 1)^{2} E_{sc}^{2}$$

(7.2)

$r_{eff}$ and $g_{eff}$ are the linear and quadratic electro-optic coefficients respectively. a and b will be non zero depending on the presence of the linear or quadratic electro-optic effect respectively. g is a real and positive parameter which we call as the waveguide parameter. This waveguide parameter represents the strength of the waveguiding which counteracts the diffraction of the light beam. In (7.1), the third term which is a function of g is a permanent change of the extraordinary refractive index due to the embedded waveguide. The incident beam envelope is,

$$\overrightarrow {E} \left( {x,z} \right) = \hat{x}\Phi \left( {x,z} \right)e^{ikz}$$

(7.3)

where $\Phi \left( {x,z} \right)$ is the slowly varying envelope of the wave and $k = k_{0} n_{e}^{\prime }$. Applying the paraxial approximation and putting (7.2) and (7.3) in (7.1), (see Note 1 at the end of the chapter),

$$i\frac{{\partial\Phi }}{\partial z} + \frac{1}{{2k_{0} n_{e} }}\frac{{\partial^{2}\Phi }}{{\partial x^{2} }} - \frac{1}{2}k_{0} n_{e}^{3} r_{eff} E_{sc}\Phi - \frac{1}{2}k_{0} n_{e}^{3} g_{eff} \in_{0}^{2} ( \in_{r} - 1)^{2} E_{sc}^{2}\Phi - gx^{2}\Phi = 0$$

(7.4)

The space charge field disregarding the diffusion effect is [9],

$$E_{sc} = \frac{{I_{\infty } + I_{d} }}{{I + I_{d} }}E_{0}$$

(7.5)

where the symbols have their usual meaning as defined previously.

Using the usual dimensionless coordinates specified before, the space charge field becomes,

$$E_{sc} = \frac{1 + \rho }{{1 + |U|^{2} }}E_{0}$$

(7.6)

and the evolution equation is obtained,

$$i\frac{\partial U}{{\partial \xi }} + \frac{1}{2}\frac{{\partial^{2} U}}{{\partial s^{2} }} - \beta_{1} \frac{1 + \rho }{{1 + |U|^{2} }}U - \beta_{2} \left( {\frac{1 + \rho }{{1 + |U|^{2} }}} \right)^{2} U - \delta s^{2} U = 0$$

(7.7)

where,

$\beta_{1} = a\frac{{(k_{0} x_{0} )^{2} n_{e}^{4} r_{eff} }}{2}E_{0}$, $\beta_{2} = b\frac{{(k_{0} x_{0} )^{2} n_{e}^{4} g_{eff} \in_{0}^{2} ( \in_{r} - 1)^{2} }}{2}E_{0}^{2}$ and $\delta = gk_{0} x_{0}^{4} n_{e}$ along with $\rho = I_{\infty } /I_{d}$. The origin of the refractive index perturbation lies in the nonlinear terms in (7.7). Equation (7.7) does not have an exact solution so we have to resort to approximate methods. There are several methods like Akhmanov’s paraxial method [10], Segev’s method [11], Anderson’s variational method [12] and Vlasov’s moment method [9] which can be used to solve (7.7). We use a variational solution along with a paraxial approximation to obtain soliton solutions which are acceptable physically. Also $\rho = 0$ since bright solitons will be considered. The slowly varying beam envelope to be expressed as,

$$U\left( {\xi ,s} \right) = U_{0} \left( {\xi ,s} \right)e^{{ - i\,\Omega \left( {\xi ,s} \right)}}$$

(7.8)

$U_{0} \left( {\xi ,s} \right)$ is a real quantity and $\Omega \left( {\xi ,s} \right)$ gives the phase. Substituting (7.8) in (7.7) we obtain,

$$\begin{aligned} & \left( {i\frac{{\partial U_{0} }}{\partial \xi } + U_{0} \frac{{\partial\Omega }}{\partial \xi }} \right) + \frac{1}{2}\left\{ {\frac{{\partial^{2} U_{0} }}{{\partial s^{2} }} - 2i\frac{{\partial U_{0} }}{\partial s}\frac{{\partial\Omega }}{\partial s} - iU_{0} \frac{{\partial^{2}\Omega }}{{\partial s^{2} }} - U_{0} \left( {\frac{{\partial\Omega }}{\partial s}} \right)^{2} } \right\} \\ & \quad - \beta_{1} \frac{1 + \rho }{{\left( {1 + U_{0}^{2} } \right)}}U_{0} - \beta_{2} \left( {\frac{1 + \rho }{{1 + U_{0}^{2} }}} \right)^{2} U_{0} - \delta s^{2} U_{0} = 0 \\ \end{aligned}$$

(7.9)

(7.9) is an equation which is a combination of real and imaginary terms. For the LHS to be zero, we need to equate the real and imaginary parts separately to zero,

$$\frac{{\partial U_{0} }}{\partial \xi } - \frac{{\partial U_{0} }}{\partial s}\frac{{\partial\Omega }}{\partial s} - \frac{1}{2}U_{0} \frac{{\partial^{2}\Omega }}{{\partial s^{2} }} = 0$$

(7.10)

$$U_{0} \frac{{\partial\Omega }}{\partial \xi } + \frac{1}{2}\frac{{\partial^{2} U}}{{\partial s^{2} }} - \frac{1}{2}U_{0} \left( {\frac{{\partial\Omega }}{\partial s}} \right)^{2} - \beta_{1}\Phi _{1} \left( {\xi ,s} \right)U_{0} - \beta_{2}\Phi _{2} \left( {\xi ,s} \right)U_{0} - \delta s^{2} U_{0} = 0$$

(7.11)

where,

$$\Phi _{1} \left( {\xi ,s} \right) = \frac{1}{{1 + |U_{0} |^{2} }}$$

(7.12)

$$\Phi _{2} \left( {\xi ,s} \right) = \frac{1}{{(1 + |U_{0} |^{2} )^{2} }}$$

(7.13)

$\Phi _{1} \left( {\xi ,s} \right)$ and $\Phi _{2} \left( {\xi ,s} \right)$ represent the contribution of the linear and quadratic electro-optic effect to the refractive index change. As mentioned previously, the last term in Eq. (7.11) represents the effect of the embedded planar waveguide. The interplay between the refractive index waveguide and the planar waveguide structure can be seen clearly from the last three terms in (7.11).

7.3 Spatial Solitons

We need to search for physically acceptable bright soliton states, which implies an intensity profile which peaks at the center of the beam and falls off with distance. Following the approach in Chap. 5 (Sect. 5.5), we shall assume a quasi soliton solution, i.e., a modified Gaussian ansatz for the soliton envelope in (7.11) as follows,

$$U_{0} \left( {\xi ,s} \right) = \frac{{U_{00} }}{{\sqrt {f\left( \xi \right)} }}e^{{ - s^{2} /2r^{2} f^{2} \left( \xi \right)}}$$

(7.14)

$$\Omega \left( {\xi ,s} \right) = \frac{{s^{2} }}{2}\Gamma \left( \xi \right)$$

(7.15)

$$\Gamma \left( \xi \right) = - \frac{1}{f\left( \xi \right)}\frac{df\left( \xi \right)}{{d\xi }}$$

(7.16)

where $P_{0} = U_{00}^{2}$ is the normalized peak power of the soliton, r is a constant which is always positive, $f\left( \xi \right)$ is the variable parameter proportional to the beam width. The spatial width of the soliton is expressed as the product $rf\left( \xi \right)$. We term the solution (7.14) as a variational solution where the variable parameters to be found are r, $f\left( \xi \right)$, $\Gamma \left( \xi \right)$. In general, we shall assume that $\frac{df}{{d\xi }} = 0$ at $\xi = 0$, i.e., the soliton beam is non-diverging at the entry point of the crystal. Also, we can assume that $f = 1$ at $\xi = 0$. The next step is to simplify the non-linear terms $\Phi _{1}$ and $\Phi _{2}$. Expanding both in a Taylor series, we get, (see Note 2 at the end of chapter)

$$\Phi _{1} \left( {\xi ,s} \right) \approx \frac{1}{{\left( {1 + \frac{{U_{00}^{2} }}{f}} \right)}} + s^{2} \frac{{\frac{{U_{00}^{2} }}{{r^{2} f^{3} \left( \xi \right)}}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)^{2} }}$$

(7.17)

$$\Phi _{2} \left( {\xi ,s} \right) \approx \frac{1}{{\left( {1 + \frac{{U_{00}^{2} }}{f}} \right)^{2} }} + 2s^{2} \frac{{\frac{{U_{00}^{2} }}{{r^{2} f^{3} \left( \xi \right)}}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)^{3} }}$$

(7.18)

where we approximate to the first order.

Substituting (7.14)–(7.18) in (7.11), we obtain an equation in various powers of $s^{2}$. Considering the coefficients of $s^{2}$ in LHS and RHS and equating them, we get,

$$\frac{{d^{2} f\left( \xi \right)}}{{d\xi^{2} }} = \frac{1}{{r^{4} f^{3} \left( \xi \right)}} - 2\beta_{1} \frac{{\frac{{P_{0} }}{{r^{2} f^{2} \left( \xi \right)}}}}{{\left( {1 + \frac{{P_{0} }}{f\left( \xi \right)}} \right)^{2} }} - 4\beta_{2} \frac{{\frac{{P_{0} }}{{r^{2} f^{2} \left( \xi \right)}}}}{{\left( {1 + \frac{{P_{0} }}{f\left( \xi \right)}} \right)^{3} }} - 2\delta f\left( \xi \right)$$

(7.19)

(7.19) can said to be an equation which details the spatial evolution of the parameter $f\left( \xi \right)$. Higher order terms of s, i.e., s³, s⁴ will not be considered since we take the first order approximation [r f(ξ)] > s in (7.17)–(7.18). Now, the light beam’s propagation in the photorefractive crystal may proceed in the following three ways: it may travel stably with an unchanging intensity profile, it may diverge, or it may be compressed. From (7.19), we can see that this depends upon the magnitudes of the power $P_{0}$ and the parameters $\beta_{1} ,\beta_{2}$. A soliton, or a stable self trapped beam needs the beam width parameter $f\left( \xi \right)$ to remains constant with propagation. Hence equating the LHS in (7.19) to zero,

$$\frac{1}{{r^{4} }} = 2\delta + \frac{{2\beta_{1} P_{0t} }}{{r^{2} (1 + P_{0t} )^{2} }} + \frac{{4\beta_{2} P_{0t} }}{{r^{2} (1 + P_{0t} )^{3} }}$$

(7.20)

In (7.20), we see an equilibrium condition which is known as quartic equilibrium condition because it is a polynomial equation of fourth order and has four roots. From (7.20), we can find out the threshold power $P_{0t}$ needed for stationary propagation of the optical beam. The region of existence of optical spatial solitons in the photorefractive waveguide can be found from (7.20) and hence it is known as the existence equation. Examining the solutions of the above equation, two roots are imaginary, one root is negative and only one root is positive. Neglecting the imaginary and negative values of r for spatial solitons as being unphysical, we are left with only one solution.

7.3.1 Waveguides in Photorefractive Crystals Having Both Electro-Optic Effects

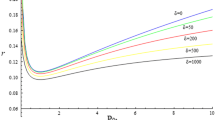
For illustration of soliton behavior in such waveguides, PMN-0.33PT crystal will be considered which exhibits both electro-optic effects simultaneously. The parameters taken for the aforementioned crystal are shown in Table 7.1. Figure 7.1 shows the graph of r versus the threshold power $P_{0t}$ for various strengths of the waveguide. The spatial width of the soliton first decreases with an increase in power when the power is low, while the soliton width increases with an increase in power when the power is high. A similar dependence remains for each value of the waveguide parameter but the curve becomes less steep as the waveguide parameter increases. The presence of bistable states is clear from Fig. 7.1 since we can infer two values for the threshold powers for a single value of r and f(ξ) is constant. The two values of the threshold power at which a soliton can just form are known as $P_{0t1}$ and $P_{0t2}$.

Table 7.1 Parameters taken in the our calculation [5]^a

Fig. 7.1

The dependence of the r the stable spatial width of the soliton on the threshold power of the spatial solitons,$\beta_{1} = 30.9224$, $\beta_{2} = 4.6896$. (Reprinted from Wave Motion, 77, Aavishkar Katti, R.A. Yadav, Awadhesh Prasad, Bright optical spatial solitons in photorefractive waveguides having both the linear and quadratic electro-optic effect, 64–76, Copyright 2018, with permission from Elsevier)

In the absence of waveguiding, we shall see the behavior of solitons in distinct power regions. Consider four values of power, $P_{1} \left( { = 0.0999} \right) < P_{0t1}$,$P_{2} \left( { = 0.2692} \right) = P_{0t1}$,$P_{0t1} < P_{3} \left( { = 1} \right) < P_{0t2}$, $P_{4} \left( { = 26.92} \right) > P_{0t2}$. In Fig. 7.2, the change in f (which is a parameter related to the soliton width) with the scaled propagation distance $\xi$ is plotted in the four power regimes. Figure 7.2 shows that the beam width deviates to a large value with propagation when P = P₁. Since $P_{1}$ is less than the threshold power, so we do not expect the soliton to form. If the power exactly equals the threshold power, $= P_{0t1}$, the parameter f = 1 and hence the soliton width rf is constant in Fig. 7.2. So we obtain a spatial soliton which travels without changing its shape, i.e., a stable self trapping. If the value of the peak power P lies between the two threshold powers, i.e., P_0t2 < P < $P_{0t1}$, we find from Fig. 7.2 that the soliton’s width oscillates. This oscillation is with amplitude less than unity so we can conclude that there is a reasonable amount of self trapping and this is in fact a “soliton”. If the soliton peak power P is larger than P_0t2, the soliton width again oscillates with propagation but now the oscillation amplitude is greater than unity and hence it cannot be termed as a soliton. As rf is the soliton width, we use it to plot the soliton’s propagation in Figs. 7.3, 7.4, 7.5 and 7.6 using (7.14).

Fig. 7.2

Variable beam width parameter $f\left( \xi \right)$ versus the normalized distance of propagation $\xi$ considering various peak powers of the soliton, $\beta_{1} = 30.9224$, $\beta_{2} = 4.6896$, r = 0.2793. (Reprinted from Katti [5], Copyright 2018, with permission from Elsevier)

Fig. 7.3

Propagation of the soliton when there is no embedded waveguide. P = 0.0999. $\beta_{1} = 30.9224$, $\beta_{2} = 4.6896$, r = 0.2793. (Reprinted from Wave Motion, 77, Aavishkar Katti, R.A. Yadav, Awadhesh Prasad, Bright optical spatial solitons in photorefractive waveguides having both the linear and quadratic electro-optic effect, 64–76, Copyright 2018, with permission from Elsevier)

Fig. 7.4

Propagation of the soliton when there is no embedded waveguide. P = 0.2692. $\beta_{1} = 30.9224$, $\beta_{2} = 4.6896$, r = 0.2793. (Reprinted from Wave Motion, 77, Aavishkar Katti, R.A. Yadav, Awadhesh Prasad, Bright optical spatial solitons in photorefractive waveguides having both the linear and quadratic electro-optic effect, 64–76, Copyright 2018, with permission from Elsevier)

Fig. 7.5

Propagation of the soliton when there is no embedded waveguide. P = 1. $\beta_{1} = 30.9224$, $\beta_{2} = 4.6896$, r = 0.2793. (Reprinted from Katti [5], Copyright 2018, with permission from Elsevier)

Fig. 7.6

Propagation of the soliton when there is no embedded waveguide. P = 26.92. $\beta_{1} = 30.9224$, $\beta_{2} = 4.6896$, r = 0.2793. (Reprinted from Wave Motion, 77, Aavishkar Katti, R.A. Yadav, Awadhesh Prasad, Bright optical spatial solitons in photorefractive waveguides having both the linear and quadratic electro-optic effect, 64–76, Copyright 2018, with permission from Elsevier)

Fig. 7.7

Beam width parameter $f\left( \xi \right)$ versus propagation distance $\xi$ for different waveguide strengths, $\beta_{1} = 30.9224$, $\beta_{2} = 4.6896$, $P_{0} = 0.055$ and r = 0.2831. (Reprinted from Wave Motion, 77, Aavishkar Katti, R.A. Yadav, Awadhesh Prasad, Bright optical spatial solitons in photorefractive waveguides having both the linear and quadratic electro-optic effect, 64–76, Copyright 2018, with permission from Elsevier)

In order to investigate what effect waveguiding has on the self trapping, we shall now take a finite nonzero value for the waveguide parameter and investigate the propagation of the soliton. How the soliton width parameter f changes while propagating is plotted in Fig. 7.3 considering various values of the waveguide parameters $\delta$. If we take, $\delta = 0$ implying no waveguide effect at all, the wave diverges as seen in Fig. 7.3. Again, as the value $\delta$ increases, we can see in Fig. 7.3 that the behavior of f changes. For a certain value of $\delta$, the value of f is seen to be oscillatory with respect to increasing distance of propagation but the oscillation amplitude is less than one. This indicates very clearly that self trapping can occur even at peak powers much less than the threshold power due to the waveguiding effect of the embedded planar waveguide. With even greater values of $\delta$, the power required to self trap the soliton reduces even more. Considering the case when the power of the light beam is less than the threshold power, i.e. P < P_0t1, the propagation of the light beam is shown in Figs. 7.8, 7.9, 7.10, 7.11 and 7.12 for various strengths of the waveguide.

Fig. 7.8

Propagation of soliton in the absence of the waveguide when P = 0.055 and r = 0.2831. (Reprinted from Wave Motion, 77, Aavishkar Katti, R.A. Yadav, Awadhesh Prasad, Bright optical spatial solitons in photorefractive waveguides having both the linear and quadratic electro-optic effect, 64-76, Copyright 2018, with permission from Elsevier)

Fig. 7.9

Propagation of soliton when the waveguding parameter is augmented to δ = 10. P = 0.055 and r = 0.2831. (Reprinted from Wave Motion, 77, Aavishkar Katti, R.A. Yadav, Awadhesh Prasad, Bright optical spatial solitons in photorefractive waveguides having both the linear and quadratic electro-optic effect, 64–76, Copyright 2018, with permission from Elsevier)

Fig. 7.10

Propagation of soliton when the waveguding parameter is augmented to δ = 30. P = 0.055 and r = 0.2831. (Reprinted from Wave Motion, 77, Aavishkar Katti, R.A. Yadav, Awadhesh Prasad, Bright optical spatial solitons in photorefractive waveguides having both the linear and quadratic electro-optic effect, 64–76, Copyright 2018, with permission from Elsevier)

Fig. 7.11

Propagation of soliton when the waveguding parameter is augmented to δ = 50. P = 0.055 and r = 0.2831. (Reprinted from Wave Motion, 77, Aavishkar Katti, R.A. Yadav, Awadhesh Prasad, Bright optical spatial solitons in photorefractive waveguides having both the linear and quadratic electro-optic effect, 64–76, Copyright 2018, with permission from Elsevier)

Fig. 7.12

Propagation of soliton when the waveguding parameter is augmented to δ = 100. P = 0.055 and r = 0.2831. (Reprinted from Wave Motion, 77, Aavishkar Katti, R.A. Yadav, Awadhesh Prasad, Bright optical spatial solitons in photorefractive waveguides having both the linear and quadratic electro-optic effect, 64–76, Copyright 2018, with permission from Elsevier)

7.3.2 Photorefractive Waveguides with the Linear Electro-Optic Effect

In (7.19), we shall put b = 0 since we consider conventional non centrosymmetric photorefractive media which does not have the quadratic electro-optic effect,

$$\frac{{d^{2} f\left( \xi \right)}}{{d\xi^{2} }} = \frac{1}{{r^{4} f^{3} \left( \xi \right)}} - 2\beta_{1} \frac{{\frac{{P_{0} }}{{r^{2} f^{2} \left( \xi \right)}}}}{{\left( {1 + \frac{{P_{0} }}{f\left( \xi \right)}} \right)^{2} }} - 2\delta f\left( \xi \right)$$

(7.21)

We have to look for points of equilibrium of (7.21) as a soliton forms when the beam width $f\left( \xi \right)$ remains constant. Hence, in (7.21), putting LHS equal to zero we obtain,

$$\frac{1}{{r^{4} }} = 2\delta + \frac{{2\beta_{1} P_{0t} }}{{r^{2} (1 + P_{0t} )^{2} }}$$

(7.22)

(7.22) signifies an equilibrium condition containing four roots and hence which is quartic. The threshold power $P_{0t}$ for stationary propagation of the light beam as a soliton can be inferred from (7.22) which serves to identify the existence for screening solitons in a photorefractive waveguide. As in the previous case, only one of the four solutions is real and positive so is physically acceptable.

We now need to consider a Lithium Niobate (LN) crystal for illustrating the characteristics of solitons in this case. The parameters taken in our investigation are shown clearly in Table 7.2. Bistable states can again be inferred from Fig. 7.13.

Table 7.2 Parameters for LN crystal taken in our theoretical investigation [13]

Fig. 7.13

Equilibrium spatial width r versus the threshold power P_0t of the spatial solitons, $\beta_{1} = 173$. (Reprinted by permission from Springer Nature: Springer Optical and Quantum Electronics Bright screening solitons in a photorefractive waveguide, Aavishkar Katti, Copyright 2018)

We shall proceed similarly to the previous case to predict the behavior of spatial solitons in absence of the waveguiding effect. For illustration, we take four different values of power, $P_{1} \left( { = 0.0999} \right) < P_{0t1}$,$P_{2} \left( { = 0.3225} \right) = P_{0t1}$,$P_{0t1} < P_{3} \left( { = 1} \right) < P_{0t2}$, $P_{4} \left( { = 32.25} \right) > P_{0t2}$. The variation in the variable beam width parameter with propagation is plotted in Fig. 7.14. As explained previously, we observe a self trapping if the power of the light beam falls within the two threshold powers. Self trapping is not observed for powers below the threshold power. The change induced by the embedded waveguide in the self trapping is investigated in Fig. 7.15 where the change in the variable beam width parameter is plotted with propagation considering diverse waveguide strengths. The conclusions remain same that a soliton of peak power lesser than the threshold power can still be self trapped by the use of an embedded waveguide in the photorefractive crystal.

Fig. 7.14

Variable beam width parameter $f\left( \xi \right)$ versus the distance of propagation $\xi$ for ddiverse values of soliton peak powers, $\beta_{1} = 173$, r = 0.125. (Reprinted by permission from Springer Nature: Springer Optical and Quantum Electronics Bright screening solitons in a photorefractive waveguide, Aavishkar Katti, Copyright 2018)

Fig. 7.15

Variable beam width parameter $f\left( \xi \right)$ versus distance of propagation $\xi$ for different waveguide strengths, $\beta_1= 173$, $P_{0} = 0.075$ and $r = 0.161$. (Reprinted by permission from Springer Nature: Springer Optical and Quantum Electronics Bright screening solitons in a photorefractive waveguide, Aavishkar Katti, Copyright 2018)

7.3.3 Centrosymmetric Photorefractive Waveguides

In (7.19), we shall put a = 0 since we consider centrosymmetric non centrosymmetric photorefractive media which does not exhibit the linear electro-optic effect,

$$\frac{{d^{2} f\left( \xi \right)}}{{d\xi^{2} }} = \frac{1}{{r^{4} f^{3} \left( \xi \right)}} - 4\beta_{2} \frac{{\frac{{P_{0} }}{{r^{2} f^{2} \left( \xi \right)}}}}{{\left( {1 + \frac{{P_{0} }}{f\left( \xi \right)}} \right)^{3} }} - 2\delta f\left( \xi \right)$$

(7.23)

We have to look for points of equilibrium of (7.23) as a soliton forms when the beam width $f\left( \xi \right)$ remains constant. Hence, in (7.23), putting LHS equal to zero, we obtain,

$$\frac{1}{{r^{4} }} = 2\delta + \frac{{4\beta_{2} P_{0t} }}{{r^{2} (1 + P_{0t} )^{3} }}$$

(7.24)

(7.24) signifies an equilibrium condition containing four roots and hence which is quartic. The threshold power $P_{0t}$ for stationary propagation of the light beam as a soliton can be inferred from (7.24) which serves to identify the existence for screening solitons in a photorefractive waveguide. As in the previous case, only one of the four solutions is real and positive so is physically acceptable [7].

We now need to consider a Potassium Lithium Tantalate Niobate (KLTN) crystal for illustrating the characteristics of solitons in this case. Taking typical parameters [7], we get,$\beta_{2} = 157.9$. The value of the equilibrium spatial width is plotted with respect to the threshold power in Fig. 7.16. Bistable states can again be inferred from Fig. 7.16.

Fig. 7.16

Equilibrium spatial width r as a function of the threshold peak power P_0t of the spatial solitons, β₂ = 157.9. (Reprinted by permission from Springer Nature: Springer Journal of Optics, Waveguiding effect on optical spatial solitons in centrosymmetric photorefractive materials, Binay P Akhouri et al, Copyright 2016)

We shall now proceed to predict the propagation behavior of spatial solitons when there is no waveguide. Consider four different values of power,$P_{1} \left( { = 0.0999} \right) < P_{0t1}$,$P_{2} \left( { = 0.3341} \right) = P_{0t1}$,$P_{0t1} < P_{3} \left( { = 1} \right) < P_{0t2}$, $P_{4} \left( { = 33.41} \right) > P_{0t2}$. We plot the variation in f with the normalized propagation distance $\xi$ in Fig. 7.17. As explained previously, we observe a self trapping if the power of the light beam falls within the two threshold powers. Self trapping is not observed for powers below the threshold power. For investigating the effect of waveguide embedded in the photorefractive crystal, we plot the beam width parameter as a function of the scaled distance of propagation for various strengths of the waveguide in Fig. 7.18. The conclusions remain same that a soliton of peak power lesser than the threshold power can still be self trapped by the use of an embedded waveguide in the photorefractive crystal.

Fig. 7.17

Variable beam width parameter f(ξ) versus distance of propagation ξ at four different soliton peak powers, β = 157.9. (Reprinted by permission from Springer Nature: Springer Journal of Optics, Waveguiding effect on optical spatial solitons in centrosymmetric photorefractive materials, Binay P Akhouri et al, Copyright 2016)

Fig. 7.18

Variable beam width parameter f(ξ) versus the distance of propagation ξ at different waveguide strengths, β = 157.9, P₀ = 0.06947, r = 0.1489. (Reprinted by permission from Springer Nature: Springer Journal of Optics, Waveguiding effect on optical spatial solitons in centrosymmetric photorefractive materials, Binay P Akhouri et al, Copyright 2016)

7.3.4 Pyroelectric Photorefractive Waveguides

We shall now consider waveguide embedded in a photorefractive crystal with a finite pyroelectric coefficient. If the photorefractive crystal is unbiased, then we can say that the external bias has been replaced by the transient pyroelectric field which in turn induces a space charge field modulating the refractive index resulting in self trapping.

As before, we consider an optical beam propagating along the z-direction in a pyroelectric photorefractive waveguide embedded in a photorefractive crystal. The photorefractive crystal is placed between an insulating cover and a metallic plate whose temperature is precisely controlled by a Peltier cell. The optical c-axis of the photorefractive waveguide is along the x-direction and the beam is polarized along the x-direction. Also it is assumed diffraction is allowed along the x-direction only. Here the space charge field which is formed is due to the pyroelectric effect only and hence, $E_{sc} = E_{pysc}$. The slowly varying envelope of the electric field of the incident beam is expressed as,$\vec{E}\left( {x,z} \right) = \hat{x}\,\Phi \left( {x,z} \right)e^{ikz}$ where $\Phi \left( {x,z} \right)$ is the slowly varying envelope of the wave. Proceeding as previously, we obtain the dynamical evolution equation,

$$i\frac{{\partial\Phi }}{\partial z} + \frac{1}{{2k_{0} n_{e} }}\frac{{\partial^{2}\Phi }}{{\partial x^{2} }} - \frac{1}{2}k_{0} n_{e}^{3} r_{eff} E_{pysc}\Phi - gx^{2}\Phi = 0$$

(7.25)

The induced space charge field in a photorefractive material due to exclusively the pyroelectric effect has been derived previously in Chap. 2,

$$E_{pysc} = - E_{py} \frac{I}{{I + I_{d} }}$$

(7.26)

where we also neglect the diffusion effects.

$E_{py}$ is the transient pyroelectric field which is expressed as,

$$E_{py} = - \frac{1}{{ \in_{0} \in_{r} }}\frac{\partial P}{{\partial T}}{\Delta }T$$

(7.27)

In (7.27), $\frac{\partial P}{{\partial T}}$ is the pyroelectric coefficient, $\in_{0}$ is the vacuum permittivity, ${\Delta }T$ is the temperature change of the photorefractive crystal, $\in_{r}$ is the dielectric constant. Using dimensionless coordinates mentioned before, the evolution equation becomes,

$$i\frac{\partial U}{{\partial \xi }} + \frac{1}{2}\frac{{\partial^{2} U}}{{\partial s^{2} }} + \alpha \frac{{|U|^{2} }}{{1 + |U|^{2} }}U - \delta s^{2} U = 0$$

(7.28)

where,

$\alpha = \frac{{(k_{0} x_{0} )^{2} n_{e}^{4} r_{33} }}{2}E_{py}$ and $\delta = gk_{0} x_{0}^{4} n_{e}$.

Equation (7.28) cannot be solved exactly, so we have to resort to the variational method using the paraxial approximation. The light beam envelope can be expressed as,

$$U\left( {\xi ,s} \right) = U_{0} \left( {\xi ,s} \right)e^{{ - i\,\Omega \left( {\xi ,s} \right)}}$$

(7.29)

$U_{0} \left( {\xi ,s} \right)$ is a real quantity and $\Omega \left( {\xi ,s} \right)$ represents the phase. Substituting (7.29) in (7.28) gives,

$$\begin{aligned} & \left( {i\frac{{\partial U_{0} }}{{\partial \xi }} + U_{0} \frac{{\partial \Omega }}{{\partial \xi }}} \right) + \frac{1}{2}\left\{ {\frac{{\partial ^{2} U_{0} }}{{\partial s^{2} }} - 2i\frac{{\partial U_{0} }}{{\partial s}}\frac{{\partial \Omega }}{{\partial s}} - iU_{0} \frac{{\partial ^{2} \Omega }}{{\partial s^{2} }} - U_{0} \left( {\frac{{\partial \Omega }}{{\partial s}}} \right)^{2} } \right\} \\ & \quad + \alpha \frac{{U_{0}^{2} }}{{\left( {1 + U_{0}^{2} } \right)}}U_{0} - \delta s^{2} U_{0} = 0 \\ \end{aligned}$$

(7.30)

The real and imaginary parts can be separately equated to give,

$$\frac{{\partial U_{0} }}{\partial \xi } - \frac{{\partial U_{0} }}{\partial s}\frac{{\partial\Omega }}{\partial s} - \frac{1}{2}U_{0} \frac{{\partial^{2}\Omega }}{{\partial s^{2} }} = 0$$

(7.31)

$$U_{0} \frac{\partial \Omega }{{\partial \xi }} + \frac{1}{2}\frac{{\partial^{2} U_{0} }}{{\partial s^{2} }} - \frac{1}{2}U_{0} \left( {\frac{\partial \Omega }{{\partial s}}} \right)^{2} + \alpha\Theta _{1} \left( {\xi ,s} \right)U_{0} - \delta s^{2} U_{0} = 0$$

(7.32)

where

$$\Theta _{1} \left( {\xi ,s} \right) = \frac{{|U_{0} |^{2} }}{{1 + |U_{0} |^{2} }}$$

(7.33)

The last term in (7.32) refers to the contribution of the embedded planar waveguide. The last two terms represent the counteracting effect on diffraction leading to a stable self trapping.Again, following our previous analysis and taking the following Gaussian ansatz for a quasi soliton in our investigation,

$$U_{0} \left( {\xi ,s} \right) = \frac{{U_{00} }}{{\sqrt {f\left( \xi \right)} }}e^{{ - s^{2} /2r^{2} f^{2} \left( \xi \right)}}$$

(7.34)

$$\Omega \left( {\xi ,s} \right) = \frac{{s^{2} }}{2}\Gamma \left( \xi \right)$$

(7.35)

$$\Gamma \left( \xi \right) = - \frac{1}{f\left( \xi \right)}\frac{df\left( \xi \right)}{{d\xi }}$$

(7.36)

where the symbols have their usual meanings as defined in Sect. 7.3.1. We define the spatial width of the soliton as the product $rf\left( \xi \right)$. We term the solution (7.34) as a variational solution where the variable parameters to be found are are r, $f\left( \xi \right)$, $\Gamma \left( \xi \right)$. In general, we shall assume that $\frac{df}{{d\xi }} = 0$ at $\xi = 0$, i.e., the soliton beam is non-diverging at the entry point of the crystal. Also, we can assume that $f = 1$ at $\xi = 0$. The next step is to simplify the non-linear term $\Theta _{1}$. Expanding in a Taylor series to first order, we get,

$$\Theta _{1} \left( {\xi ,s} \right) \approx \frac{{\frac{{U_{00}^{2} }}{f\left( \xi \right)}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f}} \right)}} + s^{2} \frac{{\frac{{U_{00}^{2} }}{{r^{2} f^{3} \left( \xi \right)}}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)^{2} }}$$

(7.37)

Substituting (7.34)–(7.37) in (7.28) results in an equation in several powers of $s^{2}$. Equating the coefficients of various powers of $s^{2}$, we obtain an evolution equation for $f\left( \xi \right)$,

$$\frac{{d^{2} f\left( \xi \right)}}{{d\xi^{2} }} = \frac{1}{{r^{4} f^{3} \left( \xi \right)}} - 2\alpha \frac{{\frac{{P_{0} }}{{r^{2} f^{2} \left( \xi \right)}}}}{{\left( {1 + \frac{{P_{0} }}{f\left( \xi \right)}} \right)^{2} }} - 2\delta f\left( \xi \right)$$

(7.38)

The normalized power of the soliton is $P_{0} = U_{00}^{2}$. Higher order terms of s, i.e., s³, s⁴ will not be considered since we take the first order approximation [r f(ξ)] > s in (7.37). Now, the light beam’s propagation in the photorefractive crystal may proceed in the following three ways: it may travel stably with an unchanging intensity profile, it may diverge, or it may be compressed. From (7.38), we can see that this depends upon the magnitudes of the power $P_{0}$ and the parameters $\alpha$. A soliton will be formed when the variable beam width parameter $f\left( \xi \right)$ remains unchanged with propagation. Hence equating the LHS in (7.38) to zero,

$$\frac{1}{{r^{4} }} = 2\delta + \frac{{2\alpha P_{0t} }}{{r^{2} (1 + P_{0t} )^{2} }}$$

(7.39)

In (7.39), we see an equilibrium condition which is known as quartic equilibrium condition because it is a polynomial equation of fourth order and has four roots. From (7.39), we can find out the threshold power $P_{0t}$ needed for stationary propagation of the optical beam. (7.39) is the existence equation for pyroelectric solitons travelling in a pyroelectric photorefractive waveguide. Examining the solutions of the above equation, two roots are imaginary, one root is negative and only one root is positive. Neglecting the imaginary and negative values of r for spatial solitons as being unphysical, we have one solution which remains physical.

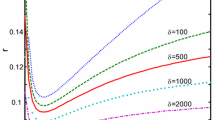
For illustration of dynamical evolution of the solitons in such waveguides, SBN crystal will be considered which exhibits a strong pyroelectric effect. The parameters taken for the aforementioned crystal are shown in Table 7.3. Figure 7.19 shows the graph of r versus the threshold power $P_{0t}$ for various strengths of the waveguide. We can see that the soliton width decreases with an increase in power for low powers, while the it increases with an increase in power for high powers. A similar dependence remains for each value of the waveguide parameter but the curve becomes less steep as the waveguide parameter increases. The existence of bistable states is clear from Fig. 7.19 since we can infer two values for the threshold powers for a single value of r and f(ξ) is constant. The two values of the threshold power at which a soliton can just form are known as $P_{0t1}$ and $P_{0t2}$. Also, the soliton width decreases with an increase in power in the low power region while the soliton width increases with an increase in power in the high power region.

Table 7.3 Parameters for SBN crystal taken in our theoretical investigation[4]

Fig. 7.19

The variation of equilibrium spatial width r with threshold peak power P_0t of the spatial solitons.$\alpha = 40.2$. (Reprinted from Optik - International Journal for Light and Electron Optics, 156, Aavishkar Katti, Bright pyroelectric quasi-solitons in a photorefractive waveguide, 433-438, Copyright 2018, with permission from Elsevier)

It is worthwhile to first investigate the behaviour of the quasi-solitons when there is no waveguide present. As before, take four different values of power, below the first threshold power, at the first threshold power, between the two threshold powers and above the second threshold power, $P_{1} \left( { = 0.0999} \right) < P_{0t1}$, $P_{2} \left( { = 0.2435} \right) = P_{0t1}$, $P_{0t1} < P_{3} \left( { = 1} \right) < P_{0t2}$, $P_{4} \left( { = 24.35} \right) > P_{0t2}$. The change in f with the normalized propagation distance $\xi$ is plotted in Fig. 7.20. To investigate the effect of the waveguide structure embedded in the photorefractive crystal, we plot the variation of the beam width parameter f with the normalized distance of propagation for different waveguide parameter $\delta$ in Fig. 7.21.

Fig. 7.20

The variation of variable beam width parameter f(ξ) with normalized distance of propagation ξ at four different soliton peak powers $\alpha = 40.2$. (Reprinted from Optik - International Journal for Light and Electron Optics, 156, Aavishkar Katti, Bright pyroelectric quasi-solitons in a photorefractive waveguide, 433–438, Copyright 2018, with permission from Elsevier)

Fig. 7.21

Variable beam width parameter f(ξ) versus the propagation distance ξ for different waveguide strengths, $\alpha = 40.2$,$P_{0} = 0.055$, $r = 0.2810$. (Reprinted from Optik - International Journal for Light and Electron Optics, 156, Aavishkar Katti, Bright pyroelectric quasi-solitons in a photorefractive waveguide, 433–438, Copyright 2018, with permission from Elsevier)

7.3.5 Photovoltaic Photorefractive Waveguides

If we consider the photorefractive crystal with a finite photovoltaic coefficient, the space charge field responsible for screening photovoltaic solitons has been found previously as,

$$E_{sc} = \frac{{I_{\infty } + I_{d} }}{{I + I_{d} }}E_{0} + \frac{{I_{\infty } - I_{d} }}{{I + I_{d} }}E_{p}$$

(7.40)

Substituting this in (7.4) alongwith b = 0,

$$i\frac{\partial U}{{\partial \xi }} + \frac{1}{2}\frac{{\partial^{2} U}}{{\partial s^{2} }} - \beta \left( {\frac{1 + \rho }{{1 + |U|^{2} }}} \right)U - \alpha \left( {\frac{{\rho - |U|^{2} }}{{1 + |U|^{2} }}} \right)U - \delta s^{2} U = 0$$

(7.41)

where,

$\beta_{1} = a\frac{{(k_{0} x_{0} )^{2} n_{e}^{4} r_{eff} }}{2}E_{0}$, $\alpha = \frac{{(k_{0} x_{0} )^{2} n_{e}^{4} r_{eff} }}{2}E_{p}$ and $\delta = gk_{0} x_{0}^{4} n_{e}$ alongwith $\rho = I_{\infty } /I_{d}$. Also $\rho = 0$ since bright solitons will be considered. The beam envelope in the slowly varying envelope approximation is expressed as [6],

$$U\left( {\xi ,s} \right) = U_{0} \left( {\xi ,s} \right)e^{{ - i\,\Omega \left( {\xi ,s} \right)}}$$

(7.42)

$U_{0} \left( {\xi ,s} \right)$ is the amplitude which is real and the phase is given by $\Omega \left( {\xi ,s} \right)$. Substituting (7.42) in (7.41) we obtain,

$$\begin{aligned} & \left( {i\frac{{\partial U_{0} }}{\partial \xi } + U_{0} \frac{\partial \Omega }{{\partial \xi }}} \right) + \frac{1}{2}\left\{ {\frac{{\partial^{2} U_{0} }}{{\partial s^{2} }} - 2i\frac{{\partial U_{0} }}{\partial s}\frac{{\partial\Omega }}{\partial s} - iU_{0} \frac{{\partial^{2}\Omega }}{{\partial s^{2} }} - U_{0} \left( {\frac{{\partial\Omega }}{\partial s}} \right)^{2} } \right\} \\ & \quad - \beta_{1} \frac{1 + \rho }{{\left( {1 + U_{0}^{2} } \right)}}U_{0} - \beta_{2} \left( {\frac{1 + \rho }{{1 + U_{0}^{2} }}} \right)^{2} U_{0} - \delta s^{2} U_{0} = 0 \\ \end{aligned}$$

(7.43)

(7.43) is an equation which is a combination of real and imaginary terms. For the LHS to be zero, we need to equate the real and imaginary parts separately to zero,

$$\frac{{\partial U_{0} }}{\partial \xi } - \frac{{\partial U_{0} }}{\partial s}\frac{\partial \Omega }{{\partial s}} - \frac{1}{2}U_{0} \frac{{\partial^{2} \Omega }}{{\partial s^{2} }} = 0$$

(7.44)

$$U_{0} \frac{\partial \Omega }{{\partial \xi }} + \frac{1}{2}\frac{{\partial^{2} U}}{{\partial s^{2} }} - \frac{1}{2}U_{0} \left( {\frac{\partial \Omega }{{\partial s}}} \right)^{2} - \beta_{1}\Phi _{1} \left( {\xi ,s} \right)U_{0} + \alpha\Phi _{2} \left( {\xi ,s} \right)U_{0} - \delta s^{2} U_{0} = 0$$

(7.45)

where,

$$\Phi _{1} \left( {\xi ,s} \right) = \frac{1}{{1 + |U_{0} |^{2} }}$$

(7.46)

$$\Phi _{2} \left( {\xi ,s} \right) = \frac{{|U_{0} |^{2} }}{{(1 + |U_{0} |^{2} )}}$$

(7.47)

$\Phi _{1} \left( {\xi ,s} \right)$ and $\Phi _{2} \left( {\xi ,s} \right)$ represent the contributions to the refractive index change due to the (linear) electro-optic effect. We shall be searching for physically acceptable bright soliton states and like before, assume a quasi-soliton solution for (7.45) as follows,

$$U_{0} \left( {\xi ,s} \right) = \frac{{U_{00} }}{{\sqrt {f\left( \xi \right)} }}e^{{ - s^{2} /2r^{2} f^{2} \left( \xi \right)}}$$

(7.48)

$$\Omega \left( {\xi ,s} \right) = \frac{{s^{2} }}{2}\Gamma \left( \xi \right)$$

(7.49)

$$\Gamma \left( \xi \right) = - \frac{1}{f\left( \xi \right)}\frac{df\left( \xi \right)}{{d\xi }}$$

(7.50)

where $P_{0} = U_{00}^{2}$ is the normalized peak power of the soliton, r is a constant which is always positive, $f\left( \xi \right)$ is the variable parameter related to the beam width such that the product $rf\left( \xi \right)$ is the spatial width of the soliton. The ansatz used in (7.48) can be said to be a variational solution. The variable parameters to be found are r, $\left( \xi \right)$, $\Gamma \left( \xi \right)$. In general, we shall assume that the soliton beam is stable and not diverging when it enters the photorefractive crystal, i.e., $\frac{df}{{d\xi }} = 0$ at $\xi = 0$. Also, we can assume that $f = 1$ at $\xi = 0$. The next step is to simplify the non-linear terms $\Phi _{1}$ and $\Phi _{2}$. By a simple Taylor expansion in first order analogous to the calculation in Sect. 7.3.1, we get,

$$\Phi _{1} \left( {\xi ,s} \right) \approx \frac{1}{{\left( {1 + \frac{{U_{00}^{2} }}{f}} \right)}} + s^{2} \frac{{\frac{{U_{00}^{2} }}{{r^{2} f^{3} \left( \xi \right)}}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)^{2} }}$$

(7.51)

$$\Phi _{2} \left( {\xi ,s} \right) \approx \frac{{\frac{{U_{00}^{2} }}{f}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f}} \right)^{2} }} - s^{2} \frac{{\frac{{U_{00}^{2} }}{{r^{2} f^{3} \left( \xi \right)}}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)^{2} }}$$

(7.52)

Substituting (7.14)–(7.18) in (7.11), we obtain an equation which contains several powers of $s^{2}$. Considering the coefficients of $s^{2}$ in LHS and RHS and equating them, we get the following evolution equation for the parameter $f\left( \xi \right)$,

$$\frac{{d^{2} f\left( \xi \right)}}{{d\xi^{2} }} = \frac{1}{{r^{4} f^{3} \left( \xi \right)}} - 2\left( {\beta + \alpha } \right)\frac{{\frac{{P_{0} }}{{r^{2} f^{2} \left( \xi \right)}}}}{{\left( {1 + \frac{{P_{0} }}{f\left( \xi \right)}} \right)^{2} }} - 2\delta f\left( \xi \right)$$

(7.53)

Higher order terms of s, i.e., s³, s⁴ will not be considered since we take the first order approximation [r f(ξ)] > s in (7.51)–(7.52). Now, the optical beam may diverge, be compressed or travel stably after self trapping. From (7.53), we can see that this depends upon the magnitudes of the power $P_{0}$ and the parameters $\beta_{1} ,\beta_{2}$. A soliton, which is a stable self trapped solitary wave will be formed when the beam width $f\left( \xi \right)$ remains exactly constant. So the LHS in (7.53) should equal zero,

$$\frac{1}{{r^{4} }} = 2\delta + \frac{{2\left( {\alpha + \beta } \right)P_{0t} }}{{r^{2} (1 + P_{0t} )^{2} }}$$

(7.54)

In (7.54), we see an equilibrium condition which is known as quartic equilibrium condition because it is a polynomial equation of fourth order and has four roots. From (7.54), we can find out the threshold power $P_{0t}$ needed for stationary propagation of the optical beam. It can be said to be an existence equation for optical spatial solitons propagating through the photorefractive waveguide. Examining the solutions of the above equation, two roots are imaginary, one root is negative and only one root is positive. Neglecting the imaginary and negative values of r for spatial solitons as being unphysical, we are left with only one solution (Fig. 7.22).

Fig. 7.22

Variation of equilibrium spatial width r with threshold peak power P_0t of the spatial solitons, β = 157.9, α = 31.58. (Reprinted with permission from: S Shwetanshumala and S Konar, Bright optical spatial solitons in a photorefractive waveguide, Physica Scripta, 82, 4, 045404, First Published 2010-09-15, doi: 10.1088/0031-8949/82/04/045404)

We shall proceed similarly to the previous case to predict the behavior of spatial solitons in absence of the waveguiding effect. Considering typical parameters of the LN crystal with external bias field, we have, For illustration, we take four different values of power, $P_{1} \left( { = 0.0999} \right) < P_{0t1}$, $P_{2} \left( { = 0.3341} \right) = P_{0t1}$, $P_{0t1} < P_{3} \left( { = 1} \right) < P_{0t2}$, $P_{4} \left( { = 33.41} \right) > P_{0t2}$. We plot the variation in f with the normalized propagation distance $\xi$ in Fig. 7.23. As explained previously, we observe a self trapping if the power of the light beam falls within the two threshold powers. Self trapping is not observed for powers below the threshold power. For investigating the effect of waveguide embedded in the photorefractive crystal, we plot the change in the soliton width parameter f with the normalized distance of propagation for different waveguide parameters $\delta$ in Fig. 7.24. The conclusions remain same that a soliton of peak power lesser than the threshold power can still be self trapped by the use of an embedded waveguide in the photorefractive crystal.

Fig. 7.23

Variable beam width parameter f(ξ) versus the propagation distance ξ at four different soliton peak powers, β = 157.9, α = 31.58. (Reprinted with permission from: S Shwetanshumala and S Konar, Bright optical spatial solitons in a photorefractive waveguide, Physica Scripta, 82, 4, 045404, First Published 2010-09-15, doi: 10.1088/0031-8949/82/04/045404)

Fig. 7.24

The variation of variable beam width parameter f(ξ) with of propagation distance ξ for different waveguide strengths, $\alpha = 31.58,\beta = 157.9$, $P_{0} = 0.06947$, $r = 0.1489$. (Reprinted with permission from: S Shwetanshumala and S Konar, Bright optical spatial solitons in a photorefractive waveguide, Physica Scripta, 82, 4, 045404, First Published 2010-09-15, doi: 10.1088/0031-8949/82/04/045404)

7.4 Concluding Remarks

In conclusion, a comprehensive investigation of optical spatial solitons propagating in a photorefractive crystal having an embedded planar waveguide has been discussed. The paraxial diffraction equation is now modified to incorporate the waveguide term. In contrast to a numerical solution for the soliton enevelope, a modified Gaussian ansatz is used to solve this paraxial Helmholtz equation by means of a variational method. The planar waveguide structure increases the self-focusing while decreasing the minimum or threshold power required for self trapping. A soliton of lesser power which could not form can be formed with assistance from the self focusing due to the waveguide. The propagation of the solitons is visualized with and without the presence of the waveguide structure. The theory reduces to studying solitons in conventional photorefractive waveguides and centrosymmetric photorefractive waveguides. Lastly, this theory is extended for spatial solitons propagating in photovoltaic photorefractive crystals and pyroelectric photorefractive waveguides.

Note 1:

We shall take,

$$\vec{E} =\Phi \left( {x,z} \right)e^{ikz}$$

(7.55)

where the plane wave propagates along the z-axis and $\Phi \left( {x,z} \right)$ is the transverse modulation of the amplitude. Applying the paraxial approximation which implies a slow variation of $\Phi \left( {x,z} \right)$ with z compared to the wavelength.

The variation is expressed as, $\delta\Phi = \frac{{\partial\Phi }}{\partial z}\delta z \ll\Phi$ with $\delta z\sim \lambda$. So that

$$\frac{{\partial\Phi }}{\partial z} \ll\Phi /\lambda \sim k\,\Phi$$

(7.56)

Hence,

$$\frac{{\partial^{2}\Phi }}{{\partial z^{2} }} \ll k\frac{{\partial\Phi }}{\partial z} \ll k^{2}\Phi$$

(7.57)

Now, we have to evaluate,

$$\nabla^{2} \overrightarrow {E} + (k_{0} n_{e}^{\prime } )^{2} \overrightarrow {E} - gx^{2} \overrightarrow {E} = 0$$

(7.58)

The Laplacian can be expressed as a combination of the transverse and longitudinal parts,

$$\nabla^{2} = \left[ {\nabla_{ \bot }^{2} + \partial_{z}^{2} } \right]$$

(7.59)

So,

$$\nabla^{2} \vec{E} = \left[ {\nabla_{ \bot }^{2} + \partial_{z}^{2} } \right]\vec{E}$$

(7.60)

Now,

$$\partial_{z}^{2} \vec{E} = \partial_{z}^{2} \left[ {\Phi \left( {x,z} \right)e^{ikz} } \right]$$

(7.61)

Solving (7.61),

$$\partial_{z}^{2} \left[ {\Phi \left( {x,z} \right)e^{ikz} \left] = \right[\partial_{z}^{2}\Phi + 2ik\partial_{z}\Phi - k^{2}\Phi } \right]e^{ikz}$$

(7.62)

Substitute in (7.58),

$$\begin{aligned} & \nabla _{ \bot }^{2} \left[ {\Phi \left( {x,z} \right)e^{{ikz}} } \right] + \partial _{z}^{2} \Phi \left( {x,z} \right) + 2ik\partial _{z} \Phi \left( {x,z} \right) - k^{2} \Phi \left( {x,z} \right)]e^{{ikz}} \\ & \quad + (k_{0} n_{e}^{\prime } )^{2} \Phi \left( {x,z} \right)e^{{ikz}} - gx^{2} \Phi \left( {x,z} \right)e^{{ikz}} \\ \end{aligned}$$

(7.63)

The term $\partial_{z}^{2}\Phi \left( {x,z} \right)$ can be neglected due to the paraxial approximation. So,

$$\begin{aligned} & \nabla _{ \bot }^{2} \left[ {\Phi \left( {x,z} \right)e^{{ikz}} } \right] + 2ik\partial _{z} \Phi \left( {x,z} \right) - k^{2} \Phi \left( {x,z} \right)]e^{{ikz}} \\ & \quad + (k_{0} n_{e}^{\prime } )^{2} \Phi \left( {x,z} \right)e^{{ikz}} - gx^{2} \Phi \left( {x,z} \right)e^{{ikz}} \\ \end{aligned}$$

(7.64)

From (7.2),

$$n_{e}^{\prime 2} = n_{e}^{2} - n_{e}^{4} r_{33} E_{sc} - n_{e}^{4} g_{eff} \in_{0}^{2} ( \in_{r} - 1)^{2} E_{sc}^{2}$$

(7.65)

Substitute $k = k_{0} n_{e}$ and (7.65) in (7.64),

$$\begin{aligned} & i\frac{{\partial \Phi }}{{\partial z}} + \frac{1}{{2k_{0} n_{e} }}\left( {\frac{{\partial ^{2} \Phi }}{{\partial x^{2} }} + \frac{{\partial ^{2} \Phi }}{{\partial y^{2} }}} \right) - \frac{1}{2}k_{0} n_{e}^{3} r_{{eff}} E_{{sc}} \Phi \\ & \quad - \frac{1}{2}k_{0} n_{e}^{3} g_{{eff}} \in _{0}^{2} ( \in _{r} - 1)^{2} E_{{sc}}^{2} \Phi - gx^{2} \Phi = 0 \\ \end{aligned}$$

(7.66)

Since the diffraction effects are considered only in the in the x-direction, (7.66) becomes,

$$\begin{aligned} & i\frac{{\partial \Phi }}{{\partial z}} + \frac{1}{{2k_{0} n_{e} }}\frac{{\partial ^{2} \Phi }}{{\partial x^{2} }} - \frac{1}{2}k_{0} n_{e}^{3} r_{{eff}} E_{{sc}} \Phi \\ & \quad - \frac{1}{2}k_{0} n_{e}^{3} g_{{eff}} \in _{0}^{2} ( \in _{r} - 1)^{2} E_{{sc}}^{2} \Phi - gx^{2} \Phi = 0 \\ \end{aligned}$$

(7.67)

Note 2

We want to calculate,

$$\Phi _{1} \left( {\xi ,s} \right) = \frac{1}{{1 + |U_{0} |^{2} }}$$

(7.68)

From (7.14),

$$U_{0} \left( {\xi ,s} \right) = \frac{{U_{00} }}{{\sqrt {f\left( \xi \right)} }}e^{{ - s^{2} /2r^{2} f^{2} \left( \xi \right)}}$$

(7.69)

Hence, we get,

$$|U_{0} |^{2} = \frac{{U_{00}^{2} }}{f\left( \xi \right)}e^{{ - s^{2} /r^{2} f^{2} \left( \xi \right)}}$$

(7.70)

Now, expanding the exponential function in (7.70),

$$e^{{ - s^{2} /r^{2} f^{2} \left( \xi \right)}} = 1 - \frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}} + \frac{1}{2!}\left( {\frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}}} \right)^{2} - \cdots$$

(7.71)

Substituting in (7.70),

$$|U_{0} |^{2} = \frac{{U_{00}^{2} }}{f\left( \xi \right)}\left\{ {1 - \frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}} + \frac{1}{2!}\left( {\frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}}} \right)^{2} - \cdots } \right\}$$

(7.72)

Substitute (7.72) in (7.68), we have,

$$\Phi _{1} = \frac{1}{{1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}\left\{ {1 - \frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}} + \frac{1}{2!}\left( {\frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}}} \right)^{2} - \cdots } \right\}}}$$

(7.73)

Simplifying,

$$\Phi _{1} = \left[ {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}\left\{ {1 - \frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}} + \frac{1}{2!}\left( {\frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}}} \right)^{2} - \cdots } \right\}} \right]^{ - 1}$$

(7.74)

$$\Rightarrow\Phi _{1} = \left[ {\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)\left\{ {1 - s^{2} \frac{{\frac{{U_{00}^{2} }}{{r^{2} f^{3} \left( \xi \right)}}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)}} + \frac{{\frac{{U_{00}^{2} }}{f\left( \xi \right)}\frac{1}{2!}\left( {\frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}}} \right)^{2} }}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)}} - \cdots } \right\}} \right]^{ - 1}$$

(7.75)

$$\Rightarrow\Phi _{1} = \left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)^{ - 1} \left\{ {1 - s^{2} \frac{{\frac{{U_{00}^{2} }}{{r^{2} f^{3} \left( \xi \right)}}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)}} + \frac{{\frac{{U_{00}^{2} }}{f\left( \xi \right)}\frac{1}{2!}\left( {\frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}}} \right)^{2} }}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)}} - \cdots } \right\}^{ - 1}$$

(7.76)

Following the approach of Refs. [28, 29], the term in curly brackets is expanded in a Taylor series. Considering the first order approximation we get,

$$\Phi _{1} \approx \left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)^{ - 1} \left\{ {1 + s^{2} \frac{{\frac{{U_{00}^{2} }}{{r^{2} f^{3} \left( \xi \right)}}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)}}} \right\}$$

(7.77)

$$\Phi_{1} \left( {\xi ,s} \right) \approx \frac{1}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)}} + s^{2} \frac{{\frac{{U_{00}^{2} }}{{r^{2} f^{3} \left( \xi \right)}}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)^{2} }}$$

(7.78)

Proceeding similarly for $\Phi _{2} \left( {\xi ,s} \right) = \frac{1}{{(1 + |U_{0} |^{2} )^{2} }}$, we get,

$$\Phi _{2} = \frac{1}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}\left\{ {1 - \frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}} + \frac{1}{2!}\left( {\frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}}} \right)^{2} - \cdots } \right\}} \right)^{2} }}$$

(7.79)

Simplifying,

$$\Rightarrow\Phi _{2} = \left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)^{ - 2} \left\{ {1 - s^{2} \frac{{\frac{{U_{00}^{2} }}{{r^{2} f^{3} \left( \xi \right)}}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)}} + \frac{{\frac{{U_{00}^{2} }}{f\left( \xi \right)}\frac{1}{2!}\left( {\frac{{s^{2} }}{{r^{2} f^{2} \left( \xi \right)}}} \right)^{2} }}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)}} - \cdots } \right\}^{ - 2}$$

(7.80)

Expanding the second term in Taylor series in first order,

$$\Phi _{2} \left( {\xi ,s} \right) \approx \frac{1}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)^{2} }} + 2s^{2} \frac{{\frac{{U_{00}^{2} }}{{r^{2} f^{3} \left( \xi \right)}}}}{{\left( {1 + \frac{{U_{00}^{2} }}{f\left( \xi \right)}} \right)^{3} }}$$

(7.81)