Keywords

4.1 Introduction

In the field of industrial sector, there is a some problems between seller and buyer regarding optimal profit as well as total cost from the both side and such type of problems have been tried to short out by Adad and Jaggi (2003) with the help of mathematical model in which has shown the effects of credit financing policy. Shinn and Hwang (2003) calculated the maximum price for the seller as well as lot size using the policy of credit financing. The total cost acts as major role in the inventory system.

An inventory model has been presented by Hung and Chung (2003) which is the extended form of Goyal (1985) which explained how to minimize the total cost under credit financing and payment rebate policy. A mathematical model has been developed for best costing and batch sizing in which assuming that purchase quantity and selling price both are different under credit financing policy when demand is a function of selling price. The EOQ model has been developed to easy manner as per suggested by Hung (2007) and given new idea how to find out the optimal lot size for the seller. Luo (2007) has been proposed an inventory model for the good coordination between seller and buyer under the credit financing policy. A stock model has been formulated for the optimal economic order quantity as guided by Sarmah et al. (2007) and in this model, a seller has connected to the many buyers under the credit financing to got more profit through coordinated strategy. In recent times, authors improved stock representation with the two-level credit policy. An inventory mathematical representation has been improved by Hung (2003) using the two-level credit policy and demand is stimulated as per consideration.

The research work of Huang (2003) has been investigated by Huang (2006) and improved this model by using two-level credit financing and restricted storage space. A stock model has been presented by Teng and Goyal (2007) for the customers when customer used to credit policy provided by buyer during the business. The construction of economic order quantity has been balanced by Huang (2007) which is the extended form of Haung (2003) with the help of two-level credit financing policy. An inventory model has improved for organization by Su et al. (2007) with the help of credit financing policy.

A two-level credit financing model has developed by Huang and Hsu (2008) with the help of partial credit policy. An economic order quantity formulation has been presented by Jaggi et al. (2008) under two-level credit policy with credit dependent demand. Jaber et al. (2008) has explained economic production quantity model for items with imperfect quality subjected to learning effects. Research task of the Huang (2007) have modified by Teng and Chang (2009) with the policy of two-level credit financing system which is the benefit for the customers. A model has been developed by Chen and Kang (2010) for business system under two-level credit policy with price dependent demand and conciliation situation. A lot of review article has been provided by Shah et a1. (2010) for the inventory system under two-level credit financing policy. Shah et al. (2012) explained an EOQ model in fuzzy environment and trade credit. Shah et al. (2016) presented a deteriorating inventory model under permissible delay in payments and fuzzy environment.

Wright (1936) analyzed that factor affecting the cost of airplane. The present article combined the effect of two- level trade credit and leaning effect with preservation atmosphere. Jayaswal et al. (2019) has proposed the effects of learning on retailer ordering policy for imperfect quality items with trade credit financing. Agarwal and Mittal (2019) explained an inventory classification using multilevel association rule mining. Mittal et al. (2017) represented a mathematical model on retailer’s ordering policy for deteriorating imperfect quality items when demand and price are time-dependent under inflationary conditions and permissible delay in payments. Jaggi et al. (2011) proposed a credit financing for deteriorating imperfect-quality items under inflationary conditions. Jayaswal et al. (2021) proposed a mathematical model with the ordering policies for deteriorating imperfect quality items with trade-credit financing under learning effect.

4.2 Assumptions and Notations

The mathematical model is derived using following notations and assumptions.

4.2.1 Assumptions

  • Replenishment rate is infinite.

  • There are no shortages in this model.

  • The lead-time is considered to be zero.

  • Unit purchasing cost is less than the unit selling price.

  • No replacement policy of perishable items during cycle length.

  • Two level trade credits are allowed.

4.2.2 Notations

R :

Annual constant demand.

ξ :

Preservation cost.

A :

Ordering cost which follows the learning effect.

P :

Selling price per unit.

θ :

Decaying rate per unit time.

C :

Unit purchase cost.

h :

Unit holding cost which follows the learning effect.

Q :

Order quantity.

M :

The offered trade credit by the supplier to the retailer to settle the account.

N :

The credit financing period for customer offered by the retailer.

I c :

Interest charged.

I e :

Interest gained.

T :

Cycle length.

q(t):

The inventory level in the interval, 0 ≤ t ≤ T .

K1(T):

The whole inventory level under the condition M ≤ T .

K2(T):

The whole inventory level under the condition N ≤ T ≤ M.

K3(T):

The whole inventory level under the condition N ≥ T.

T 1 :

Cycle length under the M ≤ T .

T 2 :

Cycle length under the case N ≤ T ≤ M.

T 3 :

Cycle length under the N ≥ T.

4.3 Mathematical Formulation

Suppose that, \(q\left( t \right)\) is the inventory level in the interval \(\left( {0 \le t \le T} \right)\). Initially, the stock level is \(Q\). The present stock is reducing due to demand and deterioration and finally, it has finished at \(t = T.\) The rate of decreasing of inventory stock are given as follows:

$$\frac{dq\left( t \right)}{{dt}} + \theta q\left( t \right) = - R,\quad 0 \le t \le T$$
(4.1)

With initial and boundary conditions

$$q\left( 0 \right) = Q\,{\text{and}}\,q\left( T \right) = 0$$
(4.2)

the solution of Eq. (4.1) is

$$q\left( t \right) = \frac{R}{\theta }\left( {e^{{\theta \left( {T - t} \right)}} - 1} \right),\quad 0 \le t \le T$$
(4.3)

Using the Eq. (4.2), the order quantity given as

$$Q = q\left( 0 \right) = \frac{R}{\theta }\left( {e^{\theta T} - 1} \right)$$
(4.4)

Now, the ordering cost per cycle,

$$OC = \frac{1}{T}\left( {C_{1} + \frac{{C_{2} }}{{n^{\beta } }}} \right)$$
(4.5)

The holding cost per cycle,

$${\textit{IHC}} = \frac{{\left( {h_{1} + \frac{{h_{2} }}{{n^{\beta } }}} \right)R}}{{\theta^{2} T}}\left( {e^{\theta T} - \theta T - 1} \right)$$
(4.6)

The deterioration cost per cycle,

$$CD = C(Q - RT) = \frac{CR}{{\theta T}}(e^{\theta T} - \theta T - 1)$$
(4.7)
$${\text{Preservation cost}},\quad PV = \xi \,T$$
(4.8)

Now the whole cost per cycle

$$K\left( T \right) = \frac{1}{T}\left[ {IHC + OC + CD + PV - IE + IC} \right]$$

Regarding interest charged and interest earned, based on the length of the cycle time \(T\), three cases may arise:

Case-1: \(M \le T\).

Case-2: \(N \le T \le M\).

Case-3: \(N \ge T\).

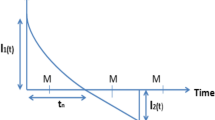
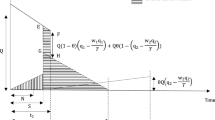
These three cases are represented in Figs. 4.1, 4.2 and 4.3 respectively.

Fig. 4.1
figure 1

The total accumulation of interest earned when \(M \le T \) (Source own)

Full size image
Fig. 4.2
figure 2

The total accumulation of interest earned when \(N \le T \le M\)

Full size image
Fig. 4.3
figure 3

The total accumulation of interest earned when \(N \ge T \) (Source own)

Full size image

Case-1: \(M \le T\) (Fig. 4.1).

During the credit period, the retailer sells items and deposits the generated revenue into an amount bearing account at the interest rate \(I_{e}\) per dollar per year.

Therefore, the interest earned per unit time is

$$IE_{1} = \frac{{PI_{e} }}{T}\int\limits_{N}^{M} {Rt} {\text{d}}t = \frac{{PI_{e} R\left( {M^{2} - N^{2} } \right)}}{2T}$$
(4.9)

The unsold items in stock are charged at interest rate \(I_{c}\) by the supplier at the beginning of time \(T\).

Therefore, the interest charged per unit time is

$$IC_{1} = \frac{{CI_{c} }}{T}\int\limits_{M}^{T} {q\left( t \right)} {\text{d}}t = \frac{{CI_{c} R}}{{\theta^{2} T}}\left[ {e^{{\theta \left( {T - M} \right)}} - \theta \left( {T - M} \right) - 1} \right]$$
(4.10)

Hence, the total cost per time unit is

$$K_{1} \left( T \right) = OC + IHC + CD + PV + IC_{1} - IE_{1}$$
(4.11)

Case 2: \(N \le T \le M\) (Fig. 4.2).

In this case, the total interest earned per unit time is,

$$\begin{aligned} IE_{2} & = \frac{{PI_{e} }}{T}\left[ {\int_{N}^{T} {Rt{\text{d}}t + RT\left( {M - T} \right)} } \right] \\ & = \frac{{PI_{e} R}}{2T}\left( {2MT - N^{2} - T^{2} } \right) \\ \end{aligned}$$
(4.12)

In this case, total interest charged = 0

Hence, the total cost per time unit is

$$K_{2} \left( T \right) = OC + IHC + PV + CD - IE_{2}$$
(4.13)

Case 3: \(N \ge T\) (Fig. 4.3).

The interest earned per unit time is,

$$IE_{3} = PI_{e} R\left( {M - N} \right)$$
(4.14)

Similar as case 2, total interest charged equal to zero.

Hence, the total cost per unit time is,

$$K_{3} \left( T \right) = OC + IHC + PV + CD - IE_{3}$$
(4.15)

Hence, the total relevant cost \(K\left( T \right)\) per unit time is,

$$K\left( T \right) = \left\{ {\begin{array}{*{20}l} {K_{1} \left( T \right),} \hfill & {{\text{if}}\,M \le T} \hfill \\ {K_{2} \left( T \right),} \hfill & {{\text{if}}\,N \le T \le M} \hfill \\ {K_{3} (T),} \hfill & {{\text{if}}\,N \ge T} \hfill \\ \end{array} } \right.$$
(4.16)

where under series approximation and assumption that \(\theta T < 1\), ignoring higher powers of \(\theta\), then we get,

$$\begin{aligned} K_{1} \left( T \right) & = \frac{{\left( {C_{1} + \frac{{C_{2} }}{{n^{\beta } }}} \right)}}{T} + \frac{{\left( {h_{1} + \frac{{h_{2} }}{{n^{\beta } }}} \right)RT}}{2} + \frac{CR\theta T}{2} + \frac{{CI_{c} RT}}{2} \\ & \quad + \frac{{CI_{c} RM^{2} }}{2T} + \frac{\xi T}{T} - CI_{c} RM - \frac{{PI_{e} R\left( {M^{2} - N^{2} } \right)}}{2T} \\ \end{aligned}$$
(4.17)

and

$$\begin{aligned} K_{2} \left( T \right) & = \frac{{\left( {C_{1} + \frac{{C_{2} }}{{n^{\beta } }}} \right)}}{T} + \frac{{\left( {h_{1} + \frac{{h_{2} }}{{n^{\beta } }}} \right)RT}}{2} + \frac{{\xi T}}{T} \\ & \quad + \frac{{CR\theta T}}{2} - \frac{{PI_{e} R}}{{2T}}\left( {2MT - N^{2} - T^{2} } \right) \\ \end{aligned}$$
(4.18)

and

$$K_{3} \left( T \right) = \frac{{\left( {C_{1} + \frac{{C_{2} }}{{n^{\beta } }}} \right)}}{T} + \frac{{\left( {h_{1} + \frac{{h_{2} }}{{n^{\beta } }}} \right)RT}}{2} + \frac{\xi T}{T} + \frac{CR\theta T}{2} - PI_{e} R\left( {M - N} \right)$$
(4.19)

The necessary and sufficient conditions for \(K_{1} \left( T \right)\) to be optimum is

$$\begin{aligned} \frac{{{\text{d}}K_{1} \left( T \right)}}{{{\text{d}}T}} & = - \frac{{\left( {C_{1} + \frac{{C_{2} }}{{n^{\beta } }}} \right)}}{{T^{2} }} + \frac{{\left( {h_{1} + \frac{{h_{2} }}{{n^{\beta } }}} \right)R}}{2} + \frac{CR\theta }{2} \\ & \quad + \frac{{CI_{c} R}}{2}\left( {1 - \frac{{M^{2} }}{{T^{2} }}} \right) + \frac{{PI_{e} R\left( {M^{2} - N^{2} } \right)}}{{2T^{2} }} \\ \end{aligned}$$
(4.20)

and

$$\frac{{{\text{d}}^{2} K_{1} \left( T \right)}}{{{\text{d}}T^{2} }} = \frac{{2\left( {C_{1} + \frac{{C_{2} }}{{n^{\beta } }}} \right)}}{{T^{3} }} + \frac{{CI_{c} RM^{2} }}{{T^{3} }} - \frac{{PI_{e} R\left( {M^{2} - N^{2} } \right)}}{{T^{3} }} > 0$$
(4.21)

For the optimal cycle time \(T_{1}\), set \(\frac{{{\text{d}}K_{1} \left( T \right)}}{{{\text{d}}T}} = 0\) which gives

$$T = T_{1} ({\text{say}}) = \sqrt {\frac{{2\left( {C_{1} + \frac{{C_{2} }}{{n^{\beta } }}} \right) + RCI_{c} M^{2} + RPI_{e} \left( {N^{2} - M^{2} } \right)}}{{R\left\{ {h_{1} + \frac{{h_{2} }}{{n^{\beta } }} + C\left( {\theta + I_{c} } \right)} \right\}}}}$$
(4.22)

Now,

$$\frac{{{\text{d}}K_{2} \left( T \right)}}{{{\text{d}}T}} = - \frac{{C_{1} + \frac{{C_{2} }}{{n^{\beta } }}}}{{T^{2} }} + \frac{{\left( {h_{1} + \frac{{h_{2} }}{{n^{\beta } }}} \right)R}}{2} + \frac{CR\theta }{2} + \frac{{PI_{e} R}}{2} - \frac{{PI_{e} RN^{2} }}{{2T^{2} }}$$
(4.23)

and

$$\frac{{{\text{d}}^{2} K_{2} \left( T \right)}}{{{\text{d}}T^{2} }} = \frac{{2\left( {C_{1} + \frac{{C_{2} }}{{n^{\beta } }}} \right)}}{{T^{3} }} + \frac{{PI_{e} RN^{2} }}{{T^{3} }} > 0$$
(4.24)

For the optimal cycle time \(T_{2}\), set \(\frac{{dK_{2} \left( T \right)}}{dT} = 0\) which gives

$$T = T_{2} ({\text{say}}) = \sqrt {\frac{{2\left( {C_{1} + \frac{{C_{2} }}{{n^{\beta } }}} \right) + PI_{e} RN^{2} }}{{R\left( {h_{1} + \frac{{h_{2} }}{{n^{\beta } }} + PI_{e} + C\theta } \right)}}}$$
(4.25)

Now,

$$\frac{{{\text{d}}K_{3} \left( T \right)}}{{{\text{d}}T}} = - \frac{{C_{1} + \frac{{C_{2} }}{{n^{\beta } }}}}{{T^{2} }} + \frac{{\left( {h_{1} + \frac{{h_{2} }}{{n^{\beta } }}} \right)R}}{2} + \frac{CR\theta }{2}$$
(4.26)

and

$$\frac{{{\text{d}}^{2} K_{3} \left( T \right)}}{{{\text{d}}T^{2} }} = \frac{{2\left( {C_{1} + \frac{{C_{2} }}{{n^{\beta } }}} \right)}}{{T^{3} }} > 0$$
(4.27)

For the optimal cycle time \(T_{3}\), set \(\frac{{{\text{d}}K_{3} \left( T \right)}}{{{\text{d}}T}} = 0\) which gives,

$$T = T_{3} ({\text{say}}) = \sqrt {\frac{{2\left( {C_{1} + \frac{{C_{2} }}{{n^{\beta } }}} \right)}}{{R(h_{1} + \frac{{h_{2} }}{{n^{\beta } }} + C\theta )}}}$$
(4.28)

4.3.1 Algorithm

  • Step-1: Compute \(T_{1}\), \(T_{2}\) and \(T_{3}\) from the Eqs. (4.22), (4.25) and (4.28) with the help of input parameters.

  • Step-2: If \(M \le T_{1}\), then calculate \(K_{1} \left( {T_{1} } \right)\), otherwise go to step-3.

  • Step-3: If \(N \le T_{2} \le M\), then calculate \(K_{2} \left( {T_{2} } \right)\), otherwise go to step-4.

  • Step-4: If \(N \ge T_{3}\), then calculate \(K_{3} \left( {T_{3} } \right)\).

  • Step-5: Find corresponding cycle time and total optimal cost.

4.3.2 Numerical Example

$$\begin{aligned} R & = 500\,{\text{units}},h_{1} = 2,h_{2} = 1,C_{1} = 30,C_{2} = 10,\beta = 0.23,\theta = 0.20,\xi = 0.15\,{\text{per}}\,{\text{items}}, \\ {\text{Ie}} & = {{\$ 0.14} \mathord{\left/ {\vphantom {{\$ 0.14} {{\$ \mathord{\left/ {\vphantom {\$ {{\text{year}}}}} \right. \kern-\nulldelimiterspace} {{\text{year}}}}}}} \right. \kern-\nulldelimiterspace} {{\$ \mathord{\left/ {\vphantom {\$ {{\text{year}}}}} \right. \kern-\nulldelimiterspace} {{\text{year}}}}}},Ip = {{\$ 0.15} \mathord{\left/ {\vphantom {{\$ 0.15} {{\$ \mathord{\left/ {\vphantom {\$ {{\text{year}}}}} \right. \kern-\nulldelimiterspace} {{\text{year}}}}}}} \right. \kern-\nulldelimiterspace} {{\$ \mathord{\left/ {\vphantom {\$ {{\text{year}}}}} \right. \kern-\nulldelimiterspace} {{\text{year}}}}}},C = \$ 50,M = {{45} \mathord{\left/ {\vphantom {{45} {365}}} \right. \kern-\nulldelimiterspace} {365}}\,{\text{year}},N = {{25} \mathord{\left/ {\vphantom {{25} {365}}} \right. \kern-\nulldelimiterspace} {365}}\,{\text{year}}, \\ & {\text{optimal cycle length}},T^{*} = 2.7217\,{\text{year}}\,{\text{and}}\,{\text{minimum}}\,{\text{total}}\,\cos t \\ & \psi _{1} \left( {T^{*} } \right) = 3253\,\$ \,{\text{per}}\,{\text{year}} \\ \end{aligned}$$

4.3.3 Sensitive Analysis and Discussion Part

Sensitive Analysis

The sensitive analysis has been studied on the effective parameters and retailer total cost will be analyzed.

Managerial Insights

  • From Table 4.1, if learning rate increases, cycle length almost fixed and retailer’s total cost decreases.

    Table 4.1 Impact of learning rate under cycle time and whole cost per cycle (Source own)
    Full size table

  • From Table 4.2, if number of shipments increases, cycle length increases marginally and retailer’s cost decreases due to the learning effect.

    Table 4.2 Impact of the number of shipments on cycle time and whole cost (Source own)
    Full size table

  • From Table 4.3, if \(M\) increases then cycle length and retailer’s total cost decrease due to the learning and credit financing.

    Table 4.3 Impact of the number of credit period on cycle time and whole cost (Source own)
    Full size table

  • From Table 4.4, if deterioration rate increases, cycle length decreases and retailer’s cost decreases.

    Table 4.4 Impact of the decaying rate on cycle time and whole cost (Source own)
    Full size table

  • From Table 4.5, if customer’s credit period increases then, cycle length is fixed and retailer’s total cost increases marginally.

    Table 4.5 Impact of the customer’s credit period on retailer’s cycle time and whole cost (Source own)
    Full size table

  • From Table 4.6, if preservation cost increases then, cycle length is fixed and retailer’s total cost increases.

    Table 4.6 Impact of the preservation cost on retailer’s cycle time and whole cost (Source own)
    Full size table

Discussion Part

In this part, we have discussed about the distinct cases and have tried to determine as to which case should be better for this model after we procured the solution with the assistance of the concerned algorithm. Post getting all the values from the above three cases, we concluded that the minimum cost was given by Case 1 which is \(N \le M \le T\) and it was beneficial due to suitable credit period which have obtained from the algorithm and other cases are not consider due the large value of credit period and have been analyzed from the algorithm. This case provided the optimal values of all the parameters. The learning effect will reduce the total cost with trade-credit policy.

4.4 Conclusion

This article developed an inventory model to determine cycle length and the corresponding total cost for the buyer with the help of the two-level trade credit financing with learning effect applied over the holding cost and the ordering cost. Eventually, we have concluded that results of this model showed that the retailer’s total cost reduces as learning parameter value increases. When items are perishable then preservation of the items are must to control the deterioration rate, but the total cost increases marginally. This article reveals that the combination of trade-credit financing and learning concept is very beneficial to get more profit in real scenario. Findings together with mathematical analysis clearly recommended that the existence of two-level trade-credit and effect of leaning have positive effects on the total cost. Present work can be extended such as stock depended demand, and cloudy environment etc.