Keywords

1 Introduction

The advancement in materials has been associated with the man’s evolution since ancient time. Yesterday, it was the age of stone, bronze, and iron and today it is the age of advanced materials, such as advanced composites, smart materials and functionally graded materials (FGMs). The most lightweight composite materials with high specific-strength and weight have been used successfully in the aircraft and defense industries and other engineering applications. However, due to strong mismatch of material properties at the interface in the structures made from traditional composites have several disadvantages, like debonding, delamination, plastic deformation and cracking problems, especially at high temperatures and pressures. In order to manufacture thermal barrier materials and also to get rid of the issues associated with the use of conventional laminated composites, a concept of FGMs was proposed in 1984 by the material scientists of Japan (Shiota and Miyamoto 1997). Functionally graded materials (FGMs), the next generation composites, are inhomogeneous material with a smooth and gradual variation in their properties along some specified direction(s), obtained by varying the volume fractions of the constituents (Suresh and Mortensen 1998).

Normally, there are two constituents of FGMs—ceramics and metals. Ceramic provides better thermal, wear and oxidation characteristics, whereas metal imparts high toughness, mechanical strength, and machinability properties to an FGM. Owing to the favorable mechanical and thermal properties, FGM offers a wide range of applications in various engineering fields requiring high temperature resistance combined with good mechnical strength. The promising advantages of using FGMs include decreased thermal stresses (Choules and Kokini 1996), good bonding strength in between joints of dissimilar materials (Howard et al. 1994), and the reduced possibility of catastrophic failure of brittle ceramic materials (Bao and Wang 1995). Further, FGMs are also used in many other applications; for instance, in rocket heat shields, heat engine components, heat exchanger tubes, plasma facings, fusion reactors, nuclear reactor plant, thermo-electric generators, and electrical insulating applications (Mahamood and Akinlabi 2017).

Further, thin-walled elements, such as plates and shells, widely used in many engineering fields, such as civil, aerospace, mechanical, naval, space engineering, and more recently, in micro-engineering, are more vulnerable towards buckling failure due to large deflections, and/or high stresses under in-plane thermo-mechanical loading conditions. Due to the fact that the membrane stiffness of plate-like structures is significantly higher than the bending stiffness that causes these types of structures to absorb a large amount of membrane strain energy with less deformations. However, the deformations are much higher when these structures absorb the same amount of bending energy. If the plate is loaded in such a way that most of its strain energy is contributed by the membrane energy, and under some conditions, such as initial imperfection, eccentric loading, etc., if the stored membrane energy is converted into the equivalent bending energy at some critical load point (called buckling load), then the plate becomes unstable and deforms dramatically in transverse direction producing excessive out-of-plane deflection. This destabilizing phenomenon is well known as buckling. It is well known that for the plate like structures, the buckling does not mean the ultimate failure, and these structures can carry extra load beyond the buckling point which is known as postbuckling strength (Singh and Kumar 1999).

In some applications, these plate-like structural elements are required primarily to resist buckling, and in others, they must carry a load well into the postbuckling range to yield weight savings. Thus, understanding their buckling and postbuckling behavior is needed for the efficient design of these structural elements.

Moreover, it is also noteworthy to mention that the structural failure can occur due to the material failure and/or geometrical instability. Before the material failure, the structure may show inelastic response producing plastic deformation which in turn causes a destabilizing effect on structures under in-plane compression and/or shear loads produced by mechanical and/or thermal loading conditions. Further, due to the safety reasons, machine elements working under the elastic limit, are also designed to carry overloads that can lead to inelastic deformations (Bazant et al. 1993). Therefore, elastic–plastic analysis is required to ensure safe and reliable design of such machine components. Being an important design criterion, the elastic–plastic buckling and postbuckling analysis of homogenous isotropic and composite plates has been reported in various studies (Narayanan and Chow 1984; Shanmugam et al. 1999; El-Sawy, and Martini 2004; Paik 2005; Ghavami and Khedmati 2006; Estefen et al. 2016). In addition, a few studies have also been reported on the inelastic buckling and postbuckling response of FGM structures (Huang and Han 2014; Zhang et al. 2015). The elastic–plastic stability and failure analysis of both imperforated and perforated FGM plates under thermal and/or mechanical loading conditions have been carried out by authors (Sharma and Kumar 2017a, b).

In this chapter, the research findings, along with the complete mathematical formulation, of elastic–plastic buckling, postbuckling and failure analysis of FGM plate under thermomechanical loading conditions, considering the temperature dependent material properties, are reported. The thermoelastic properties (i.e., elastic constants and thermal expansion coefficients) of FGM plate are calculated using theoretical and numerical micromechanics based models—Voigt’s model, and Tamura-Tomota-Ozawa model (TTO model). As per the assumption of TTO model, the ceramic phase of FGM is considered to be elastic, whereas the metal phase is assumed to be elastic–plastic. The non-linear FEM formulation for plate analysis is based on the first-order shear deformation theory (FSDT) and von-Kármán’s nonlinear kinematics. Further, J2-plasticity with isotropic hardening is adopted to perform the elastic–plastic analysis of FGM plate. The incremental solution technique based on Newton–Raphson method is utilized for the solution of nonlinear algebraic equations. Numerical studies are conducted on the buckling, postbuckling and failure responses of elastic–plastic FGM plate, considering the temperature-dependent as well as temperature-independent material properties, under thermomechanical loading condition.

2 Layer-Wise Model of FGM Plate

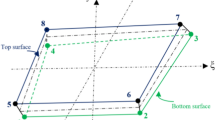
An FGM plate with continuously varying properties along thickness direction is modeled as a laminate, as shown in Fig. 1, with multiple perfectly-bonded layers of isotropic material having layer-wise constant composition, as used in many of the previous studies (Jin 2002; Shao 2005; Shakeri et al. 2006; Shakeri and Mirzaeifar 2009; Cinefra et al. 2010; Cinefra and Soave 2011; Yaghoobi et al. 2015). The FGM plate is assumed to be consisting of ceramic and metal phases and the volume fractions of the material constituents are assumed to follow a power law distribution in the thickness direction. In the present study, a coordinate system (x, y, z) is attached, as shown in Fig. 1, in the mid-plane of the plate measuring a, b and h as length, width, and thickness, respectively.

Fig. 1
figure 1

Layer wise model of a continuous FGM plate

Full size image

The temperature-dependent material properties Young’s modulus E and thermal expansion coefficient \({ }\alpha\) of FGM plate are calculated as follows (Touloukian and Center 1967).

$$P_{j} \left( T \right) = \left\{ {\begin{array}{*{20}l} {P_{0} \left( {P_{ - 1} T^{ - 1} + 1 + P_{1} T + P_{2} T^{2} + P_{3} T^{3} } \right), } & {for\, T > 0^{\circ}\,\text{K}} \\ {P_{0} } & {for\, T \le 0^{\circ}\,\text{K}} \\ \end{array} } \right.$$
(1)

In Eq. (1), \(P_{j} \left( T \right)\) represents the temperature-dependent material properties (E or \(\alpha\)), and \({ }P_{0}\),\(P_{ - 1}\), \(P_{1}\), \(P_{2}\), and \(P_{3}\) are material specific coefficients given in the Table 1 for both the constituents of FGM: Al2O3 (a ceramic phase) and Ni (a metal phase). The effect of temperature on the values of material properties of Al2O3 and Ni is depicted in Fig. 2.

Table 1 Temperature-dependent coefficients for thermo-elastic properties of Al2O3 and Ni (Reddy and Chin 1998)
Full size table
Fig. 2
figure 2

Variation of Young’s modulus (E) and thermal expansion coefficient (\(\alpha\)) with temperature

Full size image

2.1 Effective Thermoelastic Material Properties of FGM Plate

The volume fractions of ceramic and metallic constituents of FGM plate are varied in the thickness direction according to the power law, as given below:

$$V_{m} \left( z \right) = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{n} ;\quad V_{c} \left( z \right) = 1 - V_{m} \left( z \right).$$
(2)

Here, subscripts c and m represent the ceramic and the metallic constituents, respectively, and n denotes power law exponent that determines the material gradation profile across the thickness coordinate z, varying from \(\frac{h}{2}\,{\text{to}}\, - h/2\).

In the present study, the effective elastic material properties of two-phase FGM are calculated using TTO model (i.e., also called modified rule-of-mixtures) (Giannakopoulos et al. 1995). The TTO model has been used extensively in the literature (Giannakopoulos et al. 1995; Jin et al. 2003; Gunes et al. 2011) for accurately predicting the thermoelastic constants of FGM. In TTO model, the effective Young’s modulus of two-phase materials, like FGM, is given in terms of Young’s moduli (i.e., \(E_{c}\) and \({ }E_{m}\)) and volume fractions (i.e., \(V_{c}\) and \(V_{m}\)) of the constituting phases (i.e., ceramic and metallic phases), and it is expressed as under (Tamura et al. 1973):

$$\begin{aligned} E\left( {z,T} \right) & = \left\{ {V_{m} \left( z \right)E_{m} \left( T \right)\frac{{q + E_{c} \left( T \right)}}{{q + E_{m} \left( T \right)}} + \left( {1 - V_{m} \left( z \right)} \right)E_{c} \left( T \right)} \right\} \\ & \quad \times \left\{ {V_{m} \left( z \right)\frac{{q + E_{c} \left( T \right)}}{{q + E_{m} \left( T \right)}} + \left( {1 - V_{m} \left( z \right)} \right)} \right\}^{ - 1} , \\ \end{aligned}$$
(3)

where, q represents the stress transfer parameter and it depends upon the properties of constituent materials as well as on the microstructure interaction in the FGM material. The value of q ranges from 0 to \(\infty\); \(q \to \infty\) represents the case when the constituent materials deform identically in the loading direction (i.e., Voigt model), while \(q = 0\) corresponds to the case wherein the constituent materials experience the same stress level (i.e., Reuss model). Due to the complicated microstructure of FGM, the constituent elements in FGM neither experience equal deformation nor equal stress. Generally, a nonzero finite value of q is assumed to approximately reflect the actual effects of micro-structural interaction in FGM. For instance, for Ni-Al2O3 (Giannakopoulos et al. 1995) and TiB-Ti (Jin et al. 2003) FGMs, the value of q is assumed to be 4.5 GPa and for FGM containing Al and SiC phases (Bhattacharyya et al. 2007; Gunes et al. 2011), it is taken as 91.6 GPa.

In the present study, the Poisson’s ratio is assumed to be constant (equal to the average value of of Poisson’s ratio of metal and ceramic phases) i.e., \(\nu = 0.31\), along the thickness of the FGM plate is used. Equation (3) is used to calculate the Young’s modulus of FGM plate at a particular value of thickness coordinate. The thermal expansion coefficient at a particular thickness coordinate of FGM plate is calculated using the simple rule-of-mixtures, as expressed below:

$$\alpha \left( {z,T} \right) = \alpha_{c} \left( T \right)V_{c} \left( z \right) + \alpha_{m} \left( T \right)V_{m} \left( z \right).$$
(4)

2.2 Effective Elastic–Plastic Material Properties of FGM Plate

The yield strength and plastic tangent modulus of FGM are calculated by the same TTO model, as described in the previous Sect. 2.1. According to the TTO model, the overall failure, after elastic–plastic response, of an in-homogenous material, having brittle and ductile phases, is governed by the ductile constituent (Jin et al. 2003). This assumption of TTO model is applicable for FGMs (containing ceramic—a brittle phase, and metal—a ductile phase). This is because of the reason that the ductility and good shear strength induced in the FGM by the metal phase relax the stress concentration induced around the inherited cracks and flaws of ceramics through the plastic deformation and hence, eliminate the possibility of brittle failure of FGM (Bandyopadhyay et al. 2000; Soh et al. 2000).

Based on the aforementioned assumption, the overall yield strength and tangent modulus of the FGM plate are calculated using q (stress transfer parameter), \(\sigma_{ym}\) (yield strength of metal) and \(H_{m}\) (tangent modulus of metal), as follows (Giannakopoulos et al. 1995):

$$\sigma_{y} \left( {z,T} \right) = \sigma_{ym} \left( T \right)\left[ {V_{m} \left( z \right) + \left( {\frac{{q + E_{m} \left( T \right)}}{{q + E_{c} \left( T \right)}}} \right)\frac{{E_{c} \left( T \right)}}{{E_{m} \left( T \right)}}\left( {1 - V_{m} \left( z \right)} \right)} \right],$$
(5)
$$\begin{aligned} H\left( {z,T} \right) & = \left\{ {V_{m} \left( z \right)H_{m} \left( T \right)\frac{{q + E_{c} \left( T \right)}}{{q + H_{m} \left( T \right)}} + \left( {1 - V_{m} \left( z \right)} \right)E_{c} \left( T \right)} \right\} \\ & \quad \times \left\{ {V_{m} \left( z \right)\frac{{q + E_{c} \left( T \right)}}{{q + H_{m} \left( T \right)}} + \left( {1 - V_{m} \left( z \right)} \right)} \right\}^{ - 1} . \\ \end{aligned}$$
(6)

In the present study, the metallic phase is assumed to follow bilinear hardening behavior, and the elastic–plastic behavior of FGM is also predicted under the same assumption (Giannakopoulos et al. 1995; Williamson et al. 1995). The values of coefficients to calculate the temperature-dependent yield strength \(\sigma_{ym}\) and tangent modulus \(H_{m}\) of Ni (i.e., using Eq. 1) are given in Table 2 (Williamson et al. 1995).

Table 2 Temperature-dependent coefficients to evaluate yield strength and tangent modulus of Ni (Williamson et al. 1995)
Full size table

3 FGM Plate Formulation

3.1 Displacement Field

In the present study, the displacement field is based on first-order shear deformation theory (FSDT), wherein the displacement field, as expressed in Eq. (7), is written in terms of the mid-plane (z = 0) translations \(u_{0} ,v_{0} ,w_{0}\) and the independent normal rotations \(\theta_{x}\) and \(\theta_{y}\) in the xz- and yz-planes, respectively.

$$\begin{aligned} & u\left( {x, y, z} \right) = u_{0} \left( {x,y} \right) + z\theta_{x} \left( {x,y} \right) \\ & v\left( {x, y, z} \right) = v_{0} \left( {x,y} \right) + z\theta_{y} \left( {x,y} \right) \\ & w\left( {x, y, z} \right) = w_{0} \left( {x,y} \right) \end{aligned}$$
(7)

3.2 Strain–Displacement Relationship

Incorporating the von-Kármán’s assumptions—derivatives of \(u\) and \(v\) with respect to \(x,y,\) and \(z\) are small—and noting that \(w\) is independent of \(z,\) the strain components for moderately large deformations can be written in the following forms (Reddy 2004):

$$\begin{aligned} & \varepsilon_{x} = \frac{{\partial u_{0} }}{\partial x} + z\left( {\frac{{\partial \theta_{x} }}{\partial x}} \right) + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2}, \\&\varepsilon_{y} = \frac{{\partial v_{0} }}{\partial y} + z\left( {\frac{{\partial \theta_{y} }}{\partial y}} \right) + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} , \\& \gamma_{xy} = \frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x} + z\left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right) + \left( {\frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial y}} \right), \\& \gamma_{xz} = \frac{{\partial w_{0} }}{\partial x} + \theta_{x} , \\ & \gamma_{yz} = \frac{{\partial w_{0} }}{\partial y} + \theta_{y} .\end{aligned}$$
(8)

Rewriting Eq. (8) into matrix form as

$$\left\{ \epsilon \right\} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\epsilon_{x} } \\ { \epsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left\{ \epsilon \right\}^{l} + \left\{ \epsilon \right\}^{nl} ,\quad \left\{ \epsilon \right\}^{l} = \left\{ {\begin{array}{*{20}c} {\epsilon_{p}^{0} } \\ 0 \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {z\epsilon_{b}^{0} } \\ {\epsilon_{s}^{0} } \\ \end{array} } \right\},$$
(9)
$$\left\{ \epsilon \right\}^{nl} = \left\{ {\begin{array}{*{20}c} {\epsilon_{p}^{NL} } \\ 0 \\ \end{array} } \right\},$$
(10)

wherein, the linear in-plane strain \(\epsilon_{p}^{0} ,\) the bending strain \(\epsilon_{b}^{0} ,\) shear strain \(\epsilon_{s}^{0} ,\) and the nonlinear in-plane strain terms \(\epsilon_{p}^{NL}\) are written as follows:

$$\left\{ {\epsilon_{p}^{0} } \right\} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial x}} \\ {\frac{{\partial v_{0} }}{\partial y}} \\ {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \\ \end{array} } \\ \end{array} } \right\}, \quad \left\{ {\epsilon_{b}^{0} } \right\} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{{\partial \theta_{x} }}{\partial x}} \\ {\frac{{\partial \theta_{y} }}{\partial y}} \\ {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \\ \end{array} } \\ \end{array} } \right\}$$
(11)
$$\left\{ {\epsilon_{s}^{0} } \right\} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{{\partial w_{0} }}{\partial x} + \theta_{x} } \\ {\frac{{\partial w_{0} }}{\partial y} + \theta_{y} } \\ \end{array} } \\ \end{array} } \right\},\quad {\text{and}}\quad \left\{ {\epsilon_{p}^{NL} } \right\} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \\ \end{array} } \\ {\frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} } \\ {\left( {\frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial y}} \right)} \\ \end{array} } \\ \end{array} } \right\}.$$
(12)

3.3 Constitutive Relations

The elastic and elastic–plastic stress–strain relationship for FGM plate with temperature dependent material properties under thermomechanical loading conditions are discussed in the following paragraphs:

3.3.1 Elastic Constitutive Relations

Based on the generalized Hooke’s law, the elastic stress–strain relations are given by Reddy (2003) and Sharma and Kumar (2018):

$$\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\begin{array}{*{20}c} {\tau_{xy} } \\ {\tau_{yz} } \\ {\tau_{xz} } \\ \end{array} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{44} } & 0 & 0 \\ 0 & 0 & 0 & {k_{1}^{2} Q_{55} } & 0 \\ 0 & 0 & 0 & 0 & {k_{2}^{2} Q_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { \epsilon_{x} } \\ { \epsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \\ \end{array} } \right\}$$
(13)

or, in the matrix form, we can write:

$$\left\{ \sigma \right\} = \left[ D \right]\left\{ \varepsilon \right\},$$
(14)

Here, \(k_{1}^{2}\) and \(k_{2}^{2}\) are the shear correction factors, and \(Q_{ij}\) are the stiffness matrix components through the thickness of FGM plate and they are functions of material properties, as mentioned below:

$$\begin{aligned} Q_{11} & = \frac{{E\left( {z,T} \right)}}{{1 - \nu^{2} }},\quad Q_{12} = Q_{13} = Q_{23} = \nu Q_{11} ,\quad Q_{22} = Q_{33} = Q_{11} , \\ Q_{44} & = Q_{55} = Q_{66} = \frac{{E\left( {z,T} \right)}}{{\left( {1 + \nu } \right)}}, \\ \end{aligned}$$
(15)

where, \({ }E\left( {z,T} \right)\) is Young’s modulus that varies across the thickness of FGM plate at any temperature T and is calculated using Eq. (3), and \({\upnu }\) is the Poisson’s ratio that is assumed to be constant through the thickness of FGM plate.

3.3.2 Thermo-Elasto-Plastic Constitutive Relations

The elastic–plastic analysis is carried out under the assumption of von-Mises yielding criterion, and a uniform expansion is assumed to be followed by the yield surface in the stress space with increasing plastic deformation (Hill 1998). The yield function can be expressed as:

$$f = \sqrt {3J_{2} } - \sigma_{Yield} ,$$
(16)

where,

$$J_{2} = \frac{1}{6}\left[ {\left( {\sigma_{x} - \sigma_{y} } \right)^{2} + \left( {\sigma_{y} - \sigma_{z} } \right)^{2} + \left( {\sigma_{x} - \sigma_{z} } \right)^{2} + 6\left( {\tau_{xy}^{2} + \tau_{yz}^{2} + \tau_{xz}^{2} } \right)} \right].$$
(17)

Under the strain hardening effect, the initial yield surface expands with plastic deformation, and the equation of yield surface for thermo-elasto-plastic deformation can be written as:

$$f = f\left( {\sigma ,\kappa ,T} \right),$$
(18)

wherein, \(\kappa\) and T are the strain hardening parameter and temperature, respectively.

Using chain rule to differentiate \(f\):

$$df = \left( {\frac{\partial f}{{\partial \sigma }}} \right)^{T} d\sigma + \frac{\partial f}{{\partial \kappa }}d\kappa + \frac{\partial f}{{\partial T}}dT.$$
(19)

As hardening parameter (\(\kappa\)) is a function of plastic strain (\(\varepsilon_{p}\)), Eq. (19) can be rewritten as:

$$df = \left( {\frac{\partial f}{{\partial \sigma }}} \right)^{T} d\sigma + \frac{\partial f}{{\partial \kappa }}\left( {\frac{\partial \kappa }{{\partial \varepsilon_{p} }}} \right)d\varepsilon_{p} + \frac{\partial f}{{\partial T}}dT.$$
(20)

The equilibrium conditions under small incremental plastic deformations are maintained only if the plastic strain energy is put equal to zero; hence, we have:

$$df = \left( {\frac{\partial f}{{\partial \sigma }}} \right)^{T} d\sigma + \frac{\partial f}{{\partial \kappa }}\left( {\frac{\partial \kappa }{{\partial \varepsilon_{p} }}} \right)d\varepsilon_{p} + \frac{\partial f}{{\partial T}}dT = 0.$$
(21)

Now the total incremental strain includes the incremental parts of elastic strain (\({\Delta }\varepsilon_{e}\)), thermal strain (\({\Delta }\varepsilon_{T}\)), strain due to temperature-dependent material properties \(\left( {{\Delta }\varepsilon_{TD} } \right)\), and the plastic strain \(\left( {{\Delta }\varepsilon_{p} } \right)\), i.e.,

$${\Delta }\varepsilon = {\Delta }\varepsilon_{e} + {\Delta }\varepsilon_{T} + {\Delta }\varepsilon_{TD} + {\Delta }\varepsilon_{p} .$$
(22)

Using Hooke’s law, to calculate the total incremental stress (\({\Delta }\sigma\))

$${\Delta }\sigma = \left[ D \right]\left\{ {{\Delta }\varepsilon - \left( {{\Delta }\varepsilon_{T} + {\Delta }\varepsilon_{TD} + {\Delta }\varepsilon_{p} } \right)} \right\}.$$
(23)

Putting the value of total incremental stress (\(d\sigma\)) into Eq. (21), we get

$$\begin{aligned} df & = \left( {\frac{\partial f}{{\partial \sigma }}} \right)^{T} \left[ D \right]\left\{ {{\Delta }\varepsilon - \left( {{\Delta }\varepsilon_{T} + {\Delta }\varepsilon_{TD} + {\Delta }\varepsilon_{p} } \right)} \right\}\\ &\quad + \frac{\partial f}{{\partial \kappa }}\left( {\frac{\partial \kappa }{{\partial \varepsilon_{p} }}} \right){\Delta }\varepsilon_{p} + \frac{\partial f}{{\partial T}}{\Delta }T = 0. \end{aligned}$$
(24)

In the associative flow rule of plasticity, the plastic potential function is taken same as the yield function (Chakrabarty 2012) by which the incremental plastic strain can be written as:

$$\Delta \varepsilon_{p} = d\lambda \frac{\partial f}{{\partial \sigma }}.$$
(25)

The thermal strain (\({\Delta }\varepsilon_{T}\)) and the strain due to temperature-dependent material properties \(\left( {{\Delta }\varepsilon_{TD} } \right)\) can be written as:

$$\Delta \varepsilon_{T} = \alpha \Delta T, \quad and\quad \Delta \varepsilon_{TD} = \frac{{\partial \left[ D \right]^{ - 1} }}{\partial T}\sigma \Delta T.$$
(26)

Let,

$$\left( {\frac{\partial f}{{\partial \sigma }}} \right)^{T} \left[ D \right]\left( {\frac{\partial f}{{\partial \sigma }}} \right) - \frac{\partial f}{{\partial k}}\left( {\frac{\partial k}{{\partial \varepsilon_{p} }}} \right)^{T} \left( {\frac{\partial f}{{\partial \sigma }}} \right) = \eta^{i} .$$
(27)

Substituting Eqs. (25)–(27) into Eq. (24), to obtain the flow variable \(d\lambda\) as:

$$d\lambda = \left[ {\frac{{\left( {\frac{\partial f}{{\partial \sigma }}} \right)^{T} \left[ D \right]\left\{ {{\Delta }\varepsilon - \left( {\alpha {\Delta }T + \frac{{\partial \left[ D \right]^{ - 1} }}{\partial T}\sigma {\Delta }T} \right)} \right\} + \frac{\partial f}{{\partial T}}{\Delta }T}}{{\eta^{i} }}} \right]$$
(28)

The expression for incremental stress \({\Delta }\sigma\) can be evaluated inserting Eqs. (24)–(28) into Eq. (23) as:

$$\begin{aligned} \Delta \sigma & = \left[ D \right]\left[ {\left( {\Delta \varepsilon } \right) - \left( {\alpha dT + \frac{{\partial \left[ D \right]^{ - 1} }}{\partial T}\sigma dT} \right)} \right] \\ & \quad - \left[ D \right]\frac{\partial f}{{\partial \sigma }}\left[ {\frac{{\left( {\frac{\partial f}{{\partial \sigma }}} \right)^{T} \left[ D \right]\left\{ {\Delta \varepsilon - \left( {\alpha dT + \frac{{\partial \left[ D \right]^{ - 1} }}{\partial T}\sigma dT} \right)} \right\} + \frac{\partial f}{{\partial T}}dT}}{{\eta^{i} }}} \right] \\ \end{aligned}$$
(29)

Rearranging Eq. (29) to obtain:

$$\begin{aligned} \Delta \sigma & = \left[ {\left[ D \right] - \frac{1}{{\eta^{i} }}\left[ D \right]\frac{\partial f}{{\partial \sigma }}\left( {\frac{\partial f}{{\partial \sigma }}} \right)^{T} \left[ D \right]} \right]\left[ {\left( {\Delta \varepsilon } \right) - \left( {\alpha \Delta T + \frac{{\partial \left[ D \right]^{ - 1} }}{\partial T}\sigma \Delta T} \right)} \right] \\ & \quad - \frac{1}{{\eta^{i} }}\left[ D \right]\frac{\partial f}{{\partial \sigma }}\frac{\partial f}{{\partial T}}\Delta T. \\ \end{aligned}$$
(30)

The term \(\left[ {\left[ D \right] - \frac{1}{{\eta^{i} }}\left[ D \right]\frac{\partial f}{{\partial \sigma }}\left( {\frac{\partial f}{{\partial \sigma }}} \right)^{T} \left[ D \right]} \right]\) in Eq. (30) is the elasto-plastic constitutive matrix \(\left[ {D_{ep} } \right]^{i}\), that establishes the thermo-elasto-plastic constitutive relationship as follows:

$${\Delta }\sigma = \left[ {D_{ep} } \right]^{i} \left\{ {{\Delta }\varepsilon^{{\prime}} } \right\}$$
(31)
$${\Delta }\varepsilon^{{\prime}} = \left( {{\Delta }\varepsilon } \right) - \left( {{\Delta }\varepsilon^{t} } \right)$$
(32)
$${\Delta }\varepsilon^{t} = \alpha {\Delta }T + \frac{{\partial \left[ D \right]^{ - 1} }}{\partial T}\sigma {\Delta }T + \frac{1}{{\eta^{i} }}\left[ D \right]\left[ {D_{ep} } \right]^{ - 1} \frac{\partial f}{{\partial \sigma }}\frac{\partial f}{{\partial T}}{\Delta }T$$
(33)

3.4 Non-linear FEM Formulation for Thermo-Elastic–Plastic Analysis

The procedure to derive the finite element equations for thermo-elastic–plastic analysis of FGM plate is presented in this section. The incremental displacement vector (\(\Delta \overline{u}^{e}\)) within an element is interpolated as:

$$\Delta \overline{u}^{e} = N\Delta \overline{a},$$
(34)

where, \(\Delta \overline{a}\) is the incremental nodal displacement vector and \(N\) is the interpolation functions. The incremental strain tensor (\(\Delta \varepsilon\)) is expressed in the terms of incremental nodal displacement vector (\(\Delta \overline{a}\)) and strain–displacement matrix (B), as

$${\Delta }\varepsilon = B{\Delta }\overline{a},$$
(35)

the incremental strain energy (\({\Delta }U\)) may be written as

$$\Delta U = \frac{1}{2}\mathop \int \limits_{V} \Delta \varepsilon^{\prime T} \Delta \sigma dV,$$
(36)

using Eqs. (31), (32) and (35), to rewrite Eq. (36) in the following form:

$$\begin{aligned} \Delta U & = \frac{1}{2}\Delta \overline{a}^{T} \mathop \int \limits_{V} B^{T} \left[ {D_{ep} } \right]^{i} B\overline{\Delta a} dV - \Delta \overline{a}^{T} \mathop \int \limits_{V} B^{T} \left[ {D_{ep} } \right]^{i} \Delta \varepsilon^{t} dV \\ & \quad + \frac{1}{2}\mathop \int \limits_{V} \Delta \varepsilon^{t} \left[ {D_{ep} } \right]^{i} \Delta \varepsilon^{t} dV, \\ \end{aligned}$$
(37)

The incremental external work (\({\Delta }W_{ex}\)) due to incremental tractions at plate surfaces (i.e., \(z = \pm h/2\)) and plate edges can be written as:

$${\Delta }W_{ex} = {\Delta }a^{T} \mathop \int \limits_{A} N^{T} \overbrace {\Delta P}\,dA + {\Delta }a^{T} \mathop \int \limits_{s} N^{T} \overbrace {{\Delta P_{e} }}\,ds,$$
(38)

where,

$$\overbrace {\Delta P} = \left[ {\begin{array}{*{20}c} {\Delta P_{x} } & {\Delta P_{y} } & {\Delta \begin{array}{*{20}c} {P_{z} } & {\overline{\Delta M}_{x} } & {\overline{\Delta M}_{y} } \\ \end{array} } \\ \end{array} } \right]^{T} ,$$
(39)

and, the edge forces are given by

$$\begin{aligned} \overbrace {{\Delta P_{e} }} & = \left[ {\begin{array}{*{20}c} {\overline{\Delta P}_{x}^{e} } & {\overline{\Delta P}_{y}^{e} } & {\Delta \begin{array}{*{20}c} {\overline{P}_{z}^{e} } & {\overline{\Delta M}_{x}^{e} } & {\overline{\Delta M}_{y}^{e} } \\ \end{array} } \\ \end{array} } \right]^{T} \\ & = \mathop \int \limits_{h/2}^{h/2} \left[ {\left( {\begin{array}{*{20}c} {\Delta P_{x}^{e} } & {\Delta P_{y}^{e} } & {\begin{array}{*{20}c} {\Delta P_{z}^{e} } & {\Delta M_{x}^{e} } & {\Delta M_{y}^{e} } \\ \end{array} } \\ \end{array} } \right)dz} \right]^{T} \\ \end{aligned}$$
(40)

The associated equilibrium equation is obtained by applying the principle of variation over the functional (\(\Delta {\Pi } = \Delta U - \Delta W_{ex}\)) with respect to the incremental displacement (\(\Delta a\)), as:

$$\frac{{\partial \left( {\Delta {\Pi }} \right)}}{{\partial \left( {\Delta \overline{a}} \right)}} = \frac{{\partial \left( {{\Delta }U - \Delta W_{ex} } \right)}}{{\partial \left( {\Delta \overline{a}} \right)}} = 0$$
(41)

Using Eqs. (37) and (38) into Eq. (41) to get the equilibrium equation:

$$\begin{aligned} & \left( {\mathop \int \limits_{V} B^{T} \left[ {D_{ep} } \right]^{i} BdV} \right)\Delta \overline{a} - \mathop \int \limits_{V} B^{T} \left[ {D_{ep} } \right]^{i} \Delta \varepsilon^{t} dV \\ &\quad - \mathop \int \limits_{A} N^{T} \overbrace {\Delta P}\,dA - \mathop \int \limits_{s} N^{T} \overbrace {{\Delta P_{e} }}\,ds = 0. \end{aligned}$$
(42)

Value of \({\Delta }\varepsilon^{t}\) is substituted from Eq. (33) to rewrite Eq. (42) in the following manner:

$$\begin{aligned} & \left( {\mathop \int \limits_{V} B^{T} \left[ {D_{ep} } \right]^{i} BdV} \right){\Delta }\overline{a} - \mathop \int \limits_{V} B^{T} \left[ {D_{ep} } \right]^{i} \\ & \quad \times \left\{ {\alpha \Delta T + \frac{{\partial \left[ D \right]^{ - 1} }}{\partial T}\sigma \Delta T + \frac{1}{{\eta^{i} }}\left[ D \right]\left[ {D_{ep} } \right]^{ - 1} \frac{\partial f}{{\partial \sigma }}\frac{\partial f}{{\partial T}}\Delta T} \right\}dV \\ & \quad - \mathop \int \limits_{A} N^{T} \overbrace {\Delta P}\,dA - \mathop \int \limits_{s} N^{T} \overbrace {{\Delta P_{e} }}\,ds = 0. \\ \end{aligned}$$
(43)

Finally, the set of nonlinear algebraic equations is obtained in the following marix form:

$$\left[ K \right]\Delta \overline{a} = \Delta R,$$
(44)

where, \(\left[ K \right]\) is the structural stiffness matrix given by:

$$\left[ K \right] = \mathop \int \limits_{V} B^{T} \left[ {D_{ep} } \right]^{i} BdV,$$
(45)

In Eq. (44), \(\Delta R\) represents combined thermomechanical incremental load vector due to mechanical loading \(\left( {{\Delta }R_{M} } \right)\) and thermal loading \(\left( {{\Delta }R_{T} } \right)\), i.e.,

$${\Delta }R = {\Delta }R_{M} + {\Delta }R_{T} ,\quad {\text{having}}$$
(46)
$${\Delta }R_{M} = \mathop \int \limits_{A} N^{T} \overbrace {{{\Delta }P}}\,dA + \mathop \int \limits_{s} N^{T} \overbrace {{{\Delta }P_{e} }}\,ds,$$
(47)

and

$$\Delta R_{T} = \mathop \int \limits_{V} B^{T} \left[ {D_{ep} } \right]^{i} \left( {\alpha \Delta T + \frac{{\partial \left[ D \right]^{ - 1} }}{\partial T}\sigma \Delta T + \frac{1}{{\eta^{i} }}\left[ D \right]\left\{ {[D_{ep} ]^{i} } \right\}^{ - 1} \frac{\partial f}{{\partial \sigma }}\frac{\partial f}{{\partial T}}\Delta T} \right)dV$$
(48)

The solution for nonlinear algebraic equations posted in Eq. (44) is obtained using Newton–Raphson iterative solution technique. Newton–Raphson solution technique is based on Taylor’s series expansion, and it is convenient to rewrite Eq. (44) as:

$$\psi \left\{ \delta \right\} = \left[ {K\left( \delta \right)} \right]\left\{ \delta \right\} - \Delta R,$$
(49)

where, \(\psi\) is the residual force and \(\left[ {K\left( \delta \right)} \right]\) is structural stiffness matrix, which is a function of unknown deflection \(\delta\). If for an initial estimate of the displacement vector \(\left\{ \delta \right\}_{i}\) (i.e., for ith iteration) we obtain residual forces \(\psi \left\{ \delta \right\}_{i} \ne 0\), then an improved solution \(\left\{ \delta \right\}_{i + 1}\) is obtained by equating the linearized Taylor’s series expansion of \(\psi \left\{ \delta \right\}_{i + 1}\) in the neighborhood of \(\left\{ \delta \right\}_{i}\) to zero, as below:

$$\psi \left\{ \delta \right\}_{i + 1} \cong \psi \left\{ \delta \right\}_{i} + K_{T } \Delta \left\{ \delta \right\}_{i} = 0,$$
(50)

where, \(\Delta \left\{ \delta \right\}_{i}\) is the incremental displacement vector, and KT is the tangent stiffness matrix evaluated at \(\left\{ \delta \right\}_{i}\) and is given by:

$$K_{T} = \left[ {\frac{{\partial \psi \left\{ \delta \right\}_{i} }}{\partial \left[ \delta \right]}} \right].$$
(51)

The improved solution is then obtained as:

$$\left\{ \delta \right\}_{i + 1} = \left\{ \delta \right\}_{i} + {\Delta }\left\{ \delta \right\}_{i} .$$
(52)

To improve on the numerical stability and convergence of the solution, the load is applied in small increments. The iterative solution is continued until the following convergence criterion is satisfied.

$$\delta_{i + 1} - \delta_{i} \le \beta ,$$
(53)

where,\(\beta\) is sufficiently small number, i.e., 0.005%.

3.5 Ultimate Load Capacity of FGM Plate

An FEM based strategy that is followed by many authors in the literature (Narayanan and Chow 1984; Shanmugam et al. 1999; El-Sawy and Martini 2004; Paik 2005; Ghavami and Khedmati 2006; Estefen et al. 2016) to predict the ultimate load capacity of elastic–plastic homogeneous isotropic plates is extended to predict ultimate load capacity of elastic–plastic FGM plate. To get the ultimate load carrying capacity of FGM plate, the plate is subjected to the in-plane compressive load in an incremental manner that initially produces recoverable elastic stress and strain. However, a large value of load causes yielding in FGM plate which is followed by recoverable elastic strains as well as irrecoverable plastic strains. As the load further increases, beyond a particular value of load the proportion of plastic strain reaches to an extent where the plate completely loss of its stiffness resulting in the complete collapse and hence, ultimate failure of the FGM plate; the corresponding load is termed as ultimate load capacity. It is noteworthy that in the present elastic–plastic analysis the load is applied in small incremental load steps to ensure that the analysis closely follows the actual load-response curve of FGM plate.

3.6 Computer Implementation

A general purpose finite element package ANSYS® (Ansys Inc 2014) [by encrypting a macro in APDL (i.e., ANSYS Parametric Design Language)] was utilized to implement the formulation and perform thermomechanical elastic–plastic buckling, postbuckling and failure analysis of FGM plate, with temperature-dependent material properties.

The layerwise elastic–plastic FGM plate is modeled using eight-noded shell element, wherein the thermo-elastic–plastic analysis of FGM plate is carried out in two stages. In the first stage the linear buckling analysis is conducted to obtain the critical buckling load and corresponding mode shape of the FGM plate. The linear analysis is followed by nonlinear incremental procedure in which the load is applied gradually in small increments and the corresponding deformation is obtained by updating the temperature-dependent material properties at each load step. It is evident that some sort of imperfection must be introduced into the perfect geometry of the plate to trace its postbuckling response, without any numerical issues, using incremental finite element analysis (Barbero 2013). In the present analysis, the bifurcation buckling in the FGM plate is initiated by superimposing the imperfection equal to b/1000 (where, b represents width of the plate) and of the form corresponding to the first buckling mode shape.

4 Elastic–Plastic Analysis of FGM Plate

The aim of this section is to present the findings, reported by the authors (Sharma and Kumar, 2017b), obtained by the application of the developed computational model to investigate the thermo-elastic–plastic respose of Ni/Al2O3 FGM plate under in-plane compressive loading conditions..

The thermoelastic material properties as well as elastic–plastic strength parameters of FGM plate are taken as non-linear function of temperature, as defined by Eq. (1). Temperature-dependent coefficients for calculating the thermo-elastic properties of Al2O3 and Ni are given in Table 1, whereas the elastic–plastic strength coefficients to evaluate yield strength and tangent modulus of metallic phase (i.e., Ni) are given in Table 2. The thermoelastic and elastic–plastic material properties of FGM plate are calculated using rule of mixtures and TTO model, respectively, as discussed in Sect. 2.

Numerical studies are conducted to examine the effects of material, geometrical, and loading parameters on the thermo-elastic–plastic response of FGM plate, and the results are presented in the following form as:

  • Non-dimensional applied load, \({\Lambda } = \frac{{N_{{{\text{x }}\left( {{\text{or }}y} \right)}} {\text{ b}}^{2} }}{{E_{{\text{m}}} {\text{h}}^{3} }}\);

  • Non-dimensionalized maximum transverse deflection, \(\overline{w} = \frac{{w_{{{\text{max}}}} }}{{\text{h}}}\);

  • Magnitude of maximum plastic strain, \(\left( {\varepsilon_{p} } \right)_{eq} = \left( {\frac{2}{3}\varepsilon_{p}{:}\,\varepsilon_{p} } \right)^{1/2}\).

where, \(E_{{\text{c}}}\) is the Young’s modulus of ceramic; \(h\) represents the thickness of FGM plate; \(b\) is the width of plate; \(N_{{x \left( {or y} \right)}}\) is the in-plane compressive load in x- direction (or y-direction) per unit edge length, applied at x = a (or y = b); \(w_{{{\text{max}}}}\) is the maximum transverse deflection, and \(\varepsilon_{p} :\varepsilon_{p}\) is the scalar product of the plastic strain tensor corresponding to failure point (Fig. 3).

Fig. 3
figure 3

In-plane boundary conditions for a simply-supported (i.e., w = 0 on all edges) FGM plate

Full size image

The postbuckling and failure response of both elastic and elastic–plastic simply-supported FGM (for power law exponent, n = 1) square plate (of side 1 m) with b/h = 100 having temperature-dependent (TD) material properties under various thermomechanical loading conditions are shown in Fig. 4. The corresponding values of yield and failure loads are also marked in the Fig. 4 for the elastic–plastic case. It is to mention here that the yielding point on a particular load–deflection curve corresponds to the minimum value of the load at which elastic to plastic transition of the metallic phase present anywhere in the FGM takes place, whereas the failure point corresponds to the load at which the FGM plate completely losses its stiffness due to excessive plasticity.

Fig. 4
figure 4

Buckling and postbuckling response for elastic and elastic–plastic FGM plate under different thermomechanical loadings

Full size image

It can be observed from the results that irrespective of thermal load, the postbuckling response of FGM plate is significantly affected by the consideration of plasticity and the elastic–plastic FGM plate depicts decrease in the postbuckling strength followed by the ultimate failure.

Morover, the effect of material property variation and temperature rise on the buckling and postbuckling behaviors of an elastic–plastic FGM plate subjected to uni-axial mechanical compressive loading combined with different thermal load values (i.e., \(\Delta T = 25,\,50\,{\text{and}}\, 100\,^{ \circ } {\text{C}})\) is also examined and the corresponding postbuckling paths are shown in Fig. 4. It is to mention here that different material gradation profiles across the thickness of FGM plate are obtained by changing the value of power law exponent n (i.e., 1, 2 and 3) in Eq. (2).

As depicted in Fig. 5, the postbuckling strength of FGM plate (at a specific value of maximum transverse deflection) decreases considerably with increasing temperature rise. It is also noteworthy that the effect of temperature rise is to increase the rate of plastic flow (as observed subsequently in Fig. 6) which leads to ultimate failure of FGM plate at a relatively lower value of mechanical load. Figure 4 also shows that irrespective of temperature rise, the ultimate load carrying capacity of FGM plate increases with the increase in value of power law index that can be attributed to the higher proportion of ceramic (i.e., Al2O3), possessing higher resistance towards buckling failure.

Fig. 5
figure 5

Nonlinear buckling, postbuckling and failure reasponse of elastic–plastic FGM plate with different value of power law exponent (n) under thermomechanical loading

Full size image
Fig. 6
figure 6

Varition in the equivalent plastic strain across the thickness of FGM plate with different power law exponents (i.e., n) under thermomechancial loading

Full size image

Furthermore, the effect of material gradation profile on the equivalent plastic strain across the thickness of FGM plate at a particular value (taken equal to the failure load for FGM with n = 1) of thermomechanical loading is shown in Fig. 6. The flow of plasticity in FGM plate for a particular value of n, is found to be more dominating at the upper region (with higher metal proportion) in comparison to the lower part (with higher ceramic proportion).

Moreover, at a particular value of thickness, the plasticity effect is more pronounced in the case of FGM plate with n = 1. It is again demonstrated in Fig. 6 that the effect of higher temperature is to provoke more plasticity effects in the FGM plate.

The postbuckling paths for elastic–plastic FGM plate (n = 1) subjected to uni-axial and biaxial loading with different load ratios (i.e., Ny/Nx) under uniform temperature rise (i.e., \(\Delta T\)) are depicted in Fig. 7. It can be observed from Fig. 7 that irrespective of the value of temperature rise, the maximum buckling load, postbuckling strength (for a particular value of deflection) and failure load are obtained for FGM plate under uni-axial compression (i.e., for \(N_{y} /N_{x} = 0\)), and with the addition of compressive load in y-direction, the values of buckling load, postbuckling strength (for a particular value of deflection) and failure load decrease.

Fig. 7
figure 7

Effect of loading on elastic–plastic buckling and postbuckling behavior of FGM (for n = 1) plate under thermomechanical loading (Sharma and Kumar 2017b)

Full size image

5 Conclusions

A mathematical formulation for elastic–plastic buckling and postbuckling analysis of FGM plate with temperature-dependent material properties is presented. A layer-wise modeling approach of FGM plate is used, wherein the graded thermoelastic material properties of FGM plate are assumed to be governed by the rule of mixtures and TTO model, whereas the elastic–plastic material characteristics (i.e., yielding strength and tangent modulus) are varied as per the TTO model.

The governing equations for elastic–plastic FGM plate are developed using variational principle. Subsequently, the nonlinear finite element formulation based on the first-order shear deformation theory and the von Karman’s nonlinear kinematics is presented. The incremental solution algorithm based on Newton–Raphson method is used to solve the resulting nonlinear algebraic equations. A computer implementation, through ANSYS®, of the formulation is also presented to carry out the analysis. Thereafter, a study on elastic–plastic analysis of FGM plate under in-plane compression caused by the mechanical loading combined with uniform and constant temperature rise is conducted. The effects of plasticity, material inhomogenity, and thermomechanical loading on elastic–plastic buckling, postbuckling behavior and ultimate load capacity of FGM plate are analyzed under the framework of J2 deformation theory associated with the isotropic hardening flow rule.

Based on the study, the following important conclusions are drawn:

  • Postbuckling response of FGM plate is found to be greatly affected by the plasticity consideration. FGM plate with elastic material properties exhibits a continous increase in the postbuckling strength; whereas, the postbuckling strength of an elastic–plastic FGM plate decreases initially and finally, ultimate failure occurs.

  • Along the thickness of FGM plate, the effect of plastic flow is observed to be more dominating in the metal rich region of FGM plate than the ceramic rich region.

  • Effect of rise in temperature difference (i.e., \(\Delta T\)) is to develop more plastic strain, irrespective of the value of material gradation index n and the mechanical loading condition.

  • Buckling load and postbuckling strength of elastic–plastic FGM plate are found to be significantly affected by its material gradation profile; an FGM plate with higher ceramic proportion depicted higher buckling load and postbuckling strength.

  • Effect of bi-axial loading is to reduce the buckling load, postbuckling strength (for a particular value of deflection), and failure loads, for all values of temperature difference.