Oscillation-Preserving Integrators for Highly Oscillatory Systems of Second-Order ODEs

Abstract

In this chapter, from the point of view of Geometric Integration, i.e. the numerical solution of differential equations using integrators that preserve as many as possible the geometric/physical properties of them, we first introduce the concept of oscillation preservation for Runge–Kutta–Nyström (RKN)-type methods and then analyse the oscillation-preserving behaviour of RKN-type methods in detail. This chapter is also accompanied by numerical experiments which show the importance of the oscillation-preserving property for a numerical method, and the remarkable superiority of oscillation-preserving integrators for solving nonlinear multi-frequency highly oscillatory systems.

In this chapter, from the point of view of Geometric Integration, i.e. the numerical solution of differential equations using integrators that preserve as many as possible the geometric/physical properties of them, we first introduce the concept of oscillation preservation for Runge–Kutta–Nyström (RKN)-type methods and then analyse the oscillation-preserving behaviour of RKN-type methods in detail. This chapter is also accompanied by numerical experiments which show the importance of the oscillation-preserving property for a numerical method, and the remarkable superiority of oscillation-preserving integrators for solving nonlinear multi-frequency highly oscillatory systems.

1.1 Introduction

This chapter focuses on oscillation-preserving integrators for ordinary differential equations and time-integration of partial differential equations with highly oscillatory solutions. As is known, one of the most difficult problems in the numerical simulation of evolutionary problems is to deal with highly oscillatory problems, and here we refer to two important review articles on this subject by Petzold et al. [1] and Cohen et al. [2]. These type of problems occur in a variety of fields in science and engineering such as quantum physics, fluid dynamics, acoustics, celestial mechanics and molecular dynamics, including the semidiscretisation of nonlinear wave equations and Klein–Gordon (KG) equations. The computation of highly oscillatory problems contains numerous enduring challenges (see, e.g. [1,2,3,4,5,6,7,8]). It is important to note that standard methods need a very small stepsize and hence a long runtime to reach an acceptable accuracy for highly oscillatory differential equations. In this chapter, we focus on the following initial value problem of nonlinear multi-frequency highly oscillatory second-order ordinary differential equations

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &y''+My=f(y,y'),\quad t\in[0,T],\\ &y(0)=y_0,\quad y'(0)=y^{\prime}_0, \end{aligned} \right. \end{aligned} $$

(1.1)

where $y\in \mathbb {R}^d$, and $M\in \mathbb {R}^{d\times d}$ is a positive semi-definite matrix that implicitly contains the dominant frequencies of the highly oscillatory problem and $\|M\|\gg \max \left \{1,\left \|\dfrac {\partial f}{\partial y}\right \|\right \}$. In some applications, the dimension d of the matrix M refers to the number of degrees of freedom in the space semidiscretisation such as semilinear wave equations, and then ∥M∥ will tend to infinity as finer space semi-discretisations are carried out. Among typical examples of this type are semi-discretised KG equations (see, e.g. [9,10,11]).

In the case where M = 0, (1.1) reduces to the conventional initial value problem of second-order differential equations

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &y''=f(y,y'),\quad t\in[0,T],\\ &y(0)=y_0,\quad y'(0)=y^{\prime}_0. \end{aligned} \right. \end{aligned} $$

(1.2)

As is known, the standard RKN methods (see [12]) are very popular for solving (1.2). However, it may be believed that the standard RKN methods were not initially designed for the nonlinear multi-frequency highly oscillatory system (1.1). The standard RKN methods, including symplectic and symmetric RKN methods may result in unfavorable numerical behaviour when applied to highly oscillatory systems (see, e.g. [10, 13]). As a result, various RKN-type methods for solving highly oscillatory differential equations have received a lot of attention (see, e.g. [1, 2, 6, 8, 11, 13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]).

In designing numerical integrators for efficiently solving (1.1), the so-called matrix-variation-of-constants formula plays an important role, which is summarised as follows:

Theorem 1.1 (Wu et al. [25])

If $M\in \mathbb {R}^{d\times d}$ is a positive semi-definite matrix and $f:\mathbb {R}^{d}\times \mathbb {R}^{d}\rightarrow \mathbb {R}^{d}$ in (1.1) is continuous, then the exact solution of (1.1) and its derivative satisfy the following formula

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} y(t)= &\phi_0\big(t^2M\big)y_0+t\phi_1\big(t^2M\big)y_0^{\prime} +\intop\nolimits_{0}^{t}(t-\tau)\phi_1\big((t-\tau)^2M\big)\hat f(\tau)\mathrm{d}\tau,\\ y^{\prime}(t) = &-tM\phi_1\big(t^2M\big)y_0+\phi_0\big(t^2M\big)y_0^{\prime} +\intop\nolimits_{0}^{t}\phi_0\big((t-\tau)^2M\big)\hat f(\tau)\mathrm{d}\tau,\\ \end{aligned}\right. {} \end{aligned} $$

(1.3)

for t ∈ [0, T], where

$$\displaystyle \begin{aligned}\hat{f} (\tau)=f\big(y(\tau), y'(\tau)\big)\end{aligned}$$

and the matrix-valued functions ϕ ₀(V ) and ϕ ₁(V ) of $V\in \mathbb {R}^{d\times d}$ are defined by

$$\displaystyle \begin{aligned} \phi_{i}(V)&=\sum_{k=0}^{\infty}\dfrac{(-1)^{k}V^{k}}{(2k+i)!}, \end{aligned} $$

(1.4)

for i = 0, 1, 2, ⋯ .

Remark 1.1

Actually, the matrix-variation-of-constants formula (1.3) provides an implicit expression of the solution of the nonlinear multi-frequency highly oscillatory system (1.1), which gives a valuable insight into the underlying highly oscillatory solution. The formula (1.3) also makes it possible to gain a new insight into the standard RKN methods for (1.2) (see Sect. 1.2 for details).

If f(y, y′) = 0, (1.3) yields

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} y(t)= &\phi_0\big(t^2M\big)y_0+t\phi_1\big(t^2M\big)y_0^{\prime} ,\\ y^{\prime}(t) = &-tM\phi_1\big(t^2M\big)y_0+\phi_0\big(t^2M\big)y_0^{\prime} ,\\ \end{aligned}\right. {} \end{aligned} $$

(1.5)

which exactly solves the system of multi-frequency highly oscillatory linear homogeneous equations

$$\displaystyle \begin{aligned} \left\{\begin{aligned}&y''+My=0,\\ &y(0)=y_0,\quad y'(0)=y^{\prime}_0,\end{aligned}\right.\end{aligned} $$

(1.6)

associated with the nonlinear highly oscillatory system (1.1).

Assume that both y(t _n) and y ^′(t _n) at t = t _n ∈ [0, T] are prescribed, it follows from the formula (1.3) that

$$\displaystyle \begin{aligned}\left\{\begin{aligned} y(t_{n}+\mu h)=&~\phi_0(\mu^2V)y(t_{n})\\&+\mu h\phi_1(\mu^2V)y'(t_{n})+h^2\intop\nolimits_0^\mu (\mu-\zeta)\phi_1\big((\mu-\zeta)^2V\big)\hat f\big(t_{n}+\zeta h\big)\,\mathrm{d}\zeta,\\ y'(t_{n}+\mu h)=&-\mu hM\phi_1(\mu^2V)y(t_{n}) \\&+\phi_0(\mu^2V)y'(t_{n})+h\intop\nolimits_0^\mu\phi_0\big((\mu-\zeta)^2V\big)\hat f\big(t_{n}+\zeta h\big)\,\mathrm{d}\zeta, \end{aligned} \right. \end{aligned} $$

(1.7)

where V = h ² M and $0<\mu \leqslant 1$. The special case where μ = 1 in (1.7) gives

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &y(t_n+h)=\phi_0(V)y(t_n)+h\phi_1(V)y^{\prime}(t_n)+ h^2\intop\nolimits_{0}^1(1-z)\phi_1\big((1-z)^2V\big)\hat f(t_n+hz)\mathrm{d}z,\\ &y^{\prime}(t_n+h)=-hM\phi_1(V)y(t_n)+\phi_0(V)y^{\prime}(t_n) +h\intop\nolimits_{0}^{1}\phi_0\big((1-z)^2V\big)\hat f(t_n+hz)\mathrm{d}z.\\ \end{aligned}\right. {} \end{aligned} $$

(1.8)

Remark 1.2

We here remark that since the formula (1.3) is an implicit expression of the solution of the nonlinear multi-frequency highly oscillatory system (1.1), the formula (1.7) with 0 < μ < 1 exposes the structure of the internal stages, and (1.8) expresses the structure of the updates in the design of an RKN-type integrator specially for solving the nonlinear multi-frequency highly oscillatory system (1.1).

In applications, an important special case of (1.1) is that the right-hand side function f does not depend on y′, i.e.,

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &y''+My=f(y),\quad t\in[0,T],\\ &y(0)=y_0,\quad y'(0)=y^{\prime}_0. \end{aligned} \right. \end{aligned} $$

(1.9)

The case where M = 0 in (1.9) gives

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &y''=f(y),\quad t\in[0,T],\\ &y(0)=y_0,\quad y'(0)=y^{\prime}_0. \end{aligned} \right. \end{aligned} $$

(1.10)

Remark 1.3

Here it is important to realise that the matrix-variation-of-constants formula (1.3) is also valid for the nonlinear multi-frequency highly oscillatory system (1.9), and so are the formulae (1.5), (1.7) and (1.8), provided we replace $\hat f(\tau )=f\big (y(\tau ), y'(\tau )\big )$ appearing in (1.3) with $\hat f(\tau )=\hat f\big (y(\tau )\big )$.

Obviously, the formula (1.5) implies that if y _n = y(t _n) and $y^{\prime }_n=y'(t_n)$, then we have

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} y(t_n+c_ih)= &\phi_0\big(c_i^2V\big)y_n+c_ih\phi_1\big(c_i^2V\big)y_n^{\prime} ,\\ y^{\prime}(t_n+c_ih) = &-c_ihM\phi_1\big(c_i^2V\big)y_n+\phi_0\big(c_i^2V\big)y_n^{\prime} ,\\ \end{aligned}\right. {} \end{aligned} $$

(1.11)

for any t _n, t = t _n + c _i h ∈ [0, T], where h > 0 and $0<c_i\leqslant 1$ for i = 1, ⋯ , s.

In what follows, it is convenient to introduce the block vector which will be used in the analysis of oscillation preservation in Sect. 1.4:

$$\displaystyle \begin{aligned}\hat Y=(\hat Y_1^{\intercal},\cdots,\hat Y_s^{\intercal})^{\intercal},\end{aligned} $$

(1.12)

where

$$\displaystyle \begin{aligned}\hat Y_i=y(t_n+c_ih),\end{aligned}$$

express the exact solutions to the multi-frequency highly oscillatory linear homogeneous equation (1.6) at t = t _n + c _i h for i = 1, ⋯ , s. It is clear from (1.11) and (1.12) that $\hat Y$ is a block vector, which can be expressed in the block-matrix notation with Kronecker products as

$$\displaystyle \begin{aligned} \hat Y &= \phi_0(C^2\otimes V)(e\otimes y_{n}) + h(C\otimes I_d)\phi_1(C^2\otimes V)(e\otimes y^{\prime}_n),\\ \end{aligned} $$

(1.13)

where $e=(1,1,\cdots ,1)^{\intercal }$ is an s × 1 vector,

$$\displaystyle \begin{aligned}C=\mathrm{diag}(c_1,\cdots, c_s)\end{aligned}$$

is an s × s diagonal matrix, and the block diagonal matrices are given by

$$\displaystyle \begin{aligned} \phi_0(C^2\otimes V)&=\mathrm{diag}(\phi_0(c_1^2V),\cdots, \phi_0(c_s^2V)),\\ (C\otimes I_d)\phi_1(C^2\otimes V)&=\mathrm{diag}(c_1\phi_1(c_1^2V),\cdots,c_s\phi_1(c_s^2V)). \end{aligned}$$

If t = t _n + h, namely, c _i = 1, the formula (1.11) is identical to

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} y(t_n+h)= &\phi_0\big(V\big)y_n+h\phi_1\big(V\big)y_n^{\prime} ,\\ y^{\prime}(t_n+h) = &-hM\phi_1\big(V\big)y_n+\phi_0\big(V\big)y_n^{\prime}.\\ \end{aligned}\right. {} \end{aligned} $$

(1.14)

Historically, the ARKN methods and ERKN integrators were successively proposed and investigated in order to solve the highly oscillatory system (1.1) and (1.9), respectively. Although both ARKN methods and ERKN integrators were proposed and developed from single frequency to multi-frequency oscillatory problems in chronological order, throughout this chapter we are only interested in nonlinear multi-frequency highly oscillatory systems.

1.2 Standard Runge–Kutta–Nyström Schemes from the Matrix-Variation-of-Constants Formula

It is interesting to point out that the formula (1.7) provides an enlightening approach to standard RKN methods for solving second-order initial value problems (1.2) numerically, although Nyström established them in 1925 (see Nyström [12]). To clarify this, using the matrix-variation-of-constants formula (1.7) with M = 0, we are easily led to the following formulae of integral equations for second-order initial value problems (1.2):

$$\displaystyle \begin{aligned} \left\{\begin{aligned} &y(t_n+\mu h)=y(t_n)+\mu hy'(t_n)+h^2\intop\nolimits_0^\mu (\mu-z)\hat f(t_n+hz)\,\mathrm{d}z,\\ &y'(t_n+\mu h)=y'(t_n)+h\intop\nolimits_0^\mu\hat f(t_n+hz)\,\mathrm{d}z, \end{aligned}\right. \end{aligned} $$

(1.15)

for 0 < μ < 1, and

$$\displaystyle \begin{aligned} \left\{\begin{aligned} &y(t_n+ h)=y(t_n)+ hy'(t_n)+h^2\intop\nolimits_0^1 (1-z)\hat f(t_n+hz)\,\mathrm{d}z,\\ &y'(t_n+ h)=y'(t_n)+h\intop\nolimits_0^1\hat f(t_n+hz)\,\mathrm{d}z, \end{aligned}\right. \end{aligned} $$

(1.16)

for μ = 1, where $\hat f(\nu ):= f\big (y(\nu ),y'(\nu )\big )$.

Clearly, the formulae (1.15) and (1.16) contain and generate the structure of the internal stages and updates of a Runge–Kutta-type integrator for solving (1.2), respectively. This indicates the standard RKN scheme in a quite simple and natural way compared with the original idea (with the block vector $(y^{\intercal },y^{\prime \intercal })^{\intercal }$ regarded as the new variable, (1.2) can be transformed into a system of first-order differential equations of doubled dimension, and then we apply Runge–Kutta methods to the system of first-order differential equations, accompanying some simplifications). Approximating the integrals in (1.15) and (1.16) by using a suitable quadrature formula with nodes c ₁, ⋯ , c _s, we straightforwardly obtain the standard RKN methods (see Nyström [12]) as follows.

Definition 1.1

An s-stage RKN method for the initial value problem (1.2) is defined by

$$\displaystyle \begin{aligned} \left\{ \begin{array}{ll} Y_i=y_n+c_ihy^{\prime}_n+h^2\displaystyle\sum_{j=1}^{s}\bar a_{ij}f(Y_j,Y^{\prime}_j),& i=1,\cdots,s,\\ Y^{\prime}_i=y^{\prime}_n+h\displaystyle\sum_{j=1}^{s}a_{ij}f(Y_j,Y^{\prime}_j),& i=1,\cdots,s,\\ y_{n+1}=y_n+hy^{\prime}_n+h^2\displaystyle\sum_{i=1}^{s}\bar b_i f(Y_i,Y^{\prime}_i),\\ y^{\prime}_{n+1}=y^{\prime}_n+h\displaystyle\sum_{i=1}^{s} b_i f(Y_i,Y^{\prime}_i), \end{array}\right. \end{aligned} $$

(1.17)

where $\bar a_{ij},\ a_{ij},\bar b_i,\ b_i,\ c_i$ for i, j = 1, ⋯ , s are real constants.

The standard RKN method (1.17) also can be expressed in the partitioned Butcher tableau as follows:

where $\bar b=(\bar b_1,\cdots ,\bar b_s)^{\intercal },\ b=(b_1,\cdots ,b_s)^{\intercal }$ and $c=(c_1,\cdots ,c_s)^{\intercal }$ are s-dimensional vectors, and $\bar A=(\bar a_{ij})$ and A = (a _ij) are s × s constant matrices.

1.3 ERKN Integrators and ARKN Methods Based on the Matrix-Variation-of-Constants Formula

The integration of highly oscillatory differential equations has been a challenge for numerical computation for a long time. Much effort has been focused on preserving important high-frequency oscillations. The adapted RKN (ARKN) methods and extended RKN (ERKN) integrators were proposed one after another.

1.3.1 ARKN Integrators

What is the difference between a standard RKN method and an ARKN method for (1.1)? Inheriting the internal stages of standard RKN methods (ignoring the matrix-variation-of-constants formula (1.7)) and approximating the integrals appearing in (1.8) by a suitable quadrature formula with nodes c ₁, ⋯ , c _s to modify only the updates of standard RKN methods yields the ARKN methods for the nonlinear multi-frequency highly oscillatory system (1.1).

Definition 1.2 (Wu et al. [29])

An s-stage ARKN method with stepsize h > 0 for solving the multi-frequency highly oscillatory system (1.1) is defined by

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} & Y_i=y_n+hc_iy^{\prime}_n+h^2\sum_{j=1}^{s}\bar{a}_{ij}\big(f(Y_j,Y^{\prime}_j)-MY_j\big),\qquad i=1,\cdots,s, \\ &Y_i^{\prime}=y_n^{\prime}+h\sum_{j=1}^s a_{ij}\big(f(Y_j,Y^{\prime}_j)-MY_j\big),\qquad \qquad \quad ~\, i=1,\cdots,s,\\ &y_{n+1}=\phi_0(V)y_n+h\phi_1(V)y^{\prime}_n+h^2\sum_{i=1}^s\bar{b}_i(V)f(Y_i,Y^{\prime}_i),\\ &y^{\prime}_{n+1}=-hM\phi_1(V)y_n+\phi_0(V)y^{\prime}_n+h\sum_{i=1}^sb_i(V)f(Y_i,Y^{\prime}_i), \end{aligned}\right. {} \end{aligned} $$

(1.18)

where $\bar {a}_{ij}, a_{ij}, c_i$ for i, j = 1, ⋯ , s are real constants, and $\bar b_{i}(V), b_{i}(V)$ for i = 1, ⋯ , s in the updates are matrix-valued functions of V = h ² M. The ARKN method (1.18) can also be denoted by the partitioned Butcher tableau

In the block-matrix notation with Kronecker products, (1.18) can be expressed as

$$\displaystyle \begin{aligned} \left\{ \begin{aligned}& Y = e\otimes y_{n} + h c\otimes y^{\prime}_n+ h^2(\bar A\otimes I_{d})\big(f(Y,Y')-(I_s\otimes M)Y\big) ,\\ &Y'=e\otimes y^{\prime}_n + h(A\otimes I_{d})\big(f(Y,Y')-(I_s\otimes M)Y\big), \\ &y_{n+1} = \phi_0(V)y_n+h\phi_1(V)y^{\prime}_n+ h^2\bar b^{\intercal}(V)f(Y,Y'),\\ &y^{\prime}_{n+1}= -hM\phi_1(V)y_n+\phi_0(V)y^{\prime}_n+ h b^{\intercal}(V)f(Y,Y'), \end{aligned}\right. \end{aligned} $$

(1.19)

where e is an s × 1 vector of units, and the block vectors involved are defined by

$$\displaystyle \begin{aligned}Y=\big(Y_1^{\intercal},\cdots,Y_s^{\intercal}\big)^{\intercal},\quad Y^{\prime}=\big({Y_{1}^{\prime}}^{\intercal},\cdots,{Y_{s}^{\prime}}^{\intercal}\big)^{\intercal},\end{aligned}$$

$$\displaystyle \begin{aligned} f(Y,Y^{\prime})=\big(f(Y_{1},Y_{1}^{\prime})^{\intercal},\cdots,f(Y_{s},Y_{s}^{\prime})^{\intercal}\big)^{\intercal}.\end{aligned}$$

It is noted again that the internal stages of an ARKN method are the same as those of standard RKN methods, and only its updates have been modified. Concerning single-frequency ARKN methods, readers are referred to [14, 30], and the research on symplectic ARKN methods can be found in [31, 32]. Besides, Franco was the first to attempt to extend his single-frequency ARKN methods in [14] to multi-frequency systems (1.9), but his order conditions are based on single-frequency theory (see [30, 33]).

It is also important to emphasise that the internal stages and the updates for an RKN-type method when applied to (1.1) should play the same role in the approximation based on its matrix-variation-of-constants formula (1.7), and the well-known fact that

$$\displaystyle \begin{aligned}Y_i\approx y(t_n+c_ih),\quad Y^{\prime}_i\approx y'(t_n+c_ih),\end{aligned}$$

for i = 1, ⋯ , s and

$$\displaystyle \begin{aligned}y_{n+1}\approx y(t_{n+1})=y(t_n+h),\quad y^{\prime}_{n+1}\approx y'(t_{n+1})=y'(t_n+h).\end{aligned}$$

Unfortunately, from this point of view, it can be observed from (1.18) that the internal stages of an ARKN method are not put on an equal footing in the light of the matrix-variation-of-constants formula (1.7). This means that the revision or modification of an ARKN method for the multi-frequency highly oscillatory system does not go far enough and is still far from being satisfactory from both a theoretical and practical perspective. This key observation motivates ERKN integrators for the nonlinear multi-frequency highly oscillatory system (1.9), which can also be thought of as improved ARKN methods.

1.3.2 ERKN Integrators

Since we have mentioned that the ARKN method is still not satisfactory due to its internal stages, it is natural to improve both the internal stages and updates of an RKN method in the light of the matrix-variation-of-constants formulae (1.7) and (1.8) with $\hat {f} (\zeta )=f\big (y(\zeta )\big )$. To this end, approximating the integrals appearing in the formulae by using a suitable quadrature formula with nodes c ₁, ⋯ , c _s leads to the following ERKN integrator for the nonlinear multi-frequency highly oscillatory system (1.9).

Definition 1.3 (Wu et al. [25])

An s-stage ERKN integrator for the numerical integration of the nonlinear multi-frequency highly oscillatory system (1.9) with stepsize h > 0 is defined by

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &Y_i=\phi_0(c_i^2 V)y_n+c_ih\phi_1(c_i^2 V)y^{\prime}_n+h^2\sum_{j=1}^{s}\bar a_{ij}(V)f(Y_j), \quad i=1,\cdots,s, \\ &y_{n+1}=\phi_0(V)y_n+h\phi_1(V)y^{\prime}_n+h^2\sum_{i=1}^s\bar{b}_i(V)f(Y_i),\\ &y^{\prime}_{n+1}=-hM\phi_1(V)y_n+\phi_0(V)y^{\prime}_n+h\sum_{i=1}^sb_i(V)f(Y_i), \end{aligned}\right. {} \end{aligned} $$

(1.20)

where c _i for i = 1, ⋯ , s are real constants, b _i(V ), $\bar b_{i}(V)$ for i = 1, ⋯ , s, and $\bar a_{ij}(V)$ for i, j = 1, ⋯ , s are matrix-valued functions of V = h ² M.

The scheme (1.20) can also be denoted by the following partitioned Butcher tableau

It will be convenient to express the equations of (1.20) in block-matrix notation in terms of Kronecker products

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &Y = \phi_0(C^2\otimes V)(e\otimes y_{n}) + h(C\otimes I_d)\phi_1(C^2\otimes V)(e\otimes y^{\prime}_n)+ h^2\bar A(V)f(Y) ,\\ &y_{n+1} = \phi_0(V)y_n+h\phi_1(V)y^{\prime}_n+ h^2\bar b^{\intercal}(V)f(Y),\\ &y^{\prime}_{n+1}= -hM\phi_1(V)y_n+\phi_0(V)y^{\prime}_n+ h b^{\intercal}(V)f(Y), \end{aligned}\right. {} \end{aligned} $$

(1.21)

where $e=(1,1,\cdots ,1)^{\intercal }$ is an s × 1 vector of units, $c=(c_1,\cdots ,c_s)^{\intercal }$ is an s × 1 vector of nodes, C = diag(c ₁, ⋯ , c _s) is an s × s diagonal matrix, and the block vectors and block diagonal matrices are given by

$$\displaystyle \begin{aligned} Y= \begin{bmatrix} Y_{1}\\ \vdots\\ Y_{s} \end{bmatrix} ,\qquad f(Y)= \begin{bmatrix} f(Y_{1})\\ \vdots\\ f(Y_{s}) \end{bmatrix} , \end{aligned}$$

$$\displaystyle \begin{aligned}\phi_0(C^2\otimes V)=\mathrm{diag}(\phi_0(c_1^2V),\cdots, \phi_0(c_s^2V)),\end{aligned}$$

$$\displaystyle \begin{aligned} (C\otimes I_d)\phi_1(C^2\otimes V)=\mathrm{diag}(c_1\phi_1(c_1^2V),\cdots,c_s\phi_1(c_s^2V)). \end{aligned}$$

Here, it should be remarked that both internal stages and updates of an ERKN integrator have been revised and improved in terms of the matrix-variation-of-constants formulae (1.7) and (1.8) with $\hat {f} (\zeta )=f\big (y(\zeta )\big )$. This class of ERKN integrators has been well developed, and we will further present their stability and convergence analysis in Chap. 3. Moreover, we will also make an attempt to discuss ERKN integrators combined with Fourier pseudospectral discretisation for solving semilinear wave equations in Chap. 3.

If f(y) = 0 in (1.9), then accordingly (1.20) reduces to

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &Y_i=\phi_0(c_i^2 V)y_n+c_ih\phi_1(c_i^2 V)y^{\prime}_n, \quad i=1,\cdots,s, \\ &y_{n+1}=\phi_0(V)y_n+h\phi_1(V)y^{\prime}_n,\\ &y^{\prime}_{n+1}=-hM\phi_1(V)y_n+\phi_0(V)y^{\prime}_n. \end{aligned}\right. {} \end{aligned} $$

(1.22)

In terms of Kronecker products with block-matrix notation, (1.22) can be expressed by

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &Y = \phi_0(C^2\otimes V)(e\otimes y_{n}) + h(C\otimes I_d)\phi_1(C^2\otimes V)(e\otimes y^{\prime}_n),\\ &y_{n+1} = \phi_0(V)y_n+h\phi_1(V)y^{\prime}_n,\\ &y^{\prime}_{n+1}= -hM\phi_1(V)y_n+\phi_0(V)y^{\prime}_n. \end{aligned}\right. {} \end{aligned} $$

(1.23)

It follows from (1.13) and (1.14) that both the internal stages and updates of an ERKN integrator exactly solve the multi-frequency highly oscillatory linear homogeneous equation (1.6) on noticing the fact that

$$\displaystyle \begin{aligned}Y=\hat Y,~y_{n+1}=y(t_{n+1}),~y^{\prime}_{n+1}=y'(t_{n+1}).\end{aligned} $$

(1.24)

It is worth pointing out that (1.24) is an essential feature of ERKN integrators, especially for the effective treatment of nonlinear multi-frequency highly oscillatory systems and this property inherits and develops the idea of the Filon-type method for highly oscillatory integrals (see, e.g. [34, 35]), since the dominant oscillation source introduced by the linear term My has been calculated explicitly.

It is known that energy-preserving methods can be expressed as so-called continuous stage Runge–Kutta methods. Here, from the perspective of the continuous-stage Runge–Kutta methods (see, e.g. [36,37,38,39,40,41]), it is also worth noting that continuous-stage ERKN integrators for (1.9) have not received enough attention. We will next introduce the definition of continuous-stage ERKN integrators.

Definition 1.4

A continuous-stage ERKN integrator for solving the nonlinear Hamiltonian system (1.9) is given by

$$\displaystyle \begin{aligned} \left\{\begin{aligned} &Y_{\tau}=\phi_0(\tau^2V)y_n+\tau h\phi_1(\tau^2V)y^{\prime}_n+ h^2 \displaystyle\intop\nolimits_{0}^{1}\bar{A}_{\tau,\sigma}(V)f(Y_{\sigma})\mathrm{d}\sigma,\quad 0\leqslant \tau\leqslant1,\\ &y_{n+1}=\phi_0(V)y_n+h\phi_1(V)y^{\prime}_n+h^2 \displaystyle\intop\nolimits_{0}^{1}\bar{b}_{\tau}(V) f(Y_{\tau})\mathrm{d}\tau,\\ &y^{\prime}_{n+1}=-hM\phi_1(V)y_n+\phi_0(V)y^{\prime}_n+h\displaystyle\intop\nolimits_{0}^{1}b_{\tau}(V) f(Y_{\tau})\mathrm{d}\tau, \end{aligned}\right.{} \end{aligned} $$

(1.25)

where $\bar {b}_{\tau }(V), b_{\tau }(V)$ are matrix-valued functions of τ and V , and $\bar {A}_{\tau ,\sigma }(V)$ is a matrix-valued function depending on τ, σ and V .

We will further discuss continuous-stage extended Runge–Kutta–Nyström methods for highly oscillatory Hamiltonian systems in Chap. 2. Continuous-stage Leap-frog schemes for semilinear Hamiltonian wave equations will be investigated in detail in Chap. 12.

1.4 Oscillation-Preserving Integrators

It is well known that efficiency is often an important consideration for solving multiple high-frequency oscillatory ordinary differential equations over long-time intervals, although standard RKN methods are popular and effective for second-order ordinary differential equations in many applications. One needs to select an appropriate mathematical or numerical approach to track the high-frequency oscillation in order to use larger stepsizes over long-time intervals.

In the last few decades, geometric numerical integration for differential equations has received more and more attention in order to respect their structural invariants and geometry. The geometric numerical integration for nonlinear differential equations has led to the development of numerical schemes which systematically incorporate qualitative features of the underlying problem into their structures. Accordingly, first of all, a numerical algorithm should respect the highly oscillatory structure of the underlying continuous system (1.1) or (1.9), in the sense of Geometric Integration. On noticing that the Filon-type method (see, e.g. [34, 35]) for highly oscillatory integrals is very successful, and the idea behind this method is that the oscillatory part involved in these integrals must be calculated explicitly, this point is also essential for efficiently solving the nonlinear multi-frequency highly oscillatory system (1.1) or (1.9). This idea for exponential or trigonometric integrators, in fact, has been used for decades by many authors (see, e.g. [4, 15, 16, 42,43,44,45,46]).

It is noted that a comprehensive review of exponential integrators can be found in Hochbruck and Ostermann [46], in which Gautschi-type methods, impulse and mollified impulse methods (see, e.g. Grubmüller et al. [47]), multiple time-stepping methods (see Hairer et al. [15], Chapter VIII. 4), and adiabatic integrators (see Lorenz et al. [48]) were reviewed in detail for the highly oscillatory second-order differential equation, and for the singularly perturbed second-order differential equation, respectively. Hence, in this chapter, we won’t cover them again.

Here, it is clear that high oscillations are brought by the linear part My of (1.1) or (1.9) which should be solved explicitly and exactly for an efficient numerical integrator. Therefore, it will be convenient to introduce the concept of oscillation-preserving numerical methods for solving the nonlinear highly oscillatory system (1.1) or (1.9). Taking into account the significant fact that the internal stages Y _i for i = 1, ⋯ , s, must be nonlinearly involved in the updates y _n+1 and $y^{\prime }_{n+1}$ at each time step for an RKN-type method when applied to (1.1) or (1.9), we present the following definition of oscillation-preserving numerical methods for efficiently solving the nonlinear multi-frequency highly oscillatory system (1.1) or (1.9).

Definition 1.5

An RKN-type method for solving the nonlinear multi-frequency highly oscillatory system (1.1) or (1.9) is oscillation preserving, if its internal stages Y _i for i = 1, ⋯ , s, together with its updates y _n+1 and $y^{\prime }_{n+1}$ at each time step explicitly and exactly solve the highly oscillatory homogeneous linear equation (1.6) associated with (1.1) or (1.9). Apart from this, if only the updates of an RKN-type method can exactly solve the highly oscillatory homogeneous linear equation (1.6), then the RKN-type method is called to be partly oscillation preserving.

Theorem 1.2

An ERKN integrator is oscillation preserving, but an ARKN method is partly oscillation preserving, and a standard RKN method is neither oscillation preserving, nor partly oscillation preserving.

Proof

In the light of Definition 1.5, it is very clear from (1.22) or (1.23) that an ERKN integrator is oscillation preserving.

Unfortunately, an ARKN method is not oscillation preserving due to its internal stages. In fact, applying the internal stages of the ARKN method (1.18) to (1.6) gives

$$\displaystyle \begin{aligned} Y_i=y_n+c_ihy^{\prime}_n-h^2M\sum_{j=1}^s\bar a_{ij}Y_j, \end{aligned}$$

for i = 1, ⋯ , s, which leads to

$$\displaystyle \begin{aligned} Y = e\otimes y_{n} + h(C\otimes I_{d})(e\otimes y^{\prime}_n)- h^2(\bar A\otimes I_{d})(I_s\otimes M)Y, \end{aligned} $$

(1.26)

where e is an s × 1 vector of units,

$$\displaystyle \begin{aligned}h(C\otimes I_{d})=\mathrm{diag}(hc_1I_d,\cdots,hc_sI_d),\end{aligned}$$

and ⊗ represents Kronecker products. We then obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} Y& =&\displaystyle \big(I_s\otimes I_d+h^2(\bar A\otimes I_{d})(I_s\otimes M)\big)^{-1}\big(e\otimes y_{n} + h(C\otimes I_{d})(e\otimes y^{\prime}_n)\big)\\& =&\displaystyle \big(I_s\otimes I_d+h^2(\bar A\otimes I_{d})(I_s\otimes M)\big)^{-1}\big(e\otimes y_{n}\big)\\& &\displaystyle +\big(I_s\otimes I_d+h^2(\bar A\otimes I_{d})(I_s\otimes M)\big)^{-1}h(C\otimes I_{d})\big(e\otimes y^{\prime}_n\big), \end{array} \end{aligned} $$

(1.27)

provided $\det \big (I_s\otimes I_d+h^2(\bar A\otimes I_{d})(I_s\otimes M)\big )\neq 0.$ In comparison with $\hat Y$ defined in (1.13), this implies that

$$\displaystyle \begin{aligned}Y\neq\hat Y= \phi_0(C^2\otimes V)(e\otimes y_{n}) + h(C\otimes I_d)\phi_1(C^2\otimes V)(e\otimes y^{\prime}_n),\end{aligned}$$

i.e.,

$$\displaystyle \begin{aligned}Y_i\neq \hat Y_i= \phi_0\big(c_i^2V\big)y_n+c_ih\phi_1\big(c_i^2V\big)y_n^{\prime},\end{aligned}$$

for i = 1, ⋯ , s, on noticing the fact that

$$\displaystyle \begin{aligned}(C\otimes I_d)\phi_1(C^2\otimes V)=\phi_1(C^2\otimes V)(C\otimes I_d)\end{aligned}$$

and

$$\displaystyle \begin{aligned}\phi_0\big(c_i^2V\big)\neq\phi_1\big(c_i^2V\big),\end{aligned}$$

for i = 1, ⋯ , s. Therefore, it follows from Definition 1.5 that an ARKN method cannot be oscillation preserving, although it is partly oscillation preserving due to its updates. Since the internal stages of standard RKN methods are the same as those of ARKN methods, a standard RKN method is not oscillation preserving. Moreover, in a similar way, it can be shown that the updates of a standard RKN method cannot exactly solve (1.6). This implies that a standard RKN method is neither oscillation preserving nor partly oscillation preserving, because both its internal stages and updates fail to exactly solve the highly oscillatory homogeneous linear equation (1.6) associated with (1.1) or (1.9).

The proof is complete. □

Clearly, it follows from (1.25) that a continuous-stage ERKN method for (1.9) is also oscillation preserving.

Theorem 1.2 presents and confirms a fact that an ERKN integrator possesses excellent oscillation-preserving behaviour for solving the nonlinear highly oscillatory system (1.9) in comparison with RKN and ARKN methods.

With regard to the construction of arbitrary order ERKN integrators for (1.9), readers are referred to a recent paper (see [18]). Concerning the order conditions of ERKN integrators for (1.9), readers are referred to [26, 49].

1.5 Towards Highly Oscillatory Nonlinear Hamiltonian Systems

As is known, Hamiltonian systems have very important applications. Nonlinear Hamiltonian systems with highly oscillatory solutions frequently occur in areas of physics and engineering such as molecular dynamics, classical and quantum mechanics. Numerical methods used to treat them also depend on the knowledge of certain other characteristics of the solution besides high-frequency oscillation.

We now consider the initial value problem of the nonlinear multi-frequency highly oscillatory Hamiltonian system

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &\ddot q+Mq=f(q), \qquad t\in[0,T],\\ &q(0)=q_0,\quad \dot q(0)=\dot q_0, \end{aligned}\right. {} \end{aligned} $$

(1.28)

where M is a d × d symmetric positive semi-definite matrix and $f:\mathbb {R}^{d}\rightarrow \mathbb {R}^{d}$ is a continuous nonlinear function of q with f(q) = −∇U(q) for a real-valued function U(q). Then, the highly oscillatory Hamiltonian system (1.28) can be rewritten as the standard format

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} & \dot{p}=-\nabla_q H(p,q), \\ &\dot{q}=\nabla_p H(p,q),\\ \end{aligned}\right. {} \end{aligned} $$

(1.29)

with the initial values $q(0)=q_{0},\ p(0)=p_0=\dot q_{0}$ and the Hamiltonian

$$\displaystyle \begin{aligned}H(p,q)=\dfrac{1}{2}p^{\intercal}p+\dfrac{1}{2}q^{\intercal}Mq+U(q).{} \end{aligned} $$

(1.30)

It is well known that two remarkable features of a Hamiltonian system are the symplecticity of its flow and the conservation of the Hamiltonian. Consequently, for a numerical integrator for (1.29), in addition to oscillation preservation, these two features should be respected as much as possible in the spirit of geometric numerical integration. In the development of symplectic integration, the earliest significant contributions to this field were due to Feng Kang, who was a pioneer in stressing the importance of using symplectic integrators when the equations to be solved are Hamiltonian systems (see [50,51,52]). It is also worth noting the earlier important work on symplectic integration by J. M. Sanz-Serna, who first found and analysed symplectic Runge–Kutta schemes for Hamiltonian systems (see Sanz-Serna [53]). For the survey papers and monographs on numerical approaches to dealing with nonlinear Hamiltonian differential equations with highly oscillatory solutions, readers are referred to [1, 2, 13, 15, 54, 55].

1.5.1 SSMERKN Integrators

Symplecticity is an important characteristic property of Hamiltonian systems and symplectic methods have been well developed (see, e.g. [15, 52, 53, 56,57,58,59,60]). Symplectic ERKN methods for highly oscillatory Hamiltonian systems have been analysed (see Wu et al. [24]). Symplectic and symmetric multi-frequency ERKN integrators (SSMERKN integrators) have been proposed and analysed for the nonlinear multi-frequency highly oscillatory Hamiltonian system (1.29) in Wu et al. [49].

We now state the coupled conditions of explicit SSMERKN integrators for (1.29).

Theorem 1.3

An s-stage explicit multi-frequency ERKN integrator for integrating (1.29) is symplectic and symmetric if its coefficients are given by

$$\displaystyle \begin{aligned} \left\{\begin{array}{lll} c_{i}=1-c_{s+1-i},\ \ \ \ d_{i}=d_{s+1-i}\neq0, &\ i=1,2,\cdots,s,\\ {}b_{i}(V)=d_i\phi_{0}(c_{s+1-i}^{2}V), &\ i=1,2,\cdots,s,\\ {}\bar{b}_{i}(V)=d_ic_{s+1-i}\phi_{1}(c_{s+1-i}^{2}V), &\ i=1,2,\cdots,s,\\ {}\bar{a}_{ij}(V)=\dfrac{1}{d_i}\big(b_{i}(V)\bar{b}_{j}(V)-\bar{b}_{i}(V)b_{j}(V)\big), &\ i>j,\ \ i,\ j=1,2,\cdots,s. \end{array}\right. {} \end{aligned} $$

(1.31)

The detailed proof of this theorem can be found in Wu et al. [49]. It is noted that when V →0 _d×d, the ERKN methods reduce to standard RKN methods for solving Hamiltonian systems with the Hamiltonian $H(p,q)=\dfrac {1}{2}p^{\intercal }p+U(q)$. The following result can be deduced from Theorem 1.3.

Theorem 1.4

An s-stage explicit RKN method with the coefficients

$$\displaystyle \begin{aligned} \left\{\begin{array}{ll} c_{i}=1-c_{s+1-i},\ \ \ \ d_{i}=d_{s+1-i}\neq0,\quad \ &i=1,2,\cdots,s, \\ {}b_{i}=d_i,\ \ \ \bar{b}_{i}=d_ic_{s+1-i},& i=1,2,\cdots,s,\\ {}\bar{a}_{ij}=\dfrac{1}{d_i}\big(b_{i}\bar{b}_{j}-\bar{b}_{i}b_{j}\big),& i>j,\ \ i,\ j=1,2,\cdots,s, \end{array}\right. {} \end{aligned} $$

(1.32)

is symplectic and symmetric. In (1.32), d _i for $i=1,2,\cdots ,\left \lfloor \dfrac {s+1}{2}\right \rfloor ,$ are real numbers and can be chosen based on the order conditions of RKN methods or other requirements, where $\left \lfloor \dfrac {s+1}{2}\right \rfloor$ denotes the integer part of $\dfrac {s+1}{2}$.

The proof of Theorem 1.4 can be found in [49].

Theorem 1.5

An SSMERKN integrator is oscillation preserving. However, a symplectic and symmetric RKN method is neither oscillation preserving, nor partly oscillation preserving.

Proof

It follows directly from the definition of oscillation preservation (Definition 1.5). □

Hence, we conclude from Theorem 1.5 that a symplectic and symmetric RKN method may not be a good choice for efficiently solving the nonlinear multi- frequency and highly oscillatory Hamiltonian system (1.29) due to its lack of oscillation preservation, whereas an SSMERKN integrator is preferred. This point will also be observed from the results of numerical experiments in Sect. 1.7.

With regard to energy-preserving continuous-stage extended Runge–Kutta–Nyström methods for nonlinear Hamiltonian systems with highly oscillatory solutions, see Chap. 2 for details.

1.5.2 Trigonometric Fourier Collocation Methods

Geometric numerical integration is still a very active subject area and much work has yet to be done. Accordingly, the exponential/trigonometric integrator has become increasingly important (see, e.g. [8, 13, 15, 20, 61,62,63,64]). The original attempts at exploring exponential/trigonometric algorithms for the oscillatory system (1.28) with the special structure brought by the linear term Mq were motivated by many fields of research such as mechanics, astronomy, quantum physics, theoretical physics, molecular dynamics, semidiscrete wave equations approximated by the method of lines or spectral discretisation. The exponential/trigonometric methods take advantage of the special structure to achieve an improved qualitative behaviour, and produce a more accurate long-time integration than standard methods.

We next consider the highly oscillatory system (1.28) which is restricted to the interval [0, h] : 

$$\displaystyle \begin{aligned} \ddot q(t)+Mq(t)=f(q(t)), \qquad q(0)=q_0,\ \ \dot q(0)=\dot q_0,\qquad t\in[0,h].{} \end{aligned} $$

(1.33)

It follows from the matrix-variation-of-constants formula that the exact solution of the system (1.33) and its derivative satisfy

$$\displaystyle \begin{aligned} \left\{\begin{aligned} &q(h)=\phi_0(V)q_0+h\phi_1(V)p_0+ h^2\intop\nolimits_{0}^1(1-z)\phi_1\big((1 -z)^2V\big)f(q(hz))\mathrm{d}z,\\ &p(h)=-hM\phi_1( V)q_0+\phi_0(V)p_0 +h\intop\nolimits_{0}^{1}\phi_0\big((1 -z)^2V\big)f(q(hz))\mathrm{d}z, \end{aligned}\right. {} \end{aligned} $$

(1.34)

for stepsize h > 0, where V = h ² M.

Choose an orthogonal polynomial basis $\{\widetilde {P}_j\}_{j=0}^{\infty }$ on the interval [0, 1]: e.g., the shifted Legendre polynomials over the interval [0, 1], scaled in order to be orthonormal. Hence, we have

$$\displaystyle \begin{aligned}\intop\nolimits_{0}^{1}\widetilde{P}_i(x)\widetilde{P}_j(x)\mathrm{d}x=\delta_{ij},\qquad \deg \big(\widetilde{P}_j\big)=j,\qquad i,j\geqslant0,\end{aligned}$$

where δ _ij is the Kronecker symbol. The right-hand side of (1.33) can be rewritten as

$$\displaystyle \begin{aligned}f(q(\xi h))=\sum_{j=0}^ {\infty}\widetilde{P}_j(\xi )\gamma_j(q), \ \ \xi \in[0,1]; \qquad \gamma_j(q):=\intop\nolimits_{0}^{1}\widetilde{P}_j(\tau)f(q(\tau h))\mathrm{d}\tau.{} \end{aligned} $$

(1.35)

For the sake of simplicity we now use γ _j(q) to denote the coefficients γ _j(h, f(q)) involved in the Fourier expansion.

We now state a result which follows from (1.34) and (1.35), and the proof can be found in Wang et al. [8].

Theorem 1.6

The solution of (1.33) and its derivative satisfy

$$\displaystyle \begin{aligned} \left\{\begin{aligned} &q(h)=\phi_0(V)q_0+h\phi_1(V)p_0+ h^2\sum_{j=0}^ {\infty}I_{1,j}\gamma_j(q),\\ &p(h)=-hM\phi_1( V)q_0+\phi_0(V)p_0 +h\sum_{j=0}^ {\infty}I_{2,j}\gamma_j(q), \end{aligned}\right. {} \end{aligned} $$

(1.36)

where

$$\displaystyle \begin{aligned} &I_{1,j}:=\intop\nolimits_{0}^1\widetilde{P}_j(z)(1-z)\phi_1\big((1 -z)^2V\big)\mathrm{d}z,\ \ I_{2,j}:=\intop\nolimits_{0}^{1}\widetilde{P}_j(z)\phi_0\big((1 -z)^2V\big)\mathrm{d}z. \end{aligned} $$

(1.37)

Naturally, a practical scheme to solve (1.28) needs to truncate the series (1.35) after r (r⩾2) terms and this means replacing the initial value problem (1.28) with the following approximate problem

$$\displaystyle \begin{aligned} \left\{\begin{aligned} &\tilde{q}'(\xi h)=\tilde{p}(\xi h), \quad \tilde{q}(0)=q_{0},\\ &\tilde{p}'(\xi h)=-M\tilde{q}(\xi h)+\sum_{j=0}^ {r-1}\widetilde{P}_j(\xi )\gamma_j(\tilde{q}),\quad \tilde{p}(0)=p_{0}.\end{aligned}\right. {} \end{aligned} $$

(1.38)

We then obtain the implicit solution of (1.38) as follows:

$$\displaystyle \begin{aligned} \left\{\begin{aligned} &\tilde{q}(h)=\phi_0(V)q_0+h\phi_1(V)p_0+ h^2\sum_{j=0}^ {r-1}I_{1,j}\gamma_j(\tilde{q}),\\ &\tilde{p}(h)=-hM\phi_1( V)q_0+\phi_0(V)p_0 +h\sum_{j=0}^ {r-1}I_{2,j}\gamma_j(\tilde{q}). \end{aligned}\right. {} \end{aligned} $$

(1.39)

The analysis stated above leads to the following definition of the trigonometric Fourier collocation methods.

Definition 1.6 (Wang et al. [8])

A trigonometric Fourier collocation (TFC) method for integrating the oscillatory system (1.28) or (1.29) is defined by

$$\displaystyle \begin{aligned} \left\{\begin{aligned} &v_i=\phi_0(c_i^2V)q_0+c_ih\phi_1(c_i^2V)p_0+ (c_ih)^2\sum_{j=0}^ {r-1}I_{1,j,c_i} \sum_{l=1}^ {k}b_l\widetilde{P}_j(c_l)f(v_l),\\ &\quad i=1,2,\cdots,k,\\ &v(h)=\phi_0(V)q_0+h\phi_1(V)p_0+ h^2\sum_{j=0}^ {r-1}I_{1,j}\sum_{l=1}^ {k}b_l\widetilde{P}_j(c_l)f(v_l),\\ &u(h)=-hM\phi_1( V)q_0+\phi_0(V)p_0 +h\sum_{j=0}^ {r-1}I_{2,j}\sum_{l=1}^ {k}b_l\widetilde{P}_j(c_l)f(v_l), \end{aligned}\right. {} \end{aligned} $$

(1.40)

where h is the stepsize, r is an integer satisfying $2\leqslant r\leqslant k$, $\widetilde {P}_j$ are defined by

$$\displaystyle \begin{aligned} \widetilde{P}_j(x)=(-1)^j\sqrt{2j+1}\sum_{k=0}^ {j}~{j \choose{k}}~{j+k \choose{k}}~(-x)^k,\qquad j=0,1,\cdots,\qquad x\in[0,1], {} \end{aligned} $$

(1.41)

and c _l, b _l for l = 1, 2, ⋯ , k, are the nodes, and the quadrature weights of a quadrature formula, respectively. I _1,j, I _2,j, and $I_{1,j,c_i}$ are well determined by the generalised hypergeometric functions (see Wang et al. [8] for details):

(1.42)

In (1.42), the Pochhammer symbol (z)_l is recursively defined by (z)₀ = 1 and $(z)_l=z(z+1)\cdots (z+l-1),\ l\in \mathbb {N},$ and the parameters α _i and β _i are arbitrary complex numbers, except that β _i can be neither zero nor a negative integer.

Remark 1.4

We remark that ϕ ₀(V ) and ϕ ₁(V ) defined by (1.4) can also be expressed by the generalised hypergeometric function ₀ F ₁:

(1.43)

The other ϕ _j(V ) for $j\geqslant 2$ can be recursively obtained from ϕ ₀(V ) and ϕ ₁(V ) (see, e.g. [54]). This hypergeometric representation is useful, and most modern software, e.g., Maple, Mathematica, and Matlab, is well equipped for the calculation of generalised hypergeometric functions.

Remark 1.5

Although the TFC method (1.40) approximates the solution q(t), p(t) of the system (1.28) or (1.29) only in the time interval [0, h], the values v(h), u(h) can be considered as the initial values for a new initial value problem approximating q(t), p(t) in the next time interval [h, 2h]. In such a time-stepping routine manner, we can extend the TFC methods to the interval [(i − 1)h, ih] for any $i\geqslant 2$ and finally obtain a TFC method for q(t), p(t) in an arbitrary interval [0, Nh]. For more details, readers are referred to Wang et al. [8].

Concerning the order of TCF methods, we assume that the quadrature formula for γ _j(q) in (1.35) is of order m − 1. Then the order of TFC methods is of order $n=\min \{m,2r\}$. The details can be found in Wang et al. [8].

Theorem 1.7

The TFC method (1.40) is oscillation preserving.

Proof

Clearly, it follows from the definition of TFC method (1.40) that the TFC method (1.40) is a kind of k-stage RKN-type method, and both its internal stages and updates exactly solve the system of multi-frequency highly oscillatory linear homogeneous equations (1.6). Consequently, the TFC method (1.40) is oscillation preserving. □

It is worth mentioning that the TFC method (1.40) is based on the variation-of-constants formula and a local Fourier expansion of the underlying problem, via the approximation of orthogonal polynomial basis. The approximation of orthogonal trigonometric basis is another possible strategy in the effort to solve (1.33).

1.5.3 The AAVF Method and AVF Formula

It is known that one of the important characteristic properties of a Hamiltonian system is energy conservation. The study of numerical energy conservation for oscillatory systems has appeared in the literature (see, e.g. Hairer et al. [65, 66], Li et al. [7]). In particular, the average-vector-field (AVF) formula (see, e.g. [67, 68]) for (1.10) is of great importance, once (1.10) is a Hamiltonian system.

It follows from the matrix-variation-of-constants formula (1.3) that the solution of (1.28) and its derivative satisfy the following equations:

$$\displaystyle \begin{aligned}\left\{ \begin{aligned} q(t)=&\phi_0\big(t^2M\big)q_0+t\phi_1\big(t^2M\big)p_0+\intop\nolimits_{0}^{t}(t-\zeta)\phi_1\big((t-\zeta)^2M\big)\hat f(\zeta)\mathrm{d}\zeta,\\ p(t)=&-tM\phi_1\big(t^2M\big)q_0+\phi_0\big(t^2M\big)p_0+\intop\nolimits_{0}^{t}\phi_0\big((t-\zeta)^2M\big)\hat f(\zeta)\mathrm{d}\zeta,\\ \end{aligned}\right. {} \end{aligned} $$

(1.44)

where t is any real numbers and $\hat {f} (\zeta )=f\big (q(\zeta )\big )$.

The formula (1.44) motivates the following integrator with stepsize h of the form:

$$\displaystyle \begin{aligned}\left\{ \begin{array} [c]{ll} q_{n+1}&=\phi_0(V)q_n+h\phi_1(V)p_n+h^2IQ^1,\\ {}p_{n+1}&=-hM\phi_1(V)q_n+\phi_0(V)p_n+hIQ^2, \end{array}\right.{} \end{aligned} $$

(1.45)

where V = h ² M, and IQ ¹, IQ ² can be determined by the energy-preserving condition at each time step:

$$\displaystyle \begin{aligned}H(p_{n+1},q_{n+1})=H(p_{n},q_{n}).\end{aligned}$$

We now state a sufficient condition (see, e.g. Wang and Wu [21]) for the scheme (1.45) to yield energy preservation.

Theorem 1.8

If

$$\displaystyle \begin{aligned}IQ^1=\phi_2(V)\intop\nolimits_{0}^{1}f\big((1-\tau)q_{n}+\tau q_{n+1}\big)\mathrm{d}\tau,\ IQ^2=\phi_1(V)\intop\nolimits_{0}^{1}f\big((1-\tau)q_{n}+\tau q_{n+1}\big)\mathrm{d}\tau,{} \end{aligned} $$

(1.46)

then the scheme (1.45) exactly preserves the Hamiltonian (1.30), i.e.,

$$\displaystyle \begin{aligned}H(p_{n+1},q_{n+1})=H(p_{n},q_{n}),\ n=0,1,\cdots.{} \end{aligned} $$

(1.47)

Thus, we state the adapted average-vector-field (AAVF) method (see [21, 23]) as follows:

Definition 1.7

An adapted average-vector-field (AAVF) method with stepsize h for the multi-frequency highly oscillatory Hamiltonian system (1.28) is defined by

$$\displaystyle \begin{aligned}\left\{ \begin{array} [c]{ll} q_{n+1}=\phi_0(V)q_n+h\phi_1(V)p_n+h^2\phi_2(V)\displaystyle\intop\nolimits_{0}^{1}f\big((1-\tau)q_{n}+\tau q_{n+1}\big)\mathrm{d}\tau,\\ p_{n+1}=-hM\phi_1(V)q_n+\phi_0(V)p_n+h\phi_1(V)\displaystyle\intop\nolimits_{0}^{1}f\big((1-\tau)q_{n}+\tau q_{n+1}\big)\mathrm{d}\tau, \end{array}\right.{} \end{aligned} $$

(1.48)

where ϕ ₀(V ), ϕ ₁(V ) and ϕ ₂(V ) are determined by (1.4).

It follows from Theorem 1.8 that the AAVF method (1.48) is energy preserving.

It can be observed that when M = 0 in (1.48), the AAVF method reduces to the well-known AVF formula for (1.10) with y = q and f(q) = −∇U(q) (see, e.g. [67, 68]):

$$\displaystyle \begin{aligned}\left\{ \begin{array} [c]{ll} q_{n+1}=q_n+hp_n+\dfrac{h^2}{2}\displaystyle\intop\nolimits_{0}^{1}f\big((1-\tau)q_{n}+\tau q_{n+1}\big)\mathrm{d}\tau,\\ p_{n+1}=p_n+h\displaystyle\intop\nolimits_{0}^{1}f\big((1-\tau)q_{n}+\tau q_{n+1}\big)\mathrm{d}\tau. \end{array}\right.{} \end{aligned} $$

(1.49)

Remark 1.5.1

This class of discrete gradient methods is very important in Geometric Integrators, and the first actual appearance of the integrator that came to be known as the AVF method was in [68]. On the basis of this idea, we will analyse linearly-fitted conservative (dissipative) schemes for nonlinear wave equations in Chap. 8. We also consider the volume-preserving exponential integrators for different vector fields in Chap. 6. Furthermore, we will present energy-preserving integrators for Poisson systems in Chap. 4 and energy-preserving schemes for high-dimensional nonlinear KG equations in Chap. 9.

Many physical problems have time reversibility and this structure of the original continuous system can be preserved by symmetric integrators (readers are referred to Chapter V of Hairer et al. [15] for a rigorous definition of reversibility). The AAVF methods were also proved to be symmetric (see, e.g. [21]). However, it follows from the definition of oscillation preservation (Definition 1.5) that an AAVF method is neither oscillation preserving nor is the AVF method. Fortunately, an AAVF method is partly oscillation preserving due to its updates, and the result is stated as follows.

Theorem 1.9

The AAVF method for (1.28) is partly oscillation preserving.

Proof

Similarly to the AVF method, the AAVF method defined by (1.48) is also dependent on the integral and, in practice, the integral usually must be approximated by a numerical integral formula (see, e.g. [23]), a weighted summation of the evaluations of function f at s different values Y _i = (1 − τ _i)q _n + τ _i q _n+1 for i = 1, ⋯ , s, which can be regarded as the internal stages of the AAVF method. Obviously, the updates of an AAVF method can exactly solve the highly oscillatory homogeneous linear equation (1.6), but the internal stages cannot. The proof is complete. □

Remark 1.6

It is worth mentioning that in a recent paper, the AAVF methods have been extended to the computation of high-dimensional semilinear KG equations. Readers are referred to Chap. 9 for details. Moreover, long-time momentum and actions behaviour of the AAVF methods for Hamiltonian wave equations are presented in Chap. 14. Furthermore, the global error bounds of one-stage ERKN integrators for semilinear wave equations are analysed in Chap. 7. We also discussed the resonance instability for AAVF methods (see [54]).

1.6 Other Concerns Relating to Highly Oscillatory Problems

Gautschi-type methods have been intensively studied in the literature, and general ERKN methods for highly oscillatory problems have been proposed. Here, it is also important to recognise that the numerical solution of semilinear Hamiltonian wave equations is closely related to oscillation-preserving integrators.

1.6.1 Gautschi-Type Methods

This section starts from the Gautschi-type methods which have been well investigated in the literature (see, e.g. [4, 16, 69]). Gautschi-type methods for the nonlinear highly oscillatory Hamiltonian system (1.29) can be traced back to a profound paper of Gautschi [43]. Gautschi-type methods are special explicit ERKN methods of order two (see [10]). An error and stability analysis of the Gautschi-type methods can be found in [16]. Thus, Gautschi-type methods are oscillation preserving in the light of Definition 1.5. However, it is noted that ERKN methods for the highly oscillatory Hamiltonian system (1.29) can be of an arbitrarily high order which can be thought of as generalised Gautschi-type methods.

1.6.2 General ERKN Methods for (1.1)

We next turn to the general ERKN methods for solving nonlinear multi-frequency highly oscillatory second-order ordinary differential equations (1.1).

Definition 1.8 (You et al. [27])

An s-stage general extended Runge–Kutta–Nyström (ERKN) method for the numerical integration of the IVP (1.1) is defined by

$$\displaystyle \begin{aligned}\left\{\begin{aligned} &Y_i=\phi_0(c_i^2V){y}_n+c_i\phi_1(c_i^2V)h{y}^{\prime}_n +h^2\sum_{j=1}^{s}\bar{a}_{ij}(V){f}(Y_j,Y^{\prime}_j), \qquad i=1,\cdots,s, \\ &hY^{\prime}_{i}=-c_iV\phi_1(c_i^2V){y}_n+\phi_0(c_i^2V)h{y}^{\prime}_n +h^2\sum_{j=1}^{s}a_{ij}(V){f}(Y_j,Y^{\prime}_j), \qquad i=1,\cdots,s, \\ &{y}_{n+1}=\phi_0(V){y}_n+\phi_1(V)h{y}^{\prime}_n +h^2\sum_{i=1}^s\bar{b}_i(V){f}(Y_i,Y^{\prime}_i),\\ &h{y}^{\prime}_{n+1}=-V\phi_1(V){y}_n+\phi_0(V)h{y}^{\prime}_n +h^2\sum_{i=1}^sb_i(V){f}(Y_i,Y^{\prime}_i), \end{aligned}\right.\end{aligned} $$

(1.50)

where ϕ ₀(V ), ϕ ₁(V ), $\bar {a}_{ij}(V)$, a _ij(V ), $\bar {b}_{i}(V)$ and b _i(V ) for i, j = 1, ⋯ , s, are matrix-valued functions of V = h ² M.

The general ERKN method (1.50) in Definition 1.8 can also be represented briefly in a partitioned Butcher tableau of the coefficients:

(1.51)

Obviously, the general ERKN method (1.50) for the nonlinear multi-frequency highly oscillatory system (1.1) is oscillation preserving in the light of Definition 1.5. The general ERKN method (1.50) can be of an arbitrarily high order and the analysis of order conditions for the general ERKN method (1.50) can be found in [13, 28].

1.6.3 Towards the Application to Semilinear KG Equations

We note a fact that one of the major applications of oscillation-preserving integrators is to solve semilinear Hamiltonian wave equations such as semilinear KG equations:

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &u_{tt}-a^2{\Delta} u=f(u),\qquad t_0< t\leqslant T,\quad x\in{\varOmega},\\ &u(x,t_0)=\varphi_1(x),\quad u_t(x,t_0)=\varphi_2(x), \ x\in{\bar\varOmega}, \end{aligned} \right. \end{aligned} $$

(1.52)

where u(x, t) represents the wave displacement at position x and time t, and the nonlinear function f(u) is the negative derivative of a potential energy $V(u)\geqslant 0$:

$$\displaystyle \begin{aligned}V(u)=-\intop\nolimits_0^uf(\sigma)\mathrm{d}\sigma.\end{aligned}$$

Here, suppose that the initial value problem (1.52) is subject to the periodic boundary condition on the domain Ω = (−π, π),

$$\displaystyle \begin{aligned} u(x,t)=u(x+2\pi,t),\qquad x\in(-\pi,\pi], \end{aligned} $$

(1.53)

where 2π is the fundamental period with respect to x. It is known that, as a relativistic counterpart of the Schrödinger equation, the KG equation is used to model diverse nonlinear phenomena, such as the propagation of dislocations in crystals and the behaviour of elementary particles and of Josephson junctions (see [70] Chap. 2). Its efficient computation, without a doubt, induces numerous enduring challenges (see, e.g. [9, 11, 71]).

In practice, a suitable space semidiscretisation for semilinear KG equations can lead to (1.9), where the matrix M is derived from the space semidiscretisation. If we denote the total number of spatial mesh grids by N, then the larger N is, the larger $\left \Vert M \right \Vert$ becomes. This means that the semidiscrete wave equation is a highly oscillatory system. In our recent work (see Mei et al. [10]), it has been proved under the so-called finite-energy condition that the error bound of ERKN integrators when applied to semilinear wave equations is independent of $\left \Vert M \right \Vert$. This point is crucial to the numerical solution of the underlying semilinear KG equation.

Another approach to the numerical solution of KG equations is that we try to gain an abstract formulation for the problem (1.52)–(1.53), and then deal with it numerically. To this end, we first consider the following differential operator $\mathbb {A}$ defined by

$$\displaystyle \begin{aligned} (\mathbb{A}v)(x)=-a^2v_{xx}(x). \end{aligned} $$

(1.54)

In (1.54), $\mathbb {A}$ is a linear, unbounded positive semi-definite operator, whose domain is

$$\displaystyle \begin{aligned} D(\mathbb{A}):=\left\{v\in H^1({\varOmega}): v(x)=v(x+2\pi)\right\}. \end{aligned}$$

Fortunately, however, the operator $\mathbb {A}$ has a complete system of orthogonal eigenfunctions $\big \{\mathrm {e}^{\mathrm {i} kx}: k\in \mathbb {Z}\big \}$ and the linear span of all these eigenfunctions

$$\displaystyle \begin{aligned} X:=\mathrm{lin}\big\{\mathrm{e}^{\mathrm{i} \ell x}: \ell\in\mathbb{Z}\big\} \end{aligned} $$

(1.55)

is dense in the Hilbert space L ²(Ω). We then obtain the orthonormal basis of eigenvectors of the operator $\mathbb {A}$ with the corresponding eigenvalues a ² ℓ ² for $\ell \in \mathbb {Z}$.

Define the bounded functions through the following series (see [72])

$$\displaystyle \begin{aligned} \phi_k(x):=\sum_{j=0}^{\infty}\dfrac{(-1)^jx^j}{(2j+k)!},\qquad k\in\mathbb{N}\quad \mbox{for}\quad \forall x\geqslant 0. \end{aligned} $$

(1.56)

Accordingly, these functions (1.56) can induce the bounded operators

$$\displaystyle \begin{aligned} \phi_k(t\mathbb{A}):\ L^2({\varOmega})\rightarrow L^2({\varOmega}) \end{aligned}$$

for $k\in \mathbb {N}$ and $t_0\leqslant t\leqslant T$:

$$\displaystyle \begin{aligned} \phi_k(t\mathbb{A})v(x)=\sum_{\ell=-\infty}^{\infty}\hat v_\ell\phi_k(ta^2\ell^2)\mathrm{e}^{\mathrm{i}\ell x}\quad \mbox{for}\quad v(x)=\sum_{\ell=-\infty}^{\infty}\hat v_\ell \mathrm{e}^{\mathrm{i}\ell x}, \end{aligned} $$

(1.57)

and the boundedness follows from the definition of the operator norm that

$$\displaystyle \begin{aligned} \|\phi_k(t\mathbb{A})\|{}^2_{*}=\sup_{\|v\|\neq 0}\dfrac{\|\phi_k(t\mathbb{A})v\|{}^2}{\|v\|{}^2} \leqslant\sup_{t_0\leqslant t\leqslant T}|\phi_k(ta^2\ell^2)|{}^2\leqslant \gamma_k^2, \end{aligned} $$

(1.58)

where ∥⋅∥_∗ is the Sobolev norm $\|\cdot \|{ }_{L^2({\varOmega })\leftarrow L^2({\varOmega })}$, and γ _k for $k\in \mathbb {N}$ are the uniform bounds of the functions |ϕ _k(x)| for $k\in \mathbb {N}$ and $x\geqslant 0$. With regard to the analysis for the boundedness, readers are referred to Liu and Wu [72].

We are now in a position to define u(t) as the function that maps x to u(x, t), u(t) := [x↦u(x, t)], and in this way the system (1.52)–(1.53) can be formulated as an abstract second-order ordinary differential equation

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &u''(t)+\mathbb{A}u(t)=f\big(u(t)\big),\quad t_0< t\leqslant T,\\ &u(t_0)=\varphi_1(x),\quad u'(t_0)=\varphi_2(x). \end{aligned} \right. \end{aligned} $$

(1.59)

on the closed subspace

$$\displaystyle \begin{aligned} \mathbb{X}:=\Big\{u(x,\cdot)\in X\ \big|\ u(x,\cdot)\ {\mbox{satisfies the corresponding boundary conditions}}\Big\}\subseteq L^2({\varOmega}). \end{aligned} $$

(1.60)

With this premise, the solution of the abstract second-order ordinary differential equations (1.59) can be expressed by the following operator-variation-of-constants formula (see, e.g. [73,74,75]).

Theorem 1.10

The solution of (1.59) and its derivative satisfy the following operator-variation-of-constants formula

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} u(t)=&\,\phi_0\big((t-t_0)^2\mathbb{A}\big)u(t_0)+(t-t_0)\phi_1\big((t-t_0)^2\mathbb{A}\big)u'(t_0) \\&+\intop\nolimits_{t_0}^t(t-\zeta)\phi_1\big((t-\zeta)^2\mathbb{A}\big)f\big(u(\zeta)\big)\mathrm{d}\zeta,\\ u'(t)=&-(t-t_0)\mathbb{A}\phi_1\big((t-t_0)^2\mathbb{A}\big)u(t_0)+\phi_0\big((t-t_0)^2\mathbb{A}\big)u'(t_0) \\&+\intop\nolimits_{t_0}^t\phi_0\big((t-\zeta)^2\mathbb{A}\big)f\big(u(\zeta)\big)\mathrm{d}\zeta, \end{aligned} \right. \end{aligned} $$

(1.61)

for $t_0\leqslant t \leqslant T$ , where both $\phi _0\big ((t-t_0)^2\mathbb {A}\big )$ and $\phi _1\big ((t-t_0)^2\mathbb {A}\big )$ are bounded operators.

Remark 1.6.1

We here remark that the special case where f(u) = 0, the operator-variation-of-constants formula (1.61) yields the closed-form solution to (1.59). Moreover, the idea of the operator-variation-of-constants formula (1.61) also provides a useful approach to the development of the so-called semi-analytical ERKN integrators for solving high-dimensional nonlinear wave equations. See Chap. 13 for details.

According to Theorem 1.10, the solution of (1.59) and its derivative at a time point t _n+1 = t _n +  Δt, $n\in \mathbb {N}$ are given by

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} u(t_{n+1})=&\phi_0\big(\mathbb{V}\big)u(t_n)+{\Delta} t\phi_1\big(\mathbb{V}\big)u'(t_n)+{\Delta} t^2\intop\nolimits_0^1(1-z)\phi_1\big((1-z)^2\mathbb{V}\big)\tilde f(z)\mathrm{d}z,\\ u'(t_{n+1})=&-{\Delta} t\mathbb{A}\phi_1\big(\mathbb{V}\big)u(t_n)+\phi_0\big(\mathbb{V}\big)u'(t_n)+{\Delta} t\intop\nolimits_0^1\phi_0\big((1-z)^2\mathbb{V}\big)\tilde f(z)\mathrm{d}z, \end{aligned} \right. \end{aligned} $$

(1.62)

where $\mathbb {V}={\Delta } t^2\mathbb {A}$ and $\tilde f(z)=f\big (u(t_n+z{\Delta } t)\big )$.

If the nonlinear integrals

$$\displaystyle \begin{aligned} I_1:=\intop\nolimits_0^1(1-z)\phi_1\big((1-z)^2\mathbb{V}\big)\tilde f(z)\mathrm{d}z\quad {\mbox{and}}\quad I_2:=\intop\nolimits_0^1\phi_0\big((1-z)^2\mathbb{V}\big)\tilde f(z)\mathrm{d}z \end{aligned} $$

(1.63)

are efficiently approximated, then we are hopeful of obtaining some new integrators based on (1.62). For example, using the operator-variation-of-constants formula (1.62) and the two-point Hermite interpolation, we developed a class of arbitrarily high-order and symmetric time integration formulae (see Chap. 10). The preservation of symmetry by a numerical scheme is also very important because the KG equation (1.52) is time reversible. Hairer et al. [15] have emphasised that symmetric methods have excellent long-time behaviour when solving reversible differential systems. Therefore, the preservation of time symmetry for a numerical scheme is also one of the favourable features.

Here it is worth emphasising that since $\mathbb {A}$ is a linear, unbounded positive semi-definite operator, it is a wise choice to approximate the operator $\mathbb {A}$ by a symmetric and positive semi-definite differentiation matrix M on a d-dimensional space when spatial discretisations of the underlying KG equation are carried out, and this will assist in structure preservation.

It is noted that a symmetric and arbitrarily high order time integration formula can be designed in operatorial terms in an infinite-dimensional function space $\mathbb {X}$ (see, e.g. [73, 74]). Using this approach, we also consider symplectic approximations for semilinear KG equations in Chap. 11. In practice, the differential operator $\mathbb {A}$ must be replaced with a suitable differentiation matrix M so that we may obtain a proper full discrete numerical scheme. Fortunately, there exist many research publications discussing the replacement of spatial derivatives of the semilinear KG equation (1.52) with periodic boundary conditions (1.53) in the literature. Thus, it is not a main point in this chapter. Here, however, again it is notable that the operator $\mathbb {A}$ should be approximated by a symmetric and positive semi-definite differentiation matrix M and the norm of M will change with the accuracy requirement of spatial discretisations. The higher the accuracy of spatial discretisations is required, the larger $\left \Vert M \right \Vert$ will be. This implies that the spatial structure preservation is required for the full discretisation of KG equation (1.52). A full discretisation for the KG equation (1.52) with periodic boundary conditions (1.53) is spatially structure-preserving if the operator $\mathbb {A}$ is approximated by a d × d symmetric and positive semi-definite differentiation matrix M, and the norm of M, $\left \Vert M \right \Vert$, tends to infinity as d tends to infinity, where d is the number of degrees of freedom in the space discretisation.

Obviously, the global error of a fully discrete scheme for the KG equation (1.52) depends on the accuracy of both time integrators and space discretisations. As the mesh partition in the space discretisation increases for (1.59), ∥M∥ will increase, and the larger ∥M∥ is, the higher the accuracy will be increased in space approximations.

Remark 1.7

Actually, the family of matrices {M _d×d} approximates the infinite-dimensional, unbounded, operator $\mathbb {A}$. $\left \Vert M_{d\times d} \right \Vert$ tends to infinity with d, where d is the dimension of the matrix M _d×d; i.e., the number of degrees of freedom in the spatial discretisation. Consequently, the family of matrices {M _d×d} inherits the unbounded property of $\mathbb {A}$. This objectively reflects an important fact that the norm of the differentiation matrix M _d×d could be arbitrarily large, depending on the requirement of computational accuracy, and the corresponding system of second-order differential equations must be a multi-frequency highly oscillatory system once high global accuracy is required. In this case, an oscillation-preserving time integrator is needed for the numerical simulation of semilinear wave equations, including the KG equation (1.52), during a long-time computation. Moreover, the accuracy of the oscillation-preserving time integrator will be required to match that of the space discretisation. Hence, oscillation-preserving ERKN integrators of arbitrarily high order are favourable in applications, especially when applied to the semidiscrete KG equation, and high-accuracy time integrators will be required for the underlying PDEs in practice.

1.7 Numerical Experiments

This section concerns numerical experiments, and we will consider four problems which are closely related to (1.1) or (1.9). Since explicit methods are cheaper (use less CPU time in general) than implicit methods, we use three explicit RKN-type methods and two implicit methods. These methods are chosen as follows:

• ERKN3s4: the explicit three-stage ERKN method of order four presented in [18] (with its Butcher tableau given by Table 1.1);

  Table 1.1 Butcher tableau of ERKN3s4

• ARKN3s4: the explicit three-stage ARKN method of order four proposed in [76] (with its Butcher tableau given by Table 1.2);

  Table 1.2 Butcher tableau of ARKN3s4

• ERKN7s6: the explicit seven-stage ERKN method of order six derived in [77] with the coefficients

  $$\displaystyle \begin{aligned} \begin{array}{ll} c_5=1-c_3 =0.06520862987680341024,\\ {}c_6=1-c_2 =0.65373769483744778901,\\ {}c_7=1-c_1 =0.05586607811787376572,\\ {}c_4=0.5,\\ {}d_4=0.26987577187133640373,\\ {}d_5=d_3=0.92161977504885189358,\\ {}\end{array} \end{aligned} $$
  $$\displaystyle \begin{aligned} \begin{array}{ll} d_6=d_2 =0.13118241020105280626,\\[1.5mm] d_7=d_1=-0.68774007118557290171,\\[1.5mm] \bar{b}_{i}(V)=d_ic_{8-i}\phi_{1}\big(c_{8-i}^{2}V\big),\ b_{i}(V)=d_i\phi_{0}\big(c_{8-i}^{2}V\big),\\[1.5mm] {for}\ \ i=1,2,\cdots,7,\\[1.5mm] \bar{a}_{ij}(V)=d_j(c_{i}-c_{j})\phi_{1}\big((c_{i}-c_{j})^{2}V\big),\\[1.5mm] {for}\ \ i=2,3,\cdots ,7,\ \ \ j=1,2,\cdots ,i-1; \end{array} \end{aligned}$$

• TFCr2: the TFC method (1.40) of order four described in [8] (with its Butcher tableau given by Table 1.3 with the coefficients $c_1=\dfrac {3-\sqrt {3}}{6}, c_2=\dfrac {3+\sqrt {3}}{6}$, $b_1=b_2=\dfrac {1}{2},$ and r = 2);

  Table 1.3 Butcher tableau of TFCr2

• TFCr3: the TFC method (1.40) of order six described in [8] (with its Butcher tableau given by Table 1.4 with the coefficients $c_1=\dfrac {5-\sqrt {15}}{10},c_2=\dfrac {1}{2}, c_3=\dfrac {5+\sqrt {15}}{10}$, $b_1=\dfrac {5}{18}, b_2=\dfrac {4}{9}, b_3=\dfrac {5}{18}$, and r = 3).

  Table 1.4 Butcher tableau of TFCr3

We remark that an ERKN method reduces to an RKN method when M →0. Hence, the reduced method ERKN3s4 is assigned as the corresponding RKN method, which is denoted by RKN3s4. In the numerical experiments, we use fixed-point iteration for the implicit TFC methods. We set 10⁻¹⁶ as the error tolerance and 10 as the maximum number of each iteration. It will be observed from the numerical experiments that the numerical behaviour of the ERKN methods and TFC methods is much better than that of the ARKN and RKN methods.

In these methods, the matrix-valued functions ϕ _i(V ), for i = 0, 1, ⋯ , 4, are defined by (1.4).

Problem 1.1

Consider the Duffing equation (see, e.g. [10, 13, 78, 79])

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &\ddot{q} + \omega^2 q=k^2(2q^3-q), \\ &q(0)=0,\quad \dot{q}(0)=\omega, \end{aligned} \right. \end{aligned}$$

where $0\leqslant k<\omega$. As is known, this is a Hamiltonian system with the Hamiltonian

$$\displaystyle \begin{aligned} H(p,q)=\dfrac{1}{2}p^2 + \dfrac{1}{2}\omega^2 q^2 + \dfrac{k^2}{2}(q^2-q^4). \end{aligned}$$

The analytic solution is given by

$$\displaystyle \begin{aligned}q(t)=sn(\omega t,k/\omega),\end{aligned}$$

where sn denotes the Jacobian elliptic function (see, e.g. [80]).

Problem 1.1 is solved on the interval [0, 10000] with k = 0.03 and ω = 50. Figure 1.1a presents the global errors results (in logarithmic scale) with the stepsizes $h=\dfrac {0.1}{2^j}$ for j = 1, ⋯ , 4. We here remark that some global errors for RKN3s4 are too large to be plotted in Fig. 1.1a due to its instability and nonconvergence with the stepsize h = 0.05. In the next problems, similar situations are encountered and the corresponding points are not plotted either. We also show the global errors against the CPU time in Fig. 1.1b. It can be observed from these figures, ERKN3s4, ERKN7s6 and TFC methods are much more accurate than ARKN3s4 and RKN3s4, and RKN3s4 gives disappointing accuracy in comparison with the other methods, although it is a symplectic and symmetric method. This observation implies that the property of oscillation preservation for numerical methods is also of great importance in Geometric Integration. What can we learn from this observation? This experiment demonstrates that for a nonlinear highly oscillatory differential equation, the most important consideration should be the oscillation preservation when concerning numerical solutions.

Fig. 1.1

Results for Problem 1.1. (a) The log-log plot of global error GE against h. (b) The log-log plot of global error GE against CPU time. (c) The logarithm of the global energy error GE against t

Meanwhile, we also show the curves of the Hamiltonian error growth with $h=\dfrac {1}{40}$ as the integration interval is extended in Fig. 1.1c for all the methods, where the ERKN methods and TFC methods show better numerical energy preservation than the reduced RKN method: RKN3s4, and ARKN3s4 method. It follows from Fig. 1.1c that both the ERKN and RKN methods can preserve the energy approximately, whereas the ARKN3s4 method cannot. In fact, it is clear from Fig. 1.1c that the energy of the ARKN3s4 method grows as the integration interval is extended. This is because both the ERKN and RKN methods are symplectic and symmetric methods, whereas the ARKN3s4 method is not a symplectic method. Another important aspect is that, just as its algebraic accuracy, the accuracy of energy preservation of RKN3s4 method is also disappointing, even though RKN3s4 method possesses both favourable properties of symplecticity preservation and symmetry preservation. It is worth noting that, although the TFC methods are not symplectic, they are oscillation preserving and preserve the energy approximately. Hence, we should take full account of the oscillation-preserving structure in the design of numerical methods for efficiently solving a highly oscillatory nonlinear Hamiltonian system, although we cannot ignore the other structures.

Problem 1.2

Consider the sine-Gordon equation (see, e.g. [81])

$$\displaystyle \begin{aligned} \dfrac{\partial^2 u}{\partial t^2} = \dfrac{\partial^2 u}{\partial x^2} - \sin u, \end{aligned}$$

on the region $-10\leqslant x\leqslant 10$ and $t_0\leqslant t\leqslant T$ with the initial conditions

$$\displaystyle \begin{aligned} u(x,t_0)=&-4{arctan}\big(c^{-1}{sech}(\kappa x)\sin{}(-t_0c\kappa)\big), \\ u_t(x,t_0)=&\dfrac{4\kappa\cos{}(-t_0c\kappa){sech}(\kappa x)} {1+c^{-2}{sech}^2(\kappa x)\sin^2(-t_0c\kappa)},\\ \end{aligned}$$

and the boundary conditions

$$\displaystyle \begin{aligned}u(-10,t)= u(10,t)=-4{arctan}\big(c^{-1}{sech}(10\kappa)\sin{}(c\kappa t)\big), \end{aligned}$$

where $\kappa =1/\sqrt {1+c^2}$. The exact solution is

$$\displaystyle \begin{aligned}u(x,t)=-4\arctan\big(c^{-1}{sech}(\kappa x)\sin{}(c\kappa t)\big). \end{aligned}$$

For this problem, we use the Chebyshev pseudospectral discretisation with 240 spatial mesh grids and select the parameter c = 0.5, which leads to a discretisation of the type (1.9). This equation is solved on the interval [0, 100]. Figure 1.2a, b show the global errors results (in logarithmic scale) with the stepsizes $h=\dfrac {1}{2^k}$ for k = 1, ⋯ , 4. We then integrate this equation with the stepsize $h=\dfrac {1}{10}$ on the interval [0, 10000] and the numerical energy conservation is presented in Fig. 1.2c.

Fig. 1.2

Results for Problem 1.2. (a) The log-log plot of global error GE against h. (b) The log-log plot of global error GE against CPU time. (c) The logarithm of the global energy error GE against t

Again it can be observed from the numerical results that the numerical behaviour of ERKN methods and TFC methods is much better than that of ARKN3s4 and RKN3s4. In summary, an oscillation-preserving numerical method gives much better results than those methods which are not oscillation preserving. In particular, the symplectic and symmetric RKN3s4 performs badly and leads to completely disappointing numerical results in this numerical experiment.

Problem 1.3

Consider the semilinear wave equation

$$\displaystyle \begin{aligned} \begin{array}{rcl}\left\{\begin{array}{ll} \dfrac{\partial^2u}{\partial t^2}-a(x)\dfrac{\partial^2u}{\partial x^2}+92u=f(t,x,u),\ \ \ 0<x<1,\ \ t>0,\\\\ u(x,0)=a(x),\ \ \ u_t(x,0)=0,\\\\ u(0,t)=0,\ \ \ u(1,t)=0,\ \ \\ \end{array}\right. \end{array} \end{aligned} $$

where

$$\displaystyle \begin{aligned} a(x) = 4x(1-x)\end{aligned}$$

and

$$\displaystyle \begin{aligned} f(t,x,u)=u^5-a^2(x)u^3+\dfrac{a^5(x)}{4}\sin^2(20t)\cos{}(10t).\end{aligned}$$

The exact solution of this problem is

$$\displaystyle \begin{aligned}u(x,t) = a(x) \cos{}(10t),\end{aligned}$$

which represents a vibrating string.

Differently from Problem 1.2, we now consider semidiscretisation of the spatial variable with second-order symmetric differences, and this results in

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \begin{array}{ll} \dfrac{\mathrm{d}^2U}{\mathrm{d}t^2}+MU=F(t,U),\ \ U(0)=\big(a(x_1),\cdots,a(x_{N-1})\big)^{\intercal},\ \ U'(0)=\mathbf{0},\qquad \qquad \end{array} \end{array} \end{aligned} $$

(1.64)

where $U(t)\!=\!\big (u_{1}(t),\cdots ,u_{N-1}(t)\big )^{\intercal }$ with u _i(t) ≈ u(x _i, t), x _i  =  i Δx for $i\!=\!1,\cdots ,N-1$, and Δx = 1∕N.

$$\displaystyle \begin{aligned} \begin{array}{rcl} M=92I_{N-1}+\dfrac{1}{{\Delta} x^2}\left( \begin{array} [c]{ccccc} 2a(x_1)& -a(x_1) &\displaystyle &\displaystyle &\displaystyle \\ -a(x_2) & 2a(x_2) &\displaystyle -a(x_2)&\displaystyle &\displaystyle \\ & \ddots&\displaystyle \ddots&\displaystyle \ddots&\displaystyle \\ & &\displaystyle -a(x_{N-2}) &\displaystyle 2a(x_{N-2}) &\displaystyle -a(x_{N-2})\\ & &\displaystyle &\displaystyle -a(x_{N-1})&\displaystyle 2a(x_{N-1}) \\ \end{array} \right), \end{array} \end{aligned} $$

and

$$\displaystyle \begin{aligned} \begin{array}{rcl} F(t,U)=\big( f(t,x_1,u_1), \cdots, f(t,x_{N-1},u_{N-1})\big)^{\intercal}. \end{array} \end{aligned} $$

(1.64) is a highly oscillatory system, but not a Hamiltonian system. We solve this problem on the interval [0, 10] with N = 256 and $h=\dfrac {0.1}{2^j}$ for j = 1, ⋯ , 4. The global errors are shown in Fig. 1.3. Once again, it can be observed from Fig. 1.3 that the numerical behaviour of the oscillation-preserving ERKN methods and TFC methods is much better than the others. In Fig. 1.3, the global errors figures of both ERKN methods and TFC methods almost coincide with each other.

Fig. 1.3

Results for Problem 1.3. (a) The log-log plot of global error GE against h. (b) The log-log plot of global error GE against CPU time

We next consider a damped wave equation. For this problem, we choose time integrators as follows:

• ERKN3s3: the explicit three-stage ERKN method of order three proposed in [27] and denoted by the Butcher tableau

  

  where

  $$\displaystyle \begin{aligned} b_{1}(V)=&\phi_{1}(V)-\dfrac{9}{2}\phi_{2}(V)+9\phi_{3}(V),\\ b_{2}(V)=&6\phi_{2}(V)-18\phi_{3}(V),\\ b_{3}(V)=&-\dfrac{3}{2}\phi_{2}(V)+9\phi_{3}(V),\\ \bar{b}_{1}(V)=&\phi_{2}(V)-\dfrac{9}{2}\phi_{3}(V)+9\phi_{4}(V),\\ \bar{b}_{2}(V)=&6\phi_{3}(V)-18\phi_{4}(V),\\ \bar{b}_{3}(V)=&-\dfrac{3}{2}\phi_{3}(V)+9\phi_{4}(V).\\ \end{aligned}$$

• ARKN3s3: the explicit three-stage ARKN method of order three given in [82] and denoted by the Butcher tableau

  

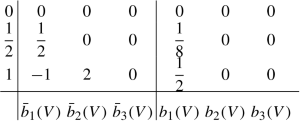
  where

  $$\displaystyle \begin{aligned} b_{1}(V)=&\phi_{1}(V)-3\phi_{2}(V)+4\phi_{3}(V), \\ b_{2}(V)=&4\phi_{2}(V)-8\phi_{3}(V),\\ b_{3}(V)=&-\phi_{2}(V)+4\phi_{3}(V),\\ \bar{b}_{1}(V)=&\phi_{2}(V)-\dfrac{3}{2}\phi_{3}(V), \\ \bar{b}_{2}(V)=&\phi_{3}(V),\qquad \qquad \\ \bar{b}_{3}(V)=&\dfrac{1}{2}\phi_{3}(V).\\ \end{aligned}$$

• RKN3s3: the explicit three-stage RKN method of order three with the Butcher tableau

  

Problem 1.4

Consider the damped wave equation (see, e.g. [27, 82])

$$\displaystyle \begin{aligned} \begin{array}{rcl}\left\{\begin{array}{ll} \dfrac{\partial^2u}{\partial t^2}+\dfrac{\partial u}{\partial t}- \dfrac{\partial^2u}{\partial x^2}=f(u),\ \ \ -1<x<1,\ \ t>0,\\\\ u(-1,t)=u(1,t). \end{array}\right. \end{array} \end{aligned} $$

A semidiscretisation in the spatial variable by using second-order symmetric differences yields the type of (1.1)

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \begin{array}{ll} \ddot{U}+MU=F(U,\dot{U}), \end{array} \end{array} \end{aligned} $$

(1.65)

where $U(t)=\big (u_{1}(t),\cdots ,u_{N}(t)\big )^{\intercal }$ with u _i(t) ≈ u(x _i, t), x _i = −1 + i Δx for i = 1, ⋯ , N, Δx = 2∕N,

$$\displaystyle \begin{aligned} \begin{array}{rcl} M= \dfrac{1}{{\Delta} x^2}\left( \begin{array} [c]{ccccc} 2& -1 &\displaystyle &\displaystyle &\displaystyle -1\\ -1 & 2 &\displaystyle -1&\displaystyle &\displaystyle \\ & \ddots&\displaystyle \ddots&\displaystyle \ddots&\displaystyle \\ & &\displaystyle -1 &\displaystyle 2 &\displaystyle -1\\ -1 & &\displaystyle &\displaystyle -1&\displaystyle 2 \\ \end{array} \right), \end{array} \end{aligned} $$

and

$$\displaystyle \begin{aligned} \begin{array}{rcl} F(U,\dot{U})=\big( f(u_1)-\dot{u}_1, \cdots, f(u_N)-\dot{u}_N\big)^{\intercal}. \end{array} \end{aligned} $$

Inthis experiment, we consider the damped sine-Gordon equation with $f(u)=-\sin u$ and with the initial conditions

$$\displaystyle \begin{aligned} U(0)=(\pi)_{i=1}^{N},\ \ \ \dot{U}(0)=\sqrt{N}\Big(0.01+\sin{}(\dfrac{2 \pi i} {N})\Big)_{i=1}^{N}. \end{aligned}$$

This equation is integrated on [0, 100] with N = 256 and $h=\dfrac {0.1}{2^i}$ for i = 2, 3, 4, 5. The global errors against the stepsizes and the CPU time are shown in Fig. 1.4. It can be observed again from the results that the oscillation-preserving integrator ERKN3s3 performs much better than the other methods. It is easy to see that the ERKN3s3 integrator provides a considerably more accurate numerical solution than other methods.

Fig. 1.4

Results for Problem 1.4. (a) The log-log plot of global error GE against h. (b) The log-log plot of global error GE against CPU time

1.8 Conclusions and Discussion

In practice, nonlinear second-order differential equations with highly oscillatory solution behaviour are ubiquitous in science and engineering applications. The overarching question now is how to preserve high frequency oscillations in the numerical treatment of nonlinear multi-frequency highly oscillatory second-order ordinary differential equations (1.1) or (1.9). This chapter presented systematic oscillation-preserving analysis, which began with the concept of oscillation preservation for RKN-type methods, and then analysed oscillation-preserving behaviour for RKN-type methods, including ERKN integrators, TFC methods, AVF methods, AAVF methods, ARKN methods, symplectic and symmetric RKN methods, and standard RKN methods, designed to solve the initial value problem of nonlinear multi-frequency highly oscillatory second-order ordinary differential equations (1.1) or (1.9). It was found that the ERKN integrators and TFC methods are oscillation preserving, whereas neither the ARKN methods nor the standard RKN methods, including symplectic and symmetric RKN methods, and AVF methods, are oscillation preserving. However, ARKN and AAVF methods are partly oscillation preserving. An oscillation-preserving integrator shows much better numerical behaviour than those methods which are not oscillation preserving when applied to nonlinear multi-frequency highly oscillatory second-order ordinary differential equations. The least favourable results are for the RKN method, in comparison with the ARKN method and ERKN method when solving nonlinear multi-frequency highly oscillatory problems. Here the most interesting conclusion is that the oscillation-preserving property depends essentially on the internal stages rather than the updates of an RKN-type method when applied to highly oscillatory second-order systems. This chapter also mentioned the potential developments of ERKN integrators and TCF methods for the nonlinear multi-frequency highly oscillatory second-order ordinary differential equation (1.9).

An important concern relating to oscillation-preserving integrators is to efficiently solve a semidiscrete nonlinear wave equation, which usually is approximated by a system of nonlinear highly oscillatory second-order ordinary differential equations derived from a suitable space discretisation of semilinear wave equations such as KG equations, i.e., the operator $\mathbb {A}$ appearing in (1.59) is approximated by a d × d symmetric and positive semi-definite differentiation matrix M. Therefore, the analysis of oscillation-preserving behaviour for RKN-type methods in this chapter is also significant for numerical PDEs. In this case, the standard RKN method, in comparison with an oscillation-preserving integrator such as the ERKN method, may not be a satisfactory choice for efficiently dealing with such highly oscillatory problems.

This chapter focuses on highly oscillatory second-order differential equations (1.1) or (1.9). Other highly oscillatory systems will also be discussed in this monograph. For instance, in Chap. 5, using exponential collocation methods, we will deal with the following highly oscillatory system:

$$\displaystyle \begin{aligned} q^{\prime\prime}(t)-N q^{\prime}(t)+\varUpsilon q(t)=-\nabla U(q(t)), \qquad q(0)=q_0,\ \ q'(0)=q^{\prime}_0,\qquad t\in[0,T], \end{aligned}$$

where N is a symmetric negative semi-definite matrix, Υ is a symmetric positive semi-definite matrix, and $U: \mathbb {R}^{d}\rightarrow \mathbb {R}$ is a differentiable function.

Last, but not least, we believe that the oscillation-preserving concept introduced and analysed in this chapter for numerical methods for solving nonlinear multi-frequency highly oscillatory differential equations is significant and interesting within the broader framework of the subject of Geometric Integration. The results of numerical experiments in this chapter have strengthened the impression that an oscillation-preserving integrator is required when efficiently solving a nonlinear multi-frequency highly oscillatory system, or a semidiscrete nonlinear wave equation.

The material in this chapter is based on the work by Wu et al. [83].