An M/M/1 Queueing Model Subject to Differentiated Working Vacation and Customer Impatience

Abstract

This paper deals with the stationary and transient analysis of a single server queueing model subject to differentiated working vacation and customer impatience. Customers are assumed to arrive according to a Poisson process and the service times are assumed to be exponentially distributed. When the system empties, the single server takes a vacation of some random duration (Type I) and upon his return if the system is still empty, he takes another vacation of shorter duration (Type II). Both the vacation duration are assumed to follow exponential distribution. Further, the impatient behaviour of the waiting customer due to slow service during the period of vacation is also considered. Explicit expressions for the time dependent system size probabilities are obtained in terms of confluent hyper geometric series and modified Bessel’s function of first kind using Laplace transform, continued fractions and generating function methodologies. Numerical illustrations are added to depict the effect of variations in different parameter values on the time dependent probabilities.

1 Introduction

A vacation queueing system that distinguishes between two kinds of vacation that a server can take, namely, a shorter duration and a longer duration vacation is termed as queues subject to differentiated vacation. Ibe and Isijola (2014) obtained the analytical expressions for the steady-state system size probabilities of the M/M/1 queueing model subject to differentiated vacation. Phung Duc (2015) considered the same model introduced by Ibe and Isijola (2014) to derive the expressions for the sojourn time and the queue length and subsequently extended the model with working vacations to obtain steady-state results for system size probabilities and certain other performance measures. Vijayashree and Janani (2018) extended the studies of Ibe and Isijola (2014) on steady-state system size probabilities of the queueing model to the corresponding time dependent analysis using the probability generating function and Laplace transforms. Customer’s impatience is another important aspect of queueing models and it may occur due to the long wait in the queue. Recently, Suranga Sampth and Liu (2018) derived the transient solution for an M/M/1 queue with impatient customers, differentiated vacations and a waiting server. In many practical situations, it is reasonable to assume an alternate server during the vacation duration who works at a relatively slower pace. In this context, this paper studies an M/M/1 multiple vacation queueing models with two kinds of differentiated working vacations considering the impatient behaviour of the waiting customer during the vacation period of the server. Explicit expressions for the steady state and time-dependent system size probabilities are obtained. The model under consideration is relevant in several human involved systems like a clerk in a bank, a cashier in the super market and many more.

In recent years, the available bandwidth in communication system needs to meet several services such as video conferencing, video gaming, data off loading etc. thereby resulting in higher energy consumption. Hence, there arises a need to save the energy being consumed. With the advent of increase in mobile usage, various energy saving strategies were introduced. The IEEE.802.16e defines a sleep mode operation for conserving the power of mobile terminals. Sleep mode plays a central role for energy efficient usage in recent mobile technologies such as WiFi, 3G and WiMax. The sleep mode is characterized by the non-availability of the Mobile Stations (MS) as observed by the serving Base Stations (BS) to downlink and uplink traffic. In the data transfer between MS and BS, the MS can be modelled as a single server which in normal state is in active mode and switches off to sleep mode (Type I) and continues in listen interval (Type II) when no data packets are waiting in the buffer. In the IEEE standard the sleep state is peer specific and has two different modes of operations - light sleep and deep sleep mode. Chakraborthy (2016) revealed that there exists interesting performance tradeoffs among light sleep mode and deep sleep mode that can be explored to design an efficient power profile for mesh networks. Certain theoretical analysis work was carried out by various authors are Seo et al. (2014), Xiao (2005), Niu et al. (2001) to study the sleep mode operation employed in IEEE 802.16e. Among them, Xiao (2005) and Niu et al. (2001) construct queueing models with multiple vacations to analyse the power consumption and the delay.

2 Model Description

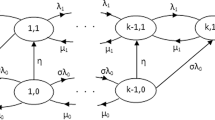
Consider a single server queueing model in which arrivals are allowed to join the system according to a Poisson process with parameter $\lambda$ and service takes place according to an exponential distribution with parameter $\mu$. The server takes a vacation of some random duration (type 1) if there are no customers in the system. When the server finds an empty system upon his return, the server takes another vacation of shorter duration (type 2). It is assumed that the server continues to provide service even during the vacation period, but at a slower rate rather than completely stopping the service. Such an assumption agrees well with most of the real time situations. The service time during type I and type II vacation are assumed to be exponentially distributed with parameters $\mu_{1} ( < \mu )$ and $\mu_{2} ( < \mu )$ respectively. Customers arriving while the system is in vacation state become impatient due to slow service. Each customer, upon arrival, activates an individual timer, which is exponentially distributed with parameter $\xi$ for both vacation types (type I and type II). If the customer’s service has not been completed before the customer’s timer expires, he abandons the system never to return. It is assumed that the inter-arrival times, service times, waiting times and vacation times are mutually independent and the service discipline is First-In First-Out. Furthermore, the vacation times of the server during type I and type II vacation are also assumed to follow exponential distribution with parameters $\gamma_{1}$ and $\gamma_{2}$ respectively. The state transition diagram for the queueing model under study is given in Fig. 1.

Fig. 1.

State Transition Diagram of an M/M/1 queueing system subject to differentiated working vacation and customer impatience.

Let $X\left( t \right)$ denote the number of the customer in the system and $S\left( t \right)$ represent the state of the server at time t, where $S\left( t \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\text{if}\,\text{ the}\,\text{ server}\,\text{ is}\,\text{ busy}} \hfill \\ {1,} \hfill & {\rm{if}\,\text{ the }\,\text{server}\,\text{ is}\,\text{ in}\,\text{ type}\,\text{ I}\,\text{ vacation}} \hfill \\ {2,} \hfill & {\rm{if}\,\text{ the}\,\text{ server}\,\text{ is}\,\text{ in}\,\text{ type}\,\text{ II}\,\text{ vacation}\rm{.}} \hfill \\ \end{array} } \right.$

It can be readily seen that the process $\left\{ {X \left( t \right), S \left( t \right) } \right\}$ forms a Markov process on the state space

$$ \Omega = \left\{ {\left( {0,1} \right) \cup \left( {0,2} \right) \cup \left( {n,j} \right);n = 1,2..;j = 0,1,2} \right\} . $$

2.1 Governing Equations

Let $P_{n,j} \left( t \right)$ denote the time dependent probability for the system to be in state j with n customers at time t. Assume that initially the system is empty and the server is in type I vacation. By standard methods, the system of Kolmogorov differential difference equations governing the process are given by

$$ P_{1,0}^{'} \left( t \right) = - \left( {\lambda + \mu } \right)P_{1,0} \left( t \right) + \mu P_{2,0} \left( t \right) + \gamma_{1} P_{1,1} \left( t \right) + \gamma_{2} P_{1,2} \left( t \right) $$

(2.1)

$$ \begin{aligned} P_{n,0}^{'} \left( t \right) = - \left( {\lambda + \mu } \right)P_{n,0} \left( t \right) + \mu P_{n + 1,0} \left( t \right) + \lambda P_{n - 1,0} \left( t \right) + \gamma_{1} P_{n,1} \left( t \right) + \gamma_{2} P_{n,2} \left( t \right) , \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,n = 2,3.. \hfill \\ \end{aligned} $$

(2.2)

$$ P_{0,1}^{'} \left( t \right) = - \left( {\lambda + \gamma_{1} } \right)P_{0,1} \left( t \right) + \mu P_{1,0} \left( t \right) + (\mu_{1} + \xi )P_{1,1} \left( t \right) $$

(2.3)

$$ P_{n,1}^{'} \left( t \right) = - \left( {\lambda + \gamma_{1} + \mu_{1} + n\xi } \right)P_{n,1} \left( t \right) + \lambda P_{n - 1,1} \left( t \right) + (\mu_{1} + \left( {n + 1} \right)\xi )P_{n + 1,1} \left( t \right) $$

(2.4)

$$ P_{0,2}^{'} \left( t \right) = - \lambda P_{0,2} \left( t \right) + (\mu_{2} + \xi )P_{1,2} \left( t \right) + \gamma_{1} P_{0,1} \left( t \right) $$

(2.5)

$$ P_{n,2}^{'} \left( t \right) = - \left( {\lambda + \gamma_{2} + \mu_{2} + n\xi } \right)P_{n,2} \left( t \right) + \lambda P_{n - 1,2} \left( t \right) + (\mu_{2} + \left( {n + 1} \right)\xi )P_{n + 1,2} \left( t \right) $$

(2.6)

with $P_{0,1} \left( 0 \right) = 1, P_{0,2} \left( 0 \right) = 0 \,{\text{and}} \,P_{n,j} \left( 0 \right) = 0$ for n = 1,2,3… and j = 0,1,2,..

3 Transient Analysis

In this section, the time–dependent system size probabilities for the model under consideration are obtained using Laplace transform, continued fractions and probability generating function method in terms of modified Bessel functions of first kind and confluent hypergeometric function.

3.1 Evaluation of $\varvec{P}_{{\varvec{n},1}} \left( \varvec{t} \right)$ and $\varvec{P}_{{\varvec{n},2}} \left( \varvec{t} \right)$

Let $\hat{P}_{n,j} \left( s \right)$ be the Laplace transform of $P_{n,j} \left( t \right); n = 0,1 \ldots \,{\text{and}}\, \,\,j = 0,1,2.$ Taking Laplace transform of the Eqs. (2.4) and (2.6) leads to

$$ \begin{aligned} & s\hat{P}_{n,1} \left( s \right) - P_{n,1} \left( 0 \right) = - \left( {\lambda + \gamma_{1} + \mu_{1} + n\xi } \right)\hat{P}_{n,1} \left( s \right) + \lambda \hat{P}_{n - 1,1} \left( s \right) \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,(\mu_{1} + \left( {n + 1} \right)\xi )\hat{P}_{n + 1,1} \left( s \right) \\ \end{aligned} $$

(3.1)

and

$$ \begin{aligned} & s\hat{P}_{n,2} \left( s \right) - P_{n,2} \left( 0 \right) = - \left( {\lambda + \gamma_{2} + \mu_{2} + n\xi } \right)\hat{P}_{n,2} \left( s \right) + \lambda \hat{P}_{n - 1,2} \left( s \right) \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,(\mu_{2} + \left( {n + 1} \right)\xi )\hat{P}_{n + 1,2} \left( s \right) \\ \end{aligned} $$

(3.2)

Using the boundary conditions and rewriting Eq. (3.1) yields

$$ \frac{{\hat{P}_{n,1} \left( s \right)}}{{\hat{P}_{n - 1,1} \left( s \right)}} = \frac{\lambda }{{s + \lambda + \gamma_{1} + \mu_{1} + n\xi - (\mu_{1} + \left( {n + 1} \right)\xi )\frac{{\hat{P}_{n + 1,1} \left( s \right)}}{{\ddot{P}_{n,1} \left( s \right)}}}} $$

which further yields the continued fraction given by

$$ \frac{{\hat{P}_{n,1} \left( s \right)}}{{\hat{P}_{n - 1,1} \left( s \right)}} = \frac{\lambda }{{\left( {s + \lambda + \gamma_{1} + \mu_{1} + n\xi } \right) - \frac{{\lambda (\mu_{1} + \left( {n + 1} \right)\xi )}}{{\left( {s + \lambda + \gamma_{1} + \mu_{1} + \left( {n + 1} \right)\xi } \right) - \frac{{\lambda (\mu_{1} + \left( {n + 2} \right)\xi )}}{{\left( {s + \lambda + \gamma_{1} + \mu_{1} + \left( {n + 2} \right)\xi } \right)}} - \ldots }}}} $$

Using the identity (Refer Lorentzen and Waadeland 1992) relating continued fractions and hypergeometric series given by

$$ \frac{{{}_{1}{\text{F}}_{1} \left( {a + 1 ;c + 1;z} \right)}}{{{}_{1}{\rm{F}}_{1} \left( {a ;c;z} \right)}} = \frac{\text{c}}{{{\rm{c}} - {\text{z}}}} \frac{{\left( {{\rm{a}} + 1} \right){\text{z}}}}{{ + {\rm{c}} - {\text{z}} + 1}} \frac{{\left( {{\rm{a}} + 2} \right){\text{z}}}}{{{\rm{c}} - {\text{z}} + 2}} \ldots , $$

where ${}_{1}{\text{F}}_{1} \left( {a ;c;z} \right)$ is the confluent hypergeometric function, we get

$$ \frac{{\hat{P}_{n,1} \left( s \right)}}{{\hat{P}_{n - 1,1} \left( s \right)}} = \frac{\lambda }{{\xi \left( {\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + n} \right)}} \frac{{{}_{1}{\text{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + n + 1 ;\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + n + 1; - \frac{\lambda }{\xi }} \right)}}{{{}_{1}{\rm{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + n ;\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + n; - \frac{\lambda }{\xi }} \right)}}, $$

for $n = 1,2,3 \ldots$ . Hence, we recursively obtain

$$ \hat{P}_{n,1} \left( s \right) = \hat{\phi }_{n} \left( s \right)\hat{P}_{0,1} \left( s \right) $$

(3.3)

where

$$ \hat{\phi }_{n} \left( s \right) = \left( {\frac{\lambda }{\xi }} \right)^{n} \frac{1}{{\mathop \prod \nolimits_{i = 1}^{n} \left( {\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + i} \right)}}\frac{{{}_{1}{\text{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + n + 1 ;\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + n + 1; - \frac{\lambda }{\xi }} \right)}}{{{}_{1}{\rm{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + 1 ;\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + 1; - \frac{\lambda }{\xi }} \right)}} . $$

In particular, when $n = 1$, Eq. (3.3) becomes

$$ \hat{P}_{1,1} \left( s \right) = \hat{\phi }_{1} \left( s \right)\hat{P}_{0,1} \left( s \right). $$

(3.4)

Now, taking Laplace transform of Eq. (2.3) and applying the boundary conditions leads to

$$ s\hat{P}_{0,1} \left( s \right) - P_{0,1} \left( 0 \right) = - \left( {\lambda + \gamma_{1} } \right)\hat{P}_{0,1} \left( s \right) + \mu \hat{P}_{1,0} \left( s \right) + (\mu_{1} + \xi )\hat{P}_{1,1} \left( s \right), $$

and hence

$$ \hat{P}_{0,1} \left( s \right) = \frac{1}{{s + \lambda + \gamma_{1} }} + \frac{\mu }{{s + \lambda + \gamma_{1} }}\hat{P}_{1,0} \left( s \right) + \frac{{(\mu_{1} + \xi )}}{{s + \lambda + \gamma_{1} }}\hat{P}_{1,1} \left( s \right). $$

(3.5)

Substituting Eq. (3.4) in the Eq. (3.5) and after some algebra, we get

$$ \hat{P}_{0,1} \left( s \right) = \left( {1 + \mu \hat{P}_{1,0} \left( s \right)} \right)\mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\hat{\phi }_{1} \left( s \right)} \right]^{r} }}{{\left( {s + \lambda + \gamma_{1} } \right)^{r + 1} }} . $$

(3.6)

Substituting Eq. (3.6) in Eq. (3.3) yields

$$ \hat{P}_{n,1} \left( s \right) = \left( {1 + \mu \hat{P}_{1,0} \left( s \right)} \right)\hat{\phi }_{n} \left( s \right)\mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\hat{\phi }_{1} \left( s \right)} \right]^{r} }}{{\left( {s + \lambda + \gamma_{1} } \right)^{r + 1} }}, n = 1,2,3. $$

(3.7)

Applying the boundary conditions to Eq. (3.2) and using the same procedure as above to evaluate $\hat{P}_{n,1} \left( s \right)$, it is seen that $\hat{P}_{n,2} \left( s \right)$ can be expressed as

$$ \hat{P}_{n,2} \left( s \right) = \hat{\psi }_{n} \left( s \right)\hat{P}_{0,2} \left( s \right) $$

(3.8)

where

$$ \hat{\psi }_{n} \left( s \right) = \left( {\frac{\lambda }{\xi }} \right)^{n} \left( {\frac{1}{{\mathop \prod \nolimits_{i = 1}^{n} \left( {\frac{{s + \gamma_{2} + \mu_{2} }}{\xi } + i} \right)}}} \right)\left( {\frac{{{}_{1}{\text{F}}_{1} \left( {\frac{{\mu_{2} }}{\xi } + n + 1 ;\frac{{s + \gamma_{2} + \mu_{2} }}{\xi } + n + 1; - \frac{\lambda }{\xi }} \right)}}{{{}_{1}{\rm{F}}_{1} \left( {\frac{{\mu_{2} }}{\xi } + 1 ;\frac{{s + \gamma_{2} + \mu_{2} }}{\xi } + 1; - \frac{\lambda }{\xi }} \right)}}} \right) . $$

In particular, when $n = 1$, Eq. (3.8) becomes

$$ \hat{P}_{1,2} \left( s \right) = \hat{\psi }_{1} \left( s \right)\hat{P}_{0,2} \left( s \right). $$

(3.9)

Again taking Laplace transform of Eq. (2.5) leads to

$$ s\hat{P}_{0,2} \left( s \right) - P_{0,2} \left( 0 \right) = - \lambda \hat{P}_{0,2} \left( s \right) + (\mu_{2} + \xi )\hat{P}_{1,2} \left( s \right) + \gamma_{1} \hat{P}_{0,1} \left( s \right), $$

and hence

$$ \hat{P}_{0,2} \left( s \right) = \frac{{(\mu_{2} + \xi )}}{s + \lambda }\hat{P}_{1,2} \left( s \right) + \frac{{\gamma_{1} }}{s + \lambda }\hat{P}_{0,1} \left( s \right). $$

(3.10)

Substituting Eq. (3.6) and Eq. (3.9) in the Eq. (3.10) and after some algebra, we get

$$ \hat{P}_{0,2} \left( s \right) = \gamma_{1} \left( {1 + \mu \hat{P}_{1,0} \left( s \right)} \right)\mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\hat{\phi }_{1} \left( s \right)} \right]^{r} }}{{\left( {s + \lambda + \gamma_{1} } \right)^{r + 1} }}\mathop \sum \limits_{m = 0}^{\infty } \frac{{\left( {\mu_{2} + \xi } \right)^{m} \left[ {\hat{\psi }_{1} \left( s \right)} \right]^{m} }}{{\left( {s + \lambda } \right)^{m + 1} }} . $$

(3.11)

Substituting Eq. (3.11) in Eq. (3.8) yields

$$ \hat{P}_{n,2} \left( s \right) = \gamma_{1} \left( {1 + \mu \hat{P}_{1,0} \left( s \right)} \right)\hat{\psi }_{n} \left( s \right)\mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\hat{\phi }_{1} \left( s \right)} \right]^{r} }}{{\left( {s + \lambda + \gamma_{1} } \right)^{r + 1} }}\mathop \sum \limits_{m = 0}^{\infty } \frac{{\left( {\mu_{2} + \xi } \right)^{m} \left[ {\hat{\psi }_{1} \left( s \right)} \right]^{m} }}{{\left( {s + \lambda } \right)^{m + 1} }} $$

(3.12)

Taking Laplace inverse for Eq. (3.7) and Eq. (3.12) leads to

$$ \begin{aligned} & P_{n,1} \left( t \right) = \left( {\delta \left( t \right) + \mu P_{1,0} \left( t \right)} \right)*\phi_{n} \left( t \right)*\mathop \sum \limits_{r = 0}^{\infty } \left( {\mu_{1} + \xi } \right)^{r} \left[ {\phi_{1} \left( t \right)} \right]^{*r} *e^{{ - \left( {\lambda + \gamma_{1} } \right)t}} \frac{{\left( t \right)^{r} }}{r!}, \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varvec{ }n = 0,1,2, \ldots \\ \end{aligned} $$

(3.13)

and

$$ \begin{aligned} & P_{n,2} \left( t \right) = \gamma_{1} \left( {\delta \left( t \right) + \mu P_{1,0} \left( t \right)} \right)*\psi_{n} \left( t \right)*\mathop \sum \limits_{r = 0}^{\infty } \left[ {\phi_{1} \left( t \right)} \right]^{*r} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;*e^{{ - \left( {\lambda + \gamma_{1} } \right)t}} \frac{{\left( {\left( {\mu_{1} + \xi } \right)t} \right)^{r} }}{r!}\mathop \sum \limits_{m = 0}^{\infty } \left[ {\psi_{1} \left( t \right)} \right]^{*m} *e^{{- \lambda t }} \frac{{\left( {\left( {\mu_{2} + \xi } \right)t} \right)^{m} }}{m!}, \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n = 0,1,2 \ldots . \\ \end{aligned} $$

(3.14)

ltiple vacation queueing systems with

where $\delta \left( t \right)\varvec{ }$ is the Kronecker delta function and $\phi_{\varvec{n}} \left( \varvec{t} \right)$ and $\psi_{n} \left( t \right)$ for all values of n are derived in the Appendix. Therefore, all the time dependent probabilities of the number in the system during the vacation period of the server (both type I and type II vacation) are expressed in terms of $P_{1,0} \left( t \right).$ It still remains to determine  $P_{1,0} \left( t \right).$

3.2 Evaluation of $\varvec{P}_{n,0} \left( \varvec{t} \right)$

Towards this end, define the probability generating function, $Q\left( {z,t} \right)\varvec{ }$ as $Q\left( {z,t} \right) = \sum\nolimits_{n = 1}^{\infty } {P_{n,0} \left( t \right)z^{n} .}$ Then, $\frac{{\partial Q\left( {z,t} \right)}}{\partial t} = \sum\nolimits_{n = 1}^{\infty } {P_{n,0}^{'} \left( t \right)z^{n} .}$

Multiplying Eq. (2.2) by $z^{n}$ and summing it over all possible values of n leads to

$$ \begin{aligned} & \mathop \sum \limits_{n = 2}^{\infty } P_{n,0}^{'} \left( t \right)z^{n} = - \left( {\lambda + \mu } \right)\mathop \sum \limits_{n = 2}^{\infty } P_{n,0} \left( t \right)z^{n} + \lambda z\mathop \sum \limits_{n = 2}^{\infty } P_{n - 1,0} \left( t \right)z^{n - 1} + \frac{\mu }{z}\mathop \sum \limits_{n = 2}^{\infty } P_{n + 1,0} \left( t \right)z^{n + 1} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,\,\, + \,\gamma_{1} \mathop \sum \limits_{n = 2}^{\infty } P_{n,1} \left( t \right)z^{n} + \gamma_{2} \mathop \sum \limits_{n = 2}^{\infty } P_{n,2} \left( t \right)z^{n} + \left( {\lambda + \mu } \right)P_{1,0} \left( t \right)z. \\ \end{aligned} $$

(3.15)

Multiplying Eq. (2.1) by $z$, we get

$$ P_{1,0}^{'} \left( t \right)z = - \left( {\lambda + \mu } \right)P_{1,0} \left( t \right)z + \mu P_{2,0} \left( t \right)z + \gamma_{1} P_{1,1} \left( t \right)z + \gamma_{2} P_{1,2} \left( t \right) z . $$

(3.16)

Now, adding the above two equations yields

$$ \begin{aligned} & \frac{{\partial Q\left( {z,t} \right)}}{\partial t} - \left( { - \left( {\lambda + \mu } \right) + \frac{\mu }{z} + \lambda z} \right)Q\left( {z,t} \right) \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \gamma_{1} \mathop \sum \limits_{n = 1}^{\infty } P_{n,1} \left( t \right)z^{n} + \gamma_{2} \mathop \sum \limits_{n = 1}^{\infty } P_{n,2} \left( t \right)z^{n} - \mu P_{1,0} \left( t \right). \\ \end{aligned} $$

Integrating the above linear differential equation with respect to ‘$t$’ leads to

$$ \begin{aligned} & Q\left( {z,t} \right) = \gamma_{1} \int_{0}^{t} {\left( {\mathop \sum \limits_{n = 1}^{\infty } P_{n,1} \left( y \right)z^{n} } \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} e^{{\left( {\frac{\mu }{z} + \lambda z} \right)\left( {t - y} \right)}} dy} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \,\gamma_{2} \int_{0}^{t} {\left( {\mathop \sum \limits_{n = 1}^{\infty } P_{n,2} \left( y \right)z^{n} } \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} e^{{\left( {\frac{\mu }{z} + \lambda z} \right)\left( {t - y} \right)}} dy} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \,\mu \int_{0}^{t} {P_{1,0} \left( y \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} e^{{\left( {\frac{\mu }{z} + \lambda z} \right)\left( {t - y} \right)}} dy.} \\ \end{aligned} . $$

(3.17)

It is well known that if $\alpha = 2\sqrt {\lambda \mu }$ and $\beta = \sqrt {\frac{\lambda }{\mu } }$, then the generating function of the modified Bessel function of the first kind of order n represented by $I_{n} \left( . \right)$ is given by

$$ exp\left( {\frac{\mu t}{z} + \lambda zt} \right) = \mathop \sum \limits_{n = - \infty }^{\infty } \left( {\beta z} \right)^{n} I_{n} \left( {\alpha t} \right). $$

Comparing the coefficients of $z^{n}$ in Eq. (3.17) for $n = 1,2,3 \ldots .$ leads to

$$ \begin{aligned} & P_{n,0} \left( t \right) = \gamma_{1} \int_{0}^{t} {\mathop \sum \limits_{k = 1}^{\infty } P_{k,1} \left( y \right)\beta^{n - k} I_{n - k} \left( {\alpha \left( {t - y} \right)} \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \,\gamma_{2} \int_{0}^{t} {\mathop \sum \limits_{k = 1}^{\infty } P_{k,2} \left( y \right)\beta^{n - k} I_{n - k} \left( {\alpha \left( {t - y} \right)} \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \,\mu \int_{0}^{t} {P_{1,0} \left( y \right)\beta^{n} I_{n} \left( {\alpha \left( {t - y} \right)} \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy.} \\ \end{aligned} $$

(3.18)

Comparing the coefficients of $z^{ - n}$ in Eq. (3.17) yields

$$ \begin{aligned} & 0 = \gamma_{1} \int_{0}^{t} {\mathop \sum \limits_{k = 1}^{\infty } P_{k,1} \left( y \right)\beta^{ - n - k} I_{ - n - k} \left( {\alpha \left( {t - y} \right)} \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \,\gamma_{2} \int_{0}^{t} {\mathop \sum \limits_{k = 1}^{\infty } P_{k,2} \left( y \right)\beta^{ - n - k} I_{ - n - k} \left( {\alpha \left( {t - y} \right)} \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\, - \,\mu \int_{0}^{t} {P_{1,0} \left( y \right)\beta^{ - n} I_{ - n} \left( {\alpha \left( {t - y} \right)} \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy . } \\ \end{aligned} $$

Multiplying the above equation by $\beta^{2n}$ and using the property $I_{ - n} \left( t \right) = I_{n} \left( t \right)$, we get

$$ \begin{aligned} & 0 = \gamma_{1} \int_{0}^{t} {\mathop \sum \limits_{k = 1}^{\infty } P_{k,1} \left( y \right)\beta^{n - k} I_{n + k} \left( {\alpha \left( {t - y} \right)} \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\; + \,\gamma_{2} \int_{0}^{t} {\mathop \sum \limits_{k = 1}^{\infty } P_{k,2} \left( y \right)\beta^{n - k} I_{n + k} \left( {\alpha \left( {t - y} \right)} \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\; - \,\mu \int_{0}^{t} {P_{1,0} \left( y \right)\beta^{n} I_{n} \left( {\alpha \left( {t - y} \right)} \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy. } \\ \end{aligned} $$

(3.19)

Subtracting Eq. (3.18) from Eq. (3.19) leads to

$$ \begin{aligned} & P_{n,0} \left( t \right) = \gamma_{1} \int_{0}^{t} {\mathop \sum \limits_{k = 1}^{\infty } P_{k,1} \left( y \right)\beta^{n - k} (I_{n - k} \left( {\alpha \left( {t - y)} \right) - I_{n + k} \left( {\alpha \left( {t - y} \right)} \right)} \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \,\gamma_{2} \int_{0}^{t} {\mathop \sum \limits_{k = 1}^{\infty } P_{k,2} \left( y \right)\beta^{n - k} (I_{n - k} (\alpha \left( {t - y)} \right)} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \,I_{n + k} \left( {\alpha \left( {t - y} \right)} \right))e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy. \\ \end{aligned} $$

(3.20)

for $n = 1,2,3, \ldots$. Thus $P_{n,0} \left( t \right)$ is expressed in terms of $P_{k,1} \left( t \right)$ and $P_{k,2} \left( t \right)$ which are expressed in terms of $P_{1,0} \left( t \right)$ in Eq. (3.13) and Eq. (3.14) respectively. It still remains to determine $P_{1,0} \left( t \right)$ explicitly. Substituting $n = 1$ in Eq. (3.20) yields

$$ \begin{aligned} & P_{1,0} \left( t \right) = \gamma_{1} \int_{0}^{t} {\mathop \sum \limits_{k = 1}^{\infty } P_{k,1} \left( y \right)\beta^{1 - k} (I_{1 - k} \left( {\alpha \left( {t - y)} \right) - I_{1 + k} \left( {\alpha \left( {t - y} \right)} \right)} \right)e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \,\gamma_{2} \int_{0}^{t} {\mathop \sum \limits_{k = 1}^{\infty } P_{k,2} \left( y \right)\beta^{1 - k} (I_{1 - k} (\alpha \left( {t - y)} \right)} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \,I_{1 + k} \left( {\alpha \left( {t - y} \right)} \right))e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy. \\ \end{aligned} $$

Using the property $I_{k - 1} \left( t \right) - I_{k + 1} \left( t \right) = \frac{{2kI_{k} \left( t \right)}}{t}$ and $I_{1 - k} \left( t \right) = I_{k - 1} \left( t \right)$, we get

$$ \begin{aligned} & P_{1,0} \left( t \right) = \gamma_{1} \int_{0}^{t} {\mathop \sum \limits_{k = 1}^{\infty } P_{k,1} \left( y \right)\beta^{1 - k} \frac{{2kI_{k} (\alpha \left( {t - y)} \right)}}{{\alpha \left( {t - y} \right)}}e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy} \\ & \;\;\;\;\;\;\;\;\;\;\; + \,\gamma_{2} \int_{0}^{t} {\mathop \sum \limits_{k = 1}^{\infty } P_{k,2} \left( y \right)\beta^{1 - k} \frac{{2kI_{k} (\alpha \left( {t - y)} \right)}}{{\alpha \left( {t - y} \right)}}e^{{ - \left( {\lambda + \mu } \right)\left( {t - y} \right)}} dy .} \\ \end{aligned} $$

(3.21)

Taking Laplace transform of Eq. (3.21) leads to

$$ \begin{aligned} & \hat{P}_{1,0} \left( s \right) = 2\gamma_{1} \mathop \sum \limits_{k = 1}^{\infty } \hat{P}_{k,1} \left( s \right)\beta^{1 - k} \frac{1}{{\alpha ^{{{-}k + 1}} \left( {p + \sqrt {p^{2} - \alpha^{2} } } \right)^{k} }} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \,2\gamma_{2} \mathop \sum \limits_{k = 1}^{\infty } \hat{P}_{k,2} \left( s \right)\beta^{1 - k} \frac{1}{{\alpha ^{{{-}k + 1}} \left( {p + \sqrt {p^{2} - \alpha^{2} } } \right)^{k} }} \\ \end{aligned} $$

(3.22)

where $p = s + \lambda + \mu .$ Substituting for $\hat{P}_{k,1} \left( s \right)$ and $\hat{P}_{k,2} \left( s \right)$ from Eq. (3.7) and Eq. (3.12) in Eq. (3.22) leads to

$$ \begin{aligned} \hat{P}_{1,0} \left( s \right) = 2\gamma_{1} \sum\limits_{k = 1}^{\infty } {\beta^{1 - k} \frac{{\left( {1 + \mu \hat{P}_{1,0} \left( s \right)} \right)}}{{\alpha ^{{{-}k + 1}} \left( {p + \sqrt {p^{2} - \alpha^{2} } } \right)^{k} }}\hat{\phi }_{k} \left( s \right)\mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\hat{\phi }_{1} \left( s \right)} \right]^{r} }}{{\left( {s + \lambda + \gamma_{1} } \right)^{r + 1} }} } \hfill \\ \;\;\;\;\;\;\;\;\;\;\; + \,2\gamma_{2} \gamma_{1} \mathop \sum \limits_{k = 1}^{\infty } \beta^{1 - k} \frac{{\left( {1 + \mu \hat{P}_{1,0} \left( s \right)} \right)}}{{\alpha ^{{{-}k + 1}} \left( {p + \sqrt {p^{2} - \alpha^{2} } } \right)^{k} }}\hat{\psi }_{k} \left( s \right)\mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\hat{\phi }_{1} \left( s \right)} \right]^{r} }}{{\left( {s + \lambda + \gamma_{1} } \right)^{r + 1} }} \hfill \\ \end{aligned} $$

$$ \mathop \sum \limits_{m = 0}^{\infty } \frac{{\left( {\mu_{2} + \xi } \right)^{m} \left[ {\hat{\psi }_{1} \left( s \right)} \right]^{m} }}{{\left( {s + \lambda } \right)^{m + 1} }}, $$

which further yields

$$ \hat{P}_{1,0} \left( s \right)\left( {1 - \hat{H}\left( s \right)} \right) = \frac{{\hat{H}\left( s \right)}}{\mu }, $$

where

$$ \begin{aligned} \hat{H}\left( s \right) = \gamma_{1} \mathop \sum \limits_{k = 1}^{\infty } \left( {\frac{1}{\beta }} \right)^{k} \left( {\frac{{p - \sqrt {p^{2} - \alpha^{2} } }}{\alpha }} \right)^{k} \mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\hat{\phi }_{1} \left( s \right)} \right]^{r} }}{{\left( {s + \lambda + \gamma_{1} } \right)^{r + 1} }} \hfill \\ \,\,\quad \quad \quad \left( {\hat{\phi }_{k} \left( s \right) + \gamma_{2} \hat{\psi }_{k} \left( s \right)\mathop \sum \limits_{m = 0}^{\infty } \frac{{\left( {\mu_{2} + \xi } \right)^{m} \left[ {\hat{\psi }_{1} \left( s \right)} \right]^{m} }}{{\left( {s + \lambda } \right)^{m + 1} }}} \right). \hfill \\ \end{aligned} $$

Therefore, we get

$$ \hat{P}_{1,0} \left( s \right) = \frac{{\hat{H}\left( s \right)}}{{\mu \left( {1 - \hat{H}\left( s \right)} \right) }} = \frac{{\hat{H}\left( s \right)}}{\mu }\mathop \sum \limits_{k = 0}^{\infty } \left( {\hat{H}\left( s \right)} \right)^{k} = \frac{1}{\mu }\mathop \sum \limits_{k = 0}^{\infty } \left( {\hat{H}\left( s \right)} \right)^{k + 1} $$

Laplace inversion of the above equation yields

$$ P_{1,0} \left( t \right) = \frac{1}{\mu }\mathop \sum \limits_{k = 0}^{\infty } \left( {H\left( t \right)} \right)^{{*\left( {k + 1} \right)}} , $$

(3.23)

where $H\left( t \right)$ is given by

$$ \begin{aligned} & H\left( t \right) = \gamma_{1} \mathop \sum \limits_{k = 1}^{\infty } \left( {\frac{1}{\beta }} \right)^{k} \frac{{kI_{k} \left( {\alpha t} \right)}}{t} e^{{ - \left( {\lambda + \mu } \right)t}} *\mathop \sum \limits_{r = 0}^{\infty } \left( {\mu_{1} + \xi } \right)^{r} \left[ {\phi_{1} \left( t \right)} \right]^{*r} *e^{{ - \left( {\lambda + \gamma_{1} } \right)t}} \frac{{\left( t \right)^{r} }}{r!} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;*\,\left( {\phi_{k} \left( t \right) + \gamma_{2} \psi_{k} \left( t \right)*\mathop \sum \limits_{m = 0}^{\infty } \left[ {\psi_{1} \left( t \right)} \right]^{*m} *e^{ - \lambda t} \frac{{\left( {\left( {\mu_{2} + \xi } \right)t} \right)^{m} }}{m!}} \right) \\ \end{aligned} $$

Note that Eqs. (3.13) and (3.14) present explicit expressions for $P_{n,1} \left( t \right)$ and $P_{n,2} \left( t \right)$ in terms of $P_{1,0} \left( t \right)$ where $P_{1,0} \left( t \right)$ is given by Eq. (3.23). All other probabilities, namely $P_{n,0} \left( t \right)$ are determined in terms of $P_{n,1} \left( t \right)$ and $P_{n,2} \left( t \right)$ in Eq. (3.20). Therefore, all the time –dependent probabilities are explicitly obtained in terms of modified Bessel function of the first kind using generating function methodology. Having determined the transient state probabilities, all other performance measures can be readily analysed.

4 Steady State Probabilities

Let $\pi_{n,j}$ denote the steady – state probability for the system to be in state j with n customers. Mathematically,

$$ \pi_{n,j} = \mathop {\lim }\limits_{t \to \infty } P_{n,j} \left( t \right) $$

Using the final value theorem of Laplace transform, which states

$$ \mathop {\lim }\limits_{t \to \infty } P_{n,j} \left( t \right) = \mathop {\lim }\limits_{s \to 0} s \,\hat{P}_{n,j} \left( s \right). $$

It is observed that

$$ \pi_{n,j} = \mathop {\lim }\limits_{s \to 0} s\,\hat{P}_{n,j} \left( s \right), $$

From Eq. (3.17), we get

$$ \mathop {\lim }\limits_{s \to 0} s \hat{P}_{n,1} \left( s \right) = \mathop {\lim }\limits_{s \to 0} s\left\{ {\left( {1 + \mu \hat{P}_{1,0} \left( s \right)} \right)\hat{\phi }_{n} \left( s \right)\mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\hat{\phi }_{1} \left( s \right)} \right]^{r} }}{{\left( {s + \lambda + \gamma_{1} } \right)^{r + 1} }}} \right\}, $$

and hence

$$ \pi_{n,1} = \left[ {\mu \phi_{n} \mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\phi_{1} } \right]^{r} }}{{\left( {\lambda + \gamma_{1} } \right)^{r + 1} }}} \right]\pi_{1,0} . $$

where

$$ \phi_{n} = \mathop {\lim }\limits_{s \to 0} s\hat{\phi }_{n} \left( s \right) = \left( {\frac{\lambda }{\xi }} \right)^{n} \frac{1}{{\mathop \prod \nolimits_{i = 1}^{n} \left( {\frac{{\gamma_{1} + \mu_{1} }}{\xi } + i} \right)}}\frac{{{}_{1}{\text{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + n + 1 ;\frac{{\gamma_{1} + \mu_{1} }}{\xi } + n + 1; - \frac{\lambda }{\xi }} \right)}}{{{}_{1}{\rm{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + 1 ;\frac{{\gamma_{1} + \mu_{1} }}{\xi } + 1; - \frac{\lambda }{\xi }} \right)}} $$

Similarly, from Eq. (3.10), we get

$$ \begin{aligned} \mathop {\lim }\limits_{s \to 0} s \hat{P}_{n,2} \left( s \right) = \mathop {\lim }\limits_{s \to 0} s\left\{ {\gamma_{1} \left( {1 + \mu \hat{P}_{1,0} \left( s \right)} \right)\hat{\psi }_{n} \left( s \right)\mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\hat{\phi }_{1} \left( s \right)} \right]^{r} }}{{\left( {s + \lambda + \gamma_{1} } \right)^{r + 1} }}} \right. \hfill \\ \left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathop \sum \limits_{m = 0}^{\infty } \frac{{\left( {\mu_{2} + \xi } \right)^{m} \left[ {\hat{\psi }_{1} \left( s \right)} \right]^{m} }}{{\left( {s + \lambda } \right)^{m + 1} }}} \right\} \hfill \\ \end{aligned} $$

and hence

$$ \pi_{n,2} = \left[ {\gamma_{1} \mu \psi_{n} \mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\phi_{1} } \right]^{r} }}{{\left( {\lambda + \gamma_{1} } \right)^{r + 1} }}\mathop \sum \limits_{m = 0}^{\infty } \frac{{\left( {\mu_{2} + \xi } \right)^{m} \left[ {\psi_{1} } \right]^{m} }}{{\left( \lambda \right)^{m + 1} }}} \right]\pi_{1,0} . $$

where

$$ \psi_{n} = \mathop {\lim }\limits_{s \to 0} s\hat{\psi }_{n} \left( s \right) = \left( {\frac{\lambda }{\xi }} \right)^{n} \frac{1}{{\mathop \prod \nolimits_{i = 1}^{n} \left( {\frac{{\gamma_{2} + \mu_{2} }}{\xi } + i} \right)}}\frac{{{}_{1}{\text{F}}_{1} \left( {\frac{{\mu_{2} }}{\xi } + n + 1 ;\frac{{\gamma_{2} + \mu_{2} }}{\xi } + n + 1; - \frac{\lambda }{\xi }} \right)}}{{{}_{1}{\rm{F}}_{1} \left( {\frac{{\mu_{2} }}{\xi } + 1 ;\frac{{\gamma_{2} + \mu_{2} }}{\xi } + 1; - \frac{\lambda }{\xi }} \right)}} $$

Also, consider the Laplace transform of Eq. (3.20) given by

$$ \begin{aligned} \hat{P}_{n,0} \left( s \right) = \mathop \sum \limits_{n = 1}^{\infty } \left\{ {\gamma_{1} \mathop \sum \limits_{k = 1}^{\infty } \hat{P}_{k,1} \left( s \right)\beta^{n - k} \left\{ {\frac{{\left( {p - \sqrt {p^{2} - \alpha^{2} } } \right)^{n - k} }}{{\alpha^{n - k} \sqrt {p^{2} - \alpha^{2} } }} - \frac{{\left( {p - \sqrt {p^{2} - \alpha^{2} } } \right)^{n + k} }}{{\alpha^{n + k} \sqrt {p^{2} - \alpha^{2} } }} } \right\}} \right. \hfill \\ \left. {\quad \quad \quad \quad + \,\gamma_{2} \mathop \sum \limits_{k = 1}^{\infty } \hat{P}_{k,2} \left( s \right)\beta^{n - k} \left\{ {\frac{{\left( {p - \sqrt {p^{2} - \alpha^{2} } } \right)^{n - k} }}{{\alpha^{n - k} \sqrt {p^{2} - \alpha^{2} } }} - \frac{{\left( {p - \sqrt {p^{2} - \alpha^{2} } } \right)^{n + k} }}{{\alpha^{n + k} \sqrt {p^{2} - \alpha^{2} } }} } \right\}} \right\}, \hfill \\ \end{aligned} $$

where $p = s + \lambda +\upmu$. It is seen that

$$ \begin{aligned} & \mathop {\lim }\limits_{s \to 0} s\,\hat{P}_{n,0} \left( s \right) = \gamma_{1} \mathop \sum \limits_{k = 1}^{\infty } \pi_{k,1} \beta^{n - k} \frac{1}{\lambda - \mu }\left\{ {\left( {\frac{2\mu }{\alpha }} \right)^{n - k} - \left( {\frac{2\mu }{\alpha }} \right)^{n + k} } \right\} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \,\gamma_{2} \mathop \sum \limits_{k = 1}^{\infty } \pi_{k,2} \beta^{n - k} \frac{1}{\lambda - \mu }\left\{ {\left( {\frac{2\mu }{\alpha }} \right)^{n - k} - \left( {\frac{2\mu }{\alpha }} \right)^{n + k} } \right\}. \\ \end{aligned} $$

On simplification, we get

$$ \pi_{n,0} = \frac{1}{\lambda - \mu }\left\{ {\mathop \sum \limits_{k = 1}^{\infty } \left[ {\gamma_{1} \pi_{k,1} + \gamma_{2} \pi_{k,2} } \right]\left( {1 - \left( {\frac{\mu }{\lambda }} \right)^{k} } \right)} \right\}, $$

which reduces to

$$ \begin{aligned} & \pi_{n,0} = \frac{{\pi_{1,0} }}{\lambda - \mu }\left\{ {\sum\limits_{k = 1}^{\infty } {\left[ {\gamma_{1} \left( {\mu \phi_{k} \mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\phi_{1} } \right]^{r} }}{{\left( {\lambda + \gamma_{1} } \right)^{r + 1} }}} \right)} \right.} } \right. \\ & \quad \quad \quad \left. { + \,\gamma_{2} \left( {\gamma_{1} \mu \psi_{k} \mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\phi_{1} } \right]^{r} }}{{\left( {\lambda + \gamma_{1} } \right)^{r + 1} }}\mathop \sum \limits_{m = 0}^{\infty } \frac{{\left( {\mu_{2} + \xi } \right)^{m} \left[ {\psi_{1} } \right]^{m} }}{{\left( \lambda \right)^{m + 1} }}} \right)} \right]\left. {\left( {1 - \left( {\frac{\mu }{\lambda }} \right)^{k} } \right)} \right\}, \\ \end{aligned} $$

Therefore,

$$ \begin{aligned} \hfill \\ \pi_{n,0} = \frac{{\gamma_{1} \mu }}{\lambda - \mu }\left\{ {\mathop \sum \limits_{k = 1}^{\infty } \left[ {\mathop \sum \limits_{r = 0}^{\infty } \frac{{\left( {\mu_{1} + \xi } \right)^{r} \left[ {\phi_{1} } \right]^{r} }}{{\left( {\lambda + \gamma_{1} } \right)^{i + 1} }}\left[ {\phi_{k} + \gamma_{2} \psi_{k} \mathop \sum \limits_{m = 0}^{\infty } \frac{{\left( {\mu_{2} + \xi } \right)^{m} \left[ {\psi_{1} } \right]^{m} }}{{\left( \lambda \right)^{m + 1} }}} \right]} \right]} \right. \hfill \\ \left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {1 - \left( {\frac{\mu }{\lambda }} \right)^{k} } \right)} \right\}\pi_{1,0} . \hfill \\ \end{aligned} $$

As a special case, when $\mu_{1} = 0 = \mu_{2}$ and $\xi = 0$ the results are seen to coincide with Vijayashree and Janani (2018) .

5 Numerical Illustrations

This section illustrates the behaviour of time-dependent state probabilities of the system during the functional state and vacation states (type 1 and type 2) of the server against time for appropriate choice of the parameter values. Though the system is of infinite capacity, the value of n is restricted to 25 for the purpose of numerical study.

Figure 2 depicts the behaviour of $P_{n,0} \left( t \right)$ against time for varying values of n with the values $\lambda = 0.4,\mu = 0.6,\gamma_{1} = 0.8,\gamma_{2} = 1,\mu_{1} = 0.1,\mu_{2} = 0.05 \,{\text{and}} \,\xi = 0.01$. It is seen that for a particular value of n the transient state probability increases as time progresses and converges to the corresponding steady state probabilities. However, for a particular value of t the value of the probability decreases with increase in the number of customer in the system.

Fig. 2.

Behaviour of $P_{n,0} \left( t \right)$ against t for varying values of $n$.

Figure 3 and Fig. 4 depicts the variation of $P_{n,1} \left( t \right)$ and $P_{n,2} \left( t \right)$ against time t for varying values of n with the same parameter values. All the values of $P_{n,1} \left( t \right)$ and $P_{n,2} \left( t \right)$ are start at 0 and converges to the corresponding to the steady state probability $.$ It is observed that for a particular instant of time the probability values decreases as n increases. However, for a particular value of n the probability values increases reaches a peak and gradually decreases till it converges.

Fig. 3.

Behaviour of  $P_{n,1} \left( t \right)$ against t for varying values of $n$.

Fig. 4.

Behaviour of  $P_{n,2} \left( t \right)$ against t for varying values of $n$.

6 Conclusions

This paper presents a time dependent analysis of an M/M/1 queueing model subject to differentiated working vacation and customer impatience. Closed form expressions for the transient state probabilities of the state of the system are obtained using generating function and continued fraction methodologies. Numerical illustrations are added to support the theoretical results. The study can be further extended to an M/M/1 queueing model subject to m kinds of differentiated working vacation with impatience.

Appendix: Derivation of \( \phi_{n} \left( t \right) \,{\text{and}} \,\psi_{n} \left( t \right) \)

The confluent hypergeometric function represented by ${}_{1}{\text{F}}_{1} \left( {{\rm{a}};{\text{c}};{\rm{z}}} \right)$ has a series representation given by

$$ {}_{1}{\text{F}}_{1} \left( {{\rm{a}};{\text{c}};{\rm{z}}} \right) = 1 + \frac{\text{a}}{\rm{c}} \frac{\text{z}}{1!} + \frac{\rm{a}}{\text{c}} \frac{{{\rm{a}}\left( {{\text{a}} + 1} \right)}}{{\left( {{\rm{c}} + 1} \right)}} \frac{{{\text{z}}^{2} }}{2!} + \ldots = 1 + \sum\limits_{k = 1}^{\infty } {\frac{{\mathop \prod \nolimits_{j = 1}^{k - 1} \left( {a + i} \right)}}{{\mathop \prod \nolimits_{i = 0}^{k - 1} \left( {c + i} \right)}} \frac{{z^{k} }}{k!}} $$

Consider the repression for $\hat{\phi }_{n} \left( s \right)$ obtained as

$$ \hat{\phi }_{n} \left( s \right) = \left( {\frac{\lambda }{\xi }} \right)^{n} \frac{1}{{\mathop \prod \nolimits_{i = 1}^{n} \left( {\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + i} \right)}}\frac{{{}_{1}{\text{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + n + 1 ;\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + n + 1; - \frac{\lambda }{\xi }} \right)}}{{{}_{1}{\text{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + 1 ;\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + 1; - \frac{\lambda }{\xi }} \right)}} . $$

(A.1)

Using the definition of confluent hypergeometric function, we obtain

$$ {}_{1}{\text{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + n + 1 ;\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + n + 1; - \frac{\lambda }{\xi }} \right) = \sum\limits_{k = 0}^{\infty } {\frac{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{1} + \left( {n + j} \right)\xi } \right)}}{{\mathop \prod \nolimits_{i = 1}^{n + k} \left( {s + \gamma_{1} + \mu_{1} + i\xi } \right)}} \frac{{\left( { - \lambda } \right)^{k} }}{{\xi^{k - n} k!}}} $$

And hence

$$ \frac{{{}_{1}{\text{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + n + 1 ;\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + n + 1; - \frac{\lambda }{\xi }} \right)}}{{\mathop \prod \nolimits_{i = 1}^{n} \left( {\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + i} \right)}} = \sum\limits_{k = 0}^{\infty } {\frac{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{1} + \left( {n + j} \right)\xi } \right)}}{{\mathop \prod \nolimits_{i = 1}^{n + k} \left( {s + \gamma_{1} + \mu_{1} + i\xi } \right)}} \frac{{\left( { - \lambda } \right)^{k} }}{{\xi^{k - n} k!}}} $$

Applying partial fraction in the above equation, we get

$$ \begin{aligned} \frac{{{}_{1}{\text{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + n + 1 ;\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + n + 1; - \frac{\lambda }{\xi }} \right)}}{{\mathop \prod \nolimits_{i = 1}^{n} \left( {\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + i} \right)}} = \mathop \sum \limits_{k = 0}^{\infty } \frac{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{1} + \left( {n + j} \right)\xi } \right)}}{k!} \frac{{\left( { - \lambda } \right)^{k} }}{{\xi^{2k - 1} }} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathop \sum \limits_{i = 1}^{ n + k} \left( {\frac{{\left( { - 1} \right)^{i - 1} }}{{\left( {i - 1} \right)!\left( {n + k - i} \right)!}}} \right) \left( {\frac{1}{{s + \gamma_{1} + \mu_{1} + i\xi }}} \right) \hfill \\ \end{aligned} $$

(A.2)

Now, consider the term in the denominator of $\hat{\phi }_{n} \left( s \right)$ as

$$ \begin{aligned} {}_{1}{\text{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + 1 ;\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + 1; - \frac{\lambda }{\xi }} \right) = \mathop \sum \limits_{k = 0}^{\infty } \frac{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{1} + j\xi } \right)}}{{\mathop \prod \nolimits_{i = 1}^{k} \left( {s + \gamma_{1} + \mu_{1} + i\xi } \right)}} \frac{{\left( { - \lambda } \right)^{k} }}{{\xi^{k} k!}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop \sum \limits_{k = 0}^{\infty } \left( { - \lambda } \right)^{k} \hat{a}_{k} \left( s \right) \hfill \\ \end{aligned} $$

Where $\hat{a}_{k} \left( s \right) = \frac{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{1} + j\xi } \right)}}{{\mathop \prod \nolimits_{i = 1}^{k} \left( {s + \gamma_{1} + \mu_{1} + i\xi } \right)}}\left( {\frac{1}{{\xi^{k} k!}}} \right)\, {\text{and}} \,\hat{a}_{0} \left( s \right) = 1.$ By resolving into partial fractions, we have

$$ \hat{a}_{k} \left( s \right) = \frac{1}{{\xi^{2k - 1} k!}}\mathop \sum \limits_{r = 1}^{k} \frac{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{1} + j\xi } \right)\left( { - 1} \right)^{r - 1} }}{{\left( {r - 1} \right)!\left( {k - r} \right)!}}\frac{1}{{s + \gamma_{1} + \mu_{1} + r\xi }} , \,{\text{for}} \, k = 1,2,3 \ldots $$

Using the identity is given by Gradshteyn et al. (2007), it is seen that

$$ \left[ {{}_{1}{\text{F}}_{1} \left( {\frac{{\mu_{1} }}{\xi } + 1 ;\frac{{s + \gamma_{1} + \mu_{1} }}{\xi } + 1; - \frac{\lambda }{\xi }} \right)} \right]^{ - 1} = \left[ {\mathop \sum \limits_{k = 0}^{\infty } \hat{a}_{k} \left( s \right)\left( { - \lambda } \right)^{k} } \right]^{ - 1} = \mathop \sum \limits_{k = 0}^{\infty } \hat{b}_{k} \left( s \right)\lambda^{k} $$

(A.3)

where $\hat{b}_{0} \left( s \right) = 1 \,{\text{and }}\,{\rm{for}}\, k = 1,2,3 \ldots$

$$ \begin{aligned} & \hat{b}_{k} \left( s \right) = \left| {\begin{array}{*{20}c} {\hat{a}_{1} \left( s \right)} & 1 & {} & \ldots & {} & {} \\ {\hat{a}_{2} \left( s \right)} & {\hat{a}_{1} \left( s \right)} & 1 & \ldots & {} & {} \\ { \hat{a}_{3} \left( s \right)} & {\hat{a}_{2} \left( s \right)} & { \hat{a}_{2} \left( s \right)} & \ldots & {} & {} \\ {} & \ldots & \ldots & \ldots & \ldots & {} \\ {\hat{a}_{k - 1} \left( s \right)} & { \hat{a}_{k - 2} \left( s \right)} & { \hat{a}_{k - 3} \left( s \right)} & \ldots & {\hat{a}_{1} \left( s \right)} & 1 \\ {\hat{a}_{k} \left( s \right)} & {\hat{a}_{k - 1} \left( s \right)} & {\hat{a}_{k - 2} \left( s \right)} & \ldots & {\hat{a}_{2} \left( s \right)} & {\hat{a}_{1} \left( s \right)} \\ \end{array} } \right| \\ & \quad \quad \quad = \,\mathop \sum \limits_{i = 1}^{k} \left( { - 1} \right)^{i - 1} \hat{a}_{i} \left( s \right)\hat{b}_{k - i} \left( s \right). \\ \end{aligned} $$

Substituting Eq. (A.3) and Eq. (A.2) in Eq. (A.1), we get

$$ \hat{\phi }_{n} \left( s \right) = \lambda^{n} \xi^{n} \mathop \sum \limits_{k = 0}^{\infty } \left( { - \lambda } \right)^{k} \frac{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{1} + \left( {n + j} \right)\xi } \right)}}{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{1} + j\xi } \right)}}\hat{a}_{n + k} \left( s \right)\mathop \sum \limits_{j = 1}^{\infty } \lambda^{j} \hat{b}_{j} \left( s \right) . $$

Taking inverse Laplace transform of the above equation leads to

$$ \phi_{n} \left( t \right) = \lambda^{n} \xi^{n} \mathop \sum \limits_{k = 0}^{\infty } \left( { - \lambda } \right)^{k} \frac{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{1} + \left( {n + j} \right)\xi } \right)}}{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{1} + j\xi } \right)}}a_{n + k} \left( t \right)*\mathop \sum \limits_{j = 1}^{\infty } \lambda^{j} b_{j} \left( t \right) , $$

where

$$ a_{k} \left( t \right) = \frac{1}{{\xi^{2k - 1} k!}}\mathop \sum \limits_{r = 1}^{k} \frac{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{1} + j\xi } \right)\left( { - 1} \right)^{r - 1} }}{{\left( {r - 1} \right)!\left( {k - r} \right)!}}e^{{ - \left( {\gamma_{1} + \mu_{1} + r\xi } \right)t}} , k = 1,2, \ldots $$

and

$$ b_{k} \left( t \right) = \mathop \sum \limits_{i = 1}^{k} \left( { - 1} \right)^{i - 1} a_{i} \left( t \right)*b_{k - i} \left( t \right), k = 2,3, \ldots , b_{1} \left( t \right) = a_{1} \left( t \right) $$

Similarly equation of $\hat{\psi }_{n} \left( s \right)$ as

$$ \hat{\psi }_{n} \left( s \right) = \lambda^{n} \xi^{n} \mathop \sum \limits_{k = 0}^{\infty } \left( { - \lambda } \right)^{k} \frac{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{2} + \left( {n + j} \right)\xi } \right)}}{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{2} + j\xi } \right)}}\hat{c}_{n + k} \left( s \right)\mathop \sum \limits_{j = 1}^{\infty } \lambda^{j} \hat{d}_{j} \left( s \right) . $$

Proceeding in the similar manner as that of $\hat{\phi }_{n} \left( s \right)$, it is seen that the Laplace inverse of $\hat{\psi }_{n} \left( s \right)$ is

$$ \psi_{n} \left( t \right) = \lambda^{n} \xi^{n} \mathop \sum \limits_{k = 0}^{\infty } \left( { - \lambda } \right)^{k} \frac{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{2} + \left( {n + j} \right)\xi } \right)}}{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{2} + j\xi } \right)}}c_{n + k} \left( t \right)*\mathop \sum \limits_{j = 1}^{j} \lambda^{j} d_{j} \left( t \right). $$

where

$$ c_{k} \left( t \right) = \frac{1}{{\xi^{2k - 1} k!}}\mathop \sum \limits_{r = 1}^{k} \frac{{\mathop \prod \nolimits_{j = 1}^{k} \left( {\mu_{2} + j\xi } \right)\left( { - 1} \right)^{k} }}{{\left( {r - 1} \right)!\left( {k - r} \right)!}}e^{{ - \left( {\gamma_{2} + \mu_{2} + r\xi } \right)t}} , k = 1,2, \ldots $$

and

$$ d_{k} \left( t \right) = \mathop \sum \limits_{i = 1}^{k} \left( { - 1} \right)^{i - 1} c_{i} \left( t \right)*d_{k - i} \left( t \right), k = 2,3, \ldots $$