Quantum Optical Phenomena in Nuclear Resonant Scattering

Abstract

With the advent of high-brilliance, accelerator-driven light sources such as modern synchrotron radiation sources or x-ray lasers, it has become possible to extend quantum optical concepts into the x-ray regime. Owing to the availability of single photon x-ray detectors with quantum efficiencies close to unity and photon-number resolving capabilities, fundamental phenomena of quantum optics can now also be studied at Angstrom wavelengths. A key role in the emerging field of x-ray quantum optics is taken by the nuclear resonances of Mössbauer isotopes. Their narrow resonance bandwidth facilitates high-precision studies of fundamental aspects of the light-matter interaction. A very accurate tuning of this interaction is possible via a controlled placement of Mössbauer nuclei in planar thin-film waveguides that act as cavities for x-rays. A decisive aspect in contrast to conventional forward scattering is that the cavity geometry facilitates the excitation of cooperative radiative eigenstates of the embedded nuclei. The multiple interaction of real and virtual photons with a nuclear ensemble in a cavity leads to a strong superradiant enhancement of the resonant emission and a strong radiative level shift, known as collective Lamb shift. Meanwhile, thin-film x-ray cavities and multilayers have evolved into an enabling technology for nuclear quantum optics. The radiative coupling of such ensembles in the cavity field can be employed to generate atomic coherences between different nuclear levels, resulting in phenomena including electromagnetically induced transparency, spontaneously generated coherences, Fano resonances and others. Enhancing the interaction strength between nuclei in photonic structures like superlattices and coupled cavities facilitates to reach the regime of collective strong coupling of light and matter where phenomena like normal mode splitting and Rabi oscillations appear. These developments establish Mössbauer nuclei as a promising platform to study quantum optical effects at x-ray energies. In turn, these effects bear potential to advance the instrumentation and applications of Mössbauer science as a whole.

3.1 Introduction

The study and applications of light-matter interactions in the optical regime have undergone a revolutionary development over the last decades, to the point where now quantum technologies become a reality. Quantum mechanical phenomena in this interaction are the domain of quantum optics, which encompasses semiclassical setups exploiting the quantum-mechanical nature of the matter, as well as cases in which the quantum character of the light has to be taken into account [1,2,3,4]. A key driver for the advancement continues to be the progress in laser source technology, also beyond the visible light regime.

3.1.1 Light Sources for X-Ray Quantum Optics

X-ray quantum optics has not been very prominent in the early phase of x-ray science, not least because of source limitations. For instance, unlike a laser source, typical x-ray sources emit photons into a large number of electromagnetic-field modes, severly restricting the control possibilities offered by the light. This is no longer the case for experimental conditions that can be realized with modern synchrotron radiation sources and x-ray free-electron lasers, together with increasing source brilliance and advances in x-ray optical elements and detection techniques (for a view on the evolution of the brilliance of x-ray sources, see Fig. 3.1). As a result, the study of quantum optical effects in the interaction of light and matter moves within reach at hard x-ray energies, and is becoming increasingly relevant for new enabling experimental possibilities and for the interpretation of data obtained at these radiation sources. Broadly speaking, the long-term goals of this approach are to fully exploit the capabilities offered by the new x-ray sources, and to continue the success story of quantum optics at hard x-ray energies.

Fig. 3.1

Evolution of brilliance (a.k.a brightness) of x-ray sources since the discovery of x-rays. The advent of synchrotron radiation sources enabled the first accelerator-based nuclear resonant scattering experiments following the proposal by Ruby [5]. The further increase in brilliance resulting from the improvement of storage-ring technology facilitated a multitude of unique applications throughout the natural sciences [6]. The ultimate limit in storage ring technology is reached when the diffraction limit of electron and photon beams is encountered (USR = ultimate storage ring). A further increase in brilliance is possible with x-ray free electron lasers (XFEL) based on the SASE process (SASE = self-amplified spontaneous emission). At these levels, the x-ray pulses may contain several photons within the resonance bandwidth of the nuclear transition, which enables the realization of coherent multiphoton excitations for experiments in quantum and nonlinear optics. Ultimate brilliance values are expected when the SASE process is amplified in a cavity as proposed in the XFEL-oscillator (XFELO) concept [7, 8]

3.1.2 X-Ray Quantum Optics with Atomic Resonances

Two key concepts of quantum optics are coherence and interference. Sharp resonances are favorable in this regard, since the narrow linewidth translates into comparably long lifetimes of coherent superpositions of the involved atomic states. At hard x-ray energies, however, it becomes increasingly difficult to find sharp electronic resonances in atoms because they are intrinsically lifetime-broadened due to strong competing interactions within the inner electron shell, see Fig. 3.2. A fortunate exception from this rule are nuclear resonances. If they are of sufficiently low energy (< 100 keV) and if the nucleus is bound in a solid, we observe the Mössbauer effect of recoilless absorption and emission of photons. This leads to the immediate consequence of coherence in the scattering of radiation from nuclear resonances because the interaction is completely elastic (the final state and the initial state are identical). As a result, nuclear resonances of Mössbauer isotopes are particularly promising in terms of coherence and interference effects. On the other hand, the Mössbauer resonances are much more narrow than the spectra of the pulses delivered by modern x-ray sources, such that it is challenging to strongly drive nuclear resonances as compared to corresponding electronic resonances. Already these general observations separate electronic and nuclear resonances into complementary platforms to establish quantum optical concepts at x-ray energies. This review will focus on how quantum optical phenomena can be realized in the regime of hard x-rays via the nuclear resonances of Mössbauer isotopes.

Fig. 3.2

Bound states of electrons or nucleons in atoms are the origin of electromagnetic resonances in matter. While the keV excited states of inner-shell electrons are affected by several competing decay channels and thus are strongly lifetime broadened, the isolated keV nuclear resonances can be observed with their ultranarrow natural linewidth if the nuclei are bound in a solid. This is due to the Mössbauer effect, in which the whole solid with its large mass acts as a recoil partner so that the recoil energy exchanged with the solid during absorption or emission is negligibly small. The right graph shows the real and imaginary parts of the atomic scattering amplitudes $f'$ and $f''$, respectively, in the vicinities of the Fe K-edge at 7.1 keV and the 14.4 keV nuclear resonance of $^{57}$Fe. Please note the relative amplitudes of the electronic and nuclear scattering amplitudes as well as their largely different energy scales and spectral shapes. While the Fe K-edge absorption proceeds from a bound state into the continuum, the 14.4 keV transition can be considered as an almost ideal two-level system connecting two discrete nuclear levels

3.1.3 Collective and Virtual Effects in Quantum Optics

Next to coherence and interference, the structure and control of field modes, photon correlations, entanglement, vacuum fluctuations and virtual processes, spontaneous and stimulated emission, and nonlinear optical interactions are important elements of quantum optics. They are fundamentally affected if many identical atoms are interacting with the same radiation field. This has led to the development of the research area of cooperative emission in quantum optics, which has been mostly developed on theoretical grounds during many decades because the preparation of ensembles of identical emitters was by far not trivial for a long time. This situation has changed significantly in recent years, e.g., due to the development of storing and manipulating of atoms in electromagnetic traps, but also by the possibility to prepare resonant atoms in solid state environments in a very controlled fashion. It turns out that such a controlled preparation of identical atoms is naturally realized for certain experimental settings involving Mössbauer isotopes, and that the engineering of cooperative effects in turn is indispensable for implementing advanced quantum optical schemes with nuclei.

Collective and virtual effects in the interaction of identical atoms with single photons are the source of intriguing phenomena in atomic physics and quantum optics [9,10,11,12,13,14,15,16,17,18,19,20,21,22] extending into the regime of hard x-rays [23,24,25,26,27,28,29]. The cooperative character of the interaction modifies the decay rate [30] (see Fig. 3.3) and shifts the resonance energy of the atomic ensemble as compared to a single atom [31], also known as the collective Lamb shift. Nowadays, these effects are becoming increasingly attractive to create entangled atomic ensembles [32] for applications ranging from quantum memories [33], quantum information processing [14] to radiative transport of energy in light-harvesting systems [34]. In particular, as discussed in this review, they also allow for the design of cooperative nuclear level schemes [28, 29, 35,36,37,38,39,40].

The collective decay rate of an ensemble of identical resonant atoms was introduced by Dicke in his pioneering work on superradiance [30]. In contrast to the atomic Lamb shift, the collective Lamb shift emerges when a virtual photon emitted from one atom is not absorbed by the same atom but by another atom within the ensemble [31, 41]. The investigation of the collective Lamb shift induced by virtual processes has received stimulated theoretical interest [15, 18, 19, 31, 41,42,43,44] that has been accompanied by recent experimental studies [27, 45,46,47,48]. Virtual transitions not only lead to a shift of the transition energy, but have an interesting effect on the collective decay rate as well [19,20,21]: They partially transfer population from the initially superradiant state into slowly decaying states, resulting in a trapping of the atomic excitation. On the other hand, virtual transitions open additional decay channels for otherwise trapped states. It lies at the heart of superradiance that the presence of many identical atoms opens a large number of potential decay channels for collective excitations. From that perspective such systems are appealing examples for open and marginally stable quantum many-body systems [49].

3.1.4 X-Ray Cavities as Enabling Tool for Nuclear Quantum Optics

Today it is possible to experimentally access collections of identical resonators in a controlled fashion, ranging from atomic Bose-Einstein condensates to quantum dots in solid state systems. Moreover, laser technology has reached a level of advancement that allows to control the light-matter interaction down to timescales of attoseconds. Currently this field of research progresses to shorter and shorter wavelengths into the regime of hard x-rays. However, it is not only the sharpness of the nuclear resonances and their favorable coherence properties which render Mössbauer nuclei an ideal candidate to experimentally explore cooperative phenomena at x-ray energies. Also, the possibility to engineer the interaction of x-rays with nuclei and the coupling between nuclei via their geometric arrangement or by embedding them into photonic nanostructures opens many fascinating routes to realize quantum optical concepts with nuclei. In this respect, thin-film x-ray cavities and multilayers have become an enabling technology for nuclear quantum optics. These cavities transform the propagating x-ray field delivered by the source into a standing wave field structure, and the precise placement of the nuclei within this standing wave allows for an accurate tuning of the interaction of the nuclei with the x-rays. Another decisive aspect is that the cavity geometry facilitates the excitation of single cooperative radiative eigenstates of the embedded nuclei, and to tailor the superradiant enhancement of the resonant emission as well as the collective Lamb shift. The possibilities are further enriched if the magnetic substructure of the nuclei is exploited, or if different nuclear ensembles are embedded within a single thin film structure. Then, the cavity fields can be employed to generate atomic coherences between different nuclear states, and to induce couplings between nuclear states up to the regime of strong collective coupling, opening additional new possibilities. This enabled the implementation of archetype quantum optical phenomena such as electromagnetically induced transparency, spontaneously generated coherences, Fano resonances and others. While much progress has already been achieved on the level of single excitations, we anticipate further enrichment of this fascinating field of physics facilitated by the ongoing development of modern x-ray sources like high-brilliance synchrotrons and x-ray lasers, see Fig. 3.1. These sources are capable of delivering many resonant photons in each single radiation pulse, providing a direct route towards multiphoton x-ray optics, and opening perspectives for associated effects like stimulated emission, x-ray lasing, nonlinear optics and more.

Fig. 3.3

Illustration of single-photon superradiance according to Dicke [30]. If a sample consisting of N identical resonant atoms is excited by a single photon, each of the atoms can be excited (red dots), but we do not know which one. Therefore, each Fock state of the system with one atom exited (red arrow up) contributes with the same probability to the state vector $|\psi \rangle$ of the whole sample. Since all the singly excited states decay to the same ground state, the sample can radiate its energy via N different pathways, so the decay proceeds N times faster than the decay of a single atom. This applies for the case that the linear dimensions of the sample are smaller than the wavelength. In the opposite case, the relative spatial phases of the atoms have to be taken into account which leads to a complex non-exponential temporal evolution of the collective decay that is strongly directional [26, 50]. In experiments with x-rays, samples are typically much larger than the radiation wavelength, so this is the most frequently encountered case. For the description of collective nuclear resonant scattering the states $|\psi \rangle _{k_0}$ have been coined ‘nuclear excitons’ [26], in a more general perspective they are referred to as ‘timed Dicke states’ [9]

3.1.5 Outline of this Review

This review is organized as follows. In Sect. 3.2 of this chapter we review the properties of nuclear resonances as almost ideal two-level systems that can be prepared as identical emitters in various structural arrangements. This leads us then in Sect. 3.3 to discuss general properties of ensembles of Mössbauer isotopes forming a cooperative atomic environment concerning their radiative properties. Specifically, in Sect. 3.4 we will discuss the properties of the nuclear exciton, i.e., the state that is formed after impulsive excitation of a nuclear ensemble by a radiation pulse, the duration of which is much shorter than the collective nuclear lifetime. Section 3.5 describes the most fundamental effect of cooperative emission, the collective Lamb shift, the observation of which was enabled via the application of planar x-ray cavities. While this section contains a semiclassical description of the underlying physics to illustrate the basic concepts of x-ray cavities as ‘enabling technology’ for this field, the following Sect. 3.6 provides a fully quantum optical description of the Mössbauer nuclei in x-ray cavities, setting the stage for inclusion of multiphoton excitation conditions. Section 3.7 is then devoted to quantum optical effects in x-ray cavities that result from the formation of coherences in this particular environment, like Fano resonance control, electromagnetically induced transparency, spontaneously generated coherences, and slow light. Further engineering of the atomic environment to form superlattices or coupled cavities allows one to reach the regime of collective strong coupling. This is discussed in Sect. 3.8, illustrated by the observation of normal-mode splitting and Rabi oscillations between nuclear ensembles. Finally, Sect. 3.9 provides an outlook on the ongoing development of modern high-brilliance x-ray sources and how they will contribute to further development of this exciting research field.

3.2 Nuclear Resonances of Mössbauer Isotopes as Two-Level Systems

In the x-ray regime, the nuclear resonances of Mössbauer isotopes provide almost ideal two-level systems to study the effects of cooperative emission. After being proposed by Ruby in [5], the use of synchrotron radiation for nuclear resonant scattering was demonstrated first by Gerdau et al. in 1985 for nuclear Bragg diffraction [51] and by Hastings et al. in [52] for nuclear resonant forward scattering. Since then the technique became an established method at many synchrotron radiation sources around the world with a multitude of applications in various fields of the natural sciences [6, 53, 54]. The most widely used isotope in this field is $^{57}$Fe with a transition energy of $E_0$ = 14.4125 keV, a natural linewidth of $\Gamma _0$ = 4.7 neV, corresponding to a lifetime of $\tau _0$ = 141 ns. Beamlines at present-day 3rd generation synchrotron radiation sources like ESRF, APS, SPring8 and PETRA III deliver a spectral flux of about $10^5$ photons/s/$\Gamma _0$. The radiation comes typically in pulses with a duration of a few 10 ps, so that excitation and subsequent emission can be treated as independent processes.

Before discussing cooperative effects in the resonant interaction of many identical nuclei with a common radiation field, it is instructive to discuss first the scattering behavior of a single atom. The scattered field of an atom in momentum-frequency space is given by [55]:

$$\begin{aligned} \mathbf{A}(\mathbf{k},\omega ) = -c \frac{\delta _+(k,\omega )}{(2\pi )^4} \int \langle {\Psi _f}| \mathbf{M}(\mathbf{k},\omega ,\mathbf{k}',\omega ')|{\Psi _i}\rangle \, \mathbf{A}_0(\mathbf{k}',\omega ')d^3k'\,d\omega ' \end{aligned}$$

(3.1)

The scattering process described by this equation can be read from right to left: The incoming field is represented by $\mathbf{A}_0(\mathbf{k}',\omega ')$, which may be understood as the wave function of a photon. In fact, $|\mathbf{A}_0(\mathbf{k},\omega )|^2 d^3k\,d\omega$ is the probability of finding the incoming photon in the mode characterized by the wave vector $\mathbf{k}$ and energy $\omega$. $\mathbf{M}$ is the scattering operator of the atom for scattering an incident photon with $\mathbf{k}',\omega '$ into an outgoing photon with $\mathbf{k},\omega$ and $\delta _+(k,\omega ) = -4\pi c/(\omega ^2 - k^2 c^2 + i\epsilon )$ is the propagator of the outgoing photon. The scattering operator $\mathbf{M}$ depends on the electromagnetic current $\mathbf{b}$, on the Hamiltonian $\mathbf{H}$ and on the propagator $\mathbf{G}_0$ of the atom:

$$\begin{aligned}&\mathbf{M}(\mathbf{k},\omega ,\mathbf{k}',\omega ') \\= & {} \frac{i}{c}\int e^{-i(\mathbf{k}\mathbf{x}- \omega t)} e^{i\mathbf{H}t}\,\mathbf{b}(x)\, \mathbf{G}_0(t-t')\,\mathbf{b}(x')\, e^{-i\mathbf{H}t'}\,e^{i(\mathbf{k}'\mathbf{x}' - \omega ' t')} d^3x\,d^3x'\,dt\,dt' \nonumber \end{aligned}$$

(3.2)

The propagator $\mathbf{G}_0$ itself can be expressed in terms of the Hamiltonian $\mathbf{H}$ and the level-shift operator ${\varvec{\Delta }}$ :

$$\begin{aligned} \mathbf{G}_0(t - t') = \frac{i}{2\pi } \int \frac{e^{-i\omega (t - t')}}{\omega - \mathbf{H}- {\varvec{\Delta }}(\omega )}\, d\omega \end{aligned}$$

(3.3)

The level-shift operator is in general non-Hermitian. ${\varvec{\Delta }}$ consists of a radiative contribution ${\varvec{\Delta }}_{\gamma }$ resulting from the perturbation of the atom by its own photon field (the self energy) and of a non-radiative contribution ${\varvec{\Delta }}_{\alpha }$ that originates from internal conversion. The real part of ${\varvec{\Delta }}$ gives the single-atom Lamb shift [56] while the imaginary part is the decay width of the transition. The smaller this imaginary contribution becomes, the more pronounced is the resonance behavior of the propagator. This leads to a strong enhancement of the scattering in the vicinity of sharp nuclear resonances.

Since we are interested here in coherent elastic scattering $(\omega = \omega ')$ we consider only the diagonal elements of the operator $\mathbf{M}$. The currents $\mathbf{b}$ of the atom are split into the nuclear and the electronic part. This gives three contributions to the scattering operator: the pure electronic part $\mathbf{E}$, the pure nuclear part $\mathbf{N}$, and an interference term between the nuclear and electronic currents that can be neglected in most cases. The nuclear contribution to the atomic scattering operator for an unsplit (single-line) nuclear resonance is given by:

$$\begin{aligned} \mathbf{N}(\mathbf{k},\omega ,\mathbf{k}',\omega )= & {} e^{i(\mathbf{k}- \mathbf{k}')\cdot \mathbf{R}}\,\frac{f_0\,(\Gamma _0/2)}{\omega - \omega _0 - i \Delta } \quad \text{ with } \quad f_0 = \frac{f_{LM}}{2k_0}\frac{2I_e + 1}{2I_g + 1}\frac{1}{1 + \alpha } \end{aligned}$$

(3.4)

where $f_{LM}$ is the Lamb-Mössbauer factor, $I_g$ and $I_e$ are the spins of the ground and excited nuclear states, respectively, and $\alpha$ is the coefficient of internal conversion. Effectively, the situation of an unsplit ground and excited state justifies a scalar approach to the scattering problem. As we will see in the next section, $\Delta$ is not a property of the single atom only, but can be greatly affected by cooperative effects, i.e., by the radiative coupling of many identical atoms.

Fig. 3.4

Photon scattering from a resonant atom (vertical double line: excited state) involving the exchange of virtual photons (horizontal wavy lines) with other atoms in the ensemble. The total amplitude is given by the sum over all possible diagrams

3.3 The Nuclear Level Width in a Cooperative Atomic Environment

In an ensemble of many identical atoms a radiated photon may interact not only with the same atom but also with identical atoms within the same ensemble. To describe this interaction a diagrammatical approach was introduced by Friedberg et al. in [31] that is illustrated in Fig. 3.4.

This leads to the complex-valued self-energy correction $\Delta _C = L_C + i\,\Gamma _C$ of the collective resonance energy of the atomic ensemble. To sum all these repeated diagrams in Fig. 3.4 we note that the Fourier transform $\tilde{\mathbf{G}}(\omega )$ of the excited-state propagator $\mathbf{G}(t - t')$ satisfies the Dyson equation

$$\begin{aligned} \tilde{\mathbf{G}}(\omega ) = \tilde{\mathbf{G}}_0(\omega ) - i \tilde{\mathbf{G}}_0(\omega )\,\tilde{{\varvec{\Delta }}}_C(\omega )\,\tilde{\mathbf{G}}(\omega ) \end{aligned}$$

(3.5)

where $\tilde{\mathbf{G}}_0(\omega ) = 1/(\omega - \mathbf{H}- {\varvec{\Delta }}(\omega ))$ is the uncorrected propagator of the single atom. Solving Eq. (3.5) for the corrected propagator yields:

$$\begin{aligned} \tilde{\mathbf{G}}(\omega ) = \frac{1}{\omega - \mathbf{H}- {\varvec{\Delta }}(\omega ) - {\varvec{\Delta }}_C(\omega )}\,. \end{aligned}$$

(3.6)

It should be noted that the Dyson equation above only provides the proper summing of the repeated diagrams in Fig. 3.4. The amplitudes of the individual diagrams have to be calculated before. The diagrammatical technique has been applied in a pioneering paper [31] to calculate the collective Lambshift. Since then the CLS has been calculated for various geometries (sphere, cylinder, slab) and models for the electromagnetic field (scalar/vector) [11, 31, 41, 57, 58]. The result of these calculations in the large-sample limit, i.e., for $k_0\,R \gg 1$ with R being the size of the sample can be summarized as follows :

$$\begin{aligned} \Delta _C \approx i \Gamma _C\left( 1 - \frac{i \,S}{k_0 R}\,\right) \quad \text{ with } \quad \Gamma _C = \frac{3}{2}\frac{N}{(k_0 R)^2}\,\Gamma _0 = \frac{\rho \uplambda ^2 R}{2\pi }\,\Gamma _0\,, \end{aligned}$$

(3.7)

where $\rho$ is the number density of resonant atoms in the sample. S is a factor that depends on the shape of the sample and on the scalar/vector model of the field. Thus, for the CLS to be observable, the quantity $\rho \,\uplambda ^3$ has to be sufficiently high. In gaseous samples, however, an increase of the density goes along with the increase of interactions between atoms, leading to collisional broadening of the resonance line. In condensed matter systems significantly higher number densities than in gases can be reached without these perturbing effects. In this case a detrimental effect that could quench cooperative emission is the inhomogeneous broadening of atomic and nuclear resonances due to interactions of the resonators with their environment. While atomic resonances are most susceptible to the interaction with their surrounding, nuclear resonances are much less affected. In fact, by controling the environment of the Mössbauer isotopes in solids it is possible to prepare ensembles of identical resonators with high number density while still keeping the natural linewidth of the transition. It appears that the narrow nuclear resonances of Mössbauer isotopes provide an almost ideal two-level system for the study of cooperative effects in the interaction of x-rays with matter.

In the following we will describe a procedure how to calculate the eigenmodes of an ensemble of resonant atoms that yields the eigenfrequencies together with the complex self-energy correction $\Delta _C$. The derivation follows in great parts the treatment given in [26], p. 234ff.

3.4 The Nuclear Exciton, Radiative Eigenstates and Single-Photon Superradiance

Soon after the discovery of the Mössbauer effect it became clear that ensembles of nuclei collectively excited by single photons bear a number of fascinating properties. These states have been called ‘nuclear excitons’ and the physics of them was explored theoretically by Afanas’ev and Kagan [23] as well as Hannon and Trammell [24, 25]; for an extensive review see [26]. With the advent of high-brilliance synchrotron radiation it became possible to prepare such states and study their properties systematically. Due to the small number of photons per mode of the radiation field at these sources, however, there is in most cases only one photon interacting with the resonant ensemble at a time. In the following we investigate collectively excited atomic (nuclear) states that have been created by short-pulse excitation containing one photon at most. Since we do not know which nucleus is excited, all possible Fock states $|{b_1\,b_2 \ldots a_j \ldots b_N}\rangle$ containing one excited nucleus $(a_j)$ while the others $(b_i)$ are in the ground state, contribute with equal weight to the state vector of the whole system. In this sense, the superradiant excitonic states are those of maximum delocalization of the excitation energy.

For the case that the sample extension R is much smaller than the wavelength of the radiation, $k_0 R \ll 1$, the exciton state is written as

$$\begin{aligned} |{\Psi _e}\rangle = \frac{1}{\sqrt{N}} |{b_1\,b_2 \ldots a_j \ldots b_N}\rangle . \end{aligned}$$

(3.8)

This state is fully symmetric with respect to exchange of any two atoms, therefore it is often called the symmetric Dicke state. In most cases of optical physics up into the x-ray regime, however, the opposite limit is encountered where $k_0 R \gg 1$, so that the spatial position of the atoms within the ensemble has to be taken into account:

$$\begin{aligned} |{\Psi _e(\mathbf{k}_0)}\rangle = \frac{1}{\sqrt{N}} \sum _j e^{\mathrm{i}\,\mathbf{k}_0\cdot \mathbf{R}_j} |{b_1\,b_2 \ldots a_j \ldots b_N}\rangle , \end{aligned}$$

(3.9)

where $\mathbf{k}_0$ is the wave vector of the incident photon and $\mathbf{R}_j$ denotes the position of the jth atom. This state was introduced to describe coherent nuclear resonant scattering as ‘nuclear exciton’ [23, 26] or more recently as ‘timed Dicke state’ [41], because atoms at various locations within the extended sample are excited at different times.

3.4.1 Radiative Normal Modes

The collective spectral response of a given ensemble of emitters and the temporal evolution of its decay can be obtained by determination of the radiative normal modes. The scattering of an external wave proceeds via virtual excitation of these modes as intermediate states. The decay of a collectively excited state is then a superposition of exponentially decaying normal modes of the system. In the following we will summarize how to obtain the Hamiltonian equation of motion of the system that determines the complex normal mode frequencies $\omega _n$, based on the formalism layed out in Ref. [26]. Due to retardation effects in the ‘timed Dicke state’ of Eq. (3.9), the Hamiltonian is symmetric rather than Hermitian. For that reason the eigenmodes $|{\Psi _n}\rangle$ are transpose orthogonal rather than Hermitian orthogonal. A general superposition exciton state $|{\Psi _e}\rangle = \sum a_n\,|{\Psi _n}\rangle$, prepared by pulsed excitation, will develop dynamical beats in the time evolution of its decay, resulting from destructive interference effects between the light emitted from the normal modes. Under certain conditions, however, a single superradiant eigenmode $|{\Psi _e(\mathbf{k}_0)}\rangle$ can be excited that exhibits a simple enhanced exponential decay. This is the case for single crystalline samples if the wavevector $\mathbf{k}_0$ of the incident photons satisfies a symmetric Bragg condition or if $\mathbf{k}_0$ excites a single mode in a cavity [59]. If $\mathbf{k}_0$ is off-Bragg (i.e. transmission in forward direction) then $|{\Psi _e(\mathbf{k}_0)}\rangle$ is a superposition of normal modes. The spread of frequencies of these modes and their Hermitian nonorthogonality determine the superradiant decay at early times and the emergence of dynamical beats thereafter. Because the energy bandwidth of the synchrotron radiation pulses (meV - eV, depending on the degree of monochromatization) is much larger than the natural linewidth of the nuclear transition (4.7 neV for $^{57}$Fe), the incident pulse covers the energies of all radiative eigenmodes of the sample, such that their excitation only depends on arrangement of the nuclei.

In a classical system of resonators with oscillating dipole moments, the coupled equations of motion lead to an eigenvalue equation from which the eigenfrequencies and the eigenvectors of the semi-stationary (decaying) normal modes can be determined:

$$\begin{aligned} \tilde{h}\,\mathbf{X}= \omega \,\mathbf{X}\end{aligned}$$

(3.10)

with $\mathbf{X}$ being an N-component vector that contains the amplitudes of all N oscillators. $\tilde{h}$ is the Hamitonian of the system. In a quantum mechanical description one obtains the equations of motion by taking the Fourier transform of the decaying exciton $\mathbf{G}_0(t -t')\,|{\Psi _e(\mathbf{k}_0)}\rangle$ with $\mathbf{G}_0(t-t')$ given by Eq. (3.3) [26]. The Hamiltonian equation of motion has the same shape as Eq. (3.10) where the state vector is now the nuclear exciton

$$\begin{aligned} \mathbf{X}= |{\Psi _e}\rangle = \sum _j c_j\,|{b_1\,b_2 \ldots a_j \ldots b_N}\rangle = \left( \begin{array}{c} c_1\\ c_2\\ \vdots \\ c_N \end{array} \right) \end{aligned}$$

(3.11)

where here and in the following for notational simplicity we identify the quantum mechanical states with their vector representation in the basis of Fock states $|{b_1\,b_2 \ldots a_j \ldots b_N}\rangle$. The Hamiltonian is given by

$$\begin{aligned} h_{ii} = \omega _0 - \frac{i\Gamma }{2} \text{ and } h_{ij}(i \ne j) = -\frac{\Gamma _{\gamma }}{2}\kappa _{ij}\frac{e^{ik_0R_{ij}}}{k_0 R_{ij}} \end{aligned}$$

(3.12)

with

$$\begin{aligned} \kappa _{ij} \approx \left\{ \begin{array}{ll} \frac{3}{2} \left( \,3 \cos ^2\Theta - 1\,\right) \left[ \frac{1}{(k_0 R_{ij})^2} - \frac{i}{k_0 R_{ij}}\right] &{} (\text{ near } \text{ zone } \quad R_{ij} \ll \uplambda )\\[2mm] \frac{3}{2} \sin ^2\Theta &{} (\text{ far } \text{ zone } \quad R_{ij} \gg \uplambda ) \end{array}\right. \end{aligned}$$

(3.13)

where $\Theta$ is the angle between the wavevector of the outgoing photon and the polarization direction of the oscillator as determined by the polarization of the incident photon. The complex frequencies $\omega _m = \omega '_m - i \Gamma _m/2$ of the normal modes are obtained via the determinant equation

$$\begin{aligned} \text{ Det }[\tilde{h} - \omega \,\tilde{\mathbf{1}}] = 0 \end{aligned}$$

(3.14)

where $\tilde{\mathbf{1}}$ is the $N \times N$ unity matrix. The resulting frequencies $\omega '_m$ and the decay widths $\Gamma _m$ will generally be different from the corresponding values of an isolated nucleus. After determination of the eigenvectors $\mathbf{X}_m$ we obtain the $N \times N$ matrix U that diagonalizes the Hamiltonian $\tilde{h}$ (the rows of U are the transpose eigenvectors $\mathbf{X}_m^T$):

$$\begin{aligned} U\,\tilde{h}\,U^{-1} = \tilde{\omega } \end{aligned}$$

(3.15)

with $U^{-1} = U^T$ and $\tilde{\omega }$ being the diagonal eigenvalue matrix $[\tilde{\omega }]_{mn} = \omega _m\,\delta _{mn}$. Since the trace of a matrix is an invariant under a similarity transformation, we have Tr($\tilde{h}$) = Tr($\tilde{\omega }$), which is equivalent to:

$$\begin{aligned} \sum _m \omega _m = N \left( \omega _0 - \frac{i\Gamma }{2}\right) \end{aligned}$$

(3.16)

From this equation two important sum rules for the real and imaginary part follow:

$$\begin{aligned} \sum _m \delta \omega = \sum _m (\omega '_m - \omega _0)= & {} 0\end{aligned}$$

(3.17)

$$\begin{aligned} \sum _m \Gamma _m= & {} N\,\Gamma _0 \end{aligned}$$

(3.18)

The frequency shift sum rule, Eq. (3.17), means that the frequency shifts of all modes average to zero. If some modes are selectively excited or unequally populated, one may nevertheless observe an overall net shift. The decay width sum rule, Eq. (3.18), states that the decay width averaged over all modes equals that of a single resonator. With the normal mode state vectors $|{\Psi _m}\rangle$ and their complex frequencies $\omega _m$ now at hand, we can calculate the time evolution of any single-exciton state $|{\Psi _e}\rangle$ via

$$\begin{aligned} |{\Psi _e(t)}\rangle = \sum _m a_m\,e^{-i\omega _m t} |{\Psi _m}\rangle \quad \text{ with } \quad a_m = \langle {\Psi _m^T}|{\Psi _e}\rangle \end{aligned}$$

(3.19)

In a synchrotron experiment with broadband excitation, we observe the decay of the excitation probability that is given by 

$$\begin{aligned} I(t) = \langle {\Psi _e(t)}|{\Psi _e(t)}\rangle = \sum _{m,n} a_n^{*} a_m\,e^{i(\omega _n^{*} - \omega _m) t} \langle {\Psi _n}|{\Psi _m}\rangle \end{aligned}$$

(3.20)

Since the normal modes $|{\Psi _m}\rangle$ are transpose orthogonal rather than Hermitian orthogonal, we have in general $\langle {\Psi _n}|{\Psi _m}\rangle \ne 0$. This gives rise to dynamical beats between the modes in the temporal evolution I(t) of the decay. In the following subsections we discuss the most frequently encountered cases, i.e., forward scattering and Bragg scattering with particular emphasis on cooperative effects encountered in these geometries.

3.4.2 Forward Scattering

The state vector in Eq. (3.8) corresponds to the small sample limit, also called the simple Dicke limit. The time evolution of the decay of this state to the ground state is strictly exponential, but due to the lack of spatial phasing there is no directionality involved. On the other hand, for extended samples ($kR \gg 1$) the spatial phasing in Eq. (3.9) leads to directional emission that is the situation most frequently encountered in experiments, especially in the regime of hard x-rays.

The exciton $|{\Psi _e(\mathbf{k}_0)}\rangle$ created by the synchrotron pulse can be considered a Bloch wave given by Eq. (3.9). However, the Bloch waves are generally not the true radiative normal modes in a crystal. In general, the Bloch state $|{\Psi _e(\mathbf{k}_0)}\rangle$ is a superposition of radiative eigenmodes, which exhibit a distribution of eigenfrequencies and decay rates. In all cases, the initial decay is always superradiant but the decay at delayed times is drastically different, depending on whether the exciton $|{\Psi _e(\mathbf{k}_0)}\rangle$ is an eigenmode or not.¹ In the case of an eigenmode, the scattered signal I(t) exhibits a pure exponential decay with an enhanced decay rate. On the other hand, if $|{\Psi _e(\mathbf{k}_0)}\rangle$ is a superposition of eigenmodes, the superradiant components die out quickly, leaving a superposition of slowly decaying components with a distribution of eigenmode frequencies. This leads to a slowly decaying beating signal at delayed times, referred to as dynamical beats or propagation quantum beats, as illustrated in Fig. 3.5. They have been observed not only for nuclear resonant scattering [50], but also for coherent forward scattering from excitons in the optical domain [60]. Quantitatively, the response function of the sample, characterizing the amplitude of the scattered light for an incident field $~\delta (t)$, is given by

$$\begin{aligned} A(t) = \delta (t) - e^{-\Gamma _0 t/2\hbar }\, \frac{\Gamma _C}{\hbar }\, \frac{J_1(\sqrt{4 \Gamma _C t/\hbar })}{\sqrt{\Gamma _C t/\hbar }}, \end{aligned}$$

(3.21)

where $\Gamma _C$ depends on the thickness of the sample, see Eq. (3.7) with $R = L_{\parallel }$. At early times the decay is essentially superradiant with an enhanced decay width given by $\Gamma _0 + \Gamma _C$. At delayed times the decay of the exciton proceeds with an envelope given by $1/\sqrt{t^3}$ and an onset of dynamical beats $\sim \cos ^2(\sqrt{t})$. The width $\Gamma _C$ for the initial radiative decay is given by [26]

$$\begin{aligned} \Gamma _C(\mathbf{k}_0) = \frac{\Gamma _{\gamma }}{4\pi N} \int d\Omega \,\sin ^2\Theta \,|S(\mathbf{k}-\mathbf{k}_0)|^2 \end{aligned}$$

(3.22)

with

$$\begin{aligned} S(\mathbf{k}-\mathbf{k}_0) = \sum \limits _{j = 1}^{N}\exp [-i(\mathbf{k}- \mathbf{k}_0)\cdot \mathbf{R}_j] \end{aligned}$$

(3.23)

where $\mathbf{k}$ is the wavevector of the outgoing photon, and the sum runs over all N atoms in the sample. $|S(\mathbf{k}-\mathbf{k}_0)|^2 = N^2$ in those directions $\mathbf{k}$ where constructive interference takes place for the amplitudes emitted from all nuclei, as it applies for forward scattering. In this case the decay width is given by

$$\begin{aligned} \Gamma _C(\mathbf{k}_0) = \Gamma _{\gamma }\frac{N}{4\pi }\,\Delta \Omega \end{aligned}$$

(3.24)

where $\Delta \Omega$ is the solid angle around $\mathbf{k}_0$ for which $(\mathbf{k}- \mathbf{k}_0) \cdot (\mathbf{R}_i - \mathbf{R}_j) < 1$ for all interatomic distances. Thus, due to the phasing, the emission preferentially proceeds into the direction of the incident photon wave vector.²

Fig. 3.5

Reprinted from [61], Copyright 2012, with permission from Wiley

a Dynamical beats in nuclear resonant forward scattering through an optically thick foil of D = 20 $\upmu$m stainless steel, where the $^{57}$Fe nuclei act as single-line resonators. For times later than $t \sim \!\hbar /\Gamma _C$ after excitation the temporal evolution is dominated by dynamical beats described by Eq. (3.21). The dashed line in the graph illustrates the initial superradiant part of the temporal evolution that proceeds as $I(t) = I_0\,\exp [-(1 + \chi )\,t/\tau _0]$ with a speedup factor of $\chi$ = 60. b $\chi = \Gamma _C/\Gamma _0 \sim \rho \,\uplambda ^2\,L_{\parallel }$ is the number of resonant atoms N in the column of cross section $\uplambda ^2$.

Equation (3.24) implies that $\Delta \Omega$ strongly depends on the dimensionality and the shape of the sample. For a 3-dimensional sample we find that $\Delta \Omega \approx (\uplambda /L_{\perp })^2$, where $L_{\perp }$ is the dimension of the sample transverse to $\mathbf{k}_0$. In this case we obtain

$$\begin{aligned} \Gamma _C(\mathbf{k}_0) = \frac{1}{4\pi }\,\rho \,\uplambda ^2\,L_{\parallel }(\mathbf{k}_0)\,\Gamma _{\gamma }, \end{aligned}$$

(3.25)

where $L_{\parallel }(\mathbf{k}_0)$ is the dimension of the sample along the direction of $\mathbf{k}_0$ and $\rho = N/(L_{\perp }^2\,L_{\parallel })$ is the number density of resonant atoms in the sample. The product $\rho \,\uplambda ^2\,L_{\parallel }$ has an interesting interpretation: It is the number of resonant atoms in a column with cross section $\uplambda ^2$ and length $L_{\parallel }$, as illustrated in Fig. 3.5.

It is instructive to take another view on forward scattering by dividing the sample into M thin layers (see Fig. 3.5) and solve for the time dependent response of the oscillators in each layer as they act under the influence of the radiation fields from all the other layers after pulsed excitation. The initial phasing of the emitters in each layer is assumed to be symmetrical, i.e., they radiate equally in both forward and backward directions. In forward scattering, however, there is no radiative coupling with another scattering channel (as it is in Bragg geometry), and this leads to an asymmetry: While the mth layer acts under the influence of the $(m-1)$ upstream layers, the downstream $(M - m)$ layers have no effects on the mth layer. As a result, the emitters in the first layer radiate at their natural resonance energy $\omega _0$ and decay rate $\Gamma _0$ while the emitters in the Mth layer are driven by the fields from all upstream layers. This strong driving eventually forces the downstream layers out of phase with the upstream layers resulting in dynamical beats and a nonexponential decay at late times. On the other hand, if the incident wave vector satisfies the symmetrical Bragg condition, then the radiated waves are constructive in both transmitted and reflected directions. As a result, the driving forces on each oscillator in the sample are equal, leading to a normal mode oscillation with superradiant decay width $\Gamma _C$ at the natural resonance frequency $\omega _0$.

It should be noted that the formalism outlined so far is valid only in the local or Markov approximation, i.e., for slowly evolving systems that do not change much while the signal propagates through the sample. In case of large samples that violate the local approximation the dynamics becomes nonlocal in time and one expects collective oscillations in the atomic population resulting from subsequent emission and reabsorption of radiation within the sample [15, 62, 63].

3.4.3 Bragg Scattering

In contrast to forward scattering, the Bragg exciton is an eigenmode that radiates at the natural resonance frequency $\omega _0$ with an exponential accelerated decay. This can be understood via the normal mode analysis presented above. For a crystal consisting of M resonant layers, each layer separately has two-dimensional normal modes corresponding to Bloch waves. The layers scatter into the same outgoing field modes, which at the same time couples the different layers. As a result, the crystal of M layers with a spacing of d will give rise to M different linear combinations of the single-layer solutions [26]. Factorizing out the two-dimensional component corresponding to the single-layer Bloch waves, the part of the excitonic state characterizing the superposition of the different layers is given by 

$$\begin{aligned} |{\Psi _e(\mathbf{k}_0)}\rangle = \frac{1}{\sqrt{M}} \left( \begin{array}{c} 1\\ e^{i g_0 d}\\ \vdots \\ e^{i g_0 d (M-1)} \end{array} \right) , \end{aligned}$$

(3.26)

with $g_0 = k_0\,\sin \Theta _B$. At the Bragg angle $\Theta _B$ we have $n \uplambda = 2d\sin \Theta _B$ with a natural number n, so that $g_0 d = n \pi$ if the Bragg condition is fulfilled. Thus, at the exact Bragg angle for a symmetric Bragg reflection, the phasing is such that only the superradiant eigenmode state is excited. With increasing deviation from the Bragg angle, in addition to the superradiant eigenmode, various other normal modes are virtually excited. As a result, the weighted resonance energy is shifted from $\omega _0$, and the effective decay width is reduced. Quantitatively, the reflectivity of a thin crystal consisting of M resonant layers in the vicinity of the resonance energy $\omega _0$ is given by [26]:

$$\begin{aligned} R(\omega ,\delta ) = \frac{1}{1 - i M \delta }\, \frac{i \Gamma _C/2}{[\,\omega _0 - \omega - i \Gamma _0/2 - i (\Gamma _C/2)/(1 - i M /\delta )]} \end{aligned}$$

(3.27)

with $\delta = k_0 d \cos \Theta _B\,\delta \Theta$. d is the spacing of the lattice planes, $\delta \Theta = \Theta - \Theta _B$ is the deviation of the incidence angle $\Theta$ from the exact Bragg angle $\Theta _B$, and $\Gamma _C$ is given by Eq. (3.25). Thus, in Bragg geometry, the effect of the collective resonant scattering is an enhancement of the decay width to

$$\begin{aligned} \Gamma = \Gamma _0 + \frac{\Gamma _C}{1 + (M\delta )^2} \end{aligned}$$

(3.28)

while the resonance frequency $\omega '_0$ is shifted relative to $\omega _0$ by the amount

$$\begin{aligned} \Delta \omega _c(\delta ) = \omega '_0 - \omega _0 = \frac{M\delta }{1+ (M\delta )^2}\,\frac{\Gamma _c}{2} \end{aligned}$$

(3.29)

Accordingly, in Bragg geometry the collective Lamb shift $\Delta \omega _c$ changes from negative to positive values if the angle of incidence crosses the Bragg angle from below. Such a behaviour has been experimentally observed in nuclear Bragg diffraction from perfect single crystals of FeBO$_3$ [64]. It was also reported in a theoretical study for a density modulated slab of material [65].

3.5 Cooperative Emission and the Collective Lamb Shift in a Cavity

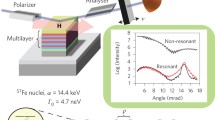
It has been shown in the previous Sect. 3.4.3 that radiative eigenstates of a resonant collection of identical atoms can be selectively excited by proper phasing of the resonators. This is the case, for example, if the atoms are arranged in a crystal and the incident wavevector matches a symmetric Bragg reflection. Here we discuss another phasing scheme for a superradiant eigenstate that leads to large cooperative effects and exhibits a high degree of experimental tunability. This is the case if the resonant atoms are embedded in a planar cavity that is excited in its first-order mode, as sketched in Fig. 3.6. An ultrathin layer of $^{57}$Fe atoms is located in the plane at $z = 0$ the center of the cavity. The layer system that forms the planar cavity consists of a material of low electron density (e.g., carbon) as a guiding layer that is sandwiched between two layers of high electron density (e.g., Pt) acting as total reflecting mirrors.

Fig. 3.6

a Structure of the planar cavity and scattering geometry used for calculation of the CLS for an ensemble of resonant $^{57}$Fe nuclei embedded in the center of its guiding layer. b Depth dependence of the normalized radiation field intensity in the first-order guided mode of the cavity. Dashed lines mark the interfaces between layers

The two phasing schemes are in fact closely related. In the Bragg case, the phasing leads to constructive interference if the condition $n \uplambda = 2 d \sin \Theta _B$ is satisfied. Then, different scattering pathways through the crystal add up in phase. We can relate this expression to the cavity case by rewriting $\uplambda = 2\pi /k_{\uplambda }$ with the wave number $k_\uplambda$, and evaluating the corresponding wave number normal to the cavity surface via $\sin \Theta _B = k_\perp /k_\uplambda$. Using $\uplambda _\perp = 2\pi /k_\perp$, the Bragg condition becomes $d = n\uplambda _\perp /2$, which is the usual resonance condition for the nth mode of a perfect resonator with length d. One may therefore interpret a cavity as a Bragg setting “folded” into one layer via the action of the mirrors. This way, also the scattering pathways shown in Fig. 3.6 can be related to the corresponding pathways in the Bragg case.

To find the complex eigenfrequencies of the system we reverse the solution precedure outlined above, first obtaining the eigenmodes by symmetry and then solving for the eigenfrequencies. We find for the electric field in the regions above and below the resonant layer at $z = 0$

$$\begin{aligned} E(z) = \left\{ \begin{array}{l} A\,(e^{ik_z z} + r_m\,e^{-ik_z z}),\quad (z > 0)\\ B\,(e^{-ik_z z} + r_m\,e^{ik_z z}),\quad (z < 0) \end{array} \right. \end{aligned}$$

(3.30)

where $k_z$ is the wavevector in z direction and $r_m$ is the reflection coefficient of the mirrors. The reflection and transmission coefficients of the ultrathin resonant layer (thickness d) are given by

$$\begin{aligned} r_r = \frac{ifd}{1 - ifd}, \quad t_r = 1 + r_r, \quad \text{ with } \quad f_n = f_n(\omega ) = \frac{2\pi \rho }{k_0^2}\,\frac{f_0 (\Gamma _0/2)}{\omega - \omega _0 - i(\Gamma _0/2)} \end{aligned}$$

(3.31)

where $f_n$ is the nuclear scattering amplitude with $f_0$ defined in Eq. (3.4). Matching the fields in Eq. (3.30) above and below the resonant layer under conditions of resonant transmission and reflection leads to

$$\begin{aligned} \left( \!\begin{array}{c}{A}\\[1mm]{B}\end{array}\!\right) = \left( \!\begin{array}{cc}{r_r r_m\,} &{} {t_r r_m}\\[1mm]{t_r r_m\,} &{} {r_r r_m} \end{array}\!\right) \left( \!\begin{array}{c}{A}\\[1mm]{B}\end{array}\!\right) \end{aligned}$$

(3.32)

The eigenfrequencies are determined from the coresponding determinant equation:

$$\begin{aligned} r_m (r_r \pm t_r) = 1 \end{aligned}$$

(3.33)

where the sign distinguishes between the odd and even solutions for the field in the cavity. Odd modes are those with a minus sign; they have a node at $z = 0$ and thus do not interact with the resonant layer. For the even modes Eq. (3.33) turns into $r_m(2r_r + 1) = 1$ from which we derive that $fd = i\,(1 - r_m)/(1 + r_m)$ which yields the complex eigenfrequency

$$\begin{aligned} \omega = \omega _0 - \frac{i\Gamma _0}{2}\,\left[ 1 - \frac{2\pi \rho f_0 d}{k_0^2} \left( \frac{1 + r_m}{1 - r_m}\right) \right] . \end{aligned}$$

(3.34)

From this expression we obtain the frequency shift

$$\begin{aligned} L_C = \frac{2\pi \rho f_0 d}{k_0^2}\,\Gamma _0\,\text{ Im } \left( \frac{1 + r_m}{1 - r_m}\right) . \end{aligned}$$

(3.35)

For highly reflecting mirrors with $|r_m| \approx 1$ the expression on the right can become quite large. Effectively, the cavity promotes the exchange of real and virtual photons between the resonant atoms within the ensemble, leading to large values for the cooperative decay width and the collective Lamb shift.

For a more rigorous description we treat the propagation of x-rays in stratified media within a transfer matrix formalism [66]. Owing to the high energies of x-rays compared with electronic binding energies in atoms, the refractive index n of any material is slightly below unity. Thus, n is commonly written as $n(E) = 1 - \delta$. Accordingly, in the X-ray regime, every material is optically thinner than vacuum, thus total reflection occurs for angles of incidence (measured relative to the surface) below the critical angle $\phi _c = \sqrt{2 \delta }$. Since $\delta = 10^{-6} \ldots 10^{-5}$ for hard X-rays with energies between about 10 and 20 keV, the critical angle $\varphi _C$ is typically a few mrad. In the regime of total reflection, the radiation penetrates only a few nm into the material via the evanescent wave. In the example shown in Fig. 3.6, the top Pt layer is thin enough (2.2 nm) so that x-rays impinging under grazing angles can evanescently couple into the cavity.

Constructive superposition of the partial waves inside the cavity occurs at certain angles when the thickness of the guiding layer equals an integer multiple of the standing wave period that is given by $(\uplambda /2)/\sqrt{\varphi ^2 - \varphi _C^2}$, where $\varphi _C$ is the critical angle of total reflection of the guiding layer material. This leads to a strong amplification of the local photonic density of states, limited only by the photoabsorption in the guiding layer material. In the first-order mode excited at about $\varphi$ = 2.5 mrad, illustrated in Fig. 3.6, one obtains a 25-fold enhancement of the normalized intensity in the center of the cavity.

In the following we calculate the spectral response of this system around the nuclear resonance energy to determine the collective decay width and the collective Lamb shift of the nuclei in the cavity. This can be accomplished via a perturbation expansion of the resonant reflectivity R of the cavity in powers of the nuclear scattering amplitude $f_n$ at the angular position $\varphi = \varphi _1$ of the first-order mode [27]. Each order of the perturbation series of R corresponds to one of the outgoing partial waves $A_i$ that are emitted from the nuclear ensemble at the ‘vertices’ (denoted by the black dots) in the diagram. In order to sum up all the partial waves $A_i$, we note that the scattered amplitude in the nth outgoing wave is related to the $(n-1)$th amplitude via

$$\begin{aligned} A_n = (\mathrm{i}\,d\,f_n)\,p\,q\,A_{n-1} \end{aligned}$$

(3.36)

Here d is the thickness of the $^{57}$Fe layer and p and q are the amplitudes of the wavefields (at the position of the resonant nuclei) propagating in the directions of the incident and the reflected beams, respectively. The depth dependence of the relevant product $p\,q$ for the first-order mode of the cavity used here is shown in Fig. 3.6b. For the first vertex we have $A_1 = (\mathrm{i}\,d\,f_n)\,p^2\,A_0$ that also includes the coupling of the radiation into the cavity. Finally, the sum over all orders results in

$$\begin{aligned} R = \mathrm{i}\, d\, f_n p^2 \sum _{k=0}^{\infty } \left( \mathrm{i}\,d\,p\,q\,f_n \right) ^k = \frac{\mathrm{i}\,d p^2 f_n}{1 - \mathrm{i}\,d\,p\,q\,f_n}. \end{aligned}$$

(3.37)

Inserting $f_n(\omega )$ as defined in Eq. (3.31) we obtain a spectral response that is again a Lorentzian resonance line

$$\begin{aligned} R(\omega ) = \frac{C\,d\,p^2\,(\Gamma _0/2)}{\omega - \omega _0 + L_C + \mathrm{i}(\Gamma _0 + \Gamma _C)/2} \quad \text{ with }\quad C = \frac{2\pi \rho \,c_n}{k_0\,k_{0z}} \end{aligned}$$

(3.38)

that exhibits a decay width of $\Gamma _C = C\,d\,|\text{ Re }(p\,q)|\,\Gamma _0 =: \chi \,\Gamma _0$ and an energy shift of $L_C = -C\,d\,\text{ Im }(p\,q)\,\Gamma _0/2$. Combining these results into one expression for the complex-valued frequency shift $\Delta _C$, we obtain

$$\begin{aligned} \Delta _C = \mathrm{i}\,\Gamma _C\,\left( 1 + \mathrm{i}\,\frac{\text{ Im }(p\,q)}{|\text{ Re }(p\,q)|} \right) \end{aligned}$$

(3.39)

The collective Lamb shift in single-photon $\gamma$-ray superradiance has been experimentally confirmed in an experiment at the European Synchrotron Radiation Facility (ESRF) [27], see Fig. 3.7.

Fig. 3.7

Reprinted from [67], Copyright 2015, with permission from Springer Nature

a Measured time response of a 1.2 nm thick layer of $^{57}$Fe atoms embedded in the center of the planar cavity (Fig. 3.6), excited in the first-order mode. The decay proceeds exponentially over two orders of magnitude with a speedup of $\chi = 65$ compared to the natural decay (upper dashed line). At later times the decay levels off into a curve with a much smaller slope, resulting from residual hyperfine interactions of the nuclei in the C matrix. b Experimental setup to record the energy spectrum of the radiation reflected from the cavity. The analyzer is a 6 $\upmu$m thick foil of stainless steel $^{57}$Fe${}_{0.55}$Cr${}_{0.25}$Ni${}_{0.20}$ where the $^{57}$Fe exhibits a single-line nuclear resonance. It is mounted on a Doppler drive in order to obtain the spectrum by recording resonantly scattered photons as function of the drive’s velocity. c The measured energy spectrum is strongly broadened due to the superradiant enhancement. Its center is shifted by about -9 $\Gamma _0$ which is the collective Lamb shift for this sample [27].

While for a spherical atomic cloud the collective Lamb shift scales with the quantity $\rho \uplambda ^3$ [31, 41], in this setting it scales with $\rho _A \uplambda ^2$, where $\rho _A$ is the areal density of the resonant nuclei in the sample. Here the ensemble of resonant nuclei effectively appears to be two-dimensional because all nuclei within the thin layer are confined to a dimension that is small compared to the period of the standing wave in the cavity. As a result, the cooperative emission from the nuclei in the cavity takes place in the limit $k_{0z} d \ll 1$, so that essentially the small-sample limit of Dicke superradiance is realized here, while the directionality of the emission is kept because the resonant nuclei interact only with one guided mode of the cavity with a well defined wavevector. One may speculate that if the resonant atoms are confined in a 1-dimensional structure like a fiber, the collective Lamb shift might scale as $\rho _L\uplambda$, where $\rho _L$ is the linear density of the atoms [61, 68]. This could lead to relatively large values of the CLS. The preparation of corresponding samples is certainly more demanding, although x-ray waveguides with a 2-dimensional confinement of the photon field have already be demonstrated [69]. Even more interesting it is to consider a 0-dimensional confinement of the atoms, e.g., in a 3D cavity. This will be practically impossible for x-rays, but has been demonstrated with microcavities in the optical regime [70].

The cavity is an ideal laboratory to study features of cooperative emission. In the following we exploit this to study the dependence of the CLS on the size of the sample. For that purpose we increased the thickness of the resonant layer while keeping the areal density of the resonant atoms constant. Calculations of the cavity reflectivity for an extended ensemble of atoms distributed over the standing wave within a 3rd order guided mode are shown in Fig. 3.8a. A close inspection reveals two prominent features: First, one observes a sharp dip in the reflectivity spectrum at the exact resonance energy ($\Delta$ = 0). This structure is very reminiscent of the transparency dips that appear in the phenomenon of electromagnetically induced transparency (EIT) in quantum optics [71, 72]. As will be discussed in Sect. 3.7.2, there is indeed a mechanism which leads to EIT in the case of nuclear resonant scattering from a cavity that contains resonant atoms. Second, the CLS (determined from the center of gravity of the curve), is a non-monotonous function of the thickness of the atomic ensemble within the cavity. This behavior can be studied particularly well if higher-order modes are employed where the resonant atoms can be distributed over a large range of kR values within the cavity, see Fig. 3.8b. The results are displayed in Fig. 3.8c. For comparison, we have used the function $a + b (\sin 2kR)/(2kR)$ (dashed lines) to pinpoint the functional dependence of the oscillations in the CLS with increasing sample size as it was predicted first in [31] and recently experimentally verified [45]. A rigorous theory to describe this behaviour on the basis of the cavity geometry used here, however, still has to be developed.

Fig. 3.8

Reprinted from [61], Copyright 2012, with permission from Wiley

The collective Lamb shift (CLS) for an extended layer of resonant atoms within the cavity. Left column: cavity reflectivity in the third-order guided mode for increasing thickness D of the resonant layer. The insets show the cavity cross section with the resonant layer (red) and the standing wave intensity pattern (solid line). Right column: CLS as function of $k_z D$ for the 7th and 11th order mode in a Pt/C/Pt cavity with a 100 nm thick guiding layer. Similar curves have been observed recently in an experiment involving thin layers of atomic vapor [45].

3.6 Quantum Optics of Mössbauer Nuclei in X-Ray Cavities

The reflectance and spectral response of an x-ray cavity can be calculated using different techniques (see Fig. 2 in [40]). One approach is Parratt’s formalism [73], in which all possible scattering pathways arising from the material boundaries are summed up. A generalization of this technique which enables one to include resonant multipole scattering with its polarization dependence has been formulated in a transfer-matrix formalism (for an overview, see [6]). A numerical implementation of this formalism is provided via the CONUSS software package [74]. An alternative approach involves the direct numerical integration of Maxwell’s equations, via a finite-difference time-domain method [75]. The analysis so far, however, focused to the case of linear light-matter interaction with classical light fields. Moreover, these methods do not enable one to interpret the obtained spectra in terms of the underlying nuclear dynamics. In the following, we therefore focus on a recently developed quantum optical framework for the description of ensembles of nuclei in x-ray cavities [35, 37]. The key idea of this approach is to relate the entire system comprising the x-ray cavity and the large ensemble of multi-level nuclei to that of a corresponding “artificial atom”, that is, a quantum optical few-level structure which for low probing fields gives rise to the same response. This method has the advantage that it treats the x-ray field as quantized, enables one to explore non-linear and quantum effects, allows for a full interpretation, and for a quantitative modeling of experiments. On the other hand, designing the cavity geometry and the nuclear level structure in a suitable way enables one to design artificial atoms with properties which reach beyond what is available in natural atoms [29, 68]. We note that the quantum optical model presented here recently was promoted to an ab-initio theory, in which the model parameters and the realized artificial quantum system can directly be calculated from a given cavity structure [40, 76]. As compared to previous models, this ab-initio theory further predicts qualitatively new phenomena, e.g., related to the effect of off-resonant cavity modes on the nuclear dynamics.

3.6.1 Quantum Optics of the Empty Cavity

To illustrate the photonic environment in a cavity without nuclei, we restrict the discussion to a single cavity mode and neglect the light polarization for the moment. The probing x-rays have frequency $\omega$ and a wave vector $\mathbf {k}$ that defines the incidence angle $\theta$. The cavity modes are characterized by discrete wave number components perpendicular to the cavity surface, but continuous wave number components along the surface. The boundary conditions impose that the wave vector $\mathbf {k}_C$ inside the cavity has a component $|\mathbf {k}_C|\,\cos (\theta )$ along the cavity surface. The component transverse to the cavity surface, however, is fixed by the guided mode standing wave condition to $|\mathbf {k}|\,\sin (\theta _0)$, if $\theta _0$ is the incidence angle under which this mode is driven resonantly for incident wave number $|\mathbf {k}|$. Thus, $|\mathbf {k}_C| = \sqrt{|\mathbf {k}|^2 \cos ^2(\theta ) + |\mathbf {k}|^2 \sin ^2(\theta _0)}$, and a detuning $\Delta _C = \omega _C - \omega \approx -\omega \theta _0 \Delta \theta$ between the cavity resonance frequency and the frequency of the incident light can be defined, which can be tuned via small variations in the incidence angle $\Delta \theta = \theta - \theta _0$ from the resonance condition. With this detuning, the Heisenberg equation of motion for the cavity mode in the absence of nuclear resonances characterized by annihilation [creation] operators a [$a^\dagger$] is given by

$$\begin{aligned} \frac{d}{dt}a = -(\kappa + i\Delta _C) a + \sqrt{2\kappa _R}\,a_\text {in}\,, \end{aligned}$$

(3.40)

where $\kappa$ is the overall damping rate of the cavity mode, $\kappa _R$ characterizes the evanescent coupling into and out of the cavity mode, and $a_\text {in}$ the applied x-ray field. In practice, $\kappa _R$ can be adjusted, e.g., by choosing the thickness of the cavity top layer through which the x-rays evanescently couple into the cavity mode. From the cavity field operators, the empty cavity reflectance $|{R_\text {c}}|^2$ can be obtained via the input-output relations [77] $a_\text {out} = - a_\text {in} + \sqrt{2\kappa _R}\,a$, using ${R_\text {c}} = \langle a_\text {out}\rangle /\langle a_\text {in}\rangle$. In the stationary state (SS) $\dot{a}^{(SS)} = 0$, such that

$$\begin{aligned} a^{(SS)} = \frac{\sqrt{2\kappa _R}\, a_\text {in}}{\kappa + i\Delta _C} \end{aligned}$$

(3.41)

and

$$\begin{aligned} R_\text {c} = \frac{2\kappa _R}{\kappa + i\Delta _C} - 1. \end{aligned}$$

(3.42)

At the so-called critical coupling condition $2\kappa _R = \kappa$, the reflectance $|R_\text {c}|^2$ vanishes on resonance $\Delta _C=0$, which can be interpreted as destructive interference between light reflected from the outside of the cavity with that coupling out of the cavity mode. If operated in this regime, the cavity can be employed to suppress a significant part of the background photons, facilitating the detection.

3.6.2 Quantum Optics of a Cavity Containing Resonant Nuclei

Next we consider the effect of the nuclei on the cavity, restricting the discussion to the single-excitation subspace spanned by the two collective states $|G\rangle$ and $|E\rangle$. The nuclei effectively act as a source term for x-ray photons in the empty cavity equation of motion (3.40), which is modified to

$$\begin{aligned} \frac{d}{dt}a = -(\kappa + i\Delta _C) a + \sqrt{2\kappa _R}\,a_\text {in} - i g^*\sqrt{N}|G\rangle \langle E|, \end{aligned}$$

(3.43)

where g is the x-ray-nucleus coupling constant. Thus the reflectance Eq. (3.42) becomes

$$\begin{aligned} R =R_\text {c} -\frac{i}{a_\text {in}} \frac{2\kappa _R}{\kappa + i\Delta _C} g^* \sqrt{N} \langle E| \hat{\rho }| G\rangle , \end{aligned}$$

(3.44)

where $\hat{\rho }$ is the density operator characterizing the nuclei. If the empty cavity reflectance $R_\text {c}$ vanishes on resonance in critical coupling, then the observable reflectance originates from the nuclei alone, and therefore ideally forms a signal without any background.

The result Eq. (3.44) can be generalized in a straightforward way to accomodate for arbitrary input and output photon polarizations, as well as the magnetic sub-structure of the nuclear levels, as it may result from nuclear Zeeman splitting in the presence of a magnetic hyperfine interaction in a ferromagnetic environment. We denote the input [output] polarization unit vectors as $\hat{a}_\text {in}$ [$\hat{a}_\text {out}$], the two cavity mode polarization unit vectors as $\hat{a}_1$ and $\hat{a}_2$, and define $\mathbf {1}_\perp = \hat{a}_1\hat{a}_1^* + \hat{a}_2\hat{a}_2^*$. The different transitions from the ground state manifold to the excited state manifold within each nucleus are labeled with index $\mu$, and have a dipole moment $\mathbf {d}_\mu$ and a Clebsch-Gordan coefficient $c_\mu$. Since the nuclei initially are distributed over the different ground states, we further define the number of nuclei in the ground state of transition $\mu$ as $N_\mu$, and generalize the exciton Eq. (3.9) to $|E_\mu \rangle$ as the exciton created upon excitation on transition $\mu$. Then,

$$\begin{aligned} R =R_\text {c}\, \hat{a}_\text {out}^* \hat{a}_\text {in} -\frac{i}{a_\text {in}} \frac{2\kappa _R}{\kappa + i\Delta _C} g^* \sum _\mu (\hat{a}_\text {out}^*\cdot \mathbf {1}_\perp \cdot \hat{d}_\mu )\,c_\mu \sqrt{N_\mu } \langle E_\mu | \hat{\rho }| G\rangle . \end{aligned}$$

(3.45)

It can be seen that the empty cavity response $R_\text {c}$ can be filtered out using orthogonal input and output polarizations, as expected. The nuclei, however, can scatter between these two orthogonal modes, such that this crossed polarization setting again is a method to detect the nuclear response without background via a high-purity polarimetry setup [78]. Further, the different transitions $\mu$ can be interpreted as a collective few-level system, with number of relevant states determined by the input and output polarization, as well as the nuclear quantization axis defining the magnetic substates. This setting with magnetic sublevels therefore enables one to realize quantum optical few-level systems [35, 37]. As evidenced by the coherent addition of the scattering channels, the responses of the different transitions within this few-level system may interfere, providing access to a rich variety of quantum optical phenomena.

3.6.3 Nuclear Dynamics in the Cavity

It remains to determine the nuclear dynamics, i.e., its evolution under the action of an x-ray pulse, in order to determine the density matrix $\rho$ entering the reflectance in Eqs. (3.44) and (3.45). Here we want to illustrate this for the simplest case of two-level nuclei and a single cavity mode a. The original Hamiltonian is of Jaynes-Cummings-type [2, 29], and contains interaction terms of the form $S_+^{(n)}a$, describing the annihilation of a cavity photon (a) together with an excitation of nucleus n ($S_+^{(n)}$), as well as the reverse process. The problem can be simplified considerably be exploiting that the fastest timescale in the problem typically is given by the cavity lifetime $1/\kappa$. In this “bad cavity” limit characterized by short photon trapping times, the cavity modes adiabatically follow the much slower evolution of the nuclei. As a consequence, the cavity operators can approximately be replaced by their steady-state values Eq. (3.43), which results in an effective Hamiltonian for the nuclei alone. In the radiative eigenmode basis it is given by [35, 37]

$$\begin{aligned} H = -\hbar \Delta |E\rangle \langle E| + \hbar (\Omega _\text {eff} \, |E\rangle \langle G| + \text {H.c.}) + \hbar \Delta _{LS}\, |E\rangle \langle E|. \end{aligned}$$

(3.46)

The interpretation of this Hamiltonian is straightforward. It is equivalent to the Rabi model for a driven two-level system [2]. However, the effective Rabi coupling constant $\Omega _\text {eff} = g\sqrt{N}\, a^{(SS)}$ in $H_\Omega$ is not given by the bare nucleus-cavity coupling g, but modified by cooperative effects as indicated by the superradiant enhancement factor $\sqrt{N}$, as well as by the cavity field as indicated by the presence of the steady-state value of the field operator $a^{(SS)}$. Furthermore, the usual detuning $\Delta$ between x-ray frequency and bare nuclear transition frequency is augmented by an additional contribution

$$\begin{aligned} \Delta _\text {LS} = |g|^2 N\, \text {Im}[(\kappa +i\Delta _C)^{-1}], \end{aligned}$$

(3.47)

which arises due to the radiative coupling between the nuclei and which can be interpreted as the cooperative Lamb shift. Similar to the Hamiltonian parts, also the incoherent spontaneous emission of the individual nuclei $\gamma$ is modified by

$$\begin{aligned} \Gamma = 2|g|^2 N\, \text {Re}[(\kappa +i\Delta _C)^{-1}]. \end{aligned}$$

(3.48)

In linear response, the desired nuclear polarization $\langle E|\rho |G\rangle$ is governed by

$$\begin{aligned} \langle E|\dot{\rho }|G\rangle = -i \Omega _\text {eff} + i\left[ \left( \Delta -\Delta _{LS}\right) + \frac{i}{2}\left( \gamma + \Gamma \right) \right] \langle E|\rho |G\rangle . \end{aligned}$$

(3.49)

Inserting the steady state solution obtained from $\langle E|\dot{\rho }|G\rangle =0$ into Eq. (3.44) finally yields

$$\begin{aligned} R = R_\text {c} -i \left( \frac{\kappa -i\Delta _C}{\kappa + i\Delta _C} \, \frac{2\kappa _R}{\kappa } \right) \, \frac{\Gamma /2}{\left( \Delta -\Delta _{LS}\right) + \frac{i}{2}\left( \gamma + \Gamma \right) }, \end{aligned}$$

(3.50)

with the empty cavity reflectance $R_\text {c}$ defined in Eq. (3.42). The nuclear response therefore comprises a Lorentzian shifted with respect to the bare nuclear resonance frequency by the collective Lamb shift $\Delta _\text {LS}$, and with superradiant broadening $\Gamma$ of the natural line width $\gamma$, as already found using a different formalism in Eq. (3.38).

3.7 Quantum Optical Effects in Cavities

3.7.1 Interferometric Phase Detection via Fano Resonance Control

In Sect. 3.5 it was found that a resonantly driven cavity containing resonant two-level nuclei features a Lorentzian spectral response, broadened by superradiance, and shifted by the cooperative Lamb shift. Having the expression for the cavity reflectance Eq. (3.50) at hand, we can start by exploring the cavity response off-resonance with the cavity mode [79]. Close to the resonance, $\Delta _C = \delta _C(\theta -\theta _\text {min})$, such that the detuning between x-rays and cavity mode can experimentally be tuned by varying the x-ray incidence angle $\theta$ around the resonance angle $\theta _{\text {min}}$.

To simplify the analysis, we specialize to strongly superradiant cavities ($\gamma \ll \Gamma$) in critical coupling ($\kappa = 2\kappa _R$) and rewrite Eq. (3.50) using Eq. (3.48) to give

$$\begin{aligned} |R|^2&= \frac{|\varepsilon + q|^2}{1+\varepsilon ^2} \sigma _0\,, \end{aligned}$$

(3.51)

where we defined the dimensionless energy $\varepsilon =(\Delta - \Delta _\text {LS})/(\Gamma /2)$, the prefactor $\sigma _0 = [1 + \kappa ^2/\Delta _C^2]^{-1}$, and the so-called q-factor $q = \kappa /\Delta _C$. The cavity response thus takes the form of a Fano resonance [80], which is an ubiquitous spectroscopic signature in light-matter interactions [81, 82]. The Fano resonance arises, because there are two interfering pathways for the light to propagate through the sample. First, the spectrally broad cavity response, which is of relevance it the light does not interact with the nuclei. Second, a spectrally narrow bound-state contribution arising from the scattering on the nuclei. The relative phase between the two contributions is given by $\phi = -\text {arg}(q-i)$, and it turns out that this phase determines the line shape, which may range from Lorentzian absorption features via dispersion-like asymmetric structures up inverted Lorentzian lines [83]. Conversely, external control over this relative phase can be used to manipulate the lineshape [83, 84]. Since close to resonance, $q = \kappa /[\delta _C(\theta - \theta _\text {min})]$, we find that changing the incidence angle allows one to tune the Fano parameter and thus the spectral lineshape. Example lineshapes are shown in Fig. 3.9, clearly demonstrating the control mechanism.

Fig. 3.9

Reprinted from [79], Copyright 2015, with permission from the American Physical Society

Fano lineshape control with nuclei embedded in a thin film cavity. The panels show the reflectance recorded at incidence angles deviating from the resonance angle by $\Delta \theta$ indicated in the panels. The figure shows raw data without baseline subtraction such that the absolute scaling cannot directly be compared. Red lines show fits with a generic Fano line shape. The cavity is a Pd(4 nm)/C(36 nm)/Pd(14 nm) structure with a 1.2 nm thick layer of ${}^{57}$Fe nuclei in the middle of the guiding C-layer.

The analytic expression Eq. (3.51) enables one to interpret the cavity spectra on- and off-resonance as Fano resonances. But more importantly, the phase-sensitivity of the spectra together with the possibility to control the relative phase of the two interfering channels open the possibility to exploit the setup as an interferometer. Note that the cavity setup discussed here enables one to control the phase in a static manner via the x-ray incidence angle, but it has been demonstrated that also a dynamical control over the phase is possible [83, 84]. This approach enables one to measure tiny phase shifts via the asymmetry of the line shape. On the other hand, manipulating the phase can be used to control the light-matter interaction. As an example, the complex nuclear dipole moment induced by the x-rays could be measured using this interferometric approach [79]. From a broader perspective, the line shape control discussed here provides a route towards the implementation of a diverse range of applications relying on Fano interference [81, 82] at x-ray energies. One example, electromagnetically induced transparency, will be discussed in the next Sect. 3.7.2.

3.7.2 Electromagnetically Induced Transparency

As shown in Sect. 3.6, an ensemble of nuclei in a cavity can be effectively considered as an artificial atom with an enhanced decay width and a self-energy correction of its resonance energy given by the collective Lamb shift. The strong spatial variation of the photonic density of states inside the cavity opens the possibility to tune these properties via placement of the atoms within the wavefield of the cavity. An ensemble in an antinode of the cavity field displays a strong superradiant enhancement, which defines a new evolution time scale which is much faster than the usual single-nucleus single decay. Relative to this accelerated time scale, ensembles in a node will remain subradiant, since their dynamics is not accelerated. Thus, a cavity with two atomic ensembles at positions with such markedly different photonic densities of states can be considered as an artificial atom with three levels: one belonging the common ground state and two excited state levels that correspond to the superradient and subradiant ensembles, respectively. Effectively, the subradiant ensemble represents a metastable level because its radiative lifetime is much longer than that of the superradiant ensemble. In this three-level system, all levels are radiatively coupled through the vacuum field of the cavity. Such a coupling gives rise to a key phenomenon of quantum optics, electromagnetically induced transparency (EIT) [72].

The EIT effect arises from the cancellation of resonant absorption due to quantum interference between atomic levels with significantly different radiative lifetimes. In the original version of EIT, the quantum interference is induced by an external laser field tuned to the transition between a metastable level and a shortlived excited state in a three-level system. The basic ingredients for EIT are illustrated in Fig. 3.11a, where a three-level system is shown, represented by the ground state, $|{1}\rangle$, and two upper states, $|{2}\rangle$ and $|{3}\rangle$ with respective energies $E_2$ and $E_3$. A strong laser field with Rabi frequency $\Omega _C$ induces an atomic coherence between states $|{2}\rangle$ and $|{3}\rangle$. Tuning a (weak) probe laser field across the resonant transition 1 $\rightarrow$ 3 leads to a Fano-type quantum interference [80] that renders the medium almost transparent in a narrow window around the exact resonance frequency. The transparency arises since due to the coherent superposition of the two states $|1\rangle$ and $|2\rangle$, the two excitation pathways $|1\rangle \rightarrow |3\rangle$ and $|2\rangle \rightarrow |3\rangle$ interfere destructively, such that no excitation takes place. The degree of transparency is limited by the dephasing of the atomic coherence resulting from the decay of state $|{2}\rangle$ or external perturbations. Thus, maximum transparency is observed if $|{2}\rangle$ can be considered metastable, i.e., if it has a decay width, $\gamma _2$, that is negligibly small relative to the radiative decay width, $\gamma _3$, of the state $|{3}\rangle$.

To investigate the possibility of EIT in the $^{57}$Fe containing cavity, we replace the spatially extended $^{57}$Fe layer in Fig. 3.8 by two layers with a separation of half the period of the standing wave in the cavity, as shown in Fig. 3.10. Energy spectra of the cavity reflectivity are calculated via the transfer matrix formalism already employed in Sect. 3.4.2. Quite remarkably, the appearance of the dip in the reflectivity very sensitively depends on the location of this pair of layers in the cavity. The dip is most pronounced (Fig. 3.10a) if the first of the resonant layers (seen from the top) is located in a node of the wavefield and the second one is located in an antinode of the wavefield. The dip gradually vanishes if the two layers are displaced by half a period of the standing wave (Fig. 3.10b, c). To determine the spectral shape of the transparency dip we subtract the two spectra in Fig. 3.10a, c. The resulting difference spectrum (Fig. 3.10d) exhibits an asymmetric shape corresponding to a Fano profile [80], thus providing clear evidence for the type of quantum interference that is typical for EIT [85].

Fig. 3.10

Reprinted from [61], Copyright 2012, with permission from Wiley

Top row: sample geometry of planar cavities for X-rays containing two 2-nm-thick layers of $^{57}$Fe (red) together with the normalized field intensity (solid line) in the 3rd-order guided mode, excited at an angle of incidence of $\varphi$ = 3.5 mrad. Bottom row: calculated energy spectra of the cavities reflectivity around the nuclear resonance, together with the difference of the spectra in (a) and (c), displayed in (d). The fundamental difference between the spectra in (a) and (c) results from the asymmetry of the boundary conditions for the electromagnetic field in the cavity, see supplementary material for Ref. [28].

In order to analyse the analogy with EIT more closely we expand the cavity reflectivity around the nuclear resonance (details of the derivation are given in the supplementary information of Ref. [28]), resulting in:

$$\begin{aligned} R(\Delta )= & {} \frac{d_2\,f_0\,\gamma _0 E_{2-+}(i\Delta + \gamma _0)}{(i\Delta + \gamma _0) (i\Delta + \gamma _0 [1 + d_2\,f_0\,\,E_{2--}]) + d_1\,d_2\,f_0^2\,\gamma _0^2\, E_{2-+} E_{1+-}} \end{aligned}$$

(3.52)

The quantities $E_{2-+}, E_{2--}$, and $E_{1+-}$ are elements of the transfer matrices that describe the propagation of the photon field in the unperturbed cavity. Equation (3.52) is basically identical to the standard expression for the complex susceptibility in case of EIT [72] if one identifies (see Fig. 3.11)

$$\begin{aligned} \gamma _2= & {} \gamma _0 \nonumber \\ \gamma _3= & {} \gamma _0 [1 + d_2\,f_0\,\,E_{2--}]\\ \Omega _c^2= & {} d_1\,d_2\,(f_0\,\gamma _0)^2 E_{2-+} E_{1+-} \nonumber \end{aligned}$$

(3.53)

This result prompts an obvious interpretation, supported by the illustration in Fig. 3.11b, c: The two ensembles of nuclei in the node and the antinode of the standing wave field experience two significantly different photonic densities of states, leading to two different collective decay rates $\gamma _2$ and $\gamma _3$. This effectively converts the nuclei in the cavity into three-level systems with two degenerate upper levels represented by the states $|{2}\rangle$ and $|{3}\rangle$, as illustrated in the level scheme of Fig. 3.11c. The expression for $\Omega _C^2$ is proportional to the two transfer matrix elements $E_{2-+}$ and $E_{1+-}$ that describe the transition amplitudes between the two counterpropagating fields in the cavity at the position of the two resonant layers. This indicates that the coupling field arises from the radiative coupling of the two resonant layers via the cavity field: An excited atom in the antinode $|{3}\rangle$ decays back to the ground state $|{1}\rangle$ and releases a photon into the cavity. This photon can promote an atom in the node from the ground state into state $|{2}\rangle$ that eventually decays and again releases a photon into the cavity, and so on. As a result, the two excited states $|{2}\rangle$ and $|{3}\rangle$ are coupled through their common ground state $|{1}\rangle$ via the vacuum field of the cavity, which effectively establishes a control field between the two upper states, represented by the horizontal arrow in Fig. 3.11c. The resulting arrangement of levels in Fig. 3.11c and their coupling resembles closely a $\Lambda$-type level scheme as in Fig. 3.11a. It should be noted that the control field Rabi frequency of Eq. (3.53) enters Eq. (3.52) as a complex-valued quantity $\Omega _C^2$ rather than a real number $|\Omega _C|^2$ in the usual expression for an EIT susceptibility. A closer inspection reveals that the imaginary part of $\Omega _C^2$ is small compared to its real part for the cavity configurations employed here. It remains to be investigated in which way the imaginary part of $\Omega _C^2$ affects EIT in these systems.

Fig. 3.11

Reprinted from [67], Copyright 2015, with permission from Springer Nature

a Typical, $\Lambda$-shaped level scheme of EIT in quantum optics: a strong laser field with Rabi frequency $\Omega _C$ induces an atomic coherence between the metastable level $|{2}\rangle$ and the upper state $|{3}\rangle$. The decoherence rate $\gamma _2$ can be neglected compared to the decay rate $\gamma _3$. The system appears to be transparent for the probe field at resonance ($\Delta$ = 0) with the transition $|{1}\rangle \rightarrow |{3}\rangle$. b Cavity geometry with two layers of $^{57}$Fe that can be translated into a $\Lambda$-shaped level scheme, if plotted with the decay width as vertical axis, shown in (c). While level $|{3}\rangle$ in the antinode is superradiant, level $|{2}\rangle$ in the node is subradiant so that $\gamma _{2} \ll \gamma _{3}$. d Measured reflectivity spectrum of the cavity shown in (b) that clearly shows the EIT transparency dip at the exact resonance energy where the system would be completely opaque without the $^{57}$Fe layer in the node [28].

We want to emphasize that cooperative emission is critical to EIT in this system. While one of the atomic ensembles undergoes single-photon superradiant enhancement leading to a decay width of $\Gamma _C = 2\gamma _3 = d_2\,f_0\,$Re$[E_{2--}]\,\Gamma _0$ and a collective Lamb shift of $L_C$ = $-d_2\,f_0\,$Im$[E_{2--}]\,\Gamma _0/2$, the decay width $2\gamma _2$ of the other’subradiant’ ensemble is given by just the natural line width $\Gamma _0$, so that $\gamma _3 \approx 50\,\gamma _2$ in the example shown in Fig. 3.10. Thus, in the presence of a strong superradiant enhancement of state $|{3}\rangle$, the state $|{2}\rangle$ is relatively long-lived and thus can be considered as metastable. This is an important condition for a pronounced EIT effect. The superradiantly broadened transition of the nuclei in the antinode provides the continuum of states relative to which the Fano interference in this system takes place. The collective Lamb shift of this level introduces an asymmetry that leads to the characteristic Fano profile of the transparency window. For vanishing CLS, the profile would simply be a Lorentzian line [79, 82, 83].

For an experimental verification of EIT in the x-ray regime, we have prepared an x-ray cavity, shown in Fig. 3.11b, that consists of a Pt(3 nm)/C(38 nm)/Pt(10nm) sandwich structure containing two 3 nm $^{57}$Fe layers that occupy a node and an antinode of the cavity field. These two layers represent the subradiant state $|{2}\rangle$ and the superradiant state $|{3}\rangle$ that are radiatively coupled via the vacuum field of the cavity, and thereby realize the EIT scheme. Drawing these states and their coupling in a level diagram with the decay width as vertical axis, one obtains a $\Lambda$ type level system as shown in Fig. 3.11c. Using a spectroscopic detection scheme similar to that employed for measurement of the collective Lamb shift [27], we could record the energy spectrum of one of the hyperfine-split resonances of the Fe in this system, shown in Fig. 3.11d, clearly displaying a pronounced EIT transparency dip at the exact resonance where the system would be completely opaque otherwise [28].

The modulation of the photonic density of states in the cavity facilitates the preparation of ensembles of resonant atoms with greatly different radiative lifetimes. In other words, it lifts the radiative degeneracy of the atoms in the cavity, effectively creating extra excited levels that are radiatively coupled amongst each other via the cavity field. Note that this approach is general, as illustrated by the fact that the EIT mechanism discussed here has been adapted to qubits operating at microwave frequencies [86]. The degeneracy of the excited-state levels can also be lifted energy-wise by a magnetic hyperfine interaction (nuclear Zeeman effect). In this case the vacuum field of the cavity then leads to coherences between the excited states that are subject of the following section.

3.7.3 Spontaneously Generated Coherences

So far, we have focused on nuclei without magnetic substructure. In an environment with magnetic fields, e.g., $^{57}$Fe exhibits two ground ($I=1/2$) and four excited ($I=3/2$) states, which result in a splitting of the Mössbauer spectra into six lines. Superradiant broadening can overcome this splitting, such that the different spectral lines overlap. Naively, one might expect an incoherent addition of the individual spectral contributions of the different transitions. However, deep minima can arise in the spectrum, which suggest the presence of destructive interference. These will turn out to be a consequence of so-called spontaneously generated coherences (SGC) [87,88,89]. While SGC are linked to numerous potential applications including the suppression of spontaneous decay, stringent conditions on their presence so far have limited the experimental exploration.

Fig. 3.12

Reprinted from [67], Copyright 2015, with permission from Springer Nature

Elementary processes in the interaction of the nuclei with the electromagnetic vacuum. Green straight arrows indicate the nuclear dynamics. Red curved arrows depict the corresponding emission and re-absorbtion of a virtual photon. a Emission and absorption of the virtual photon within a single nucleus on a single transition leads to a complex energy correction, contributing to Lamb shift and spontaneous emission. b The photon exchange between two nuclei induces dipole-dipole couplings. c If the virtual photon couples different transitions within a single nucleus, spontaneously generated coherences arise.

The origin of SGC can be understood as follows. In second order perturbation theory, the interaction of the nuclei with the surrounding electromagnetic vacuum field leads to processes as visualized in Fig. 3.12. In (a), an initially excited nucleus deexcites and emits a virtual photon (red line), which subsequently is reabsorbed on the same transition. This process results in a complex correction of the transition energy, the real and imaginary part of which can be interpreted as single-particle Lamb shift and spontaneous decay rate. Similarly, the virtual photon can be reabsorbed by another particle (b), giving rise to dipole-dipole energy exchange between nuclei. This corresponds to the exchange of virtual photons already discussed in Sect. 3.3. To be added is the process shown in (c), where the virtual photon is re-absorbed within the same particle, but on another transition. This state transfer establishes SGC between the two excited states, arising from the interaction with the vacuum only. As a consequence of this coherence, the spontaneous emission from a superposition of the excited states $|-\rangle = (|a\rangle - |b\rangle )/\sqrt{2}$ is suppressed, since the two decay channels $|a\rangle \rightarrow |g\rangle$ and $|b\rangle \rightarrow |g\rangle$ destructively interfere. In contrast, $|+\rangle = (|a\rangle + |b\rangle )/\sqrt{2}$ decays with double decay rate due to constructive interference. Figure 3.13 shows the corresponding temporal evolution. Initially, the nuclei are in state $|a\rangle$. Without SGC, the excited state exponentially decays, and the ground state population grows accordingly (a). With SGC in (b), population is transfered from $|a\rangle$ to $|b\rangle$, establishing a coherence. As a result, half of the nuclei remain trapped in $|-\rangle$, which corresponds to the contribution to the initial state $|\langle - |a\rangle |^2 = 1/2$. In the optical spectra, such trapping states translate into dark lines.

However, the generation of SGC is limited by stringent conditions, which usually are not met for atoms in free space. First, the dipole moments of emitting and absorbing transitions must be non-orthogonal. Second, the energy difference between the upper states should be small compared to the natural line width, since for non-degenerate upper states the free time evolution converts the trapping state $|-\rangle$ into the decaying state $|+\rangle$. Thus, with increasing energy difference the time over which population can be trapped in the excitated states becomes smaller (see Fig. 3.13c), until it eventually can be neglected compared to the natural lifetime. A final condition is that the two involved transitions should share a common ground state $|g\rangle$ to enable the re-absorption, even though there are also effects in the spectrum of the emitted light associated to SGC on transitions with different ground states [90].

Fig. 3.13

Reprinted from [67], Copyright 2015, with permission from Springer Nature

Spontaneous emission dynamics for nuclei initially in state $|a\rangle$ of Fig. 3.12c. a Regular spontanous decay without the presence SGC, as it could be observed, e.g., in two-level nuclei. b As in (a), but with SGC in the three-level system shown in Fig. 3.12c. Part of the nuclei evolve into state $|b\rangle$, and half of the nuclei remain trapped in the excited states. c Similar to (b), but with energy splitting $\gamma /2$ between $|a\rangle$ and $|b\rangle$, which limits the time over which population can be trapped in the excited states.

With large ensembles of nuclei in x-ray cavities, these limitations can be overcome. One reason is that the coupling between the different transitions is mediated via the cavity rather than free space. Then the condition of non-orthogonal dipole moments $\mathbf {d}_\mu ^*\cdot \mathbf {d}_\nu \ne 0$ is relaxed to $(\hat{d}_\mu ^*\cdot \mathbf {1}_\perp \cdot \hat{d}_\nu )\ne 0$, where $\mathbf {1}_\perp$ is a projector onto the cavity polarization space [see Eq. (3.45)]. To illustrate the consequence of this, we introduce a coordinate system with cavity surface normal unit vector $\hat{\pi } = \hat{x}$, wave vector $\mathbf {k}= \hat{z}$, and $\hat{\sigma } = \hat{k}\times \hat{\pi } = \hat{y}$. In this case, $\mathbf {1}_\perp = \hat{x}\hat{x}^* + \hat{y}\hat{y}^*$, where the vectors are multiplied with the outer product to form a matrix. If the nuclear magnetization $\mathbf {B}_\text {hf}\propto \hat{\pi }$, the two circularly polarized transitions have dipole moments $\hat{d}_1 = (\hat{k}+i\hat{\sigma })/\sqrt{2}$ and $\hat{d}_2 = (\hat{k}-i\hat{\sigma })/\sqrt{2}$. Then, $(\hat{d}_\mu ^*\cdot \mathbf {1}_\perp \cdot \hat{d}_\nu ) = 1/2$ for $\mu ,\nu \in \{1,2\}$. Since the cross terms $\mu \ne \nu$ have the same weight as the diagonal terms $\mu = \nu$, maximum SGC arises. This is possible since the contribution due to $\hat{x}\hat{x}^*$ vanishes in this particular cavity geometry. In contrast, in free space, contributions of different polarizations would cancel each other and $\hat{d}^*_1 \cdot \hat{d}_2 = 0$. Thus, the spatial anisotropy of the cavity vacuum leads to the formation of SGC [91, 92]. A second mechanism for SGC in x-ray cavities involves the coupling between different nuclei. In our approach, the combined system of the large ensemble of nuclei and the cavity is described as a single effective nucleus. Within this model, the probing x-ray beam does not resolve the microscopic structure of the system. As a consequence, the dipole-dipole coupling between different nuclei appears as a radiative coupling between different states of the single effective nucleus. Therefore, the nuclear many-body system enables one to engineer an effective single nucleus with properties going beyond those naturally found in nuclei. Finally, in both cases, the superradiant enhancement of spontaneous emission enables one to reduce the perturbing effect of the energy splitting between the different states.

Fig. 3.14

Reprinted from [67], Copyright 2015, with permission from Springer Nature

Experimental realization of SGC. a Theoretical predictions of the quantum optical model, as well as corresponding results obtained by artificially omitting the SGC contributions. b Experimental data from [29], together with a theoretical fit using CONUSS including details of the detecion procedure. The deep minima indicating the presence of SGC can clearly be seen.

We implemented SGC in a Pd(5 nm)/C(20 nm)/$^{57}$Fe(2.5 nm)/C(20 nm)/Pd(20 nm) layer system, in which the magnetization of the ferromagnetically ordered Fe layer can be controlled via a weak external magnetic field. An example is shown in Fig. 3.14 for the half-Faraday geometry, in which the magnetization $\mathbf {B}_{\text {hf}} \parallel (\hat{k} + \hat{\sigma })$. The input and detection polarization were chosen along $\hat{\sigma }$ and $\hat{\pi }$, respectively. It can be seen that the quantum optical model predicts deep interference minima at around $\Delta = \pm 30 \gamma$, which disappear if the mechanism leading to SGC is artificially omitted in the analysis. The corresponding experimental results clearly verify the presence of these minima, and thus of SGC [29]. The experimental data is overlayed by a theoretical calculation obtained using CONUSS [55, 74] which in addition takes into account the details of the detection method. Interestingly, the intensity drops down to the background baseline, which indicates full interference visibility. This indicates a nuclear quantum system essentially free of perturbations.

From a broader perspecitive, the large ensembles of nuclei with magnetic sublevels in x-ray cavities thus enable one to engineer a variety of tunable quantum optical level schemes, including the possibility to implement SGC.

3.7.4 Tunable Subluminal Propagation of Resonant X-Rays

As discussed in Sect. 3.7.2, the key signature of electromagnetically induced transparency is the vanishing of the linear absorption of a probe beam within a narrow spectral transparency window. However, next to the transparency, EIT is also accompanied by characteristic modifications to the medium’s dispersion [72]. In particular, within the transparency window, a steep linear dispersion appears, which can be facilitated to control the group velocity of a light pulse passing through the medium. To see this, we consider the propagation of an electromagnetic wave packet through a medium, given in one dimension by

$$\begin{aligned} E(x,t) = \frac{1}{2\pi } \int \limits _{-\infty }^{\infty } d\omega E(\omega )\, e^{i(\omega t - kx)} . \end{aligned}$$

(3.54)

We assume that the spectral width of the wave packet is narrow as compared to the EIT window, and expand the wave number $k = k_R + i k_I$ in leading order of a Taylor series around the center of the EIT window at $\omega _0$ to give $k_R(\omega ) \approx k_R(\omega _0) + \frac{\partial k_R}{\partial \omega }|_{\omega _0}\, (\omega - \omega _0)$ and $k_I(\omega ) \approx k_I(\omega _0)$. Note that the linear order of $k_I$ is zero since the absorption has a minimum at $\omega _0$. Inserting this into Eq. (3.54) gives

$$\begin{aligned} E(x,t) \approx \frac{1}{\sqrt{2\pi }} e^{-k_I(\omega _0) x}\times e^{k_R(\omega _0)\,(x-v_{ph} t )}\times \int \limits _{-\infty }^{\infty } d\omega E(\omega ) e^{i\frac{\omega -\omega _0}{v_{gr}} (x-v_{gr}t)} . \end{aligned}$$

(3.55)

The three parts separated by “$\times$” have a clear interpretation. The first part is the linear attenuation because of the imaginary part of the resonant refractive index $n_I(\omega _0) \propto k_I(\omega _0)$, following the Lambert-Beer law. The second part describes the propagation of the carrier frequency plane wave through the medium. It moves with the phase velocity $v_{ph} = \omega _0/k_R(\omega _0) = c/n_R(\omega _0)$, that is, with the vacuum speed of light c divided by the real part of the index of refraction. The third part shows that the wave packet propagates with the group velocity

$$\begin{aligned} v_{gr} = \left( \frac{\partial k_R}{\partial \omega }\bigg |_{\omega _0} \right) ^{-1} = \frac{c}{n_R(\omega _0) + \omega _0 \frac{\partial n_R}{\partial \omega }|_{\omega _0}}. \end{aligned}$$

(3.56)

This expression illustrates that without dispersion $\partial n_R/\partial \omega$, the group velocity of the wave packet is equal to the phase velocity. Otherwise, depending on the sign and the magnitude of the dispersion, the group velocity can be much lower than the vacuum speed of light c (“slow light”, sub-luminal propagation), larger than c (“fast light”, super-luminal propagation), or even negative. All cases have been experimentally implemented with atomic gases, and the control of the group velocity has found numerous applications [72].

Fig. 3.15

Reprinted from [36], Copyright 2015, with permission from the American Physical Society

Schematic setup of the experiment. The lower panel shows the temporal and the spectral structure of the x-ray pulse at different points throughout the propagation through the setup.

Recently, group velocity control and slow light has also been achieved at x-ray energies using Mössbauer nuclei [36]. The concept of the experiment is shown in Fig. 3.15. The setup is motivated by two main experimental challenges. First, a resonant medium with steep positive linear dispersion has to be implemented in order to achieve $v_{gr}\ll c$. For this, a suitably prepared cavity containing ${}^{57}$Fe nuclei was used. Second, a spectrally narrow x-ray pulse must be generated, whose spectrum lies entirely within the linear dispersion part of the medium, i.e., within a bandwidth of about 10–100 neV. This is impossible with conventional monochromators, but can be realized, e.g., using pure nuclear Bragg reflections [93,94,95] or mechanical choppers [96]. For the experiment, instead another method was developed, based on a single line absorber together with a high-purity polarimetry setup [78].

To explain the generation of the spectrally narrow pulse, we follow the propagation of the x-rays through the setup in Fig. 3.15. In the time domain, the incident spectrally broad synchrotron pulse is well approximated as a Dirac delta function at time $t=0$, see the lower left panel. Upon passing through the single line absorber, the x-ray pulse is split into two parts. The part which did not interact remains a delta function. The other part which did interact with the nuclei in the single line analyzer leads to a temporally long response of the nuclei, and correspondingly to a narrow spectral absorption resonance which will become the desired spectrally narrow x-ray pulse. Note that because of the thickness of the single line absorber, dynamical beats appear in the time domain, which will turn out to be crucial for the analysis of the experiment. Afterwards, the x-rays pulse is polarized, which does not lead to notable changes because of the natural polarization of the synchrotron radiation, but improves the purity of the polarimetry setup. Next, the x-rays interact with the cavity. As explained below, the nuclei in the cavity are operated in such a way that they slow down and delay the narrow pulse component by a time $\tau$, and at the same time rotate the polarization of part of the scattered light. The analyzer is operated in crossed setting, such that only light with rotated polarization may pass. As a consequence, only light which interacted with the nuclei in the cavity can pass the analyzer. The light seen by the detector thus contains two parts. The first part interacted with the cavity, but not with the single line analyzer. The second part interacted with the cavity and the single line analyzer. At late times, the latter signal dominates, because it is delayed by both the single line analyzer and the cavity, and it comprises the desired signal of a spectrally narrow x-ray pulse which interacted with the cavity. As the lower right panel of Fig. 3.15 shows, this signal in the time domain approximately is a copy of the input pulse, but delayed by $\tau$. This delay is easily visualized independent of the total count rate by the position of the dynamical beat minima.

In order to implement the steep dispersion, we used a variety of the cavity featuring spontaneously generated coherences (see Sect. 3.7.3) optimized for the linear dispersion. Both EIT (see Sect. 3.7.2) and SGC may feature transparency windows and steep linear dispersion, and in fact are related [35, 37]. The advantage of the SGC cavities is the simpler design, and that previous experiments [29] had already demonstrated the possibility to reach almost perfect transparency, see Fig. 3.14. Furthermore, the SGC cavities rely on the magnetic substructure of the nuclei in a way which allows to rotate the polarization of the scattered light as required for the polarimetry method to generate spectrally narrow x-ray pulses.

To analyze light propagation in the cavity setting, in analogy to the procedure leading to Eq. (3.55), we expand the cavity response $R(\omega )$ around the transparency resonance $\omega _0$ in linear order. We find $R(\omega ) \approx R(\omega _0) e^{i(\omega -\omega _0)\tau }$, where $\tau = \frac{\partial }{\partial \omega } \text {arg}[R(\omega _0)]$. The action of the cavity on an input pulse $E_{in}(t)$ with spectrum $E_{in}(\omega )$ is therefore given by

$$\begin{aligned} E_{out}(t)&\propto \int E_{in}(\omega ) R(\omega ) e^{-i\omega t} d\omega \nonumber \\&\approx R(\omega _0) e^{-i\omega _0 \tau } \int E_{in}(\omega ) e^{-i\omega (t-\tau )} d\omega \nonumber \\&\propto E_{in}(t-\tau )\,. \end{aligned}$$

(3.57)

We thus find that the input pulse preserves its shape, but is delayed by the time $\tau$, as desired for slow light. The expression of $\tau$ can be understood by noting that in a cavity setting, the real and imaginary parts of the medium susceptibility are in fact related to the phase arg(R) and the logarithm of the modulus log(|R|) of the cavity reflectance R [36].

Fig. 3.16

Reprinted from [36], Copyright 2015, with permission from the American Physical Society

Results of the experiment. a Shows the recorded intensity as function of time and the detuning of the single line absorber, as well as the corresponding theory result. Dashed lines in the theory plot indicate the position of the undelayed dynamical beat minima. White lines indicate the actual positions of the minima predicted from theory. b Shows two cuts through (a) at detunings $\Delta _D = 0.56\gamma$ and $\Delta _D = 46.1\gamma$, respectively. The two curves coincide at late times except for a delay $\tau$, indicated by the black arrow. c Shows the observed delay as function of the single line analyzer detuning, i.e., the center frequency of the spectrally narrow x-ray pulse. The corresponding theoretical result is shown in blue. Delays exceeding 35 ns are observed, corresponding to group velocities below $10^{-4}\,c$.

In the experiment, a cavity consisting of a Pd(2 nm)/C(20 nm)/${}^{57}$Fe(3 nm)/C(21 nm)/Pd(10 nm)/Si layer system was probed in grazing incidence, coupling the x-rays into the fundamental mode. A magnetic field was applied along the beam direction in order to align the magnetization of the nuclei in the so-called Faraday configuration. In this setting, spontaneously generated coherences occur, which lead to a steep linear dispersion [29]. Since full transparency of the medium corresponds to zero intensity of the scattered x-ray, the cavity was designed to avoid full transparency in order to measure the delay of the x-rays also on resonance. The single line analyzer comprised a 10$\mu$m thick stainless steel foil (${}^{57}$Fe${}_{55}$Cr${}_{25}$Ni${}_{20}$) mounted on a Doppler drive, which generates a spectrally narrow pulse of about 10 ns duration with tunable central frequency. The results of the experiment are shown in Fig. 3.16. (a) presents the experimentally recorded intensity as function of the time after excitation and the detuning of the single line absorber. (b) shows the corresponding theoretical fit, which agrees very well. The white dashed lines indicate the position of the dynamical beats expected without pulse delay. It can be seen that close to resonance $\Delta _D = 0$, the dynamical beat minima observed in the experiment are systematically shifted to later times, as expected for slow light. To illustrate this further, (c) shows cuts through (a) and (b) for $\Delta _D = 0.56\gamma$ and $\Delta _D = 46.1\gamma$, respectively. For the lower detuning, the spectrally narrow x-ray pulse experiences the steep linear dispersion, and thus is slowed down. The higher detuning is outside the steep linear dispersion region and does not lead to slow light. As a result, at late times, the two data sets are essentially identical, except for a temporal delay indicated by the black arrow. Note that at early times the two curves differ, because of the residual contribution of light which did not interact with the single line absorber. Finally, panel (d) shows the experimentally observed delay $\tau$ as function of detuning $\Delta _D$. The solid line shows the corresponding theoretical prediction. We find that our cavity allows to induce delays exceeding 35 ns, which corresponds to group velocities below $10^{-4}\,$c [36].

These results constitute another proof of the possibility of manipulating the x-ray optical response of nuclei embedded in cavities to one’s desire. Further theoretical calculations predict that with a suitable time-dependent manipulation of the applied magnetic fields, also a complete stopping of the x-ray pulse could be achieved [97]. Possible applications of such techniques include the delay and synchronization of x-ray photons, and the coherence-based enhanced of nonlinear interactions between x-rays and nuclei [72].

3.8 Collective Strong Coupling of Nuclei in Coupled Cavities and Superlattices

A central subject of quantum optics is to manipulate the interaction of light and matter. To achieve this, two important parameters must be controlled. One is the strength of the light-matter interaction. It has to be strong enough that emitted photons have a chance to act back on their emitters. This is the so-called strong-coupling limit in quantum optics [98]. It can be achieved in special environments into which the emitters are embedded. Strong coupling is used in the optical and infrared regimes, for instance, to produce non-classical states of light, enhance optical nonlinearities even at relatively low intensities [99] and control quantum states [100]. The other parameter is the number of modes of the electromagnetic field that the resonant system interacts within this environment. If the number of these modes is too large, the emitted photons might get irreversibly lost when they are distributed over these modes. Strong coupling has been achieved for a variety of systems and energy ranges, but until now not with X-rays. Here we report about the first observation of collective strong coupling of hard X-rays at the nuclear resonance of $^{57}$Fe.

3.8.1 Strong Coupling of X-Rays and Nuclei in Photonic Lattices: Normal-Mode Splitting

The usual route to strong coupling between light and resonant atoms is to insert the atoms into a cavity, the Q-factor of which is on the order or larger than that of the atomic resonance [98]. A good cavity restricts the interaction with the light to the one mode allowed by the cavity; furthermore, the intensity of the light within the cavity is large, leading to an enhanced interaction. The strong interaction leads to the coupling of two degrees of freedom; two normal modes form, which are superpositions of the otherwise uncoupled components of the system. If the cavity is probed, for instance by monitoring its reflectivity or transmissivity, its spectral signature shows two dips, which are detuned from the sample resonance and the cavity mode. Upon varying the detuning between cavity mode and resonance, it turns out that the dips undergo a very well-known anti-crossing dispersion; the minimal distance between the branches of the dispersion relation is given by the interaction strength.

While X-ray cavities have been successfully applied to realize quantum optical concepts in the linear regime, fabricating a cavity of sufficient quality to reach the strong coupling regime is not possible yet in the X-ray range. Even in the angular range of grazing incidence, the reflectivity of the cladding mirrors is $\sim \!95\%$ only. Compared to the reflectivity achieved for microwave and visible light cavities of $\>\!99.999\%$ this is not sufficient. The problem is rooted in the fact that the spectral width of the cavity is much larger than the coupling strength. Essentially, the two dispersive dips mentioned above cannot be resolved [27, 79].

This points the way to another method of coherent control. Since our nuclear exciton interacts with only one mode anyway, we can focus on enlarging the interaction without making use of a cavity, but by enlarging the number of nuclei that contribute to the nuclear exciton, as the collective interaction strength depends on that number. In the following, we will focus our attention on periodic multilayers or periodic resonant systems. These, often referred to as resonant photonic crystals or resonant optical lattices, also restrict the number of modes the resonant matter interacts with.

The propagation of light through periodic arrays of resonant media such as optical lattices or multiple quantum wells has opened intriguing possibilities to control the interaction of light and matter [102,103,104,105]. One of the most interesting features of these systems is the appearance and dispersion of bandgaps [106,107,108,109], see Fig. 3.17.

Fig. 3.17

Figures a, b reprinted from [101], Copyright 2016, with permission from Springer Nature

a Dispersion relation (plotted as frequency $\omega$ against wavevector $k_{0z}$) for photons in different media: in a medium with uniform refractive index (blue dashed line) and in a photonic crystal with an interlayer spacing d (black solid curves). b Brillouin diagram for a material with a modulated refractive index, showing the allowed and forbidden regions for the real wavevector, implying propagation and reflection, respectively. Pink bands indicate photonic bandgap formation. A periodic nuclear resonance structure can result in the formation of an excitonic Bragg reflection feature. c A stack of 30 [(1.64 nm $^{56}$Fe)/(1.12 nm $^{57}$Fe)] bilayers was used to modulate the refractive index of the material for light at the nuclear resonance.

Here we describe an optical lattice-like structure with bandgaps in the regime of hard X-rays, consisting of a multilayer with alternating layers of non-resonant $^{56}$Fe and nuclear-resonant $^{57}$Fe. The electronic part of the index of refraction is identical for both isotopes. The system can thus be modelled as having a uniform background refractive index, with a periodic resonant refractive index superimposed. The resulting bandgap can be observed by measuring the spectrally resolved X-ray reflectivity of the sample close to the Bragg angle of the multilayer. Although similar isotopic multilayer structures have been discussed before [110,111,112,113], mainly the angular dependence of the reflectivity has been studied instead of its spectral properties. Here we report about high-resolution spectroscopic studies, and reveal the strong collective interaction between resonant X-rays and nuclei, which leads to the formation of photonic bandgaps. In the following we discuss the connection between the photonic dispersion relation and the reflectivity of the multilayer, the latter being the observable that allows us to experimentally assess the signatures of strong coupling.

Fig. 3.18

Figures reprinted from [38]

Angular-dependent dispersion relation of a $^{56}$Fe/$^{57}$Fe multilayer. The dispersion of the out-of-plane component $k_z$ of an infinite stack of 1.64 nm $^{56}$Fe/1.12 nm $^{57}$Fe bilayers around the Bragg position is shown. a The real part of $k_z$ is encoded in the colour bar in units of $\pi /d$. b Magnification of the small, dispersionless gap in (a). c Imaginary part of $k_z$, logarithmically encoded in the colour bar. d The extinction coefficient contribution to the imaginary part, encoded logarithmically. It characterizes how well a sample reflects light and is due to dispersion, not absorption of the materials. An anticrossing is visible at the Bragg position. In comparison with (c), it is obvious that the extinction coefficient is a weak contribution to the imaginary part both at the energetic resonance and very far from it, but is dominant in the intermediate range.

Figure 3.18 shows the real and imaginary parts of the dispersion relation around the nuclear resonance and the Bragg peak. There are three distinct contributions to the imaginary part: (1) the uniform electronic absorption, (2) the nuclear absorption, which exhibits a Lorentzian energy dependence around the resonance and (3) the extinction, which determines how deeply the radiation penetrates into the multilayer. The higher the extinction, the fewer periods contribute to the reflection. Nuclear absorption dominates around the resonance, absorbing most incoming radiation. Off resonance, the extinction becomes stronger relative to the absorption, indicating enhanced reflection. Far off resonance and off-Bragg, the electronic absorption suppresses the reflection. The shape of the real part results from a polaritonic effect: X-rays of suitable energy impinging on resonant matter undergo nuclear-resonant forward scattering, which leads to an energy-dependent phase shift of the scattered photons. In periodic media, polaritons excited at certain angles and with certain energies radiate in phase, such that the outgoing radiation has a different direction from the incoming one because the electromagnetic waves interfere destructively in all other directions. In other words, the Bragg condition $k_{0z} = \pi /d$ is fulfilled. Tuning the angle across the Bragg peak, one can observe an angularly resolved polaritonic dispersion relation and the corresponding anticrossing behaviour, as well as a narrow, almost dispersionless contribution around resonance that is visible in Fig. 3.18a, b. This interpretation is supported by a simple quantum-optical model [38] to explain the dispersion relation in microscopic terms [114, 115]. To account for the finite thickness of the resonant layers, we model our system as a so-called bichromatic optical lattice (containing two atoms per unit cell) and simplify the Hamiltonian until it can be numerically diagonalized for a range of k-vectors at a particular angle. Figure 3.19 compares the resulting quantum mechanical dispersion relation to the reflectivities of two multilayers with a finite number of periods. In Fig. 3.19a (30 periods) a splitting is readily observable, but in Fig. 3.19b (100 periods) the almost fully formed bands seem to diverge at the Bragg angle, because the collective coupling-enhanced splitting is too large for the displayed energy range. We also see that the reflectivity of the 30-period structure exhibits peaks rather than fully formed bandgaps. The peaks correspond to the lower edges of the bandgaps; here the extinction coefficient is largest and even for a few-period structure there is a sizable reflection. Alternatively, the peaks can be described as superradiant modes, which, on adding more periods to the structure, turn into bandgaps [116]. Note that the descriptions by the transfer matrix formalism and the quantum optical model are qualitatively identical for infinite systems, thus supporting our interpretation of the observed phenomena. The low-dispersion bandgap that appears close to resonance is probably caused by nuclei weakly coupling to the electromagnetic field, for example at the layer interfaces. Although the bandgaps we observe are photonic bandgaps, their dispersion is due to the (strong) collective interaction of light and the nuclei.

Fig. 3.19

Figures reprinted from [38]

Calculated reflectivity of the $^{56}$Fe/$^{57}$Fe multilayer. a Calculated reflectivity of a 30-period multilayer and b of a 100-period multilayer. c Quantum mechanically calculated dispersion relation. The reflectivity of a many-period multilayer is well-described by the model of the multilayer with an infinite number of layers. For 30 periods, the bandgaps are not fully formed and the splitting is smaller. This is due to the collectivity of the light-matter interaction. More layers result in a stronger interaction and a larger splitting. In (b) and (c), the interaction and splitting are so large that the bandgaps are not observed together in an experimentally accessible energy range.

In the case where the wavevector of the incoming light approximately fulfills the Bragg condition, the quantum-optical model yields an analytic dispersion relation given by

$$\begin{aligned} \omega _{j,\pm }(q) = \frac{\omega _{k_{0z}} + \omega }{2} \pm \sqrt{(\frac{\omega _{k_{0z}} - \omega }{2})^2 + 2Ng^2\left[ 1-(-1)^j \cos (q\rho )\right] } \end{aligned}$$

(3.58)

where index j = 1,2, g is the coupling constant, N is the number of unit cells, $\rho$ is the distance between atoms of the same unit cell and q is the reciprocal lattice vector. The similarity to a standard strong coupling dispersion relation [98, 117] with the corresponding Rabi splitting is obvious. In our case, multiple bands undergo this splitting, leading to two bandgaps. The splitting between them is the signature of collective strong coupling. This microscopic model does not include dissipation. However, it has the advantage of giving our results an intuitive and qualitative explanation. The dispersion relation derived from the transfer matrix model is quantitatively more reliable because it includes dissipation and absorption.

Fig. 3.20

Right figure reprinted from [38]

Left: measured energy spectra of the multilayer reflectivity for different angular positions around the Bragg angle $\theta _B$. Displayed is the energy region around the outer resonance line of $^{57}$Fe in ferromagnetic Fe. The spectra reveal a splitting of the line, the angular dependence of which displays the characteristic anticrossing behavior (see blue lines as guide to the eye) that is indicative of strong coupling. On the the right hand side the measured intensity is plotted as a colour map; the background baseline is normalized to one. The upper right panel shows simulations, the lower shows the data. The white bar in the upper panel indicates the dip distance which gives the collective coupling strength. The white lines in the lower bar indicate the edges of the photonic band gaps.

To experimentally verify the particular shape of the dispersion relation for a nuclear optical lattice, we prepared a multilayer sample consisting of 30 periods of (1.64 nm $^{56}$Fe)/(1.12 nm $^{57}$Fe) (average thicknesses) sandwiched between two 4 nm Ta layers, altogether deposited on a Si substrate. This facilitated to measure the splitting in a suitable energy range, but did not permit an accurate quantitative comparison to the model. However, the reflectivity can be simulated by the transfer matrix model. Measurements were performed at the Nuclear Resonance Beamline ID18 of the European Synchrotron Radiation Facility (ESRF). Reflectivity spectra of the sample are shown in Fig. 3.20 together with simulations using the program package CONUSS [55, 74]. Owing to the magnetic hyperfine interaction in the sample, the nuclear resonance of $^{57}$Fe is split into four well-separated lines, each of which can be treated as a single-line nuclear resonance (displayed in Fig. 3.18). The outer lines in the measured spectra exhibit the strongest collective coupling, manifesting in a clearly resolved Rabi splitting at the Bragg position. The bands at zero detuning, i.e., at the Bragg angle, have the frequencies $\pm \sqrt{2Ng^2(1-(-1)^j\cos (q\rho ))}$ around the nuclear resonance. The splitting is then $4g\sqrt{N}f_j(q\rho )$, where $f_1(q\rho ) = \cos (q\rho /2)$ and $f_2(q\rho ) = \sin (q\rho /2)$. Depending on whether $\rho$ is smaller or larger than 0.25a, the bands marked by $j=1$ or $j=2$ form the inner bands. We assume that $\rho$ is smaller, giving a splitting of $4g\sqrt{N}\cos (q\rho /2) \approx 8 \Gamma _0 \approx 57.3$ MHz. Again, this is the result for 30 layers and should not uncritically be equated with the formula resulting from the infinite model. Nevertheless, the agreement between transfer matrix model simulations and measurements is excellent. An exception is the almost dispersionless gap visible in Fig. 3.18a which could not be resolved experimentally since the energetic width of the analyzer foil smears out sharp spectral features.

To summarize, we have simulated and measured the energy-resolved reflectivities of an isotopic 1.64 nm $^{56}$Fe/1.14 nm $^{57}$Fe multilayer around the nuclear resonant Bragg peak. The results were explained in terms of the polaritonic propagation of light and excitations of nuclear resonant matter. Within a quantum optical model, we could connect the dispersion to the coupling of x-rays with nuclear excitons and have given a lower bound to the collective coupling strength. Dissipation and the interface roughness that grow with the number of layers thwart any attempt to observe fully-formed band-gaps, and therefore precise values cannot be determined. However, the distinctly observable dispersion and splitting of bands is the first unambiguous evidence of collective strong coupling in the hard x-ray energy range.

Nuclear optical lattices display several unique features absent in other systems, such as extremely high number densities (on the order of $10^{28}$m$^{-3}$) and stability over a wide temperature range. This work could be extended to other isotopes with higher energies and less electronic interaction, such as $^{119}$Sn (23.9 keV) or $^{61}$Ni (67.4 keV). We therefore anticipate that nuclear resonant periodic multilayers will stimulate x-ray quantum optics research and bring it closer to coherent control of the x-ray-matter interaction. Even further, the concept of polaritons in bichromatic optical lattices or other periodic systems itself is a subject that holds great interest far beyond the x-ray range.

To put our results into perspective we briefly summarize previous work in similar systems, as given in [118]. To the best of our knowledge, two physical systems have yielded phenomena and observations similar to those described here: genuine optical lattices [104, 106, 107] and gratings of excitonic quantum wells. In excitonic quantum wells, a semiconductor is doped periodically; that way, the background refractive index is identical throughout, but there are periodically spaced regions where quantum well excitations are possible [119]. This medium is particular interesting, since it suffers from a similar drawback as ours: too few layers result in an unclear or incomplete formation of band gaps. Since the early 1990s, the results obtained from excitonic quantum wells have been described in a different framework. Instead of assuming an infinite structure, researchers calculated the eigenmodes of these systems for a small number ($\sim$10) of layers [120, 121]. In that case, the eigenmodes are one superradiant Bragg mode, which reflects the radiation in a band much wider than the exciton resonance, and a number of dark modes. In a sense, this is the incipient Bragg band gap. However, experiments [108, 122] showed that with an increasing number of layers, dips in the superradiant mode and a saturation of its width appeared; researchers explained this later in terms of band gaps and standing waves within the band gaps [116, 123], much as the quantum optical model of this chapter. A system resembling a bichromatic array of quantum wells was examined in [102]; although that paper has a different focus, the observed phenomena resemble those presented here.

3.8.2 Rabi Oscillations via Strong Coupling of Two Nuclear Cavities

In the regime of strong coupling, the reversible exchange of photons between a cavity mode and an electromagnetic resonance leads to an oscillatory energy transfer between the two systems, the so-called Rabi oscillations. Collective strong coupling of X-rays and nuclei has recently been demonstrated in a periodic multilayer [39], as described in the previous section. The mode splitting and anticrossing dispersion typical of strong coupling was observed in energy-resolved reflectivity measurements. However, the Zeeman splitting of the Mössbauer resonance into several resonance lines together with dissipation and structural imperfections of the layer system prevented a clear detection of Rabi oscillations. Moreover, a conclusive proof of strong coupling requires that the splitting of the resonance is solely due to the interaction between the ensembles and is not affected by Lamb shift contributions. This requires a particular arrangement of the resonant ensembles, as explained in the following.

The central requirement for the strong coupling regime is that the coupling of the mode and the resonant layer be larger than their decay rates given by the the spectral width of the cavity (that is, the inverse of the time a photon is stored in the cavity) and the decay width of the nuclear ensemble. For a single thin-film cavity system, the coupling strength, although larger than the nuclear decay width, is still much smaller than the cavity linewidth. We circumvent this difficulty by introducing a novel double cavity setup (Fig. 3.21), which is described by an effective Hamiltonian fulfilling the desired strong coupling conditions. This ansatz follows the general approach of simulating a complex physical system that mimics a simple Hamiltonian that cannot be implemented straightforwardly. Similar approaches are used extensively in contemporary research, for example to observe the Dicke phase transition [124, 125] or in the use of ultracold quantum gases to simulate magnetism [126] and correlated materials [127, 128].

Fig. 3.21

Sketch of the coupled cavity system and experimental geometry to observe Rabi oscillations between two ensembles of $^{57}$Fe nuclei. Each cavity consists of a Pd/C/$^{57}$SS/C/Pd layer stack, where $^{57}$SS denotes stainless steel (Fe$_{0.55}$Cr$_{0.25}$Ni$_{0.2}$) with its iron content enriched to 95$\%$ with $^{57}$Fe. Stainless steel does not exhibit ferromagnetic order, so in this alloy the $^{57}$Fe isotope presents a single-line resonance at 14.413 keV with no Zeeman splitting. This layer structure realizes two almost identical cavities coupled via a thin Pd interlayer, which also constitutes the top cladding of the lower cavity and bottom cladding of the upper cavity. The layer system was positioned on a goniometer that permitted to control the cavity detunings via adjustment of the angle of incidence $\theta$ and to perform ($\theta - 2\theta$) reflectivity measurements

In the following we discuss a quantum optical description of the double cavity setup in order to show that it indeed fulfills the conditions to observe Rabi oscillations between the two nuclear layers. The interaction between the X-ray field and the two nuclear layers embedded in the double cavity can be described by means of a recently developed quantum-optical model [29, 79] adapted to the particular sample geometry. The Hamiltonian of this interaction is given by

$$\begin{aligned} H= & {} \Delta _{1} a^{+}_{1} a_{1}+\Delta _{2} a^{+}_{2} a_{2}+J(a^{+}_{1}a_{2}+a^{+}_{2}a_{1}) \nonumber \\- & {} \Delta (| E_1 \rangle \langle E_1 |+| E_2 \rangle \langle E_2 |) \\+ & {} g_1\sqrt{N_1}\left( {a}_{1}| E_{1} \rangle \langle G |+a^{+}_{1}| G \rangle \langle E_1 |\right) \nonumber \\+ & {} g_2\sqrt{N_2}\left( {a}_{2}| E_2 \rangle \langle G |+a^{+}_{2}| G \rangle \langle E_2 |\right) \nonumber , \end{aligned}$$

(3.59)

where $|G\rangle = |g_1 g_2 0_1 0_2\rangle$ denotes the nuclear ground state and $|E_1\rangle = |e_1 g_2 0_1 0_2\rangle$, $|E_2\rangle = |g_1 e_2 0_1 0_2\rangle$ denote the states with a single excitation in either of the nuclear layers, respectively. The first line in Eq. (3.59) gives the energies of the cavity modes and their interaction term; the second one likewise the energies of the nuclear ensembles. The third line describes the interaction between the first mode and its nuclear ensemble, while the fourth one depicts the interaction between the second mode and its ensemble. The creation (annihilation) operators of the cavity mode in the first cavity are $a_1^{\dagger }(a_1)$. A second cavity is coupled to this first one by a strength J. The second cavity mode’s creation (annihilation) operators are $a_2^{\dagger }(a_2)$. The detunings of these two cavities are denoted by $\Delta _1$ and $\Delta _2$, respectively.

In each cavity, there is a nuclear ensemble coupled to it. In our experiments with synchrotron radiation there is at most one photon in the system, i.e., we work in the one-excitation limit. This allows us to truncate the Hamiltonian and to take into account only the first symmetric timed Dicke state [29] of these ensembles that is coupled to these modes [79]. The Dicke states are denoted as $|E_1\rangle$ and $|E_2\rangle$, and their excitation and deexcitation operators are $|E_{1(2)}\rangle \langle G|$ and $|G\rangle \langle E_{1(2)}|$, respectively. They are coupled to their respective cavity modes with a collective coupling strength $g_1 \sqrt{N_1}, g_2\sqrt{N_2}$, where the $N_{1(2)}$ is the number of nuclei per ensemble, and $g_{1(2)}$ the coupling strength of an individual nucleus to the respective cavity mode. An additional term $\Delta$ describes the energy of the nuclei and their detuning from the incoming beam.

We then continue by prediagonalizing the interaction between the cavity modes, resulting in two cavity supermodes $a_{\pm }$, both coupling to the two nuclear ensembles (see Methods in [39]). We then heuristically add driving terms for both of these cavity modes, which are $i\sqrt{2\kappa _{R\pm }}(a_{in}a_{\pm }^{\dagger } + a_{in}^*a_{\pm }$). The energy bandwidth of the empty cavities is very large, on the order of 100 eV, which renders them highly dissipative, i.e., their interactions and the temporal evolution of their modes take place on extremely fast timescales, orders of magnitude faster than the evolution of the nuclear decay. Therefore, the common practice is to adiabatically eliminate the cavity modes and solely follow the temporal evolution of the three states $|g_1g_20_10_2\rangle$, $|g_1g_20_10_2\rangle$ and $|g_1e_20_10_2\rangle$, corresponding to states with no nuclear excitation or one delocalised, collective excitation in layer 1 or 2, respectively, as depicted in Fig. 3.22d. Thus we reduce the problem to that of two interacting low-excitation nuclear ensembles similar to Ref. [79]. The effective Hamiltonian then reads (see Methods in [39]):

$$\begin{aligned} H = \begin{pmatrix} 0 &{} \Omega _1 &{} \Omega _2 \\ \Omega _1^* &{} \Delta -\delta _1 + i\gamma _1 &{} g_{12} - i\gamma _{12}\\ \Omega _2^* &{} g_{12} - i\gamma _{12} &{} \Delta -\delta _2 + i\gamma _2 \end{pmatrix}, \end{aligned}$$

(3.60)

where the Hamiltonian is made up of a series of effective parameters given by:

Fig. 3.22

Figures b, d reprinted from [39]

Illustration of the quantum optical models for description of the two coupled cavities. a Each cavity contains a thin $^{57}$Fe layer located in the antinode of the first mode of each cavity so that the coupling constants $g_1$ and $g_2$ are roughly equal. The first cavity is illuminated by a classical driving field. Both cavities are at the same time divided and coupled via a thin cladding layer, the thickness of which must be carefully adjusted to ensure a large coupling constant J. b Level scheme of the setup in (a). There are four states that are labeled by g or e, describing the states of the nuclear ensemble in layer 1 and layer 2, and by 0 or 1, which denote the number of photons in the first guided modes of cavity 1 and cavity 2. $g_i$ describes the situation when all atoms in layer i are in the ground state, and $e_i$ stands for the first symmetric Dicke state after the delocalized excitation of one nucleus in layer i. c, d Sketches of the effective set-up achieved after adiabatic elimination of the cavity modes. The original energies of the layers are replaced by those of the Dicke states in individual layers and undergo collective Lamb shifts, denoted $\delta _1$ and $\delta _2$. Their decay is superradiantly enhanced, with decay widths $\gamma _1$ and $\gamma _2$, and there is an effective interaction $\Omega _R$ between the layers. The latter is stronger than the respective superradiant decay rates, leading to strong coupling between the upper two levels. The decay of these dressed states shows Rabi oscillations.

(i) the effective driving strengths of both layers:

$$\begin{aligned} \Omega _{1}= & {} g_{1}\sqrt{N}\left( \frac{\sqrt{2\kappa _{R+}}}{\kappa _{+}+i\Delta _{+}}+\frac{\sqrt{2\kappa _{R-}}}{\kappa _{-}+i\Delta _{-}}\right) a_{in}, \end{aligned}$$

(3.61)

$$\begin{aligned} \Omega _{2}= & {} g_{2}\sqrt{N}\left( \frac{\sqrt{2\kappa _{R+}}}{\kappa _{+}+i\Delta _{+}}-\frac{\sqrt{2\kappa _{R-}}}{\kappa _{-}+i\Delta _{-}}\right) a_{in}, \end{aligned}$$

(3.62)

(ii) The effective decay widths, consisting of real and imaginary part, $\delta$ and $\gamma$, respectively:

$$\begin{aligned} \delta _{i}= & {} -\frac{g_i^2N}{2}\left( \frac{\Delta _{+}}{\kappa _{+}^2+\Delta _{+}^2}+\frac{\Delta _{-}}{\kappa _{-}^2+\Delta _{-}^2}\right) , \end{aligned}$$

(3.63)

$$\begin{aligned} \gamma _{i}= & {} \frac{g_i^2N}{2}\left( \frac{\kappa _{+}}{\kappa _{+}^2+\Delta _{+}^2}+\frac{\kappa _{-}}{\kappa _{-}^2+\Delta _{-}^2}\right) , \end{aligned}$$

(3.64)

(iii) the effective cavity-mediated coupling strength (real and imaginary part):

$$\begin{aligned} g_{12}= & {} -\frac{g_1g_2N}{2}\left( \frac{\Delta _{+}}{\kappa _{+}^2+\Delta _{+}^2}-\frac{\Delta _{-}}{\kappa _{-}^2+\Delta _{-}^2}\right) , \end{aligned}$$

(3.65)

$$\begin{aligned} \gamma _{12}= & {} \frac{g_1g_2N}{2}\left( \frac{\kappa _{+}}{\kappa _{+}^2+\Delta _{+}^2}-\frac{\kappa _{-}}{\kappa _{-}^2+\Delta _{-}^2}\right) . \end{aligned}$$

(3.66)

Originally, the cavity modes were driven by an outside X-ray beam. Because we have adiabatically eliminated the cavity modes, in our new picture that driving term is now applied to both nuclear ensembles. In this picture the beam effectively drives both ensembles directly, but with an extra dispersion inherited from the cavity mode. $\Delta$ is the X-ray detuning to the nuclear resonance energy, considered to be the same in both layers. $\Delta _{\pm }$ is the detuning of the supermodes from the incoming beam energy.

The new effective Hamiltonian in Eq. (3.60) can be interpreted as follows: The new energies of the states representing collective excitations in layer i are given by $\Delta - \delta _i + i \gamma _i$. $\gamma _i$ is the cavity-enhanced superradiant decay rate of the Dicke state, and $\delta _i$ is the cavity-induced collective Lamb shift [27]. The two states are connected by an effective interaction given by the real part $g_{12}$ and an imaginary part $\gamma _{12}$. All parameters in the effective Hamiltonian can be derived from $g_{1(2)}\sqrt{N_{1(2)}}, \kappa _{\pm }$ and $\Delta _{\pm }$, and $\kappa _{R\pm }$. While the latter three can be extracted from an off-resonant reflectivity curve, the quantity $g_i\sqrt{N_i}$ must be fitted from the experimental data. Note that these new, effective parameters can be tuned via the angle of incidence $\theta$ through a wide range of values, as they all depend on the detuning, which is given by $\Delta _{\pm } = (\sin (\theta _{\pm })/\sin (\theta ) - 1)\,\omega _0$. Here, $\theta _{\pm }$ is the angle for which one cavity supermode is exactly at resonance at the nuclear transition energy $\omega _0$.

We can essentially regard the new, effective Hamiltonian as a three-level system (Fig. 3.22d). The first level, corresponding to the ground state (no excited ensemble) serves only to probe the properties of the other two through the (very weak) driving terms. The energies of these two states, in turn, can be tuned via the collective Lamb shifts, as can their superradiant decay terms and their mutual interaction. These upper two levels form a two-level system with tunable energies, decay constants and a tunable mutual interaction. Just as for a regular two-level system interacting with a cavity mode, strong coupling and Rabi oscillations between the two levels can be achieved if the interaction term is larger than the two respective decay terms, in this case $g_{12} > \gamma _1, \gamma _2$. If this can be reached by appropriate tuning, the two upper states will exchange a photon multiple times before the whole system decays, giving rise to Rabi oscillations [129]. This is an equivalent of the standard strong-coupling set-up, where the coupling strength between an atom and a cavity must exceed the latter’s decay constants [130,131,132,133]. This effective three-level system may also be regarded as the implementation of an artificial Autler-Townes set-up, which also consists of two upper levels whose interaction is probed from a lower ground state. A crucial difference is that the interaction here is cavity-induced, whereas in the Autler-Townes case, a laser beam tuned to the energy difference between the two levels couples them.

The equivalent of the classical Rabi frequency in our case is given by

$$\begin{aligned} \Omega _R = \sqrt{g_{12}^2 + \gamma _{12}^2 + (\delta _1-\delta _2)^2}, \end{aligned}$$

(3.67)

which includes the cavity-mediated coupling strength $g_{12}$ between the two ensembles/states, as well as their relative energy detuning $\delta _1 -\delta _2$. The behaviour of $\Omega _R$ in comparison with the superradiant decay rates, and the collective Lamb shifts as a function of the incident angle, are shown in Figs. 3.23b,c. Any change in the incident angle $\theta$ leads to modifications of all parameters $\delta _i$, $\gamma _i$ and $g_{12}$, which makes it difficult to reach the desired behaviour of the coupling and the decay properties of the system. This raises the question of whether we can find an angle $\theta$ at which the strong coupling conditions ($g_{12} >\gamma _i$) are fulfilled. This is indeed the case: In between both supermodes, at large detunings from them, the superradiant decay widths $\gamma _1, \gamma _2$ are insignificant compared to the interaction strength between the two layers. This can be explained because the real part $g_{12}$ of the interaction strength is suppressed by $1/\Delta _{\pm }^{-1}$ at angles sufficiently far away from the cavity angle of zero detuning, while the imaginary part $\gamma _{12}$ describing the superradiant decay is suppressed by $1/\Delta _{\pm }^{-2}$. However, the collective Lamb shifts do not go to zero as quickly, and, according to Eq. (3.67), they are also involved in determining the oscillation rate $\Omega _R$. To observe pure Rabi oscillation - that is, the case when the oscillations are solely induced by the coupling constant, i.e. $\Omega _R = g_{12}$, it is necessary to have zero Lamb shift detuning between the layers. This, in turn, requires that both layers either have the same collective Lamb shift, or none at all.

Fig. 3.23

Figures reprinted from [39]

a Reflectivity and b, c effective parameters (given by Eqs. (3.61)–(3.66)) of the Hamiltonian that describes the coupled cavities. $\varphi _M$ is the optimum coupling angle at which the conditions for the observation of pure Rabi oscillations between the two resonant layers are fulfilled. $\varphi _m$ lies in the middle between the two cavity modes that show up as dips in the reflectivity displayed in (a). At $\varphi _m$, the collective Lamb shifts (b) in the two layers cancel, and the superradiant enhancements (c) are minimal, meaning that according to Eq. (3.67) the splitting is exclusively due to the interaction $\Omega _R$.

A brief inspection of the Hamiltonian reveals that this is possible if the Lamb shifts caused by the two cavity modes cancel exactly for both layers. This can be accomplished if the two cavity modes both couple to the nuclear layers with identical strength. The double cavity is precisely the set-up that matches all these requirements: the field modes couple equally strong to both layers, so the Lamb shifts of both layers will always be equal. There are, however, always imperfections in real samples that may lead to slightly different coupling strengths. An easy way to ameliorate this, relies on the fact that the Lamb shift is highly dependent on the sign of the relative detuning. Between two modes, the corresponding contributions will cancel and the Lamb shifts of both layers will be exactly zero. At that particular angular position, illustrated in Fig. 3.23a, we perform our experiment.

The experiment was performed at the nuclear resonance beamline ID18 of the European Synchrotron Radiation Facility (ESRF). The beam was pre-monochromatized to a bandwidth of 1 meV around the nuclear resonance energy by the successive use of high-heat load and high-resolution monochromators.

Fig. 3.24

Figures reprinted from [39]

Left: measured energy-resolved reflectivity at the optimum coupling angle $\varphi _m$. The two peaks indicated by the arrows are due to the normal mode splitting that translates to the frequency of the Rabi oscillations in (b). The modulation of the background (yellow dashed line is a guide to the eye) is due to the detection method involving time gating and has been taken into account in the numerical simulation. Right: temporal response of the double cavity, showing pronounced Rabi oscillations. The theoretical curves are a Fourier transform of the energy-resolved reflectivity, derived from the quantum optical model, and an exponentially damped cosine with a period that corresponds to the Rabi frequency, respectively. Note that these temporal oscillations are evenly spaced, in contrast to dynamical beats [50, 134], the period of which increases with increasing time after excitation.

The sample system for the experiment consists of two thin-film cavities stacked on top of each other, coupled through a thin interlayer as sketched in Fig. 3.21. A resonant $^{57}$Fe nuclear ensemble is embedded into each cavity. Specifically, the sample was a (15 nm Pd)/(19 nm C)/2 nm $^{57}$SS)/(19 nm C)/(2 nm Pd)/(16 nm C)/(2 nm $^{57}$SS)/(19 nm  C)/(2 nm Pd) multilayer (Fig. 3.21) fabricated by sputter deposition on a superpolished Si wafer. Here, $^{57}$SS indicates stainless steel (Fe$_{0.55}$Cr$_{0.25}$Ni$_{0.2}$) with its iron content enriched to 95$\%$ with the resonant $^{57}$Fe isotope. Stainless steel does not display ferromagnetic order, so the $^{57}$Fe isotope presents a single-line resonance at 14.4125 keV with no Zeeman splitting. A weak hyperfine magnetic field distribution in the sample, however, effectively broadens the $^{57}$Fe-resonance linewidth to $\sim$2–3 $\Gamma _0$ [135]. This design effectively implements two almost identical cavities coupled via a thin Pd interlayer, which also constitutes the top cladding of the lower cavity and bottom cladding of the upper cavity.

For an energy analysis of the reflected radiation, a 1-$\upmu$m-thick $^{57}$Fe-enriched stainless steel foil was inserted into the beampath. In this foil the $^{57}$Fe nuclei exhibited a single-line resonance with a FWHM width of 1.5 $\Gamma _0$. This stainless-steel foil was mounted on a Mössbauer drive, which was then moved at velocities of ±10 mm/s. The ensuing Doppler shifts of ±100 $\Gamma _0$ covered the spectral range of interest. To obtain the energy spectrum of the reflectivity at the optimum angle of incidence $\varphi = \varphi _m$ (Fig.3.24a) the delayed, resonantly reflected photons at that angular setting were detected together with the actual velocity of the Mössbauer drive. The non-resonantly scattered radiation was rejected from being recorded by a temporal gating from 0 to 7 ns after excitation. The temporal gating ensured that the huge background of nonresonantly scattered radiation was rejected from the detection, but the associated time-window effect introduced an unphysical background modulation that is visible in the spectrum. Moreover, because the non-resonant background is already subtracted in the detection process, dips in the reflectivity appear as peaks in the spectrum measured at the APD detector. For the time-resolved measurement, the Mössbauer drive with the analyzer foil was removed. The measured temporal beat pattern in Fig. 3.24b shows a clear, exponentially damped cosine pattern with a period that corresponds the energy splitting of the line in (a), the typical fingerprint of Rabi oscillations.

To summarize, we have succeeded in observing Rabi oscillations in the X-ray regime by using a double cavity set-up, and confirmed the collective strong coupling regime via a quantum optical model. The temporal evolution of the system is marked by the coherent exchange of a photon between two different collective excited nuclear states. The result also points the way to coherent control of X-rays over matter. Already minor changes in the layer structure, such as the positioning of the layers, can create new effective multilevel systems with completely different dynamics, and facilitate artificial quantum optical systems in the X-ray range, with tunable dispersions and interactions.

3.9 Nuclear Quantum Optics with Advanced Sources of X-Rays

A further boost for the field of nuclear quantum optics will be enabled not only by an increase of the spectral flux provided by the x-ray source, but also by qualitatively new properties of the radiation source. One of those is the so-called photon degeneracy $\eta$, which is a parameter that gives the number of resonant photons per mode of the radiation field. In the case of a pulsed radiation source where the pulse length is much shorter than the nuclear lifetime, $\eta$ is simply given by the number of photons per pulse within the nuclear resonance bandwidth. If $\eta$ is significantly larger than 1, one obviously enters the regime of multiphoton excitation of nuclear ensembles which could open new avenues for nuclear quantum optics, ranging from stimulated emission to nonlinear optics. At most present-day sources, however, values for $\eta$ are typically much lower than 1, implying that in the majority of the pulses that interact with the sample there is no resonant photon. This means that there is typically only one nuclear resonant photon at a time in the setup. Under favorable conditions, e.g., when large bunch charges like in few-bunch filling mode of the storage ring are realized, there can be a sufficiently large fraction of bunches containing two or more resonant photons. The situation changes drastically with the advent of x-ray laser sources operating in the regime of hard x-rays like the LCLS in Stanford (USA) [136], SACLA in Himeji (Japan) [137], and the European XFEL in Hamburg (Germany) [138,139,140,141]. At these sources, values for $\eta$ larger than 10$^2$ at 14.4 keV can be expected. In fact, a first experiment devoted to NRS has been recently been performed at SACLA, demonstrating superradiant emission from nuclear excited states with close to 10$^2$ photons per pulse [142]. In this section we are going to discuss two new types of future sources of x-rays that have great potential to further stimulate the field of nuclear quantum optics. These are the ultimate realizations of synchrotron radiation sources, i.e., diffraction limited storage rings (DLSR) and x-ray free electron laser oscillators (XFELO).

3.9.1 Diffraction-Limited Storage Rings

A new generation of accelerator-based x-ray sources is presently emerging that relies on a novel type of electron optics for the storage-ring, the so-called multi-bend achromat (MBA) [143,144,145]. The new concept allows for a significant reduction of the horizontal emittance $\epsilon _x$ compared to existing facilities. The emittance is a property of a radiation source and is given by the product of beam diameter and beam divergence. The smaller the emittance, the higher is the degree of spatial coherence of the source, which is the most desirable property of a radiation source for focusing or imaging applications. The emittance cannot be arbitrarily decreased, but is limited by the fundamental effect of diffraction of the beam by the shape of its own beam cross section. For that reason there are worldwide great efforts undertaken to reduce the emittance of synchrotron radiation sources as much as possible to reach the diffraction limit. The synchrotron radiation source MAX IV in Lund, Sweden, is the first light source that was successfully commissioned with this new lattice type [146], and SIRIUS in Campinas, Brazil, is currently under construction. Amongst the high-energy synchrotron radiation sources (electron energy equal or larger than 6 GeV), the European Synchrotron Radiation Source (ESRF) in Grenoble, France, will undergo an upgrade starting in winter 2018 to the fourth generation light source ESRF-EBS with an emittance as low as $\epsilon _x \approx$ 130 picometer-radian (pmrad) at an electron beam energy of 6 GeV [147]. Many other sources worldwide have upgrade plans along these lines, among which are also the high-energy storage-ring sources Advanced Photon Source (APS) at Argonne National Laboratory (USA) [148], SPring-8 in Harima (Japan), and PETRA IV at DESY in Hamburg (Germany) [149]. The latter facility will be the first source reaching the diffraction limit for hard x-rays at 10 keV photon energy. The implementation of the new electron optics in the storage ring allows for an increase of the spectral brightness by one to two orders of magnitude. This will dramatically change the landscape of synchrotron radiation facilities in the next decade, see Fig. 3.25.

Fig. 3.25

Reprinted from [149], the authors licensed under CC-BY 4.0

Diffraction limit for selected synchrotron radiation sources and their future upgrades.

The benefit of diffraction-limited storage rings for the field of nuclear quantum optics will not be an increase in the photon degeneracy parameter $\eta$, but primarily the concentration of more resonant photons in a given scattering volume as compared to present-day sources. This is enabled by the high degree of lateral coherence which facilitates a very efficient collimation and focusing of x-rays, leading to an enhanced coupling of x-rays to nuclear ensembles, e.g., in cavities and photonic nanostructures.

3.9.2 X-Ray Free-Electron Lasers: SASE-XFEL and XFELO

A tremendous increase of the photon degeneracy $\eta$ will be reached by x-ray sources that rely on a fundamentally different mechanism of radiation generation. This is the principle of self-amplified spontaneous emission (SASE) which forms the basis for free-electron lasers (FEL). The SASE principle leads to a increase in the brilliance of the radiation by several orders of magnitude compared to synchrotron radiation sources, going along with a corresponding increase in $\eta$. The ultimate performance for nuclear resonant scattering experiments, however, will be achieved if the SASE process takes place in a specially designed cavity where the relativistic electrons interact with the x-rays that are circulating in the cavity. Such a device has been termed x-ray free-electron laser oscillator (XFELO), conceptually introduced about ten years ago [7, 150, 151].

An XFELO is a low-gain device, in which an X-ray pulse that circulates in a cavity formed by diamond crystal Bragg mirrors is amplified every time it overlaps with an electron bunch in the undulator, illustrated in Fig. 3.26 . Due to its high reflectivity and excellent thermo-mechanical properties, diamond is the preferred material for the Bragg crystals employed to form the X-ray cavity [152]. An XFELO will work at any photon energy for which the Bragg reflectivity of diamond is sufficiently high and the bandwidth is sufficiently broad so that the initial exponential gain of the intra-cavity pulse energy can be sustained for a reasonable set of electron beam and undulator parameters. This range is expected to extend from 5 to 25 keV [151]. The photon energy can be continuously tuned for a given setting within a range of about 5$\%$ by changing the Bragg angle and adjusting the crystal positions so that the cavity roundtrip time remains fixed.

Fig. 3.26

Figure adopted from [8]

A schematic illustration of an XFELO. Four crystals form a closed X-ray cavity via Bragg reflection.

An XFELO will open up completely new possibilities in the field of nuclear resonance scattering (NRS) for isotopes with resonance energies between 5 and 25 keV. Due to the narrow resonance linewidths of Mössbauer transitions, NRS will benefit from the extremely intense, narrow-bandwidth radiation from the XFELO in several ways: The anticipated hard X-ray spectral flux of 3$\times 10^{9}$ ph/sec/neV is more than 4 orders of magnitude larger than at existing 3rd generation synchrotron radiation sources [8].

As an example, at 14.4 keV (the transition energy of the $^{57}$Fe Mössbauer resonance) the number of photons per pulse is expected to be 1$\times 10^{10}$ within a pulse length of 680 fs (FWHM) and a spectral bandwidth of 3 meV (FWHM). This amounts to an average spectral flux of about 3$\times 10^{15}$ photons/sec/meV or 1.5$\times 10^{10}$ photons/sec/$\Gamma _0$, which corresponds to $\eta =$ 1.5$\times 10^{4}$ photons/pulse/$\Gamma _0$ where $\Gamma _0$ = 4.7 neV is the natural linewidth of the $^{57}$Fe Mössbauer resonance. These numbers are four orders of magnitude larger than those observed at the best third-generation synchrotron radiation sources to date. This allows one to push Mössbauer science far beyond the single photon regime, opening new perspectives for X-ray quantum optics and nonlinear science with nuclear resonances. The full transverse coherence of the radiation will allow for efficient focusing to extremely small spot sizes in the range of 10 nm, enabling one to combine NRS with high-resolution imaging techniques. Moreover, a frequency stabilized XFELO would enable a hard X-ray frequency comb with pulse-to-pulse coherence for unique applications in X-ray coherent control and extreme metrology.

The longitudinal coherence of optical fields is the core requisite to induce and control interference between different quantum pathways in atoms. In nuclei, similar developments so far were restricted to single photons interfering with themselves, due to the lack of sufficiently coherent photon sources. With an XFELO this situation will fundamentally change. Its full coherence and spectral brightness provides new avenues for studying the interaction between X-rays and nuclei under multiphoton excitation conditions, thus offering unique possibilities for nonlinear spectroscopy of the nucleus, as well as for novel approaches to nuclear state preparation and detection.

For example, at low orders of nonlinearity quantum aspects involving X-ray photons could naturally be explored with two or more correlated photons. Potential approaches encompass both the generation of X-ray photon entanglement and its applications, and the exploration of quantum states in the nuclei by subsequent spectroscopic detection of scattered X-ray photons [153]. The availability of multiple coherent photons per pulse in turn enables detection of multiple correlated X-ray photons, providing access to higher-order correlation functions characterizing, e.g., density fluctuations, phonons or similar excitations. This will fuel the development of a broad class of new detection and analysis techniques. With multiple potentially phase-locked driving fields, multi-dimensional spectroscopy techniques come within reach, providing further insight into the dynamics. 2D nuclear spectroscopy might reveal couplings among nuclear transitions that could provide fundamental insight into intra-nuclear interactions, analogous to what is revealed in two-dimensional spectroscopy throughout radio frequency to optical spectral ranges [154, 155]. This and the other 2D measurements mentioned above will require at least phase-related X-ray pulse pairs, which could be generated by splitting one XFELO output pulse by an X-ray split-and-delay line or by applying temporal control of resonantly scattered photons via ultrafast piezo modulation [84].

Further progress is anticipated in the engineering of advanced nuclear level schemes. First steps have recently been demonstrated at 3rd generation light sources, by designing suitable target structures utilizing Mössbauer nuclei embedded in superlattices [38] and planar X-ray cavities [27, 29, 39]. The XFELO will enhance these capabilities by its unique source properties, which, aside from the spectral brightness also includes coherent multi-pulse or multi-color excitation. The XFELO could also facilitate novel nuclear resonance excitation processes, such as non-linear two-photon excitation [156] or four-wave mixing.

Fig. 3.27

Modified from [157], Copyright 2016, with permission from Springer Nature

Diagram of Mössbauer isotopes and nuclear isomers together with atomic and nuclear clock transitions in the parameter space of transition energy and half-life. The shaded regions covers the energy range of the XFELO (light blue) and the XFELO with a high-gain high-harmonic (HGHG) extension to reach photon energies above 25 keV (light brown).

The pulse-to-pulse coherence of an energy stabilized XFELO enables one to realize a hard X-ray frequency comb (see Sect. 3.6), facilitating ultrahigh-resolution X-ray spectroscopy of nuclear transitions. Examples include multi-level nuclear transition measurements, probing ultra-narrow X-ray Mössbauer resonances, dynamics of X-ray driven nuclear—electronic transitions, and X-ray + laser double resonance experiments. Facilitated by X-ray comb spectroscopy, fascinating possibilities come into reach: X-ray frequency and wavelength metrology would be enabled by extending the optical frequency comb technologies and techniques to X-ray wavelengths. In addition to probing nuclear physics with unprecedented precision, linking nuclear transitions to the Cs standard can be used to search for the variation of fundamental constants with improved sensitivity [158, 159]. Nonlinear phase-coherent driving and probing at X-ray wavelengths will be possible over long times >10 s. High-quality-factor nuclear transitions like the 12.4 keV level of $^{45}$Sc with a lifetime of $\sim$300 ms and $\Gamma _0/E_0 \sim \!10^{-19}$ (see Fig. 3.27) can be established as new and improved frequency standards. Importantly, the pulse-to-pulse coherence allows to excite these narrow resonances using a sequence of pulses, offering the possibility of orders of magnitude higher excitation fraction than expected from SASE [153].

With sufficient temporal coherence and high intensity, coherent processes including nuclear coherent population transfer in the stimulated Raman adiabatic passage (STIRAP) technique [160, 161] or nuclear Rabi oscillations [162] are rendered possible. Coherent population transfer would enable controlled pumping, storage and release of energy stored in long-lived nuclear excited states. In addition, also nuclear reactions starting from excited nuclear states driven by the XFELO can be envisaged.

3.10 Concluding Remarks

We have shown in this review that planar cavities and photonic nanostructures like multilayers and superlattices containing Mössbauer nuclei constitute interesting systems to explore quantum optical effects in the x-ray regime. Since the period of the x-ray standing waves in these structures is typically much larger than the thickness of ultrathin layers of Mössbauer atoms embedded in them, one is able to realize the small-sample limit of Dicke superradiance. This is instrumental for the preparation of single radiative eigenmodes of these nuclear ensembles. Accurately controlling their placement within the standing wave field facilitates to tailor their radiative decay width. In the vacuum field of the cavity this leads to several possibilities to prepare coherences between nuclear levels. One of those coupling schemes leads to electromagnetically induced transparency (EIT), another one to spontaneously generated coherences (SGC), and many others are still to be explored, opening exciting perspectives for future research in the field of cooperative emission and quantum optics with hard x-rays. Further engineering of photonic structures in one, two, or even three dimensions with modern thin-film deposition methods and lateral structuring techniques enables one to reach the regime of collective strong coupling between x-rays and nuclear resonances. We have demonstrated the basic effects encountered in this regime, namely normal mode splitting of the resonances and Rabi oscillations between nuclear ensembles. While all these effects could be explored in the limit of single-photon excitation, new avenues could open up under conditions of multiphoton excitation. This includes stimulated emission, nonlinear x-ray optics, multiphoton cooperative emission, novel hybrid light-matter states in cavities, to name a few. Especially intriguing in this area would be the simultaneous coupling of different types of photonic structures like cavities and multilayers to further enhance the multiphoton light-matter coupling with nuclear resonances. Moreover, the concepts presented in this review even open the possibility to transfer them into other wavelength regimes of the electromagnetic spectrum. One could explore these effects also with narrow resonance of inner-shell resonances, where first measurements on the collective Lamb shift have been performed [163]. Further applications could be to realize concepts of quantum memory with nuclear resonances which could even form a bridge into the area of quantum computing implementations.