The Prediction Analysis of COVID-19 Cases Using ARIMA and KALMAN Filter Models: A Case of Comparative Study

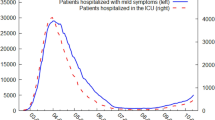
Abstract

The time series technique in machine learning is one of the important spaces for analysis and prediction. It includes many approaches to predict that involves time component. In the chapter, two approaches, i.e., autoregressive integrated moving average (ARIMA) and KALMAN filter models were demonstrated on the corona data (India) that was obtained from Ministry of Health and Family Welfare Web site. On modeling, it was found that ARIMA model gave better performance model over the KALMAN filter model. ARIMA (1, 1, 0) gave the approximate value of 35,303 for May 1, 2020 with sigma equal to 199.32, whereas the state-space model and error model of KALMAN filter generated the value of 33,116 and variance equal to 1356.18. The key purpose of the study is to understand and estimate the number of hospital beds and nursing care beds for the COVID-19 (CV-19) patients and make the indispensable arrangement for the patient treatment and avoid delay in action. In recovery cases, the highest value of difference is observed as 1153 on April 27, 2020, whereas the increases in reported cases are 2082 on April 28, 2020. More number of cases are reported with the peak in Maharashtra of 9915 (confirmed) and 1593 (recovery) on April 30, 2020. COVID-19 data visualization was carried out geographical information system with red color referring to the danger or more number of COVID-19 affected areas/state. Green color refers to normal and blue color refers to safe zone with no or single digit cases reported.

1 Introduction

In machine learning, the analysis of time series is found to be very popular and standard that is performed using various models. The experimental data analysis was observed at various points in time leads to new and unique complications in statistical modeling and inference [1]. In this chapter, ARIMA and KALMAN filter models are discussed for predicting COVID-19 cases. The prediction approach of events through a time sequence is referred as time series forecasting. By analyzing the historical trends of the past, assumption is favored for future trends. Time series (TS) are used in every field from medicine to finance, business, inventory planning, and dynamic system theory. The modern application of TS forecasting uses computer technologies that include machine learning, artificial neural networks, support vector machines, and so on. It is well-quoted by a data scientist that “time series forecasting is something of a dark horse in data science.” On the other hand, according to Tealab [2] time series is a general problem solution of great practical interest in various disciplines. TS have evidence about the predictor variables of any system which determines dynamically. It is a sequence of values over the time of a system y(t) which registers a sequence of experimental values given as y (t₁), y (t₂), y (t₃),…, y (t_n) for certain interval t = n where t₀ < t₁ < … < t_n. The aim of the study is to have the count of hospital beds and nursing beds made available on the prediction made to avoid delays and rushing. This would help the healthcare centers to arrange and be vigilant.

2 Predictive Modeling

Predictive modeling (PM) is a practice that uses data and mathematics to predict outcomes with data models. On the other hand, machine learning (ML) algorithms build the mathematical model based on the training data for prediction; ML algorithms uses statistical techniques to allow a computer to construct PMs. Predictive model stirs relations between ML, pattern recognition, and data mining. PM includes much more than the tools and techniques for unveiling patterns within data. PM training defines the development of a model process in a way that can understand and quantify the model’s prediction accuracy on future, yet-to-be-seen data. The prime aim of PM is to produce accurate predictions and next is to interpret the model and understand how it works. But unfortunate reality/certainty is that as the model is pushed toward higher accuracy, models become more complex and their interpretability becomes more difficult [3]. PM performs curve and surface fitting, TS regression, or/and ML methods. One such example of TS regression; where the key convention of regression methods is that the patterns in the past data will be repeated in the future [4]. In this work, time series approach is carried out using ARIMA and KALMAN filter approach, the predictive results of CV-19 were analyzed to find that the ARIMA model gave the nearest results of the confirmed cases in India. The objective of this prediction study is to understand the need of hospital beds and nursing care beds for CV-19 patients. This study helps to make the necessary arrangements for number of patient in-advance and to be cared for.

3 Time Series Using COVID-19 Datasets

A time series (TS) is a set of series of data points listed in the time order. A sequence that is successive equal spread out in points with time. The analysis encompasses methods for analyzing TS data to extract meaningful statistics and other data characteristics. The forecasting model of TS uses future values based on previously observed values for prediction. The time series data components are trend, seasonal variation, cyclical variation, and other irregular fluctuations.

Elmousalami [5] in their case study of CV-19 of analysis and modeling performed single exponential smoothing (SES) on the datasets of international confirmed cases. Figure 1 shows the graph of SES obtained and the Eq. 1 of SES is given as

Fig. 1

SES for predicting the confirmed cases (international) [5]

$$F_{t + 1} = \left( {1 - \alpha } \right)F_{t} + \alpha \,D_{t}$$

(1)

The results in Table 1 show that SES has the most accurate model for forecasting recovered cases of CV-19 with 517.54, 523335.16, 723.42, and 16.38% for mean absolute deviation (MAD), mean square error (MSE), root mean square error (RMSE), mean absolute percentage error (MAPE), respectively, against moving average (MA) and weighted moving average WMA.

Table 1 Forecasting models for international confirmed cases [5]

Siedner [6] in their study of CV-19 in USA suggests that the due to social distancing, there is a lot of reduction in mean daily growth rate of CV-19 cases. The study involved a cumulative epidemic size of 4,171 cases (USA) where the reduction in growth rate estimated corresponds with a reduction in total cases from 26,356 to 23,266 at 7 days, and from 156,360 to 88,105 at 14 days after implementation. In brief, the uninterrupted TS model suggests that social distancing reduced the total number of CV-19 cases by nearly about 3,090 cases in 7 days after implementation and by 68,255 cases in 14 days. Table 2 displays the outcome of regression model for the growth rate daily wise after the social distancing was implemented.

Table 2 Linear regress for daily growth rate before versus after implementation of the first state-wide social distancing measure and state-wide restrictions on the internal movement [6]

In this study of CV-19 with dataset of different states of India, TS graph was implemented to understand the visualization of reported and recovery cases at a time. The data was obtained from https://www.mohfw.gov.in/ and the analysis is carried out on STATA-12 software.

The graph displays the different states confirmed (Fig. 2) and recovery (Fig. 3), in both the graphs Maharashtra is at the peak with 9915 (confirmed) and 1593 recovery cases on April 30, 2020.

Fig. 2

Reported cases of different Indian states affected due to COVID-19

Fig. 3

Recovery cases in different states of India

Figure 4 shows the recovery cases of CV-19 in India from March 14, 2020 to April 30, 2020. The graph represents slight decrease on April 13, 2020 giving April 14 on subtracting from April 12, 2020 recovery data. Figure 5 shows the comparison of two—reported cases (Fig. 5a) and recovery cases (Fig. 5b) with increase/decrease in the number of cases. The peak value in recovery difference is 1153 on April 27, 2020, whereas the highest increase in confirmed case is 2082 on April 28, 2020.

Fig. 4

Day-wise recovery cases graph

Fig. 5

a Day-wise increase in confirm cases, b increase/decrease graph for recovery cases

4 ARIMA

In TS exploration, an autoregressive integrated moving average (ARIMA) model is a generalization of an autoregressive moving average (ARMA) model. ARIMA (ARM) models are the best models for the statistical models for analyzing and forecasting TS data. An ARM model is a filter that separates the data from the noise, and the data is then extrapolated to obtain forecasts. The forecasting equation of ARM for stationary TS is a linear (regress) equation in which the predictors include of lags of the response variable and/or lags of the forecast errors. Predicted value (Y) is calculated with a constant and/or a weighted sum of one or more current values of Y and/or a weighted sum of one or more current values of the errors.

ARM models complex data pattern; and uses the export modeler for outlier detection, and produces for the drive of eXtended Markup Language (XML) files for prediction modeling of future data.

4.1 The Notation of ARIMA (P, D, Q)

The ARM model consists of autoregressive (AR), moving average (MA), and seasonal autoregressive integrated moving average (SARIMA) models [7]. The autoregressive terms are lags of the stationaries series in the forecasting equation; moving average are lags of the forecast errors, and a TS which needs to be differenced to be made stationary is integrated of a stationary series.

A non-seasonal ARM model is written as an ARIMA (p, d, q) model where p is the sum of autoregressive terms, d is the sum of integrated differences order, and q is the sum of moving average (lagged forecast errors) in the prediction equation.

Hence, the forecasting Eqs. 2, 3, and 4 is built as follows [8, 9].

$$\left( {1 - \varPhi_{1} B - \ldots - \varPhi_{p} B^{p} } \right)\left( {1 - \varPhi_{1} B^{s} - \ldots - \varPhi_{p} B^{\text{ps}} } \right)\left( {1 - B} \right)^{d}$$

(2)

$$\left( {1 - B^{s} } \right)^{D} y_{t} = \left( {1 + \theta_{1} B + \ldots + \theta_{q} B^{q} } \right)\left( {1 + \ominus_{1} B^{s} + \ldots + \ominus_{Q} B^{QS} } \right) \in_{t}$$

(3)

where B represents the backshift operator that is defined by the following operation:

$$B^{m} y_{t} = y_{t} {-}m$$

(4)

whenever the parameter has a value of 0 is used; it represents that not to use that element of the model.

4.2 ARIMA in COVID-19 Cases—Datasets

In a case study of ARIMA model, [10] used the model for predicting the electricity prices. The two ARIMA models −1 and 2 were used predicted hourly prices in the electricity markets of Spain and California. The model of Spanish requires 5 h to predict future prices, as opposed to the 2 h needed by the Californian model. The spot markets and long-term contracts, price forecasts are essential for developing bid strategies or negotiation skills.

Model 1 is given as

$$\begin{aligned} & \left( {1 - \varPhi_{1} B^{1} {-}\varPhi_{2} B^{2} {-}\varPhi_{3} B^{3} {-}\varPhi_{4} B^{4} {-}\varPhi_{5} B^{5} } \right) \\ & \quad \times \left( {1 - \varPhi_{23} B^{23} {-}\varPhi_{24} B^{24} {-}\varPhi_{47} B^{47} } \right. \\ & \quad {-}\left. {\varPhi_{48} B^{48} {-}\varPhi_{72} B^{72} {-}\varPhi_{96} B^{96} {-}\varPhi_{120} B^{120} {-}\varPhi_{144} B^{144} } \right) \\ & \quad \times \left( {1 - \varPhi_{168} B^{168} {-}\varPhi_{336} B^{336} {-}\varPhi_{504} B^{504} } \right)\log p_{t} = c \\ & \quad + \left( {1 - \theta_{1} B^{1} {-}\theta_{2} B^{2} } \right) \, \left( {1 - \theta_{24} B^{24} } \right) \\ & \quad \times \left( {1 - \theta_{168} B^{168} - \theta_{336} B^{336} - \theta_{504} B^{504} } \right)\varepsilon_{t} \\ \end{aligned}$$

(5)

Model 2 is given as

$$\begin{aligned} & \left( {1 - \varPhi_{1} B^{1} {-}\varPhi_{2} B^{2} } \right) \times \left( {1 - \varPhi_{23} B^{23} {-}\varPhi_{24} B^{24} {-}\varPhi_{47} B^{47} {-}\varPhi_{48} B^{48} } \right. \\ & \quad {-}\left. {\varPhi_{72} B^{72} {-}\varPhi_{96} B^{96} {-}\varPhi_{120} B^{120} {-}\varPhi_{144} B^{144} } \right) \\ & \quad \times \left( {1 - \varPhi_{167} B^{167} {-}\varPhi_{169} B^{169} {-}\varPhi_{192} B^{192} } \right) \times \left( {1 - B} \right)\left( {1 - B^{24} } \right)\left( {1 - B^{168} } \right) \\ & \quad \log p_{t} = c + \left( {1 - \theta_{1} B^{1} {-}\theta_{2} B^{2} } \right)\left( {1 - \theta_{24} B^{24} {-}\theta_{48} B^{48} {-}\theta_{72} B^{72} {-}\theta_{96} B^{96} } \right) \\ & \quad \times \left( {1 - \theta_{144} B^{144} } \right) \times \left( {1 - \theta_{168} B^{168} - \theta_{336} B^{336} - \theta_{504} B^{504} } \right)\varepsilon_{t} \\ \end{aligned}$$

(6)

Tables 3 and 4 are the statistical values of forecast mean square of errors (FMSE) was obtained on application of model 1 and 2. Table 5 displays the estimated and parameter values of two countries models.

Table 3 Statistical without explanatory variables [10]

Table 4 Statistical with explanatory variables [10]

Table 5 Estimated parameter values of the Spanish and Californian ARIMA models [10]

Noureen [9] in a case study of ARIMA in forecasting is a small-scale agricultural load. For the TS data, ARIMA method was applied on the stationary TS data. As seasonal variations make a TS nonstationary, this study presented an analyses on testing stationarity and transforming non-stationarity into stationarity. The model was developed with a specific order selection for autoregressive terms, moving average terms, differencing and seasonality and the forecasting performance has been tested and compared with the actual value. After the plotting of ACF and PACF, augmented Dickey fuller (ADF) test is performed for hypothesis testing to confirm stationarity of TS. ADF is also known as unit root test. The model for the ADF test is shown in Eq. (7):

$$\partial Y_{t} = \mu + \beta t + \rho Y_{t - 1} + \partial Y_{t - 1} + \ldots + \partial_{p} Y_{t - p} + e_{t}$$

(7)

The seasonal ARIMA model is implemented to forecast the agricultural loads for the last one year of the three-year data. The mean absolute error (MAE) of our forecast is calculated to be 13.23%.

Benvenuto [7] implemented ARIMA on a dataset consisting of 22 number determinations. The overall prevalence of CV-19 presented an increasing trend that reached the epidemic plateau as shown in Fig. 6 and Table 6 gives the predicted values for the two days. The difference between cases of a day and cases of the previous day ∆(Xn-Xn-1) showed a non-constant increase in the number of confirmed cases. Figure 7 displays the correlogram and ARIMA forecast graph for the 2019-nCoV incidence.

Fig. 6

Correlogram and ARIMA forecast graph for the 2019-nCoV prevalence [7]

Table 6 Forecast value for two days after the analysis for the prevalence and for the incidence of the CV-19 [7]

Fig. 7

Correlogram and ARIMA forecast graph for the 2019-nCoV incidence [7]

4.3 ARIMA Model on COVID-19—India Dataset

In this case study of COVID-19 (India), ARIMA (ARM) model was built using STATA software. Here, the comparative study on the prediction results obtained from the two models state that ARIMA (1,1,0) model gives much better accurate results over the KF predicted values. The number of cases reported is shown in Table 7 and ARIMA (1,1,0) was modeled to obtain Table 8 with log likelihood value of −316.86; and the predicted value of both the models is shown in Table 15.

Table 7 Number of cases reported

Table 8 ARIMA model—ARIMA(1,1,0)

Using ARM model, when the parameters of the model were given as p = 1, d = 1, and q = 0; then the p-value = 0 and the predicted values were to the nearest data values. The z-test statistic for the predictor (ConfirmCases) is 823.3/554.8 = 1.48. Coefficient of ARMA(ar) = 0.96; wald chi2(1) is wald chi-square statistic. It is mainly used for hypothesis test where at least one of the predictors’ regression coefficients is not equal to zero. Here, in this case, 1 refers to the number of degrees of freedom of the chi-square distribution used to test the wald chi-square statistic and is distinct by the number of predictors (1)./sigma is the estimated standard error of the ARM regression with 199.32 value.

Correlograms/autocorrelation function (ACF) and partial correlograms/partial autocorrelation function (PACF) are shown in Fig. 8, with confidence interval (CI) of −0.9–0.9 in ACF and in PACF, CI is −0.03–0.03. The x-axis denotes the lag and y-axis represents the first-order differential of cases. The blue dot represents the autocorrelation between the lag variable and unlag variable of cases in this study. The dots which are well-outside the interval are known to be large and will be least equal to 1, i.e., p = 1. Each spike that rises above or falls below the CI range is considered to be statistically significant. ACF and PACF table is mentioned in Table 9.

Fig. 8

ACF and PACF graph of COVID cases

Table 9 ACF and PACF values

The analysis procedures include ACF and PACF that are used to calculate correlation in the data [11].

5 KALMAN Filter

KALMAN filter (KF) is widely known as an optimal estimator—i.e., infers factors of interest from indirect, inaccurate, and uncertain observations. The new measurements are processed by the recursive property of KF. KF minimizes the mean square error of the estimated parameters, if the noise is Gaussian; and it is a best linear estimator, given the mean and standard deviation of the noise. The technique of finding the best estimate from noisy data amounts to filter out the noise is referred as filtering; and this practice is carried out by KF (Kleeman). KF is a two-step process, namely prediction and update steps. For the likelihood, one has to find f (y_t|Y_t-1) [12]. The two steps are given in Eqs. 8 and 9. (prediction) and Eqs. 10, 11, and 12 (update).

• 1. Prediction equation

  $${\hat{\mathbf{x}}}_{k}^{ - } = A\,{\hat{\mathbf{x}}}_{k - 1}^{ - } + BU_{k}$$

  (8)
  $${\mathbf{P}}_{k}^{ - } = A\,{\mathbf{P}}_{k - 1}^{ - } + A^{T} + {\mathbf{Q}}$$

  (9.)

• 2. Updating equation

  $${\mathbf{K}}_{\text{k}} = {\mathbf{P}}_{\text{k}} {\mathbf{C}}^{T} \left( {{\mathbf{CP}}_{{\mathbf{k}}}^{ - } {\mathbf{C}}^{\text{T}} + {\mathbf{R}}} \right)^{ - 1}$$

  (10)
  $$\widehat{{\mathbf{x}}}_{{\mathbf{k}}} = \widehat{{\mathbf{x}}}_{{\mathbf{k}}}^{ - } + {\mathbf{K}}_{{\mathbf{k}}} \left( {{\mathbf{Y}}_{{\mathbf{k}}} - {\mathbf{C}}\widehat{{\mathbf{x}}}_{{\mathbf{k}}}^{ - } } \right)$$

  (11)
  $$P_{k} = \left( {1 - K_{k} C} \right)P_{k}^{ - }$$

  (12)

The state-space model consists of covariance and error forms; both the forms follow two equations first one is state Eq. 13 and observation Eq. 14. The notation of a state-space model is as follows:

$$y_{t} = Z_{t} \alpha_{t} + S_{t} \xi_{t}$$

(13)

$$\alpha_{t} = T_{t} \alpha_{t - 1} + R_{t} \eta_{t}$$

(14)

with $\left( {\begin{array}{*{20}c} {\eta_{t} } \\ {\xi_{t} } \\ \end{array} } \right)$ ~ iid N $\left( {0,\left[ {\begin{array}{*{20}l} Q \hfill & 0 \hfill \\ 0 \hfill & H \hfill \\ \end{array} } \right]} \right)$ and the initial observation is given as y₁ ~ N(y_1|0, F₁).

5.1 KALMAN Filter—for Prediction in Different Studies

Rhudy [13] in their work of KF using MATLAB gives an illustration of a simple object in freefall presuming that there is no air resistance. The purpose of filter is to determine the location of the object based on uncertain information about the starting location of the object as well as measurements of the location provided by a laser rangefinder. The acceleration of the given object will be the same to the acceleration due to gravity. In their study, the measurement system has a standard deviation of error of 2 m, and variance of 4 m². In the measurement noise, uncertainty in the initial state is considered. The starting point is known to be 105 m before the ball is dropped, while the actual starting point is 100 m as shown in Fig. 9. The initial guess was roughly determined and has a relatively high corresponding initial covariance. The error of 10 m² for the initial position is assumed as the object starts from rest; a smaller uncertainty value of 0.01 m²/s² is obtained as shown in Fig. 10.

Fig. 9

Example of KF estimated and true states [13]

Fig. 10

Example of KF using estimation errors [13]

Laaraiedh [14] in a case study of KF in telecommunications used on the mobile tracking user connected to a wireless network. A simple tracking algorithm was implemented using Python language by a mobile user who is moving in a room and connected to at least three wireless antennas. The estimated position of the mobile using a trilateration algorithm is indicated by matrix of measurement Y with at least three values of time of arrival (ToA) at time step k as shown in Fig. 11. The values are computed using ranging procedures between the mobile and the three antennas. Initialization of different matrices and using the updated matrices for each step and iteration; estimated, and the real trajectory of the mobile user, and the measurements are performed by the least square-based trilateration. KF enhances the tracking accuracy compared to the static least square-based estimation.

Fig. 11

KF applied to ToA-based localization [14]

Rankin [15] in their case study of KF for the market price application was based on yearly, quarterly, monthly, weekly, and daily prices. A study was also carried out on open, high, low, and close prices. The use of averages (e.g., weekly or monthly) or stock indexes may alter the results of a study. Table 10 shows the comparison of expenses for the consumer strategy. The first sample (DJT#1) consisted of 1036 hourly readings from February 22, 1985 to September 23, 1985. The second (DJT#2) was of 896 hourly readings from January to June, 1984. The third sample (DJT#3) was gathered from July through December, 1983 and consisted of 896 samples from the 128 day period. KF program produced N-step ahead forecasts for TS. MSE of the forecast errors are calculated to measure model accuracy.

Table 10 Expense comparison for consumer strategy [15]

Malleswari [16] in a case study of KF in the error modeling (like ionospheric delays, atmospheric delays, tropospheric delays, and so on) affecting the GPS signals as they travel from satellite to the user who is on earth. In this methodology, it showed that the variations in the signal related to WGS—84 data can be smoothened using KF with the studies made and the analysis yielded better accuracies as shown in Tables 11 and 12 that Φkf—the latitude in degrees on KF application is 0.004221766 for Gandipet and 0.00003667424 for Hussain Sagar. Similarly, λkf—longitude in degrees on KF application KF is 0.03084715 for Gandipet and 0.0006331302 for Hussain Sagar.

Table 11 Comparison of longitude for Gandipet (left) and Hussain Sagar (right) [16]

Table 12 Comparison of latitude for Gandipet (left) and Hussain Sagar (right) [16]

5.2 KALMAN Filter—for COVID-19 Prediction—India Dataset

There are two forms in state-space model, namely covariance and error form models. There are shown in Tables 13 and 14, respectively.

Table 13 State-space model—covariance

Table 14 State-space model—error form

5.2.1 Covariance

See Table 13.

5.2.2 Error Form

In Fig. 12, the dotted lines show the prediction of CV-19 data obtained using ARIMA and KF model. The solid blue line indicates cases of training data. The results of KF model—covariance and error model are shown in Tables 13 and 14, respectively. The log likelihood in refine estimates is −77.19, wald chi2(1) is 2923.86. Z-test of predictor (Confirm_Cases1) is 73018.58/31135.21 = 2.35 and z-test of date is 1392.43/25.75 = 54.07. The variance is given as 1356.18. Two models are best fit model; as all of the p-values are very significant with p < 0.001 and p < 0.05.

Fig. 12

Comparison of ARIMA and KALMAN filter prediction graphs

Table 15 shows the ARM and KF predicted value from May 1, 2020 and the data. The prediction was calculated from May 1, 2020 up to May 20, 2020. The predicted values are thus compared with the data to check if it lies within the nearest range. Figure 13 describes the prediction of ARM and KF along with data in a single graph and on comparison one can see the predictive curve of ARM increases accurately with the dates, whereas the KF would not give accurate predicted values.

Table 15 Predicted values using ARIMA and KALMAN filter from April 27, 2020 to May 20, 2020

Fig. 13

Two models prediction graph of COVID-19 India cases

6 Geographic Information Systems—Visualization and Prediction—COVID-19 Datasets

Geographic information systems (GIS) are a computer-based tool that examines spatial relationships, patterns, and trends. This through connecting geography with data, GIS better understands data using a geographic context. It stores, analyze, and visualize data for geographic positions on earth’s surface. The four main characteristics of GIS create geographic data, manage it in a database, analyze and find patterns, and visualize it on a global map. In viewing and analyzing data on maps gives better understanding of data, and one can make better decisions. It helps in understanding what is where. Spatial-temporal GIS, or 4D GIS, has become necessary in areas where GIS is needed for predicting dimensions across time. GIS is increasingly needed with a real-time platform that offers not just monitoring of events but can take input and predict what could happen as a type of forecasting tool. Figure 14 shows the GIS visualization of CV-19 in different states of India. The color red in Maharashtra indicates that the numbers of reported cases (confirmed cases) are more in number and is known as red zone. The less brightness of red indicates the little less than Maharashtra state. The green color indicates normal with less number of CV-19 cases. The color blue refers to safe zone where no or single digit confirmed cases are reported. In red and green zone states, one find lockdown implemented to overcome the increase in the number of cases. If no lockdown was implemented in India, one would find more number of cases as in aboard along with death cases.

Fig. 14

GIS visualization on COVID-19 in different states on India

7 Conclusions

In a comparative study of two predictive models of TS, ARIMA, and KALMAN filter in this chapter predicts day-wise cases in COVID-19 of India. Both the models are used on the stationary TS datasets. But, it was found that ARIMA model gave better results over KALMAN filter model for the COVID-19 dataset.