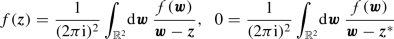Abstract
Meta-conformal invariance is a novel class of dynamical symmetries, with dynamical exponent \(z=1\), and distinct from the standard ortho-conformal invariance. The meta-conformal Ward identities can be directly read off from the Lie algebra generators, but this procedure implicitly assumes that the co-variant correlators should depend holomorphically on time- and space coordinates. Furthermore, making this assumptions leads to un-physical singularities in the co-variant correlators. We show how to carefully reformulate the meta-conformal Ward identities in order to obtain regular, but non holomorphic expressions for the co-variant two-point functions, both in \(d=1\) and \(d=2\) spatial dimensions.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Many brilliant applications of conformal invariance are known, ranging from string theory and high-energy physics [36], or to two-dimensional phase transitions [9, 16, 19] or the quantum Hall effect [11, 17]. These applications are based on a geometric definition of conformal transformations, considered as local coordinate transformations \(\textit{\textbf{r}}\mapsto \textit{\textbf{r}}'=\textit{\textbf{f}}(\textit{\textbf{r}})\), of spatial coordinates \(\textit{\textbf{r}}\in \mathbb {R}^2\) such that angles are kept unchanged. The associated Lie algebra is called the ‘conformal Lie algebra’.
In Table 1, examples of infinite-dimensional Lie groups of time-space transformations are shown. They represent attempts to answer the question “Is it possible to adapt conformal invariance to dynamical problems ?” A minimal requirement is to distinguish time and space variables through their global rescaling, according to \(t\mapsto t'=b t\) and  which defines the dynamical exponent
which defines the dynamical exponent  . In what follows, we shall consider infinitesimal transformations where \(b=1+\varepsilon \), with \(|\varepsilon |\ll 1\). Then a rescaling transformation is described by an infinitesimal generator, which for global dilatations on time- and space-coordinates takes the form
. In what follows, we shall consider infinitesimal transformations where \(b=1+\varepsilon \), with \(|\varepsilon |\ll 1\). Then a rescaling transformation is described by an infinitesimal generator, which for global dilatations on time- and space-coordinates takes the form  . The parameter \(\delta \) is the scaling dimension of the scaling operator \(\varphi =\varphi (t,\textit{\textbf{r}})\) on which the generator \(X_0\) is thought to act. Practical use of this is made for the computation of n-point correlation functions \(C^{[n]}=C^{[n]}(t_1,\ldots ,t_n;\textit{\textbf{r}}_1,\ldots ,\textit{\textbf{r}}_n) := \left\langle \varphi _1(t_1,\textit{\textbf{r}}_1)\cdots \varphi _n(t_n,\textit{\textbf{r}}_n)\right\rangle \). The dilatation-invariance of such a correlator is expressed via a Ward identity, which for the global dilatations described by \(X_0\) takes the form
. The parameter \(\delta \) is the scaling dimension of the scaling operator \(\varphi =\varphi (t,\textit{\textbf{r}})\) on which the generator \(X_0\) is thought to act. Practical use of this is made for the computation of n-point correlation functions \(C^{[n]}=C^{[n]}(t_1,\ldots ,t_n;\textit{\textbf{r}}_1,\ldots ,\textit{\textbf{r}}_n) := \left\langle \varphi _1(t_1,\textit{\textbf{r}}_1)\cdots \varphi _n(t_n,\textit{\textbf{r}}_n)\right\rangle \). The dilatation-invariance of such a correlator is expressed via a Ward identity, which for the global dilatations described by \(X_0\) takes the form

and it becomes explicit how the dynamical exponent  distinguishes between temporal and spatial coordinates. Different symmetries will lead to different Ward identities which describe together constraints on the form of the n-point correlator \(C^{[n]}\). Explicit examples will be given in later sections. These differential equation constraints are only consistent if the generators, such as \(X_0\), belong to a well-defined algebraic structure, e.g. a Lie algebra.
distinguishes between temporal and spatial coordinates. Different symmetries will lead to different Ward identities which describe together constraints on the form of the n-point correlator \(C^{[n]}\). Explicit examples will be given in later sections. These differential equation constraints are only consistent if the generators, such as \(X_0\), belong to a well-defined algebraic structure, e.g. a Lie algebra.
It follows from time-space rotation-invariance that conformal invariance must have  . In general,
. In general,  has a non-trivial value
[44]. In \(1+1\) time-space dimensions, there exists an infinite hierarchy of models with dynamical exponent
has a non-trivial value
[44]. In \(1+1\) time-space dimensions, there exists an infinite hierarchy of models with dynamical exponent  [37]. Lower bounds on
[37]. Lower bounds on  are derived from hydrodynamic projections of many-body dynamics
[13]. Attempts of identifying dynamical conformal invariance goes back at least to critical dynamics of a two-dimensional statistical system
[12]. In Table 1, we distinguish the well-studied ‘ortho-conformal’ transformations
[9], which in the two-dimensional space made from time-space points \((t,r)\in \mathbb {R}^2\) are angle-preserving, from recently constructed groups of ‘meta-conformal’ transformations
[20, 25, 28, 42], which in general are not angle-preserving but which share certain algebraic properties with ortho-conformal transformations in Table 1.
are derived from hydrodynamic projections of many-body dynamics
[13]. Attempts of identifying dynamical conformal invariance goes back at least to critical dynamics of a two-dimensional statistical system
[12]. In Table 1, we distinguish the well-studied ‘ortho-conformal’ transformations
[9], which in the two-dimensional space made from time-space points \((t,r)\in \mathbb {R}^2\) are angle-preserving, from recently constructed groups of ‘meta-conformal’ transformations
[20, 25, 28, 42], which in general are not angle-preserving but which share certain algebraic properties with ortho-conformal transformations in Table 1.
 of this standard representation and the physical nature of the co-variant n-point functions is also indicated.
of this standard representation and the physical nature of the co-variant n-point functions is also indicated.The most simple prediction of ortho-conformal invariance concerns the form of the co-variant two-point function \(C = C(z_1,\bar{z}_1,z_2,\bar{z}_2) = \left\langle \phi _1(z_1,\bar{z}_1) \phi _2(z_2,\bar{z}_2)\right\rangle \) built from so-called ‘quasi-primary’ scaling operators \(\phi _j\), with ‘conformal weights’ \(\varDelta _j\) and \(\overline{\varDelta }_j\) [9]. In complex light-cone coordinates \(z=t+\mathrm{i}\mu r\), \(\bar{z}=t-\mathrm{i}\mu r\), one has
up to normalisation. Herein, \(1/\mu \) has the dimensions of a velocity. In deriving this kind of result, auxiliary assumptions are made. Analogously with Eq. (1), the requirement of ortho-conformal co-variance leads to a set of linear partial first-order differential equations for C, the so-called global ortho-conformal Ward identities. Their joint solutions Eq. (2) are necessarily holomorphic (or anti-holomorphic) functions in the variables \(z_j, \bar{z}_j\) [29].
In this work, we shall examine the analogous question for meta-conformal invariance. Known physical examples of confirmed meta-conformal invariance are of two types. First, there exist spatially non-local representations, which arise as a dynamical symmetry of certain non-local equations of motion which occur for example in diffusion-limited erosion [34], the kink-terrace-step model for vicinal surfaces [39] or the associated quantum chain [31] which is a conformal field-theory with central charge \(c=1\) [38]. Some predictions of meta-conformal invariance for response functions have been confirmed in these models [26, 27]. Second, a different type of meta-conformal invariance, with spatially local representations, has been identified recently in the kinetics of biased spin systems, see Fig. 1, such as the kinetic 1D Glauber-Ising model with a bias, sufficiently long-ranged initial conditions and quenched to zero temperature [28, 43]. The influence of transverse dimensions on the representations of meta-conformal transformations is currently under investigation. However, the focus of this work rather is on the formal study of meta-conformal representations as time-space transformations and the boundedness of the resulting two-point correlators.
In order to do so, we begin by analysing the consequences of writing analogous global Ward identities for meta-conformal invariance [20, 28, 42]. As we shall see in Sect. 2, the straightforward implementation of the global meta-conformal Ward identities leads to un-physical singularities in the time-space behaviour of such correlators. These singularities arise since the meta-conformally co-variant correlators are no longer holomorphic functions of their arguments. Therefore, a more careful approach is required, which we shall explicitly describe in Sects. 3 and 4, respectively, for \(d=1\) and \(d=2\) spatial dimensions. Our main result is the explicit form of a meta-conformally co-variant two-point function which remains bounded everywhere, as stated in Eqs. (33, 34) in Sect. 5. An appendix contains mathematical background on Hardy spaces in restricted geometries, for both \(d=1\) and \(d=2\).
2 Global Meta-conformal Ward Identities
Meta-conformal invariance arises as a dynamical symmetry of the simple equation \(\mathscr {S}\varphi (t,\textit{\textbf{r}})= \left( - \mu \partial _t + \partial _{r_{\Vert }}\right) \varphi (t,\textit{\textbf{r}})=0\), which distinguishes a single preferred direction [41], with coordinate \(r_{\Vert }\), from the transverse direction(s), with coordinate \(\textit{\textbf{r}}_{\perp }\). This is sketched in Fig. 1. Throughout, we shall admit rotation-invariance in the transverse directions, if applicable. Therefore, in more than three spatial dimensions, the consideration of the two-point function can be reduced to the case of a single transverse direction, \(r_{\perp }\). Therefore, it is enough to discuss explicitly either (i) the case of one spatial dimension, referred from now one as the 1D case (then there is no transverse direction), or else (ii) the case of two spatial dimensions, called the 2D case (with a single transverse direction).
The Lie algebra generators of meta-conformal invariance read off from Table 1 as follows. In the 1D case, in terms of time- and space-coordinates [20] (with \(n\in \mathbb {Z}\))
and in the 2D case [28]
with the short-hands \(\partial _{\Vert }=\frac{\partial }{\partial r_{\Vert }}\) and \(\partial _{\perp }=\frac{\partial }{\partial r_{\perp }}\). The constants \(\delta \) and \(\gamma \) (respectively \(\gamma _{\Vert ,\perp }\)) are the scaling dimension and the rapidity of the scaling operators on which these generators act and \(\mu ^{-1}\) is a constant with the dimension of a velocity. Each of the infinite families of generators in (3, 4) produces a Virasoro algebra (with zero central charge). Therefore, the 1D meta-conformal algebra is isomorphic to a direct sum of two Virasoro algebras. In the 2D case, there is an isomorphism with the direct sum of three Virasoro algebras. Their maximal finite-dimensional Lie sub-algebras (isomorphic to a direct sum of two or three \(\mathfrak {sl}(2,\mathbb {R})\) algebras) fix the form of two-point correlators \(C(t,\textit{\textbf{r}}) = \left\langle \varphi _1(t,\textit{\textbf{r}}) \varphi _2(0,\textit{\textbf{0}}) \right\rangle \) built from quasi-primary scaling operators. Since the generators (3, 4) already contain the terms which describe how the scaling operators \(\varphi =\varphi (t,\textit{\textbf{r}})\) transform under their action, the global meta-conformal Ward identities can simply be written down. The requirement of meta-conformal co-variance leads to
and where \(\textit{\textbf{r}}=r\in \mathbb {R}\) for \(d=1\) and \(\textit{\textbf{r}}=(r_{\Vert },r_{\perp })\in \mathbb {R}^2\) for \(d=2\) where we also write \(\gamma := \gamma _{\Vert }-\mathrm{i}\gamma _{\perp }\) and \(\bar{\gamma } :=\gamma _{\Vert }+\mathrm{i}\gamma _{\perp }\). In addition, the constraints \(\delta _1=\delta _2\) and \(\gamma _1=\gamma _2\) in 1D or \(\gamma _{\Vert ,1}=\gamma _{\Vert ,2}\) and \(\gamma _{\perp ,1}=\gamma _{\perp ,2}\) in 2D are implied.
Real part (orange) and imaginary part (blue) of the 1D meta-conformally co-variant two-point function C(t, r), with \(\delta _1=0.22\), \(\gamma _1=0.33\) and \(\mu =1\). Left panel: Spurious singularities arise in (5). Right panel: Regularised form after correction of the spurious singular behaviour.
Formally, the procedure to derive (5) is completely analogous to the used above for the derivation of (2) from ortho-conformal co-variance. The explicit forms (5) make it apparent that \(C_\mathrm{meta}(t,\textit{\textbf{r}})\) is not necessarily bounded for all t or \(\textit{\textbf{r}}\). In Fig. 2, we illustrate this for the 1D case—a spurious singularity appears whenever \({\mu }r=-t\).
In the limit \(\mu \rightarrow 0\), the meta-conformal algebras contract into the galilean conformal algebras [18]. Carrying out the limit on the correlator (4), one obtains, as has been stated countless times in the literature, see e.g. [3,4,5,6, 35]
with the definition \(\varvec{\gamma }=(\gamma _{\Vert },\gamma _{\perp })\). While this correlator decays in one spatial direction (where \(\gamma _1 r>0\) or \(\varvec{\gamma }_1\cdot \textit{\textbf{r}}>0\) and assuming \(t>0\)), it diverges in the opposite direction. In view of the large interest devoted to conformal galilean field-theory, see [1, 6,7,8, 10, 14, 15, 30, 33, 35] and refs. therein, it appears important to be able to formulate well-defined correlators which remain bounded everywhere in time-space. We mention in passing that the 1D form of (6) can also be obtained from 2D ortho-conformal invariance: it is enough to consider complex conformal weights \(\varDelta =\frac{1}{2}\left( \delta -\mathrm{i}\gamma /\mu \right) \) and \(\overline{\varDelta }=\frac{1}{2}\left( \delta +\mathrm{i}\gamma /\mu \right) \). Then (2) can be rewritten as
In what follows, we shall describe how to find correlators bounded everywhere. Since the implicit assumption of holomorphicity in the coordinates gave the unbounded results (5, 6), we shall explore how to derive non-holomorphic correlators. Our treatment follows [25], to be generalised to the case \(d=2\) where necessary.
3 Regularised Meta-conformal Correlator: The 1D Case
Non-holomorphic correlators can only be found by going beyond the local differential operators derived from the meta-conformal Ward identities. We shall do so in a few simple steps [25], restricting for the moment to the 1D case. First, we consider the ‘rapidity’ \(\gamma \) as a new variable. Second, it is dualised [22,23,24] through a Fourier transformation, which gives the quasi-primary scaling operator
This leads to the following representation of the dualised meta-conformal algebra
such that meta-conformal Lie algebra is given by
This form will be more convenient for us than the one used in [25], since the parameter \(\mu \) does no longer appear in the Lie algebra commutators (10). Third, it was suggested [22, 25] to look for a further generator N in the Cartan sub-algebra \(\mathfrak {h}\), viz. \(\mathrm{ad}_N \mathscr {X} = \alpha _\mathscr {X} \mathscr {X}\) for any meta-conformal generator \(\mathscr {X}\). It can be shown that
is the only possibility [25], where the functions \(\kappa (\mu )\) and \(\nu (\mu )\) remain undetermined. Since in this generator, the parameter \(\mu \) is treated as a further variable, we see the usefulness of the chosen normalisation of the generators in (9). On the other hand, the generator of spatial translations now reads \(Y_{-1}=-\mu ^{-1}\partial _r\), with immediate consequences for the form of the two-point correlator. In dual space, the two-point correlator is defined as
Lifting the generators from the representation (9) to two-body operators, the global meta-conformal Ward identities (derived from the maximal finite dimensional sub-algebra isomorphic to \(\mathfrak {sl}(2,\mathbb {C})\oplus \mathfrak {sl}(2,\mathbb {C})\)) become a set of linear partial differential equations of first order for the function \(\widehat{F}\). While the solution will certainly be holomorphic in its variables, the back-transformation according to (8) can introduce non- holomorphic behaviour but will also lead to a correlator bounded everywhere.
The function \(\widehat{F}\) is obtained as follows. First, co-variance under \(X_{-1}\) and \(Y_{-1}\) gives
The action of the generators \(Y_0\) and \(Y_1\) on \(\widehat{F}\) is best described by introducing the new variables \(\eta := \mu _1\zeta _1 + \mu _2 \zeta _2\) and \(\zeta := \mu _1\zeta _1 - \mu _2\zeta _2\). Then the corresponding Ward identities become
Finally, the Ward identities coming from the generators \(X_0\) and \(X_1\) become
The second of these gives the constraint \(\delta _1=\delta _2\). The two remaining equations have the general solution
with an undetermined function \(\widehat{\mathscr {F}}\). Spatial translation-invariance only holds in a more weak form, which could become useful for the description of physical situations where the propagation speed of each scaling operator can be different.
In [25], we tried to use co-variance under the further generator N in order to fix the function \(\widehat{\mathscr {F}}\). However, therein a choice of basis in the meta-conformal Lie algebra was used where the parameter \(\mu \) appears in the structure constants, but it became possible to fix \(\widehat{\mathscr {F}}\) and furthermore to show that \(\widehat{F}\) with respect to the variable \(\eta \) is in the Hardy space \(H_2^+\), see the appendix for the mathematical details. If we want to consider \(\mu \) as a further variable, as it is necessary because of the explicit form of N, objects such as “\(\mu Y_{n+m}\)” are not part of the meta-conformal Lie algebra. Therefore, it is necessary, to use the normalisation (9) which leads to the Lie algebra (10) which is independent of \(\mu \). In order to illustrate the generic consequences, let \(\nu =\nu (\mu )\) and \(\sigma =-\mu \kappa (\mu )\) be constants. The co-variance condition \(N\widehat{F}=0\) gives

where the function  remains undetermined. In contrast to our earlier treatment, we can no longer show that \(\widehat{F}\) had to be in the Hardy space \(H_2^+\). On the other hand, this mathematical property had turned out to be very useful for the derivation of bounded correlators. This motivates the following.
remains undetermined. In contrast to our earlier treatment, we can no longer show that \(\widehat{F}\) had to be in the Hardy space \(H_2^+\). On the other hand, this mathematical property had turned out to be very useful for the derivation of bounded correlators. This motivates the following.
First, we re-write the result (16) as follows (with the constraint \(\delta _1=\delta _2\))
and we also denote \(\widehat{\mathscr {F}}_{\lambda }(\zeta _+) := \widehat{\mathscr {F}}(\zeta _+ +\mathrm{i}\lambda )\). Then, we require:
Postulate
If \(\lambda >0\), then \(\widehat{\mathscr {F}}_{\lambda }\in H_2^+\) and if \(\lambda <0\), then \(\widehat{\mathscr {F}}_{\lambda }\in H_2^-\).
The Hardy spaces \(H_2^{\pm }\) on the upper and lower complex half-planes \(\mathbb {H}_{\pm }\) are defined in the appendix. There, it is also shown that, under mild conditions, that if \(\lambda >0\) and if there exist finite positive constants \(\widehat{\mathscr {F}}^{(0)}\), \(\varepsilon \) such that \(|\widehat{\mathscr {F}}(\zeta _+ +\mathrm{i}\lambda )| <\widehat{\mathscr {F}}^{(0)} e^{-\varepsilon \lambda }\), then \(\widehat{\mathscr {F}}_\lambda \) is indeed in the Hardy space \(H_2^{+}\). Physically, this amounts to a requirement of an algebraic decay with respect to the scaling variable.
The utility of our postulate is easily verified, following [25]. From Theorem 1 of the appendix, especially (A.3), we can write
where the Heaviside functions \(\varTheta (\pm \lambda )\) select the two cases. For \(\lambda >0\), we find
where the definitions (18) were used. Similarly, for \(\lambda <0\) we obtain
Combining these two forms gives our final 1D two-point correlator
up to normalisation. As shown in Fig. 2, this is real-valued and bounded in the entire time-space, although not a holomorphic function of the time-space coordinates.
Finally, it appears that our original motivation for allowing the \(\mu _j\) to become free variables, is not very strong. We might have fixed the \(\mu _j\) from the outset, had not included a factor \(1/\mu \) into the generators \(Y_n\) (such that the spatial translations are generated by \(Y_{-1}=-\partial _r\) and continue immediately with our Postulate. Since a consideration of the meta-conformal three-point function shows that \(\mu _1=\mu _2=\mu _3\) [21, chap. 5], we can then consider \(\mu ^{-1}\) as an universal velocity.Footnote 1
4 Regularised Meta-conformal Correlator: The 2D Case
The derivation of the 2D meta-conformal correlator starts essentially along the same lines as in the 1D case, but is based now on the generators (3). The dualisation is now carried out with respect to the chiral rapidities \(\gamma =\gamma _{\Vert }-\mathrm{i}\gamma _{\perp }\) and \(\bar{\gamma }=\gamma _{\Vert }+\mathrm{i}\gamma _{\perp }\) and we also use the light-cone coordinates \(z=r_{\Vert }+\mathrm{i}r_{\perp }\) and \(\bar{z}=r_{\Vert }-\mathrm{i}r_{\perp }\). Taking the translation generators \(A_{-1}, B_{-1}^{\pm }\) into account, we consider the dual correlator
where we defined the variables
In complete analogy with the 1D case, we further define the variables
such that the correlator \(\widehat{F}=\widehat{F}(\eta ,\bar{\eta },t,\xi ,\bar{\xi },\mu _1,\mu _2)\) obeys the equations
along with the constraint \(\delta _1=\delta _2\). The most general solution of this system is
with the abbreviations (\(\bar{u}\) is obtained from u by replacing \(\zeta _j\mapsto \bar{\zeta }_j\))
and we simplified the notation by letting \(\mu _1=\mu _2=\mu \) and assumed translation-invariance in time and space. As before, we expect that a Hardy space will permit to derive the boundedness, see the appendix for details. We define \(\widehat{\mathscr {F}}_{\lambda }(u,\bar{u}) :=\widehat{\mathscr {F}}(u+\mathrm{i}\lambda ,\bar{u}+\mathrm{i}\lambda )\) and require:
Postulate
If \(\lambda >0\), then \(\widehat{\mathscr {F}}_{\lambda }\in H_2^{++}\) and if \(\lambda <0\), then \(\widehat{\mathscr {F}}_{\lambda }\in H_2^{--}\).
Theorem 2 in the appendix, especially (A.11), then states that
Then, we can write the two-point function in the case \(\lambda >0\), with the short-hand \(\mathscr {D}\zeta := \mathrm {d}\zeta _1\mathrm {d}\bar{\zeta }_1\mathrm {d}\zeta _2\mathrm {d}\bar{\zeta }_2\) and the abbreviations from (28)
Herein, variables were changed according to \(\zeta _1 = \zeta _+ + \zeta _-\) and \(\zeta _2 = \zeta _+-\zeta _-\) and similarly for the \(\bar{\zeta }_j\). The case \(\lambda <0\) is treated in the same manner
In order to understand the meaning of these expression, we return to the physical interpretation of the conditions \(\lambda >0\) and \(\lambda <0\). From (28), the most restrictive case occurs for \(r_{\perp }=0\). Then \(\lambda >0\) is equivalent to \(r_{\Vert }/t>0\). On the other hand, since \(\gamma _1/\mu \) will have a definite sign, it is a fortiori also real. Hence \(\gamma _{1,\perp }=0\) and we can conclude that
up to normalisation, is the final form for the 2D meta-conformally co-variant correlator which is bounded in the entire time-space.
5 Conclusions
It has been shown that via a dualisation procedure of the rapidities in the meta-conformal generators, a refined form of the global Ward identities can be found which leads to expressions of the quasi-primary two-point functions which remain bounded in the entire time-space. Herein, we postulate that the dualised two-point functions, whose dual variables are naturally seen to occur in a tube of the first (or the forth) quadrant, belong to a Hardy space. In this way, we can formulate a sufficient condition for the construction of bounded two-point functions, namely
(up to normalisation) in \(d=1\) spatial dimensions and
in \(d\ge 2\) spatial dimensions, where rotation-invariance in the \(d-1\) transverse directions is assumed (provided \(\varvec{\gamma }_{\perp }=\textit{\textbf{0}}\)).
Notes
- 1.
In the conformal galilean limit \(\mu \rightarrow 0\), recover the bounded result \(F\sim \exp \left( -2 |\gamma _1 r|/t\right) \) [25].
References
Aizawa, N., Kuznetsova, Z., Toppan, F.: Invariant partial differential equations with two-dimensional exotic centrally extended conformal Galilei symmetry. J. Math. Phys. 57, 041701 (2016). arXiv:1512.02290
Akhiezer, N.I.: Lectures on Integral Transforms. American Mathematical Society, Providence (1988)
Bagchi, A., Gopakumar, R.: Galilean conformal algebras and AdS/CFT. JHEP 0907, 037 (2009). arXiv:0902.1385
Bagchi, A., Gopakumar, R., Mandal, I., Miwa, A.: CGA in 2D. JHEP 1008, 004 (2010). arXiv:0912.1090
Bagchi, A., Detournay, S., Fareghbal, R., Simón, J.: Holographies of \(3D\) flat cosmological horizons. Phys. Rev. Lett. 110, 141302 (2013). arxiv:1208.4372
Bagchi, A., Gary, M., Zodinmawia: Bondi-Metzner-Sachs bootstrap. Phys. Rev. D96, 025007 (2017). arxiv:1612:01730
Barnich, G., Compère, G.: Classical central extension for asymptotic symmetries at null infinity in three spacetime dimensions. Class. Quant. Grav. 24 F15 (2007). Corrigendum 24, 3139 (2007). [arxiv:gr-qc/0610130]
Barnich, G., Gomberoff, A., González, H.A.: Three-dimensional Bondi-Metzner-Sachs invariant two-dimensional field-theories as the flat limit of Liouville theory. Phys. Rev. D 87, 124032 (2007). arxiv:1210.0731
Belavin, A.A., Polykaov, A.M., Zamolodchikov, A.B.: Infinite conformal symmetry in two-dimensional quantum field-theory. Nucl. Phys. B 241, 333 (1984)
Bondi, H., van der Burg, M.G.J., Metzner, A.W.K.: Gravitational waves in general relativity. Proc. Roy. Soc. London A 269, 21 (1962)
Cappelli, A., Dunne, G.V., Trugenberger, C.A., Zemba, G.R.: Conformal symmetry and universal properties of quantum Hall states. Nucl. Phys. B 398, 531 (1993). [arXiv:hep-th/9211071]
Cardy, J.L.: Conformal invariance and critical dynamics. J. Phys. A 18, 2271 (1985)
Doyon, B.: Diffusion and superdiffusion from hydrodynamic projection. arxiv:1912.01551
Duval, C., Gibbons, G.W., Horváthy, P.A.: Conformal Carroll groups. J. Phys. A: Math. Theor. 47, 335204 (2014). arXiv:1403.4213
Duval, C., Gibbons, G.W., Horváthy, P.A.: Conformal Carroll groups and BMS symmetry. Class. Quantum Gravity 34, 092001 (2014). arXiv:1402.5894
di Francesco, P., Mathieu, P., Sénéchal, D.: Conformal Field Theory. Springer, Heidelberg (1997)
Hansson, T.H., Hermanns, M., Simon, S.H., Viefers, S.F.: Quantum Hall physics: hierarchies and conformal field-theory techniques. Rev. Mod. Phys. 89, 025005 (2017). arXiv:1601.01697
Havas, P., Plebanski, J.: Conformal extensions of the Galilei group and their relation to the Schrödinger group. J. Math. Phys. 19, 482 (1978)
Henkel, M.: Conformal Invariance and Critical Phenomena. Springer, Heidelberg (1999)
Henkel, M.: Phenomenology of local scale-invariance: from conformal invariance to dynamical scaling. Nucl. Phys. B 641, 405 (2002). [arxiv:hep-th/0205256]
Henkel, M., Pleimling, M.: Non-equilibrium Phase Transitions. Volume 2: Ageing and Dynamical Scaling far from Equilibrium. Springer, Heidelberg (2010)
Henkel, M.: Causality from dynamical symmetry: an example from local scale-invariance. In: Makhlouf, A., et al. (eds.) Algebra, Geometry and Mathematical Physics. Springer Proceedings in Mathematics & Statistics, vol. 85, p. 511 (2014). arxiv:1205.5901
Henkel, M.: Dynamical symmetries and causality in non-equilibrium phase transitions. Symmetry 7, 2108 (2015). arxiv:1509.03669
Henkel, M., Stoimenov, S.: Physical ageing and Lie algebras of local scale-invariance. In: Dobrev, V. (ed.) Lie Theory and its Applications in Physics. Springer Proceedings in Mathematics & Statistics, vol. 111, p. 33 (2015). arxiv:1401.6086
Henkel, M., Stoimenov, S.: Meta-conformal invariance and the boundedness of two-point correlation functions. J. Phys A: Math. Theor. 49, 47LT01 (2016). arxiv:1607.00685
Henkel, M.: Non-local meta-conformal invariance, diffusion-limited erosion and the XXZ chain. Symmetry 9, 2 (2017). arxiv:1611.02975
Henkel, M., Stoimenov, S.: Infinite-dimensional meta-conformal symmetries: \(1D\) diffusion-limited erosion and ballistic transport in (1+2) dimensions. In: Dobrev, V. (ed.) Quantum Theory and Symmetries with Lie Theory and Its Applications in Physics Volume 1. Springer Proceedings in Mathematics and Statistics, vol. 263, p. 113 (2018)
Henkel, M., Stoimenov, S.: Infinite-dimensional meta-conformal Lie algebras in one and two spatial dimensions. J. Stat. Mech. 084009 (2019). arxiv:1810.09855v3
Hille, E.: Ordinary Differential Equations in the Complex Domain. Wiley, New York (1976); Dover, New York (1997)
Hosseiny, A., Rouhani, S.: Affine extension of galilean conformal algebra in \(2+1\) dimensions. J. Math. Phys. 51, 052307 (2016). arXiv:0909.1203
Karevski, D., Schütz, G.M.: Conformal invariance in driven diffusive systems at high currents. Phys. Rev. Lett. 118, 030601 (2017). arXiv:1606.04248
Koosis, P.: Introduction to \(H_p\) Spaces, 2nd edn. Cambridge University Press, Cambridge (1998)
Krivonos, S., Lechtenfeld, O., Sorin, A.: Minimal realization of \(\ell \)-conformal Galilei algebra, Pais-Uhlenbeck oscillators and their deformation. JHEP 1610, 073 (2016). arxiv:1607.03756
Krug, J., Meakin, P.: Kinetic roughening of laplacian fronts. Phys. Rev. Lett. 66, 703 (1991)
Martelli, D., Tachikawa, Y.: Comments on Galilean conformal field theories and their geometric realization. JHEP 1005, 091 (2010). arXiv:0903.5184
Polchinski, J.: String Theory, vol. 2. Cambridge University Press, Cambridge (2001)
Popkov, V., Schadschneider, A., Schmidt, J., Schütz, G.M.: Fibonacci family of dynamical universality classes. Proc. Nat. Acad. Sci. 112, 12645 (2019). arxiv:1505.04461
Schütz, G.M.: Conformal invariance in conditioned stochastic particle systems. J. Phys. A 50, 314002 (2017)
Spohn, H.: Bosonization, vicinal surfaces, and hydrodynamic fluctuation theory. Phys. Rev. E60, 6411 (1999). arxiv:cond-mat/9908381
Stein, E.M., Weiss, G.: Fourier Analysis in Euclidean Spaces. Princeton University Press, Princeton (1971)
Stoimenov, S., Henkel, M.: From conformal invariance towards dynamical symmetries of the collisionless Boltzmann equation. Symmetry 7, 1595 (2015). arxiv:1509.00434
Stoimenov, S., Henkel, M.: Construction of meta-conformal algebras in \(d\) spatial dimensions. In: AIP Conference Proceedings, vol. 2075, p. 090026 (2019)
Stoimenov, S., Henkel, M.: Meta-conformal invariance in the directed Glauber-Ising chain. In: Dobrev, V. (ed.) Lie Theory and its Applications in Physics, vol. 335, pp. 463–471. Springer, Singapore (2020). https://doi.org/10.1007/978-981-15-7775-8_37
Täuber, U.C.: Critical Dynamics. Cambridge University Press, Cambridge (2014)
Acknowledgements
Most of this work was done during the visits of S.S. at Université de Lorraine Nancy and of M.H. at the workshop “Lie theories and its applications in physics LT13”. These visits were supported by PHC Rila. M.H. thanks the MPIPKS Dresden for warm hospitality, where other parts of this work were done.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix. Background on Hardy Spaces
Appendix. Background on Hardy Spaces
In the main text, we need precise statements on the Fourier transform on semi-infinite spaces. These can be conveniently formulated in terms of Hardy spaces. Here, we restrict to the special case \(H_2\). Our brief summary is based on [2, 40].
We begin with the case of functions of a single complex variable z, defined in the upper half-plane \(\mathbb {H}_+ := \left\{ z\in \mathbb {C}\left| z=x+\mathrm{i}y, y\ge 0\right. \right\} \).
Definition 1:
A function \(f:\mathbb {H}_+\rightarrow \mathbb {C}\) belongs to the Hardy space \(H_2^+\) if it is holomorphic on \(\mathbb {H}_+\) and if
The main results of interest to us can be summarised as follows.
Theorem 1
[2]: Let \(f:\mathbb {H}_+\rightarrow \mathbb {C}\) be a holomorphic function. Then the following statements are equivalent:
-
1.
\(f\in H_2^+\)
-
2.
there exists a function
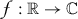 , which is square-integrable
, which is square-integrable 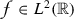 , such that
, such that 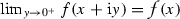 and
and 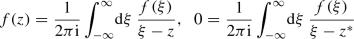 (A.2)
(A.2)where \(z^*=x-\mathrm{i}y\) denotes the complex conjugate of z. For notational simplicity, one often writes \(f(x) = \lim _{y\rightarrow 0^+} f(x+\mathrm{i}y)\), with \(x\in \mathbb {R}\).
-
3.
there exists a function \(\widehat{f}:\mathbb {R}_+\rightarrow \mathbb {C}\), \(\widehat{f}\in L^2( \mathbb {R}_+)\), such that for all \(y>0\)
$$\begin{aligned} f(z) = f(x+\mathrm{i}y) = \frac{1}{\sqrt{2\pi \,}\,} \int _0^{\infty } \!\mathrm {d}\zeta \, e^{\mathrm{i}(x+\mathrm{i}y) \zeta } \widehat{f}(\zeta ) \end{aligned}$$(A.3)
The property (A.3) is of major interest to us in the main text.
If \(f\in H_2^+\), one has the following bounds [2]
Equation (A.4a) follows from the bound (in turn obtained from (A.3)), see also [32]
which holds for all \(x\in \mathbb {R}\) and where the constant \(f_{\infty }>0\) depends on the function f. There is a simple sufficient criterion which can be used to establish that a given function f is in the Hardy space \(H_2^+\):
Lemma:
If the complex function \(f(z)=f(x+\mathrm{i}y)\) is holomorphic for all \(y\ge 0\), obeys the bound \(|f(z)| < f_0 e^{-\delta y}\), with the constants \(f_0>0\) and \(\delta >0\) and if \(\int _{-\infty }^{\infty } \!\mathrm {d}x\, |f(x)|^2< \infty \), then \(f\in H_2^+\).
Proof:
Since f(z) is holomorphic on the closure \(\overline{\mathbb {H}_+}\) (which includes the real axis), one has the Cauchy formula
where the integration contour \(\mathscr {C}\) consists of the segment \([-R,R]\) on the real axis and the superior semi-circle \(\mathscr {C}_\mathrm{sup}\). One may write \(w=u+\mathrm{i}v = R e^{\mathrm{i}\theta }\in \mathscr {C}_\mathrm{sup}\). It follows that on the superior semi-circle \(|f(w)| < f_0 e^{-\delta v} = f_0 e^{-\delta R \sin \theta }\). Now, for R large enough, one has \(|w-z|= | w(1-z/w)| \ge R \frac{1}{2}\), for \(z\in \overline{\mathbb {H}_+}\) fixed and \(w\in \mathscr {C}_\mathrm{sup}\). We can then estimate the contribution \(F_2(z)\) of the superior semi-circle
Hence, the integral representation \(f(z) = \frac{1}{2\pi \mathrm{i}}\int _{\mathbb {R}} \!\mathrm {d}w\, f(w) (w-z)^{-1}\) holds for \(R\rightarrow \infty \). Since \(f\in L^2(\mathbb {R})\), the assertion follows from Eq. (A.2) of Theorem 1. q.e.d.
Clearly, one may also define a Hardy space \(H_2^-\) for functions holomorphic on the lower complex half-plane \(\mathbb {H}_-\), by adapting the above definition. All results transpose in an evident way.
Further conceptual preparations are necessary for the generalisation of these results to higher dimensions. Here, we shall merely treat the 2D case, which is enough for our purposes (and generalisations to \(n>2\) will be obvious). We denote \(\textit{\textbf{z}}=(z_1,z_2)\in \mathbb {C}^2\) and write the scalar product \(\textit{\textbf{z}}\cdot \textit{\textbf{w}}=z_1 w_1 + z_2 w_2\) for \(\textit{\textbf{z}},\textit{\textbf{w}}\in \mathbb {C}^2\). Following [40], \(H_2\)-spaces can be defined as follows.
Definition 2:
If \(B\subset \mathbb {R}^2\) is an open set, the tube \(T_B\) with base B is
A function \(f: T_B\rightarrow \mathbb {C}\) which is holomorphic on \(T_B\) is in the Hardy space \(H_2(T_B)\) if
However, it turns out that this definition is too general. More interesting results are obtained if one uses cônes as a base of the tubes.
Definition 3:
(i) An open cône \(\varGamma \subset \mathbb {R}^n\) satisfies the properties \(0\not \in \varGamma \) and if \(\textit{\textbf{x}},\textit{\textbf{y}}\in \varGamma \) and \(\alpha ,\beta >0\), then \(\alpha \textit{\textbf{x}}+\beta \textit{\textbf{y}}\in \varGamma \). A closed cône is the closure \(\overline{\varGamma }\) of an open cône \(\varGamma \). (ii) If \(\varGamma \) is a cône, and if the set
has a non-vanishing interior, then \(\varGamma ^*\) is the dual cone with respect to \(\varGamma \). The cône \(\varGamma \) is called self-dual, if \(\varGamma ^* = \overline{\varGamma }\).
For illustration, note that in one dimension (\(n=1\)) the only cône is \(\varGamma =\left\{ x\in \mathbb {R}\left| x>0\right. \right\} = \mathbb {R}_+\). It is self-dual, since \(\varGamma ^*=\overline{\varGamma }=\mathbb {R}_{0,+}\). In two dimensions (\(n=2\)), consider the cône \(\varGamma ^{++}:= \left\{ \textit{\textbf{x}}\in \mathbb {R}^2\left| \textit{\textbf{x}}=(x_1,x_2) ~\mathrm{with}~ x_1>0, x_2>0\right. \right\} \) which is the first quadrant in the 2D plane. Since
the set \(\varGamma ^{++}\) is a self-dual cône.
Hardy spaces defined on the tube \(T_{\varGamma ^{++}}\) of the first quadrant provide the structure required here.
Definition 4
[40]: If \(\varGamma ^{++}\) denotes the first quadrant of the plane \(\mathbb {R}^2\), a function \(f: T_{\varGamma ^{++}}\rightarrow \mathbb {C}\) holomorphic on \(T_{\varGamma ^{++}}\) is in the Hardy space \(H_2^{++} :=H_2(T_{\varGamma ^{++}})\) if
Theorem 2
[40]: Let the function \(f:T_{\varGamma ^{++}}\rightarrow \mathbb {C}\) be holomorphic. Then the following statements are equivalent:
-
1.
\(f\in H_2^{++}\)
-
2.
there exists a function
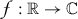 , which is square-integrable
, which is square-integrable 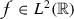 , such that
, such that 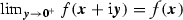 and
and 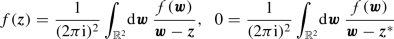 (A.10)
(A.10)where \((\textit{\textbf{w}}-\textit{\textbf{z}})^{-1} := (w_1-z_1)^{-1} (w_2-z_2)^{-1}\) and \(\textit{\textbf{z}}^*=\textit{\textbf{x}}-\mathrm{i}\textit{\textbf{y}}\) denotes the complex conjugate of \(\textit{\textbf{z}}\). For notational simplicity, one often writes \(f(\textit{\textbf{x}}) = \lim _{\textit{\textbf{y}}\rightarrow \textit{\textbf{0}}^+} f(\textit{\textbf{x}}+\mathrm{i}\textit{\textbf{y}})\), with \(\textit{\textbf{x}}\in \mathbb {R}^2\).
-
3.
there exists a function \(\widehat{f}:\mathbb {R}_+\oplus \mathbb {R}_+\rightarrow \mathbb {C}\), with \(\widehat{f}\in L^2( \mathbb {R}_+\oplus \mathbb {R}_+)\) and \(z_i\in \mathbb {H}_+\)
$$\begin{aligned} f(\textit{\textbf{z}}) = \frac{1}{2\pi } \int _{\varGamma ^{++}} \!\mathrm {d}\textit{\textbf{t}}\, e^{\mathrm{i}\textit{\textbf{z}}\cdot \textit{\textbf{t}}} \widehat{f}(\textit{\textbf{t}}) = \frac{1}{2\pi } \int _0^{\infty } \!\mathrm {d}t_1 \int _0^{\infty } \!\mathrm {d}t_2\, e^{\mathrm{i}(z_1 t_1 + z_2 t_2)} \widehat{f}(\textit{\textbf{t}}) \end{aligned}$$(A.11)
The property (A.11) is of major interest to us in the main text. Summarising, the restriction to the first quadrant \(\varGamma ^{++}\) allows to carry over the known results from the 1D case, separately for each component.
Of course, one may also define a Hardy space \(H_2^{--} :=H_2(T_{\varGamma ^{--}})\) on the forth quadrant, in complete analogy.
Rights and permissions
Copyright information
© 2020 Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Henkel, M., Stoimenov, S. (2020). Meta-conformal Invariance and Their Covariant Correlation Functions. In: Dobrev, V. (eds) Lie Theory and Its Applications in Physics. LT 2019. Springer Proceedings in Mathematics & Statistics, vol 335. Springer, Singapore. https://doi.org/10.1007/978-981-15-7775-8_5
Download citation
DOI: https://doi.org/10.1007/978-981-15-7775-8_5
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-15-7774-1
Online ISBN: 978-981-15-7775-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





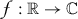 , which is square-integrable
, which is square-integrable 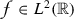 , such that
, such that 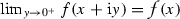 and
and 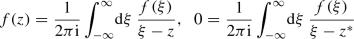
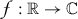 , which is square-integrable
, which is square-integrable 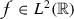 , such that
, such that 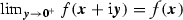 and
and