Effect of Non-uniform Heating on Electroosmotic Flow Through Microchannel

Abstract

The effect of non-uniform heating on the heat transfer characteristics for electroosmotic flow through a microchannel has been investigated numerically. The temperature field and Nusselt number are studied by changing the normalized wavelength of non-uniform heat flux $\left( \gamma \right)$ and thermal Peclet number $\left( {\text{Pe}} \right)$ in the range of $1.5 \le \gamma \le 6$ and $1 \le {\text{Pe}} \le 100$, respectively. It is found that the intensity of maximum temperature reduces for non-uniform heating as compared to the uniform heating. The maxima of local Nusselt number increases with a decrease in the wavelength of the non-uniform heat flux. The critical Peclet number $\left( {{\text{Pe}}_{\text{c}} } \right)$ is found such that average Nusselt number shows the monotonic and non-monotonic variation with $\gamma$.

1 Introduction

Electroosmotic flow (EOF) has several advantages over the pressure-driven flow (PDF) in the microchannel. The micro-electro-mechanical systems (MEMS) gain more importance in recent years and these types of devices are used in many biochemical and biomedical industries. For the micro-level flow, interfacial interaction is important as the surface to volume ratio is high. Therefore, the mechanical pump may fail for such systems. To overcome these problems, electroosmotic flow is the best solution option for such transport [1, 2]. The thermal transport characteristics for EOF through microchannel have got immense interest from research community in the past few years. Dey et al. [3] investigated the effect of steric effect on heat transfer characteristics for EOF through a  microchannel and found that the steric factor alters the results drastically when the zeta potential is very high as compared to point charge assumption. For many applications of micro-level-flow in heat sinks like CPUs and ICs, the discrete heat generation occurs due to the micro-arrangement of electronics components [4,5,6]. Azari et al. [7] investigated the distributed wall heat flux on the heat transfer characteristic for combined EOF and PDF in micro-slit. It is found that the Nusselt number decreases with EDL thickness and PDF velocity for any wall heat flux distribution. Pati et al. [8] used different heat flux profiles to identify the optimal heating strategy for minimization of peak temperature and entropy generation for forced convective flow through a circular pipe. From the available work in literature, it is found that the effect of non-uniform heating for EOF needs to be explained in detail, as the effects of wavelength or undulation of hot spots are not investigated till now. Hence, the objective of this work is to investigate the effect of wavelength of non-uniform heating on the temperature field and heat transfer characteristics for EOF through a microchannel.

2 Theoretical Formulation

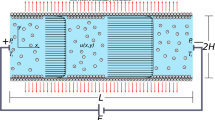
The EOF of a Newtonian fluid through a microchannel is considered. The non-uniform heat flux $q\left( x \right) = 0.5q_{o} \left[ {1 + \sin \left( {{{2\pi x} \mathord{\left/ {\vphantom {{2\pi x} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }} \right)} \right]$ is imposed at the walls [5] as shown in Fig. 1. The applied  electric field strength is $E$. It is assumed that the flow is steady, laminar, hydrodynamically fully developed, and incompressible and thermo-physical properties are temperature independent. The charge is considered as a point, as well as, zeta potential is assumed to be uniform at the wall for the entire length. The convective term is neglected in the momentum equation as the Reynolds number is very small. The viscous dissipation term is also neglected for the energy equation. Under these assumptions, for single valance ions (e.g. KCl, NaCl, etc.), transport equation can be written as [3, 7]:

Fig. 1

Physical domain

$$\frac{{{\text{d}}^{2} \psi }}{{{\text{d}}Y^{2} }} = \kappa^{2} \sinh \left( \psi \right)$$

(1)

$$0 = - \frac{{\partial^{2} U}}{{\partial Y^{2} }} + \frac{{\kappa^{2} }}{\zeta }\sinh \left( \psi \right)$$

(2)

$${\text{Pe}}\,U\frac{\partial \theta }{{\partial X}} = \frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }} + G$$

(3)

Equations (1) to (3) represent the Poisson-Boltzmann equation for EDL potential, momentum equation, and energy equation, respectively. Here, $\psi ,\;U\;{\text{and}} \;\;\theta$ are normalized EDL potential, flow velocity, and dimensionless temperature, respectively, $X\;{\text{and}} \;Y$ are the dimensionless axial and transverse co-ordinate normalized with $H$. The other normalized parameters are: $\psi = {{\psi^{*} } \mathord{\left/ {\vphantom {{\psi^{*} } {\zeta_{{{\text{ref}}}} }}} \right. \kern-\nulldelimiterspace} {\zeta_{{{\text{ref}}}} }}$, $U = {u \mathord{\left/ {\vphantom {u {u_{HS} }}} \right. \kern-\nulldelimiterspace} {u_{HS} }}$, $\theta = {{\left( {T - T_{{{\text{in}}}} } \right)k} \mathord{\left/ {\vphantom {{\left( {T - T_{{{\text{in}}}} } \right)k} {q_{o} H}}} \right. \kern-\nulldelimiterspace} {q_{o} H}}$, Peclet number is ${\text{Pe}} = {{u_{HS} H} \mathord{\left/ {\vphantom {{u_{HS} H} {\left( {{k \mathord{\left/ {\vphantom {k {\rho c_{p} }}} \right. \kern-\nulldelimiterspace} {\rho c_{p} }}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{k \mathord{\left/ {\vphantom {k {\rho c_{p} }}} \right. \kern-\nulldelimiterspace} {\rho c_{p} }}} \right)}}$, Joule heating term is $G = {{HE^{2} } \mathord{\left/ {\vphantom {{HE^{2} } {q{}_{o}\sigma }}} \right. \kern-\nulldelimiterspace} {q{}_{o}\sigma }}$. Reference velocity is $u_{HS} \left( { = {{ - \varepsilon \varepsilon_{o} E\xi_{{{\text{ref}}}} } \mathord{\left/ {\vphantom {{ - \varepsilon \varepsilon_{o} E\xi_{{{\text{ref}}}} } \mu }} \right. \kern-\nulldelimiterspace} \mu }} \right)$, $\zeta_{{{\text{ref}}}}$ is the reference zeta potential, dimensionless Debye parameter is $\kappa = H\left( {{{2n_{o} z^{2} e^{2} } \mathord{\left/ {\vphantom {{2n_{o} z^{2} e^{2} } {\varepsilon \varepsilon_{o} }}} \right. \kern-\nulldelimiterspace} {\varepsilon \varepsilon_{o} }}k_{B} T} \right)^{0.5}$. Note that $\mu ,\,\rho ,\;c_{p} ,\;k,\;\sigma ,\;k_{B} ,\;z,e\;{\text{and}} \;\varepsilon_{o}$ are the dynamic viscosity, density, specific heat capacity, thermal conductivity, electric conductivity, Boltzmann constant, valency, the charge on single electron and permittivity of the free space, respectively.

To solve the above transport equations, the imposed boundary conditions are the following [7]:

At inlet

$$\frac{{{\text{d}}\psi }}{{{\text{d}}X}} = 0,\;\;\frac{\partial U}{{\partial X}} = 0,\;\theta = 0$$

(4)

At wall $\left( {Y = 1} \right)$:

$$\psi = \zeta ,\;U = 0,\;\frac{\partial \theta }{{\partial Y}} = 0.5\left( {1 + \sin \left( {{{2\pi X} \mathord{\left/ {\vphantom {{2\pi X} \gamma }} \right. \kern-\nulldelimiterspace} \gamma }} \right)} \right)$$

(5)

At outlet:

$$\frac{{{\text{d}}\psi }}{{{\text{d}}X}} = 0,\;P_{G} = 0,\;\;\frac{\partial \theta }{{\partial X}} = 0$$

(6)

At centerline $\left( {Y = 0} \right)$:

$$\frac{{{\text{d}}\psi }}{{{\text{d}}Y}} = 0,\;\frac{{{\text{d}}U}}{{{\text{d}}Y}} = 0,\;\frac{\partial \theta }{{\partial Y}} = 0$$

(7)

where $P_{G}$ is the gauge pressure. The heat transfer rate can be calculated in terms of the local Nusselt number $\left( {Nu} \right)$. Mathematically, it can be represented as: ${\text{Nu}} = {{hH} \mathord{\left/ {\vphantom {{hH} k}} \right. \kern-\nulldelimiterspace} k}$. Here, $h$ is the heat transfer coefficient and given by $h = q{{\left( x \right)} \mathord{\left/ {\vphantom {{\left( x \right)} {\left( {T_{{\text{W}}} - T_{{\text{m}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {T_{{\text{W}}} - T_{{\text{m}}} } \right)}}$ [4, 7], where $T_{{\text{W}}}$ and $T_{{\text{m}}}$ is the wall and bulk mean temperature, respectively. Hence, local Nusselt number can be expressed as: ${\text{Nu}} = {{\left[ {0.5\left( {1 + \sin \left( {{{2\pi X} \mathord{\left/ {\vphantom {{2\pi X} \gamma }} \right. \kern-\nulldelimiterspace} \gamma }} \right)} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {0.5\left( {1 + \sin \left( {{{2\pi X} \mathord{\left/ {\vphantom {{2\pi X} \gamma }} \right. \kern-\nulldelimiterspace} \gamma }} \right)} \right)} \right]} {\left( {\theta_{{\text{W}}} - \theta_{{\text{m}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\theta_{{\text{W}}} - \theta_{{\text{m}}} } \right)}}$. The normalized bulk mean temperature can be represented as: $\theta_{{\text{m}}} = {{\int_{0}^{1} {\theta U{\text{d}}Y} } \mathord{\left/ {\vphantom {{\int_{0}^{1} {\theta U{\text{d}}Y} } {\int_{0}^{1} {U{\text{d}}Y} }}} \right. \kern-\nulldelimiterspace} {\int_{0}^{1} {U{\text{d}}Y} }}$.

3 Numerical Method and Validation

The finite element method is used to solve the governing transport equations. The domain under consideration is divided into smaller subdomains of triangular geometry of non-uniform size. These subdomains are known as elements. The flow variables are approximated by using proper interpolation functions within each subdomains. Thus, the governing equations are converted into closed-form, which are then solved using iterative techniques. The relative convergence criterion for the residuals of all the transport variables is set to $10^{ - 6}$. The details of the numerical procedure can be seen in [9, 10]. The grid independency has been done for the present study and the maximum difference in calculating Nusselt number for the selected mesh is less than 0.1% as compared to very fine mesh. For the selected fine mesh, number of nodes and elements are 35,500 and 68,614, respectively. Before presenting the findings of the current investigation, we first ascertain the accuracy of the numerical scheme used to stimulate the results. For validation purpose, we consider electroosmotic flow through a square microchannel similar to the work of Hsieh et al. [11]. They have conducted an experimental study on the velocity distribution of EOF using micro-particle velocimetry. Figure 2 depicts the comparison of velocity distribution for the present study and by Hsieh et al. [11]. The comparison is shown for electroosmotic flow of TAE buffer for 1000 and 5000 V/m intensity of electric field, zeta potential is $- 42.24\,{\text{mV}}$ and dielectric constant 77.232. The comparison shows a good match with the available results [11]. Hence, the present model is accepted for the numerical simulation.

Fig. 2

Validation for velocity profile along the transverse direction of the rectangular microchannel with the experimental results of Hsieh et al. [11] for TAE buffer at E = 5000 V/m and 1000 V/m, zeta potential is $- 42.24\,{\text{mV}}$ and dielectric constant 77.232

4 Results and Discussions

The effect of non-uniform heating on the temperature field and heat transfer characteristics for EOF through a microchannel has been investigated by changing the normalized wavelength of non-uniform heat flux $\left( \gamma \right)$ and thermal Peclet number $\left( {\text{Pe}} \right)$ in the range $1.5 \le \gamma \le 6$ and $1 \le {\text{Pe}} \le 100$, respectively [2, 4, 7]. The values of other parameters are taken as: $\zeta = - 2,\;G = 1,\;E = 10{,}000{\text{V}} /\text{m}\;{\text{and}} \;\kappa = 20$ [4, 12].

To study the effect of non-uniform heating on the temperature field for EOF, isotherms contours are presented in Fig. 3 at different $\gamma \left( { = 1.5\;{\text{and}} \;6} \right)$ and uniform heating case at Pe = 10. It can be seen that the uniform heating case causes higher temperature intensity as compared to the non-uniform heating cases. It can be also noted that in transverse direction temperature distribution is more uniform in total length for the non-uniform heating case for smaller wavelength $\gamma = 1.5$, and this uniformity is smaller at higher wavelength $\gamma = 6$ as compared to uniform heating case. It can be explained as the heating load in given length is distributed for smaller $\gamma$, whereas at higher $\gamma$ it is concentrated. Thus for smaller $\gamma$ gives more uniform transverse temperature distribution.

Fig. 3

Isotherm contours for non-uniform case with $\gamma = 1.5\;{\text{and}} \;6$, and uniform heating at Pe = 10

The variation of wall temperature $\left( {\theta_{{\text{W}}} } \right)$ and bulk mean temperature $\left( {\theta_{{\text{m}}} } \right)$ along the channel length is presented in Fig. 4 for non-uniform heating at $\gamma = 1.5\;{\text{and}} \;6$, and uniform heating case at Pe = 100. It can be seen that wall temperature for smaller $\gamma \left( { = 1.5} \right)$ is more uniform as the line of local maxima is inside the corresponding limit at $\gamma = 6$. It is because of the higher uniformity of temperature due to the higher undulation as discussed. On the other hand, the effect of $\gamma$ on $\theta_{{\text{m}}}$ is minimal. Although, the higher $\theta_{{\text{m}}}$ is found at the position of maximum heat flux undulation for $\gamma = 6$ due to the highly concentrated heat flux as compared to smaller $\gamma$ in given length. The uniform heating shows small difference in variation of wall temperature $\left( {\theta_{{\text{W}}} } \right)$ and bulk mean temperature $\left( {\theta_{{\text{m}}} } \right)$ near to inlet and gradually tends to a constant value in the downstream direction.

Fig. 4

Variation of bulk mean and surface temperature for $\gamma = 1.5\;$, $\gamma = 6\;$ and uniform heating for Pe = 100

Variation of local heat transfer enhancement in terms of local Nusselt number (Nu) is presented in Fig. 5 for the uniform and non-uniform cases at different thermal Peclet number. Figure 5a depicts the variation of ${\text{Nu}}$ at Pe = 1. It can be noted that the local minima and maxima of ${\text{Nu}}$ are induced for the non-uniform heating case as reported in [13]. The minima of Nu for all $\gamma$ is zero due to the zero flux at that position, whereas maxima of Nu increases with decrease in $\gamma$. It can be noted that all maxima of Nu for non-uniform heating case is higher than the uniform heating case. The increase in Nu with the decrease in $\gamma$ can be explained by the fact of decrease in difference of wall and mean temperature with the decrease in $\gamma$ at that maxima heat flux position. (See Fig. 4). Whereas, for uniform heating case, the higher wall temperature creates higher difference in bulk mean and wall temperature, thereby reducing Nu. Similar effect has been observed for Pe = 10, only difference is that the similar undulation of ${\text{Nu}}$ for uniform and non-uniform case, respectively has reached relatively far from the inlet as shown in Fig. 5b. For Pe = 100, the developed region of Nu increases far towards the downstream. It is because of the increase in Pe allows relatively higher advection strength, as compared to the conductive or diffusive strength. It can be noted that for the downstream region of Nu for Pe = 1 and 10, maxima of Nu increases with Pe for all $\gamma$. It is because of the decrease in the difference of wall and mean temperature with Pe. It can be also noted that with increase in Pe, the rate of decrease in maxima of Nu with $\gamma$ decreases. It can be explained by analying the rate of decrease in the difference of the bulk mean temperature and wall temperature at the corresponding location with increase in Pe. It is important to mention that the peak of Nu for higher wavelength $\left( {\gamma = 6} \right)$ is more flat, whereas, increasing Pe corresponding peak becomes sharper. This can be explained by the difference between wall and bulk-mean temperature at lower and higher Pe. At lower Pe, for higher wavelength $(\gamma = 6)$ $\left( {\theta_{{\text{w}}} - \theta_{{\text{m}}} } \right)$ approaches near to zero at the maxima of heat flux position, whereas for higher values of Pe, the value of $\left( {\theta_{{\text{w}}} - \theta_{{\text{m}}} } \right)$ is relatively higher at the maxima heat flux position. This variation affects the average Nusselt number variation with Pe.

Fig. 5

Variation of local Nusselt number for uniform and non-uniform heating case with different normalized wavelength of heat flux at a Pe = 1, b Pe = 10 and c Pe = 100

The variation of average Nusselt number $\left( {\overline{{{\text{Nu}}}} } \right)$ with Peclet number is shown in Fig. 6 for uniform and non-uniform heating case for different $\gamma$. The value of $\overline{{{\text{Nu}}}}$ is always higher for the uniform heating case because of the minima of Nu for non-uniform heating approaches to zero, and $\overline{{{\text{Nu}}}}$ for both the cases increase with Pe. Form the figure it can be seen that the two regimes of Pe are found such that beyond the critical limit $\left( {{\text{Pe}}_{{\text{c}}} } \right)$, [regime 2], $\overline{{{\text{Nu}}}}$ shows the monotonic trend with $\gamma$ and increases with the decrease in $\gamma$. For ${\text{Pe}} < {\text{Pe}}_{\text{c}}$ [regime 1], the non-monotonic behavior of $\overline{{{\text{Nu}}}}$ can be explained by the fact of occurrence of more flat peak of Nu for higher $\gamma \left( { = 6} \right)$ at smaller Pe as discussed above. On the other hand, the decrease in $\gamma$ results in smaller effect of flatness on the peak of Nu, as reduced wavelength itself increases its sharpness. Therefore, for ${\text{Pe}} < {\text{Pe}}_{\text{c}}$ $\overline{{{\text{Nu}}}}$ is higher for $\gamma = 1.5$ and smaller for $\gamma = 3$. For the present study the value of ${\text{Pe}}_{\text{c}}$ is 11.5.

Fig. 6

Variation of average Nusselt number with Pe for uniform and non-uniform heating case with different normalized wavelength ($\gamma = 1.5,3,6$) of heat flux

5 Conclusions

The heat transfer for EOF through a microchannel has been investigated numerically under the effect of non-uniform heating. The temperature field and Nusselt number have been studied by varying the wavelength of non-uniform heat flux $\left( \gamma \right)$ and thermal Peclet number $\left( {Pe} \right)$. The important findings from the present work are summarized as follows:

• The hot spot intensity in the domain decreases for the non-uniform heating as compared to the uniform heating case. The uniformity of temperature profile increases with a decrease in wavelength of the non-uniform heat flux.

• The maximum intensity of the wall temperature increases with an increase in wavelength of non-uniform heat flux.

• The maxima of local Nusselt number increases with a decrease in wavelength of non-uniform heat flux. The rate of decrement in local Nusselt number with the wavelength of non-uniform heat flux increases with an increase in thermal Peclet number.

• The average  Nusselt number $\left( {\overline{{{\text{Nu}}}} } \right)$ for uniform heating case is always higher as compared to the non-uniform heating case. The critical value of Peclet number $\left( {\text{Pe}_{\text{c}} } \right)$ is found such that for ${{\text{Pe}}} < \text{Pe}_{\text{c}}$, the value of $\overline{{{\text{Nu}}}}$ shows the non-monotonic variation with non-uniform heat flux wavelength and opposite effect for ${\text{Pe}} > \text{Pe}_{\text{c}}$. For the present study the value of ${\text{Pe}}_{\text{c}}$ is 11.5.