Keywords

1 Introduction

Cognitive radio is one of the most promising techniques for the efficient utilization of the available radio frequency spectrum. According to the FCC report [1], a large portion of radio frequency (RF) spectrum remains under-utilized. Motivated by it, the concept of cognitive radio (CR) was first proposed in [2] as a possible solution to the under-utilization of the limited RF spectrum. CR exploits the under-utilized frequency bands by identifying spectrum holes. Spectrum sensing is one of the most important functions of CR system where unlicensed user or secondary user (SU) at the CR terminal continuously monitors the spectrum to detect the presence or absence of licensed user or primary user [2]. Most spectrum sensing algorithms such as energy detection (ED) and improved energy detection (IED) [3], the eigenvalue based spectrum sensing [4], the goodness-of-fit based spectrum sensing [5] assumes Gaussian noise (AWGN) into consideration. In real scenarios, the noise may be non-Gaussian. Possible impairments which result in non-Gaussian background noise include artificial impulsive noise, co-channel interference from other PUs, emission from microwave ovens etc. [6]. Further, the previously mentioned detection schemes degrade heavily in non-Gaussian noise.

It has been shown in [6, 7] that Gaussian mixture model, Middleton class A noise model, and Laplace distribution (Laplacian noise) are used for approximately characterizing the statistics of multiple access interference (MAI) in TH-UWB communication system. It has been shown that Laplacian noise accurately model MAI than other noise models [7]. Motivated by it, Laplacian noise has been addressed by advanced test-statistics such as suprathreshold stochastic resonance (SSR) [8], polarity coincidence array (PCA) [9], non-linear function Kernel function [10], soft limiting PCA (SL-PCA) [11], AVCD [12], i-AVCD [13] among others. AVCD is based on fixed fractional lower order statistics (FLOS) while i-AVCD is based on a flexible FLOS strategy with exponent p ranging from 0 to 2 [13].

In this paper, i-AVCD based on the CSS scheme is proposed as a test statistic to improve the detection performance in additive Laplacian noise. Performance of CSS is shown for AND, OR, and majority \((n/K)\) rule. Optimum value of \(p\) for all three CSS schemes (AND, OR, majority rule) is derived using simulations. Optimum number of CRs out of a specified number of CRs is also expressed analytically. Performance of CSS schemes for AVCD, i-AVCD, SL-PCA, SSR is compared and it is shown here that by choosing optimum p for CSS based i-AVCD test-statistics, performance can be improved greatly in case of CSS-OR rule but the same is not necessarily true in case of AND (CSS-AND) rule and majority (CSS-n/K) rule.

2 System Model

Let y = [\(y_{1} ,y_{2} , \ldots ,y_{N}\)] be a vector of N observations of a PU received at the cognitive terminal where \(N \ge 1\). It is assumed that all the received observations are real, independent, and identically distributed (i.i.d.). Each received observations \(y_{i}\) can be represented as

$$\begin{aligned} & H_{0} :\,y_{i} = w_{i} \\ & H_{1} :\,y_{i} = \sqrt \gamma hx_{i} + w_{i} , \\ \end{aligned}$$
(1)

where h is the channel coefficient and it is assumed to be constant (h = 1), i = 1, 2, …, N, γ denotes the average signal-to-noise ratio (SNR), ni is Laplacian noise which follows Laplace distribution with mean 0 and variance 2b2 i.e., wi ~ L(0, b), b is the scale parameter of Laplace distribution, xi is BPSK PU signal, i.e., \(x_{i} \in \left\{ { - 1,1} \right\}\) p is the exponent (power) of received samples at the cognitive terminal (SU).

2.1 Decision Statistics

i-AVCD based decision rule can be expressed as

$$Z = \sum\limits_{i = 1}^{N} {\left| {y_{i} } \right|}^{p} .$$
(2)

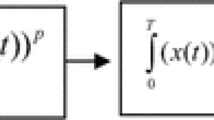
Decision statistics of i-AVCD can be expressed as

$$\begin{aligned} & H_{0} :\,Z < \lambda ,{\text{ PU}}\,{\text{absent,}} \\ & H_{1} :\,Z \ge \lambda ,{\text{ PU}}\,{\text{present,}} \\ \end{aligned}$$

where γ is the detection threshold of AVCD. It is should be noted that p = 1 denotes AVCD. Here, CSS scheme is applied where multiple CRs are present in a cognitive radio system. Each CR makes independent binary decisions in the form of 0 or 1. Then each CR forwards their independent binary decisions (hard decisions) to the fusion center (FC). FC then combines the received decisions to determine the presence or absence of PU as shown below:

$$S = \sum\limits_{i = 1}^{K} {s_{i} } ,$$
(3)

where K is the total number of CRs present, S is the sum of independent binary decisions from each CR. si is the hard decision made by each CR based on i-AVCD test-statistics. The hypotheses H0 (null hypothesis) and H1 (alternative hypothesis) at the FC using the CSS scheme can be expressed as

$$\begin{aligned} \,H_{0} :\,S < n,\quad {\text{PU}}\,{\text{absent,}} \hfill \\ \,H_{1} :\,S \ge n,\quad {\text{PU}}\,{\text{present}} \hfill \\ \end{aligned}$$

where \(n < K\) denotes majority rule, \(n = 1\) denotes OR rule and \(n = K\) denotes AND rule.

3 Detection Probability and False Alarm Probability

Probability density function (pdf) of received samples \(y_{i}\) at each CR under hypotheses \(H_{0} \,\) and \(H_{1}\) can be expressed as

$$f_{{y_{i} \left| {H_{0} } \right.}} (x) = \frac{1}{2b}{\text{e}}^{{ - \frac{\left| x \right|}{b}}}$$
(4)
$$f_{{y_{i} |H_{1} }} (x) = \frac{1}{4b}\left[ {{\text{e}}^{{ - \frac{{\left| {x - \sqrt \gamma } \right|}}{b}}} + {\text{e}}^{{ - \frac{{\left| {x + \sqrt \gamma } \right|}}{b}}} } \right].$$
(5)

Using (4) \(f_{{\left| {y_{i} } \right|\left| {H_{0} } \right.}} (x)\) can be expressed as [13]

$$\begin{aligned} f_{{\left| {y_{i} } \right|\left| {H_{0} } \right.}} (x) & = \frac{1}{b}{\text{e}}^{{ - \left| {b^{ - 1} x} \right|}} , \\ & = 0,x < 0. \\ \end{aligned}$$
(6)

Mean \(E\left[ {\left| {y_{i} } \right|^{p} \left| {H_{0} } \right.} \right]\) and variance \(D\left[ {\left| {y_{i} } \right|^{p} \left| {H_{0} } \right.} \right]\) can be expressed as [13]

$$E\left[ {\left| {y_{i} } \right|^{p} \left| {H_{0} } \right.} \right] = \, b^{p} \varGamma \left( {p + 1} \right)$$
(7)
$$D\left[ {\left| {y_{i} } \right|^{p} \left| {H_{0} } \right.} \right] = b^{2p} \varGamma \left( {2p + 1} \right) - b^{2p} \varGamma^{2} \left( {p + 1} \right).$$
(8)

False alarm probability \((P_{\text{F}} )\) at each CR can be expressed as

$$P_{\text{F}} = Q\left( {\frac{{\lambda - N \times E\left[ {\left| {y_{i} } \right|^{p} \left| {H_{0} } \right.} \right]}}{{\sqrt {N \times D\left[ {\left| {y_{i} } \right|^{p} \left| {H_{0} } \right.} \right]} }}} \right) .$$
(9)

Similarly, detection probability \((P_{\text{D}} )\) at each CR can be expressed as

$$P_{\text{D}} = Q\left( {\frac{{\lambda - N \times E\left[ {\left| {y_{i} } \right|^{p} \left| {H_{1} } \right.} \right]}}{{\sqrt {N \times D\left[ {\left| {y_{i} } \right|^{p} \left| {H_{1} } \right.} \right]} }}} \right) .$$
(10)

Similarly, expressions of \(E[\left| {y_{i} } \right|^{p} \left| {H_{1} } \right.]\) and \(D[\left| {y_{i} } \right|^{p} \left| {H_{1} } \right.]\) can be derived [13] similarly as done in case of PF.

Finally, at FC, detection probability \((Q_{\text{D}} )\) and false alarm probability \((Q_{\text{F}} )\) can be expressed as [14]

$$Q_{\text{F}} = \sum\limits_{l = n}^{K} {\left( {\begin{array}{*{20}c} K \\ l \\ \end{array} } \right)} \,P_{\text{F}}^{l} \left( {1 - P_{\text{F}} } \right)^{K - l}$$
(11)
$$Q_{\text{D}} = \sum\limits_{l = n}^{K} {\left( {\begin{array}{*{20}c} K \\ l \\ \end{array} } \right)} \,P_{\text{D}}^{l} \left( {1 - P_{\text{D}} } \right)^{K - l}$$
(12)

Total error probability \(\left( {P_{\text{e}} } \right)\) at the FC can be expressed as

$$P_{\text{e}} = Q_{\text{m}} + Q_{\text{F}} ,$$
(13)

where \(Q_{\text{m}} = 1 - Q_{\text{D}}\) is the missed detection probability at the FC.

3.1 Optimum Values of p, N, and K

Optimum values of \(p(p^{*} )\) at each CR can be obtained by partially differentiating \(P_{\text{D}}\) w.r.t. p and equating it to zero.

$$p^{*} = \arg \mathop { \text{max} }\limits_{p} (P_{\text{D}})$$
(14)

Similarly, optimum values of n can be obtained as

$$n^{*} = \arg \mathop { \hbox{min} }\limits_{n} \left( {P_{\text{e}} } \right) = \hbox{min} \left( {K,\left\lceil {\frac{K}{1 + \alpha }} \right\rceil } \right)$$
(15)

where \(\alpha = \frac{{\ln \left( {\frac{{P_{\text{F}} }}{{1 - P_{\text{m}} }}} \right)}}{{\ln \left( {\frac{{P_{\text{m}} }}{{1 - P_{\text{F}} }}} \right)}}\) and \(\left\lceil . \right\rceil\) denotes ceiling function.

Thus, for specified values of K, and \(P_{\text{m}}\), \(n^{*}\) can be easily found out.

4 Simulation Results

Figure 1 shows \(P_{\text{D}}\) versus SNR (in dB) comparison of i-AVCD with ED and AVCD using CSS-\(n/K\) (majority) rule at SNR of −4 dB, \(N = 30\) and \(P_{\text{F}} = 0.1\). It can be seen clearly that at low values of SNR, i-AVCD with n/K rule underperform the test-statistics without \(n/K\) rule. However, as SNR increases, n/K rule improves the performance of i-AVCD. Figure 2 shows \(P_{\text{D}}\) versus SNR comparison of i-AVCD using CSS-AND rule. It is clear from figure that AND rule of CSS doesn’t perform better than that without AND rule in case of the test-statistics ED, AVCD and i-AVCD. Figure 3 shows \(P_{\text{D}}\) versus SNR comparison of i-AVCD using CSS-OR rule. It is clear from figure that OR rule of CSS improves the performance of ED, AVCD and i-AVCD significantly. Figure 4 shows optimum p of i-AVCD with CSS-OR rule for different \(P_{\text{F}}\). It can be clearly seen from the figure that optimum \(p(p^{*} )\) increases with decrease in \(P_{\text{F}}\). Values \(p^{*}\) at different values of \(P_{\text{F}}\) and at \(\gamma = - 4\) dB are given in Table 1. Figure 5 shows the optimum values of K comparison to achieve a certain target error probability for different \(P_{\text{F}}\). From the simulation result, it is found that to achieve total error probability of 0.001739, optimum values of CR are 30 out of total 60 taken CRs. Similarly, to achieve an error target of 0.02311, only 15 CRs will be sufficient out of 60 CRs. Figure 6 shows performance comparison of i-AVCD with SL-PCA, SSR, ED, AVCD using CSS-OR rule at \(P_{\text{F}} = 0.1\) and \(N = 30\). i-AVCD at \(p^{*}\) = 0.101 shows better performance than all the mentioned test-statistics at optimum p. However, as p increases \((p = 1.5)\), performance of i-AVCD decreases. Figure 7 shows receiver operating characteristic (ROC) plot of i-AVCD, AVCD, and ED at \(N = 50\) and \(\gamma = - 4\) dB at different values of p. ROC improves as p decreases. Further, both simulations and analytical results closely match for the three compared test-statistics in the figure.

Fig. 1
figure 1

Performance comparison of i-AVCD, AVCD and ED with CSS (n/K rule) for n = 2, K = 3 at \(\gamma = - 4\) dB, N = 30

Full size image
Fig. 2
figure 2

Performance comparison of i-AVCD, AVCD and ED with CSS (AND rule) for n = 3, K = 3 at \(\gamma = - 4\) dB, N = 30

Full size image
Fig. 3
figure 3

Performance comparison of i-AVCD, AVCD and ED with CSS (OR rule) for n = 1, K = 3 at \(\gamma = - 4\) dB, N = 30

Full size image
Fig. 4
figure 4

\(P_{\text{D}}\) versus p at \(\gamma = - 4\) dB and N = 30 at different values of \(P_{\text{F}}\) showing optimum \(p\)

Full size image
Table 1 Optimum values of p of i-AVCD with CSS at \(N = 30\) and \(\gamma = - 4\) dB
Full size table
Fig. 5
figure 5

\(P_{\text{e}}\) versus \(K\) at \(\gamma = - 4\) dB and N = 30 with i-AVCD at \(p = 1\) for different detection threshold \((\lambda )\)

Full size image
Fig. 6
figure 6

Performance comparison of i-AVCD with other test-statistics using CSS scheme based on OR rule at N = 30 and \(P_{\text{F}} = 0.1.\)

Full size image
Fig. 7
figure 7

ROC comparison of i-AVCD with other test-statistics using CSS scheme based on OR rule at \(\gamma = - 4\) dB, N = 50

Full size image

5 Conclusion

Cooperative spectrum sensing with i-AVCD is discussed using different CSS rules: AND, OR, and majority (n/K) rule. It is concluded that optimum p increases with a decrease in \(P_{\text{F}}\). Further, it is also concluded that OR rule shows better performance over a wide SNR range as compared to AND rule and majority rule. n/K rule also works well but shows improved performance over only a limited SNR range. i-AVCD is compared with ED, AVCD, SSR, SL-PCA and it is concluded that by carefully selecting optimum p, detection performance increases over a wide SNR range, as compared with other test-statistics in case of CSS-OR rule.