1-Planar Graphs

Abstract

Topological graph theory discusses, in most cases, graphs embedded in the plane (or other surfaces). For example, such plane graphs are sometimes regarded as the simplest town maps. Now, we consider a town having some pedestrian bridges, which cannot be realized by a plane graph. Its underlying graph can actually be regarded as a 1-plane graph. The notion of 1-plane and 1-planar graphs was first introduced by Ringel in connection with the problem of simultaneous coloring of the vertices and faces of plane graphs. In particular, in contrast to planarity testing, testing 1-planarity of a given graph is an NP-complete problem. Even though 1-planar graphs have been widely studied recently, we still know relatively little about them. In this chapter, we begin with formally defining 1-plane and 1-planar graphs and mainly focus on “maximal”, “maximum,” and “optimal” 1-planar graphs, which are relatively easy to treat. This chapter reviews some basic properties of these graphs.

4.1 Definition and Basic Results

A drawing of a graph G on the sphere $\mathbb {S}^2$ is a representation of G, where vertices are distinct points in $\mathbb {S}^2$, and edges are Jordan arcs in the sphere joining the points corresponding to their end vertices. (Note that the sphere is the one-point compactification of the Euclidean plane. The above drawing of G on $\mathbb {S}^2$ is equivalent to a drawing of G in the plane, except that none of the faces has a special role in the sphere.) A crossing point is a transversal intersection of two arcs on the sphere. In this chapter, we consider only proper drawings such that edges are simple arcs without vertices of the graph in their interiors, two arcs having an intersection always cross-transversely, no two adjacent edges cross each other, and no more than two edges cross at a single point.

A graph G is 1-planar if it can be drawn on the sphere $\mathbb {S}^2$, so that each edge crosses at most one other edge. The notion of 1-planar graphs was first introduced by Ringel [25] in connection with the problem of simultaneous coloring of the vertices and faces of plane graphs. For aspects of 1-planar graphs that are not covered in this chapter, refer to a recent survey [16]. Note that all graphs in this chapter are assumed to be simple and connected unless otherwise specified. However, we sometimes consider 1-planar (or 1-plane) multigraphs, i.e., with loops or multiple edges, in our statements and proofs. In some cases, we still refer to “simple graphs” for clarity. By the above definition, notice that every planar graph is 1-planar. We can also regard the drawing as a continuous map $f\!:\! G \rightarrow \mathbb {S}^2$ which may not be injective, where G is regarded as a one-dimensional topological space. In this chapter, we call the above map f a 1-embedding of G into the sphere. In this case, we say that the image f(G) is a 1-plane graph; similar to the difference between “planar graph” and “plane graph”. (Sometimes, we denote a given 1-plane graph by G, instead of f(G), to simplify notation. Further, we sometimes call the image G (or f(G)) a 1-embedding on $\mathbb {S}^2$.) An edge is crossing if it crosses another edge in a 1-plane graph G on the sphere, and is non-crossing otherwise. In a 1-plane graph, if an edge $v_0v_2$ crosses another edge $v_1v_3$ and has a crossing point z, then we say that the arc $zv_i$ is a half-edge of G for each $i \in \{0,1,2,3\}$. In the above, $v_iz$ and $v_{i+1}z$ are consecutive, where the indices are taken modulo 4. Throughout the chapter, we often use the following fact in our argument.

Proposition 4.1

Let G be a connected 1-plane multigraph on $\mathbb {S}^2$. Then, each connected component of $\mathbb {S}^2 - G$ is homeomorphic to an open disk (also known as a 2-cell). Further, for any two consecutive half-edges $v_0z$ and $v_1z$, where $v_0, v_1 \in V(G)$, there exists a connected component of $\mathbb {S}^2 - G$ having $v_0$ and $v_1$ on its boundary.

Proof

Suppose that there is a connected component D of $\mathbb {S}^2 - G$ not homeomorphic to a 2-cell. Then, the boundary of D is disconnected and has components $J_1, \ldots , J_k$ with $k \ge 2$, each of which is homeomorphic to a simple closed curve. It is clear that there exists a connected component of G corresponding to $J_i$ for $i\in \{1, \ldots , k\}$, and any two of them are disjoint in G. Therefore, G is disconnected, a contradiction. The second part of the statement holds since the closed set formed by $v_0z \cup v_1z$ is on the boundary of some connected component of $\mathbb {S}^2 - G$ by the 1-planarity.    $\square$

A connected component D of $\mathbb {S}^2-G$ whose boundary contains no crossing point is called a face of the 1-plane graph G. In other words, the boundary of a face D of G corresponds to a closed walk consisting of only non-crossing edges of G. A k-gonal face of G is a face of G whose boundary walk has a length of exactly k. On the other hand, a connected component D of $\mathbb {S}^2-G$ whose boundary contains a crossing point is a fake face. Note that a fake face is not a face of G vice versa. See Fig. 4.1. It depicts a 1-embedding of a complete graph $K_5$, or a 1-plane graph isomorphic to $K_5$; as a result, $K_5$ is 1-planar. This 1-embedding has one crossing point, four triangular faces, and four triangular fake faces.

Fig. 4.1

1-plane graph $K_5$

The following is the most important fact giving the upper bound of the number of edges of 1-planar graphs; this had been proved in some papers, e.g., see [1, 24].

Proposition 4.2

Let G be a simple 1-planar graph with $|V(G)|\ge 3$. Then, we have $|E(G)| \le 4|V(G)| - 8$.

Proof

Let G be a simple 1-plane graph with $|V(G)|\ge 3$. We add edges to G on $\mathbb {S}^2$ to obtain a new 1-plane graph, admitting loops, and multiple edges, which however has neither 1- nor 2-gonal face. The resulting multigraph $G'$ is assumed to be edge maximal with respect to the above property. By Proposition 4.1 and the maximality of $G'$, if $G'$ has a pair of crossing edges $v_0v_2$ and $v_1v_3$, then there are four edges $v_0v_1, v_1v_2, v_2v_3$, and $v_3v_0$ such that the closed walk $v_0v_1v_2v_3$ bounds a 2-cell that contains no vertex and a unique crossing point. Furthermore, observe that $G'$ is connected and that every face of $G'$ is triangular; if not, we can add a diagonal edge in the face.

Let c denote the number of crossing points of $G'$. Now we remove a crossing edge from each pair of crossing edges in $G'$ and denote the resulting multigraph by $G''$; note that we have removed c edges from $G'$. Clearly, $G''$ is an embedding without crossing points and each face of $G''$ is triangular. By Euler’s formula, we have $|E(G'')| = 3 |V(G'')| - 6$ and $|F(G'')| = 2 |V(G'')| - 4$. Furthermore, we have $c\le |F(G'')| / 2$ since each crossing point in $G'$ corresponds to a pair of adjacent triangular faces in $G''$, and all other triangular faces of $G''$ are already present in $G'$. Then we obtain the inequality in the statement as follows:

$$\begin{aligned} |E(G)|\le & {} |E(G')| \\= & {} |E(G'')| + c \\\le & {} |E(G'')| + |F(G'')| / 2\\= & {} (3 |V(G'')| - 6) + (|V(G'')| - 2)\\= & {} 4|V(G'')| -8\\= & {} 4|V(G)| - 8 \end{aligned}$$

Therefore, the proposition follows.    $\square$

The following fact is easily obtained from Proposition 4.2.

Proposition 4.3

A complete graph $K_7$ with seven vertices is not 1-planar.

Proof

By Proposition 4.2, a 1-planar graph with seven vertices has at most 20 edges. However, $K_7$ has 21 edges.    $\square$

A 1-planar graph G is optimal if it satisfies the equality in Proposition 4.2, i.e., $|E(G)| = 4|V(G)| - 8$ holds. With the terminology defined above, a 1-embedded optimal 1-planar graph is called an optimal 1-plane graph.

Let G be a 1-planar graph. For any nonadjacent vertices $u, v\in V(G)$, if $G+uv$ is not 1-planar, then G is maximal. On the other hand, a 1-plane graph G is maximal if it cannot be augmented to a larger 1-plane graph by adding an edge as an arc to G on the sphere without introducing forbidden crossings. The reader notes the difference between these two notions of maximality, defined for 1-planar graphs and 1-plane graphs. Note that any 1-embedding f(G) of any maximal 1-planar graph G is maximal 1-plane, but the converse does not hold in general. Figure 4.2 depicts a maximal 1-plane graph G. However, the underlying graph of G is not maximal 1-planar since we know that $K_6$ is 1-planar (see M(6) in Fig. 4.10).

Fig. 4.2

Maximal 1-plane graph with six vertices

Furthermore, a 1-planar graph G with n vertices is maximum if $|E(G)| \ge |E(G')|$ for any other 1-planar graph $G'$ with n vertices. Clearly, every maximum 1-planar graph is maximal. It is easy to see that every optimal 1-planar graph is maximum, but the converse does not hold true. It was proved that there is an optimal 1-planar graph with n vertices if and only if $n=8$ or $n\ge 10$ (see e.g., [3, 4, 28]). In other words, if n is either 9 or at most 7, then any maximum 1-planar graph with n vertices is not optimal. Especially, if $n\le 6$, then the maximum 1-planar graph is a complete graph with n vertices (see $M(3), M_1(4), M_2(4), M(5)$, and M(6) shown in Fig. 4.10).

In the remainder of this section, we present some basic properties that hold for 1-planar graphs.

Proposition 4.4

Let G be a 1-plane graph with n vertices. Then, the number of crossing points is at most $n-2$.

Proof

Let c denote the number of crossing points of G. For every crossing point z created by two edges $v_0v_2$ and $v_1v_3$, we successively add a non-crossing edge $v_iv_{i+1}$ so that $zv_iv_{i+1}$ bounds a fake face of G if such an edge does not already exist for $i\in \{0,1,2,3\}$, where the indices are taken modulo 4. Note that we allow creating multiple edges in the above operation. After that, we remove all crossing edges of G and denote the resulting plane multigraph by $G'$. Note that $G'$ has neither a 1- nor a 2-gonal face. Now we have the following equality by Euler’s formula where $F_k$ denotes the number of k-gonal face of $G'$.

$$\begin{aligned} \sum _{k\ge 3}(k-2)F_k = 2n-4 \nonumber \end{aligned}$$

Thus, we obtain the inequality $F_4 \le n-2$. It is clear that $c\le F_4$ by our construction, and hence we have $c \le n-2$. Thus, we got our desired conclusion.    $\square$

Proposition 4.5

Let G be a maximal 1-plane graph and let $\{v_0v_2, v_1v_3\}$ be a pair of crossing edges having a crossing point z. Then, the four edges $v_0v_1, v_1v_2, v_2v_3$ and $v_3v_0$ are present in G. Furthermore, if G is 4-connected, then $zv_iv_{i+1}$, for $i\in \{0,1,2,3\}$ bounds a fake face with indices taken modulo 4.

Proof

There exists a connected component D of $\mathbb {S}^2 - G$ homeomorphic to an open disk (or a 2-cell region) whose boundary contains two half-edges $v_0z$ and $v_1z$ by Proposition 4.1. If $v_0v_1\notin E(G)$, then G would not be maximal since we can join $v_1$ and $v_2$ by an arc passing through D, a contradiction. Similarly, we can show the existence of the other three edges.

Next, suppose that G is 4-connected. Let D be a 2-cell region bounded by $v_0v_1$ and the half-edges $v_0z$ and $v_1z$. Assume, to the contrary, that D contains a vertex of G. If $v_0v_1$ is non-crossing, then $\{v_0, v_1\}$ would become a cut set, which separates vertices in D from the others, a contradiction. If $v_0v_1$ is a crossing edge and crosses $xy\in E(G)$ where y is located in D, then $\{v_0, v_1, x\}$ would become a 3-cut of G, which also separates vertices in D from the others. It contradicts the 4-connectivity condition of G.    $\square$

Proposition 4.6

Let G be a maximal 1-plane graph. Then, every face of G is either triangular or quadrangular. Furthermore, if G has a quadrangular face, then G contains $M_1(4)$, shown in Fig. 4.10, as a subgraph. Moreover, if G is 3-connected, then either every face of G is triangular or G is homeomorphic to $M_1(4)$.

Proof

Let f be a k-gonal face bounded by a closed walk $C=v_0v_1\cdots v_{k-1}$ for $k\ge 4$. If C is not a cycle, then $v_i=v_j$ for some $i\ne j$. Under the condition, it is easy to see that $v_i$ is a cut vertex of G. Then, we can join two vertices in different components of $G-v_i$ by an arc passing through f, preserving the simplicity. It contradicts the maximality of G. Thus, C is a cycle.

Since G is maximal, there exist edges $v_iv_j$ for all $\{i, j\}$ with $0\le i < j \le k-1$ which lie outside of f; otherwise, one could add a new edge inside f. If $k\ge 5$, there would be an edge $v_iv_j$ having at least two crossing points, contrary to the 1-planarity of G; e.g., $v_0v_2$ must cross $v_1v_3$ and $v_1v_4$. Thus, $k=4$ and the edges $v_0v_2$ and $v_1v_3$ cross outside of f. Then, G clearly contains $M_1(4)$ as a subgraph, as required. If G is 3-connected, then G has no vertex other than those in $V(M_1(4))$; otherwise $\{v_i, v_{i+1}\}$ would form a 2-cut for some $i\in \{0,1,2,3\}$. Therefore, we got our desired conclusion.    $\square$

4.2 Connectivity

It is well known that every triangulation of the sphere is 3-connected. However, we cannot guarantee the high connectivity of 1-planar graphs even if we assume the maximality to those graphs. We only ensure the following.

Theorem 4.1

([8]) Let G be a maximal 1-plane graph with $|V(G)|\ge 3$. Then a subgraph formed by all non-crossing edges is spanning and 2-connected.

By the above theorem proven by Eades et al., we can immediately obtain the following.

Proposition 4.7

Every maximal 1-plane graph G with $|V(G)|\ge 3$ is 2-connected.

The above “2” is the best possible since it is not difficult to construct a maximal 1-plane graph having a vertex of degree 2; insert a vertex of degree 2 in one of the two triangular fake faces sharing a non-crossing edge of a 1-embedded graph shown in Fig. 4.2.

By Proposition 4.2, the average degree of every 1-planar graph is less than 8. This implies that any 1-planar graph has a vertex of degree at most 7. This “7” is also the best possible since Fabrici and Madaras [9] exhibited a 7-regular 1-planar graph as shown in Fig. 4.3.

Fig. 4.3

7-regular 1-planar graph

A quadrangulation (resp., triangulation) of the sphere is a simple graph embedded on the sphere such that each face is bounded by a 4-cycle (resp., 3-cycle). By the argument in the proof of Proposition 4.2, the graph formed by all non-crossing edges of an optimal 1-plane graph G forms a quadrangulation of the sphere. We call it a quadrangular subgraph of G and denote it by Q(G) (see Fig. 4.4). On the other hand, the following holds for crossing edges.

Fig. 4.4

Optimal 1-planar graph and its quadrangular subgraph

Proposition 4.8

Let G be an optimal 1-plane graph. Then, a subgraph of G formed by all crossing edges is disconnected.

Proof

Let G be an optimal 1-plane graph. It is well known that every quadrangulation of the sphere is bipartite and hence Q(G) is bipartite. Thus, V(G) can be decomposed into $V_B(G)\cup V_W(G)$ so that every non-crossing edge joins vertices in different sets while every crossing edge joins vertices in the same set. This implies that the subgraph of G formed by all crossing edges has two components having vertex sets $V_B(G)$ and $V_W(G)$, respectively. Therefore, we are done.    $\square$

The following theorem gives us the clear relationship between optimal 1-plane graphs and quadrangulations of the sphere.

Theorem 4.2

([28]) Let H be a simple quadrangulation of the sphere. Then there exists a simple optimal 1-plane graph G such that $H = Q(G)$ if and only if H is 3-connected.

By the above theorem, every optimal 1-planar graph is 3-connected. (In fact, “3” is not the best possible. See the argument below.) Further, we can see that around each vertex of an optimal 1-plane graph, crossing edges and non-crossing edges appear alternately. Hence, each vertex of an optimal 1-planar graph has even degree; i.e., every optimal 1-planar graph is Eulerian. Thus, every optimal 1-planar graph has a vertex of degree 6 and the connectivity cannot be larger than 6. (Recall that the average degree of 1-planar graph is smaller than 8, and that the minimum degree is at least 6 by the simplicity.) In fact, there is an infinite series of 6-connected optimal 1-planar graph obtained as follows: At first, embed a 2k-cycle $v_1u_1v_2u_2 \cdots v_ku_k$ into the sphere without crossing point and put two vertices a and b in its interior and exterior separated by the cycle, respectively. Next, we add edges $av_i$ and $bu_i$ for $i = 1, \ldots , k$. We call the resulting graph a pseudo double wheel and denote it by $W_{2k}$ (see the left-hand side of Fig. 4.5). Since $W_2$ has multiple edges and $W_4$ has two vertices of degree 2, the smallest 3-connected pseudo-double wheel is $W_6$, which is nothing but a cube. We add pairs of crossing edges to all the faces of $W_{2k} (k \ge 3)$, and obtain the optimal 1-plane graph called a X-pseudo-double wheel denoted by $X\!W_{2k}$. See the right-hand side of Fig. 4.5. We call the vertices a and b hubs of $X\!W_{2k}$.

Fig. 4.5

Pseudo-double wheel and X-pseudo-double wheel

Proposition 4.9

For every $k \ge 3$, $X\!W_{2k}$ is 6-connected.

Proof

Let G be a X-pseudo-double wheel $X\!W_{2k}$ with hubs a and b with $k\ge 3$. In fact, $G - \{ a, b \}$ is a graph known as the square of the cycle of length $2k \ge 6$. In [12], it is proven that $G - \{ a, b \}$ is 4-connected. Since both a and b are adjacent to all the vertices in $V(G) - \{a,b\}$ and $|V(G) - \{a,b\}| \ge 6$, G is 6-connected.    $\square$

In fact, throughout the argument in [10, 28], the following theorem had been proven.

Theorem 4.3

([10, 28]) The connectivity of an optimal 1-planar graph G is either 4 or 6. If the connectivity is 4 (resp., 6), then there exists a separating 4-cycle (resp., 6-cycle) of Q(G).

4.3 Planarization

For a given 1-plane graph G, we sometimes consider a plane graph $G_P$ called a planarization of G, defined as follows. Let $\{a_1c_1, b_1d_1\}, \{a_2c_2, b_2d_2\}, \ldots , \{a_kc_k, b_kd_k\}$ denote pairs of crossing edges of G. Roughly speaking, we regard a crossing point formed by $\{a_ic_i, b_id_i\}$ as a new vertex $z_i$. Precisely, our required plane graph $G_P$ has $V(G_P)=V(G)\cup \{z_i|1\le i \le k\}$ as its vertex set and $E(G_P)=E(G) \cup \{a_iz_i, b_iz_i, c_iz_i, d_iz_i|1\le i \le k\} \setminus \{a_ic_i, b_id_i|1\le i \le k\}$ as its edge set. We call $z_i$ a false vertex of $G_P$ for $1\le i \le k$, and $v \in V(G)\subset V(G_P)$ a true vertex. Clearly, we have $\deg _{G_P}(z_i)=4$, and edges $a_iz_i, b_iz_i, c_iz_i, d_iz_i$ appear in this order around $z_i$. The following fact is easily obtained.

Proposition 4.10

Every face of $G_P$ obtained from a simple 1-plane graph G has at least two true vertices.

Proof

Clearly, $G_P$ is simple if G is simple. Hence, the length of any face of $G_P$ is bounded by a closed walk of length at least three unless $G_P \cong K_2$. If $G_P \cong K_2$, then such two vertices are true and hence the statement holds. Further, two false vertices are not adjacent by our construction of $G_P$. Thus, we are done.    $\square$

Concerning the connectivity of the planarization $G_P$ of G, the following result is known.

Theorem 4.4

([9]) If G is a 3-connected 1-plane graph with the minimum number of crossings taken over all 1-embeddings $f : G \rightarrow \mathbb {S}^2$, then $G_P$ is 3-connected.

Before reading the following proposition, recall that a planar graph is 1-planar by the definition of 1-planarity.

Proposition 4.11

A planarization $G_P$ of a 1-plane graph G is 5-connected if and only if G is a 5-connected plane graph.

Proof

If a 1-plane graph G has at least one crossing point, then $G_P$ has a vertex of degree 4. In this case, $G_P$ cannot be k-connected for $k\ge 5$. Thus, if $G_P$ is 5-connected, then G has no crossing point. That is, $G=G_P$ and hence G is a 5-connected plane graph. The converse is obvious since $G=G_P$ also holds in this case.    $\square$

By the above fact, the connectivity of the planarization $G_P$ of a 1-plane graph G is at most 4 if G has at least one crossing point. This raises the question of what condition for a 1-plane graph G is sufficient to guarantee the 4-connectivity of $G_P$? So far, we know the following.

Theorem 4.5

([13]) If a 1-plane graph G is 7-connected, then $G_P$ is 4-connected.

The “7” in the above theorem is the best possible. The 1-plane graph shown in Fig. 4.6 is 6-connected. However, the planarization of the graph clearly has a 3-vertex cut, which consists of three false vertices. Furthermore, the connectivity of a 7-regular 1-planar graph presented in Fig. 4.3 is 7.

Fig. 4.6

6-connected 1-plane graph whose planarization has a 3-cut

As noted above, we can easily construct a maximal 1-plane graph G having a vertex v of degree 2. In this case, it is easy to see that v is degree 2 also in $G_P$. That is, “maximality” does not imply lower bounds on the connectivity. However, for optimal 1-plane graphs, the following theorem holds.

Theorem 4.6

([13]) The planarization of an optimal 1-plane graph is 4-connected.

Using the above result, we can easily obtain the following proposition; a proof was previously published in [13].

Proposition 4.12

Every optimal 1-planar graph is Hamiltonian.

Proof

Let G be an optimal 1-plane graph and denote the planarization of G by $G_P$. By Theorem 4.6, $G_P$ is 4-connected and hence $G_P$ has a Hamiltonian cycle C by [29]. Now assume that C passes through a false vertex z corresponding to a crossing point created by a pair of crossing edges $\{v_0v_2, v_1v_3\}$. If a 2-path $v_izv_{i+2}$ is contained in C, then we replace the 2-path by $v_iv_{i+2}$, which is an edge of G, where the indices are taken modulo 4. On the other hand, if a 2-path $v_izv_{i+1}$ is contained in C, we replace it by an edge $v_iv_{i+1}$, which is also an edge of G by Proposition 4.5. We do the above replacement for all false vertices contained in C, and obtain a Hamiltonian cycle of G.    $\square$

At the end of this section, we show the following result using the notion of planarization. The proof is based on [6].

Theorem 4.7

([6]) A complete bipartite graph $K_{5,4}$ is not 1-planar.

Proof

For the sake of contradiction, suppose that $K_{5,4}$ is 1-planar. Let G be a 1-embedding of $K_{5,4}$, and $G_P$ denotes its planarization. It is known that $cr(K_{5,4})=8$ by [15], where cr(H) represents the crossing number of H. Thus, $G_P$ has at least 8 crossing points. This implies that G has at least 16 crossing edges and has at most 4 non-crossing edges.

Now, consider the following equation derived from Euler’s formula, where $\deg _H(f)$ denotes the length of the boundary walk of a face f:

$$\begin{aligned} \sum _{v\in V(G_P)}(\deg _{G_P}(v)-4) + \sum _{f\in F(G_P)}(\deg _{G_P}(f)-4) = -8. \nonumber \end{aligned}$$

Clearly, $G_P$ has four vertices of degree 5 and all other true and false vertices have degree 4. Thus, we have,

$$\begin{aligned} \sum _{f\in F(G_P)}(\deg _{G_P}(f)-4) = -12. \nonumber \end{aligned}$$

Since G is bipartite, G has no cycle of length 3. Thus, each triangular face has a false vertex on its boundary. Furthermore, by Proposition 4.10, such a triangular face is incident to a non-crossing edge. That is, $G_P$ has at most eight triangular faces. This contradicts the above equation.    $\square$

4.4 Edge Density

As mentioned in Sect. 4.1, every 1-planar graph with n vertices has at most $4n-8$ edges. In this section, we evaluate the number of edges of those graphs under various additional constraints.

Let $M(\mathscr {G}, n)$ and $m(\mathscr {G}, n)$ denote the maximum and the minimum number of edges taken over all graphs with n vertices in a graph class $\mathcal {G}$, respectively. For example, it is well known that $M(\mathscr {T}, n)=m(\mathscr {T}, n)=3n-6$ for the family of maximal planar graphs$\mathscr {T}$ assuming $n\ge 3$; and such graphs are known as triangulations of the sphere. However, we know that $M(\mathscr {P}, n)\ne m(\mathscr {P}, n)$ (resp., $M(\mathscr {P}', n)\ne m(\mathscr {P}', n)$) in general where $\mathscr {P}$ (resp., $\mathscr {P}'$) denotes the family of maximal 1-planar (resp., 1-plane) graphs. In fact, $M(\mathscr {P}, n)=M(\mathscr {P}', n)$ represents the number of edges of a maximum 1-planar graph with n vertices by our definition. That is, in most cases ($n=8$ and $n\ge 10$), the above value equals to $4n-8$, which is the number of edges of an optimal 1-planar graph with n vertices. Furthermore, we have $M(\mathscr {P}, n)=\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ if $n\le 6$, whose underlying graph is a complete graph $K_n$. In the remaining cases (i.e., $n\in \{7,9\}$), we have $M(\mathscr {P}, n)=4n-9$. (See Sect. 4.6. Maximum 1-plane graps with $3\le n\le 7$ vertices which are not optimal are exhibited.)

As we have seen, $m(\mathscr {P}, n)$ and $m(\mathscr {P}', n)$ are more interesting values to discuss. Here, observe that $m(\mathscr {P}, n) \ge m(\mathscr {P}', n)$ for every n by the definitions. At first, we introduce the results concerning $m(\mathscr {P}', n)$. Eades et al. [8] proved that $\frac{9n}{5}-\frac{18}{5} \le m(\mathscr {P}', n) \le \frac{7n}{3}-2$, and Brandenburg et al. [5] improved the above lower bound to $\frac{21n}{10}-\frac{10}{3}$. Further in [5], they construct maximal 1-plane graphs having $\frac{7n}{3}-3$ edges for any large n. In [5], it was also proved that $m(\mathscr {P}, n) \ge \frac{28n}{13}-\frac{10}{3}$ and that there exist maximal 1-planar graphs having $\frac{45n}{17}-\frac{84}{17}$ edges for any large n. Very recently, both lower bounds were improved to $\frac{20n}{9}-\frac{10}{3}$ by Barát and Tóth [2].

Next, we introduce some results for multipartite graphs. Karpov [14] proved that every bipartite 1-planar graph has at most $3n-8$ edges for even $n\ne 6$ and at most $3n-9$ for odd n and for $n=6$. For tripartite 1-planar graphs, we show the following result here.

Theorem 4.8

Every tripartite 1-planar graph with n vertices has at most $\frac{7}{2}n-7$ edges.

Proof

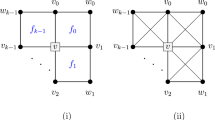
Let G be a tripartite 1-plane graph with n vertices, and let c denote the number of crossing points of G. For any pair of crossing edges $\{v_0v_2, v_1v_3\}$ of G, we perform the following operation. Observe that there exists a pair of vertices $\{v_i, v_{i+1}\}$, say $\{v_0, v_1\}$ without loss of generality, such that $v_0$ and $v_1$ belong to the same partite set. We remove an edge $v_0v_2$ from G, and add an edge $v_0v_1$ so that $v_0v_1v_3$ forms a corner of a face or a fake face (see Fig. 4.7). Now denote the resulting multigraph by $G'$. Note that $G'$ is probably not tripartite. If there exists a pair of multiple edges forming a 2-gonal face of $G'$, then such edges come from left and right pairs of crossing edges of G; note that such edges do not exist in G since each of them joins vertices in the same partite set (see Fig. 4.7 again). Therefore, $G'$ has at most $\frac{c}{2}$ such pairs of multiple edges. We remove an edge from every pair of multiple edges forming a 2-gonal face of $G'$, and obtain a plane multigraph $G''$. Combining with the result in Proposition 4.4, we obtain the following:

$$\begin{aligned} |E(G)|= & {} |E(G')| \nonumber \\\le & {} |E(G'')| + \frac{c}{2} \nonumber \\\le & {} 3n - 6 + \frac{n-2}{2} \nonumber \\= & {} \frac{7}{2}n-7 \nonumber . \end{aligned}$$

Therefore, the theorem follows.    $\square$

Fig. 4.7

Operation in the proof of Theorem 4.8

The upper bound in the above theorem is sharp. In fact, the graph depicted in Fig. 4.8 has $4k+2$ ($k\ge 2$) vertices and 14k edges. Furthermore, observe that there exist infinitely many 4-colorable optimal 1-planar graphs (see [21]). This implies that the upper bound of the number of edges for 4-partite 1-planar graphs with n vertices cannot be less than $4n-8$ if $n \ge 8$ and $n\ne 9$.

Fig. 4.8

Tripartite 1-plane graph with $\frac{7}{2}n-7$ edges

4.5 Minors and Subgraphs

For terminology around miniors of graphs, refer to a general text of graph theory, e.g., [7]. It is well known that a graph G is planar if and only if it contains neither $K_5$ nor $K_{3,3}$ as a minor. However, 1-planarity cannot be characterized in terms of forbidden minors. In contrast to planar graphs, it is easy to see that every graph is a minor of a 1-planar graph; see [11]. We prove the following stronger result.

Theorem 4.9

([27]) For every graph H, there is an optimal 1-planar graph having a topological minor of H.

Proof

We draw a given graph H on the sphere as a proper drawing. Let z be a crossing point of $v_0v_1, v_2v_3 \in E(H)$. We delete $v_0v_2$ and $v_1v_3$ from H on the sphere, and add vertices $u_i$ and edges $u_iv_i$ and $u_iu_{i+1}$ for $i\in \{0,1,2,3\}$ where the indices are taken modulo 4. By Proposition 4.1, we may assume that the above-added edges are all non-crossing such that $u_0u_1u_2u_3$ bounds a quadrangular face. We successively apply the above operation for each crossing point of H and denote the resulting plane graph by $H'$ (see the center of Fig. 4.9).

Fig. 4.9

Configurations in the proof of Theorem 4.9

Now, we subdivide edges of $H'$ if necessary, other than those of the 4-cycles around the crossing points above so that the resulting graph becomes bipartite. Furthermore, we add edges so that the resulting graph $H''$ is a simple quadrangulation of the sphere. (Note that we can add a diagonal edge to any 2l-gonal face ($l\ge 3$) in the bipartite graph preserving the simplicity by the planarity. See the right-hand side of Fig. 4.9.) If $H''$ is 3-connected, then there exists an optimal 1-plane graph G with $Q(G) = H''$ by Theorem 4.2 and then G clearly has a topological minor of H. If $H''$ is not 3-connected, then we apply the following operation to $H''$. For every face f of $H''$ bounded by $a_0a_1a_2a_3$, we put a 4-cycle $b_0b_1b_2b_3$ and edges joining $a_i$ and $b_i$ into f for each $i\in \{0,1,2,3\}$; all such edges are assumed to be non-crossing. Then, the resulting quadrangulation becomes 3-connected and the theorem follows, by the same argument as above.    $\square$

For the minors of complete graphs in optimal 1-planar graphs, we can easily obtain the following fact since Mader [19] proved that a graph with n vertices and at least $4n-9$ edges has a $K_6$-minor.

Proposition 4.13

Every optimal 1-planar graph has a $K_6$-minor.

Furthermore, Suzuki proved the following theorem for $K_7$-minors in optimal 1-planar graphs where $X\!W_{8}^+$ is the unique optimal 1-planar graph that can be obtained from $X\!W_8$ by a specific operation.

Theorem 4.10

([27]) A 6-connected optimal 1-planar graph G contains a $K_7$-minor if and only if G is isomorphic to neither $X\!W_{2k}$ $(k\ge 3)$ nor $X\!W_{8}^{+}$.

In fact, the characterization for general optimal 1-planar graphs without the connectivity condition to have a $K_7$-minor is given in the same paper. However, we do not describe it here since it would require several additional conditions.

On the other hand, if G is 1-planar, then any subgraph of G is also 1-planar; in other words, 1-planarity is closed under taking subgraphs. A graph G is a MN-graph if G is not 1-planar but for any edge e of G, $G-e$ is 1-planar. For example, Korzhic [17] proved that $K_7 -E(K_3)$ is the unique MN-graph with seven vertices. It easily follows from the above fact that any graph obtained from $K_7$ by deleting any two nonadjacent edges is 1-planar. Furthermore, it had been proven in [17, 18] that there are infinitely many MN-graphs with a minimum degree of at least 3.

However, if graphs are restricted to complete multipartite graphs, their 1-planarity is completely determined as follows.

Theorem 4.11

([6]) Let G be a complete k-partite 1-planar graph with $k\ge 2$. Then, G is isomorphic to a graph in Table 4.1:

Table 4.1 1-Planar complete multipartite graphs

In Table 4.1, $a-b$ (resp., $a-$) represents $\{i\in \mathbb {Z}|a \le i \le b \}$ (resp., $\{i\in \mathbb {Z}|a \le i \}$). For example, $K_{2-3,2,1,1}$ stands for two graphs $K_{2,2,1,1}$ and $K_{3,2,1,1}$. Furthermore, note that $K_{1,1,1,1,1,1}$ is equal to $K_6$. As we have already seen, any complete 7-partite graph G is not 1-planar since G contains $K_7$ as its subgraph.

For example, we can see that $K_{5,4}$ is not 1-planar; this fact can also be found as Theorem 4.7 in Sect. 4.3. Furthermore, we also see that $K_{4,3,2}$ is not 1-planar. However, this is clear since $K_{4,3,2}$ contains $K_{5,4}$ as its subgraph. In addition, $K_{4,3,2}$ has 26 edges and it cannot be 1-planar by Theorem 4.8.

4.6 Re-embeddings of 1-Planar Graphs

Let G be a 1-planar graph. For the precise definition below, assume that every edge $e=uv$ of G has a middle point $p \in e - \{u,v\}$ such that p corresponds to the crossing point if e is crossing in a 1-embedding. Two 1-embeddings $f_1,f_2\! :\! G \rightarrow \mathbb {S}^2$ are equivalent to each other if there exists a homeomorphism $h\! :\! \mathbb {S}^2 \rightarrow \mathbb {S}^2$ such that $hf_1 = f_2$. If not, they are inequivalent. If there is exactly one equivalence class of 1-embeddings of G, we say that G is uniquely 1-embeddable into the sphere, up to equivalence.

For two 1-embeddings $f_1$ and $f_2$ of G, if there exists an automorphism $\sigma \! :\! G \rightarrow G$ and a homeomorphism $h\! :\! \mathbb {S}^2 \rightarrow \mathbb {S}^2$ such that $hf_1 = f_2\sigma$, they are weakly equivalent to each other. Roughly speaking, they have the same picture when we ignore the labeling of vertices.

In this section, we especially discuss “re-embeddability” of maximum 1-planar graphs. The notion of “re-embeddability” of optimal 1-planar graphs was first given by Schumacher [26], who proved that if G is a 5-connected optimal 1-planar graph other than $X\!W_{2k} (k \ge 3)$, then G is uniquely 1-embeddable into the sphere, up to equivalence. In fact, the 5-connectivity condition is unnecessary in the above result, and Suzuki proved the following theorem.

Theorem 4.12

([28]) Let G be an optimal 1-planar graph other than $X\!W_{2k} (k \ge 3)$. Then G is uniquely 1-embeddable into the sphere, up to equivalence.

In fact, $X\!W_{2k}(k \ge 4)$ has only two 1-embeddings as follows. See the right-hand side of Fig. 4.5 again, and exchange the labels a and b in the figure. Then we obtain another 1-plane graph; e.g., $av_1$ is non-crossing in the original 1-plane graph while it is crossing in the latter one. Note that the underlying graph of the resulting 1-plane graph is isomorphic to $X\!W_{2k}$. That is, the two 1-embeddings of $X\!W_{2k}$ are inequivalent.

For $k=3$, $X\!W_6$ has exactly eight inequivalent 1-embeddings. In fact, $X\!W_6$ is isomorphic to $K_{2,2,2,2}$, and is obtained from a cube H by adding a pair of crossing edges to each face of H; thus, $X\!W_6$ has the rich symmetry. Furthermore, it is easy to see that all the inequivalent 1-embeddings of $X\!W_6$ are given by the same picture as the above example $X\!W_8$. Therefore, it follows that every optimal 1-planar graph is uniquely 1-embeddable into the sphere, up to weak equivalence.

The notion of the above re-embeddings of optimal 1-planar graphs is applied to the construction of maximal 1-planar graphs having small number of edges, which is discussed in Sect. 4.4. Let G be an optimal 1-planar graph with n vertices that is not isomorphic to $X\!W_{2k}(k \ge 3)$. Let $e=uv$ be a non-crossing edge of G. Then, we add a new vertex of degree 2 to G adjacent to u and v. For each non-crossing edge of G, we do the same operation, and denote the resulting graph by $G'$. It is easy to check that $G'$ is maximal 1-planar since G is uniquely 1-embeddable into the sphere by Theorem 4.12. Now, $G'$ has $n'=n+(2n-4)=3n-4$ vertices and $(4n-8)+2(2n-4)=8n-16$ edges. Consequently, $G'$ has $n'$ vertices and $\frac{8}{3}n'-\frac{16}{3}$ edges. However, the above coefficient is not better than that presented in [5] with a different construction, which was mentioned in Sect. 4.4.

Next, we consider maximum 1-planar graphs other than optimal 1-planar ones. In fact, the maximum 1-planar graphs that are not optimal in the unlabeled sense are determined as follows.

Theorem 4.13

([28]) Let G be a maximum 1-planar graph with $n\ge 3$ vertices that is not optimal. Then a 1-embedding of G in the sphere is equivalent to one of M(3), $M_1(4)$, $M_2(4)$, M(5), M(6), M(7) and $M_l(9) (l=1, \ldots , 6)$, up to weak equivalence.

Fig. 4.10

Maximum 1-planar graphs which are not optimal with $n \le 7$

The 1-plane graphs in the above theorem denoted by M(3), $M_1(4)$, $M_2(4)$, M(5), M(6) and M(7) can be found in Fig. 4.10. (The reader should refer to [28] for $M_l(9) (l=1, \ldots , 6)$.) Note that the underlying graph of both $M_1(4)$ and $M_2(4)$ is isomorphic to $K_4$. That is, $K_4$ has two inequivalent 1-embeddings, up to weak equivalence. Actually, it has been proven in [28] that $K_4$ is the unique maximum 1-planar graph having such a property; additionally, recall the result of optimal 1-planar graphs discussed above.

Let $f\!:\! G \rightarrow \mathbb {S}^2$ be a 1-embedding of a graph G into the sphere. An automorphism $\sigma \!:\! G \rightarrow G$ of G is called a symmetry of f if there is a homeomorphism $h \!:\! \mathbb {S}^2 \rightarrow \mathbb {S}^2$ such that $h f = f \sigma$. The symmetry group of f is defined as the set of all symmetries of f and is denoted by $\text{sym}(f)$ or by $\text{sym}(f(G))$. Then $\text{sym}(f)$ is a subgroup of $\text{aut}(G)$, i.e., an automorphism group of G, possibly not normal.

Let G be a 1-planar graph and f be its 1-embedding. We denote a set of 1-embeddings that are weakly equivalent to G by $\text{emb}(f)$ or by $\text{emb}(f(G))$; $\text{emb}(f)$ should be a quotient set by the equivalence of 1-embeddings. Then, the following relation is well known: $|\text{emb}(f)| = |\text{aut}(G)| / |\text{sym}(f)|$. Let $\text{Emb}(G)$ denote the quotient set of G’s 1-embeddings by the equivalence. If G admits precisely k inequivalent 1-embeddings $f_1, \ldots , f_k$, up to weak equivalence, then we have that $\text{Emb}(G) = \text{emb}(f_1) \cup \cdots \cup \text{emb}(f_k)$.

Table 4.2 presents the numbers of 1-embeddings of maximum 1-planar graphs (see the rightmost column). In the table, if G is not isomorphic to $K_4$, we have $\text{Emb}(G) = \text{emb}(f)$ for some f, as mentioned above. For example, the 1-embedding M(6) of $K_6$ attains the maximum value $|\text{emb}(M(6))|=60$, which comes from $|\text{aut}(K_6)|=6!=720$ and $|\text{sym}(M(6))|=12$. If $G \cong K_4$, we have $\text{Emb}(G) = \text{emb}(M_1(4)) \cup \text{emb}(M_2(4))$, and hence $|\text{Emb}(K_4)| = |\text{emb}(M_1(4))| + |\text{emb}(M_2(4))| = 1 + 3 = 4$.

Table 4.2 The number of 1-embeddings of maximum 1-planar graphs 

In [18], the notion of a PN-graph, defined as a 3-connected planar graph having no 1-embeddings into the sphere with at least one crossing point was introduced. It is well known that every 3-connected planar graph can be uniquely embedded into the sphere (without crossing points). That is, any PN-graph has the unique 1-embedding into the sphere. Note that, in most cases, the unique 1-embedding of a PN-graph is not maximal, and used for constructing 1-planar graphs with our desired property by adding edges; e.g., 3-connected maximal 1-planar graphs having small number of edges (see [13]).

4.7 Difference from Optimal 1-Planar Graphs

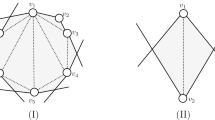
For every plane graph G, we can obtain a maximal plane graph by adding edges to G. Recall that such a maximal plane graph is a triangulation of the sphere. However, as we mentioned above, a maximal 1-plane graph is not necessarily optimal. Observe that maximum 1-plane graphs that are not optimal (listed in Theorem 4.13) are such examples. Furthermore, it is easy to see that a 1-plane graph having the subgraph shown in Fig. 4.11 clearly cannot be augmented to an optimal 1-plane graph by adding edges to it; note that we deal with only simple graphs in this chapter. Moreover, a 1-plane graph with minimum degree at least 7, e.g., the 7-regular graph shown in Fig. 4.3, cannot be augmented to an optimal 1-plane graph, either; it is an easy exercise for the readers.

Fig. 4.11

1-plane graph which cannot be augmented to an optimal one

We define the following family of graphs to relax the condition. A 1-plane graph G is near optimal, if (i) any face of a subgraph H of G formed by all non-crossing edges is either triangular or quadrangular (i.e., H is known as a mosaic), (ii) any quadrangular face bounded by $v_0v_1v_2v_3$ of H contains the unique crossing point created by a pair of crossing edges $\{v_0v_2, v_1v_3\}$, and (iii) no two triangular faces of G share any edge. For example, it is easy to check that $M(6) \cong K_6$ and M(7) in Fig. 4.10 are near optimal. Furthermore, the 7-regular graph depicted in Fig. 4.3 is also near optimal. It is clear that every optimal 1-plane graph is near optimal, and hence this notion can be regarded as a generalization of optimal 1-planar graphs. Note that any near optimal 1-plane graph has an even number of triangular faces; by applying the Handshake lemma to the dual of the mosaic H.

Proposition 4.14

Every near optimal 1-plane graph with n vertices has at least $\frac{18}{5}n-\frac{36}{5}$ edges.

Proof

Let G be a near optimal 1-plane graph with n vertices. Denote the subgraph of G formed by all non-crossing edges by H. By the above definition (i), H is a plane graph having only triangular and quadrangular faces. Let $F_3$ and $F_4$ denote the numbers of triangular and quadrangular faces of H, respectively; thus, we have $|F(H)|=F_3+F_4$ where F(H) is the set of faces of H. Further, note that $3F_3+4F_4 = 2|E(H)|$, and that $3F_3\le 4F_4$ by property (iii). Then, we have the following by substituting these into Euler’s formula:

$$\begin{aligned} 2|V(H)| - (3F_3+4F_4) +2(F_3+F_4)= & {} 4 \nonumber \\ 2|V(H)| - 4= & {} F_3 + 2F_4 \nonumber \\ 6|V(H)|-12\le & {} 4F_4 + 6F_4 \nonumber \\ \frac{3}{5}|V(H)| - \frac{6}{5}\le & {} F_4. \nonumber . \end{aligned}$$

Clearly, we have $|E(G)|=3|V(G)|-6 + F_4$ and hence the inequality in the statement follows; observe that $|V(G)|=|V(H)|$.    $\square$

The lower bound in Proposition 4.14 is sharp. See Fig. 4.12. The graph depicted in the figure is the smallest one attaining the lower bound in the proposition; in the graph, no two fake faces share a non-crossing edge of G. In fact, we can construct an infinite sequence of graphs attaining the lower bound. (The reader should try to construct such an infinite series of graphs.) Observe that if $F_3=0$ in the above proof, then G is optimal and has $4n-8$ edges.

Fig. 4.12

Near-optimal 1-plane graph with 12 vertices

Proposition 4.15

Every 5-connected maximal 1-plane graph G is near optimal.

Proof

Let G be a 5-connected maximal 1-plane graph. By Proposition 4.5, each crossing point of G lies in a quadrangular face of the subgraph of G formed by all non-crossing edges. Since G is not isomorphic to $K_4$, any face of G is triangular by Proposition 4.6.

Assume, to the contrary, that G has two triangular faces $v_0v_1v_2$ and $v_1v_2v_3$ sharing $v_1v_2$. Since G is a maximal 1-plane graph, there exists an edge joining $v_0$ and $v_3$. If $v_0v_3$ is non-crossing, then G would have a separating 3-cycle $C=v_0v_1v_3$ which consists of only non-crossing edges; otherwise, C bounds a face of G and $v_1$ would have degree 3, contrary to G being 5-connected.

If $v_0v_3$ is crossing, it crosses another edge $u_1u_2$. By Proposition 4.5 again, there exists non-crossing edges $v_0u_1, u_1v_3, v_3u_2$ and $u_2v_0$. Here, observe that we have $\{v_1,v_2\} \cap \{u_1,u_2\}=\emptyset$; otherwise, G would have a vertex of degree 4, which is either $v_1$ or $v_2$. Under the situation, either $v_0v_1v_3u_1$ or $v_0v_1v_3u_2$ is separating, contrary to G being 5-connected. Therefore, the statement holds.    $\square$

Note that Proposition 4.15 implies that every 5-connected 1-plane graph G can be augmented to a near-optimal 1-plane graph by adding edges to G. In the above proposition, the 5-connectivity condition is necessary since the unique 1-embedding M(5) of $K_5$ is not near-optimal.

To obtain an optimal 1-plane graph, we actually need stronger conditions; e.g., the 5-connectivity condition is not sufficient since M(6) in Fig. 4.10, which is the unique embedding of $K_6$ up to weak equivalence is maximum; and hence maximal but not optimal. However, we know some graph classes having our desired property. First, it is easy to see that every 3-connected quadrangulation can be augmented to an optimal 1-plane graph by adding pairs of crossing edges by Theorem 4.2. Furthermore, Noguchi and Suzuki proved the following theorem.

Theorem 4.14

([23]) Every triangulation T of the sphere contains a spanning quadrangulation as a subgraph. Furthermore, if T is 5-connected, then every spanning quadrangulation subgraph of T is 3-connected.

The lower bound 5 on the connectivity of T in Theorem 4.14 is the best possible; i.e., there exist infinitely many 4-connected triangulations of the sphere that do not have the property. As a corollary of the above theorem, it follows that every 5-connected triangulation T of the sphere can be augmented to an optimal 1-plane graph by adding edges to T. Moreover, Noguchi and Suzuki proved the following theorem.

Theorem 4.15

([23]) Let Q be a quadrangulation of the sphere with $|V(Q)|\ge 6$. Then Q can be augmented to a 4-connected triangulation of the sphere by adding a diagonal edge in every face of Q.

Using the above result, we can easily prove the following proposition, which was also shown in [23].

Proposition 4.16

Let G be an optimal 1-plane graph. Then G contains a spanning 4-connected triangulation as a subgraph.

Proof

By Theorem 4.2, G has a 3-connected quadrangulation Q as its subgraph. Since the cube having 8 vertices is the smallest 3-connected quadrangulation of the sphere, Q satisfies the condition of Theorem 4.15. Thus, we can choose one diagonal edge from each pair of crossing edges in the face of Q, so that the resulting graph becomes a 4-connected triangulation. Thus, we got a conclusion.    $\square$

The “4” in the above proposition is clearly the best possible; recall that there are optimal 1-planar graphs with connectivity 4. By the above proposition, we can prove Proposition 4.12 in Sect. 4.3 more easily by using the result [29] again.

4.8 Open Problems

At the end of this chapter, we show some open problems concerning the topics dealt in the chapter.

• 1. Is every 6-connected (or 7-connected) 1-planar graph Hamiltonian? In fact, Noguchi [22] constructed a infinite sequence of non-Hamiltonian 5-connected 1-planar graphs.

• 2. Improve the bounds for the number of edges in maximal 1-planar or 1-plane graphs, mentioned in Sect. 4.4.

• 3. Characterize optimal 1-planar graphs having no $K_n$-minor for $n\ge 8$. Furthermore, characterize optimal 1-planar multigraphs having no $K_n$-minor for $n \ge 5$.

• 4. Is every 7-connected 1-planar graph uniquely 1-embeddable into the sphere? If this is true, then “7” is the best possible since every X-pseudo double wheel, which is 6-connected by Proposition 4.9, has at least two inequivalent 1-embeddings, up to equivalence.

• 5. Is the underlying graph of every near-optimal 1-plane graph is maximal 1-planar?

• 6. Extend the problems in this chapter for 1-embeddings on non-spherical closed surfaces. In [20], it was shown that there is a one-to-one correspondence between simple optimal 1-embeddings of a non-spherical closed surface $\mathbb {F}^2$ and polyhedral quadrangulations of $\mathbb {F}^2$, i.e., 3-connected and 3-representative quadrangulations of $\mathbb {F}^2$. However, little is known about general 1-embeddings on non-spherical surfaces.