The Maximal 1-Planarity and Crossing Numbers of Graphs

Abstract

A 1-planar graph is a graph which has a drawing on the plane such that each edge has at most one crossing. Czap and Hudák showed that every 1-planar graph with n vertices has crossing number at most $n-2$. In this paper, we prove that every maximal 1-planar graph G with n vertices has crossing number at most $n-2-(2\lambda _1+2\lambda _2+\lambda _3)/6$, where $\lambda _1$ and $\lambda _2$ are respectively the numbers of 2-degree and 4-degree vertices in G, and $\lambda _3$ is the number of odd vertices w in G such that either $d_G(w)\le 9$ or $G-w$ is 2-connected. Furthermore, we show that every 3-connected maximal 1-planar graph with n vertices and m edges has crossing number $m-3n+6$.

1 Introduction

All graphs considered here are simple, finite and undirected unless otherwise stated, and all terminology not defined here are referred to [5]. A drawing of a graph $G=(V,E)$ is a mapping D that assigns to each vertex in V a distinct point in the plane and to each edge uv in E a continuous arc connecting D(u) and D(v). We often make no distinction between a graph-theoretical object (such as a vertex, or an edge) and its drawing. All drawings considered here are good unless otherwise specified, meaning that no edge crosses itself, no two edges cross more than once, and no two edges incident with the same vertex cross each other.

For any drawing D, let cr(D) denote the number of crossings in D. The crossing number of a graph G, denoted by cr(G), is the minimum value of cr(D)’s among all drawings D of G.

A drawing D of a graph is called 1-planar if each edge in D is crossed at most once. If a graph has a 1-planar drawing, then it is called 1-planar.

The notion of 1-planarity was introduced in 1965 by Ringel [13], and since then many properties of 1-planar graphs have been studied (e.g. see the survey paper [11]). It is known that any 1-planar graph on n vertices has at most $4n{-}8$ edges [10, 12, 14], and this bound is tight. A 1-planar graph with n vertices and $4n{-}8$ edges is called optimal. A 1-planar graph G is maximal if adding any edge to G yields a graph which is not 1-planar or not simple. A 1-planar drawing D is maximal if no further edge can be added to D without violating 1-planarity or simplicity. Clearly, a graph G is maximal 1-planar if and only if every 1-planar drawing of G is maximal. In this article, we always assume that a 1-planar graph has its order n at least 3.

Czap and Hudák [7] showed that for any 1-planar graph G on n vertices, $cr(D)\le n-2$ holds for each 1-planar drawing D of G, and thus $cr(G)\le n-2$. In this article, we will improve this result.

Theorem 1

Let G be a maximal 1-planar graph with n vertices. Then,

$$\begin{aligned} cr(G)\le n-2-\left( 2\lambda _1+2\lambda _2+\lambda _3\right) /6, \end{aligned}$$

where, for $i=1,2$, $\lambda _i$ denotes the number of 2i-degree vertices of G, and $\lambda _3$ is the number of odd vertices w in G such that either $d_G(w)\le 9$ or $G{-}w$ is 2-connected.

For a maximal 1-planar graph G, if G is 3-connected, then cr(G) can be expressed in terms of its vertex number and edge number.

Theorem 2

Let G be a maximal 1-planar graph with n vertices and m edges. If G is 3-connected, then $cr(G)=m-3n+6$.

A graph is IC-planar if it has a 1-planar drawing so that each vertex is incident to at most one crossed edge [1], and NIC-planar if it has a 1-planar drawing so that two pairs of crossed edges share at most one vertex [16]. A IC-planar graph (resp. NIC-planar) G is called maximal if adding any edge to G yields a graph which is not IC-planar (resp. NIC-planar). We also show that the conclusion of Theorem 2 holds for every maximal IC-planar graph or maximal NIC-planar graph with at least 5 vertices (see Theorem 3).

For any drawing D, let $D^\times$ denote the plane graph obtained by turning each crossing of D into a new vertex. A vertex in $D^{\times }$ is called false if it corresponds to some crossing of D, and is true otherwise. For a 1-planar drawing D on n vertices, in Sect. 2, we will show that cr(D) is equal to $n-2-\frac{1}{2} \sum _{f} (\epsilon (f)-2)$, where the sum runs over all faces f of $D^{\times }$ and $\epsilon (f)$ is the number of true vertices on the boundary of face f.

In Sect. 3, we consider the family ${\mathscr {M}}$ of maximal 1-planar drawings D with the property that redrawing exactly one edge in D does not decrease the number of crossings. We show that for any $D\in {\mathscr {M}}$ and a vertex w in D, if $d_D(w)\in \{2,4\}$, then w is incident with at least two $\Gamma$-faces (i.e., faces f with $\epsilon (f)\ge 3$) of $D^{\times }$; and if $d_D(w)$ is odd and either $d_D(w)\le 9$ or $D-w$ is 2-connected, then w is incident with at least one $\Gamma$-face of $D^{\times }$. The results in Sects. 2 and 3 will be applied in Sect. 4 to prove Theorems 1 and 2.

2 On The Plane Graph $D^\times$

Let D be a drawing. Clearly, $D^{\times }$ is a plane graph. Recall that a vertex in $D^{\times }$ is a false vertex if it is a crossing of two edges in D and a true vertex otherwise. A face or an edge of $D^{\times }$ is called false if it is incident with some false vertex, and is true otherwise.

A multi 1-planar drawing D is a drawing which may have parallel edges and each edge in D may have at most one crossing. A face is called a triangle if its size is 3. A triangulation is a plane graph whose all faces are triangle.

By the definition of multi 1-planar drawings, the following properties hold.

Lemma 1

For any multi 1-planar drawing D of order n and size m, the following hold:

• (i) cr(D) is the number of false vertices in $D^{\times }$;

• (ii) each false vertex in $D^{\times }$ is of degree 4 and is adjacent to true vertices only;

• (iii) $D^{\times }$ is of order $n+cr(D)$ and size $m+2cr(D)$; and

• (iv) any two true vertices are adjacent in $D^{\times }$ if and only if they are adjacent in D and the edge joining them is a true edge of $D^{\times }$.

Recall that for any face f of $D^{\times }$, $\epsilon (f)$ is the number of true vertices on the boundary of f. By Lemma 1, $\epsilon (f)\ge 2$.

Proposition 1

Let D be a 1-planar drawing with at least 3 vertices. Then, D can be extended to a multi 1-planar drawing ${\mathcal {T}}$ by adding some non-crossed edges such that ${\mathcal {T}}^{\times }$ is a triangulation and for each face f of $D^{\times }$, ${\mathcal {T}}^{\times }$ has $\epsilon (f)-2$ true faces within f, and when $\epsilon (f)\ge 3$, each true vertex of $D^{\times }$ on the boundary of f is incident with at least one of these true faces of ${\mathcal {T}}^{\times }$.

Proof

The multi 1-planar drawing ${\mathcal {T}}$ is obtained from D by turning each face of $D^{\times }$ bounded by more than three edges into many triangles.

Let f be any face of $D^{\times }$ with exactly s vertices on its boundary. As D is simple and good, $s\ge 3$. Assume that $t=\epsilon (f)$ and $v_1,v_2,\ldots , v_t$ are the true vertices of $D^{\times }$ which are on the boundary of f in the clockwise direction. By Lemma 1, any two false vertices of $D^{\times }$ are not adjacent, implying that $t\ge s/2$.

If $s=3$, no edge is added within face f. Now assume that $s\ge 4$. Then $t\ge 2$. Face f of $D^{\times }$ is turned into many triangles by adding some new non-crossed edges as stated below (see Fig. 1):

• (i) for $i=1,2,\ldots ,t$, if $v_iv_{i+1}$ is not an edge of $D^{\times }$, add a new edge within f joining $v_i$ and $v_{i+1}$, where $v_{t+1}$ is $v_1$; and

• (ii) for $i=3,\ldots , t-1$, add a new edge within f joining $v_1$ and $v_{i}$.

Observe that, for $i=2,3,\ldots , t-1$, $v_1v_iv_{i+1}v_1$ is the boundary of some face of ${\mathcal {T}}^{\times }$. Thus, ${\mathcal {T}}^{\times }$ has $t-2$ true faces (i.e.,triangles) within f, and when $t\ge 3$, each vertex in the set $\{v_1,v_2,\ldots ,v_t\}$ is incident with at least one true face of ${\mathcal {T}}^{\times }$.

The result holds. $\square$

Fig. 1

Triangulating a face

The following result was recently obtained by Biedl [4].

Proposition 2

[4] Let D be a multi 1-planar drawing with n vertices. If $D^{\times }$ is a triangulation, then $cr(D)=n-2-\tau /2$, where $\tau$ is the number of true faces of $D^{\times }$.

By applying Propositions 1 and 2, we obtain the following result which will be applied in the proof of Theorem 1.

Corollary 1

Let D be a 1-planar drawing with n vertices. Then

$$\begin{aligned} cr(D)=n-2-\frac{1}{2} \sum _{f}\left( \epsilon (f)-2\right) , \end{aligned}$$

where the sum runs over all faces f of $D^{\times }$.

Proof

By Proposition 1, D can be extended to a multi 1-planar drawing ${\mathcal {T}}$ with $cr({\mathcal {T}})=cr(D)$ such that ${\mathcal {T}}^{\times }$ is a triangulation with the following number of true faces:

$$\begin{aligned} \sum _{f} (\epsilon (f)-2), \end{aligned}$$

where the sum runs over all faces f of $D^{\times }$. By Proposition 2, the result holds. $\square$

By Corollary 1, for any 1-planar drawing D of order n, if $D^{\times }$ has at least one true face, then $cr(D)\le n-3$. This conclusion holds for any straight-line 1-planar drawing D with n vertices. A straight-line 1-planar drawing is a 1-planar drawing in which the edges are straight-line segments.

Corollary 2

Every straight-line 1-planar drawing with n vertices has at most $n-3$ crossings.

Proof

Let D be a maximal straight-line 1-planar drawing such that no non-crossed straight-line edges can be added to D (otherwise, we add them). Let f denote the exterior face of $D^{\times }$. As no more non-crossed straight-line edges can be added to D, the boundary of f is a convex polygon. Since the segments of this convex polygon correspond to true edges of $D^{\times }$, f is a true face of $D^{\times }$, i.e., $\epsilon (f)\ge 3$. By Corollary 1, $cr(D)\le n{-}3$. $\square$

Recall that every planar graph with n vertices has at most $3n{-}6$ edges. The following corollary follows immediately from Corollary 2.

Corollary 3

[8] Every straight-line 1-planar drawing with n vertices has at most $4n-9$ edges.

3 Maximal 1-Planar Drawings

3.1 Basic Properties of Maximal 1-Planar Drawings

In the following are two properties on maximal 1-planar drawings from [3, 6].

Proposition 3

[3, 6] Let D be a maximal 1-planar drawing. For any face f of $D^\times$, any two vertices of D on the boundary of f are adjacent in D.

Proposition 4

[3, 6] Let D be a maximal 1-planar drawing. If $u_1u_2$ and $v_1v_2$ are a pair of crossing edges in D, then, the subgraph of D induced by $\{u_1,u_2,v_1,v_2\}$ is the complete graph $K_4$.

By Proposition 4, any pair of edges $e_1$ and $e_2$ in a maximal 1-planar drawing D which cross each other is covered by a complete graph $K_4$, which is called a kite of D corresponding to $e_1$ and $e_2$.

Let ${\mathscr {M}}$ denote the set of maximal 1-planar drawings D such that $cr(D)\le cr(D')$ holds for any 1-planar drawing $D'$ which is obtained from D by redrawing exactly one edge of D. More properties on kites in $D\in {\mathscr {M}}$ are given below.

Lemma 2

Let $D\in {\mathscr {M}}$ and W be a kite of D. If W corresponds to edges $e_1$ and $e_2$ of D, then $e_1$ and $e_2$ are the only edges in W which are crossed edges of D.

Proof

Assume that $e=uv$ is a crossed edge in W and $e\ne e_1,e_2$. Then, one can redraw a curve $e'$ to represent e which does not cross with any other edge of D, as shown in Fig. 2. The resulting drawing is 1-planar and has lower crossing number than D, contradicting assumption that $D\in {\mathscr {M}}$. Hence the result holds. $\square$

Fig. 2

Redrawing an edge joining u and v without a crossing

For any graph G and any vertex w in G, let $E_G(w)$ denote the set of edge in G which are incident with w.

Lemma 3

Let $D\in {\mathscr {M}}$ and, let W and $W'$ be different kites of D. Then

• (i) W and $W'$ do not contain any common crossed edge of D; and

• (ii) for any vertex w in W and any vertex $w'$ in $W'$, $|E_{W}(w)\cap E_{W'}(w')|\le 1$ holds.

Proof

(i) Assume that W corresponds to edges wv and $u_1u_2$, and $W'$ corresponds to edges $w'v'$ and $u'_1u'_2$. By Lemma 2, wv and $u_1u_2$ are the only crossed edges of D in W and $w'v'$ and $u'_1u'_2$ are the only crossed edges of D in $W'$.

Assume that c is the false vertex of $D^{\times }$ at which wv and $u_1u_2$ cross each other, and $c'$ is the false vertex of $D^{\times }$ at which $w'v'$ and $u'_1u'_2$ cross each other.

Claim 1

$\{wv,u_1u_2\}\cap \{w'v',u'_1u'_2\}=\emptyset$.

Suppose that wv and $w'v'$ are the same edge of D. Then c and $c'$ are the same vertex, implying that $u_1u_2$ and $u'_1u'_2$ are the same edge of D. Thus W and $W'$ must be the same kite, a contradiction.

So Claim 1 holds and (i) also holds.

(ii) We will prove it by showing the following claims.

Claim 2

$wv\notin E_{W'}(w')$ and $w'v'\notin E_{W}(w)$.

As wv is a crossed edge of D and both $w'u'_1$ and $w'u'_2$ are non-crossed edges of D, $\{wv\}\cap E_{W'}(w')\subseteq \{wv\}\cap \{w'v'\}$. But, by Claim 1, $\{wv\}\cap \{w'v'\}=\emptyset$. The same thing happens for $w'v'$. Thus, Claim 2 holds.

Claim 3

$\{wu_1,wu_2\}\ne \{w'u'_1,w'u'_2\}$.

Suppose that $\{wu_1,wu_2\}=\{w'u'_1,w'u'_2\}$. Then $u_1u_2$ and $u'_1u'_2$ are the same edge in D, contradicting Claim 1.

Thus, Claim 3 holds. By Claims 2 and 3, (ii) holds. $\square$

3.2 $\Gamma$-Faces

Recall that for a 1-planar drawing D, a face f of $D^{\times }$ is a $\Gamma$-face if $\epsilon (f)\ge 3$. Obviously, each true face of $D^{\times }$ is a $\Gamma$-face. Some basic properties on $\Gamma$-faces follow from the definition.

Lemma 4

Let D be a 1-planar drawing. For any face f of $D^{\times }$, if one of the following conditions hold, then f is a $\Gamma$-face of $D^{\times }$:

• (i) the boundary of f contains more than 4 vertices of $D^{\times }$;

• (ii) the boundary of f contains 4 vertices of $D^{\times }$ and two consecutive vertices on this boundary are true vertices of $D^{\times }$; or

• (iii) the boundary of f contains at least two true edges.

Proof

(i) and (ii) follow from the fact that any two false vertices of $D^{\times }$ are not adjacent, while (iii) follows from the definition. $\square$

A drawing of a graph implies a rotation system. The rotation at a vertex is the clockwise order of its incident edges. In a drawing, two edges incident with some vertex w are called to be consecutive if they appear in sequence in the cyclic ordering at w. In the following, we study vertices w in $D\in {\mathscr {M}}$ which are incident with $\Gamma$-faces of $D^{\times }$.

Lemma 5

Let $D\in {\mathscr {M}}$ and w be a vertex in D. Then $d_D(w)\ge 2$ and

• (i) if $d_D(w)=2$, then w is incident with two $\Gamma$-faces of $D^{\times }$; and

• (ii) if $3\le d_D(w)\le 4$, then w is incident with at least $(d_D(w)-2)$ $\Gamma$-faces of $D^{\times }$.

Proof

It is known that every maximal 1-planar drawing is 2-connected [9, 15]. This implies that $d_D(w)\ge 2$.

(i) Assume that $d_D(w)=2$ and w is incident with edges $e_1$ and $e_2$. If both $e_1$ and $e_2$ are true edges of $D^{\times }$, by Lemma 4 (iii), w is incident with two $\Gamma$-faces of $D^{\times }$.

Suppose that some edge $e_i$ is not a true edge in $D^{\times }$, where $1\le i\le 2$. By Proposition 4, $d_D(w)\ge 3$, a contradiction. Thus, (i) holds.

(ii) Assume that $3\le d_D(w)\le 4$.

Claim 1: w is incident with at most one crossed edge of D.

Suppose that $e_1$ and $e_2$ be two crossed edges of D which are incident with w. Then w is a common vertex in two kites W and $W'$ of D. By Lemma 3,

$$\begin{aligned} d_D(w)\ge d_W(w)+d_{W'}(w)-1\ge 5, \end{aligned}$$

contradicting the condition that $d_D(w)\le 4$. Thus Claim 1 holds.

As $3\le d_D(w)\le 4$, Claim 1 implies that w is incident with at least $d_D(w)-2$ pairs of consecutive true edges of D. By Lemma 4 (iii), w is incident with at least $d_D(w)-2$ faces which are $\Gamma$-faces of $D^{\times }$.

Hence (ii) holds. $\square$

Note that an even-degree vertex w in D with $d_D(w)>4$ may be not incident with any $\Gamma$-face of $D^{\times }$. For an odd vertex w in $D\in {\mathscr {M}}$, we can show that w is incident with some $\Gamma$-face of $D^{\times }$ under certain condition.

Lemma 6

Let $D\in {\mathscr {M}}$ and w be an odd vertex in D. If either $d_D(w)\le 9$ or $D-w$ is 2-connected, then w is incident with at least one $\Gamma$-face of $D^{\times }$.

Proof

Let w be an odd vertex in D such that $d_D(w)\le 9$ or $D-w$ is 2-connected. We may assume that the conclusion holds whenever such an odd vertex is of degree less than $d_D(w)$.

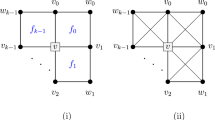
Suppose that the conclusion fails for w. By Lemma 5, $d_D(w)\ge 5$. By Lemma 4 (iii), any two consecutive edges at w cannot be both true edges of $D^{\times }$. As $d_D(w)$ is odd, w is incident with two consecutive edges $wc_1$ and $wc_2$ of $D^{\times }$ which are both false edges of $D^{\times }$, where $c_1$ and $c_2$ are false vertices of $D^{\times }$. Let $\alpha$ denote the face of $D^{\times }$ whose boundary contains vertices $w,c_1$ and $c_2$, as shown in Fig. 3a. As $\alpha$ is not a $\Gamma$-face, by Lemma 4 (i), its boundary contains at most 4 vertices. As the boundary of $\alpha$ has two false vertices $c_1$ and $c_2$, it contains two true vertices of $D^{\times }$, i.e., w and u as shown in Fig. 3a.

Fig. 3

1-planar drawing D

Since $D\in {\mathscr {M}}$, by Proposition 4 and Lemma 2, w and u are adjacent in D, and the edge joining w and u, denoted by e, is a true edge of $D^{\times }$, as shown in Fig. 3a.

For $i=1,2$, let $v_i$ be the vertex of D which is adjacent to w and $c_i$ be on the edge $v_iw$. Observe that any path in D connecting $v_1$ and $v_2$ contains either w or u, implying that $D-w$ is not 2-connected. Thus, by the given condition, $d_D(w)\le 9$ holds.

For $i=1,2$, let $C_i$ denote the cycle formed by edges wu ($=e$), $wc_i$ and $uc_i$. As $D^{\times }$ is a plane graph, each $C_i$ partitions $D^{\times }$ into three subsets $V_{i,0},V_{i,1}$ and $V_{i,2}$, where

• (i) $V_{i,0}=\{w,u,c_i\}$, i.e., the set of vertices on $C_i$;

• (ii) $V_{i,1}$ is the set of vertices of D which are in the interior regions of $C_i$; and

• (iii) $V_{i,2}$ is the set of vertices of D which are in the exterior regions of $C_i$.

Observe that either $c_1\in V_{2,1}$ or $c_2\in V_{1,1}$. Without loss of generality, assume that $c_1\in V_{2,1}$.

Let $D_1$ be the 1-planar drawing obtained from D by removing all vertices of D in $V_{1,2}$, and $D_2$ be the 1-planar drawing obtained from D by removing all vertices of D in $V_{2,1}$, as shown in Fig. 3b and c. It can be verified that both $D_1$ and $D_2$ belongs to ${\mathscr {M}}$.

Note that $d_{D_1}(w)+d_{D_2}(w)=d_{D}(w)+1$ and $d_{D_i}(w)<d_{D}(w)$ for both $i=1,2$. By the assumption on the minimality of $d_D(w)$, if $d_{D_i}(w)$ is odd for some i, then w is incident with some $\Gamma$-face of $D_i^{\times }$. Such a $\Gamma$-face of $D_i^{\times }$ is also a $\Gamma$-face of $D^{\times }$, a contradiction. Thus, both $d_{D_1}(w)$ and $d_{D_2}(w)$ are even.

Without loss of generality, assume that $d_{D_1}(w)\le d_{D_2}(w)$. Thus $d_{D_1}(w)\le (d_{D}(w)+1)/2\le 5$. As $d_{D_1}(w)$ is even, we have $d_{D_1}(w)\in \{2,4\}$. By Lemma 5, w is incident with some $\Gamma$-face f of $D_1^{\times }$. Clearly, f is also a $\Gamma$-face of $D^{\times }$.

Thus the result holds. $\square$

4 The Main Results

4.1 Proving Theorem 1

We can now apply Lemmas 5 and 6 to prove Theorem 1.

Proof of Theorem 1

Let D be a 1-planar drawing of G and $D\in {\mathscr {M}}$. By Lemma 5, each 2-degree or 4-degree vertex in D is incident with at least two $\Gamma$-faces of $D^\times$. Let $V^*$ denote the set of odd vertices v in D such that either $d_G(v)\le 9$ or $G-v$ is 2-connected. By Lemma 6, each vertex v in $V^*$ is incident with at least one $\Gamma$-face of $D^\times$.

We will complete the proof by applying Corollary 1.

Let ${\mathcal {F}}_D$ denote the set of faces in $D^{\times }$, and for any vertex v in D, let ${\mathcal {F}}_D(v)$ denote the set of faces in $D^{\times }$ which are incident with v. Recall that for each f of $D^{\times }$, $\epsilon (f)$ is the number of true vertices on the boundary of f. Then

$$\begin{aligned} \sum _{f\in {\mathcal {F}}_D} (\epsilon (f)-2) =&\sum _{v\in V(D)} \sum _{f\in {\mathcal {F}}_D(v)}\left( \frac{\epsilon (f)-2}{\epsilon (f)}\right) \nonumber \\ \ge&\sum _{\begin{array}{c} v\in V(D) \\ d_G(v)\in \{2,4\} \end{array}} \sum _{f\in {\mathcal {F}}_D(v)}\left( \frac{\epsilon (f)-2}{\epsilon (f)}\right) + \sum _{v\in V^*} \sum _{f\in {\mathcal {F}}_D(v)} \left( \frac{\epsilon (f)-2}{\epsilon (f)}\right) \nonumber \\ \ge&2(\lambda _1+\lambda _2)/3+\lambda _3/3, \end{aligned}$$

(1)

where the last expression follows from the fact that $\frac{\epsilon (f)-2}{\epsilon (f)}\ge 1/3$ holds for each $\Gamma$-face f.

Thus, by (1) and Corollary 1, $cr(G)\le cr(D)\le n-2-(2\lambda _1+2\lambda _2+\lambda _3)/6$. $\square$

Remark The maximal 1-planar graph depicted in Fig. 4 is 7-regular and of order 24. By Lemma 8 in Sect. 4.2, we know that it has crossing number 18. This implies that the upper bound in Theorem 1 is tight.

Fig. 4

A graph which shows that the upper bound in Theorem 1 is tight

From [4], we know that any 1-planar graph with minimum degree 7 has at least 24 vertices of degree 7. It is known that 1-planar graphs have minimum degree at most 7 and every 1-planar graph can be extended to a maximal 1-planar graph by adding some edges without reducing the crossing number. Thus, the following conclusion follows immediately from Theorem 1.

Corollary 4

Any 1-planar graph with n vertices and minimum degree 7 has crossing number at most $n{-}6$.

It is well-known that any graph with n vertices and m edges has crossing number at least $m-3n+6$. Hence, any optimal 1-planar graph has crossing number at least $n{-}2$. Thus, the following result holds by Theorem 1.

Corollary 5

Any optimal 1-planar graph has minimum degree 6.

4.2 Proving Theorem 2

We need to establish two results for proving Theorem 2.

Lemma 7

Let $D\in {\mathscr {M}}$ with at least 5 vertices. If D is 3-connected, then $D^{\times }$ is a triangulation.

Proof

Suppose that $D^{\times }$ is not a triangulation. Then $D^{\times }$ has a face f bounded by a cycle C with at least 4 vertices. As any two false vertices in $D^{\times }$ are not adjacent, $D^{\times }$ has two true vertices u and v in C which are not adjacent in C. As $D \in {\mathscr {M}}$, by Proposition 3, u and v must be adjacent in D.

Let e denote the edge in D joining u and v. We claim that e is non-crossed in D. Otherwise, we can redraw a curve within face f to represent edge e and the new 1-planar drawing has less crossings than D, a contradiction.

Note that C can be divided into two paths, denoted by $P_1$ and $P_2$, with end u and v. As u and v are not adjacent in C, each $P_i$ contains an internal vertex $z_i$, as shown in Fig. 5.

As $D^{\times }$ is a plane graph, it can be verified that any path in $D^{\times }$ connecting $z_1$ and $z_2$ must pass through u or v, implying that $z_1$ and $z_2$ are in different components $D_1$ and $D_2$ of $D^{\times }-\{u,v\}$. As each false vertex in $D^{\times }$ is adjacent to 4 true vertices, both $D_1$ and $D_2$ contain true vertices. Thus, $D-\{u,v\}$ is disconnected, contradicting the given condition.

Hence the result holds. $\square$

Fig. 5

A face in $D^{\times }$ bounded by at least four edges

Lemma 8

Let G be a graph with n vertices and m edges. Then, there exists a drawing D of G with each face in $D^\times$ being a triangle if and only if $cr(G)=m-3n+6$.

Proof

(Necessity) Suppose that D is a drawing of G with c crossings and each face of $D^\times$ is a triangle. Then, $D^\times$ has $n+c$ vertices and $m+2c$ edges. Let $\phi$ be the number of faces of $D^\times$. Then, $3\phi =2(m+2c).$ By Eular’s formula, we have

$$\begin{aligned} n+c-(m+2c)+2(m+2c)/3=2, \end{aligned}$$

which implies that $cr(G)\le c= m-3n+6$.

As each maximal plane graph on n vertices has exactly $3n-6$ edges, $cr(G)\ge m-3n+6$ holds. Thus the necessity holds.

(Sufficiency) Assume that $cr(G)=m-3n+6$. Then, there is a drawing D of G with exactly $m-3n+6$ crossings. So $D^\times$ has exactly $m-2n+6$ vertices and $3(m-2n+4)$ edges, i.e, $|E(D^\times )|=3|V(D^\times )|-6$. This implies that each face of $D^\times$ is a triangle. $\square$

By Lemmas 7 and 8, we can now prove Theorem 2 easily.

Proof of Theorem 2:

Let D be a 1-planar drawing of G and $D\in {\mathscr {M}}$. As G is 3-connected, D is also 3-connected. By Lemma 7, $D^\times$ is a triangulation. Then, by Lemma 8, $cr(G)=m-3n+6$. $\square$

The conclusion of Theorem 2 also holds for IC-planar and NIC-planar graphs. Bachmaier et al. [2] has showed that a NIC-planar drawing of any maximal NIC-planar graph with at least 5 vertices is a triangulation. By applying a similar argument, one can show that an IC-planar drawing of any maximal IC-planar graph with at least 5 vertices is a triangulation. Thus, by Lemma 8, the following conclusion holds.

Theorem 3

Let G be a maximal IC-planar (or NIC-planar) graph with $n\ge 5$ vertices and m edges. Then, $cr(G)=m-3n+6$.

5 Unsolved Problems

We wonder if the conclusion of Theorem 1 holds if $\lambda _3$ is changed to be the number of all odd vertices.

Problem 1

For any maximal 1-planar graph G with n vertices, does $cr(G)\le n-2-(2\lambda _1+2\lambda _2+\lambda _3)/6$, where, for $i=1,2$, $\lambda _i$ denotes the number of 2i-degree vertices of G, and $\lambda _3$ is the number of odd vertices in G?