Non-linear State Space Formulation Simulating Single Station Ride Dynamics of Military Vehicle

Abstract

Military vehicles are generally equipped with hydro-gas suspension systems that exhibit better shock-absorbing capability over drastic dynamic environments compared to linear suspension. In order to implement suspension semi-active/active control in the future, it is required to develop the mathematical model of the vehicle using non-linear state space approach by incorporating the hydro-gas suspension trailing arm dynamics in the governing equations of motion. The present study formulates the non-linear state space approach which simulates single station ride dynamics of military vehicles. Incorporating the developed trailing arm kinematics and non-linear suspension characteristics, non-linear state space approach has been used to formulate the sprung and unsprung mass governing equations of motion. The multi-body dynamics model for the single station is established in MSC.ADAMS in order to validate the non-linear state space model. The mathematical model is solved using MATLAB and compares well with the multi-body model simulations. The entire military vehicle non-linear state space model can also be developed which would be suitable for carrying out vehicle dynamics control studies with active or semi-active suspension systems.

1 Introduction

The military vehicles are generally equipped with hydro-gas suspension systems in order to have a better shock-absorbing capability over the drastic dynamic environment compared to that of linear suspension. Therefore, for future implementation of semi-active or active control system, it is an important pre-requisite to determine the transmitted vibration levels to the vehicle with passive suspension. Gillespie [1] provided a detailed overview of the fundamental theory of vehicle dynamics. Solomon and Padmanaban [2] have proposed a polytropic gas compression model to describe the spring characteristics and hydraulic conductance model to represent the damper characteristics of hydro-gas suspension system. The above spring and damper models have been incorporated in a vehicle dynamic in-plane math model and carried out simulations for sinusoidal and Axle Proving Ground (APG) terrains as well as validated with experimental measurements [2]. Dhir and Shankar [3] have derived the tracked vehicle math model by using the Lagrangian method over a hard terrain and constant vehicle speed. The track–terrain interaction has been considered and ride dynamic analysis of an Armoured Personal Carrier vehicle has been carried out [3]. Rakheja et al. [4] have carried out a comparative ride dynamic studies of a non-linear vehicle dynamic in-plane model with active and passive suspensions. However, in [2,3,4], the trailing arm dynamics for each of the suspension stations have not been considered. The equivalent vertical stiffness and damping parameters have been derived from the trailing arm kinematics. The effect of trailing arm dynamic behaviour will be quite different from the vertical suspension system which requires to be mathematically formulated. Moreover, the above studies do not include the roll mode of the vehicle. Sujatha et al. [5] have carried out an experimental ride dynamic evaluation of a 6 station military vehicle with torsion bar suspension. Accelerations have been obtained at specified locations over various dynamic environments and analysed [5]. Balamurugan [6] has developed a finite element model of a highly mobile military-tracked vehicle over a hard road for estimating the ride characteristics. Hada [7] has derived the dynamic behaviour of a 12 station tracked vehicle with torsion bar suspension. It is observed that [5,6,7] does not take into account non-linear effects of the hydro-gas suspension. Subburaj et al. [8] have described the solution methodology for structural dynamics problems through implicit procedures with a detailed description on the solution stability. Paduart et al. [9] have proposed a state space methodology that deals with Multiple Input and Multiple Output (MIMO) systems. Reddy [10] provided a detailed overview on the finite element methods and practice. Banerjee et al. [11] have described the trailing arm suspension dynamics for a single station of a tracked vehicle. In [2,3,4,5,6,7], the vehicle dynamics have not been modelled using non-linear state space approach. It is noteworthy that extensive research has undergone in the area of vehicle dynamics.

The present study describes the non-linear state space mathematical method for formulating the military vehicle single station ride dynamics by incorporating the trailing arm kinematic and dynamic behaviour. Subsequent validation studies have been carried out with numerical experiments which are based on the developed MSC.ADAMS multi-body dynamics model. Reference [11] provided a systematic approach to bring out the significance of the physical dynamic behaviour of the trailing arm suspension and effects of inertia coupling between the sprung and upsprung masses on the ride dynamics. However, in the present paper, the developed state space model of single station with trailing arm dynamic effects can be used for implementing semi-active and active control techniques for ride vibration control unlike the mathematical model described in [11]. The above mathematical state space ride model when extended for a full military vehicle model would also serve as a useful input to a driving simulator.

2 State Space Approach for Single Station Representation

Initially, the hydro-gas suspension kinematics which was derived in Sect. 2.1 [11] has further been simplified for implementation in the state space matrix. The stiffness non-linearities which pertain to various charging pressures have been expressed as binomial series in terms of axle arm angular displacement. The angular motion behaviour of trailing arm unsprung mass has been expressed with the Taylor series expansion in terms of axle arm angular displacement for suitable implementation in state space matrix. Following the above mathematical representations, non-linear state space domain matrices are formulated and solved in MATLAB. The sprung mass dynamics responses have been compared and validated with the MBD model which is subjected to standard terrain excitations.

3 Implementation of Suspension Kinematics in State Space Matrix

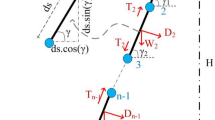
Figures 1 and 2 represent the hydro-gas suspension assembly and kinematic description of the same.

Fig. 1

Trailing arm suspension model

Fig. 2

Trailing arm suspension mechanism

Referring to Sect. 2.1 [11], the trailing arm suspension kinematic relations can be expressed as

$$ \begin{aligned} x = {\text{sqrt}}\left( {L_{p}^{2} - \left[ {L_{c} \left\{ {\cos \left( {\beta + \gamma } \right) - \cos \left( {\beta - \varphi + \gamma } \right)} \right\} + L_{p} \sin \left( \delta \right)} \right]^{2} } \right) \hfill \\ \,\,\,\,\, + L_{c} \left\{ {\sin \left( {\beta + \gamma } \right) - \sin \left( {\beta - \varphi + \gamma } \right)} \right\} - L_{p} \cos \left( \delta \right). \hfill \\ \end{aligned} $$

(1)

For the convenience of incorporation of suspension kinematics in the non-linear state space matrix, a factor $f$ is determined from Eq. (1) such that

$$ f = x/\varphi . $$

(2)

Differentiating $x$ in Eq. (2) with respect to time t,

$$ \dot{x} = \frac{dx}{dt} = \frac{dx}{d\varphi }\frac{d\varphi }{dt} . $$

$$ \therefore \dot{x} = f1 \cdot \dot{\varphi }, $$

(3)

where

$$ \begin{aligned} f1 = \frac{dx}{d\varphi } = \frac{{\left[ {L_{c} \left\{ {\cos \left( {\beta + \gamma } \right) - \cos \left( {\beta - \varphi + \gamma } \right)} \right\} + L_{p} \sin \left( \delta \right)} \right]\left\{ {L_{c} \sin \left( {\beta - \varphi + \gamma } \right)} \right\}}}{{{\text{sqrt}}\left( {L_{p}^{2} - \left[ {L_{c} \left\{ {\cos \left( {\beta + \gamma } \right) - \cos \left( {\beta - \varphi + \gamma } \right)} \right\} + L_{p} \sin \left( \delta \right)} \right]^{2} } \right) }} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + L_{c} { \cos }\left( {\beta - \varphi + \gamma } \right). \hfill \\ \end{aligned} $$

It is observed from Eq. (3) that the piston velocity can be related to the axle arm angular displacement and velocity. Suitable kinematic simplifications are carried out through Eqs. (2) and (3) for incorporation in the state space matrix. It may be noted that hydro-gas suspension kinematics have a mild non-linearity. The following sections describe the method of incorporating non-linearity due to suspension stiffness in state space matrix domain.

4 Determination of Non-linear Stiffness Characteristics of Suspension

Referring to Sect. 4.2 [11], the suspension kinematics have been used to determine the non-linear stiffness characteristics which are highlighted through Eqs. (4)–(6) as

$$ P_{reb} V_{o}^{n} = P\left( {V_{o} - V_{1} } \right)^{n} , $$

(4)

$$ F_{p} = P\pi d^{2} /4, $$

(5)

$$ T = F_{p} L_{o} . $$

(6)

Due to static angular rotation of the axle arm by $\varphi_{st}$, the actuator piston displacement $x_{st}$ takes place in line with the actuator cylinder axis. The reaction moment about pivot point ‘O’ is $T_{st}$ at a statically settled position. Subsequent to the static settlement, the axle arm rotation is described by $\varphi_{l}$ due to terrain excitation. This in turn causes the reaction moment $T_{l}$ due to displacement of the actuator piston by $x$ in line with the actuator cylinder axis.

From Eqs. (4)–(6),

$$ T_{st} = \frac{{p_{reb} V_{0}^{n} }}{{\left( {V_{0} - {{\pi d^{2} x_{st} } \mathord{\left/ {\vphantom {{\pi d^{2} x_{st} } \text{4}}} \right. \kern-0pt} \text{4}}} \right)^{n} }}\frac{\pi }{\text{4}}d^{ 2} L_{0}, $$

(7)

$$ T_{l} = \frac{{p_{reb} V_{0}^{n} }}{{\left( {V_{0} - {{\pi d^{2} x_{st} } \mathord{\left/ {\vphantom {{\pi d^{2} x_{st} } \text{4}}} \right. \kern-0pt} \text{4}} - {{\pi d^{2} x} \mathord{\left/ {\vphantom {{\pi d^{2} x} \text{4}}} \right. \kern-0pt} \text{4}}} \right)^{n} }}\frac{\pi }{\text{4}}d^{ 2} L_{0}. $$

(8)

Using Eq. (2), Eq. (8) may be written as

$$ T_{l} = \frac{{p_{reb} V_{0}^{n} }}{{\left( {V_{0} - {{\pi d^{2} x_{st} } \mathord{\left/ {\vphantom {{\pi d^{2} x_{st} } \text{4}}} \right. \kern-0pt} \text{4}} - {{\pi d^{2} f\varphi_{l} } \mathord{\left/ {\vphantom {{\pi d^{2} f\varphi_{l} } \text{4}}} \right. \kern-0pt} \text{4}}} \right)^{n} }}\frac{\pi }{\text{4}}d^{ 2} L_{0}. $$

(9)

The non-linear force–displacement characteristics can be derived from the above equations which are highlighted in Fig. 3 for different rebound gas pressures.

Fig. 3

Gas restoring force variation with piston displacement for rebound pressures of 11.4 and 13 MPa

4.1 Taylor Series Approximation of Hydro-Gas Suspension Spring Restoring Moment

Subsequent to the achievement of the static equilibrium configuration (described in [11]), the hydro-gas suspension spring restoring moment about the static position $(T_{l} - T_{st} )$ is required to be expressed in terms of $\varphi_{l}$ in order to facilitate the transformation of the coupled equations of motion into matrix domain.

From Eqs. (8) and (9), if

$$ \frac{{V_{o} }}{{\frac{\pi }{4}d^{2} }} - x_{st} = l_{2} \,\,{\text{and }}\frac{{p_{reb} V_{o}^{n} }}{{\left( {\frac{\pi }{4}d^{2} } \right)^{n} }} \frac{\pi }{4}d^{2} L_{o} = K , $$

Then

$$ \left( {T_{l} - T_{st} } \right) = \frac{K}{{\left( {l_{2} - x} \right)^{n} }} - \frac{K}{{\left( {l_{2} } \right)^{n} }} = \frac{K}{{\left( {l_{2} } \right)^{n} }}\left[ {\left( {1 - {\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x {l_{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${l_{2} }$}}} \right)^{ - n} - 1} \right]. $$

(10)

Also, the expression $\left( {1 - {\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x {l_{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${l_{2} }$}}} \right)^{ - n}$ in Eq. (10) may be expanded in binomial series which is truncated after the fifth term as

$$ \begin{aligned} \left( {1 - {\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x {l_{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${l_{2} }$}}} \right)^{ - n} = 1 + \frac{nx}{{l_{2} }} + \frac{{n\left( {n + 1} \right)}}{{2l_{2}^{2} }}x^{2} + \frac{{n\left( {n + 1} \right)\left( {n + 2} \right)}}{{6l_{2}^{3} }}x^{3} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{n\left( {n + 1} \right)\left( {n + 2} \right)\left( {n + 3} \right)}}{{24l_{2}^{4} }}x^{4} + \frac{{n\left( {n + 1} \right)\left( {n + 2} \right)\left( {n + 3} \right)\left( {n + 4} \right)}}{{120l_{2}^{5} }}x^{5}. \hfill \\ \end{aligned} $$

The truncation was based on a trial and error method. Simulations have also been carried out with higher order terms in the state space matrix; but, an insignificant difference in results has been obtained. Therefore, the binomial series have been truncated accordingly. This is a reasonable approximation by considering the dynamic range of angular operation of the axle arm which is normally limited within 30° from static equilibrium position. Using the above binomial series and Eq. (2) in Eq. (10),

$$ \left( {T_{l} - T_{st} } \right) = K\left( {\varphi_{l} } \right)\varphi_{l}, $$

(11)

where

$$ \begin{gathered} K\left( {\varphi _{l} } \right) = \frac{K}{{l_{2} ^{n} }}\left[ {\frac{{nf}}{{l_{2} }} + \frac{{n\left( {n + 1} \right)f^{2} }}{{2l_{2} ^{2} }}\varphi _{l} + \frac{{n\left( {n + 1} \right)\left( {n + 2} \right)f^{3} }}{{6l_{2} ^{3} }}\varphi _{l} ^{2} {\text{~}}} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{n\left( {n + 1} \right)\left( {n + 2} \right)\left( {n + 3} \right)f^{4} }}{{24l_{2} ^{4} }}\varphi _{l} ^{{3~}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { + \frac{{n\left( {n + 1} \right)\left( {n + 2} \right)\left( {n + 3} \right)\left( {n + 4} \right)f^{5} }}{{120l_{2} ^{5} }}\varphi _{l} ^{{4~}} } \right]. \hfill \\ \end{gathered} $$

Equation (11) relates the spring dynamics restoring moment and rotational angle of the axle arm. Equation (11) is of non-linear nature in terms of the angular rotation of axle arm about the static position. This relation may be directly implemented while transforming the coupled equations of motion into non-linear state space matrix domain.

5 Formulation of State Space Mathematical Single Station Ride Model

The model description is similar to Sect. 5 [11]. It may be noted that in practice, the unsprung mass is distributed partly on the axle arm. However, the axle arm mass is less compared to that of the road-wheel and track pad. Therefore, the unsprung mass has been lumped at the road-wheel centre. However, the present mathematical formulation may similarly be extended for a distributed unsprung mass.

5.1 Single Station Mathematical Model Using Non-linear State Space Approach

The governing differential equations of motion which are described in Sect. 5.2 [11] have been transformed into non-linear state space domain for both the sprung and unsprung masses. The state space approach has been followed subsequent to the static settlement of the two degree of freedom single station model. The static equilibrium equations have been derived in Sect. 5.1 [11]. With reference to Sect. 5.3 [11], the dynamic behaviour of the single station model as well as free body diagrams for the sprung and unsprung masses are shown in Fig. 4a, b and c, respectively. The state space mathematical model comprises similar nomenclature as described in Table 1 [11].

Fig. 4

a Application of ground excitation to the single station model, b Sprung mass force representation, c Unsprung mass moment representation

5.2 Sprung Mass Bounce Motion in the State Space Domain

With reference to Sect. 5.3 [11], the sprung mass bounce is described by Eq. (12) as

$$ \left( {M + m_{l} } \right)\ddot{X} + m_{l} \ddot{X}_{\varphi } + k_{t} \left( {X + X_{\varphi } - Y} \right) = 0\,, $$

(12)

where

$$ X_{\varphi } = L{ \cos }\left( {\rho_{l} } \right) - L{ \cos }\left( {\rho_{l} + \varphi_{l} } \right); \rho_{l} = \alpha_{l} + \varphi_{st}, $$

$$ \ddot{X}_{\varphi } = L\dot{\varphi }_{l}^{2} \cos \left( {\rho_{l} + \varphi_{l} } \right) + L\ddot{\varphi }_{l} { \sin }\left( {\rho_{l} + \varphi_{l} } \right) = L\dot{\varphi }_{l}^{2} \cos \left( {\rho_{l} + \varphi_{l} } \right) + L_{\varphi } \ddot{\varphi }_{l}, $$

$$ L_{\varphi } = L{ \sin }\left( {\rho_{l} + \varphi_{l} } \right). $$

Now, ${ \cos }\left( {\rho_{l} + \varphi_{l} } \right) = \cos \left( {\rho_{l} } \right)\cos \left( {\varphi_{l} } \right) - \sin \left( {\rho_{l} } \right){ \sin }\left( {\varphi_{l} } \right).$

Also, $\cos \left( {\varphi_{l} } \right)$ and $\sin \left( {\varphi_{l} } \right)$ may be expanded into the Taylor series as shown below (neglecting higher order terms),

$$ \cos \left( {\varphi_{l} } \right) = 1 - \frac{{\varphi_{l}^{2} }}{2} + \frac{{\varphi_{l}^{4} }}{24} , $$

$$ \sin \left( {\varphi_{l} } \right) = \varphi_{l} - \frac{{\varphi_{l}^{3} }}{6} + \frac{{\varphi_{l}^{5} }}{120} . $$

The truncation of the above trigonometric expressions for $\varphi_{l}$ is based on trial and error method which is explained in Sect. 4.1. Using the above conversions and expressing trigonometric expressions of variable $\varphi_{l}$ as the Taylor series expansion,

$$ k_{t} X_{\varphi } = \left[ {k_{1} - k_{1} \left\{ {1 - \frac{{\varphi_{l}^{2} }}{2} - \frac{{\varphi_{l}^{4} }}{24}} \right\} + k_{2} \left\{ {\varphi_{l} - \frac{{\varphi_{l}^{3} }}{6} + \frac{{\varphi_{l}^{5} }}{120}} \right\}} \right]. $$

(13)

$$ \therefore k_{t} X_{\varphi } = k_{t} \left( {\varphi_{l} } \right)\varphi_{l} \;, $$

(14)

where $k_{1} = k_{t} L{ \cos }\left( {\rho_{l} } \right)$ and $k_{2} = k_{t} L{ \sin }\left( {\rho_{l} } \right)$,

$$ k_{t} \left( {\varphi_{l} } \right) = \left[ {k_{1} \left\{ {\frac{{\varphi_{l} }}{2} - \frac{{\varphi_{l}^{3} }}{24}} \right\} + k_{2} \left\{ {1 - \frac{{\varphi_{l}^{2} }}{6} + \frac{{\varphi_{l}^{4} }}{120}} \right\}} \right]. $$

Therefore, Eq. (14) may be written as

$$ \left( {M + m_{l} } \right)\ddot{X} + m_{l} \ddot{X}_{\varphi } + k_{t} \left( {\varphi_{l} } \right)\varphi_{l} + k_{t} X = k_{t} Y. $$

$$ \therefore \left( {M + m_{l} } \right)\ddot{X} + m_{l} \ddot{\varphi }_{l} L_{\varphi } + m_{l} L\dot{\varphi }_{l}^{2} \cos \left( {\alpha_{l} + \varphi_{st} + \varphi_{l} } \right) + k_{t} \left( {\varphi_{l} } \right)\varphi_{l} + k_{t} X = k_{t} Y . $$

(15)

5.3 Unsprung Mass Rotational Dynamics in the State Space Domain

With reference to Sect. 5.4 [11], unsprung mass rotation is described in Eq. (16) as

$$ m_{l} L^{2} \ddot{\varphi }_{l} + m_{l} \ddot{X}L_{\varphi } + \left( {T_{l} - T_{st} } \right) + c\dot{x}L_{0} + \left( {T_{t} - T_{Y} } \right) = 0, $$

(16)

where

$$ L_{\varphi } = L { \sin }\left( {\rho_{l} + \varphi_{l} } \right), $$

$$ \left( {T_{t} - T_{Y} } \right) = k_{t} \left( {X + X_{\varphi } - Y} \right) L_{\varphi } $$

$$ X_{\varphi } = L{ \cos }\left( {\rho_{l} } \right) - L{ \cos }\left( {\rho_{l} + \varphi_{l} } \right) $$

Using the previous expressions and Eq. (3), Eq. (16) may be written as

$$ m_{l} L^{2} \ddot{\varphi }_{l} + m_{l} \ddot{X}L_{\varphi } + K\left( {\varphi_{l} } \right)\varphi_{l} + cf1\dot{\varphi }_{l} L_{0} + k_{t1} \left( {\varphi_{l} } \right)\varphi_{l} + k_{t} L_{\varphi } X = k_{t} L_{\varphi } Y. $$

$$ \therefore m_{l} L^{2} \ddot{\varphi }_{l} + m_{l} \ddot{X}L_{\varphi } + \left\{ {K\left( {\varphi_{l} } \right) + k_{t1} \left( {\varphi_{l} } \right)} \right\}\varphi_{l} + cf1\dot{\varphi }_{l} L_{0} + k_{t} L_{\varphi } X = k_{t} L_{\varphi } Y, $$

(17)

where

$$ k_{t1} \left( {\varphi_{l} } \right) = k_{t} \left( {\varphi_{l} } \right)L_{\varphi } . $$

5.4 Transformation into Non-linear State Space Domain

Equations (15)–(17) can be transformed into state space domain which is highlighted in Eqs. (18)–(19), respectively.

$$ \left( {M + m_{l} } \right)\ddot{X} + m_{l} \ddot{\varphi }_{l} L_{\varphi } = - m_{l} L\dot{\varphi }_{l}^{2} \cos \left( {\rho_{l} + \varphi_{l} } \right) - k_{t} \left( {\varphi_{l} } \right)\varphi_{l} - k_{t} X + k_{t} Y. $$

(18)

$$ m_{l} L^{2} \ddot{\varphi }_{l} + m_{l} \ddot{X}L_{\varphi } = - \left\{ {K\left( {\varphi_{l} } \right) + k_{t1} \left( {\varphi_{l} } \right)} \right\}\varphi_{l} - cf1\dot{\varphi }_{l} L_{0} - k_{t} L_{\varphi } X + k_{t} L_{\varphi } Y. $$

(19)

Define $\dot{\varphi }_{l} = u_{1}$ and $\dot{X} = u_{2}$

Substituting for $\dot{\varphi }_{l}$ and $\dot{X}$ in Eqs. (18) and (19), the following state space matrix is obtained:

$$ {\dot{\mathbf{Z}}} = \frac{1}{{{\mathbf{M}}_{1} }}\left\{ {{\mathbf{A}}\left( {\varphi_{l} } \right){\mathbf{Z}} + {\mathbf{B}}\left( {\varphi_{l} } \right){\mathbf{U}}} \right\}, $$

(20)

where

$$ {\mathbf{Z}} = \left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ {\varphi_{l} } \\ X \\ \end{array} } \right] {\text{and }}{\mathbf{U}} = \left[ {\text{Y}} \right], $$

$$ {\mathbf{M}}_{1} = \left[ {\begin{array}{*{20}c} {m_{l} L_{\varphi } } & {\left( {M + m_{l} } \right)} & 0 & { 0} \\ {m_{l} L^{2} } & {m_{l} L_{\varphi } } & 0 & { 0} \\ 0 & 0 & 1 & { 0} \\ 0 & 0 & 0 & { 1} \\ \end{array} } \right], $$

$$ {\mathbf{A}}\left( {\varphi_{l} } \right) = \left[ {\begin{array}{*{20}c} { - m_{l} L\dot{\varphi }_{l} cos\left( {\rho_{l} + \varphi_{l} } \right)} & 0 & { - k_{t} \left( {\varphi_{l} } \right)} & { - k_{t} } \\ { - cf1L_{o} } & 0 & { - \left\{ {K\left( {\varphi_{l} } \right) + k_{t1} \left( {\varphi_{l} } \right)} \right\}} & { - k_{t} L_{\varphi } } \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{array} } \right] $$

$$ {\mathbf{B}}\left( {\varphi_{l} } \right) = \left[ {\begin{array}{*{20}c} {k_{t} } \\ {k_{t} L_{\varphi } } \\ 0 \\ 0 \\ \end{array} } \right]. $$

The non-linear state space form of the equations which comprises the non-linear suspension characteristics is described by Eq. 20. The matrices ${\mathbf{A}}\left( {\varphi_{l} } \right)$ and ${\mathbf{B}}\left( {\varphi_{l} } \right)$ vary with $\varphi_{l}$ and get updated with every time increment.

5.5 Solution for the Non-linear State Space Model

The solution technique for the single station non-linear state space model is similar to that described in Sect. 5.5 [11]. Since the matrices are of non-linear nature, therefore, at every computation time, the matrices get altered as per the change of axle arm angular rotations about static position which results from base excitation.

6 Single Station Multi-body Dynamics Model

Referring to Sect. 7 [11], the multi-body dynamics model which is developed in MSC.ADAMS for the non-linear state space model validation has been shown in Fig. 5. The multi-body model has been solved using a similar approach as described in [11]. The MBD model can be considered to be a numerical experiment that is solved through an implicit time integration scheme.

Fig. 5

MSC. ADAMS single station MBD model

7 Comparative Responses Between State Space and Multi-body Dynamic Models

The multi-body dynamics model for a single station has been used to validate the non-linear state space model through simulations over APG profile at vehicle speeds of 20 and 30 kmph. Generally, the vehicle negotiates APG terrain at average speeds of 20 and 30 kmph. Therefore, simulations have been carried out at the above speeds. Similar parameters which are described in Table 2 [11] have been used for the state space model.

7.1 Dynamics Analysis at 20 Kmph Over APG

The APG (Axle Proving Ground) excitation profile (shown in Fig. 6) is applied to the single station model at a vehicle speed of 20 kmph. The simulation is carried out for 20 s. In the present case, suspension charging pressure is 11.4 MPa. The input has been applied as a vertical base displacement with respect to time. The time-domain variation is obtained by dividing the spatial distance between terrain elevation profiles by the corresponding vehicle speed. For the present model, vertical base displacement input with respect to time has been applied by considering a spatial variation on the left side of the APG terrain. The vertical displacement input due to APG at 20 kmph is shown in Fig. 7. The comparative sprung mass bounce displacement and acceleration responses are shown in Figs. 8 and 9, respectively. The maximum vertical accelerations over APG at 20 kmph which are obtained from the MBD and mathematical state space models are about 26.7 m/s² and 28.8 m/s², respectively. The RMS of vertical accelerations over APG at 20 kmph which are obtained from MBD and mathematical state space models are about 4.7 m/s² and 5.2 m/s², respectively. The dynamic responses from state space model compare well with the MBD model. Figure 10 shows the frequency-domain comparison of the sprung mass bounce acceleration response.

Fig. 6

Representation of the APG terrain

Fig. 7

Vertical displacement input due to APG at 20 kmph

Fig. 8

Sprung mass bounce displacement response at CG for 20 kmph

Fig. 9

Sprung mass bounce acceleration response at CG for 20 kmph

Fig. 10

Frequency spectrum for sprung mass bounce acceleration response at CG for 20 kmph vehicle speed

7.2 Dynamics Analysis at 30 Kmph Vehicle Speed Over APG

Comparative dynamic simulations have been carried out over APG at 30 kmph vehicle speed. The simulations have been performed for 14 s. The suspension characteristics and the displacement input procedures are similar to those described in Sect. 7.1. The vertical displacement input which pertains to 30 kmph vehicle speed over APG has been shown in Fig. 11. Figures 12 and 13 highlights the comparative sprung mass bounce displacement and acceleration responses. The maximum vertical accelerations over APG at 30 kmph which are obtained from MBD and mathematical state space models are about 32.1 m/s² and 29.1 m/s², respectively. The RMS of vertical accelerations over APG at 30 kmph which are obtained from MBD and mathematical state space models are 6.3 m/s² and 5.8 m/s², respectively. The sprung mass dynamics responses which are obtained over APG at 30 kmph show good comparison with the MBD model. Also, sprung mass responses obtained from the models over APG at 30 kmph are comparatively higher than that at 20 kmph. The frequency spectrum which pertains to the sprung mass comparative bounce acceleration response at CG is shown in Fig. 14.

Fig. 11

Vertical displacement input due to APG at 30 kmph

Fig. 12

Sprung mass bounce displacement response at CG for 30 kmph

Fig. 13

Sprung mass bounce acceleration response at CG for 30 kmph

Fig. 14

Frequency-domain variation for sprung mass CG bounce acceleration response for 30 kmph speed

The above simulations have also been carried out by using higher order terms in the non-linear state space model. However, insignificant difference is observed in the results with higher order terms when compared to those highlighted above. One of the reasons for possible deviations in response is due to differences in solvers (numerical solution and interpolation techniques) which are used in math and Adams models. Very marginal response difference may also be attributed to the dropping of higher order terms during the Taylor series and binomial expansions. Irrespective of the above deviations, there is a close agreement in response between the state space model and MBD model.

8 Conclusions

The non-linear state space mathematical model for the single station incorporates the kinematics and dynamics effects of the trailing arm suspension. The non-linear equations for the single station in state space matrix domain are reformulated so that it is directly feasible for future control related studies without compromising much on accuracy. The maximum vertical accelerations over APG at 20 kmph which are obtained from the MBD and mathematical state space models are about 26.7 m/s² and 28.8 m/s², respectively. The RMS of vertical accelerations over APG at 20 kmph which are obtained from MBD and mathematical state space models are about 4.7 m/s² and 5.2 m/s², respectively. The maximum vertical accelerations over APG at 30 kmph which are obtained from MBD and mathematical state space models are about 32.1 m/s² and 29.1 m/s², respectively. The RMS of vertical accelerations over APG at 30 kmph which are obtained from MBD and mathematical state space models are 6.3 m/s² and 5.8 m/s², respectively. The sprung mass peak and RMS vertical acceleration responses which are obtained at 30 kmph speed are more when compared to that at 20 kmph. From the above results, it is observed that the non-linear mathematical state space model shows a close agreement with Adams MBD model. The entire military vehicle non-linear state space model which involves many degrees of freedom can also be derived from the present model. The present non-linear state space model provides the design and development motivation for semi-active and active suspension system in the military vehicles.