Dynamic Response Analysis of Rotating Shaft-Bearing System with an Open Crack

Abstract

The best of effective design and practices of constructive methods in the analysis of rotor excessive vibration will yield the solutions for the dynamic problems. The extensive effusion of the finite element method (FEM) strongly induced in the area of rotordynamic studies and can give accurate results. Diagnosis of a rotor shaft with crack for its operating conditions is essential to the dynamic systems design. This paper carries the analysis of a finite element model of a flexible rotor-bearing system with a transverse open crack by accounting the various crack depths and internal damping of the shaft. The effect of transverse crack on the system instability regions was found out. It is noted that the natural whirl speeds reduce with increase in crack depths. The system unbalance response and damped natural whirl speeds are presented with undamped orthotropic bearings. The stability of the rotating shaft-bearing system with transverse open crack has also been studied for the various spin speeds and disk eccentricity with the time integration procedure. The phase-plane portraits and frequency-domain diagrams are drawn to study the dynamic behavior. Further, the study is yet to be extended to a fully levitated rotor model supported in active magnetic bearings (AMBs).

1 Introduction

The growing direction of rotating dynamic systems, steer into a complicated analysis of design for the smooth operation. Dynamic analysis of rotating systems has had an extensive investigation over the last few decades. Several methods were developed for the study of shaft-disk-bearing systems over the past few decades. Effective modeling procedures can be split into two significant classes. Finite element method (FEM) is one among them, in which the rotor elements are subdivided into finite number of degrees of freedom and the system motions are represented by ordinary differential equations. Rotating structures are employed broadly through industries from all around the world for energy generation and power transmission. The large vibration amplitudes in rotating systems will lead the shaft/rotor to the propagation of cracks. Followed by these great amplitudes due to cracks allow to unpredicted shutdown and feasible damage of machine elements. The shaft with an open crack is one of the vicious havoc situations in rotordynamic systems analysis particularly in transverse direction.

An important study of the modeling and investigation to get the perfect results for multi-stepped rotor systems was carried for distributed parameters. In his three instances, first, the system is validated with FEM analysis. Second a parametric study in variation of shaft length consists of two different shafts with different diameters. And finally, an unbalance response analysis was carried out by Hong and Park [1]. A new approach for extracting the critical speeds of flexible rotor-bearing system with the transverse shear effect and distributed mass and inertia of the shaft were presented. The external loads are considered with bearing mass, damping, and coupling flexibilities. The critical speeds with the effect of coupling flexibilities were investigated by Joshi and Dang [2]. Modal analysis for continuous rotor-bearing systems for isotropic and anisotropic natural boundary conditions was analyzed. The backward and forward whirl speeds, and mode shapes are calculated for varying rotational speed and boundary conditions by Lee and Jei [3]. The finite element method is used as a key to extract the eigenvalue and stability investigation of rotors by accounting distributed stiffness of bearing and damping. For the two models of rotor on cylindrical journal bearings, tilting pad journal bearings, offset and three-lobe journal bearings were analyzed with (i) uniform and (ii) parabolic distributions, followed by the stability limits were studied by Rao et al. [4]. Sekhar and Dey [5] investigated the rotor-bearing system with transverse crack for the stability threshold by FEM analysis by accounting the different crack parameters, internal dampings and geometric parameters. They found that, the instability is reduced reasonably with an increase of crack depth.

Analysis of flexible rotor-bearing system with symmetrical single-disk derived by lump mass method including shaft stiffness and damping, bearing linear oil-film forces was used to find out the unbalance responses and the feasibilities are discussed by Sanxing et al. [6]. Nelson and McVaugh [7] presented the dynamic modeling of the shaft-disk system supported on bearings which gave the basic idea in this field of rotor dynamics. They suggested a Rayleigh shaft element for modeling a rotating shaft-disk system. The study of rotor model with finite elements incorporates the effects of rotatory inertia, axial load, and gyroscopic moments by applying the consistent matrix method. Natural whirl speeds and unbalance response were presented for two sets of undamped bearing stiffness. However, it excludes the axial torque or shear deformation effect. By employing Timoshenko beam theory, the above approach hypothesizes his previous study to obtain the shape functions by Nelson [8]. Dimarogonas [9] has presented a review article for crack in a structural member as vibration of cracked structures. He had mentioned about the two families of subharmonic critical speed. A transient vibration analysis of rotor with crack which is passing over critical speeds was studied by Sekhar and Prabhu [10]. The work from the authors shows that the time histories with harmonics and frequency spectrum of model can be obtained with further analysis. The analysis of asymmetric cracked rotor shaft systems for stability concern is much interested topic to study by the rotordynamicists: Some basic cases have been discussed in [11, 12] which generally gives the parametric instability.

2 Finite Element (FE) Model of the Shaft-Bearing System

Finite element method (FEM) is predominantly influenced in rotordynamic analysis. The spinning structures are composed of numerous particles. The equation of motion of the total particles allows the conclusion in the equilibrium of the system. Structures with ‘n’ numbers of particles will have the generalized coordinates qi which consists of nodal translational and nodal rotational displacement variables. Displacement components of the nodal commonly chosen by order to be translations and followed by rotations.

2.1 Energy Equations

All rotating particles are part of the structural system, and that it undergoes for elastic deformations. By implementing the linear stress–strain relationship to the system, the elastic potential energy of the structure can be derived. The derivative of this elastic potential energy gives the finite element stiffness matrix of the structure. The dissipative force which acts on the structure indicates the energy lost in it. The kinetic energy of these particles is damped by the above-mentioned forces.

2.2 System Configuration and Coordinates

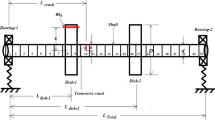
In present work, a typical flexible overhanging rotor-bearing model is analyzed to understand the system dynamic stability situation. The segment incorporates the discrete bearing, discrete disks with mass unbalances and incorporates a transverse open crack in one of the element. The dynamic equations are solved using the implied time integration procedure, and the stability at different speeds of operation is studied using phase-plane portraits and frequency response. A simplified rotor system by finite element can be standardized using Timoshenko beam theory. Figure 1 shows the typical rotor element model.

Fig. 1

Turbocharger schematic diagram

The finite element method is used to model the rotor-disk-bearing system. Here, rotor mass is M and entire length L is divided into n-number of elements along n + 1 total node for the rotor z-axis which shown in Fig. 2a. By considering the bending and shearing effects, the kinetic energy (T_s) and potential energy (U_s) of the elements (shaft) in rotation are given as:

Fig. 2

a Rotor-disk finite element system. b Bearing model of the system

$$T_{s} = \frac{1}{2}\int\limits_{0}^{\ell } {\rho \left\{ {A(\dot{v}^{2} + \dot{w}^{2} ) + I_{D} (\dot{\theta }_{y}^{2} + \dot{\theta }_{z}^{2} ) + I_{P} \left[ {\Omega ^{2} + \Omega (\dot{\theta }_{z} \theta _{y} - \dot{\theta }_{y} \theta _{z} )} \right]} \right\}{\text{d}}s}$$

(1)

$$U_{s} = \frac{1}{2}\int\limits_{0}^{\ell } {\left\{ {EI(\theta _{y}^{{\prime 2}} + \theta _{z}^{{\prime 2}} ) + kGA\left[ {(\theta _{y} - w^{\prime } )^{2} + (\theta _{z} + v^{\prime } )^{2} } \right]} \right\}{\text{d}}s}$$

(2)

2.3 Disk Model

The rigid disk with four degrees of freedom is kept in the respective elemental nodes. Since the disk is rigid, the mass/inertia center of the disks is placed on the particular node which is connecting two elements as shown in Fig. 2a. The disk kinetic energy is given as:

$$\begin{aligned} & T_{d} = \frac{1}{2}m_{d} \left( {\dot{v}^{2} + \dot{w}^{2} } \right) + \frac{1}{2}J_{d} \left( {\dot{\theta }_{y}^{2} + \dot{\theta }_{z}^{2} } \right) \\ & \quad + \frac{1}{2}J_{p} \left[ {\varOmega^{2} + \Omega (\dot{\theta }_{z} \theta_{y} - \dot{\theta }_{y} \theta_{z} )} \right] \\ \end{aligned}$$

(3)

The work generated by the disk with eccentricity of mass is:

$$W_{d} = m_{d} r_{d} \varOmega^{2} (w\cos \varOmega t + v\sin \varOmega t)$$

(4)

$$[M_{d} ] = \left[ {\begin{array}{*{20}c} {m_{d} } & {} & {} & {} \\ {} & {m_{d} } & {} & {} \\ {} & {} & {J_{d} } & {} \\ {} & {} & {} & {J_{d} } \\ \end{array} } \right];[G_{d} ] = \left[ {\begin{array}{*{20}c} 0 & {} & {} & {} \\ {} & 0 & {} & {} \\ {} & {} & 0 & {J_{p} } \\ {} & {} & { - J_{p} } & 0 \\ \end{array} } \right]$$

(5)

2.4 Bearing Model

The bearings considered in this analysis which is in Fig. 2b are restricted to follow the governing equations. The bearings were linearized and the stiffness alone is taken into account for the analysis. The stiffness matrix of the bearing elements as follows,

$$\left[ {K^{b} } \right] = \left[ {\begin{array}{*{20}c} {k_{VV}^{b} } & {k_{VW}^{b} } \\ {k_{WV}^{b} } & {k_{WW}^{b} } \\ \end{array} } \right]$$

(6)

2.5 System Modeling

The shaft model is expressed with beam elements of circular in cross section. The strain energy and kinetic energies are needed to take into account when modeling a shaft element. The distinctive shaft elemental cross section is estimated with the following equation(s):

$$\left\{ {\begin{array}{*{20}c} v \\ w \\ \end{array} } \right\} = [N_{t} (s)]\{ q\} ;\left\{ {\begin{array}{*{20}c} {\theta_{y} } \\ {\theta_{z} } \\ \end{array} } \right\} = [N_{r} (s)]\{ q\}$$

(7, 8)

where [N_t(s)] and [N_r(s)] are the shape functional matrices of translation and rotation. These shape functions are well-established by Nelson [8]. By using the above set of equations and by doing the integration along the total length by implementing Hamilton’s principle, the below equations for the finite system, disk, and bearings are obtained:

$$[M_{s} ]\{ \ddot{q}_{s} \} + \varOmega [G_{s} ]\{ \dot{q}_{s} \} + [K_{s} ]\{ q_{s} \} = \{ F_{s} \}$$

(9)

$$[M_{d} ]\{ \ddot{q}_{d} \} + \varOmega [G_{d} ]\{ \dot{q}_{d} \} = \{ F_{d} \}$$

(10)

where

$$[M_{s} ] = \int\limits_{0}^{\ell } {\rho A[N_{t} ]^{T} [N_{t} ]{\text{d}}s} + \int\limits_{0}^{\ell } {\rho I_{d} [N_{r} ]^{T} [N_{r} ]{\text{d}}s}$$

(11)

$$[G_{s} ] = \int\limits_{0}^{\ell } {\rho I_{p} [N_{r} ]^{T} \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - 1} & 0 \\ \end{array} } \right][N_{r} ]{\text{d}}s}$$

(12)

$$\begin{aligned} [K_{s} ] & = \int\limits_{0}^{\ell } {EI[N_{r}^{\prime } ]^{T} [N_{r}^{\prime } ]{\text{d}}s} \quad \\ & \quad + \kappa GA\int\limits_{0}^{\ell } {\left\{ {[N_{t} ]^{T} [N_{t} ] + [N_{r} ]^{T} [N_{r} ] + 2[N_{t} ]^{T} \left[ {\begin{array}{*{20}c} 0 & { - 1} \\ 1 & 0 \\ \end{array} } \right][N_{r} ]} \right\}{\text{d}}s} \\ \end{aligned}$$

(13)

Considering the effect of damping on the rotor, the system equation of motion is given as follows:

$$[M]\{ \ddot{q}\} + \left[ {[C] + \varOmega [G]} \right]\{ \dot{q}\} + [K]\{ q\} = \{ F\}$$

(14)

where

$$\{ q\} = [\begin{array}{*{20}c} {v_{1} } & {w_{1} } & {v_{2} } & {w_{2} } & {v_{3} } & {w_{3} } & {v_{4} } & {w_{4} } & {v_{5} } & {w_{5} } \\ \end{array} ]^{\text{T}}$$

(15)

2.6 Crack Model

The transverse crack model leads the parametric inertia or stiffness excitation to the system equation. Due to the parametric inertia, it is required to figure out the effect on the instability regions. Initially, the discrete elements equations of motions of the rotor system are formed. Further, the transverse open crack is considered into account for the current analysis as shown in Fig. 3.

Fig. 3

Finite model of the rotor-disk system with open crack

The time-varying stiffness functions of the cracked element are taken as [13],

$$\mathop k\nolimits_{oc}^{j} \left( t \right) = \mathop k\nolimits_{o1}^{j} + \mathop k\nolimits_{o2}^{j} \cos \left( {2\left( {\varOmega t + \varphi } \right)} \right)$$

(16)

2.7 Final Rotor System Model with Crack

The overall equation of motion of the cracked rotor system is given as,

$$\begin{aligned} & [M^{S} ]\{ \ddot{q}^{S} (t)\} - \varOmega [G^{S} ]\{ \dot{q}^{S} (t)\} \\ & \quad + \left( {[K^{S} ] + [\tilde{K}(t)]} \right)\{ q^{S} (t)\} = \{ Q^{S} \}_{4n\, \times 1} \\ \end{aligned}$$

(17)

where $\left[ {M^{S} } \right],\left[ {G^{S} } \right],\left[ {K^{S} } \right]$, and $\left[ {\tilde{K}\left( t \right)} \right]$ are the global mass, gyroscopic, stiffness, and cracked elemental matrices having dimensions in 4(n + 1) × 4(n + 1). The constant spin speed (Ω) brings the equation of motion of the system in the time-varying second order periodic differential equation with the open crack frequency of 2Ω.

3 Theoretical Results and Discussions

The rotor-bearing-disk system with crack is distributed as 4 elements and the disk with mass unbalance as given in Fig. 3. The values of the mechanical and physical properties are listed in Table 1. The finite element equations are solved with MATLAB. The equations compute the nodal degrees of freedom by the defined number of elements. Hence, in the beginning stage it calculates the natural frequencies of the system and subsequently gives the Campbell diagram. However, need to give the value of bearing stiffness coefficients manually to avoid further calculations. This procedure helps to verify the system assembly.

Table 1 Mechanical and physical properties of the shaft elements and rigid disk

The cracked shaft (open crack) equation of motion incorporates the stiffness matrix as constant (K − K_c) in the investigation part. Unbalance mass of m_u = 10⁻⁶ kg m is considered for the fully opened crack condition at t = 0. The result in Fig. 4a shows the unbalance response and critical speed of the rotor-bearing-disk system at 3859 and 4904 rpm with crack. The natural frequencies for various non-dimensional crack depth µ, [14] are listed in Table 2.

Fig. 4

a UBR of finite system with crack. b Campbell plot with Ω_cr of 1Xhamonic

Table 2 List of first six natural frequencies (f_n) with non-dimensional crack depth (µ) at (L_crack = 0.4235 m)

For an open crack at element 3, the natural whirl speeds were plotted for the non-dimensional crack depth µ = 0.1, 0.2, and 0.3 which shown in Fig. 4b. It clarifies the action of cracked rotor system responds for backward whirl when the crack begins to look at very minimum crack depths, and it can be also understood that the amplitude change with an increase in crack depth values for critical forward and backward whirling speeds. The frequency spectrum of the model with crack influence is plotted in Fig. 5a which shows the disturbed frequencies due to the stiffness of the rotor. For the displacements at disk nodes for both the disk at Ω = 1200 rpm were plotted and shown in Fig. 5b.

Fig. 5

a Frequency spectrum of the system. b Displacements at disk 1 & 2 at Ω = 1200 rpm

The phase portraits for the system with open crack, behave as periodic with a little unstable center at Ω = 1200 rpm which shown in Fig. 6a, b. This effect also can be observed from the disturbed frequency response curves with crack which is shown in Fig. 5a. The viscous damping factors of 0.01 and shear coefficient of 0.65 are considered in the system modeling.

Fig. 6

a Phase portraits at disk 1 in ~ x-direction. b Phase portraits at disk 2 in ~ y-direction

4 Conclusions

This study carries well-organized methods to solve and understand the behavior of the rotor shaft-bearing-disk system with crack. The general solution of the rotor shaft system with open crack has been included in the study to understand the behavior. The outcome from the method which was followed gives the important observations of the natural whirls, cracked unbalance vibration amplitudes, displacements at disk nodes, and phase-plane diagrams. The behavior of the cracked rotor-bearing-disk system for various crack depths with specific speeds was carried. Hence, the approach helps to predict the changes with rotor orbit shapes in specific rotor critical speeds considered at very minimum crack depths.