Analysis of Tristable Energy Harvesters Under Random Excitations

Abstract

This manuscript analyzes the performance of a tristable vibration energy harvester under Gaussian white noise excitation. Broadband vibration energy harvesting has attracted significant research attention and is targeted toward obtaining large power output over a wide range of frequencies. Nonlinearity can be introduced into vibration energy harvesting systems through multi-stability. In cantilever-type vibration energy harvesters, multi-stability could be achieved by the introduction of magnetic interactions. When two external magnets are used, the harvester can have up to three stable static equilibrium positions. The harvester with two stable states has been explored widely, both theoretically and experimentally. Recently, the harvester with three stable states is shown to perform better than its bistable counterpart in the presence of a linearly increasing harmonic sweep excitation. Ambient vibrations are random in nature, and the performance of tristable energy harvesters under such excitations needs to be studied. To begin with, we study the performance of tristable energy harvesters under Gaussian white noise excitation through numerical simulations. The simulations show that beyond a certain critical amplitude of excitation, the harvesters undergo inter-well oscillations and harvest more power. This implies that if the variance of the random ambient excitation is known, then the harvester could be optimized so that the mean harvested power is maximized.

1 Introduction

The current technological revolution has sparked an exponential growth in the realm of wireless communication. However, the lifetime of batteries powering the miniature sensors and wireless devices often limits their use. A self-sustainable power source would ensure that these devices are exploited to their full potential. To address this, researchers have been actively trying to harvest electrical energy from the ambient sources such as structural vibrations, temperature gradients, and radiations. Among these, low-frequency mechanical vibrations (1–100 Hz) are widely present in industrial and structural environments, and could act as a source of power for devices monitoring such environments.

The classical design of a vibration energy harvester consists of a cantilever beam carrying a tip mass and employs a piezoelectric transducer to convert mechanical vibrations to electrical energy. This design is efficient when excited harmonically at its resonant frequency and at off-resonance frequencies, the efficiency reduces immensely [1]. As the ambient vibrations are random, the bandwidth of operation of the harvester must be increased. Tunable resonators, multi-frequency arrays, and nonlinear oscillators are some of the methods by which the bandwidth could be enhanced [2, 3].

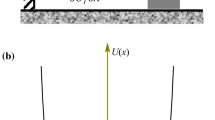
In energy harvesters, nonlinear stiffness is generally introduced by engineering more than one stable state (multi-stability). One such system that exploits this technique is the piezomagnetoelastic harvester. This harvester is based on the concept of a magneto-elastic oscillator with a nonlinear potential energy function. It consists of a cantilever beam carrying a tip magnet, oscillating in a magnetic field created by two external magnets as shown in Fig. 1. Piezoelectric transducers are attached near the base of the beam to harvest energy from the oscillator. When tuned appropriately, the system undergoes inter-well oscillations, even for low excitations, thus harvesting more power.

Fig. 1

Schematic representation of the piezomagnetoelastic harvester

The concept of magneto-elastic oscillations dates back to 1979 when Moon and Holmes [4] proposed the same as the first experimental evidence for strange attractors in structural mechanics. Depending on the distance between the magnets and their field strength, the system may have one, two, or three stable equilibrium positions and is, respectively, known as monostable, bistable, or tristable [4, 5]. The bistable and tristable configurations can oscillate in a non-resonant manner between the various stable states, leading to an increase in the bandwidth of operation.

Erturk et al. [6] introduced the concept of magneto-elastic interactions in vibration energy harvesting and investigated the broadband capabilities of a bistable energy harvester through experiments. In another instance, Zhou et al. [7] proposed a tristable energy harvester that provides better performance than its bistable counterpart. The authors have shown through simulations that the tristable energy harvester has shallower potential wells than the bistable harvester. Hence, the potential barrier in a tristable harvester can be easily overcome even at lower excitation amplitudes and the system undergoes inter-well oscillations, generating high energy output.

We, the authors of this manuscript, have previously studied the influence of potential well shapes on the harvesting performance of piezomagnetoelastic harvesters in the presence of a harmonic base excitation [8]. In this manuscript, we analyze the performance of tristable piezomagnetoelastic energy harvesters under a broadband excitation as such excitation characteristics would better approximate the ambient vibrations.

The primary aim of the study is to illustrate that beyond a certain noise level, the tristable energy harvester could undergo inter-well oscillations and harvest more power. The rest of the manuscript is arranged as follows. Section 2 introduces the governing differential equations of the harvester. Section 3 discusses the results of the numerical simulations. Conclusions are drawn thereafter.

2 The Piezomagnetoelastic Energy Harvester

A piezomagnetoelastic harvester consists of a cantilever beam carrying a tip magnet oscillating in the field created by two other external magnets, as shown in Fig. 1. The two magnets are placed symmetrically about the clamped position of the beam. Here, we consider the beam to be excited at the base with zero mean Gaussian white noise. Piezoelectric patches are pasted along the beam to convert the mechanical vibrations of the beam into electrical energy. The piezoelectric patches can be connected to a load resistance in parallel, so that electrical power can be taken out of the system.

The system is governed by two coupled differential equations, one corresponding to the mechanical oscillator and the other corresponding to the electrical circuit. The mechanical oscillator can have either one, three, or five equilibrium positions, depending on the magnet spacing and system dimensions [5]. Here, we are interested in the tristable configuration, which has a total of five equilibrium positions, among which three are stable. Thus, the mechanical oscillator is characterized by a potential that has three wells.

Considering a single degree of freedom approximation, the governing differential equation of the magneto-elastic oscillator can be put in a non-dimensional form as follows:

$$\ddot{x} + c\dot{x} + kx + \alpha x^{3} + \beta x^{5} - \chi v = f(t)$$

(1)

where x is the dimensionless transverse displacement of the tip mass and v is the dimensionless voltage. The restoring force is a polynomial in x of order five, with k, $\alpha$, and $\beta$ denoting the linear, cubic, and quintic stiffness coefficients, respectively. The system will exhibit a tristable configuration when $k > 0$, $\alpha < 0$, $\beta > 0$, and $\alpha^{2} - 4k\beta > 0$. The term $c\dot{x}$ denotes damping and the term $\chi v$ arises due to electromechanical coupling. The force $f(t)$ is proportional to the base acceleration.

In the electrical side, the circuit can be modeled as a load resistance connected across the piezoelectric transducer. The piezoelectric transducer behaves like a capacitor. Hence, the non-dimensional equation governing the circuit is

$$\dot{v} + \lambda v + \kappa \dot{x} = 0$$

(2)

where $\lambda$ denotes the decay fraction of the electrical circuit. The term $\kappa \dot{x}$ represents the dimensionless current that arises out of electromechanical coupling in the piezoelectric patches. It should be noted that $\lambda \propto 1/\left( {C_{p} R_{l} } \right)$ where $C_{p}$ and $R_{l}$ are the dimensionless capacitance and resistance, respectively.

3 Simulated Results and Discussion

Vibration energy harvesters, in general, may be put to use in environments, where the excitation could be random. Hence, we look at the harvesting performance of tristable energy harvesters under such conditions. The excitation $f(t)$ in Eq. (1) has been taken to be Gaussian white noise with zero mean and specified variance $\sigma_{f}^{2}$. Thus, Eqs. (1) and (2) can be written in the form of a system of Itô stochastic differential equations as follows:

$$dx_{1} = dx_{2} dt$$

(3)

$$dx_{2} = \sigma_{f} dW(t) - \left( {cx_{2} + kx_{1} + \alpha x_{1}^{3} + \beta x_{1}^{5} - \chi x_{3} } \right) dt$$

(4)

$$dx_{3} = - \left( {\lambda x_{3} + \kappa x_{2} } \right) dt$$

(5)

In the above equations, the state variables $x_{1}$, $x_{2}$, and $x_{3}$ denote the dimensionless displacement x, the dimensionless velocity $\dot{x}$, and the dimensionless voltage v, respectively. The forcing $f(t)$ has been taken as $\sigma_{f} \frac{dW(t)}{dt}$ where $W(t)$ denotes the one-dimensional Wiener’s process.

Equations (3), (4), and (5) are integrated using fourth-order Runge–Kutta–Maruyama algorithm [8]. The system parameters are taken from [9] as follows: $\chi = 0.05$, $\lambda = 0.01$, and $\kappa = 0.5$. The stiffness coefficients are taken as shown in Table 1. Five sets of parameters have been considered, with each set corresponding to different potential well depths, as shown in Fig. 2. For each set, the simulations have been carried for different values of the standard deviation of the excitation $\sigma_{f}$.

Table 1 Stiffness coefficients for different cases

Fig. 2

Potential wells for different cases

The influence of the width and the depth of the potential wells on the system dynamics and harvesting performance is investigated. In Fig. 2, Case 1 (solid black line) represents the reference configuration, in which three wells of equal depth. In Case 2 (dashed green line), the outer wells are shallower than the middle well. In Cases 3, 4, and 5, the outer wells are deeper than the middle well. However, their depth and width vary as shown in Fig. 2. For all the five cases, the simulations have been carried for different values of the standard deviation of the excitation $\sigma_{f}$, ranging from 0.01 to 0.12. The initial conditions are fixed as ($x_{1} (0)$, $x_{2} (0)$, $x_{3} (0)$) = (0, 0, 0) for all the simulations. The corresponding results are shown in Fig. 3.

Fig. 3

Influence of the standard deviation of the excitation on the system dynamics

Figure 3a shows the variation of $\sigma_{x} /\sigma_{f}$ as $\sigma_{f}$ varies. Here, $\sigma$ refers to the standard deviation of the subscripted variable. The presence of sharp peaks indicates the transition from intra-well to inter-well oscillations. As $\sigma_{f}$ is increased beyond a certain value, the system is able to overcome the potential barrier and undergo inter-well oscillations. This is marked by a significant increase in the ratio of the standard deviation of the output voltage to the standard deviation of the forcing. If the harvested is designed so as to operate in this range of $\sigma_{f}$, then the efficiency of the harvester $(\sigma_{v} /\sigma_{f} )$ is maximized. However, the critical value of $\sigma_{f}$ for which the inter-well oscillations onset is dependent on the depth and the width of the potential wells. This dependence is illustrated in Figs. 4, 5, 6, 7, and 8, for various cases. Figures 4, 5, 6, 7, and 8 show the projection of the phase portrait of the system on to the $x - \dot{x}$ plane for various values of $\sigma_{f}$, corresponding to Cases 1 to 5, respectively. The inferences from the projected phase portraits are explained in the following sub-sections.

Fig. 4

Projection of phase portrait on $x - \dot{x}$ plane for various values of the standard deviation of the excitation for Case 1

Fig. 5

Projection of phase portrait on $x - \dot{x}$ plane for various values of the standard deviation of the excitation for Case 2

Fig. 6

Projection of phase portrait on $x - \dot{x}$ plane for various values of the standard deviation of the excitation for Case 3

Fig. 7

Projection of phase portrait on $x - \dot{x}$ plane for various values of the standard deviation of the excitation for Case 4

Fig. 8

Projection of phase portrait on $x - \dot{x}$ plane for various values of the standard deviation of the excitation for Case 5

3.1 Influence of Potential Well Depth

As mentioned earlier, Case 1 (shown in Fig. 4) is taken as the reference for the analysis. In Case 1, when $\sigma_{f} = 0.02$, the system oscillates in the well where the initial condition lies (the middle one in this case). This is because the system does not have sufficient energy to overcome the potential barrier. When $\sigma_{f}$ is increased to 0.025, the response escapes from the middle one to the left, and then remains there. This implies that the system is slightly short of the energy to overcome the potential barrier.

If $\sigma_{f}$ is increased further to 0.03, inter-well oscillations occur in the system. The inter-well oscillations are completely developed at $\sigma_{f} = 0.035$ as shown in Fig. 4.

In Case 2 (shown in Fig. 5), the outer potential wells are slightly shallower than the middle well. For $\sigma_{f} = 0.02$, the system response is confined to the middle well, where the initial condition lies, in this case also. However, for $\sigma_{f} = 0.025$, the system undergoes inter-well oscillations intermittently, as the outer wells are shallower. With further increase in $\sigma_{f}$, the inter-well oscillations become fully developed. The responses corresponding to $\sigma_{f} = 0.03$ and 0.035 are shown in Fig. 5 as an example.

In Case 3 (shown in Fig. 6), the middle potential well is deeper than that of other cases. The outer potential wells are even deeper than the middle well. In this case, the system response is confined to the middle well even for $\sigma_{f} = 0.025$. When $\sigma_{f}$ is increased to 0.03, the response escapes from the middle well, but eventually settles on to the left one. This implies that the system has enough energy to overcome the barrier from the middle well, but not yet from the outer wells. When $\sigma_{f}$ is further increased to 0.035 such that the potential barrier of the outer wells are overcome, inter-well oscillations occur.

Case 4 is similar to Case 3, but the inter-well oscillations occur at lower values of $\sigma_{f}$ than Case 3, as the middle potential well is shallower. The outer wells of Case 5 are deeper than that of Case 4. Hence, in Case 5, at $\sigma_{f} = 0.025$, the system does not have enough energy to overcome the potential barrier of outer wells, and inter-well oscillations onset at $\sigma_{f} = 0.03$. The corresponding phase portraits for Cases 4 and 5 are shown in Figs. 7 and 8, respectively.

In a nut-shell, this analysis implies that higher the potential barrier, higher would be the value of $\sigma_{f}$ needed to undergo inter-well oscillations.

3.2 Influence of Potential Well Width

To track the effect of potential well width, Cases 3 and 4 are considered. The middle well of Case 3 is wider and deeper than the middle well of Case 4. Hence, for $\sigma_{f} = 0.03$, the inter-well oscillations are intermittent in Case 3, while they are more prominent in Case 4. Hence, after the onset of inter-well oscillations, the mean power harvested would be higher for Case 4 than Case 3 as shown in Fig. 3c. However, from the same figure, it could be observed that, at much higher excitation levels $(\sigma_{f} > 0.11)$, Case 3 gives higher mean harvested power than Case 4. This is because the potential energy function of Case 3 is wider than that of Case 4 for higher energy levels (Refer Fig. 2). Thus, for the same amount of energy supplied, Case 3 would undergo more displacement, and consequently more strain than Case 4. A higher strain means that the piezoelectric patches would harvest more power. Thus, wider potential wells result in comparatively higher mean harvested power.

3.3 Implication in Energy Harvesting

The study has four main implications in tristable energy harvesting:

• For very low excitation levels $(\sigma_{f} )$, the harvester would undergo only intra-well oscillations and produce less power. However, if the excitation levels are increased so as to overcome the potential barrier, then the system would undergo inter-well oscillations, generating high power output.

• Deeper potential wells require higher excitation levels to overcome the potential barrier. Hence, in such systems, inter-well oscillations onset at higher values of $\sigma_{f}$.

• Wider potential wells result in higher mean harvested power. In fact, this is the prime reason for inter-well oscillations to give more power than intra-well oscillations.

• The efficiency of the harvester $(\sigma_{v} /\sigma_{f} )$ is maximum just after the onset of inter-well oscillations (Refer Fig. 3b). However, with further increase in $\sigma_{f}$, the harvester efficiency decreases despite an increase in the mean harvested power $(\sigma_{v}^{2} )$ (Refer Fig. 3b, c).

4 Conclusions

The performance of tristable piezomagnetoelastic energy harvesters under Gaussian white noise excitation is analyzed here. The system is modeled as a set of coupled Itô stochastic differential equations. Numerical simulations have been performed for various noise levels for different potential well configurations. The simulated results show that the system exhibits inter-well oscillations, the onset of which depends on the depth and width of the potential wells. To maximize the efficiency, the harvester should be operated at a noise level just above the onset of inter-well oscillations. Thus, if the noise levels of the ambient excitation are known beforehand, tristable energy harvesters could be designed so as to operate under such efficient operating conditions.