Two-step approximation procedure for random analyses of tristable vibration energy harvesting systems

Abstract

Vibration energy harvesters have been of great interest for self-power sources. Various harvester designs have been developed to achieve high performance, i.e., considerable output power. The tristable energy harvester is among the best designs due to its large-amplitude oscillation and low threshold excitation intensities under some conditions. However, the theory and analysis of tristable vibration harvesters under random excitations have not been considered. Therefore, an approximate procedure, which includes two successive steps, is established to predict the performance of the tristable energy harvester under Gaussian white noise excitation. In the first step, the interaction between the auxiliary circuit and the mechanical system is decoupled with harmonic functions, and the mechanical–electrical system becomes a modified mechanical system with additional dissipative and conservative terms. In the second step, an equivalent mechanical system associated with the modified mechanical system is established through an unconventional equivalent nonlinearization technique. The statistical quantities of the tristable harvesting system are approximately equal to those of the equivalent mechanical system. The numerical results illustrate the prediction accuracy of the approximation procedure in terms of the mean output power.

1 Introduction

Vibration energy harvesters are a popular research topic because of their potential applications in low-power devices; moreover, vibration energy harvesters have a much lower maintenance cost than chemical batteries. Vibration-based energy harvesters utilize the linear resonance principle and operate with high efficiency when external excitation frequencies are near the resonant frequency of the device [1, 2]. However, any small deviations in the excitation frequency from the resonant frequency of the harvester will severely deteriorate the harvesting performance, even making the harvester ineffective. Hence, linear resonance-based harvesters are not robust to variable excitation frequencies and are suitable only for vibrations with time-invariant frequencies. Unfortunately, environmental vibrations are extremely complex, such as multifrequency and random disturbances with wide frequency bandwidths [3,4,5].

To improve the narrow operating frequency of linear vibration energy harvesters, nonlinear mechanical structures have been included to extend the bandwidth of the frequency response function [6, 7]. By using nonlinear springs or establishing bistable structures, the mechanical system can dramatically broaden the efficient operating frequencies of vibration energy harvesters. The former is usually referred to as a monostable harvesting system, whereas the latter is referred to as a bistable harvesting system; these two types of systems work with different operating principles[8, 9]. The monostable harvester works through nonlinear resonant characteristics, whereas the bistable harvester works through interwell movement. The behavior of the transitions between the two potential wells, which is a large-amplitude oscillation, enables a well-designed bistable harvesting system to be more efficient than a monostable harvesting system [10]. In addition to the high power generation and broad effective working frequencies, the bistable harvesting system is also not sensitive to varying excitation environments, which is a significant improvement over the above-mentioned linear energy harvesters [11]. The large interwell movement plays an important role in efficiently outputting power; however, this interwell movement is always accompanied by undesirable small amplitude oscillations captured in one potential well. Furthermore, the interwell oscillation cannot be excited in a wide frequency bandwidth; however, the bistable harvesting system is applicable over a wider frequency range than the monostable harvesting system. Some solutions have been proposed to improve the performance of bistable harvesters [12, 13], and additional research is still needed to realize the proposed improvements.

Instead of optimizing bistable harvesters in terms of the energy output and the frequency bandwidth, recent studies focus on novel nonlinear tristable energy harvesters [14,15,16]. The potential function of a tristable harvester is that the device has three stable equilibrium points: one point at zero and the other two points on either side. It has been verified that the effective frequency bandwidth of a tristable harvester can be wider than that of a bistable harvester if the system parameters are carefully selected; tristable harvesters also provide greater output power than bistable harvesters. To reveal the sensitivity of the dynamic behavior to the system parameters from a theoretical perspective, the steady-state system response of a tristable harvester under deterministic excitation is derived by using a harmonic balance analysis [17]. After observing the dynamic response curves with respect to the system parameters, the high-energy interwell motion is feasible even under low-level ambient excitations, which is consistent with the experimental results. To determine the design rules for the system parameters on the effective bandwidth, the multiple-scale method is utilized to determine the bifurcation points and the effective bandwidth [8]. Due to the intrinsic randomness of the ambient vibration, the performance of the tristable harvester under filtered Gaussian noise is studied via simulations and experiments, and the results show that the tristable harvester is robust to the excitation intensity and is quite suitable for practical applications [18]. However, the tristable harvester under random noise is studied only through numerical simulation or experiments, and the important theoretical analysis is still open.

This study aims to develop an efficient analytical procedure to estimate the mean output power and reveal the influence of the design parameters on the harvester performance under Gaussian white noise excitation. Due to the coupling between the mechanical system and the external circuit, it is quite difficult to obtain the exact solution of the nonlinear harvester subjected to Gaussian white noise. To date, the exact solution can be derived only for a special case in which the ratio of the mechanical system period and the circuit time constant is quite large [7]. Recently, the equivalent nonlinearization technique based on the generalized harmonic transformation was successful in yielding the approximate mean output power of a monostable nonlinear harvesting system [19]. In that study, a coupled nonlinear system was approximately decoupled, and then the modified nonlinear mechanical system, which incorporated the stiffness and electrical damping effects, was solved by the equivalent nonlinearization technique. Although the combined procedure cannot be directly used for a tristable harvesting system, the generalization from a monostable nonlinear harvester to a tristable harvester is worthwhile due to the relative simplicity and the few limitations on nonlinear stiffness and Gaussian white noise excitation intensity.

This manuscript establishes a two-step approximation procedure for the random responses of tristable harvesting systems, which possess high precision for Gaussian white noise. In the first step, one modified mechanical system from the original energy harvesting system is established by the harmonic balance method. In the second step, the equivalent mechanical system associated with the modified mechanical system is derived through an unconventional equivalent nonlinearization technique. The equivalent mechanical system is determined by an iterative process, and the statistical information of the equivalent mechanical system can be obtained, which is an approximate solution for the original harvesting system. The dependence of the mean output power and system response on the crucial system parameters is discussed.

2 Mathematical description of a tristable energy harvesting system

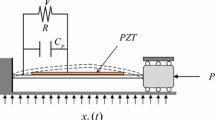
Regardless of the conversion mechanism, piezoelectric energy harvesting systems have similar mathematical descriptions. Consequently, this section concentrates on the mathematical description of a tristable vibration energy harvesting system. Moreover, the symmetric tristable potential is selected, and the piezoelectric material is directly connected with a resistance.

The coupled equations of the tristable harvester are [14]

$$\begin{aligned}&{\ddot{X}}+2\xi {\dot{X}}+\frac{\hbox {d}U\left( X \right) }{\hbox {d}X}+\kappa ^{2}V=-{\ddot{X}}_b \end{aligned}$$

(1a)

$$\begin{aligned}&{\dot{V}}+\alpha V={\dot{X}} \end{aligned}$$

(1b)

and

$$\begin{aligned} U\left( x \right) =\frac{1}{2}x^{2}-\frac{1}{4}\mu x^{4}+\frac{1}{6}\delta x^{6}, \end{aligned}$$

(2)

where the parameters $\mu$ and $\delta$ meet the conditions $\mu >0$ and $\delta >0$. One potential inequality constraint $\mu ^{2}-4\delta >0$ should be satisfied, which makes the system tristable.

According to the potential function in Eq. (2), we find that the mechanical component of the harvester possesses five equilibrium positions: two instable positions, $x=\pm \sqrt{\frac{\mu -\sqrt{\mu ^{2}-4\delta }}{2\delta }}$, and three stable positions, $x=\pm \sqrt{\frac{\mu +\sqrt{\mu ^{2}-4\delta }}{2\delta }}$ and 0, as shown in Fig. 1b. The largest range of motion, which can lead to a large strain and induce a high output voltage from the piezoelectric material, is positively related to the distance of the two outside stable equilibrium points: $x=\sqrt{\frac{\mu +\sqrt{\mu ^{2}-4\delta }}{2\delta }}$ and $x=-\sqrt{\frac{\mu +\sqrt{\mu ^{2}-4\delta }}{2\delta }}$. The distance (or the largest motion range) decreases as the nonlinear stiffness coefficient $\delta$ increases, whereas the distance increases as the nonlinear stiffness coefficient $\mu$ increases.

Fig. 1

Original coupled system: a schematic of the original coupled system and b the potential of the mechanical system

Fig. 2

Overarching flowchart of the proposed procedure

The base acceleration ${\ddot{X}}_b$ is Gaussian white noise with a zero mean. The correlation function $R\left( \tau \right) =2D\delta \left( \tau \right)$, where $\delta \left( \cdot \right)$ is the Dirac delta function and 2D is the noise intensity. The Gaussian white noise is an appropriate assumption as long as the flat spectral density of the excitation can thoroughly overlap the fundamental frequency of the harvesting system [20].

The output power is crucial for evaluating the performance of an energy harvesting system, and the output power can be expressed as [21]

$$\begin{aligned} P=\alpha \kappa ^{2}V^{2}. \end{aligned}$$

(3)

Throughout this paper, we endeavor to establish one approximate procedure to evaluate the mean output power of a tristable energy harvester under Gaussian white noise.

Before we start to give the complex derivation process, Fig. 2 shows a flowchart that presents a clear overview of the whole proposed procedure. Briefly, through two approximation steps, we successively obtain the modified mechanical system and the equivalent mechanical system. The joint probability density function of system displacement and velocity is solved from the equivalent mechanical system. Then, by using the voltage expression associated with system displacement and velocity, the mean output power is obtained, which is an approximate solution for the original system. The details of the above-mentioned processes are given in the following sections.

3 First approximation step: original coupled system to the modified mechanical system

As shown in Fig. 1, Eq. (1a) and (1b) can be interpreted as the mathematical description of a mechanical oscillator with a fixed base. The mechanical oscillator is forced by an external excitation $-{\ddot{X}}_b$ and disturbed by a complex “force” $\kappa ^{2}V$. For convenience, let us still call this the original coupled system. Due to the complex dependence on system states, the influence of the “force” $\kappa ^{2}V$ on system responses can be replaced by a certain conservative mechanism and dissipative mechanism. Consequently, the dynamic responses of the original coupled system in Fig. 1a will be consistent with those of the modified mechanical system in Fig. 3 with certain additional stiffness and additional damping. Compared with the mechanical vibration energy, the collected electrical energy through the “force” $\kappa ^{2}V$ is quite small. Therefore, the additional stiffness and damping associated with the “force” $\kappa ^{2}V$ are both very weak.

Fig. 3

Modified mechanical system: a the modified mechanical system and b the tristable potential of the modified mechanical system

The additional stiffness corresponds to an additional potential energy, and the sum of the original mechanical potential and the additional potential constitutes the total potential of the modified tristable mechanical system. Obviously, the potential shape of the modified tristable mechanical system slightly deviates from the shape of the original mechanical potential. Observing the total potential energy curve associated with the modified system plotted in Fig. 3b, we find that the minimum potential energy (denoted by $U_{cr2} )$ is at the modified stable point $P_1$, whereas the local maximum potential energy (denoted by $U_{cr1} )$ is at the modified unstable point $P_2$.

A conservative tristable oscillation system experiences two typical motions: intrawell motion and large-amplitude motion, which depend on the system energy level. When the system energy level is less than the potential barrier, the periodic and fixed-amplitude motion is confined in one well. A large, periodic, fixed-amplitude motion occurs when the system energy is greater than the potential barrier. For a nonconservative system, the total energy is influenced by the input energy of random excitation and the dissipated energy of damping. In the stationary stage, the difference in the input energy and the dissipated energy on a pseudo-period is less than the total energy, i.e., the system energy slowly varies, whereas the system displacement and velocity vary quickly [22]. The system will experience quasiperiodic motion, which can be found from one sample plotted in Fig. 4. Consequently, the displacement of the modified mechanical system can be precisely expressed by different harmonic functions [23] for intrawell motion and large-amplitude motion.

Fig. 4

Response sample of the mechanical system: a the response sample of the mechanical system displacement and b the response sample of the mechanical system velocity

For the intrawell motion, we assume that[17, 24]

$$\begin{aligned} X\left( t \right)= & {} A_1 \left( {H\left( t \right) } \right) \cdot \sin \left( {\theta _1 \left( t \right) } \right) \nonumber \\&+\,B_1 \left( {H\left( t \right) } \right) \cdot \cos \left( {\theta _1 \left( t \right) } \right) \pm x^{{*}}\left( {H\left( t \right) } \right) \end{aligned}$$

(4a)

$$\begin{aligned} V\left( t \right)= & {} C_1 \left( {H\left( t \right) } \right) \cdot \sin \left( {\theta _1 \left( t \right) } \right) +D_1 \left( {H\left( t \right) } \right) \cdot \cos \left( {\theta _1 \left( t \right) } \right) ,\nonumber \\ \end{aligned}$$

(4b)

where $x^{{*}}$ denotes the equilibrium position of the modified mechanical system and depends on energy $H\left( t \right)$. The phase $\theta _1$ is defined as $\theta _1 =\int _0^t {\omega _1 \left( s \right) d} s+\phi \left( t \right)$, which depends on the instantaneous frequency $\omega _1 \left( t \right)$, the oscillator location, and the residue phase angle $\phi \left( t \right)$. The “±” symbol distinguishes the motion in the right well and left well. The energy, equilibrium position, and terms of $A_1$, $B_1$, $C_1$, and $D_1$ in Eq. (4) slowly vary, whereas the system displacement and velocity vary quickly.

The introduction of harmonic functions Eqs. (4a) and (4b) provide an opportunity to approximately evaluate the past velocity through the current system states. The velocity is the derivative of the displacement $X\left( t \right)$ with respect to time, which can be expressed as

$$\begin{aligned} {\dot{X}}\left( t \right)= & {} \frac{\hbox {d}}{\hbox {d}t}A_1 \left( {H\left( t \right) } \right) \cdot \sin \left( {\theta _1 \left( t \right) } \right) \nonumber \\&+\,A_1 \left( {H\left( t \right) } \right) \cdot \cos \left( {\theta _1 \left( t \right) } \right) \cdot \frac{\hbox {d}}{\hbox {d}t}\theta _1 \left( t \right) \nonumber \\&+\,\frac{\hbox {d}}{\hbox {d}t}B_1 \left( {H\left( t \right) } \right) \cdot \cos \left( {\theta _1 \left( t \right) } \right) -B_1 \left( {H\left( t \right) } \right) \nonumber \\&\cdot \sin \left( {\theta _1 \left( t \right) } \right) \cdot \frac{\hbox {d}}{\hbox {d}t}\theta _1 \left( t \right) \pm \frac{\hbox {d}}{\hbox {d}t}x^{{*}}\left( {H\left( t \right) } \right) . \end{aligned}$$

(5)

The following approximation is considered [25]:

$$\begin{aligned} \theta _1 \left( {t+\tau } \right)= & {} \int _0^{t+\tau } {\omega _1 \left( s \right) d} s+\phi \left( {t+\tau } \right) \approx \theta _1 \left( t \right) \nonumber \\&+\bar{{\omega }}_1 \tau , \end{aligned}$$

(6)

where $\bar{{\omega }}_1$ is the average frequency of $\omega _1 \left( t \right)$ and can be expressed by the quasiperiod $T_1$ as $\bar{{\omega }}_1 =\frac{2\pi }{T_1 }$.

Thus, the approximation $\frac{\hbox {d}}{\hbox {d}t}\theta _1 \left( t \right) \approx \bar{{\omega }}_1$ can be made and all time derivatives of the slowly varying terms $A_1$, $B_1$, $C_1$, $D_1$, and $x^{{*}}$ can be neglected. Then, Eq. (5) can be reduced to

$$\begin{aligned} {\dot{X}}\left( t \right)= & {} A_1 \left( {H\left( t \right) } \right) \cdot \bar{{\omega }}_1 \cdot \cos \left( {\theta _1 \left( t \right) } \right) \nonumber \\&-B_1 \left( {H\left( t \right) } \right) \cdot \bar{{\omega }}_1 \cdot \sin \left( {\theta _1 \left( t \right) } \right) . \end{aligned}$$

(7)

Similar to deriving the velocity, the derivative of the voltage V with respect to time, where all time derivatives of the slowly varying terms are neglected and the approximation $\frac{\hbox {d}}{\hbox {d}t}\theta _1 \left( t \right) \approx \bar{{\omega }}_1$ is used, can be expressed as

$$\begin{aligned}&{\dot{V}}\left( t \right) =C_1 \left( {H\left( t \right) } \right) \cdot \bar{{\omega }}_1 \cdot \cos \left( {\theta _1 \left( t \right) } \right) -D_1 \left( {H\left( t \right) } \right) \nonumber \\&\quad \quad \quad \quad \cdot \bar{{\omega }}_1 \cdot \sin \left( {\theta _1 \left( t \right) } \right) \end{aligned}$$

(8)

By substituting Eqs. (4b), (5), and (8) into Eq. (1b) and balancing the coefficients of the terms $\sin \left( {\theta _1 \left( t \right) } \right)$ and $\cos \left( {\theta _1 \left( t \right) } \right)$, we can obtain the algebraic equations of $A_1$, $B_1$, $C_1$, and $D_1$, which can be expressed as

$$\begin{aligned}&\bar{{\omega }}_1 \cdot C_1 \left( {H\left( t \right) } \right) +\alpha \cdot D_1 \left( {H\left( t \right) } \right) =A_1 \left( {H\left( t \right) } \right) \cdot \bar{{\omega }}_1 \end{aligned}$$

(9a)

$$\begin{aligned}&\alpha \cdot C_1 \left( {H\left( t \right) } \right) -\bar{{\omega }}_1 \cdot D_1 \left( {H\left( t \right) } \right) =-B_1 \left( {H\left( t \right) } \right) \cdot \bar{{\omega }}_1 \end{aligned}$$

(9b)

By using Eq. (9a) and (9b), the coefficients $C_1$ and $D_1$ in the voltage expression can be solved in terms of coefficients $A_1$ and $B_1$, which can be expressed as

$$\begin{aligned}&C_1 \left( {H\left( t \right) } \right) =\frac{\bar{{\omega }}_1^2 \cdot A_1 -\alpha \bar{{\omega }}_1 \cdot B_1 }{\bar{{\omega }}_1^2 +\alpha ^{2}} \end{aligned}$$

(10a)

$$\begin{aligned}&D_1 \left( {H\left( t \right) } \right) =\frac{\alpha \bar{{\omega }}_1 \cdot A_1 +\bar{{\omega }}_1^2 \cdot B_1 }{\bar{{\omega }}_1^2 +\alpha ^{2}}. \end{aligned}$$

(10b)

By substituting Eq. (10a) and (10b) into Eq. (4b) and rewriting the voltage expression by using the mechanical displacement X and velocity ${\dot{X}}$ in Eqs. (4a) and (7), the relationship between the voltage and the mechanical state can be revealed, which is expressed as

$$\begin{aligned} V\left( t \right) =\frac{\bar{{\omega }}_1^2 }{\bar{{\omega }}_1^2 +\alpha ^{2}}\left( {X{\mp } x^{{*}}} \right) +\frac{\alpha }{\bar{{\omega }}_1^2 +\alpha ^{2}}{\dot{X}}. \end{aligned}$$

(11)

For a large-amplitude motion, we can similarly assume that

$$\begin{aligned} X\left( t \right)= & {} A_2 \left( {H\left( t \right) } \right) \cdot \sin \left( {\theta _2 \left( t \right) } \right) \nonumber \\&+\,B_2 \left( {H\left( t \right) } \right) \cdot \cos \left( {\theta _2 \left( t \right) } \right) \end{aligned}$$

(12a)

$$\begin{aligned} V\left( t \right)= & {} C_2 \left( {H\left( t \right) } \right) \cdot \sin \left( {\theta _2 \left( t \right) } \right) \nonumber \\&+\,D_2 \left( {H\left( t \right) } \right) \cdot \cos \left( {\theta _2 \left( t \right) } \right) . \end{aligned}$$

(12b)

Similar to the case of intrawell motion, the terms $A_2$, $B_2$, $C_2$, and $D_2$ in the large-amplitude motion are also slowly varying quantities, and the following approximation relation still holds:

$$\begin{aligned} \theta _2 \left( {t+\tau } \right) =\int _0^{t+\tau } {\omega _2 \left( s \right) d} s+\phi \left( {t+\tau } \right) \approx \theta _2 \left( t \right) +\bar{{\omega }}_2 \tau ,\nonumber \\ \end{aligned}$$

(13)

where $\bar{{\omega }}_2$ is the average frequency of $\omega _2 \left( t \right)$ and can be expressed by the quasiperiod $T_2$ as $\bar{{\omega }}_2 =\frac{2\pi }{T_2 }$.

Thus, the voltage $V\left( t \right)$ for the large amplitude can be given as

$$\begin{aligned} V\left( t \right) =\frac{\bar{{\omega }}_2^2 }{\bar{{\omega }}_2^2 +\alpha ^{2}}X+\frac{\alpha }{\bar{{\omega }}_2^2 +\alpha ^{2}}\dot{X}. \end{aligned}$$

(14)

Based on Eqs. (11) and (14), the algebraic expression of the complex “force” $\kappa ^{2}V$ for the intrawell motion is

$$\begin{aligned} \kappa ^{2}V= & {} \frac{\kappa ^{2}\omega _1 \left( {H\left( t \right) } \right) ^{2}}{\alpha ^{2}+\omega _1 \left( {H\left( t \right) } \right) ^{2}}\cdot \left[ {X\left( t \right) {\mp } x^{{*}}\left( {H\left( t \right) } \right) } \right] \nonumber \\&+\,\frac{\kappa ^{2}\alpha }{\alpha ^{2}+\omega _1 \left( {H\left( t \right) } \right) ^{2}}\cdot {\dot{X}}\left( t \right) . \end{aligned}$$

(15)

For the large-amplitude motion, we have a similar expression, which is expressed as

$$\begin{aligned} \kappa ^{2}V= & {} \frac{\kappa ^{2}\omega _2 \left( {H\left( t \right) } \right) ^{2}}{\alpha ^{2}+\omega _2 \left( {H\left( t \right) } \right) ^{2}}\cdot X\left( t \right) \nonumber \\&+\,\frac{\kappa ^{2}\alpha }{\alpha ^{2}+\omega _2 \left( {H\left( t \right) } \right) ^{2}}\cdot {\dot{X}}\left( t \right) . \end{aligned}$$

(16)

Note that the symbol “-” above the frequency $\omega _i$, which indicates that the average frequency, is omitted for convenience in Eqs. (15) and (16) and in the following content.

The substitution of the algebraic expressions in Eqs. (15) and (16) into Eq. (1a) yields the explicit mathematical description of the modified mechanical system in Fig. 3a, which is expressed as

$$\begin{aligned} {\ddot{X}}+2\xi {\dot{X}}+f_{\mathrm {mod}}^{\mathrm {dis}} +\frac{\hbox {d}U\left( X \right) }{\hbox {d}X}+f_{\mathrm {mod}}^{\mathrm {con}} =-{\ddot{X}}_b, \end{aligned}$$

(17)

where both the modified damping $f_{\mathrm {mod}}^{\mathrm {dis}}$ and modified stiffness $f_{\mathrm {mod}}^{\mathrm {con}}$ possess different expressions for the intrawell motion and large-amplitude motion, and they are expressed as

$$\begin{aligned} f_{\mathrm {mod}}^{\mathrm {dis}}= & {} \left\{ {{\begin{array}{l} {\frac{\kappa ^{2}\alpha }{\alpha ^{2}+\omega _1 \left( {H\left( t \right) } \right) ^{2}}{\dot{X}}\left( t \right) ,\hbox { intrawell}} \\ {\frac{\kappa ^{2}\alpha }{\alpha ^{2}+\omega _2 \left( {H\left( t \right) } \right) ^{2}}{\dot{X}}\left( t \right) ,\hbox { large amplitude}} \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$

(18a)

$$\begin{aligned} f_{\mathrm {mod}}^{\mathrm {con}}= & {} \left\{ {{\begin{array}{l} {\frac{\kappa ^{2}\omega _1 \left( {H\left( t \right) } \right) ^{2}}{\alpha ^{2}+\omega _1 \left( {H\left( t \right) } \right) ^{2}}\left[ {X\left( t \right) {\mp } x^{{*}}\left( {H\left( t \right) } \right) } \right] ,\hbox { intrawell}} \\ {\frac{\kappa ^{2}\omega _2 \left( {H\left( t \right) } \right) ^{2}}{\alpha ^{2}+\omega _2 \left( {H\left( t \right) } \right) ^{2}}X\left( t \right) ,\hbox { large amplitude}} \\ \end{array} }}. \right. \nonumber \\ \end{aligned}$$

(18b)

At this point, we have successfully derived the explicit mathematical description of the modified mechanical system in Fig. 3, as shown in Eqs. (17) and (18). For the tristable modified mechanical system, the modified damping and modified stiffness possess different expressions, as shown in Eqs. (18a) and (18b). It should be emphasized that we have derived only the explicit mathematical description of the modified system in form: The energy H, the frequency functions $\omega _{1}(H)$ and $\omega$$_{2}(H)$, and the equilibrium position $x^{{*}}\left( H \right)$ remain unknown. Thus, solving the modified tristable system is impossible, and a second approximation step is needed.

4 Second approximation step: modified mechanical system to an equivalent mechanical system

In this section, an unconventional equivalent nonlinearization technique is developed to derive the equivalent system of the modified mechanical system and is shown in Fig. 3. The solution of the equivalent mechanical system response can be derived analytically, which is an approximate result for the original coupled system. The equivalent mechanical system family from which the equivalent mechanical system will be selected is first illustrated, and then an appropriate criterion that measures the differences in the modified mechanical system and the equivalent mechanical system is proposed to derive those undetermined parameters [26, 27].

4.1 Equivalent mechanical system family of the tristable modified mechanical system

The element of the equivalent mechanical system is depicted in Fig. 3, in which $f_{\mathrm {eq}}^{\mathrm {dis}} ,f_{\mathrm {eq}}^{\mathrm {con}}$, and $U_{\mathrm {eq}}$ represent the additional damping, additional stiffness, and additional potential, respectively. The mathematical description of the equivalent mechanical system is

$$\begin{aligned} {\ddot{X}}+2\xi {\dot{X}}+f_{\mathrm {eq}}^{\mathrm {dis}} +\frac{\hbox {d}\left( {U+U_{\mathrm {eq}} } \right) }{\hbox {d}X}=-\ddot{X}_b. \end{aligned}$$

(19)

To balance the solvability and similarity between the chosen equivalent system and the modified mechanical system and equivalent system, the equivalent damping, equivalent stiffness, and equivalent potential for the tristable modified systems should be appropriately selected.

For the modified mechanical system with tristable potential, the equivalent damping, equivalent stiffness, and equivalent potential are selected as

$$\begin{aligned} f_{\mathrm {eq}}^{\mathrm {dis}}= & {} \left\{ {{\begin{array}{l} {\frac{\kappa ^{2}\alpha }{\alpha ^{2}+\omega _{\mathrm {eq1}} \left( {H_{\mathrm {eq}} } \right) ^{2}}{\dot{X}},\hbox { intrawell}} \\ {\frac{\kappa ^{2}\alpha }{\alpha ^{2}+\omega _{\mathrm {eq2}} \left( {H_{\mathrm {eq}} } \right) ^{2}}{\dot{X}},\hbox { large amplitude}} \\ \end{array} }} \right. \end{aligned}$$

(20a)

$$\begin{aligned} f_{\mathrm {eq}}^{\mathrm {con}}= & {} {\tilde{a}}_1 x-{\tilde{a}}_3 x^{3}+\tilde{a}_5 x^{5} \end{aligned}$$

(20b)

$$\begin{aligned} U_{\mathrm {eq}}= & {} \frac{1}{2}{\tilde{a}}_1 x^{2}-\frac{1}{4}\tilde{a}_3 x^{4}+\frac{1}{6}{\tilde{a}}_5 x^{6}, \end{aligned}$$

(20c)

where $H_{\mathrm {eq}} ={{\dot{x}}^{2}}/2+U+U_{\mathrm {eq}}$ is the energy of the equivalent mechanical system; $\omega _{\mathrm {eq1}} \left( {H_{\mathrm {eq}} } \right)$ and $\omega _{\mathrm {eq2}} \left( {H_{\mathrm {eq}} } \right)$ are the energy-dependent frequency functions for the intrawell motion and large-amplitude motion, respectively; and ${\tilde{a}}_1$, ${\tilde{a}}_3$, and ${\tilde{a}}_5$ are the undetermined equivalent linear and nonlinear stiffness coefficients.

The equivalent system experiences intrawell motion when $H_{\mathrm {eq}} <U_{cr1}$, where $U_{cr1}$ is shown in Fig. 1b, where as the equivalent system experiences large-amplitude motion when $H_{\mathrm {eq}} \ge U_{cr1}$. The energy-dependent frequency function $\omega _{\mathrm {eq1}} \left( {H_{\mathrm {eq}} } \right)$ for the intrawell motion can be explicitly derived as follows. Due to the relation $\hbox {d}t={\hbox {d}x}/{{\dot{x}}}$, we can obtain

$$\begin{aligned} \hbox {d}t=\frac{\hbox {d}x}{\pm \sqrt{2H_{\mathrm {eq}} -2U-2U_{\mathrm {eq}} }}, \end{aligned}$$

(21)

where the energy $H_{\mathrm {eq}}$ appears to be constant. The period is derived by integrating Eq. (21), in which the displacement x varies in one oscillation cycle, and then the average frequency can be written as

$$\begin{aligned} \omega _{\mathrm {eq1}} \left( {H_{\mathrm {eq}} } \right) ={2\pi }/{T_1 }, \end{aligned}$$

(22)

where $T_1 =2\int _{A_1 \left( {H_{\mathrm {eq}} } \right) }^{A_2 \left( {H_{\mathrm {eq}} } \right) } {\frac{\hbox {d}x}{\sqrt{2H_{\mathrm {eq}} -2U\left( x \right) -2U_{\mathrm {eq}} \left( x \right) }}} , U_{cr2} \hbox {<}H_{\mathrm {eq}} <0$ is the period of the oscillator around the right equilibrium point, and $A_{1}(H_{\mathrm {eq}} )$ and $A_{2}(H_{\mathrm {eq}} )$ represent the lower and upper boundaries, respectively, which can be determined from the equation $H_{\mathrm {eq}} =U\left( x \right) +U_{\mathrm {eq}} \left( x \right)$.

When $0\hbox {<}H_{\mathrm {eq}} <U_{cr1}$ (the oscillator still experiences intrawell motion),

$$\begin{aligned} \omega _{\mathrm {eq1}} \left( {H_{\mathrm {eq}} } \right) ={2\pi }/{T_2 }, \end{aligned}$$

(23)

where

$$\begin{aligned} T_2= & {} \frac{2}{3}\int _{A_3 \left( {H_{\mathrm {eq}} } \right) }^{A_4 \left( {H_{\mathrm {eq}} } \right) } {\frac{\hbox {d}x}{\sqrt{2H_{\mathrm {eq}} -2U\left( x \right) -2U_{\mathrm {eq}} \left( x \right) }}} \\&+\,\frac{1}{3}\int _{A_5 \left( {H_{\mathrm {eq}} } \right) }^{A_6 \left( {H_{\mathrm {eq}} } \right) } {\frac{\hbox {d}x}{\sqrt{2H_{\mathrm {eq}} -2U\left( x \right) -2U_{\mathrm {eq}} \left( x \right) }}} 0\hbox {<}H_{\mathrm {eq}} <U_{cr1} \end{aligned}$$

is the average period of the oscillator around the three stable equilibrium points; $A_{3}(H_{\mathrm {eq}} )$ and $A_{4}(H_{\mathrm {eq}} )$ represent the lower and upper boundaries around the right equilibrium point for a given energy $H_{\mathrm {eq}}$, respectively; and $A_{5}(H_{\mathrm {eq}} )$ and $A_{6}(H_{\mathrm {eq}} )$ represent the lower and upper boundaries around the 0 equilibrium point for a given energy $H_{\mathrm {eq}}$, respectively.

The energy-dependent frequency function $\omega _{\mathrm {eq2}} \left( {H_{\mathrm {eq}} } \right)$ for the large-amplitude motion is expressed as

$$\begin{aligned} \omega _{\mathrm {eq2}} \left( {H_{\mathrm {eq}} } \right) =\pi /{\int _{A_7 \left( {H_{\mathrm {eq}} } \right) }^{A_8 \left( {H_{\mathrm {eq}} } \right) } {\frac{\hbox {d}x}{\sqrt{2H_{\mathrm {eq}} -2U\left( x \right) -2U_{\mathrm {eq}} \left( x \right) }}} }, H_{\mathrm {eq}} \ge U_{cr1} \end{aligned}$$

(24)

where $A_{7}(H_{\mathrm {eq}} )$ and $A_{8}(H_{\mathrm {eq}} )$ represent the lower and upper boundaries for a given $H_{\mathrm {eq}}$, respectively, which can be determined from the equation $H_{\mathrm {eq}} =U\left( x \right) +U_{\mathrm {eq}} \left( x \right)$.

For given values of parameters ${\tilde{a}}_1$, ${\tilde{a}}_3$, and ${\tilde{a}}_5$, the stationary probability density of the equivalent system with tristable potential can be analytically obtained from the FPK equation [22], which is expressed as

$$\begin{aligned} p_{\mathrm {eq}} \left( {x,{\dot{x}}} \right) =\left\{ {{\begin{array}{l} {N_1 \cdot e^{-\frac{1}{D}\int _{U_{cr2} }^{{{\dot{x}}^{2}}/2+U\left( x \right) +U_{\mathrm {eq}} \left( x \right) } {\left[ {2\xi +\frac{\kappa ^{2}\alpha }{\alpha ^{2}+\omega _{\mathrm {eq1}} \left( u \right) ^{2}}} \right] \hbox {d}u} }\hbox {, }U_{cr2} \le u<U_{cr1} }\\ {N_2 \cdot e^{-\frac{1}{D}\int _{U_{cr2} }^{{{\dot{x}}^{2}}/2+U\left( x \right) +U_{\mathrm {eq}} \left( x \right) } {\left[ {2\xi +\frac{\kappa ^{2}\alpha }{\alpha ^{2}+\omega _{\mathrm {eq2}} \left( u \right) ^{2}}} \right] \hbox {d}u} }, u\ge U_{cr1} } \\ \end{array} }} \right. \end{aligned}$$

(25)

where $N_1$ and $N_2$ are normalized constants.

4.2 Determination of equivalent linear and nonlinear stiffness coefficients

The equivalent damping in Eq. (19) is appropriately selected according to the forms of the modified damping in Eq. (20a). However, the equivalent stiffness is selected as the form of Eq. (20b). Thus, it is reasonable to select the difference in the equivalent stiffness in Eq. (20b) and the additional stiffness in Eq. (18b) as the criterion, which can be expressed as

$$\begin{aligned} e={\tilde{a}}_1 X-{\tilde{a}}_3 X^{3}+{\tilde{a}}_5 X^{5}-f_{\mathrm {mod}}^{\mathrm {con}}. \end{aligned}$$

(26)

The equivalent linear coefficient ${\tilde{a}}_1$ and the nonlinear stiffness coefficients ${\tilde{a}}_3$ and ${\tilde{a}}_5$ can be determined by the condition of minimum mean-square value $E\left( {e^{2}} \right)$ and are defined by the stationary probability density of the modified mechanical system $p_{\bmod } \left( {x,\dot{x}} \right)$. The deviation in the mean-square difference, i.e., $\frac{\partial E\left[ {e^{2}} \right] }{\partial {\tilde{a}}_i }=0 \left( {i=1,2,3} \right)$, yields the expressions of coefficients ${\tilde{a}}_1$, ${\tilde{a}}_3$, and ${\tilde{a}}_5$.

The terms in the expressions $\frac{\partial E\left[ {e^{2}} \right] }{\partial {\tilde{a}}_i }=0 \left( {i=1,2,3} \right)$ depend on the modified stiffness $f_{\mathrm {mod}}^{\mathrm {con}}$ and the stationary probability density of the modified mechanical system $p_{\bmod } \left( {x,{\dot{x}}} \right)$. The modified stiffness $f_{\mathrm {mod}}^{\mathrm {con}}$ in Eq. (18b) depends on the energy H, the frequency functions $\omega _{1}(H)$ and $\omega$$_{2}(H)$, and the equilibrium position $x^{{*}}\left( H \right)$ of the modified mechanical system; however, all of these quantities are unknown. The stationary probability density of the modified mechanical system $p_{\bmod } \left( {x,{\dot{x}}} \right)$, however, is the function that should be determined. Thus, we replace the quantities of the modified mechanical system with those of the equivalent mechanical system:

$$\begin{aligned}&H\rightarrow H_{\mathrm {eq}} =\frac{1}{2}{\dot{x}}^{2}+U\left( x \right) +\frac{1}{2}{\tilde{a}}_1 x^{2}-\frac{1}{4}{\tilde{a}}_3 x^{4}+\frac{1}{6}{\tilde{a}}_5 x^{6}\nonumber \\ \end{aligned}$$

(27a)

$$\begin{aligned}&\omega _i \left( H \right) \rightarrow \omega _{\mathrm {eq}i} \left( {H_{\mathrm {eq}} } \right) i=1,2 \end{aligned}$$

(27b)

$$\begin{aligned}&x^{*}\left( H \right) \rightarrow x^{*}\equiv 0,\nonumber \\&\quad \sqrt{\frac{\left( {\mu +{\tilde{a}}_3 } \right) +\sqrt{\left( {\mu +{\tilde{a}}_3 } \right) ^{2}-4\left( {1+{\tilde{a}}_1 } \right) \left( {\delta +{\tilde{a}}_5 } \right) }}{2\left( {\delta +{\tilde{a}}_3 } \right) }}\nonumber \\ \end{aligned}$$

(27c)

$$\begin{aligned}&p_{\bmod } \left( {x,{\dot{x}}} \right) \rightarrow p_{\mathrm {eq}} \left( {x,{\dot{x}}} \right) . \end{aligned}$$

(27d)

Based on Eqs. (27a)–(27d), the moments of the modified mechanical system that appear in $\frac{\partial E\left[ {e^{2}} \right] }{\partial {\tilde{a}}_i }=0 \left( {i=1,2,3} \right)$ are replaced:

$$\begin{aligned} E\left[ {X^{i}} \right]= & {} \int _{-\infty }^\infty {x^{i}p_{\mathrm {eq}} \left( {x,{\dot{x}}} \right) \hbox {d}x\hbox {d}{\dot{x}}} \end{aligned}$$

(28a)

$$\begin{aligned} E\left[ {X^{i}f_{\mathrm {mod}}^{\mathrm {con}} } \right]= & {} \left\{ {{\begin{array}{l} {\int _{-\infty }^\infty {\int _{-\infty }^\infty {x^{i}\frac{\kappa ^{2}\omega _{\mathrm {eq1}} \left( {H_{\mathrm {eq}} } \right) ^{2}}{\alpha ^{2}+\omega _{\mathrm {eq}1} \left( {H_{\mathrm {eq}} } \right) ^{2}}\left( {x{\mp } x^{{*}}} \right) p_{\mathrm {eq}} \left( {x,{\dot{x}}} \right) } \hbox {d}x\hbox {d}{\dot{x}}} , U_{cr2} \le H_{eq} <U_{cr1} } \\ {\int _{-\infty }^\infty {\int _{-\infty }^\infty {x^{i\hbox {+}1}\frac{\kappa ^{2}\omega _{\mathrm {eq}2} \left( {H_{\mathrm {eq}} } \right) ^{2}}{\alpha ^{2}+\omega _{\mathrm {eq}2} \left( {H_{\mathrm {eq}} } \right) ^{2}}p_{\mathrm {eq}} \left( {x,\dot{x}} \right) } \hbox {d}x\hbox {d}{\dot{x}}} , H_{\mathrm {eq}} \ge U_{cr1} } \\ \end{array} }}, \right. \end{aligned}$$

(28b)

where $p_{\mathrm {eq}} \left( {x,{\dot{x}}} \right)$ is the stationary probability density of the equivalent mechanical system with tristable potential, as shown in Eq. (25). Note that the equivalent linear and nonlinear stiffness coefficients ${\tilde{a}}_1$, $\tilde{a}_3$, and ${\tilde{a}}_5$ should be determined through an iterative technique. Once the coefficients ${\tilde{a}}_1$, $\tilde{a}_3$, and ${\tilde{a}}_5$ are obtained, the probability density of the equivalent mechanical system can be given together with the response statistics, which are used as the approximate solution of the original coupled system. The mean-square voltage is evaluated through the algebraic voltage expression given in Eqs. (15) and (16):

$$\begin{aligned} E\left[ {V^{2}} \right] =\left\{ {{\begin{array}{l} {\int _{-\infty }^\infty {\int _{-\infty }^\infty {\left[ {\frac{\omega _{\mathrm {eq1}} \left( {H_{\mathrm {eq}} } \right) ^{2}\left( {x{\mp } x^{{*}}} \right) }{\alpha ^{2}+\omega _{\mathrm {eq}1} \left( {H_{\mathrm {eq}} } \right) ^{2}}+\frac{\alpha \dot{x}}{\alpha ^{2}+\omega _{\mathrm {eq}1} \left( {H_{\mathrm {eq}} } \right) ^{2}}} \right] ^{2}} } p_{\mathrm {eq}} \left( {x,{\dot{x}}} \right) \hbox {d}x\hbox {d}{\dot{x}}, U_{cr2} \le H_{eq} <U_{cr1} } \\ {\int _{-\infty }^\infty {\int _{-\infty }^\infty {\left[ {\frac{\omega _{\mathrm {eq}2} \left( {H_{\mathrm {eq}} } \right) ^{2}}{\alpha ^{2}+\omega _{\mathrm {eq}2} \left( {H_{\mathrm {eq}} } \right) ^{2}}x+\frac{\alpha {\dot{x}}}{\alpha ^{2}+\omega _{\mathrm {eq2}} \left( {H_{\mathrm {eq}} } \right) ^{2}}} \right] ^{2}} } p_{\mathrm {eq}} \left( {x,{\dot{x}}} \right) \hbox {d}x\hbox {d}\dot{x}, H_{\mathrm {eq}} \ge U_{cr1} } \\ \end{array} }}. \right. \end{aligned}$$

(29)

The mean output power, which is the expectation of the output power in Eq. (3), is expressed as

$$\begin{aligned} E\left[ P \right] =\alpha \kappa ^{2}\cdot E\left[ {V^{2}} \right] \end{aligned}$$

(30)

Fig. 5

Curve of the mean output power $E\left[ P \right]$ and the excitation intensity 2D. Solid lines: approximate results. Discrete markers: MCS

Fig. 6

Marginal and joint probability densities of system displacement and velocity: a the stationary displacement probability density, b the stationary velocity probability density, c the stationary joint probability density (approximate result), and d the stationary joint probability density (MCS). Solid lines: approximate results. Discrete markers: MCS

5 Examples and discussion

By comparing the system displacement and velocity responses from the proposed procedure and the numerical Monte Carlo simulation (MCS), the accuracy of the two-step approximation procedure is first illustrated. The time step of the MCS is chosen as 0.01, the number of samples is 10,000, and the total simulation time for each sample is 200. Then, the relations of the mean output power to some crucial parameters are discussed in detail. The system parameter values are set as the nonlinear stiffness coefficients $\mu =1.5$ and $\delta =0.4$, the linear electromechanical coupling coefficient $\kappa =0.1$, the time constant ratio $\alpha =0.1$, the viscous damping ratio $\xi =0.02$, and the Gaussian white noise intensity $2D=0.08$.

Fig. 7

Curve of the mean output power $E\left[ P \right]$ and the linear electromechanical coupling coefficient $\kappa$. Solid lines: approximate results. Discrete markers: MCS

Fig. 8

Curve of the mean output power $E\left[ P \right]$ and the time constant ratio $\alpha$. Solid lines: approximate results. Discrete markers: MCS

The curve of the mean output power $E\left[ P \right]$ and the excitation intensity 2D is first illustrated in Fig. 5. For the cases with small excitation intensities, the two-step approximation procedure provides accurate predictions of the mean output power. However, this approximation procedure yields worse prediction accuracy for larger excitation intensities. In Fig. 6, the system displacement and velocity responses, such as the marginal and joint probability densities, are depicted ($2D=0.08)$. The agreement of the results from the analytical technique and the Monte Carlo numerical simulation shows the effectiveness of the two-step approximate procedure. Hereafter, the relations of the mean output power to the crucial system parameters are investigated. Figure 7 illustrates the relation between the linear electromechanical coupling coefficient $\kappa$ and the mean output power $E\left[ P \right]$. As the linear electromechanical coefficient $\kappa$ decreases, the mean output power $E\left[ P \right]$ monotonously decreases. Figure 8 depicts the curve of the mean power $E\left[ P \right]$ and the time constant ratio $\alpha$. As the time constant ratio $\alpha$ increases, the mean power $E\left[ P \right]$ approaches the largest values at the associated optimal time constant ratio $\alpha \approx 1.0$, which indicates the existence of an optimal external resistance value where the tristable harvesting system generates maximal output power.

Fig. 9

Curve of the mean output power $E\left[ P \right]$ and the nonlinear stiffness coefficient $\mu$. Solid lines: approximate results. Discrete markers: MCS

Fig. 10

a Potential function for different nonlinear stiffness coefficients $\mu$. b Probability density of displacement for different nonlinear stiffness coefficients $\mu$. Solid lines: approximate results. Discrete markers: MCS

Fig. 11

Curve of the mean output power $E\left[ P \right]$ and the nonlinear stiffness coefficient $\delta$. Solid lines: approximate results. Discrete markers: MCS

Fig. 12

a Potential function for different nonlinear stiffness coefficients $\delta$. b Probability density of displacement under different nonlinear stiffness coefficients $\delta$. Solid lines: approximate results. Discrete markers: MCS

Figures 9, 10, 11, and 12 illustrate the effects of the nonlinear stiffness. Figure 9 presents the relation of the mean power $E\left[ P \right]$ to the stiffness coefficient $\mu$. As the nonlinear stiffness $\mu$ increases, the mean output power $E\left[ P \right]$ approaches the largest values at the associated optimal nonlinear stiffness $\mu$ and then decreases continuously. The occurrence of the optimal nonlinear stiffness $\mu$ indicates the existence of an optimal potential function. To obtain a better understanding, Fig. 10a and 10b shows the potential function and the stationary marginal probability density of the displacement under three different stiffness coefficients $\mu$. It is obvious that for $\mu =0.5$, the harvester is monostable [19], whereas at $\mu =1.5$ and $\mu =2.5$, the harvester is tristable. The tristable harvesting system can be superior to the monostable system under some nonlinear stiffness values (i.e., $\mu \hbox {=}1.5)$ but not all of the nonlinear stiffness values (i.e., $\mu \hbox {=}2.5)$. However, for some large values of $\mu$ (i.e., $\mu =2.5)$, the deep potential, as shown in Fig. 10a, confines the large-amplitude oscillation, and the probability density of the displacement shown in Fig. 10b reveals that the motion is intrawell with a probability of approximately one. The mean power level of the tristable harvester is even smaller than that of the monostable system. Figures 11 and 12 depict the relation of the harvesting power to the nonlinear stiffness coefficient $\delta$. As the nonlinear stiffness $\delta$ increases, the potential function in Fig. 12a changes from a tristable type to a monostable type. As the nonlinear stiffness $\delta$ increases, the collected energy decreases, as shown in Fig. 11, which is consistent with the probability density of the displacement in Fig. 12b. Generally, the efficiency of the tristable harvester depends on both the distance of the two side equilibrium points and the depth of the potential well. The balance of the distance and depth of the potential well is critically important. Finally, the influence of viscous damping is discussed in Fig. 13. Increase in the viscous damping coefficient $\xi$ significantly decreases the mean output power $E\left[ P \right]$. Therefore, system damping is an important factor in the design of tristable vibration energy harvesters and should be carefully treated.

Fig. 13

Curve of the mean output power $E\left[ P \right]$ and the viscous damping coefficient $\xi$. Solid lines: approximate results. Discrete markers: MCS

6 Conclusions

The response of the tristable harvesting system under Gaussian white noise is investigated in this study. A modified mechanical system and an equivalent mechanical system of the original coupled system are successively established by using a two-step approximation procedure. The equivalent mechanical system is determined from an iterative process, and the statistical quantities, such as the mean-square voltage and mean energy collection power, are obtained. The approximation procedure provides good predictions for the energy harvesting output power. The tristable harvester is superior to the monostable harvester in some cases (i.e., shallow potential wells), which indicates that the potential function should be constructed carefully. It should be noted that the proposed procedure not only provides an approximate solution of the tristable energy harvester but can also be easily extended to multistable energy harvesters, of which the tristable harvester is just a special case.

As an end to this study, we discuss another approximate method: stochastic averaging. After finishing the first approximation step and obtaining the modified mechanical system, we can use stochastic averaging [21] to derive the solutions. A comparison between the stochastic averaging and the proposed procedure shows that stochastic averaging provides worse predictions of the marginal probability densities than the proposed procedure, whereas stochastic averaging provides better precision for the mean output power, which seems contradictory. The main reason for this behavior is that the approximate expression in Eq. (16) underestimates the voltage value, which can be found from the fact that the nearly exact probability of the system states from the proposed procedure can only give a small mean output power estimation. However, the stochastic averaging, which overestimates the probability of large-amplitude response, reduces the error from the voltage approximation expression.