Keywords

1 Introduction

With the increasing demand for smartphones and fast mobile Internet services, the fifth generation (5G) of mobile networks is being researched to support large amounts of data traffic. One of the key performance indicators (KPIs) in future communication network design is the energy consumption, which means that spectral efficiency (SE) and energy efficiency (EE) are important factors in the 5G design. There are two techniques presented, they are: (i) Distributed antenna systems (DAS), because DAS can reduce the communication distance between mobile phones and remote access units (RAUs), the DAS has many advantages to increase capacity, improve coverage and EE [1,2,3]; (ii) device-to-device (D2D) communication, that can underlay the spectral resource of cellular users to enable a user device communicating with another nearby user device directly without extra hop from base station. It increases the overall network SE and thus allows the network to admit more users [4, 5].

It is well known that power allocation will become an urgent problem in the future. In the field of DAS and D2D communication, there are a number of efficient approaches which have been presented to solve this problem [6,7,8,9,10,11,12]. For instance, for DAS, an power allocation approach to maximize SE has been provided for generalized DAS in [6]. The authors in [7] have proposed a power allocation approach to maximize the EE, which transforms the fractional form of non-convex problem into its equivalent subtractive form. For D2D communication, the authors considered maximizing sum-rate over signal to interference and noise ratio of the system in [10]. In order to keep the quality of service (QoS) of D2D users and cellular user equipments, a three-step approach has been presented to improve the total transmit rate of the system in [11].

The above methods all improve the performance of communication system. However, among the aforementioned power allocation approaches, there is no paper considering the scenario of coexistence of DAS and D2D communication. In this paper, to further improve the performance of system, a new scenario for D2D communication underlaid DAS is proposed. We mainly focus on how to improve the SE and EE of the system. We first convert the maximizing SE and EE objective functions to a DC problem by function reorganization, CCCP algorithm and the interior point method which are presented to get optimal solutions. In particular, the Dinkelbach algorithm based on the parameter method is utilized in EE power allocation algorithm, and we transform the fractional form of EE optimization into a subtractive form that is easier to solve. In order to confirm the reliability of the proposed algorithm, we also compare with co-located antenna systems (CAS) with D2D communication [13]; experiment results demonstrate that the proposed algorithm has a better performance. Unlike the existing approaches, the proposed one has a good performance in improving system efficiency. So it is a key technique for the future communication systems.

Fig. 6.1
figure 1

DAS with D2D system model

Full size image

2 System Model and Problem Formulation

2.1 System Model

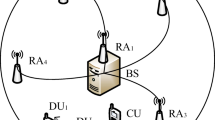
In this section, the model of D2D user underlaying the spectral resource of cellular user in DAS is established. We consider downlink transmission in a cellular network where UE and D2D pairs use the same frequency bands. The locations of N RAUs are uniformly located in the cell and connected to the central base station (e.t. RAU1) through optical fiber. In one cell, there are M cellular user equipments (UEs) and K D2D pairs, and they are both equipped with one single antenna. Each channel undergoes independent and identically distribution (i.i.d.). We can define configuration specified in the system as (N,M,K). For example, Fig. 6.1 is a (5, 1, 1) system that is discussed in this paper, where M = 1, N = 5, K = 1. In addition, there are two special cases

1. (N, M, 0) stands for the DAS with fully distributed antennas;

2. (1, M, 0) represents the co-located antenna system (base station can equip with multiple antennas).

2.2 Channel Model

In this paper, \({{h_{n,c}}}\) denotes the channel which consists of a small- and large-scale fading, which can be written as [14, 15]

$$\begin{aligned} {h_{n,c}} = {g_{n,c}}{w_{n,c}}, \end{aligned}$$
(6.1)

where

$$\begin{aligned} {w_{n,c}} = \sqrt{\frac{{c{s_{n,c}}}}{{{d_{n,c}}}}}, \end{aligned}$$
(6.2)

\({g_{n,c}}\) represents the small-scale fading, \({g_{n,c}}\sim \mathcal {CN}(0,1)\) and \({w_{n,c}}\) represent the large-scale fading factor, which has no relationship with \({g_{n,c}}\). c denotes the median of the mean path gain, \({d_{n,c}}\) denotes the communication distance between cellular user and RAU n, \(\alpha \) and \({s_{n,c}}\) are constants.

2.3 Achievable Rate

We assume that the RAUs and UEs in the system can easily get the channel state information (CSI) and the total system bandwidth is 1 MHz.

The following parameters are used in the description of the system model

  • \({p_d}\): Transmit power of the D2D transmitter.

  • \({p_{n,c}}\): Transmit power from the nth RAU to the UE.

  • \(P_{\max }^d\): Maximum transmit power of the D2D transmitter.

  • \(P_{\max }^n\): Maximum transmit power of RAU n.

  • \({{h_{n,c}}}\): The channel gain from the RAU n to cellular user.

  • \({{h_d}}\): The channel gain from the D2D transmitter to D2D receiver.

  • \({{h_{d,c}}}\): The channel gain from the D2D transmitter to UE.

  • \({{h_{n,d}}}\): The channel gain from the D2D transmitter to RAU n.

  • \(\sigma _c^2,\sigma _d^2\): The power of the white Gaussian noise (AWGN) of UE and D2D user, respectively.

  • \({R_c}\): The transmission rate of UE.

  • \({R_d}\): The transmission rate of D2D user.

The SE of UE and D2D user is expressed as follows

$$\begin{aligned} {R_c} = {\log _2}\left( 1 + \frac{{\sum \nolimits _{n = 1}^N {{p_{n,c}}{{\left| {{h_{n,c}}} \right| }^2}} }}{{{p_d}{{\left| {{h_{d,c}}} \right| }^2} + \sigma _\mathrm{{c}}^2}}\right) , \end{aligned}$$
(6.3)
$$\begin{aligned} {R_d} = {\log _2}\left( 1 + \frac{{{p_d}{{\left| {{h_d}} \right| }^2}}}{{\sum \nolimits _{n = 1}^N {{p_{n,c}}{{\left| {{h_{n,d}}} \right| }^2}} + {\sigma ^2}}}\right) . \end{aligned}$$
(6.4)

3 Objective Optimization Formulation

In the first part, the maximum SE optimization problem is discussed. Then, the EE optimization model is considered in the second part including the power consumption of circuit and optical fiber. Finally, an effective power allocation scheme is presented to maximizing the EE of system.

3.1 Maximum SE Optimization

Due to the D2D pair and UE use the same spectrum at the same time, there exists interference between them, which makes the problem becomes more complicated. It can be modeled as

$$\begin{aligned} \begin{array}{l} \mathop {\max }\limits _\mathbf{{P}} \;SE \buildrel \varDelta \over = \;{R_c} + {R_d} \\ s.t.\;\;\;\;\;{p_{n,c}} \in [0,P_{\max }^n]\;\;\;\;\;\forall n \in \{ 1,2, \cdots ,N\} , \\ \;\;\;\;\;\;\;\;\;\;{p_d} \in [0,P_{\max }^d]\;. \\ \end{array} \end{aligned}$$
(6.5)

where \(\mathbf{{P}} \buildrel \varDelta \over = \;[\mathbf{{p}},{p_d}]\), \(\;\mathbf{{p}} = \{ {p_{n,c}},\;for\;n = 1,2 \cdots ,N\} \).

Readjusting the expression of the objective function (6.5), we can find that the objective function has a special DC structure. We can exploit the similar methods based on DC structure to solve the optimization problem [16,17,18]. Let \({f_{se}}(\mathbf{{P}})\) represents the variable and objective functions in (6.5), respectively. So the (6.5) can be decoupled as

$$\begin{aligned} {f_{se}}(\mathbf{{P}}) = {f_{cave}}(\mathbf{{P}}) + {f_{vex}}(\mathbf{{P}}) \end{aligned}$$
(6.6)

where

$$\begin{aligned} \begin{array}{l} {f_{cave}}(\mathbf{{P}}) \buildrel \varDelta \over = {\log _2}\left( \sum \nolimits _{n = 1}^N {{p_{n,c}}{{\left| {{h_{n,c}}} \right| }^2}} + {p_d}{\left| {{h_{d,c}}} \right| ^2} + \sigma _\mathrm{{c}}^2\right) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + {\log _2}\left( {p_d}{\left| {{h_d}} \right| ^2} + \sum \nolimits _{n = 1}^N {{p_{n,c}}{{\left| {{h_{n,d}}} \right| }^2} + {\sigma _d}^2} \right) , \\ \end{array} \end{aligned}$$
(6.7)
$$\begin{aligned} \begin{array}{l} {f_{vex}}(\mathbf{{P}}) \buildrel \varDelta \over = - {\log _2}\left( {p_d}{\left| {{h_{d,c}}} \right| ^2} + \sigma _\mathrm{{c}}^2\right) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {\log _2}\left( \sum \nolimits _{n = 1}^N {{p_{n,c}}{{\left| {{h_{n,d}}} \right| }^2}} + {\sigma _d}^2\right) . \\ \end{array} \end{aligned}$$
(6.8)

We can learn that \({f_{cave}}(\mathbf{{P}})\) and \({f_{vex}}(\mathbf{{P}})\) are strict convex and concave functions of \(\mathbf{{P}}\), respectively. So the objective function in (6.6) is a function with DC structure.

Let\(\;{\mathbf{{S}}_R}\) represents the set of constraints of (6.5), Therefore, \({\mathbf{{S}}_R}\) is a convex set. The optimizing SE problem can be transformed into an equivalence problem containing the objective function with DC structure [16].

$$\begin{aligned} \mathop {\max }\limits _\mathbf{{P} \in {\mathbf{{S}}_R}} \mathrm{{\{ }}{f_{cave}}(\mathbf{{P}}) + {f_{vex}}(\mathbf{{P}})\mathrm{{\} }}\mathrm{{.}} \end{aligned}$$
(6.9)

In [17, 18], the author further points out that when there is a partial derivative of the convex function part in the DC objective function, the DC algorithm can be simplified to the CCCP algorithm, and its core idea is to use Majorization-Minimization (MM) method [19], stepwise iteratively linearizing the convex function part of the DC objective function.

Due to the convex function part of \({f_{vex}}(\mathbf{{P}})\) in (6.9) has a partial derivative. Therefore, we can linearize \({f_{vex}}(\mathbf{{P}})\) according to the first-order Taylor expansion in each iteration to get the iteration equation as below

$$\begin{aligned} \begin{array}{l} {\mathbf{{P}}^{\mathrm{{(k + 1)}}}}\mathrm{{ = arg}}\mathop {\max }\limits _{P \in {\mathbf{{S}}_R}} \{ {f_{cave}}(\mathbf{{P}}) + \nabla {f_{vex}}({\mathbf{{P}}^{(k)}})*{\mathbf{{P}}^\text {T}}\} \\ \;\;\;\;\;\;\; = \mathrm{{arg}}\mathop {\max }\limits _{P \in {\mathbf{{S}}_R}} \{ {f_{cave}}(\mathbf{{P}}) + \\ \;\;\;\;\;\;\;\left[ \frac{{{{\left| {{h_{d,c}}} \right| }^2}}}{{(p_{_d}^k{{\left| {{h_{d,c}}} \right| }^2} + \sigma _\mathrm{{c}}^2)\ln 2}},\frac{{\sum \nolimits _{n = 1}^N {{{\left| {{h_{n,d}}} \right| }^2}} }}{{(\sum \nolimits _{n = 1}^N {{p_{n,c}}{{\left| {{h_{n,d}}} \right| }^2}} + {\sigma _d}^2)\ln 2}}\right] *{\mathbf{{P}}^\text {T}}\} , \\ \end{array} \end{aligned}$$
(6.10)

where \({\mathbf{{P}}^\text {T}}\) is the transposition of \(\mathbf{{P}}\), \(\nabla {f_{vex}}({\mathbf{{P}}^{(k)}})\) represents the gradient of \({f_{vex}}(\mathbf{{P}})\) at \({\mathbf{{P}}^{(k)}} \buildrel \varDelta \over = \;[{\mathbf{{p}}^{(k)}},p_{_d}^{(k)}],\;\;{\mathbf{{p}}^{(k)}} = \{ p_{_{n,c}}^{(k)},\; for\;n = 1,2 \ldots ,N\} \).

At this time, the objective function in (6.10) is convex, which can be solved by traditional methods such as interior point method. The specific algorithm is showed in Table 6.1.

Table 6.1 Maximum SE power allocation algorithm
Full size table

The convergence of the CCCP algorithm can be guaranteed by the following two theorems [18, 20].

Theorem 1

The optimization objective function (6.9) increases with the power sequence \(\{ {\mathbf{{P}}^k}\} \) generated by the convex optimization problem in (6.10) monotonically.

Theorem 2

The power sequence \(\{ {\mathbf{{P}}^k}\} \) generated by the convex optimization problem in (6.10) converges to its limit point \({P^\infty }\) when \({\mathbf{{S}}_R} \ne \varPhi \), and at this point, the KKT condition in the original optimization problem (6.9) is satisfied.

3.2 Maximum EE Optimization

(1) Power Consumption

The total power consumption \({P_{total}}\) can be decoupled into two parts: the transmit power consumption of power amplifier at antennas (RAUs and D2D transmitter) and the extral circuit power consumption. The first part can be written as [21]

$$\begin{aligned} {P_{trans}} = \frac{{\sum \nolimits _{n = 1}^N {{p_{n,c}}} + {p_d}}}{\tau }, \end{aligned}$$
(6.11)

where \(\tau \) is a constant, representing the drain efficiency.

The second part is denoted as \({P_{circuit}}\), which is consisted of three parts. (i): the circuit power consumption \({P_b}\); (ii): the basic power consumption \({P_u}\); (iii): the wasted power of signals transmit through optical fiber \({P_o}\). So it can be modeled as

$$\begin{aligned} {P_{circuit}} = {P_b} + {P_u} + {P_o}, \end{aligned}$$
(6.12)

The total power consumed by DAS with D2D communication, denoted as \({P_{total}}\), is given by:

$$\begin{aligned} \begin{aligned} {P_{total}}&= {P_{trans}} + {P_{circuit}} \\&= \frac{{\sum \nolimits _{n = 1}^N {{p_{n,c}}} + {p_d}}}{\tau } + {P_b} + {P_u} + {P_o}. \\ \end{aligned} \end{aligned}$$
(6.13)

(2) EE Problem Formulation

We focus on optimizing the power allocation to maximize the system EE. It can be expressed as (unit: bits/J/Hz) [22, 23]

$$\begin{aligned} \begin{array}{l} \max \;\;EE \buildrel \varDelta \over = \frac{{{R_c} + {R_d}}}{{\frac{{\sum \nolimits _{n = 1}^N {{p_{n,c}}} + {p_d}}}{\tau } + {P_b} + {P_u} + {P_o}}} \\ s.t.\;\;\;\;\;{p_{n,c}} \in [0,P_{\max }^n]\;\;\;\;\;\;\;\forall n \in \{ 1,2, \ldots ,N\} , \\ \;\;\;\;\;\;\;\;\;{p_d} \in [0,P_{\max }^d]. \\ \end{array} \end{aligned}$$
(6.14)

(3) Maximize EE Optimization Model

Through the above analysis, the overall energy efficiency optimization problem of the user terminals can be expressed as

$$\begin{aligned} \mathop {\max }\limits _{\mathbf{{V}} \in \mathbf{{S}}} EE \buildrel \varDelta \over = \frac{{{R_c} + {R_d}}}{{\frac{{\sum \nolimits _{n = 1}^N {{p_{n,c}}} + {p_d}}}{\tau } + {P_b} + {P_u} + {P_o}}}. \end{aligned}$$
(6.15)

where \(\mathbf{{V}}\) and \(\mathbf{{S}}\) represent the optimization variables and constraint sets, respectively. According to [24], (6.15) is equivalent to the following problem

$$\begin{aligned} \mathop {\max }\limits _{\mathbf{{V}} \in \mathbf{{S}}} \left\{ {R_c} + {R_d} - {\lambda ^*}\left( \frac{{\sum \nolimits _{n = 1}^N {{p_{n,c}}} + {p_d}}}{\tau } + {P_b} + {P_u} + {P_o}\right) \right\} = 0, \end{aligned}$$
(6.16)

where \({\lambda ^*} = \mathop {\max }\limits _{\mathbf{{V}} \in \mathbf{{S}}} EE\) represents the maximum value of the optimization goal.

For the above conclusions, the [24] has a simple and constructive proof, which will not be repeated here. In addition, the [24] also gives an iterative algorithm based on the parameter method (Dinkelbach algorithm) to find the optimal solution \({\mathbf{{V}}^*} \buildrel \varDelta \over = \arg \mathop {\max }\limits _{\mathbf{{V}} \in \mathbf{{S}}} EE\) of the optimization problem in (6.15). The specific process is shown in Table 6.2.

Table 6.2 Dinkelbach algorithm
Full size table

In the Dinkelbach algorithm, the most critical step is to solve the following subproblems for a given parameter \(\lambda \)

$$\begin{aligned} ee(\lambda ) \buildrel \varDelta \over = \mathop {\max }\limits _{\mathbf{{V}} \in \mathbf{{S}}} \{ {R_c} + {R_d} - \lambda \left( \frac{{\sum \nolimits _{n = 1}^N {{p_{n,c}}} + {p_d}}}{\tau } + {P_b} + {P_u} + {P_o}\right) \}, \end{aligned}$$
(6.17)

In each iteration, if the solution of Eq. (6.17) can be obtained, then the iteration can continue until the optimal solution of the optimization problem in Eq. (6.15) is obtained. The convergence of the Dinkelbach algorithm can be ensured in each iteration, \({\lambda ^{k + 1}} \ge {\lambda ^k}\) and \(ee({\lambda ^{k + 1}}) \le ee({\lambda ^k})\;(k = 0,1 \ldots )\), and the specific proof process is in [24].

Next, we will give the solution to the sub-problem for the energy efficiency optimization problem. By the parameter transformation in the Dinkelbach algorithm, the NFP optimization problem in (6.15) can be expressed as the following subproblem

$$\begin{aligned} \begin{array}{l} \mathop {\max }\limits _{{p_{n,c}},{p_d}} \left\{ {R_c} + {R_d} - \lambda (\frac{{\sum \nolimits _{n = 1}^N {{p_{n,c}}} + {p_d}}}{\tau } + {P_b} + {P_u} + {P_o})\right\} , \\ s.t.\;\;\;\;\;{p_{n,c}} \in [0,P_{\max }^n]\;\;\;\;\;\;\;\forall n \in \{ 1,2, \cdots ,N\} , \\ \;\;\;\;\;\;\;\;\;\;{p_d} \in [0,P_{\max }^d]\;. \\ \end{array} \end{aligned}$$
(6.18)

According to the discussion of the D.C. optimization problem in the previous section, the above problems can be expressed as

$$\begin{aligned} \begin{array}{l} \mathop {\max }\limits _{{p_{n,c}},{p_d}} \{ {f_{cave}}(\mathbf{{Q}}) + {f_{vex}}(\mathbf{{Q}})\} , \\ s.t.\;\;\;\;\;{p_{n,c}} \in [0,P_{\max }^n]\;\;\;\;\;\;\;\forall n \in \{ 1,2, \ldots ,N\} , \\ \;\;\;\;\;\;\;\;\;\;{p_d} \in [0,P_{\max }^d]\;. \\ \end{array} \end{aligned}$$
(6.19)

where \(\mathbf{{Q}} = [{\mathbf{{p}}_{n,c}},{p_d}]\) represents the optimization variable,

$$\begin{aligned} \begin{array}{l} {f_{cave}}(\mathbf{{Q}}) \buildrel \varDelta \over = {\log _2}(\sum \nolimits _{n = 1}^N {{p_{n,c}}{{\left| {{h_{n,c}}} \right| }^2}} + {p_d}{\left| {{h_{d,c}}} \right| ^2} + \sigma _\mathrm{{c}}^2) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + {\log _2}({p_d}{\left| {{h_d}} \right| ^2} + \sum \nolimits _{n = 1}^N {{p_{n,c}}{{\left| {{h_{n,d}}} \right| }^2} + {\sigma _d}^2} ). \\ \end{array} \end{aligned}$$
(6.20)
$$\begin{aligned} \begin{array}{l} {f_{vex}}(\mathbf{{Q}}) \buildrel \varDelta \over = - {\log _2}({p_d}{\left| {{h_{d,c}}} \right| ^2} + \sigma _\mathrm{{c}}^2) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; - {\log _2}(\sum \nolimits _{n = 1}^N {{p_{n,c}}{{\left| {{h_{n,d}}} \right| }^2}} + {\sigma _d}^2) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; - \lambda (\frac{{\sum \nolimits _{n = 1}^N {{p_{n,c}}} + {p_d}}}{\tau } + {P_b} + {P_u} + {P_o}).\; \\ \end{array} \end{aligned}$$
(6.21)

where \({f_{cave}}(\mathbf{{Q}})\) and \({f_{vex}}(\mathbf{{Q}})\) represent concave function part and convex function part of the objective function, respectively. \({\mathbf{{S}}_T}\) is the set of constraints in (6.18). Since all constraints are linear inequalities, \({\mathbf{{S}}_T}\) is a convex set. In addition, the convex function in (6.18) has a partial derivative, so the above D.C. problem can be transformed into the following sequential convex program problem by the CCCP algorithm

$$\begin{aligned} \begin{array}{l} {\mathbf{{Q}}^{\mathrm{{(k + 1)}}}}\mathrm{{ = arg}}\mathop {\max }\limits _{\mathbf{{Q}} \in {\mathbf{{S}}_T}} \{ {f_{cave}}(\mathbf{{Q}}) + \nabla {f_{vex}}({\mathbf{{Q}}^{(k)}})*{\mathbf{{Q}}^\text {T}}\} \\ \;\;\;\;\;\;\;\;\; \mathrm{{ = arg}}\mathop {\max }\limits _{\mathbf{{Q}} \in {\mathbf{{S}}_T}} \{ {f_{cave}}(\mathbf{{Q}}) \\ \;\;\;\;\;\; \;\;\;\;\;\;\;+ [\frac{{{{\left| {{h_{d,c}}} \right| }^2}}}{{(p_{_d}^{(k)}{{\left| {{h_{d,c}}} \right| }^2} + \sigma _\mathrm{{c}}^2)\ln 2}} - \lambda ,\frac{{\sum \nolimits _{n = 1}^N {{{\left| {{h_{n,d}}} \right| }^2}} }}{{(\sum \nolimits _{n = 1}^N {p_{_{n,c}}^{(k)}{{\left| {{h_{n,d}}} \right| }^2}} + {\sigma _d}^2)\ln 2}} - \lambda ]*{\mathbf{{Q}}^\text {T}}\}. \\ \end{array} \end{aligned}$$
(6.22)

where \({\mathbf{{Q}}^\text {T}}\) is the transposition of \(\mathbf{{Q}}\), \(\nabla {f_{vex}}({\mathbf{{Q}}^{(k)}})\) represents the gradient of \({f_{vex}}(\mathbf{{Q}})\) at \({\mathbf{{Q}}^{(k)}} \buildrel \varDelta \over = \;[{\mathbf{{p}}^{(k)}},p_{_d}^{(k)}],\;\;{\mathbf{{p}}^{(k)}} = \{ p_{_{n,c}}^{(k)},\;for\;n = 1,2 \ldots ,N\} ,\).

Because the objective function in equations (6.18) is a concave function. So we can exploit the traditional methods to obtain the optimal solutions. After transformation, the optimizing energy efficiency problem in (6.15) can be solved by a three-layer nested loop algorithm, which is concluded in Table 6.3.

Table 6.3 Maximum energy-efficient power allocation algorithm
Full size table
Table 6.4 Simulation parameters.
Full size table

4 Numerical Results

In the simulations, to simplify the computational complexity, we only consider a single-cell DAS with one UE and one D2D pair in the downlink transmission, both of which are uniformly located in the cell. The parameters values are showed in Table 6.4. The system is set as a circle of radius D. The layout of the RAUs is similar to [25].

In Fig. 6.2, \(P_{\max }^c\) changes from 5 to 30 dBm to show its effects on SE of the system. It shows that the SE increases with the increase of \(P_{\max }^c\), and the performance of the power allocation methods used in DAS with D2D pair is better than used CAS with D2D pair in [13]. We also compare with two different optimization objectives of maximizing SE and EE. From Fig. 6.2, for maximizing SE in DAS with D2D communication, maximizing SE power allocation algorithm is better than the algorithm used to maximize EE. Compared to CAS with D2D communication, the maximum SE in DAS is approximately 89.9% higher than maximum SE in CAS when \(P_{\max }^c =P_{\max }^d = 30\) dBm.

In Fig. 6.3, maximizing SE and maximizing EE algorithms are both used in increasing the EE of DAS with D2D communication. In this case, the maximizing EE algorithm is much better than the algorithm of maximizing SE power allocation. We also show the impact on the overall system performance after introducing DAS. Obviously, compared to CAS with D2D communication in [13], the EE has improved significantly in DAS with D2D communication. The EE of maximum EE in DAS is approximately 408.9% higher than maximum EE in CAS when \(P_{\max }^c =P_{\max }^d = 30\) dBm.

Fig. 6.2
figure 2

SE versus maximum transmit power

Full size image
Fig. 6.3
figure 3

EE versus maximum transmit power

Full size image

5 Conclusion

We considered a coexistence scenario of DAS and D2D communication in this paper. CSI is assumed known at both receiver and transmitter side. We first presented a optimization problem with respect to the maximizing SE power allocation, and the original problem was transformed into a DC structure problem by function recombination. Then the CCCP process was exploited to solve the DC structure problem, in which the interior point method was used to get the optimal power allocation solution. Then maximizing EE of the system also considered in the following part. We proposed an algorithm to maximize EE by Dinkelbach algorithm based on parameter method. Simulation results indicated that the performance of the power allocation methods used in DAS with D2D user was better than used in CAS with D2D communication.