Close-Proximity Dynamic Operations of Spacecraft with Angles-Only Rendezvous in a Circular Phasing Orbit

Abstract

Through this paper, it is to assess a closed-loop guidance algorithm for the range of observability of angles-only by rendezvous position and proximity operation. The prominence and influence of Clohessy–Wiltshire dynamics (CWD) is an emerging area which deals with angles-only guidance coupling algorithm and relative position. Observability analysis of the of rendezvous at a low earth circular orbit, as opposed to one spacecraft remaining fixed in its orbit, and the implications for total times are expended. A closed-loop guidance design scheme is generally based on unscented Kalman filter (UKF) and coupling relationship. The proposed method is used in the analysis and the following results are obtained for an initial separation, initial state uncertainties, line-of-sight angles correctness and ΔV (change in velocity) from the navigation and guidance accuracy. The novelty of the approach is to minimize the delta-V for close-proximity operation in phasing spacecraft to the other.

1 Introduction

Autonomous spacecraft rendezvous plays an important role in many space missions to enabling technology. In 1967, a successful autonomous spacecraft rendezvous [1] was tested; since then, bounteous mission proposals have been lunched and attempted by NASA, Soviet Russia, European Space Agency (ESA), Japan Aerospace Exploration Agency (JAXA) and China National Space Association (CNSA), and methods were assorted for exploring an autonomous rendezvous and docking operation. In addition, Demonstration of Autonomous Rendezvous Technology (DART) [2], Orbital Express (OE), [3] and Experimental Small System (XSS) [4] have been developed by USA to demonstrate the possibility of autonomous rendezvous and docking technologies. Due to space race, Russian Federal Space Agency’s Soyuz progress a spacecraft, ESA has designed an Automated Transfer Vehicle (ATV) and JAXA’s H-II Transfer Vehicle (HTV) [5] and were considered to rendezvous with the International Space Station (ISS). Recently, CNSA also has conducted several rendezvous and docking tests with Tiangong-1 (TG-1) target spacecraft since 2011 [6].

Many researchers have shown a keen interest in flight safety during the process of spacecraft rendezvous and docking, on-orbit tasks, exclusively in the close-proximity operation to avoid the collision into the target [7]. In the aforementioned research [8], the authors are strenuous to safety in the rendezvous trajectory planning. Another practical approach is proposed in Ref. [8], the strategy for initial separation and considering the measurement uncertainties in a planned trajectory, for optimized collision avoidance. This case aimed to send separate spacecraft to rendezvous with the ISS. It allows the station to remain fixed in orbit, incessantly conducting experiments, while fresh crews and supplies are brought to it, from the ground.

2 Problem of Interest

This investigation will focus on close-range rendezvous in the Hill frame using the Clohessy–Wiltshire equations and phasing orbits for rendezvous of spacecraft on the same orbit. Rendezvous is important to crucial objectives such as resupply, in-orbit spacecraft servicing and repair, contingency planning (e.g. proposed Space Shuttle “rescue” missions) and in-orbit construction. One of the main literature gaps to which this research will attempt to contribute is the topic of planning of spacecraft guidance and control over multiple stages in the presence of uncertainties.

2.1 Solution Method: Relative Motion

This section describes the solution method of relative motion. Figure 1 shows the RSW (Radial, Along Track and Cross Track) coordinate frame, where R is in line with the position vector, S is in the direction of the velocity vector but aligned with the horizontal (perpendicular to the position vector), and W is normal to R and W (forming a right-handed system); Hill’s equations are a convenient way to express relative spacecraft dynamics in the RSW frame (see Fig. 1) when two spacecraft are close together. They are derived, assuming that the satellites are only a few km apart, the frame (origin of the RSW frame) is in a circular orbit and there are no external forces, such as solar radiation pressure or drag. Figure 1 shows RSW coordinate frame where x, y and z correspond to r, s and w, respectively, and the equation is as follows:

Fig. 1

RSW coordinate frame

$$ \begin{aligned} x\left( t \right) & = \frac{{x_{0} }}{\omega }\text{sin}\omega t - \left( {3x_{0} + \frac{{2y_{0} }}{\omega }} \right)\text{cos}\omega t - \left( {4x_{0} + \frac{{2y_{0} }}{\omega }} \right) \\ y\left( t \right) & = \left( {6x_{0} + \frac{{4y_{0} }}{\omega }} \right)\text{sin}\omega t + \frac{{4x_{0} }}{\omega }\cos \omega t - \left( {6x_{0} + 3y_{0} } \right)t + \left( {y_{0} + \frac{{2x_{0} }}{\omega }} \right) \\ z\left( t \right) & = z_{0} \cos \omega t + \frac{{z_{0} }}{\omega }\text{sin}\omega t \\ \end{aligned} $$

(1)

$$ \begin{aligned} y\left( t \right) & = \left( {6\omega x_{0} + 4y_{0} } \right)\text{cos}\omega t - 2x_{0} \text{sin}\omega t - \left( {6x_{0} + 3y_{0} } \right) \\ z\left( t \right) & = - z_{0} \omega \text{sin}\omega t + z_{0} \text{cos}\omega t \\ \end{aligned} $$

(2)

Setting the first three equations equal to zero (x = y=z = 0) and solving the velocities give the necessary velocities to set the spacecraft, on a trajectory to reach the origin of the RSW frame (usually centred on a target spacecraft) for a given time to rendezvous. Those equations are shown below, where $\omega = \sqrt {\frac{\mu }{{a2_{\text{tgt}} }}}$ with $a_{\text{tgt}}$ being the radius of the circular orbit of the target/origin of the RSW frame. Collectively this will be called v₀ because it is the initial velocity in the RSW frame of the intercept trajectory. Figure 2 shows that relative motion coordinates for better understanding. Note that initial velocity in the y-direction must be solved first because initial velocity in the x-direction is a function of $\frac{{{\text{d}}y_{0} }}{{{\text{d}}t}}$.

Fig. 2

Represent the coordinates of relative motion

$$ \begin{aligned} x_{0} & = \frac{{ - \omega x_{0} \left( {4 - 3\text{cos}\omega t} \right) + 2\left( {1 - \text{cos}\omega t} \right)y_{0} }}{{\text{sin}\omega t}} \\ y_{0} & = \frac{{\left( {6x_{0} \left( {\omega t - \text{sin}\omega t} \right) - y_{0} } \right)\omega \text{sin}\omega t - 2\omega x_{0} \left( {4 - 3\text{cos}\omega t} \right)\left( {1 - \text{cos}\omega t} \right) }}{{\left( {4\text{sin}\omega t - 3\omega t} \right)\text{sin}\omega t + 4\left( {1 - \text{cos}\omega t} \right)^{2} }} \\ z\left( t \right) & = - z_{0} \omega \text{cot}\omega t \\ \end{aligned} $$

(3)

2.2 Clohessy–Wiltshire Dynamics

The well-known method of Clohessy–Wiltshire equation, for the relative motion dynamics, is to the near-circular orbit. The two-body problem assumption made a space between the target and the chaser. The distance, compared from the target to the centre of Earth, is very small. The following equations are appropriate in the relative position of chaser.

$$ \begin{aligned} f_{x} & = \ddot{x} - 2\omega z \\ f_{y} & = \ddot{y} + \omega^{2} y \\ f_{z} & = \ddot{z} + 2\omega x - 3\omega^{2} z \\ \end{aligned} $$

(4)

where ω represents the angular rate of RSW frame. The axis of x, y and z describes the elements of r(t), f_x, f_y and the outward forces on the chaser element is f_z. The discrete propagating equation for the system state is X = [r; v]. Equation 4 is utilized for ignoring the disturbing forces and the pulse manoeuvre scheme, the expression of propagating equation, for X can be described below

$$ \varphi (k,0)\left[ {\begin{array}{*{20}l} 1 \hfill & 0 \hfill & {6\{ \omega (t_{k} - t_{0} )\} } \hfill & {4{ \sin }[\omega (t_{k} - t_{0} )] } \hfill & 0 \hfill & {2\{ 1 - { \cos }[\omega (t_{k} - t_{0} )]\} } \hfill \\ 0 \hfill & {\text{cos} [\omega (t_{k} - t_{0} )] } \hfill & 0 \hfill & 0 \hfill & {\frac{{{ \sin }[\omega (t_{k} - t_{0} )]}}{\omega }} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 4 \hfill & { - 3 { \cos }\left[ {\omega (t_{k} - t_{0} )\left\{ {\frac{{ 2{ \cos }[\omega (t_{k} - t_{0} )] - 1}}{\omega }} \right\}} \right]} \hfill & 0 \hfill & {\frac{{{ \sin }[\omega (t_{k} - t_{0} ) ]}}{\omega }} \hfill \\ 0 \hfill & 0 \hfill & {6\{ \omega (t_{k} - t_{0} )\} } \hfill & {\text{cos}[\omega (t_{k} - t_{0} ) - 3]} \hfill & 0 \hfill & { 2 {\text{sin[}}\omega (t_{k} - t_{0} ) ]} \hfill \\ 0 \hfill & { {-}\omega {\text{sin[}}\omega (t_{k} - t_{0} ) ] } \hfill & 0 \hfill & 0 \hfill & {{ \cos }[\omega (t_{k} - t_{0} )]} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & { 3\omega {\text{sin[}}\omega (t_{k} - t_{0} ) ]} \hfill & { - 2\text{sin}[\omega (t_{k} - t_{0} )] } \hfill & 0 \hfill & {\text{cos}[\omega (t_{k} - t_{0} )]} \hfill \\ \end{array} } \right] $$

(5)

And, Eq. 2 is re-expressed as, 


$$ X_{k} = \varPhi \left( {k,0} \right)X_{0} + G\Delta v $$

(6)

where G represents the control-driven matrix:


$$ G = \varPhi (k,0)\left[ {0_{6 \times 3} ,I_{3 \times 3} } \right] $$

(7)

3 Observation Equations

In the observation equation, two reasonable assumptions are to be made to establish the equation. It will make the analysis, easier in the following section. Initially, the RSW reference frame, of the chaser and target, can be observed, as being parallel in the setting up of the proximity operation.

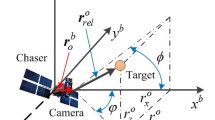
In this case, an orbital height 400 km is considered (Altitude of International Space Station) and the primary distance mark, between the chaser and target, is 10 km, and the accuracy of orbital phase angle in a deviation will be about 1.472 × 10⁻³ rad. Even the poor camera setup. In addition, make the angle deviation will be smaller, even when the equivalent, when, the chaser should not be far away from the target. The obtained measurement transformation equation is from chaser to target RSW frame. Figure 3 shows the relative measurement geometry.

Fig. 3

Relative measurement geometry

$$ \left[ {\begin{array}{*{20}c} \varepsilon \\ \theta \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - 1 0} \\ {0 - 1} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{\varepsilon }} \\ {\dot{\theta }} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ \pi \\ \end{array} } \right] $$

(8)

The second assumption can be realized by attitude control, when the camera measuring frame is coinciding with the chaser’s RSW frame which has been demonstrated in PRISMA mission. Then, an observation equation in the target’s RSW frame is to be obtained.

$$ \begin{aligned} z_{1} & = e + v_{e} = \arctan \frac{z}{{\sqrt {x^{2} + y^{2} } }} + v_{e} ; \\ z_{2} & = \theta + v_{e} = { \arctan }\frac{z}{{\sqrt {x^{2} + y^{2} } }} + v_{e} \\ \end{aligned} $$

(9)

The phase of mid-range proximity for a cooperative and non-cooperative target can be used in both Eq. 7 (observation equation) and Eq. 8 (measurements transformation equation), where x, y and z unit vectors are representing the element of the line of sight, as well as θ and ε are the azimuth angle and the elevation, respectively, vθ and vε are the measurement noises. It is commonly modelled as zero-mean Gaussian noise, i.e. v ∼ N(0, σ²) and v ∼ N(0, σ²).

3.1 Observability Analysis

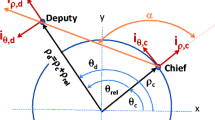
For the circular phasing rendezvous case, we have two spacecraft initially on the same circular orbit, as shown in Fig. 4. Conceptually, this method transfers the intercepting spacecraft onto a phasing orbit, with a differing period, than the initial orbit. The period, of this phasing orbit, is chosen, as such, that alerts the desired number of full orbits, when the intercepting spacecraft returns to the initial orbit, at the same time, as the target spacecraft [5], when the target leads the interceptor, the phase angle, is negative.

Fig. 4

Phasing orbit

When the target spacecraft leads the intercepting spacecraft, the intercepting spacecraft must “speed up”, and thus must enter an orbit, with the smaller semi-major axis (faster orbital period) to “catch up” to the target spacecraft. Similarly, if the target spacecraft is trailing, the intercepting spacecraft must “slow down” and enter a phasing orbit with the larger semi-major axis (slower orbital period) to allow the target spacecraft to “catch up”. Mathematically, this is performed using the equations given below [5]. Note that, this assumes two-impulse transfers, with instantaneous application of delta-V.

Figure 2 shows the phase angle θ is negative in this case where the target leads the interceptor, θ is positive, when the interceptor leads the target.

First, we must find the angular velocity of the target spacecraft $\omega_{\text{tgt}} = \sqrt {\frac{\mu }{{a2_{\text{tgt}} }}}$. Then, the time of the phasing orbit is given by

$$ \tau_{\text{phase}} = \frac{{k_{\text{tgt}} \left( {2\pi } \right) + \theta }}{{\omega_{\text{tgt}} }} $$

(10)

where $k_{\text{tgt}}$ is the desired number of orbits, the target spacecraft completes before rendezvous? Using that, the semi-major axis, of the phasing orbit, can be found with the expression

$$ a_{\text{phase}} = \left( {\mu \left( {\frac{{\tau_{\text{phase}} }}{{2\pi k_{\text{int}} }}} \right)^{2} } \right)^{{\frac{1}{3}}} $$

(11)

where $k_{\text{int }}$ is the desired number of orbits, the intercepting spacecraft completes before rendezvous? For the analyses in this project, $k_{{{\text{int}} }} = k_{\text{tgt}}$ for simplicity, though, this certainly needs not to be true. Another important consideration is the radius of perigee of the phasing orbit when the phasing orbit is smaller than the initial orbit (θ is negative). The phasing orbit must not intersect the central body (Earth for this project) or go too far into the atmosphere. $r_{\text{p}} = 2a_{\text{phase}} - r_{\text{a}}$ with $r_{\text{a}} = a_{\text{tgt}} (a_{\text{tgt}} = a_{\text{initial}} )$ for the intercepting spacecraft. For this project, r_p is not allowed to drop lower than 160 km perigee altitude above Earth. Finally, the ΔV required, for the intercepting satellite, is found by taking the difference of the velocity on the initial orbit and the velocity on the transfer orbit where it intersects the initial orbit. There will be two burns of equal magnitude and opposite direction, so the total

$$ \Delta v = 2\left| {\sqrt {\frac{2\mu }{{a_{\text{tgt}} }}} - \frac{\mu }{{a_{\text{phase}} }} - \sqrt {\frac{\mu }{{a_{\text{tgt}} }}} } \right| $$

(12)

An example solution using this method is illustrated in Fig. 5. Here, the initial orbit has a radius of 8.378 * 103 and the target spacecraft is the red spacecraft (solid orbit line). The target spacecraft has initial true anomaly of 0°, while the intercepting spacecraft (green point, dotted line) has true anomaly of 315°, giving a phase angle of −45°. Working through the process above with k = 1 gives the result below, with total delta-V = 0.6579 km/s and a time to rendezvous of 1.86 h. The designed closed-loop guidance system is represented in Fig. 6.

Fig. 5

Spacecraft orbits for circular phasing rendezvous in the PQ frame

Fig. 6

Designed closed-loop guidance model

4 Rendezvous in Circular Phasing Orbit

Given the orbital radius of the target spacecraft and the coordinates of the intercepting spacecraft in the RSW frame of the target, the ΔV, required to rendezvous in a desired amount of time, can be calculated.

4.1 Extension

The rendezvous problem in this context is typically posed, as having one spacecraft rendezvous, with a second passive spacecraft, that does not manoeuvre. In this extension, the idea, of rendezvous at an intermediate point, will be explored. This also includes investigating rendezvous locations for more than two spacecraft as well. These types of investigations are becoming more important, as mission designers increasingly utilize multi-spacecraft systems, to accomplish mission goals. For example, NASA’s Asteroid Redirect Mission requires a manned spacecraft to rendezvous, with an asteroid sample, that will be placed in lunar orbit [9].

A possible Mars sample return mission would, likely, require some type of Mars ascent vehicle to rendezvous, with a spacecraft in Mars orbit, before returning to Earth [10]. Finally, future manned Mars missions may require the coordination/rendezvous of multiple supply spacecraft, which has been sent to the planet, ahead of time [11]. There is a growing interest in future space mission concepts which involve the interaction of multiple spacecraft/satellites [12,13,14,15,16]. In each of these cases, the multiple spacecraft involved would have the ability to manoeuvre and the finding of an intermediate rendezvous point may help reduce the demand on a single spacecraft, that may not have the required ΔV or time available. It may even reduce the total ΔV or time to rendezvous.

4.2 Circular Phasing Extension

To explore intermediate rendezvous points for circular phasing rendezvous, the same process, as above, is followed with only minor modification. Here, the “target satellite” is, instead, a point in the initial orbit that, the other spacecraft’s aim to rendezvous with. This point defined, by its initial true anomaly, is at the start of the simulation thus evolves with time. The circular phasing method, as described above, is performed for each satellite in the system, across the full range of possible rendezvous locations, to examine the trends. For the two-satellite case, the minimum time case (initial true anomaly of target orbit = 240° for k = 4) is animated below, to illustrate the method.

Setting up the initial true anomaly, of the target orbit equal to the initial true anomaly of satellite 1, is equivalent to the setting up of the rendezvous point at satellite 1. Satellite 2 is leading the target orbit (θ is positive), and thus satellite 2 must enter a phasing orbit with greater semi-major axis to rendezvous with satellite 1. Recall that

$$ \Delta v = 2\left| {\sqrt {\frac{2\mu }{{a_{\text{tgt}} }}} - \frac{\mu }{{a_{\text{phase}} }} - \sqrt {\frac{\mu }{{a_{\text{tgt}} }}} } \right| $$

(13)

This expression shows, that transfer orbits with smaller required, because, all the other parameters in the equation are constant. Thus, the leading satellite should rendezvous with the trailing satellite when using phasing orbits to achieve rendezvous with two spacecraft at a minimum ΔV cost. Another interesting relation, to note, is the drop off in ΔV part way, through the plot (at around 200 degree) (Fig. 7).

Fig. 7

Delta versus true anomaly of target location

This occurs because the phase angle switches from negative (trailing the target) to positive (leading the target). This switch is a result of the phase angle, being the smaller of the two angles between the two position vectors, and changes the phasing orbit from being smaller than the initial orbit to being larger than the initial orbit. This larger orbit, however, is not as extreme, a change, as was required for the previous orbit, so ΔV is required drops (Fig. 8).

Fig. 8

Schematic approach of control system

Effect of varying target location identifies ΔV which is required for a continuous rendezvous. There are also trends observed in rendezvous time, plotted below. Note that, while using one of the satellites as a rendezvous point can minimize ΔV; this does not save total time, because the second satellite must still complete its phasing orbits. Figures 9, 10, 11, 12, 13 and 14 represent that, an intermediate rendezvous orbit is better if minimizing this time is more important than minimizing ΔV. This time minimizing point occurs, where both satellites are still trailing the target initially and thus enter phasing orbits with periods, faster than the phasing orbits needed, when leading the target. Once, one of the satellite transitions leads the target, its rendezvous time jumps up and leaves behind a minimum.

Fig. 9

Rendezvous versus true anomaly

Fig. 10

Delta-V versus altitude

Fig. 11

Delta-V versus inclination

Fig. 12

Delta-V versus RAAN

Fig. 13

Delta-V versus true anomaly

Fig. 14

Delta-V versus argument of perigee

Note that, this minimum is highly expensive in terms of ΔV, because it is the scenario with the greatest changes in orbit needed, to achieve rendezvous (the smaller the phasing orbit, the more ΔV needed to transfer to it).

4.3 Relative Motion Extension

The relative motion rendezvous problem was extended in a similar manner, with the target, being a selected arbitrary orbit rather than on a specific spacecraft. However, for this problem, the initial orbits, of the spacecraft, were defined by using the classical orbital elements and then transformed into the RSW frame [4].

$$ \begin{aligned} x & = \delta r \\ y & = r\left( {\delta \theta + \text{cos}i\delta \varOmega } \right) \\ z & = r(\text{sin}\theta i - \text{cos}\theta \sin i\delta \varOmega \\ \end{aligned} $$

(14)

$$ \begin{aligned} x & = - \frac{{v_{r} }}{2a}\delta a + \left( {\frac{1}{r} - \frac{1}{p}} \right)h\delta \varOmega \ldots \\ & \quad + \left( {v_{r} aq_{1} + h\text{sin}\theta } \right)\frac{{\delta q_{1} }}{p} + \left( {v_{r} aq_{2} - h\text{cos}\theta } \right)\frac{{\delta q_{2} }}{p} \\ y & = - \frac{{3v_{t} }}{2a}\delta a - v_{r} \delta \theta + \left( {3v_{t} aq_{1} + 2h\text{cos}\theta } \right)\frac{{\delta q_{1} }}{p} \ldots \\ & \quad + \left( {3v_{t} aq_{2} + 2h\text{sin}\theta } \right)\frac{{\delta q_{2} }}{p} + v_{r} \text{cos} i\delta \varOmega \\ z & = \left( {v_{t} \text{cos}\theta + v_{r} \text{sin}\theta } \right)\delta i + \left( {v_{t} \text{sin}\theta - v_{r} \text{cos}\theta } \right)\sin i\delta \varOmega \\ \end{aligned} $$

(15)

Equations from [5] have been used to convert from orbital elements to RSW frame. This gives the ability to see the ideal target location in terms of different orbital elements. In cases with an odd number of satellites, the optimal location, instead, appears to be on the same orbit, as the middle satellite (middle meaning the satellite in between the other satellites with respect to whichever orbit element is being varied). Thus, with an even number of satellites, it may be beneficial to look at intermediate orbits; depending on the distribution of satellites, there may not be one on an orbit that would be optimal to target for rendezvous. Of course, this analysis is only confined to these specific parameters. A more generalized investigation would give more concrete recommendations. Further, investigation, of the coupling between varying different parameters, may also be of interest.

5 Conclusion

In this project, some more conventional rendezvous problems, with goals of reaching a non-manoeuvring spacecraft, have been described. These methods used two-body dynamics for the circular phasing orbits and dynamics transformed into a relative motion frame to calculate delta-V, required for rendezvous. We then extended these same methods to look at rendezvous in intermediate orbits. We showed that for circular phasing orbits, to minimize delta-V, the leading satellite should rendezvous with the trailing satellite, if ΔV minimization is a priority and the leading satellite has sufficient ΔV. However, when minimizing time while still using circular phasing orbits, there may be a more desirable intermediate rendezvous orbit, depending on the mission and how important time versus ΔV is. In this case, for $t_{f} = 5\,{ \hbox{min} }$, ΔV₁ = 1.2918 m/s, ΔV₂ = 1.2054 m/s and ΔV_total = ΔV₁ + ΔV₂ = 2.4972 m/s.

The extension in the relative frame also gave insight into intermediate rendezvous locations and indicates that rendezvous orbits that do not coincide with a spacecraft should be considered in some cases (even number of spacecraft with certain initial conditions). Analyses, such as these, can be useful for the understanding of how to balance resource usage across multiple spacecraft, considering the different needs for each, as opposed to globally optimizing a solution, that may not be optimal for a single spacecraft. Further research would ideally extend the relative motion analysis to investigate more general conditions and to ensure that, the initial conditions of the spacecraft do not exceed the distances allowable by Hill’s equations. An even a better investigation would be the research optimal control solutions for two or more spacecraft attempting to rendezvous where the different parameters could be varied, based on needs of the mission.