Introduction

The initial inertial orbit determination problem using angles-only measurements is well known. For example, Gauss’ method of preliminary orbit determination [1, 2] is capable of determining the inertial orbit or inertial state of an orbiting object using angles-only measurements. In Gauss’ method, an Earth-based observer with a known position collects angular information of an orbiting object over a relatively short period of time to produce a preliminary estimate of the object’s state vector. The observations are the line-of-sight (LOS) vectors of the space object, equivalent to pairs of azimuth and elevation angles. Three observations, equivalent to 6 pieces of angular information, are required to estimate the object’s inertial state vector.

The initial relative orbit determination (IROD) problem is similar in many ways, but consists of an orbiting observer (chief) in a known orbit and a space object (deputy) in an unknown orbit. In this case the three LOS observations are used to estimate the deputy’s relative state vector (and since the inertial state of the chief is assumed to be known, the deputy inertial state is also determined).

The objective of this paper however is to conduct a preliminary performance analysis of the IROD problem, independent of the specific algorithm that may be chosen. The goal is to conduct this performance analysis using a geometric approach equivalent to the computation of the Cramer-Rao lower bound [3], and then apply it to the case where the chief and deputy are in nearly the same circular orbit. The final metric is the geometric dilution of precision (GDOP) for each component of the initial state vector. This will provide valuable relative orbit determination performance information based only on the geometry of the problem and the time-interval between measurements.

The standard Hill-Clohessy-Wiltshire (HCW) equations in Cartesian coordinates [4, 5] cannot be utilized for this study because Woffinden [6] showed that the angles-only relative navigation problem in this context is unobservable. A brief summary of Woffinden’s proof is given below.

The standard HCW equations in Cartesian coordinates are given by,

$$ \ddot{x}_{rel}\approx3n^{2}x_{rel}+2n\dot{y}_{rel} $$
(1.1)
$$ \ddot{y}_{rel}\approx-2n\dot{x}_{rel} $$
(1.2)
$$ \ddot{z}_{rel}\approx-n^{2}z_{rel} $$
(1.3)

where x(t), y(t), and z(t) are the radial, along-track, and cross-track components of the relative position vector r(t), and n is the constant angular rate of the chief’s circular orbit. The solution to these equations is

$$ \boldsymbol{r}(t)=\phi_{rr}(t)\boldsymbol{r}_{0}+\phi_{rv}(t)\boldsymbol{v}_{0} $$
(1.4)

where r 0 is the initial relative position, v 0 is the initial relative velocity, and ϕ r r (t) and ϕ r v (t) are known functions of time [6]. Using these equations, the LOS measurement time-history,

$$ \boldsymbol{i}_{los}(t)=\frac{\boldsymbol{r}(t)}{\left\Vert \boldsymbol{r}(t)\right\Vert} =\frac{\phi_{rr}(t)\boldsymbol{r}_{0}+\phi_{rv}(t)\boldsymbol{v}_{0}}{\left\Vert \phi_{rr}(t)\boldsymbol{r}_{0}+\phi_{rv}(t)\boldsymbol{v}_{0}\right\Vert} $$
(1.5)

is not unique to each initial position/velocity state [6]. For example, any scalar multiple of the initial state vector in the above equation will produce the exact same LOS vector time-history. Thus, a performance analysis based on the standard HCW equations in Cartesian coordinates will only show that the initial state is unobservable. This proof is easily extended to any linear relative orbital motion model in Cartesian coordinates including the Tschauner-Hempel equations [7, 8].

A number of solutions to the observability problem can be found in the literature. Observability maneuvers and associated observability criteria have been recently studied [9–11]. Although these solutions require propellant, they are valid for small or large inter-vehicle separations. To avoid the costs associated with maneuvers, [12] solves the observability problem by including a second optical sensor at a known baseline. To avoid the costs associated with using two (or more) optical sensors, [13] solves the observability problem by properly modeling the offset of a single optical sensor from the vehicle center-of-mass. These non-propulsive solutions are valid for relative small inter-vehicle separations and dependent on the length of the sensor baseline or the magnitude of the sensor offset.

In the current paper, it is hypothesized that the linearized equations of motion in cylindrical coordinates retain more information about orbit curvature and relative orbit dynamics than the HCW equations in Cartesian coordinates, and are thus more useful in investigating relative orbit state observability and conducting IROD performance analysis. The observability problem is solved by introducing the curvature of the orbit through the angular component of the cylindrical coordinates. Maneuvers, multiple optical sensors, or modeling of the sensor offset are not required. A similar analysis using relative orbital elements [14] (ROE) might be possible, since the ROE will also properly capture the curvature of the orbit.

While the linearized relative orbital equations of motion in cylindrical coordinates are well known [15, 16], a rigorous and detailed derivation of these equations in vector form using kinematics in cylindrical coordinates is difficult to find in the literature. Thus, Section “Derivation of Relative Orbital Motion Equations in Cylindrical Coordinates” presents a detailed and rigorous derivation of the relative orbital equations of motion in cylindrical coordinates. The nonlinear two-body differential equations of motion, the linearized linear-time-varying (LTV) differential equations of motion for an elliptical orbit chief, and the linearized linear-time-invariant (LTI) differential equations of motion for a circular orbit chief are all presented in cylindrical coordinates.

Section “Measurement Equation in Cylindrical Coordinates” derives and presents the nonlinear LOS measurement equation in cylindrical coordinates. To facilitate our understanding of the observability and IROD performance, the remainder of the paper focuses on the 2-dimensional problem where the deputy and the chief are in the same orbital plane. In this case there are only 4 elements of the initial relative state vector and each LOS observation consists of only 1 angle measurement, i.e., 4 observations are required to estimate the 4 elements of the initial state vector.

The nonlinear LOS measurement equation and the linearized dynamics are applied in Section “Observability” to produce strong evidence that the initial relative state is in fact observable. Although full nonlinear observability criteria for the angles-only relative motion problem is nicely provided in [17], this section empirically shows that the linearized dynamics in cylindrical coordinates can provide the observability that the linearized dynamics in Cartesian coordinates cannot.

Section “Initial Relative Orbit Determination Performance Analysis and Geometric Dilution of Precision” presents a geometric approach, based on the linearized dynamics in cylindrical coordinates, to assess IROD performance equivalent to the computation of the Cramer-Rao lower bound. Section “Results - Leader/Follower Orbits” presents IROD performance analysis results for leader-follower orbits, and Section “Results - Flyby Orbits” presents results for flyby orbits where the deputy passes directly above or below the chief. Section “Results - Summary” provides a summary of the IROD results, and conclusions are provided in Section “Conclusions”.

Derivation of Relative Orbital Motion Equations in Cylindrical Coordinates

The equations of inertial two-body orbital motion for two spacecraft (deputy and chief) are given by.

$$ \boldsymbol{a}_{c}=-\frac{\mu}{{r_{c}^{3}}}\boldsymbol{r}_{c} $$
(2.1)
$$ \boldsymbol{a}_{d}=-\frac{\mu}{{r_{d}^{3}}}\boldsymbol{r}_{d} $$
(2.2)

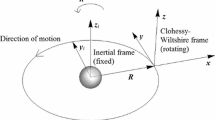
The equations of motion in cylindrical coordinates can be derived by first establishing a fixed reference orbit plane coincident with the initial orbit plane of the chief. The normal to this plane will be denoted by i z . The components of the chief’s motion in the reference plane are described using two unit vectors, \(\mathbf {i}_{\rho _{c}}\) and \(\mathbf {i}_{\theta _{c}}\), as shown in Fig. 1. A set of cylindrical coordinates ρ c (t), 𝜃 c (t), and z c (t) can then be defined to describe the motion of the chief with respect to the nominal plane where ρ c (t) and 𝜃 c (t) describe the in-plane motion, and z c (t) describes the out-of-plane motion. The chief’s inertial position, velocity, and acceleration vectors are then given by

$$ \boldsymbol{r}_{c}=\rho_{c}\mathbf{i}_{\rho_{c}}+z_{c}\mathbf{i}_{z} $$
(2.3)
$$ \boldsymbol{v}_{c}=\dot{\rho}_{c}\mathbf{i}_{\rho_{c}}+\rho_{c}\dot{\theta}_{c}\mathbf{i}_{\theta_{c}}+\dot{z}_{c}\mathbf{i}_{z} $$
(2.4)
$$ \boldsymbol{a}_{c}=\left( \ddot{\rho}_{c}-\rho_{c}\dot{\theta}_{c}^{2}\right)\mathbf{i}_{\rho_{c}}+(\rho_{c}\ddot{\theta}_{c}+2\dot{\rho}_{c}\dot{\theta}_{c})\mathbf{i}_{\theta_{c}}+\ddot{z}_{c}\mathbf{i}_{z} $$
(2.5)

By equating the components of Eq. 2.1 to the components of Eq. 2.5, the differential equations of motion for the chief in cylindrical coordinates are determined.

$$ \ddot{\rho}_{c}-\rho_{c}\dot{\theta}_{c}^{2}=-\frac{\mu\rho_{c}}{\left( {\rho_{c}^{2}}+{z_{c}^{2}}\right)^{3/2}} $$
(2.6)
$$ \rho_{c}\ddot{\theta}_{c}+2\dot{\rho}_{c}\dot{\theta}_{c}=0 $$
(2.7)
$$ \ddot{z}_{c}=-\frac{\mu z_{c}}{\left( {\rho_{c}^{2}}+{z_{c}^{2}}\right)^{3/2}} $$
(2.8)

Given appropriate initial conditions, the solution to these nonlinear differential equations will produce the time-history of the chief’s coordinates, ρ c (t), 𝜃 c (t), and z c (t).

Fig. 1
figure 1

Cylindrical coordinates geometry

Full size image

Next, using the same reference plane specified by the unit vector i z , we can setup the kinematic and dynamic equations of motion for the deputy in cylindrical coordinates using the unit vectors, \(\mathbf {i}_{\rho _{d}}\) and \(\mathbf {i}_{\theta _{d}}\), to describe the deputy’s orbital motion in the reference plane.

$$ \boldsymbol{r}_{d}=\rho_{d}\mathbf{i}_{\rho_{d}}+z_{d}\mathbf{i}_{z} $$
(2.9)
$$ \boldsymbol{v}_{d}=\dot{\rho}_{d}\mathbf{i}_{\rho_{d}}+\rho_{d}\dot{\theta}_{d}\mathbf{i}_{\theta_{d}}+\dot{z}_{d}\mathbf{i}_{z} $$
(2.10)
$$ \boldsymbol{a}_{d}=\left( \ddot{\rho}_{d}-\rho_{d}\dot{\theta}_{d}^{2}\right)\mathbf{i}_{\rho_{d}}+(\rho_{d}\ddot{\theta}_{d}+2\dot{\rho}_{d}\dot{\theta}_{d})\mathbf{i}_{\theta_{d}}+\ddot{z}_{d}\mathbf{i}_{z} $$
(2.11)

By equating the components of Eq. 2.2 to the components of Eq. 2.11, the differential equations of motion for the deputy in cylindrical coordinates are determined

$$ \ddot{\rho}_{d}-\rho_{d}\dot{\theta}_{d}^{2}=-\frac{\mu\rho_{d}}{\left( {\rho_{d}^{2}}+{z_{d}^{2}}\right)^{3/2}} $$
(2.12)
$$ \rho_{d}\ddot{\theta}_{d}+2\dot{\rho}_{d}\dot{\theta}_{d}=0 $$
(2.13)
$$ \ddot{z}_{d}=-\frac{\mu z_{d}}{\left( {\rho_{d}^{2}}+{z_{d}^{2}}\right)^{3/2}} $$
(2.14)

Given appropriate initial conditions, the solution to these nonlinear differential equations will produce the time-history of the deputy coordinates, ρ d (t), 𝜃 d (t), and z d (t).

If the relative coordinates are defined as

$$ \rho_{rel}(t)\equiv\rho_{d}(t)-\rho_{c}(t) $$
(2.15)
$$ \theta_{rel}(t)\equiv\theta_{d}(t)-\theta_{c}(t) $$
(2.16)
$$ z_{rel}(t)\equiv z_{d}(t)-z_{c}(t) $$
(2.17)

the second time-derivatives of \(\ddot {\rho }_{rel}(t)\), \(\ddot {\theta }_{rel}(t)\), and \(\ddot {z}_{rel}(t)\), can be determined by subtracting Eqs. 2.12–2.14 from Eqs. 2.6–2.8.

$$ \ddot{\rho}_{rel}=\rho_{d}\dot{\theta}_{d}^{2}-\rho_{c}\dot{\theta}_{c}^{2}-\frac{\mu\rho_{d}}{\left( {\rho_{d}^{2}}+{z_{d}^{2}}\right)^{3/2}}+\frac{\mu\rho_{c}}{\left( {\rho_{c}^{2}}+{z_{c}^{2}}\right)^{3/2}} $$
(2.18)
$$ \ddot{\theta}_{rel}=\frac{-2\dot{\rho}_{d}\dot{\theta}_{d}}{\rho_{d}}+\frac{2\dot{\rho}_{c}\dot{\theta}_{c}}{\rho_{c}} $$
(2.19)
$$ \ddot{z}_{rel}=-\frac{\mu z_{d}}{\left( {\rho_{d}^{2}}+{z_{d}^{2}}\right)^{3/2}}+\frac{\mu z_{c}}{\left( {\rho_{c}^{2}}+{z_{c}^{2}}\right)^{3/2}} $$
(2.20)

In the absence of perturbations, the chief’s motion is entirely in the reference plane, i.e., z c (t)≡0. Substituting ρ d (t) = ρ c (t) + ρ r e l (t), 𝜃 d (t) = 𝜃 c (t) + 𝜃 r e l (t), and z d (t) = z r e l (t) into the above equations produces

$$ \ddot{\rho}_{rel}=[\rho_{c}(t)+\rho_{rel}][\dot{\theta}_{c}(t)+\dot{\theta}_{rel}]^{2}-\rho_{c}(t) \dot{\theta}_{c}^{2}(t)-\frac{\mu[\rho_{c}(t)+\rho_{rel}]}{\left( [\rho_{c}(t)+\rho_{rel}]^{2}+z_{rel}^{2}\right)^{3/2}} +\frac{\mu}{{\rho_{c}^{2}}(t)} $$
(2.21)
$$ \ddot{\theta}_{rel}=\frac{-2[\dot{\rho}_{c}(t)+\dot{\rho}_{rel}][\dot{\theta}_{c}(t)+\dot{\theta}_{rel}]}{\rho_{c}(t)+\rho_{rel}}+\frac{2\dot{\rho}_{c}(t)\dot{\theta}_{c}(t)}{\rho_{c}(t)} $$
(2.22)
$$ \ddot{z}_{rel}=-\frac{\mu z_{rel}}{\left( [\rho_{c}(t)+\rho_{rel}]^{2}+z_{rel}^{2}\right)^{3/2}} $$
(2.23)

These are the exact nonlinear two-body equations of relative orbital motion in cylindrical coordinates. The coordinates of the chief ρ c (t), 𝜃 c (t), and z c (t) are assumed to be known.

Assuming \(\rho _{rel},\dot {\theta }_{rel},\dot {\rho }_{rel},z_{rel}\) are “small” (\(\rho _{rel},z_{rel}\ll R,\dot {\theta }_{rel}\ll \dot {\theta }_{c}(t),\dot {\rho }_{rel}\ll \dot {\rho }_{c}(t)\)), the above equations can be expanded to first-order in a Taylor series to produce

$$ \ddot{\rho}_{rel}\approx\left[\dot{\theta}_{c}^{2}(t)+\frac{2\mu}{{\rho_{c}^{3}}(t)}\right]\rho_{rel}+[2\rho_{c}(t)\dot{\theta}_{c}(t)]\dot{\theta}_{rel} $$
(2.24)
$$ \ddot{\theta}_{rel}\approx \left[\frac{2\dot{\rho}_{c}(t)\dot{\theta}_{c}(t)}{{\rho_{c}^{2}}(t)}\right]\rho_{rel}-\left[\frac{2\dot{\rho}_{c}(t)}{\rho_{c}(t)}\right]\dot{\theta}_{rel}-\left[\frac{2\dot{\theta}_{c}(t)}{\rho_{c}(t)}\right]\dot{\rho}_{rel} $$
(2.25)
$$ \ddot{z}_{rel}\approx-\left[\frac{\mu}{\rho_{c}(t){}^{3}}\right]z_{rel} $$
(2.26)

These are the linear-time-varying (LTV) differential equations of motion for an elliptical orbit chief in the absence of perturbations. It is important to note that since the right hand sides of Eqs. 2.21-2.23 are a function of only \(\rho _{rel},\dot {\theta }_{rel},\dot {\rho }_{rel},z_{rel}\), the above linearized equations are valid for arbitrarily large 𝜃 r e l and \(\dot {z}_{rel}\).

If the chief is in a circular orbit of constant radius R and constant orbital angular rate n, then ρ c (t)≡R, \(\dot {\rho }_{c}(t)\equiv 0\), \(\dot {\theta }_{c}(t)\equiv n\). If these relations are substituted into Eqs. 2.21-2.23, the nonlinear two-body exact equations of relative motion in cylindrical coordinates for a circular orbit chief are determined

$$ \ddot{\rho}_{rel}=[R+\rho_{rel}][n+\dot{\theta}_{rel}]^{2}-\frac{\mu[R+\rho_{rel}]}{\left( [R+\rho_{rel}]^{2}+z_{rel}^{2}\right)^{3/2}} $$
(2.27)
$$ \ddot{\theta}_{rel}=\frac{-2\dot{\rho}_{rel}[n+\dot{\theta}_{rel}]}{R+\rho_{rel}} $$
(2.28)
$$ \ddot{z}_{rel}=-\frac{\mu z_{rel}}{\left( [R+\rho_{rel}]^{2}+z_{rel}^{2}\right)^{3/2}} $$
(2.29)

Assuming \(\rho _{rel},\dot {\theta }_{rel},z_{rel}\) are “small” \((\rho _{rel},z_{rel}\ll R,\dot {\theta }_{rel}\ll n\)), the above equations can be expanded to 1st-order in a Taylor series to produce

$$ \ddot{\rho}_{rel}\approx3n^{2}\rho_{rel}+2Rn\dot{\theta}_{rel} $$
(2.30)
$$ \ddot{\theta}_{rel}\approx-\frac{2n}{R}\dot{\rho}_{rel} $$
(2.31)
$$ \ddot{z}_{rel}\approx-n^{2}z_{rel} $$
(2.32)

These are the linear-time-invariant (LTI) differential equations of relative motion for a circular orbit chief in the absence of perturbations. Notice the similarity of these equations to the HCW equations in Eqs. 1.1–1.3. However, there is a significant difference between these equations and the HCW equations. Since the right hand sides of Eqs. 2.27–2.29 are a function of only \(\rho _{rel},\dot {\theta }_{rel},\dot {\rho }_{rel},z_{rel}\), the above linearized equations are valid for arbitrarily large 𝜃 r e l and \(\dot {z}_{rel}\). This is an important result.

For subsequent analysis, only the two-dimensional in-plane relative motion will be considered. If we define the state vector as

$$ \boldsymbol{X}(t)=\left[\begin{array}{c} \rho_{rel}(t)\\ \theta_{rel}(t)\\ \dot{\rho}_{rel}(t)\\ \dot{\theta}_{rel}(t) \end{array}\right] $$
(2.33)

the solutions to Eqs. 2.30 and 2.31 are

$$ \rho_{rel}(t)=\boldsymbol{K}_{\rho}^{T}(t)\boldsymbol{X}_{0} $$
(2.34)
$$ \theta_{rel}(t)=\boldsymbol{K}_{\theta}^{T}(t)\boldsymbol{X}_{0} $$
(2.35)

where

$$ \boldsymbol{K}_{\rho}(t)=\!\left[\begin{array}{c} 4-3\cos\beta\\ 0\\ \sin\beta/n\\ 2R(1-\cos\beta)/n \end{array}\right],\quad\boldsymbol{K}_{\theta}(t)\,=\,\left[\begin{array}{c} 6(\sin\beta-\beta)/R\\ 1\\ 2(\cos\beta-1)/(Rn)\\ (4\sin\beta-3\beta)/n \end{array}\right],\quad\beta\,=\,n(t-t_{0}) $$
(2.36)

An alternative description of the relative motion can be obtained by introducing the arc-length along the chief’s circular orbit, y⌢ r e l , and the arc-length rate, \(\stackrel {\dot {\frown }}{y}_{rel}\), where

$$\stackrel{\frown}{y}_{rel}=R\theta_{rel} $$
$$\stackrel{\dot{\frown}}{y}_{rel}=R\dot{\theta}_{rel} $$

Defining x r e l = ρ r e l and \(\dot {x}_{rel}=\dot {\rho }_{rel}\), the new relative motion state vector becomes

$$ \boldsymbol{x}(t)=\left[\begin{array}{c} x_{rel}(t)\\ \stackrel{\frown}{y}_{rel}(t)\\ \dot{x}_{rel}(t)\\ \stackrel{\dot{\frown}}{y}_{rel}(t) \end{array}\right]=\left[\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & R & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & R \end{array}\right]\boldsymbol{X}(t) $$
(2.37)

where the solutions to Eqs. 2.30 and 2.31 are used to determine x r e l (t) and y⌢ r e l (t)

$$ x_{rel}(t)=\boldsymbol{k}_{x}^{T}(t)\boldsymbol{x}_{0} $$
(2.38)
$$ \stackrel{\frown}{y}_{rel}(t)=\boldsymbol{k}_{\stackrel{\frown}{y}_{rel}}^{T}(t)\boldsymbol{x}_{0} $$
(2.39)
$$ \boldsymbol{k}_{x}(t)=\left[\begin{array}{c} 4-3\cos\beta\\ 0\\ \sin\beta/n\\ 2(1-\cos\beta)/n \end{array}\right],\quad\boldsymbol{k}_{\stackrel{\frown}{y}_{rel}}(t)=\left[\begin{array}{c} 6(\sin\beta-\beta)\\ 1\\ 2(\cos\beta-1)/n\\ (4\sin\beta-3\beta)/n \end{array}\right],\quad\beta=n(t-t_{0}) $$
(2.40)

For completeness a third description of the relative motion can be obtained by introducing the arc-length along the chief’s circular orbit, y⌢ r e l , and changing the independent variable from time t to a normalized time, τ = n t. (This may also help control numerical instabilities in some numerical applications.)

$$ \mathsf{x}_{rel}=\rho_{rel} $$
(2.41)
$$ \stackrel{\frown}{\mathsf{y}}_{rel}=R\theta_{rel} $$
(2.42)
$$ \frac{d\mathsf{x}_{rel}}{d\tau}=\mathsf{x}_{rel}^{\prime}=\dot{\rho}_{rel}/n $$
(2.43)
$$ \frac{d\stackrel{\frown}{\mathsf{y}}_{rel}}{d\tau}=\stackrel{\frown}{\mathsf{y}}_{rel}^{\prime}=R\dot{\theta}_{rel}/n $$
(2.44)

Using this description, the relative motion state vector becomes

$$ \boldsymbol{\mathsf{X}}(\tau)=\left[\begin{array}{c} \mathsf{x}_{rel}(\tau)\\ \stackrel{\frown}{\mathsf{y}}_{rel}(\tau)\\ \mathsf{x}_{rel}^{\prime}(\tau)\\ \stackrel{\frown}{\mathsf{y}}_{rel}^{\prime}(\tau) \end{array}\right]=\left[\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1/n & 0\\ 0 & 0 & 0 & 1/n \end{array}\right]\boldsymbol{x}(t)=\left[\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & R & 0 & 0\\ 0 & 0 & 1/n & 0\\ 0 & 0 & 0 & R/n \end{array}\right]\boldsymbol{X}(t) $$
(2.45)

where the solutions to Eqs. 2.30 and 2.31 can be used to determine x r e l (τ) and y⌢ r e l (τ)

$$ \mathsf{x}_{rel}(\tau)=\mathsf{\mathbf{K}}_{\mathsf{x}}^{T}(\tau)\boldsymbol{\mathsf{X}}_{0} $$
(2.46)
$$ \stackrel{\frown}{\mathsf{y}}_{rel}(\tau)=\mathsf{\mathbf{K}}_{\stackrel{\frown}{\mathsf{\mathsf{y}}}_{rel}}^{T}(\tau)\boldsymbol{\mathsf{X}}_{0} $$
(2.47)
$$ \mathsf{\mathbf{K}}_{\mathsf{x}}^{T}(\tau)=\left[\begin{array}{c} 4-3\cos\beta\\ 0\\ \sin\beta\\ 2(1-\cos\beta) \end{array}\right],\qquad\mathsf{\boldsymbol{K}}_{\stackrel{\frown}{\mathsf{y}}_{rel}}(\tau)=\left[\begin{array}{c} 6(\sin\beta-\beta)\\ 1\\ 2(\cos\beta-1)\\ (4\sin\beta-3\beta) \end{array}\right],\qquad\beta=\tau-\tau_{0} $$
(2.48)

Measurement Equation in Cylindrical Coordinates

In two dimensions, the line-of-sight angle measurement with respect to the chief’s radial direction, α(t), is shown in Fig. 1. To obtain this measurement, it is assumed that the inertial position and inertial orientation of the camera is known. The error in the angle measurement is due to uncertainties in the chief’s position and attitude, uncertainties in the camera resolution/accuracy, uncertainties in the pixel location of the deputy’s center-of-mass in the camera image plane, and uncertainties in the orientation of the camera in the chief’s body frame. If the camera orientation and the chief’s position and attitude are assumed to be known perfectly, the angle measurement error is due only to camera resolution/accuracy and uncertainties in the pixel location of the deputy’s center-of-mass.

Using the geometry in Fig. 1, the position of the deputy with respect to the chief is given by

$$ \mathbf{r}_{d}-\mathbf{r}_{c}=\left[\rho_{d}\cos\theta_{rel}-\rho_{c}\right]\mathbf{i}_{\rho_{c}}+\rho_{d}\sin\theta_{rel}\mathbf{i}_{\theta_{c}} $$
(3.1)

and the angle measurement α(t) is given by

$$ \tan\alpha=\frac{\rho_{d}\sin\theta_{rel}}{\rho_{d}\cos\theta_{rel}-\rho_{c}}=\frac{(\rho_{c}+\rho_{rel}) \sin\theta_{rel}}{(\rho_{c}+\rho_{rel})\cos\theta_{rel}-\rho_{c}}=\frac{\sin\theta_{rel}}{\left[\cos\theta_{rel}-\frac{\rho_{c}}{\rho_{c}+\rho_{rel}}\right]} $$
(3.2)

or

$$ \cos\alpha=\frac{(\rho_{c}+\rho_{rel})\cos\theta_{rel}-\rho_{c}}{\sqrt{(\rho_{c}+\rho_{rel})^{2}+{\rho_{c}^{2}} -2\rho_{c}(\rho_{c}+\rho_{rel})\cos\theta_{rel}}} $$
(3.3)
$$ \sin\alpha=\frac{(\rho_{c}+\rho_{rel})\sin\theta_{rel}}{\sqrt{(\rho_{c}+\rho_{rel})^{2}+{\rho_{c}^{2}}-2\rho_{c} (\rho_{c}+\rho_{rel})\cos\theta_{rel}}} $$
(3.4)

Thus far, the above nonlinear measurement equation is completely general, i.e., no assumptions have been made except for formulating the measurement equations in two dimensions.

Another useful form of the measurement equation is the case where the chief is in a circular orbit ρ c = R and ρ r e l ≪R. This is relevant since the linearized dynamics in cylindrical coordinates make these same assumptions. In this case, Eq. 3.2 to first-order in ρ r e l becomes

$$ \tan\alpha\thickapprox\frac{\sin\theta_{rel}}{\left[\rho_{rel}/R+\cos\theta_{rel}-1\right]} $$
(3.5)

where

$$ \cos\alpha\thickapprox\frac{(R+\rho_{rel})\cos\theta_{rel}-R}{\sqrt{2R(R+\rho_{rel})(1-\cos\theta_{rel})}} $$
(3.6)
$$ \sin\alpha\thickapprox\frac{(R+\rho_{rel})\sin\theta_{rel}}{\sqrt{2R(R+\rho_{rel})(1-\cos\theta_{rel})}} $$
(3.7)

Observability

While a rigorous proof of relative state observability in cylindrical coordinates is not presented in this paper, the evidence provided below shows that the initial relative state is observable when the angles-only relative navigation problem is formulated in cylindrical coordinates. This is an important result because if analysis is conducted using the Cartesian coordinates formulation of the problem, a different conclusion will be reached.

The observability question asks whether or not the time-history of α(t) or \(\tan \alpha (t)\) is unique for every possible combination of initial conditions, ρ r e l (t 0), 𝜃 r e l (t 0), \(\dot {\rho }_{rel}(t_{0})\), \(\dot {\theta }_{rel}(t_{0})\). Alternatively, the observability question can be examined by substituting Eqs. 2.34–2.35 into Eq. 3.2

$$ \tan\alpha(t)=\frac{\sin[\boldsymbol{K}_{\theta}^{T}(t)\boldsymbol{X}_{0}]}{\left[\cos[\boldsymbol{K}_{\theta}^{T}(t)\boldsymbol{X}_{0}]-\frac{\rho_{c}}{\rho_{c}+\boldsymbol{K}_{\rho}^{T}(t)\boldsymbol{X}_{0}}\right]} $$
(4.1)

and asking whether or not the time-history of \(\tan \alpha (t)\) is unique for each initial state vector X 0. Given the highly nonlinear nature of Eq. 4.1, it seems likely that each time-history α(t) can be associated with a unique set of initial conditions. Even when the chief is in a circular orbit and ρ r e l ≪R, the measurement equation in Eq. 3.5 continues to be highly nonlinear in X 0, as seen by substituting Eqs. 2.34–2.35 into Eq. 3.5:

$$ \tan\alpha(t)=\frac{\sin\left[\boldsymbol{K}_{\theta}^{T}(t)\boldsymbol{X}_{0}\right]}{\left\{ \boldsymbol{K}_{\rho}^{T}(t)\boldsymbol{X}_{0}/R+\cos\left[\boldsymbol{K}_{\theta}^{T}(t)\boldsymbol{X}_{0}\right]-1\right\}} $$
(4.2)

indicating that the initial state may be observable.

Note however that when the relative downrange position of the deputy is small, as is required in the linearized Cartesian formulation of the problem, 𝜃 r e l must also be small. In this case, if Eqs. 3.5 and 4.2 are expanded to first-order in 𝜃 r e l they reduce to

$$ \tan\alpha(t)\approx\frac{R\theta_{rel}(t)}{\rho_{rel}(t)}=\frac{R\boldsymbol{K}_{\theta}^{T}(t)\boldsymbol{X}_{0}}{\boldsymbol{K}_{\rho}^{T}(t)\boldsymbol{X}_{0}} $$
(4.3)

where it becomes apparent that any scalar multiple of the state will produce the same LOS time-history, i.e., the initial state is unobservable. The assumption of small 𝜃 r e l is of course unnecessary in the cylindrical coordinate formation of the problem, and the evidence provided below shows that the initial relative state is observable in the cylindrical coordinates formulation of the angles-only relative navigation problem.

For example, it is known that when the deputy is in the same circular orbit as the chief, i.e., a leader-follower orbit, the Cartesian formulation of the HCW equations produces the same LOS measurements independent of the relative displacement position of the deputy as shown [6]. In the cylindrical coordinates formulation of the problem, the LOS measurements are seen to be unique to each leader-follower angular displacement. This case can be seen by setting ρ r e l =0 in Eq. 3.2

$$ \tan\alpha=\frac{\sin\theta_{rel}}{\cos\theta_{rel}-1} $$
(4.4)

and examining how the measurement α changes for each value of angular displacement 𝜃 r e l . Fig. 2 shows that the change in α from the local horizontal, Δα = α−π/2, is in fact a unique function of the relative angular displacement of the deputy 𝜃 r e l . Hence it may be possible to determine the range of the deputy for leader-follower orbits (contrary to Woffinden’s dilemma) if the LOS measuring device has sufficient accuracy. The required accuracy can be estimated by determining the sensitivity of α to changes in 𝜃 r e l . Using Eq. 4.4, the sensitivity of the measurement α to displacements along the v-bar 𝜃 r e l reduces to

$$ \frac{\partial\alpha}{\partial\theta_{rel}}=\frac{1}{2} $$
(4.5)

This rather simple result is important. If two spacecraft are known to be in leader-follower co-circular 7000 km LEO orbits, a measurement error of ±1 mrad corresponds to an orbit angular displacement error equal to ±2 mrad, equivalent to an along-track error of 7000 km ×0.002 rad =±14 km. That is, an along-track navigation error <±14 km will not be discernible by a camera measurement with ±1 mrad accuracy. For a 42,000 km GEO orbit, an angle measurement error of ±1 mrad corresponds to an along-track error of 42,000 km ×0.002 rad =±84 km.

Fig. 2
figure 2

Change in LOS measurement angle from the local horizontal, Δα = α−π/2, as a function of the relative angular displacement of the deputy

Full size image

It is also known that when the deputy is in a co-circular orbit with altitude Δh above or below the chief, i.e., a flyby orbit, the Cartesian formulation of the HCW equations produce the same LOS time-history independent of the altitude [6]. In contrast, in the cylindrical formulation of the problem the LOS measurements are seen to be unique to each flyby orbit. Consider the case where the deputy coasts from a position above and well ahead of the chief to a position above and well behind the chief. Given the initial conditions ρ r e l (t 0)=Δh, \(\dot {\rho }_{rel}(t_{0})=0\), 𝜃 r e l (t 0)=3πΔh/2R, and \(\dot {\theta }_{rel}(t_{0})=-3n{\Delta } h/2R\), Eqs. 2.34-2.35 show that the resulting relative motion is ρ r e l (t)=Δh and 𝜃 r e l (t)=3Δh(π−n t)/2R, i.e., the deputy will pass directly over the chief in one-half orbital period, and the final along-track position after one orbital period is 𝜃 r e l (t f )=−3πΔh/2R. Substituting these expressions for the flyby relative motion into Eq. 3.2 provides the LOS time-history for a particular flyby altitude Δh.2

$$ \tan\alpha=\frac{(R+{\Delta} h)\sin\left[\frac{3{\Delta} h(\pi-nt)}{2R}\right]}{(R+{\Delta} h)\cos\left[\frac{3{\Delta} h(\pi-nt)}{2R}\right]-R} $$
(4.6)

Using this equation, the time-histories of α can be computed for various values of Δh and subtracted from a baseline time-history associated with Δh=1 m. The results are shown in Fig. 3 for a 7000 km circular chief orbit, where it is seen that the LOS time-histories for flyby orbits are indeed different and unique to each Δh . This figure also shows, for example, that a measurement accuracy <2 mrad is required to discern the Δh of a 100 km flyby orbit from another nearby flyby orbit 10 km above or below. Notice also that the ability to discern Δh drops dramatically as the deputy approaches the point directly above the chief.

Fig. 3
figure 3

Flyby orbit LOS measurement angle time-histories for several values of Δh subtracted from a baseline time-history Δh=1 m using the nonlinear measurement equation and linearized relative motion dynamics in cylindrical coordinates (R=7000 km)

Full size image

Similar results can be seen in Fig. 4 for a natural motion circumnavigating football orbit with semimajor axis a. Given the initial conditions ρ r e l (t 0)=0, \(\dot {\rho }_{rel}(t_{0})=na/2\), 𝜃 r e l (t 0) = a/R, and \(\dot {\theta }_{rel}(t_{0})=0\), Eqs. 2.34-2.35 show that the resulting relative motion is periodic, \(\rho _{rel}(t)=a\sin (nt)/2\) and \(\theta _{rel}(t)=a\cos (nt)/R\), where a is the arc-length of the semi-major axis of the football orbit. Substituting these expressions for the relative motion into Eq. 3.2 provides the LOS time-history for a particular football orbit. In this case, the measurement angle time-histories α(t) are given by

$$ \tan\alpha=\frac{\left( R+\frac{a\sin nt}{2}\right)\sin\left[\frac{a\cos nt}{R}\right]}{\left( R+\frac{a\sin nt}{2}\right)\cos\left[\frac{a\cos nt}{R}\right]-R} $$
(4.7)

While the Cartesian formulation of the CW equations produces the same LOS time-history for any size football orbit, the cylindrical formulation produces different and unique LOS time-histories for each value of semimajor axis a. Similar to the flyby example, here the ability to discern the value of the semimajor axis drops dramatically at certain times \(\left (\text {in this case}~\frac {1}{2}~\text {and}~\frac {3}{4}~\text {orbital periods}\right )\).

Fig. 4
figure 4

Football orbit LOS measurement angle time-histories for several values of semi-major axis a subtracted from a baseline time-history associated with a=1 m using the nonlinear measurement equation and linearized relative motion dynamics in cylindrical coordinates (R=7000 km)

Full size image

Initial Relative Orbit Determination Performance Analysis and Geometric Dilution of Precision

Since the empirical results above indicate that the angles-only relative navigation problem is observable when formulated in cylindrical coordinates, a preliminary analysis of IROD performance utilizing the cylindrical coordinates formulation of the problem is warranted. To be useful and provide a better understanding of the IROD problem, such analysis should depend only on the geometry of the problem (i.e., the relative motion), the time-interval between measurements, and the expected sensor accuracy. It is important to point out that such an analysis using the Cartesian formulation of the problem is impossible since the results will always show that the IROD problem is unobservable. On the other hand, a preliminary performance analysis based on the full nonlinear models may produce more accurate results, but the benefits of the semi-analytical linearized models in cylindrical coordinates are the speed with which analysis can be conducted and the insight that can be gained using the semi-analytical models. Finally, since the linearized cylindrical coordinate formulation properly captures the curvature of the underlying inertial orbits, second-order effects such as J2, drag, or SRP, over relatively short (less than 1 orbit period) measurement periods, are expected to provide minimal additional observability and improvement in IROD performance.

To conduct this performance analysis, a useful metric, the Cramer-Rao lower bound, will be employed. The Cramer-Rao lower bound is given by [18]

$$ P\ge\sigma_{\alpha}^{2}\left[H^{T}H\right]^{-1} $$
(5.1)

where P is the covariance of the initial state estimate, and \(\sigma _{\alpha }^{2}\) is the variance of the LOS angle measurements. Note that the matrix H T H will be singular if the problem is unobservable.

Given 4 measurements at times t i , i=0,1,2,3, the matrix H in the above equation is given by

$$ H=\left[\begin{array}{c} \boldsymbol{h}^{T}(t_{0})\\ \boldsymbol{h}^{T}(t_{1}){\Phi}(t_{1},t_{0})\\ \boldsymbol{h}^{T}(t_{2}){\Phi}(t_{2},t_{0})\\ \boldsymbol{h}^{T}(t_{3}){\Phi}(t_{3},t_{0}) \end{array}\right] $$
(5.2)

where the state transition matrix Φ(t i ,t 0) is obtained from the linear differential equation in Eqs. 2.30-2.32 and the measurement geometry vectors h T(t i ) are computed from Eq. 3.2

$$ \boldsymbol{h}^{T}(t_{i})=\left.\frac{\partial\alpha}{\partial\boldsymbol{X}}\right|_{t_{i}}=\left[\begin{array}{cccc} \frac{\partial\alpha}{\partial\rho_{rel}} & \frac{\partial\alpha}{\partial\theta_{rel}} & 0 & 0\end{array}\right]_{t_{i}} $$
(5.3)

where

$$ \frac{\partial\alpha}{\partial\rho_{rel}}=-\cos^{2}\alpha\left( \frac{\rho_{c}\sin(\theta_{rel})}{\left\{ \rho_{d}\cos\theta_{rel}-\rho_{c}\right\}^{2}}\right)==-\frac{\rho_{c}}{d^{2}}\sin\theta_{rel} $$
(5.4)
$$ \frac{\partial\alpha}{\partial\theta_{rel}}=-\cos^{2}\alpha\left( \frac{\rho_{d}\rho_{c}\cos\theta_{rel}-{\rho_{d}^{2}}}{\left\{ \rho_{d}\cos\theta_{rel}-\rho_{c}\right\}^{2}}\right)=\frac{{\rho_{d}^{2}}-\rho_{c}\rho_{d}\cos\theta_{rel}}{d^{2}} $$
(5.5)

and where d is the distance between the chief and the deputy.

$$ d=\sqrt{{\rho_{d}^{2}}+{\rho_{c}^{2}}-2\rho_{c}\rho_{d}\cos\theta_{rel}} $$
(5.6)

Conceptually, each measurement geometry vector h T(t i ) reflects the direction and sensitivity of the information that α(t i ) provides about X i . The information in these measurement geometry vectors is effectively converted to information about the initial state X 0 using the state transition matrix in Eq. 5.2. Thus, although this has been formulated as a Cramer-Rao lower bound, it is more fundamentally a geometric problem that answers the question of how well the 4 row vectors in H span the 4-dimensional space of X 0.

Note that the above measurement geometry vectors are valid for completely arbitrary chief/deputy positions (in 2 dimensions). The state transition matrices however are based upon the linearized equations of relative motion in cylindrical coordinates in Eqs. 2.30-2.32 where the chief is assumed to be in a circular orbit with radius R. Since the 3rd and 4th elements of the measurement geometry vectors are zero, the 3rd and 4th rows of the transition matrices are not required. Thus, each row of H is given simply by

$$\begin{array}{@{}rcl@{}} \boldsymbol{h}^{T}(t_{i}){\Phi}(t_{i},t_{0})&=&-\frac{\rho_{c}(t_{i})}{d^{2}(t_{i})}\sin\theta_{rel}(t_{i}) \boldsymbol{K}_{\rho}^{T}(t_{i})\\ &&+\left[\frac{{\rho_{d}^{2}}(t_{i})-\rho_{c}(t_{i})\rho_{d}(t_{i}) \cos\theta_{rel}(t_{i})}{d^{2}(t_{i})}\right]\boldsymbol{K}_{\theta}^{T}(t_{i}),\quad i=0,1,2,3\\ \end{array} $$
(5.7)

Using this expression to populate the rows of H, Eq. 5.1 can be used to compute the relative altitude (x r e l ) geometric dilution of precision (GDOP) as defined in [19].

$$ GDOP_{x_{rel}}=\sqrt{P_{11}}/\sigma_{\alpha}=\sqrt{\left[H^{T}H\right]_{11}^{-1}} $$
(5.8)

The relative altitude GDOP is not strictly in the radial direction, it will be referred to as the radial GDOP.

The GDOP for the along-track arc-length (y⌢ r e l ), radial-rate (\(\dot {x}_{rel}\)), and along-track arc-length rate (\(\stackrel {\dot {\frown }}{y}_{rel}\)) are similarly given by

$$ GDOP_{\stackrel{\frown}{y}_{rel}}=R\times\sqrt{P_{22}}/\sigma_{\alpha}=R\times\sqrt{\left[H^{T}H\right]_{22}^{-1}} $$
(5.9)
$$ GDOP_{\dot{x}_{rel}}=\sqrt{P_{33}}/\sigma_{\alpha}=\sqrt{\left[H^{T}H\right]_{33}^{-1}} $$
(5.10)
$$ GDOP_{\stackrel{\dot{\frown}}{y}_{rel}}=R\times\sqrt{P_{44}}/\sigma_{\alpha}=R\times\sqrt{\left[H^{T}H\right]_{44}^{-1}} $$
(5.11)

Notice that the GDOP is based only on the geometry of the information vectors, i.e., the 4 measurement geometry vectors (rows) in Eq. 5.2. The measurement geometry vectors are easily computed using Eq. 5.7 when measurement time-interval, the radius of the chief’s circular orbit, and the relative motion of the deputy with respect to the chief are specified.

Results - Leader/Follower Orbits

First consider the case where the deputy is placed in the same 7000 km circular LEO orbit as the chief. Using Eqs. 5.8–5.9, the expected position GDOP in the along-track and radial directions are shown in Figs. 5 and 6 as a function of the relative angular displacement between the chief and the deputy and the time-interval between measurements Δt. These results are based only on geometry of the problem and represent the best case IROD performance given 4 angle measurements separated by a time-interval Δt, i.e., there are no unmodeled dynamics, sensor misalignment, sensor biases, etc., in the problem.

Fig. 5
figure 5

Leader-follower along-track GDOP as a function of measurement rate Δt and relative along-track position of deputy for 7000 km circular orbit chief. The relative radial position of deputy is zero

Full size image
Fig. 6
figure 6

Leader-follower radial GDOP as a function of measurement rate Δt and relative along-track position of deputy for 7000 km circular orbit chief. The relative radial position of deputy is zero

Full size image

Figure 5 shows that the along-track errors are consistently reduced as the deputy/chief separation is increased (the results for Δh=0.01 km and Δh=0.1 are off the scale of the plot). This is due to the additional curvature in the trajectory as the deputy is moved further away from the chief. The figure also shows that the along-track error is very dependent on the time increment between measurements Δt. The along-track error is seen to decrease as Δt is increased from zero and reaches a minimum in the range of 2000s<Δt<4000s, with the exception of a spike in the performance when Δt is equal to one-half the orbital period (not seen in the figure is another spike at one orbital period). Since the natural frequency of the linearized dynamics is the orbit rate, this is equivalent to the problem of estimating the amplitude of a harmonic oscillator by sampling it at intervals of n π/2.

The data also shows, for example, that a camera with an accuracy of 1 mrad will be useful only when the deputy/chief separations are on the order of 1000 km or greater, since only then will the downrange errors be less than the separation. For separations of 100 km or less, significantly more accuracy is required. Since these are best-case results, the leader-follower IROD problem with only 4 measurements will be difficult to solve when measurement accuracy is only on the order of 1 mrad. From the standpoint of practicability, measurement accuracy on the order of 0.1 mrad is possible, while to the author’s knowledge, accuracy better than 0.01 mrad is, at this time, difficult to obtain.

Figure 6 shows that the radial errors are relatively independent of deputy/chief separations (i..e most of the curves lie on top of each other), but are again dependent on Δt . The radial error is seen to decrease as Δt is increased from zero and reaches a minimum in the range of 2000s<Δt<4000s, with a spike in the error when time increment between measurements is equal to one-half the orbital period (another spike occurs at one orbital period). The data also shows that a camera with 1 mrad accuracy will be useful only when the deputy/chief separations are greater than 10 km, since only then will the radial errors be smaller than the range. For separations less than 10 km, improved measurement accuracy will be required.

The GDOP results in Figs. 5–6 reflect how well the rows of H span the 4-dimensional in-plane space. Using Eq. 5.7 it can be seen that when β i = n(t i −t 0)≪1 (i.e., small measurement time-intervals, Δt) the row vectors of H for the leader-follower case are given by

$$ \boldsymbol{h}^{T}(t_{i}){\Phi}(t_{i},t_{0})=-\frac{\rho_{c}}{d^{2}}\sin\theta_{rel}\boldsymbol{K}_{\rho}^{T}(t_{i})+\frac{{\rho_{c}^{2}}}{d^{2}}\left( 1-\cos\theta_{rel}\right)\boldsymbol{K}_{\theta}^{T}(t_{i}) $$
(6.1)

where 𝜃 r e l , d, and ρ c = ρ d are constants, and

$$\boldsymbol{K}_{\rho}(t_{i})\approx\left[\begin{array}{c} 1\\ 0\\ \beta_{i}/n\\ 0 \end{array}\right],\qquad\boldsymbol{K}_{\theta}(t_{i})\approx\left[\begin{array}{c} 0\\ 1\\ 0\\ \beta_{i}/n \end{array}\right],\qquad\beta_{i}=n(t_{i}-t_{0}),\quad i=0,1,2,3 $$

Denoting the coefficients of \(\boldsymbol {K}_{\rho }^{T}(t_{i})\) and \(\boldsymbol {K}_{\theta }^{T}(t_{i})\) by c ρ and c 𝜃 , the four rows of the H matrix are

$$ H\approx\left[\begin{array}{cccc} c_{\rho} & c_{\theta} & 0 & 0\\ c_{\rho} & c_{\theta} & c_{\rho}\beta_{1}/n & c_{\theta}\beta_{1}/n\\ c_{\rho} & c_{\theta} & c_{\rho}\beta_{2}/n & c_{\theta}\beta_{2}/n\\ c_{\rho} & c_{\theta} & c_{\rho}\beta_{3}/n & c_{\theta}\beta_{3}/n \end{array}\right] $$
(6.2)

In this case the rows of H are linear dependent, r o w 1 = β 2 r o w 2−β 1 r o w 3/(β 2−β 1), and they do not span the 4-dimensional in-plane space. This accounts for the large GDOP shown in Figs. 5–6 as Δt approaches zero.

When the measure time-interval is equal to one-half the orbital period, Δt = π/n and β i = i π, i=0,1,2,3, the rows of H are

$$ H\approx\left[\begin{array}{cccc} \quad c_{\rho}\quad & \quad c_{\theta}\quad & \quad0\quad & 0\quad\\ \quad7c_{\rho}-\frac{6\pi c_{\theta}}{R}\quad & \quad c_{\theta}\quad & \quad-\frac{4c_{\theta}}{Rn}\quad & \quad\frac{4c_{\rho}R-3\pi c_{\theta}}{n}\quad\\ \quad c_{\rho}-\frac{12\pi c_{\theta}}{R}\quad & \quad c_{\theta\quad} & \quad0 & -\frac{6\pi c_{\theta}}{n}\quad\\ \quad7c_{\rho}-\frac{18\pi c_{\theta}}{R}\quad & \quad c_{\theta\quad} & \quad-\frac{4c_{\theta}}{Rn}\quad & \quad\frac{4c_{\rho}R-9\pi c_{\theta}}{n}\quad \end{array}\right] $$
(6.3)

Although it is not as obvious as in the previous case, the rows of H are again linearly dependent, r o w 1 = r o w 2−r o w 4 + r o w 3, and they do not span the 4-dimensional in-plane space. This accounts for the large GDOP “spikes” shown in Figs. 5 and 6 when Δt = π/n .

Lastly, if the \(\sin (\theta _{rel})\) and \(\cos (\theta _{rel})\) in Eq. 6.1 are expanded to second-order (𝜃 r e l ≈d/R<0.1), the rows of H for arbitrary β i (and arbitrary fixed values of Δt) are given approximately by

$$ \boldsymbol{h}^{T}(t_{i}){\Phi}(t_{i},t_{0})\approx-\frac{1}{d}\boldsymbol{K}_{\rho}^{T}(t_{i})+\frac{1}{2}\boldsymbol{K}_{\theta}^{T}(t_{i}) $$
(6.4)

and H is given by

$$ H\approx\left[\begin{array}{cccc} \quad-\frac{1}{d}\quad & \frac{1}{2} & \quad0\quad & 0\quad\\ \quad-\frac{4-3\cos\beta_{1}}{d}+\frac{3(\sin\beta_{1}-\beta_{1})}{R}\quad & \frac{1}{2} &-\frac{\sin\beta_{1}}{dn}+\frac{\cos\beta_{1}-1}{Rn}\quad & -\frac{2R(1-\cos\beta_{1})}{dn}+\frac{3(4\sin\beta_{1}-3\beta_{1})}{2n}\quad\\ \quad-\frac{4-3\cos\beta_{2}}{d}+\frac{3(\sin\beta_{2}-\beta_{2})}{R}\quad & \frac{1}{2} & -\frac{\sin\beta_{2}}{dn}+\frac{\cos\beta_{2}-1}{Rn}\quad & -\frac{2R(1-\cos\beta_{2}}{dn}+\frac{3(4\sin\beta-3\beta_{2})}{2n}\quad\\ \quad-\frac{4-3\cos\beta_{3}}{d}+\frac{3(\sin\beta_{3}-\beta_{3})}{R}\quad & \frac{1}{2} & -\frac{\sin\beta_{3}}{dn}+\frac{\cos\beta_{3}-1}{Rn}\quad & -\frac{2R(1-\cos\beta_{3})}{dn}+\frac{3(4\sin\beta_{3}-3\beta_{3})}{2n}\quad \end{array}\right] $$
(6.5)

This H is generally non-singular (as verified by the results in the figures above and below).

However, as d approaches zero (for a fixed value of Δt), H reduces to the singular matrix below

$$ H\approx\left[\begin{array}{cccc} \quad-\frac{1}{d}\quad\, & \frac{1}{2} & \quad0\quad\, & 0\quad\\ \quad-\frac{4-3\cos\beta_{1}}{d}\quad\, & \frac{1}{2} & \quad-\frac{\sin\beta_{1}}{dn}\quad\, & -\frac{2R(1-\cos\beta_{1})}{dn}\quad\\ \quad-\frac{4-3\cos\beta_{2}}{d}\quad\, & \frac{1}{2} & \quad-\frac{\sin\beta_{2}}{dn}\quad\, & -\frac{2R(1-\cos\beta_{2})}{dn}\quad\\ \quad-\frac{4-3\cos\beta_{3}}{d}\quad\, & \frac{1}{2} & \quad-\frac{\sin\beta_{3}}{dn}\quad\, & -\frac{2R(1-\cos\beta_{3})}{dn}\quad \end{array}\right] $$
(6.6)

In this case it is easier to show that the columns of H (rather than the rows) are linearly dependent, \(col_{2}=\frac {3nd}{4R}col_{4}-\frac {d}{2}col_{1}\), and thus the columns do not span the 4-dimensional in-plane space. This is an important result — for a given fixed value of Δt the GDOP will increase as the inter-satellite separation, d = R 𝜃 r e l ,becomes smaller. This accounts for the increase in the along-track GDOP shown in Fig. 5 as the inter-satellite separation is reduced.

Results - Flyby Orbits

Next consider the case where the deputy travels from a position well ahead of a chief that is in a 7000 km circular orbit to a position well behind the chief. Given the initial conditions ρ r e l (t 0)=Δh, \(\dot {\rho }_{rel}(t_{0})=0\), 𝜃 r e l (t 0)=3πΔh/2R, and \(\dot {\theta }_{rel}(t_{0})=-3n{\Delta } h/2R\), Eqs. 2.34-2.35 show that the resulting relative motion is ρ r e l (t)=Δh and 𝜃 r e l (t)=3Δh(π−n t)/2R, i.e., the deputy will pass directly over the chief after \(\frac {1}{2}\) orbital period, and final along-track position after one orbital period is 𝜃 r e l (t f )=−3πΔh/2R. Substituting these expressions for the flyby relative motion into Eq. 3.2 provides the LOS time-history as shown in Eq. 4.6 for a particular flyby altitude Δh.

The expected position GDOP in the along-track and radial direction for this case using Eqs. 5.8-5.9 is shown in Figs. 7 and 8 for several different flyby altitudes above the chief. Once again, these results are based fundamentally on the geometry of the problem and represent best case IROD performance given 4 angle measurements.

Fig. 7
figure 7

Flyby orbit along-track GDOP as a function of measurement rate Δt and the altitude of the deputy’s flyby orbit Δh for 7000 km circular orbit chief. Deputy passes over the chief after \(\frac {1}{2}\) orbital periods

Full size image
Fig. 8
figure 8

Flyby orbit radial GDOP as a function of measurement rate Δt and the altitude of the deputy’s flyby orbit Δh for 7000 km circular orbit chief. Deputy passes over the chief after \(\frac {1}{2}\) orbital periods

Full size image

Figure 7 shows that the along-track errors are relatively independent of deputy/chief separations and very dependent on Δt. The errors are seen to decrease as Δt is increased from zero and reaches a minimum in the range of 3000s<Δ5000s. Curiously, there are 3 spikes in the along-track performance, none of which seem to be a rational fraction of the orbital period. The best results occur at approximately Δt=3500 sec and ΔT=4500 sec where the along-track errors are 6 km/mrad and 3 km/mrad, respectively.

Figure 8 shows that the radial errors are also relatively independent of deputy/chief separations, and again very dependent on Δt . Similar to the along-track error, the radial error decreases as Δt is increased from zero and reaches a minimum in the range of 3000s<Δ5000s. The 3 spikes observed in the along-track error results are also found in the radial error results. The best results occur at approximately Δt=3500 sec and ΔT=4500 sec where the radial errors are approximately 1 km/mrad.

The initial conditions for the above flyby cases were modified such that the deputy passes over the chief after 1 orbital period instead of \(\frac {1}{2}\) an orbital period. The expected position GDOP in the along-track and radial direction are shown in Figs. 9 and 10 for several different flyby altitudes above the chief. The best results are approximately 10 km/mrad in the along-track direction and 1 km/mrad in the radial direction for Δt>3000 sec. While the results in the radial direction are similar to the previous case, the GDOP in the along-track direction has increased to approximately 7-10 km/mrad. While this represents a decrease in absolute performance by a factor of 2, the deputy in this case is 2 times further away from the chief . Hence, the percent error is approximately unchanged.

Fig. 9
figure 9

Flyby orbit along-track GDOP as a function of measurement rate Δt and the altitude of the deputy’s flyby orbit Δh for 7000 km circular orbit chief. Deputy passes over the chief after 1 orbital period

Full size image
Fig. 10
figure 10

Flyby orbit radial GDOP as a function of measurement rate Δt and altitude of the deputy’s flyby orbit Δh for 7000 km circular orbit chief. Deputy passes over the chief after 1 orbital period

Full size image

The initial conditions for the above flyby cases were modified again such that the deputy passes over the chief after \(1\frac {1}{2}\) orbits. The expected position GDOP in the along-track and radial directions are shown in Figs. 11 and 12 for several different flyby altitudes above the chief. Although the best results at Δt=2500 sec and Δt=5000 sec are approximately the same as in the previous cases, a spike near 4000 sec has curiously reappeared.

Fig. 11
figure 11

Flyby orbit along-track GDOP as a function of measurement rate Δt and altitude of the deputy’s flyby orbit Δh for 7000 km circular orbit chief. Deputy passes over the chief after \(1\frac {1}{2}\) orbital periods

Full size image
Fig. 12
figure 12

Flyby orbit radial GDOP as a function of measurement rate Δt and altitude of the deputy’s flyby orbit Δh for 7000 km circular orbit chief. Deputy passes over the chief after \(1\frac {1}{2}\) orbital periods

Full size image

In the previous section, an analytic examination of the rows of H for the leader-follower orbit was used to validate many of the trends in the associated GDOP results. Unfortunately, an analytic examination of the rows of H for the flyby orbit is not possible due to the dynamics nature of the flyby orbit, i.e., 𝜃 r e l and d are functions of time, and ρ c ≠ρ d .

Results - Summary

For leader-follower orbits, the along-track position determination performance improves as the deputy/chief separation is increased. The along-track position estimation performance is strongly dependent on the time-interval between measurements and is optimum when the time-interval between measurements is somewhat less than or greater than one-half orbital period. The radial position estimation performance however is nearly independent of the deputy/chief separation, but is also strongly dependent on the time-interval between measurements exhibiting the same properties as in the along-track performance. In both cases, a singularity exists when the measurement time-interval is a multiple of \(\frac {1}{2}\) the orbit period indicating that the initial state is not observable when observations are taken at this rate.

For flyby orbits where the deputy passes directly over or under the chief, the performance analysis results are markedly different. In all cases the along-track and radial position estimation performance is nearly independent of the deputy/chief initial separation and generally improves monotonically as the time between observations increases. There are also singularities at multiple measurement time-intervals indicating that the initial state is not observable when observations are taken at these rates. These singularities however have yet to be explained, but the results show that they tend to be eliminated as the initial separations between the deputy and chief are significantly increased.

More importantly, the above results show that the IROD performance with only 4 measurements for flyby and leader-follower orbits is poor when, for example, camera accuracy is on the order of 1 mrad. In general, higher camera accuracy will be required to achieve realistic IROD performance. From the standpoint of practicability, measurement accuracy on the order of 0.1 mrad is possible, while to the author’s knowledge, accuracy better than 0.01 mrad is, at this time, difficult to obtain.

Although the effects of orbital perturbation such as J2, drag, and SRP have been ignored in this analysis, these second-order effects will likely have a minimal effect on the above results except perhaps where GDOP spikes occur, i.e., the second-order perturbations may add a bit more observability to the problem.

Additionally, it must be remembered that if this analysis had been conducted using the Cartesian coordinate formulation of the CWH equations, there would be no results to present – the problem would be deemed unobservable and the GDOP would have been infinity for all cases.

Finally, since all of the GDOP results are based on the geometry of the relative deputy/chief positions at 4 measurements times, the above results for a 7000 km LEO orbit can be scaled to obtain the results for any arbitrary circular chief orbit. For example, the GDOP results for a 42,000 km GEO leader-follower and flyby orbits can be obtained by scaling the LEO results by a factor of 42,000 km/7000 km = 6. This can be seen in the GDOP equations in Eqs. 5.1–5.9.

Conclusions

While a rigorous observability proof for the angles-only relative orbit determination problem in cylindrical coordinates has not been provided in this paper, the empirical evidence shows that the problem is observable when formulated with linearized dynamics and nonlinear measurements in cylindrical coordinates. In contrast to the Cartesian coordinates formulation, cylindrical coordinates preserve more information about the curvature of the orbits. This is primarily due to the fact that the magnitude of the relative downrange angular displacements are unrestricted in the linearized equations of motion. The evidence provided indicates full-relative-state observability, including the problem of relative range observability.

The preliminary IROD performance analysis presented in this paper shows that IROD solutions are achievable for leader-follower and flyby orbits with only 4 measurement (for the in-plane case). However, measurement accuracy on the order of 1 mrad will not yield very good performance. For example, if the measurement error is equal to 1 mrad the expected best case relative orbit determination performance for a chief in a 7000 km LEO orbit and a deputy in a nearby leader-follower or flyby orbit is on the order of 1 km of position error in the radial direction and 4 km in the along-track direction. The analysis also shows that performance is highly dependent on the time-interval between measurements. For GEO orbits, performance is reduced further by a factor of approximately R G E O /R L E O =6. In general, camera accuracy greater than 1 mrad will be required to achieve realistic IROD performance for LEO and GEO leader-follower and flyby orbits. However, this may be problematic since while measurement accuracy on the order of 0.1 mrad is possible, to the author’s knowledge, accuracy better than 0.01 mrad is, at this time, difficult to obtain.