Computational Analysis of Unsteady MHD Flow of Third Grade Fluid Between Two Infinitely Long Porous Plates

Abstract

In current work the unsteady MHD flow behaviour of a fluid of grade three between two infinitely long flat porous plates is scrutinized where the top lamina is fixed and the lower lamina moves with a velocity which vary with respect to time. Then the non linear p.d.e governing the flow behaviour are reduced to a system of algebraic equations using fully implicit finite difference scheme and numerical solution is obtained using damped-Newton method, which is then coded using MATLAB programming. Influence on velocity with variations in m, $\alpha$, $\gamma$, Re is interpreted through different graphical representation.

1 Introduction

Due to substantial use of non-Newtonian fluids in the field of industry and engineering, the modern research has captivated the attention of number of researchers in this field. A sole paradigm exhibiting every aspect of non-Newtonian fluids is unobtainable, because of which different non-Newtonian models and constitutive equations have been recommended. Second grade fluid model is one of the simplest model which is capable of predicting normal stress differences, but lacks the shear thinning and thickening property of the non-Newtonian fluids described by Joseph and Fosdick [1] which became a motivation for many researchers like Fosdick and Rajagopal [2], Erdogan [3], Ariel [4, 5], Sahoo and Poncet [6], Nayak et al. [7, 8], Awais [9], Samuel and Falade [10], Hayat et al. [11], Okoya [12].

Recently Carapau and Corria [13] have analysed the numerical solution of a third grade fluid in a tube through a contraction. Using numerical simulation they analysed the unsteady flow over a finite set or a tube with performed contraction. Saadatmandi et al. [14] used notion of Chebyshev polynomials and rational Legendre functions for numerical solution. He used the specific features of RLC, ChFD techniques to lessen the computation to a few algebraic equations and made a comparison between the result obtained by this method to results obtained by other techniques which manifested its competent accuracy and rate of convergence. Akinshilo [15] examined the stationary flow and analysed the conduction of heat transfer of fluid of grade three in the porous medium and solution was obtained to the arising non linear differential equation using a domain method. He studied the influence of thermal fluidic parameter on the flow and heat transfer, and discovered the inverse variation of porosity term and velocity distribution, and direct variation of heat and temperature distribution towards the upper plate and revealed its diverse application.

Here, we make an attempt to analyse the unsteady magnetohydrodynamics fluid flow of grade three passing through two infinitely long porous plates. The bottom plate moves instantaneously with a velocity that varies with time in its own plane in the presence of a uniform magnetic field applied transversely. After attaining a numerical solution for the problem, the influence of various physical parameters on momentum boundary layers is audited through several graphs.

The technique used here is a powerful tool to solve strong non-linear complex problem numerically for small as well as large values of elastic parameters and also handle large system of equations with insignificant cost of time which might be difficult to solve analytically. Also derivation of entire problem need not be required for every change of boundary conditions. Due to the benefits of its mathematical features and advantages of its application, the present study is worthwhile and has not been analysed by any above cited researcher to the best of my knowledge.

A brief synopsis of our work is illustrated consecutively. Section 2 is concerned with framing of the problem. Section 3 focuses on the solution strategy. Section 4 reviews influence of several parameters on the velocity field, with magnetic field being present, with the aid of graphical representations followed by the epilogue.

2 Devising the Problem

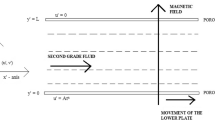
We choose $x^{'}$ along the lower wall and $y^{'}$ axis perpendicular to it. It is presumed that the walls are unbounded either side of the $x^{'}$ axis, where the top lamina is stationary and the lower plate moves suddenly with a velocity which vary with time.

Since both the plates are porous we represent the velocity of suction/injection by a constant V.

We denote $u^{'}$, $v^{'}$, the constituents of velocity in the domain of flow at any point $(x^{'} ,y^{'})$ by

$$\begin{aligned} u^{'} = u^{'}(y^{'},t^{'}) \ , \ v^{'} = V. \end{aligned}$$

(1)

The cauchy stress P for an incompressible homogeneous and thermodynamically accordant with fluid of grade three by Fosdick and Rajagopal [2] is given as

$$\begin{aligned} P = -pI + \mu A_{1} +\alpha _{1}A_{2}+\alpha _{2}{A_{1}^{2}} + \beta _{3}(tr {A_{1}^{2}})A_{1}. \end{aligned}$$

(2)

where $A_{1}$, $A_{2}$ are first two tensors by Rivlin and Ericson [16].

$\mu$ = Viscosity.

$\alpha _{1}, \ \alpha _{2}, \ \beta _{3}$ are the elastic parameters of second order and third order respectively.

p = Pressure.

I = Identity Tensor.

Under these physical assumptions and the stress components given in equation(2), the equation of momentum for the fluid of grade three becomes

$$\begin{aligned} \rho \Bigg (\frac{\partial u^{'}}{\partial t^{'}} + V\frac{\partial u^{'}}{\partial y^{'}}\Bigg )= \mu \frac{\partial ^{2} u^{'}}{\partial y^{'2}} + \alpha _{1}\frac{\partial ^{3} u^{'}}{\partial y^{'2}\partial t^{'}} + 6\beta _{3}\frac{\partial ^{2} u^{'}}{\partial y^{'2}} {\frac{\partial u^{'}}{\partial y^{'}}^{2}} + \alpha _{1}V\frac{\partial ^{3} u^{'}}{\partial y^{'3}} - \sigma {\beta _{0}^{2}}u^{'}. \end{aligned}$$

(3)

Equation (3) is subjected to the subsequent conditions

$$\begin{aligned} \begin{aligned} t^{'} = 0 : u^{'} = 0, \ \ \ \forall y^{'}, \\ t^{'} > 0:\ \ \ u^{'} = At^{n}\ \ \ \ \text {for} \ y^{'} = 0, \\ u^{'} = 0, \ \ \text {for} \ y^{'} = 1. \end{aligned} \end{aligned}$$

(4)

The dimensionless variables and parameters are introduced as:

$u = \frac{u^{'}}{A}, \ y = \frac{y^{'}}{\sqrt{\nu _{1}T}}, \; t = \frac{t^{'}}{T}$

$\text {Re}= \frac{V\sqrt{T}}{\sqrt{\nu _{1}}}, \ \alpha = \frac{\alpha _{1}}{\rho \nu _{1}T}, \ \gamma = \frac{6\beta _{3}A^{2}}{\rho \nu _{1}^{2}T}, \ m^{2} = \frac{\sigma \beta _{0}^{2}T}{\rho }$

$\nu _{1} = \frac{\mu }{\rho }$ , is the kinematic viscosity, m is Hartmann number,

Re = Reynolds number, $\alpha$ = visco-elastic parameter, $\gamma$ = third grade elastic parameter, T = Time, $\sigma$ = conductivity of the medium, $\beta _{0}$ = Magnetic Strength, A = constant, $\rho$ = Density of fluid, $\mu$ = dynamic viscosity.

The above notations are employed in the equation of motion (3) to obtain the following dimensionless form

$$\begin{aligned} \frac{\partial u}{\partial t} +\text {Re}\frac{\partial u}{\partial y} = \frac{\partial ^{2} u}{\partial y^{2}} + \alpha \frac{\partial ^{3}u}{\partial y^{2} \partial t} +\text {Re }\alpha \frac{\partial ^{3}u}{\partial y^{3}} + \gamma {\bigg (\frac{\partial u }{\partial y}}\bigg )^2 \frac{\partial ^{2} u}{\partial y^{2}} - m^{2}u. \end{aligned}$$

(5)

along with the subsequent conditions

$$\begin{aligned} \begin{aligned} t = 0 : u = 0 \ , \ \forall \ y, \\ t > 0 : u = t^{n}, \ \ \text {for} \ y = 0,\\ u = 0 \ \ \text {when} \ y = 1. \end{aligned} \end{aligned}$$

(6)

3 Solution Strategy

The solution strategy is discussed as follows.

3.1 Finite Difference Method

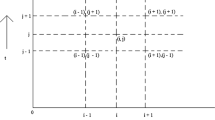
Equation (5) is solved by implementing the crank-Nickolson type implicit finite difference scheme for space discretization and time discretization with a uniform mesh of space step h and time step k. The obtained difference scheme is represented as

$d_{1i}^{j} = u_{i+1}^{j} - u_{i-1}^{j}$.

$d_{2i}^{j} = u_{i+1}^{j} - 2u_{i}^{j} + u_{i-1}^{j}$.

$d_{3i}^{j} = -u_{i-2}^{j} + 2u_{i-1}^{j }- 2u_{i+1}^{j} + u_{i+2}^{j}$.

$d_{3i}^{'j} = -3u_{i-1}^{j} + 10u_{i}^{j} - 12u_{i+1}^{j} + 6u_{i+2}^{j} - u_{i+3}^{j}$.

$d_{3i}^{''j} = u_{i-3}^{j} - 6u_{i-2}^{j} + 12u_{i-1}^{j} - 10u_{i}^{j} + 3u_{i+1}^{j}$.

We use the following notations for difference approximations for the derivatives $(ih,j\triangle t)$, $i = 0(1)N+1$ and $j = 0(1)M-1$ as

$$\begin{aligned}&\frac{\partial u}{\partial t} \approx \frac{u_{i}^{j+1} - u_{i}^{j}}{\triangle t}. \nonumber \\&\frac{\partial u}{\partial y} \approx \frac{1}{4h}(d_{1i}^{j+1}+d_{1i}^{j}).\nonumber \\&\frac{\partial ^{2} u}{\partial y^{2}} \approx \frac{1}{2h^{2}}(d_{2i}^{j+1} + d_{2i}^{j}).\nonumber \\&\frac{\partial ^{3}u}{\partial y^{3}} \approx \frac{1}{2h^{3}} (d_{3i}^{j+1} + d_{3i}^{j}) \ \ , \ i\ne 1,N.\nonumber \\&\frac{\partial ^{3}u}{\partial y^{2} \partial t} \approx \frac{(d_{2i}^{j+1} - d_{2i}^{j})}{h^{2}\triangle t}. \end{aligned}$$

(7)

The third order derivative $\frac{\partial ^{3}u}{\partial y^{3}}$ is substituted by $\frac{1}{2h^{3}} (d_{3i}^{' j+1} + d_{3i}^{ ' j})$ and $\frac{1}{2h^{3}} (d_{3i}^{'' j+1} + d_{3i}^{ '' j})$ at nodes $(1,j\triangle t)$, $(N,j\triangle t)$ respectively. The fully implicit finite difference scheme used here is unconditionally stable and satisfy second order convergence in time as well as in space.

Using the above differences for the partial derivatives, the governing velocity equation is written as

$$\begin{aligned} \begin{aligned} \frac{u_{i}^{j+1} - u_{i}^{j}}{\triangle t} + \frac{\text {Re}}{4h}(d_{1i}^{j+1}+d_{1i}^{j}) = \frac{1}{2h^{2}}(d_{2i}^{j+1} + d_{2i}^{j}) + \frac{\alpha }{h^{2}\triangle t}(d_{2i}^{j+1} - d_{2i}^{j}) \\ +\frac{\text {Re }\alpha }{2h^{3}}(d_{3i}^{j+1} + d_{3i}^{j}) + \frac{\gamma }{32h^{4}}{(d_{1i}^{j+1}+d_{1i}^{j})^{2}}(d_{2i}^{j+1} + d_{2i}^{j}) - m^{2} \frac{u_{i}^{j+1} + u_{i}^{j}}{2}. \end{aligned} \end{aligned}$$

(8)

along with the subsequent conditions in discretized form are

$$\begin{aligned} \begin{aligned} u_{i}^{0} = 0, \ \ i=0(1)N+1 ,\\ u_{0}^{j} = (j\triangle t)^{n} \ \ \ \text {and}, \\ u_{N+1}^{j} = 0, \ \ \ j =1(1)M. \end{aligned} \end{aligned}$$

(9)

The approximate choice of M is made according to the algorithm given in Jain [17], where the choice of N is made in such a way, to impose the boundary conditions at infinity so that the modulus value of the difference between the two solutions obtained by presuming the boundary conditions at infinity to hold at $((N+1)h, j\triangle t)$ and $((N+2)h, j\triangle t)$ successively, and their difference becomes less than a prescribed error $\epsilon$.

The system of non-linear equations for velocity (8) is solved using above mentioned numerical scheme, where the said method gives the quadratic convergent result for sufficiently good choice of initial solution. For better choice of initial velocity, equation of motion is arranged in tridiagonal form after making the parameter values $\alpha , \gamma , \text {and}\ m$ to zero in Eq. (8) and solution is obtained using special form of Gaussian elimination method. For applying the damped-Newton method we evaluate the residuals $(R_{i}$, where i ranges from 1 to N and the elements in Jacobian matrix $\Big (\frac{\partial R_{i}}{\partial u_{j}}\Big )$, $i = 1(1)N$ and $j = 1(1)M$ that are not equal to zero. A new approximated solution is accepted as $x^{k+1} = \Big (x^{k}+\frac{h}{2^{i}}\Big )$ for that i, where $i = \min$ $\Bigg ({j} : 0 \le j \le j_{\max } \mid {\parallel \text { residue }(x^{k}+\frac{h}{2^{j}})\parallel }_{2} < {\parallel \text { residue} (x^{k}) \parallel }_{2}\Bigg )$.

This ensures that the residual error decreases in each iteration, which guarantees about the convergence of the scheme. The MATLAB coding is verified with the existing result in Conte De Boor [18] and found exact upto fifth decimal place.

4 Results and Discussion

The flow characteristics for the concerned problem is investigated through several graphs depicted in Fig. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10.

Fig. 1

Influence on velocity with variations in m when $\alpha$ = 3, $\gamma$ = 4, Re = 7

Fig. 2

Influence on velocity with variations in m when $\alpha$ = 3, $\gamma$ = 4, Re = 8

Fig. 3

Influence on velocity with variations in m when $\alpha$ = 0, $\gamma$ = 0, Re = 8

Fig. 4

Influence on velocity with variations in $\alpha$ when $\gamma$ = 4, Re = 8, m = 9

Fig. 5

Influence on velocity with variations in $\alpha$ when, $\gamma$ = 4, Re = 8, m = 8

Fig. 6

Influence on velocity with variations in $\alpha$ when $\gamma$ = 2, Re = 9, m = 8

Fig. 7

Influence on velocity with variations in $\gamma$ when, $\alpha$ = 3, Re = 8, m = 8

Fig. 8

Influence on velocity with variations in $\gamma$ when $\alpha$ = 3, Re = 8, m = 8

Fig. 9

Influence on velocity with variations in Re when $\alpha$ = 3, $\gamma$ = 3, m = 8

Fig. 10

Effect on velocity with variations in Re when, $\alpha$ = 0.01, $\gamma$ = 1, m = 7

It is observed from Figs. 1 and 2 that the increase in the parametric values of the Hartmann number (m) leads to increase in Lorentz force of the fluid, which causes increase of resistance to the flow velocity and as a result velocity decelerates through out the flow field. A similar effect from Fig. 3 is also obtained for Newtonian fluid i.e, when $\alpha$ and $\gamma$ are considered as zero.

Visco-elasticity of the fluid rises, with increase of the visco-elastic parameter ($\alpha$) values, that gives rise to reduction of velocity in the entire flow field, for both less and bigger values of $\alpha$. When the values of elastic parameter $\alpha$ is small, the influence of it on velocity is quite opposite, when damping magnetic strength value is 8 or less.

The effect of non-newtonian parameter $\gamma$ on the velocity field is seen from Figs. 7 and 8. For large values of $\gamma$ ($\gamma > 1$), a sudden rise in the velocity field is observed near the plate, but there is a decrease in velocity through out the domain field, with an increase in the parametric value $\gamma$. For $\gamma < 1$, with other parameters kept fixed, the decreasing effect on velocity seems to be insignificant near the plates and gradually becomes noticeable at a considerably far distance from the plate and again appears to diminish.

Figure 9 shows that velocity profile gradually slows down with increase in the suction parameter Re. A similar behaviour is observed for smaller values of Re, shown in Fig. 10, which is obtained by reducing values of elastic parameters as well as magnetic factor.

5 Conclusion

The present study is concerned with the numerical study of a time- dependent flow of a third grade fluid passing through two infinite parallelly placed plates is investigated with the magnetic field being present. Using above mentioned scheme the governing constitutive equation of motion is converted into system of non-linear algebraic equations and is solved numerically using highly convergent aforesaid method and presented graphically.

The principal and noteworthy finding of this investigation is that the increase in Hartmann number m substantially decrease velocity profile, however the fluid shows newtonian or non-Newtonian behaviour. With increase of Re, $\alpha$, and $\gamma$ slow down the fluid motion both for large and small values of the parameters. For very small values of visco-elastic parameter $\alpha$, when we decrease the value of magnetic strength, a reduction in the fluid viscosity is noticed which minimises the resistance to flow velocity, resulting in remarkable gradual enhancement in velocity of the fluid. Hence it is apparent that velocity profile is controlled with proper variations of parameters $\alpha$ and m.