Keywords

1 Introduction

There are numerous fluids in the industry as well as technology whose performance fails to be described by the classical linearly viscous Newtonian fluid model. The divergence from the Newtonian comportment demonstrates itself in an assortment of manners: non-Newtonian viscosity, stress relaxation, non-linear creeping, development of normal stress differences, and yield stress. The Navier–Stokes equations are insufficient to prognosticate the activities of such a category of fluids, consequently multitudinous significative associations of non-Newtonian fluids. These substantial relations yields ascend to the differential equations, which, in comprehensive are higher perplexed and higher order compared with Navier–Stokes equations. For that reason, it is complicated to attain exact analytical solutions for Kuvshinski fluids.

Reddy et al. [1] have scrutinized radiation assimilation and Kuvshinski fluid model on unsteady MHD free convective flow all the way through an infinite non-parallel porous plate in the existence of chemical effect and heat source. Sakthikala et al. [2] investigated the influence of Kuvshinski fluid model on unsteady free convective fluid flow through an infinite moving porous plate by means of dependable as well as variable temperatures. Reddy et al. [3] examined the influence of Soret and Kuvshinski type fluid on MHD natural convective flow inside a porous medium through a semi-infinite non-parallel moving plate with heat source. In this examination, perturbation technique was employed for solving the governing equations. Buggaramulu et al. [4] have reported visco-elastic fluid model on unsteady MHD-free convective fluid stream through a porous medium in the existence of chemical effect and radiation.

Devasena et al. [5], Reddy et al. [6] and VidyaSagar et al. [7] have analyzed analytically the influence of Kuvshinski fluid on unsteady MHD natural convective flow with radiation absorption. Sharma et al. [8] have examined influence of stratified Kuvshinski fluid on MHD free convective stream through a non-parallel porous plate by means of heat and mass transfer. Chamkha [9] and Hady et al. [10] have analyzed unsteady natural convective flow through a semi-infinite porous moving plate by means of heat absorption. Hossian et al. [11] have discussed the problem of natural convection flow along a non-parallel wavy surface by means of uniform surface temperature in the existence of heat generation/absorption. Chamkha et al. [12], Muthucumaraswamy et al. [13] and Ibrahim et al. [14] investigated the influence of heat generation and chemical reaction on MHD unsteady free convection flow over perpendicular moving porous plate.

All these studies paid attention towards MHD unsteady free convection flow of Kuvshinski fluid past an inclined surface, where thermal radiation, radiation absorption, chemical reaction, heat generation, and aligned magnetic impacts are contemplated. The predominant purpose is to scrutinize the unsteady MHD free convection flow of Kuvshinski fluid past a moving inclined plate with heat production in the demeanor of mass blowing or suction and with the special effects of aligned magnetic, chemical reaction, thermal radiation, and radiation absorption.

2 Mathematical Formulation

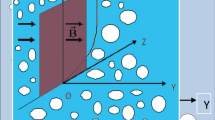
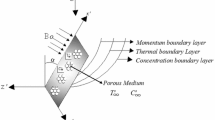
Let us contemplate the 2D unsteady MHD free convection Kuvshinski fluid flow through a semi-infinite inclined moving porous plate in a uniform porous medium under the sway of a uniform magnetic field, radiation absorption, chemical effect, heat generation and thermal radiation. Here x*-axis is taken along the porous plate in the upward direction and y*-axis perpendicular to it. The fluid is to be gray, absorbing—emitting however non-scattering medium. In the x*-way, the radiative heat flux is significantly small against to that in the y*-direction. Each and every flow variable excluding pressure are functions of y* and t* only. The plate in x*-direction is of infinite length. The induced magnetic field is insignificant. The size of the porous plate is large compared to typical microscopic length scale of the porous medium. Chemical reactions occur in the flow.

figure a

Under these suppositions, the governing equations are

$$\frac{{\partial v^{*} }}{{\partial y^{*} }} = 0$$
(1)
$$\begin{aligned} \left( {1 + \lambda_{1}^{*} \frac{\partial }{{\partial t^{*} }}} \right)\,\frac{{\partial u^{*} }}{{\partial t^{*} }} + V^{*} \frac{{\partial u^{*} }}{{\partial y^{*} }} & = \left( {1 + \lambda_{1}^{*} \frac{\partial }{{\partial t^{*} }}} \right)\frac{{\partial U_{\infty }^{*} }}{{\partial t^{*} }} + \nu \frac{{\partial^{2} U^{*} }}{{\partial y^{*2} }} \\ & \quad + g\beta \cos \phi \left( {T^{*} - T_{\infty }^{*} } \right) + g\beta^{*} \cos \phi \left( {C^{*} - C_{\infty }^{*} } \right) \\ & \quad + \left( {\frac{{\sigma B_{0}^{2} \sin^{2} \xi }}{\rho } + \frac{\nu }{{K^{*} }}} \right)\left( {1 + \lambda_{1}^{*} \frac{\partial }{{\partial t^{*} }}} \right)\left( {U_{\infty }^{*} - u^{*} } \right) \\ \end{aligned}$$
(2)
$$\begin{aligned} \frac{{\partial T^{*} }}{{\partial t^{*} }} + V^{*} \frac{{\partial T^{*} }}{{\partial y^{*} }} & = \frac{k}{{\rho C_{\text{p}} }}\frac{{\partial^{2} T^{*} }}{{\partial y^{*2} }} + \frac{{Q_{0} }}{{\rho C_{\text{p}} }}(T^{*} - T_{\infty }^{*} ) \\ & \quad - \frac{{16\sigma^{*} T_{\infty }^{{*^{3} }} }}{{3\rho C_{\text{p}} K_{1}^{*} }}\frac{{\partial^{2} T^{*} }}{{\partial y^{*2} }} - \frac{{R_{1}^{*} }}{{\rho C_{\text{p}} }}(C^{*} - C_{\infty }^{*} ) \\ \end{aligned}$$
(3)
$$\frac{{\partial C^{*} }}{{\partial t^{*} }} + V^{*} \frac{{\partial C^{*} }}{{\partial y^{*} }} = D_{\text{m}} \frac{{\partial^{2} C^{*} }}{{\partial y^{*2} }} - R^{*} (C - C_{\infty }^{*} )$$
(4)

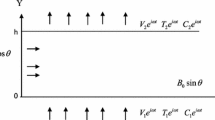
The conditions at the boundary are

$$\begin{aligned} u^{*} & = u_{\text{p}}^{*} ,\quad T^{*} = T_{\infty }^{*} + \in (T_{w}^{*} - T_{\infty }^{*} )\,{\text{e}}^{{n^{*} t^{*} }} , \\ C^{*} & = C_{w}^{*} + \in (C_{w}^{*} - C_{\infty }^{*} )\,{\text{e}}^{{n*t^{*} }} \;{\text{at}}\;y = 0 \\ \end{aligned}$$
(5)
$$u^{*} \to u_{\infty }^{*} = U_{0} (1 + \in {\text{e}}^{{n^{*} t^{*} }} ),\quad T^{*} \to T_{\infty }^{*} ,\quad C^{*} \to C_{\infty }^{*} \;{\text{at}}\;y \to \infty$$
(6)

Let us suppose that in the direction of the fluid flow, the porous plate moves by a stable velocity \(u_{p}^{*}\) and the free stream velocity \(U_{\infty }^{*}\) abide by exponentially increasing small perturbation law. In addition, the temperature, concentration and the suction velocity are exponentially varying with time. It is clear from Eq. (1) that the suction velocity at the plate surface is a function of time only and it takes the following form

$$V^{*} = - V_{0} \left( {1 + \in A{\text{e}}^{{n^{*} t^{*} }} } \right)$$
(7)

where A is a real positive constant \(\in\) and \(\in A\) are small and less than unity and V0 is a scale of suction velocity which is a non-zero positive constant.

Let us set the dimensionless variables as follows:

$$\begin{aligned} u & = \frac{{u^{*} }}{{U_{0} }},v = \frac{{v^{*} }}{{V_{0} }},y = \frac{{y^{*} V_{0} }}{v},U_{\infty }^{*} = U_{\infty } U_{0} , \\ u_{p}^{*} & = U_{p} U_{0} ,t = \frac{{t^{*} V_{0}^{2} }}{v},n = \frac{{n^{*} v}}{{V_{0}^{2} }}, \\ \theta & = \frac{{T^{*} - T_{\infty }^{*} }}{{T_{w}^{*} - T_{\infty }^{*} }},C = \frac{{C^{*} - C_{\infty }^{*} }}{{C_{w}^{*} - C_{\infty }^{*} }}, \\ {\text{Gr}} & = \frac{{vg\beta (T_{w}^{*} - T_{\infty }^{*} )}}{{V_{0}^{2} U_{0} }},{\text{Gm}} = \frac{{vg\beta^{*} (C_{w}^{*} - C_{\infty }^{*} )}}{{V_{0}^{2} U_{0} }}, \\ K & = \frac{{K^{*} V_{0}^{2} }}{{\nu^{2} }},S = \frac{{\phi_{0} \nu^{2} }}{{\kappa V_{0}^{2} }},\Pr = \frac{\mu Cp}{\kappa }{\text{Ra}} = R_{1}^{*} \left( {\frac{{C_{\omega }^{*} - C_{\infty }^{*} }}{{T_{\omega }^{*} - T_{\infty }^{*} }}} \right)\frac{{\nu^{2} }}{{V_{0}^{2} }} \\ \lambda_{1} & = \frac{{\lambda_{1}^{*} V_{0}^{2} }}{\nu },R = \frac{{4\sigma^{*} T_{\infty }^{{*^{3} }} \nu^{2} }}{{K_{1} \kappa V_{0}^{2} }},K_{\text{r}} = \frac{{R^{*} \nu }}{{\nu_{0}^{2} }},S_{\text{e}} = \frac{\nu }{{D_{\text{m}} }} \\ \end{aligned}$$
(8)

Substituting the Eq. (8) into Eqs. (2), (3) and (4), we obtain

$$\begin{aligned} \left( {1 + \lambda_{1} \frac{\partial }{\partial t}} \right)\frac{\partial u}{\partial t} - \left( {1 + \in A{\text{e}}^{nt} } \right)\frac{\partial u}{\partial y} & = \left( {1 + \lambda_{1} \frac{\partial }{\partial t}} \right)\frac{{{\text{d}}U_{\infty } }}{{{\text{d}}t}} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + {\text{Gr}}_{1} \theta + {\text{Gm}}_{1} C \\ & \quad + N\left( {1 + \lambda_{1} \frac{\partial }{\partial t}} \right)\left( {U_{\infty } - u} \right) \\ \end{aligned}$$
(9)
$$\frac{\partial \theta }{\partial t} - (1 + \in Ae^{nt} )\frac{\partial \theta }{\partial y} = \frac{1}{\Pr }\left( {1 + \frac{4R}{3}} \right)\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + \frac{S}{\Pr }\theta - \frac{\text{Ra}}{\Pr }C$$
(10)
$$\frac{\partial C}{\partial t} - (1 + \in A{\text{e}}^{nt} )\frac{\partial C}{\partial y} = \frac{1}{Sc}\frac{{\partial^{2} C}}{{\partial y^{2} }} - {\text{Kr}}C$$
(11)

The corresponding boundary conditions are

$$u = U_{\text{P}} ,\theta = 1 + \in {\text{e}}^{nt} ,C = 1 + \in {\text{e}}^{nt} \;,{\text{at}}\,{\text{y = 0}}$$
(12)
$$u \to U_{\infty } = 1 + \in {\text{e}}^{nt} ,\theta \to 0,C \to 0\;{\text{as}}\,y \to \infty$$
(13)

where, \(N = M\,\sin^{2} \,\xi + \frac{1}{K}.\,{\text{Gr}}_{1} = {\text{Gr}}\,{ \cos }\phi ,\quad {\text{Gm}}_{1} = {\text{Gm}}\,{ \cos }\phi\).

3 Solution of the Problem

To solve the Eqs. (9)–(11) subject to the boundary conditions (12) and (13), we apply the perturbation technique. Let the velocity, temperature and concentration fields as

$$\begin{aligned} u & = u_{0} (y) + \in {\text{e}}^{nt} u_{1} (y) + O( \in^{2} ) \\ \theta & = \theta_{0} (y) + \in {\text{e}}^{nt} \theta_{1} (y) + O( \in^{2} ) \\ C & = C_{0} (y) + \in {\text{e}}^{nt} C_{1} (y) + O( \in^{2} ) \\ \end{aligned}$$
(14)

Using (14) in Eqs. (9)–(11) and comparing the coefficients of the same degree terms and neglecting terms of 0(∈2), a set of ODE are obtained and on solving, the following solutions are obtained.

$$\begin{aligned} u(y,t) & = \left( {1 + L_{1} {\text{e}}^{{ - l_{1} y}} + P_{7} {\text{e}}^{{ - R_{1} y}} + P_{8} {\text{e}}^{{ - R_{3} y}} } \right) + \in {\text{e}}^{nt} \\ & \quad \left( {1 + L_{2} {\text{e}}^{{ - l_{2} y}} + P_{9} {\text{e}}^{{ - l_{1} y}} + P_{10} {\text{e}}^{{ - R_{1} y}} + P_{11} {\text{e}}^{{ - R_{2} y}} + P_{12} {\text{e}}^{{ - R_{3} y}} + P_{13} {\text{e}}^{{ - R_{4} y}} } \right) \\ \end{aligned}$$
(15)
$$\begin{aligned} \theta (y,t) & = \left( {P_{2} {\text{e}}^{{ - R_{1} y}} + \left( {1 - P_{2} } \right){\text{e}}^{{ - R_{3} y}} } \right) \\ & \quad + \in e^{nt} \left( {P_{3} {\text{e}}^{{ - R_{1} y}} + P_{4} {\text{e}}^{{ - R_{2} y}} + P_{5} {\text{e}}^{{ - R_{3} y}} + P_{6} {\text{e}}^{{ - R_{4} y}} } \right) \\ \end{aligned}$$
(16)
$$C (y,t) = e^{{ - R_{1} y}} + \in e^{nt} \left( {\left( {1 - P_{1} } \right)e^{{ - R_{2} y}} + P_{1} e^{{ - R_{1} y}} } \right)$$
(17)

Shear Stress: The skin friction at the plate y = 0 in terms of shear stress is given by

$$\begin{aligned} \tau = \left. {\frac{ - \partial u}{\partial y}} \right|_{y = 0} & = \left( {l_{1} L_{1} + R_{1} P_{7} + R_{3} P_{8} } \right) \\ & \quad + \in {\text{e}}^{nt} \left( {l_{1} L_{2} + l_{1} P_{9} + R_{1} P_{10} + R_{2} P_{11} + R_{3} P_{12} + R_{4} P_{13} } \right) \\ \end{aligned}$$
(18)

4 Results and Discussion

From analytical solutions, the numerical values for velocity, temperature, concentration, skin friction, Nusselt number as well as Sherwood number are computed by fixing diverse values of the non-dimensional parameters in the problem, i.e., n = 0.2, A = 1, ε = 0.002, t = 1, S = 0.01, Ra = 1, R = 1, Pr = 0.71, M = 1, Sc = 0.60, Gr = 5, Gm = 3, Kr = 1, Up = 1, K = 5, \(\lambda_{1}\) = 1, \(\phi = \frac{\pi }{6}\) and \(\xi = \frac{\pi }{6}\).

Figure 1 illustrated the effects on velocity of magnetic field M as well as Prandtl number Pr for cooling of the plate (Gr > 0). The velocity declined for both water (Pr = 7) as well as air (Pr = 0.71). The reason is that the magnetic field generates Lorentz force which resists the fluid flow and hence velocity falls. From Fig. 2: it is lucid that the velocity diminishes with the rise of aligned angle \(\xi\) for the reason that the influence of the applied magnetic field is higher while aligned angle accentuates. From Fig. 3, it is observed that fluid velocity decreases with the increase of angle \(\phi\). If the plate is inclined, as a result of gravity components, the buoyancy effect decrements and consequently the fluid has higher velocity for vertical surface (\(\phi\) = 0) as against that of inclined surface. The influence of radiation, heat absorption as well as absorption radiation parameters on the temperature field is revealed in Fig. 4. It is perceived that the temperature rises with the rise in radiation and radiation absorption parameters.

Fig. 1
figure 1

Velocity profiles for different values of M and Pr

Full size image
Fig. 2
figure 2

Velocity profiles for different values of \(\xi\)

Full size image
Fig. 3
figure 3

Velocity profiles for different values of ϕ

Full size image
Fig. 4
figure 4

Temperature profiles for different values of R, S, and Ra

Full size image

Conclusions

  • The velocity declines, with the incremental values of magnetic field.

  • The temperature rises with the rise in thermal radiation and radiation absorption and the skin friction rise with the rise in solutal Grashof number.

  • The rise of aligned angle or angle of inclination leads to a decrease in fluid velocity (Table 1).

    Table 1 Skin friction coefficient when Kr = R = Ra = \(\phi\) = \(\xi\) = \(\lambda_{1}\) = 0
    Full size table

Validation of the results: In this examination, the outcomes obtained herein are compared with the results of Chamkha [9] in the absence of Kr, R and Ra on skin friction τ for different values of Gm. The consequences of this comparison are in good agreement with Chamka [9].