Dichotomy: Trajectory Planning Algorithm Based on Point Group Distribution

Abstract

The historical navigation trajectory carries rich information about the spatiotemporal patterns of a moving target, as well as its transboundary potentials. To obtain the moving track of a ship or a plane, a large amount of point-to-point data is required via the measurements of satellites or aviation equipments. On the basis of time, we can easily draw a track. However, the distribution of the point-to-point data information provided by each detection unit is irregular due to the inconsistency of the standards of the data units. Some of the regional point groups are densely distributed, while the others may be very sparse. The point density can mess up the trajectory detection and make it not ideal to observe the behavior habits of a target unit. In this study, a dichotomy trajectory planning algorithm was proposed to fix the problem mentioned above. The target area was set as a grid with the points in the grid dichotomized. In that case, the distribution of the targeted point group after dichotomization can perform as similar as possible, and an approximate trajectory line was formed. Such a method considers the change of point density. Results were tested against the performance of the clustering, the random, and the greedy methods, showing that the former had a better adaptability in dealing with different data distribution. In this paper, a novel approximate estimation algorithm based on the density change rate is proposed. Finally, we will compare the performance of our dichotomous method with clustering method, random method, and greedy algorithm through experiments and show the trajectory fitting effect through different distribution data.

1 Introduction

With the rapid development of wireless communication technology, mobile terminals, and mobile positioning, the trajectories of a large number of moving targets (aircraft, ships, etc.) through mobile terminals such as smart phones and navigators can be obtained. This allows people to pay attention to spatiotemporal evolution patterns for moving targets. The goal of spatiotemporal data mining is to acquire trajectory knowledge of moving objects and provide effective decision support for modern aviation, navigation, intelligent transportation, and other directions [1,2,3]. However, due to the accuracy of equipment, weather conditions, human factors, and so on, the derived trajectory would be redundant and chaotic, which is inconvenient for geographic information system technicians to analyze whether navigation behaviors of a ship and aircraft violate relevant laws or regulations.

Generally, the point-scale trajectory analysis methods mainly include clustering analysis [4, 5], correlation analysis [6, 7], and anomaly detection [8, 9]. The purpose of clustering is to detect out the similar objects from different classes. At present, the widely used clustering algorithms are k-means, hierarchical clustering, and density clustering. For trajectory data, clustering is indeed a method of normal moving object motion rules and behavior habits; but in different scenarios, they have their own advantages and disadvantages. For example, k-means clustering is simple, fast deal with large data sets. This algorithm maintains scalability and efficiency. When the cluster is close to the Gauss distribution, its performance is better. However, if there are outliers, it will lead to bias and not suitable for non-convex clustering. DBSCAN is a density-based clustering algorithm, which assumes that categories can be determined by the compactness of sample distribution. It can be applied to a convex or non-convex sample set; however, its parameters are hard to set to make satisfactory clustering results.

In some special cases, the two methods mentioned above cannot be applicable. In our studied case, the historical track was focused on. As we will discuss in this paper, if we simply use clustering algorithm to solve the problem of historical track simplification, the final effect will be very unsatisfactory. We will ignore the important trajectory points and the moving direction of the moving target, which is not conducive to the analysis of the moving law and behavior pattern of the moving target. In paper [10], the idea of VQ-based path analysis is proposed. It is assumed that all trajectory points in a region are covered by a grid, and the point sets in each grid are clustered separately. This method solves the problem of trajectory deviation to a large extent, but the problem of trajectory deviation in each grid is not considered. This paper perfects this point. In order to express the problem more visually, take an example to illustrate. We simulate the trajectory points as desert trees. Generally speaking, the more symmetrical the distribution of trees on both sides, and the road goes along with the forest, not across it. We will feel that the road is integrated into the forest. So this road is more representative of the direction of the forest, so our problem can be expressed as to find a path that can represent the whole region and make the surrounding forest as far as possible road extension.

1.1 Summary of Key Contributions

The following is a list of our main contributions.

• We propose a trajectory analysis model, namely dichotomy algorithm method (DAM), based on symmetric distribution. Assuming that the trajectory point set ${\mathbb{P}} = \left\{ {p_{1} , \ldots ,p_{N} } \right\}$ of a region has $N$ elements and is covered by a grid, the trajectory points in ${\mathbb{P}}$ have time attributes, and the corresponding time set is ${\mathbb{T}} = \left\{ {t_{1} , \ldots ,t_{N} } \right\}$. For each grid, two representative trajectory points are selected. Finally, a new trajectory line is formed by connecting the selected point sets according to time. The trajectory line is concise and reflects the trajectory law to the greatest extent in the context of studying moving targets.

• For each mesh area, find a trajectory, so that the point set in the area can be distributed as far as possible on both sides of the trajectory and can be closely around the trajectory. Then we think that this trajectory is representative and can accurately express the law of trajectory points in this region. To this end, we propose an algorithm based on the symmetric distribution (DAM), which can find this trajectory.

• We also propose random algorithm model, greedy algorithm model, and clustering algorithm model to study trajectory. These models have their own advantages and disadvantages. In this paper, we show the trajectory fitting effect of these models through experiments.

1.2 Article Structure

The remainder of this paper is organized as follows. Section Two provides a review of the state-of-the-art research on trajectory analysis; Section Three presents system overview, random algorithm model, clustering greedy algorithm model, clustering algorithm model, and dichotomy algorithm method; Section Four introduces the mechanisms of four trajectory methods including the random algorithm model, greedy algorithm model, clustering algorithm model, and dichotomy algorithm method; Section Five evaluates performances of dichotomy algorithm method against the other three; Section Six delivers our conclusions for this paper.

2 Related Work

Song and Liu [11] framed a data compression algorithm which is developed on the basis of track data curve fitting idea. Because the core technology of the algorithm is fixed partition fitting, the error is large. Karimbergki [12] proposed a method of trajectory fitting including curvature, direction, and position parameters of circle. The method is based on the explicit solution of nonlinear least squares problem, and the error estimation of trajectory fitting parameters is reliable. Liu et al. [13] proposed a trajectory information fitting algorithm with adaptive selection of step size. Although the algorithm improves the fitting accuracy, the fitting curve is discontinuous and the inflection point is obvious. Liang and Li [14] proposed an adaptive fitting algorithm for trajectory information based on the optimization of least squares method and constrained quadratic programming method, so as to automatically select the optimal fitting interval and generate the key points and coefficients of the fitting interval. Peng and Xiguo [15] deduced a trajectory fitting method based on genetic programming (GP) and ant colony algorithm. A large number of calculations show that the fitting method has clear physical relationship, high accuracy, and fast calculation speed. Lee and Xu [16] proposed a model which is very suitable for finding the best-fitting trajectory from many examples. The model is a spline smoother considering local velocity information. The existing smoothing design only considers the position information, but does not consider the local velocity information; so it is difficult to apply to the dynamic system with time smooth trajectory. Zhang and Liu [17] proposed a mathematical model based on polynomial fitting of sliding window. The model processes the historical data sequence of target position by polynomial fitting. The main idea is that every time the target’s future position is calculated, the target data is updated with time, so as to achieve real-time prediction. This method overcomes the problem that the prediction error of general trajectory fitting increases with time. The method of trajectory fitting proposed by Ge and Chen [18] is based on Fourier series function to fit discrete trajectory points. Genetic algorithm is used to optimize the trajectory fitting model. The simulation results verify the correctness of the trajectory planning algorithm.

3 Preliminaries

The study of historical trajectory is of great significance. Generally, the original trajectory has various phenomena, such as aggregation, abnormality, round trip, and so on, which is helpful for judging and researching moving targets. It is inconvenient to judge a target (e.g., plane, ship) cross the border or break the law. So it is meaningful to select representative trajectory points and form simple and effective trajectory lines. In addition, for the sake of narrative convenience, we abbreviate “trajectory planning” as TP. In this section, we will summarize system overview, random algorithm model, greedy algorithm model, clustering algorithm model, and dichotomy algorithm method for trajectory planning.

3.1 System Overview

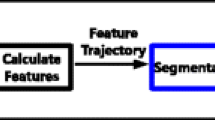
In this section, we will briefly introduce the framework of trajectory planning as shown in Fig. 1. The specific implementation process is as follows:

Fig. 1

System overview

• Firstly, the trajectory information of specified time period in specified area is collected by positioning device or smart mobile device, and the data is provided to data analysis center.

• After analyzing and extracting the data, representative trajectory points can be selected, such as random algorithm model, clustering algorithm model, greedy algorithm model, and VQ-based dichotomy model.

• A new trajectory is formed by linking the selected trajectory point data with the corresponding time information. This simple and effective trajectory is convenient for studying the behavior pattern of moving targets.

3.2 Random Algorithm Model

The idea of random algorithm model is to randomly select $k$ points from trajectory point set ${\mathbb{P}}$ and link them up according to the corresponding time information ${\mathbb{T}}$ of $K$ points. The advantage of this method is that it is simple and fast, but because of its randomness, it is difficult to capture key point information. Figure 2 shows a simple illustration of random algorithm model.

Fig. 2

Random algorithm model

3.3 Greedy Algorithm Model

Greedy algorithm means that when solving a problem, always make what seems to be the best choice at present. That is to say, without considering the global optimum, the local optimal strategy will be selected. Figure 3 shows the computational process of the greedy model.

Fig. 3

Greedy algorithm model

The aim of the greedy algorithm model is to continuously find the point with the highest density. Firstly, we assume that the scanning radius of each point as the center of the circle is $r$, and find the point with the highest density from the point set scanned and sequentially behind the center of the circle. The density of the point of $p_{i}$ is the ratio of the number of points within the radius to the area of the circle, with $p_{i}$ as the origin. Definition 1 gives the definition of distance.

Definition 1

(Distance). Suppose there are two trajectory points $p_{i}$, $p_{j}$ in two-dimensional space. We define the coordinates of two points as $\left( {x_{i} ,y_{i} } \right)$, $\left( {x_{j} ,y_{j} } \right)$, and then the distance between these two trajectory points is

$${\text{dis}}\left( {p_{i} ,p_{j} } \right) = \sqrt {\left( {x_{i} - x_{j} } \right)^{2} + \left( {y_{i} - y_{j} } \right)^{2} }$$

(1)

In order to facilitate calculation, we put forward the concept of density weight. The specific definition is shown in Definition 2.

Definition 2

(Density Widget). Assuming that a point $p_{j}$ is in a circular region with origin $p_{i}$ and radius $r$, we define the weight of this point as 1. Otherwise, we think that the weight of this point is 0.

$$\omega \left( {p_{j} } \right)_{{p_{i} ,r}} = \left\{ {\begin{array}{*{20}c} {1,} & {{\text{dis}}\left( {p_{i} ,p_{j} } \right) \le r} \\ {0,} & {{\text{otherwise}} .} \\ \end{array} } \right.$$

(2)

According to Definition 2, we can generalize the lemma of Point Density in Lemma 1.

Lemma 1

(Point Density). With point $p_{i}$ as the origin and $r$ as the radius, ${\mathcal{P}}_{ - i}$ is a set of all trajectory points without $p_{i}$; in this circular area, we define that the density of this point $p_{i}$ based on parameter $r$ is the ratio of the number of elements in the region to the area of the region, that is

$$\rho \left( {p_{i} } \right) = \frac{{\mathop \sum \nolimits_{{j:p_{j} \in {\mathcal{P}}_{ - i} }} \omega \left( {p_{j} } \right)_{{p_{i} ,r}} }}{{\pi r^{2} }}$$

(3)

3.4 Clustering Algorithm Model

Clustering algorithm is a clustering algorithm, so-called clustering; that is, according to the principle of similarity, data objects with high similarity are divided into the same cluster, and data objects with high similarity are divided into different clusters. The biggest difference between clustering and classification is that the clustering process is unsupervised; that is, the data objects to be processed do not have any prior knowledge; while the classification process is supervised, that is, there is a training data set with prior knowledge.

K-means algorithm is a partition-based clustering algorithm, which takes distance as the criterion of similarity measurement between data objects. That is, the smaller the distance between data objects, the higher their similarity, and the more likely they are in the same cluster. There are many ways to calculate the distance between data objects. K-means algorithm usually uses Euclidean distance to calculate the distance between data objects. The clustering details are shown in Fig. 4.

Fig. 4

Clustering algorithm model

3.5 Dichotomy Algorithm Model

Dichotomy is a new algorithm proposed in this paper, which is mainly an extension of the idea of symmetric distribution. Paper [10] proposed a trajectory analysis algorithm based on vector quantization. This algorithm needs to assume that a grid covers the area to be analyzed, and then a simple clustering algorithm is used for each grid element to calculate the clustering center as the representative of the grid element area. In this paper, the proposed algorithm (dichotomy algorithm) also assumes that the trajectory point distribution area is covered by meshes; but for each mesh element, we use the idea of density distribution symmetry to find the best partitioning line. If the distribution of trajectory points is mainly concentrated around the partitioning line, then assuming that the intersection point between the splitting line and the element boundary of the mesh is $a,b$, and then the two closest trajectory points $p_{\alpha }$ and $p_{\beta }$ will be the approximate optimal splitting line. The trajectory points $p_{\alpha }$ and $p_{\beta }$ can be used as the representative points of the trajectory points set in the mesh area. If the distribution of the trajectory points is mainly concentrated in the normal direction of the partition line, then we will take the clustering center of the two partitioned points set as the representative points. The representative points obtained by this scheme cannot only describe the direction of the trajectory, but also be more representative.

The ideological framework of the model is shown in Fig. 5. Firstly, the central point of each grid element is determined to be the origin of the coordinate system, and the grid element region is divided into two equal parts $A_{1} ,B_{1}$ by the linear function $y = kx$. With the change of slope $k$, we can find the most similar critical point for the distribution of two trajectory point sets $P_{\alpha } ,P_{\beta }$. The judgment of similar distribution of trajectory point set can be made by using the change rate of trajectory point set density. This algorithm is also a new algorithm proposed in this paper, which calculates the average change rate of trajectory point set density by continuously reducing the area. As shown in Fig. 5, flags 1, 2, and 3 represent three states. For area $A_{1}$, assuming that state 1 changes to state 2, the area reduction rate is $\varepsilon$, the area of state 1 is defined as $S\left( {A_{1} } \right)$, and the number of point sets of state 1 is ${\mathcal{N}}\left( {A_{1} } \right)$. Define the edge length of the grid element to be l. Then $S\left( {A_{1} } \right) = l^{2} /2$. It is easy to get that the area of state 2 and state 3 is $S\left( {A_{2} } \right) = \left( {1 - \varepsilon } \right)S\left( {A_{1} } \right)$ and $S\left( {A_{3} } \right) = (1 - \varepsilon )^{2} S\left( {A_{1} } \right)$, respectively. Densities at states 1, 2, and 3 are $\rho \left( {A_{1} } \right) = \frac{{{\mathcal{N}}\left( {A_{1} } \right)}}{{S\left( {A_{1} } \right)}}$, $\rho \left( {A_{2} } \right) = \frac{{{\mathcal{N}}\left( {A_{2} } \right)}}{{S\left( {A_{2} } \right)}}$ and $\rho \left( {A_{3} } \right) = \frac{{{\mathcal{N}}\left( {A_{3} } \right)}}{{S\left( {A_{3} } \right)}}$, respectively.

Fig. 5

Dichotomy algorithm model

Then the definition of the density (defined in Definition 3) used to judge the distribution similarity of the trajectory point set is as follows.

Definition 3

(Density Base on Area). Suppose that a grid element region is divided into two parts, $A_{1}$ and $B_{1}$, by a linear function $y = kx$. For region $A_{1}$, if the initial state area is $S\left( {A_{1} } \right)$ and the number of trajectory points is ${\mathcal{N}}\left( {A_{1} } \right)$, then the area of $A_{1}$ is $S\left( {Ar + 1} \right) = (1 - \varepsilon )^{m} S\left( {A_{1} } \right)$ with the reduction rate ε changed by m times, and the number of current trajectory points is ${\mathcal{N}}\left( {A_{m + 1} } \right)$, the area name is $A_{m + 1}$. The density base on area $A_{m + 1 }$ can be expressed as the following formula:

$$\rho \left( {A_{m + 1} } \right) = \frac{{{\mathcal{N}}\left( {A_{m + 1} } \right)}}{{S\left( {A_{m + 1} } \right)}} = \frac{{2{\mathcal{N}}\left( {A_{m + 1} } \right)}}{{l^{2} (1 - \in )^{m} }}$$

(4)

In this section, we design a trajectory planning algorithm based on dichotomy. Assuming that the trajectory points ${\mathbb{P}} = \left\{ {p_{1} , \ldots ,p_{N} } \right\}$ in a region are covered by a grid, the corresponding time series is ${\mathbb{T}} = \left\{ {t_{1} , \ldots ,t_{N} } \right\}$, and the mesh size of the grid element is $l$. For trajectory points in each grid element, we want to draw a partition line and divide the trajectory points in each grid into two parts according to the distribution, so that the distribution of the two parts should be as similar as possible. Assuming that the center of the mesh is the origin of the Cartesian coordinate system, the partition line can be expressed as a linear function $y = kx$ with slope $k$, where $k = { \tan }\theta$ ($\theta$ is the angle to the X-axis). Details are shown in Fig. 1. Then, the intersection points of the linear function $y = kx$ and the meshes are taken as the basic points of trajectory analysis, and the two points $p_{i} ,p_{j}$ closest to the intersection point in the mesh are selected to represent the group of points in the mesh. How to judge whether the distribution of two parts of point groups is similar after the linear function $y = kx$ segmentation is the key to solve the problem. We measure the similarity of distribution by area reduction.

Define a set of trajectory points in a grid element as ${\mathcal{P}} = \left\{ {p_{1} , \ldots ,p_{n} } \right\}$, the corresponding time series is ${\mathcal{T}} = \left\{ {t_{1} , \ldots ,t_{n} } \right\}$. We measure the similarity of distribution by area reduction. Assume that the linear function $y = kx$ divides a grid element into two regions $a$ and $b$, and their corresponding areas are $S\left( a \right)$ and $S\left( b \right)$, and we can get the lemma (Lemma 2) of point group distribution similarity.

Lemma 2

(PGD Similarity). Suppose that the reduction rate of edge length in $a$ and $b$ regions is defined as $\varepsilon$, and that the density of point groups in $a$ and $b$ regions can be defined as $\rho \left( a \right)$ and $\rho \left( b \right)$. Assuming that the number of area reductions is defined as $m$, for region $a$, after $m$ times of area iteration reduction, the total change of point-group density is $\Delta \rho \left( {a,m} \right) = \;|\rho (a)_{1} - \rho (a)_{2} \left| { + \cdots + } \right|\rho (a)_{\imath } - \rho (a)_{\imath + 1} \left| { + \cdots + } \right|\rho (a)_{m} - \rho (a)_{m + 1} |$, where $\rho (a)_{1} , \ldots ,\rho (a)_{m + 1}$ is the density sequence corresponding to all changes ($m > 1$). That is $\Delta \rho \left( {a,m} \right) = \sum\nolimits_{j = 1}^{m} {|\rho (a)_{j} - \rho (a)_{j + 1} |}$. Then the average density change rate about $a$ is $\overline{\Delta \rho } \left( {a,m} \right) = \frac{{\Delta \rho \left( {a,m} \right)}}{m}$. Similarly, the average density change rate about $b$ is $\overline{\Delta \rho } \left( {b,m} \right) = \frac{{\Delta \rho \left( {b,m} \right)}}{m}$. The difference of point group distribution similarity between $a$ and $b$ is $\xi = \left| {\overline{\Delta \rho } \left( {a,m} \right) - \overline{\Delta \rho } \left( {b,m} \right)} \right|$, namely

$$\xi = |\mathop \sum \limits_{j = 1}^{m} |\rho (a)_{j} - \rho (a)_{j + 1} \left| \; -\; \right|\rho (b)_{j} - \rho (b)_{j + 1} ||$$

(5)

4 Algorithm Analysis

In this paper, four kinds of trajectory analysis models are involved, which are random algorithm model (RAM), greedy algorithm model (GAM), clustering algorithm model (CAM), and dichotomy algorithm model (DAM). In this chapter, the implementation algorithms of these four models will be described in detail. Table 1 lists frequently used notations.

Table 1 Notations of follow algorithms

4.1 Random Algorithm

Random algorithm model, as its name implies, randomly extracts $k$ trajectory points from the set of trajectories as representative points and links them up according to their time characteristics. Algorithm 1 (RAFTP) shows the algorithm process.

Algorithm 1: RAFTP
Input: ${\mathbb{P}},{\mathbb{T}},k$
Output: ${\mathbb{P}} '$
1. random k elements from trajectory point set ${\mathbb{P}}$;
2. drawing trajectory line based on time series ${\mathbb{T}}$;
3. return ${\mathbb{P}} '$;

4.2 Greedy Algorithm

Greedy algorithm cannot get the overall optimal solution for all problems, and the key is the choice of greedy strategy. The greedy strategy must have no aftereffect; that is, the process before a certain state will not affect the later state, only related to the current state.

In short, the main idea of the greedy algorithm for trajectory analysis is to select the starting point of $p_{j}$, scan the surrounding area with $p_{j}$ as the starting point and $r$ as the radius to find the maximum density point. For the definition of density, see Lemma 1. After each scan, the trajectory points in the scanning area that are later than the origin time will be removed from the trajectory set to avoid repeated calculation. Through continuous iteration, until the time does not meet the conditions; that is, no longer can find the trajectory point of later time. Algorithm 2 (GAFTP) shows the detailed algorithm steps of greedy algorithm model.

Algorithm 2: GAFTP
Input: ${\mathbb{P}},{\mathbb{T}},r$
Output: ${\mathbb{P}} '$
1. ${\mathbb{Q}} \leftarrow {\mathbb{P}}$
2. $t_{max} \leftarrow t_{N}$
3. Determine the starting point as $p_{j} \in {\mathbb{Q}}$
4. ${\mathbb{P}} '\leftarrow p_{j}$
5. While $t_{j} \le t_{N} and {\mathbb{Q}} \ne \emptyset$ do
6. the set of trajectory points scanned from ${\mathbb{Q}}$ with $\varvec{p}_{\varvec{j}}$ as the center and $\varvec{r}$ radius is as the radius is ${\mathcal{P}}\left( {p_{j} } \right)$
7. ${\mathbb{Q}} \leftarrow {{\mathbb{Q}}\ominus }\backslash {\mathcal{P}}\left( {p_{j} } \right)$
8.         filter out the trajectory-point set with times are later than $\varvec{t}_{\varvec{j}}$, and get the set ${\mathcal{P}} '\left( {p_{j} } \right)$
9.         for each $p_{\imath } '\in {\mathcal{P}}\left( {p_{j} } \right)$ do
10.           if $t\left( {p_{\imath } '} \right) \ge t_{j}$ then
11. ${\mathcal{P}} '\left( {p_{j} } \right) \leftarrow p'$
12. $p_{0} \leftarrow \mathop { \hbox{max} }\limits_{{p_{j} \in {\mathcal{P}^{\prime}}\left( {p_{j} } \right)}} \rho \left( {p_{j} '} \right)$
13. ${\mathbb{P}} '\leftarrow p_{0}$
14.         return ${\mathbb{P}} '$

4.3 Clustering Algorithm

Clustering algorithm aggregates the set of trajectory points ${\mathbb{P}}$ into $k$ classes and calculates the central points of $k$ clusters. Based on the time information of the central points, the selected trajectory points are joined together to form a new trajectory line. Algorithm 3 (CAFTP) shows the steps of clustering.

Algorithm 3: CAFTP
Input: ${\mathbb{P}},{\mathbb{T}},k$
Output: $P'$
1. Using the idea of K-means algorithm, the set ${\mathbb{P}}$ of trajectory points is aggregated into $k$ classes
2. ${\mathbb{P}} '\leftarrow$ calculating $\varvec{k}$ cluster centers
3. connect trajectory points to form a new trajectory based on the time information of clustering center
4. return ${\mathbb{P}} '$

4.4 Dichotomy Algorithm

Dichotomy algorithm model divides all trajectory points into grid elements according to the idea of vector quantization and then analyzes the set of trajectory points in each grid element. DAM detailed steps in Algorithm 4 (GMFTP). Assuming that the set of elements in a grid element is ${\mathcal{P}}$, the corresponding time information sequence is ${\mathcal{T}}$, and the slope of the point set function $y = kx$ is $\theta$. Because we need to find the best dividing line by changing the slope, we need to determine the magnitude of the angle change, denoted as $\Delta \theta$. We need to use the concept of density change rate to compare the distribution of trajectory points in the two regions after segmentation. See Lemma 2 for the specific definition. This involves the concept of the number of regional area reductions used to calculate the rate of density change. Here we define the number of reductions as $m$. In Algorithm 4 (GMFTP), 2–6 rows are searched for the best segmentation line. Assuming that the segmented region is $a$ and $b$, then 8–12 rows determine the region where the trajectory points belong. Lines 13–22 determine the points within the grid area that can represent the set of trajectory points in the region. All grid elements are calculated according to Algorithm 4.

Finally, according to the time information of the selected trajectory points, the trajectory points are joined together and a new trajectory line is fitted.

Algorithm 4: GMFTP
Input: ${\mathcal{P}},{\mathcal{T}},l,\theta ,\Delta \theta ,m$
Output: $P'$
1. $\theta \leftarrow 0,\phi \leftarrow 0,\xi_{min} \leftarrow + \infty$
2. While $\theta < 2\pi$ do
3.         if $\xi \left( {y = tan\theta \cdot x} \right) < \xi_{min}$ do
4. $\xi_{min} \leftarrow \xi \left( {y = tan\theta \cdot x} \right)$
5. $\phi = \theta$
6. $\theta = \theta + \Delta \theta$
7. $k = tan\phi ,{\mathcal{P}}\left( a \right) \leftarrow \emptyset ,{\mathcal{P}}\left( b \right) \leftarrow \emptyset$
8. for each $p_{i} \in {\mathcal{P}}$ do
9.         if $y_{i} \ge kx_{i}$ then
10. ${\mathcal{P}}\left( a \right) \leftarrow p_{i}$
11.         if $y_{i} \le kx_{i}$ then
12. ${\mathcal{P}}\left( b \right) \leftarrow p_{i}$
13. $P \leftarrow \emptyset ,{\mathcal{I}} \leftarrow \emptyset$
14. if $\mathop \sum \limits_{{i:p_{i} \in {\mathcal{P}}}} \frac{{\left| {kx_{i} - y_{i} } \right|}}{{\sqrt {k^{2} + 1} }} \le \mathop \sum \limits_{{i:p_{i} \in {\mathcal{P}}}} \frac{{\left| {x_{i} + ky_{i} } \right|}}{{\sqrt {k^{2} + 1} }}$ then
15. the intersection set of linear function $y = kx$ and $y = \pm l/2$,$x = \pm l/2$ is ${\mathcal{I}} = \left\{ {\left( {x_{1} ,y_{1} } \right) \ldots } \right\}$
16. for each $I_{\varsigma } \in {\mathcal{I}}$ do
17.           // $\left( {\varvec{x}_{\varvec{\varsigma }} ,\varvec{y}_{\varvec{\varsigma }} } \right)$ is the coordinate of $\varvec{I}_{\varvec{\varsigma }}$ with the center of the grid element as its origin.
18.           if $x_{\varsigma } ,y_{\varsigma } \in \left[ { - l/2,l/2} \right]$ then
19.              $p' \leftarrow { \arg }_{{p_{\gamma } :p_{\gamma } \in {\mathcal{P}}}} min dis\left( {I_{\varsigma } ,p_{\gamma } } \right)$
20.              $P \leftarrow p'$
21. else
22.         $P \leftarrow {\mathcal{P}}\left( a \right) clustering center,P \leftarrow {\mathcal{P}}\left( b \right) clustering center$
23. return $P$

5 Performance Evaluation

5.1 Simulation Setup

In order to better see the performance of the trajectory analysis model, we use simulation experiments to test. We set up two sets of data. In Set one, the X, Y coordinates of the trajectory points are randomly within [0, 200], and the incremental step size is 10 at each time. In order to make the effect more real, we make the step size fluctuate within [−8, 2]. For stochastic model and clustering model, we define that the number of substituted trajectory points is 15, the scanning radius of greedy algorithm is 15, and the pixel size of dichotomy grid is 15. In Set two, we expand the data quantity of trajectory points. The X, Y coordinates of trajectory points are random in [0, 400]. Each random incremental step is 10, and the fluctuation range of step size is [−10,2]. The number of representative points selected by random model and clustering model is 30, the scanning radius of greedy algorithm is 30, and the pixel size of dichotomy grid is 30. Detailed parameters are given in Table 2.

Table 2 Parameter setting

5.2 Simulation Results

Figure 6 shows the effect of trajectory fitting of random algorithm model, in which original represents the original trajectory. From Fig. 6a, b, we can find that although RAM can simplify trajectory to a great extent, it largely ignores the original characteristics of trajectory. For example, the random model does not capture the broken line feature at the passing point (150, 100) in Fig. 6a and the bending feature at the passing point (50, 100) in Fig. 6b.

Fig. 6

Random model for trajectory fitting

Figure 7a, b shows the trajectory fitting effect of the greedy model. From Fig. 7a, we find that if there are no outliers or clutter in the trajectory, the greedy strategy can well show the characteristics of the original trajectory. On the contrary, in Fig. 7b, there will be the same shortcomings as the random model, ignoring some characteristics of the original trajectory. Figure 8 shows the trajectory fitting effect of the clustering model. It is easy to find that the model algorithm can capture the region with dense trajectory points and achieve better trajectory simplification effect. However, the model cannot express the characteristics of discrete points very well. Figure 9 shows the trajectory fitting effect of the dichotomy model. We find that the fitting effect is close to the original trajectory and can well reflect the trajectory direction and inflection point characteristics. There is no obvious abnormal phenomenon. Generally speaking, the experimental results show that compared with the other three models, the algorithm model has obvious advantages.

Fig. 7

Greedy model for trajectory fitting

Fig. 8

Clustering model for trajectory fitting

Fig. 9

Dichotomy model for trajectory fitting

6 Conclusion

In this paper, we design random algorithm model (RAM), greedy algorithm model (GAM), clustering algorithm model (CAM), and dichotomy algorithm model (DAM) for trajectory analysis. Through these four algorithms, representative trajectory point sets are selected. According to the corresponding time information, a new trajectory is fitted. Experiments show that RAM has high efficiency and low-time complexity, but RAM cannot describe the trajectory well. If the trajectory is not complicated, then GAM will be a good choice as it is capable of updating with the current state information, because GAM can make the best strategy that conforms to the current state. CAM has a good performance in dense cases. The DAM is the key research algorithm in this paper. It solves the problem from the point of view of the distribution of trajectory points. This method can combine the ideas from VQ and clustering methods with a dynamic strategy to deal with the change of point density, which allows it to be powerful for studying the trajectory pattern.