A Sharp-Interface Immersed Boundary Method for High-Speed Compressible Flows

Abstract

Numerical simulation of hypersonic flows is important owing to their applications to the design of launch vehicles and re-entry capsules. We describe the development and application of a hybrid Cartesian–immersed boundary (HCIB) approach in a finite volume (FV) framework for inviscid and viscous compressible flows with a focus on the hypersonic regime. The HCIB approach employs a local one-dimensional reconstruction to obtain the near-wall solutions thereby enforcing the boundary conditions exactly on the sharp geometric interface. The role of the reconstruction on solution accuracy and discrete conservation is discussed, and the IB-FV solver is applied to several hypersonic flow problems involving inviscid as well as viscous flows. The studies demonstrate the efficacy of the HCIB approach for inviscid flows with stationary as well as moving bodies while also highlighting some of the drawbacks for heat transfer predictions in high Reynolds number flows. Some directions for future research are also outlined.

1 Introduction

Numerical simulation of flow past bodies offers several challenges especially when the geometry is complex in nature. Ensuring a good quality body-conformal mesh for the underling geometry is not a trivial proposition and demands user expertise while also being time-consuming. The challenge of creating a good quality body-conformal mesh becomes even more severe when the geometries undergo motion. For such scenarios, Cartesian grid-based methods offer a significant advantage because of the ease with which the complex bodies can be treated on a simple orthogonal grid. This reduces the cost and time associated with grid generation and can be extended in a straightforward manner for moving body problems. The use of a fixed background grid provides the user with significant leverage by avoiding mesh movement and re-meshing that would be necessitated on flow solvers with conformal meshes. One of the approaches in this class is the “cut–cell” method that has been used quite extensively (Clarke et al. 1986; Udaykumar and Shyy 1995; Ye et al. 1999). However, this approach suffers from stability issues due to small cells near the boundary that limit the time step and requires cell-merging strategies to overcome this problem. Another class of Cartesian grid-based methods that have gained popularity in the last few years is the immersed boundary method, originally proposed by Peskin in his seminal work in 1972 (Peskin 1972). Over the last two decades, there have been several variants of the immersed boundary methods, although the development of these techniques for fluid flows and heat transfer has been largely for incompressible flows. A good and comprehensive review of IB methods can be found in Mittal and Iaccarino (2005) and Sotiropoulos and Yang (2014), with the latter highlighting some of the interesting applications of IB techniques for complex incompressible flows.

The use of IB approaches for compressible flows has not been as widespread when compared to its incompressible counterparts. The earliest studies in this direction were carried out by Ghias et al. (2007) and de Palma et al. (2006). While the former discussed mostly low subsonic flows using ghost-cell IB methods, the latter extended the IB methodology to low supersonic flows. This was followed by the work on sharp-interface IB methods for transonic flows using local grid refinement by de Tullio et al. (2007). Cho et al. (2007) employed the Brinkman penalisation method, which belongs to the class of “diffuse" interface IB methods for compressible flows over a wide range of Mach numbers. Studies using a hybrid Cartesian immersed boundary (HCIB) method in the subsonic and transonic regimes were carried out by Zhang and Zhou (2014). Sambasivan and Udayakumar devised a sharp-interface variant for multi-material compressible flows (Sambasivan and UdayKumar 2010), and ghost-cell immersed boundary approaches have been employed to study shock diffraction and explosion with moving bodies (Mo et al. 2016). There have also been efforts to develop higher-order finite difference IB methods for compressible flow (Brehm et al. 2015) but most studies have been targeted at flows in the high subsonic and low supersonic flow regimes. Furthermore, while most studies have addressed Euler flows, only a few efforts concentrate on viscous compressible flows (Palma et al. 2006; de Tullio et al. 2007; Ghosh et al. 2010; Pu and Zhou 2018). Importantly, there have been only a handful of studies that have attempted to use the IB approach for high Mach number flows. In particular, the recent studies of Das et al. (2017) and Qu et al. (2018) have employed immersed boundary methods for shocked particle-laden flows and moving rigid bodies, respectively. Nevertheless, even these studies in high-speed viscous flows do not address the issue of resolution of the thin boundary layers and consequently the prediction of wall heat flux and skin friction. To the best of the authors’ knowledge, only the studies of Arslanbekov et al. (2011) and Sekhar and Ruffin (2013) have attempted to study the stagnation heat flux estimation using IB methods. While their investigations discussed hypersonic flows, the Reynolds numbers in their studies were quite moderate. An important aspect of immersed boundary approaches that also has not been deeply probed is the issue of discrete conservation. Unlike cut-cell-based methods, IB approaches are clearly not discretely conservative and there have been no major efforts to look into the conservation errors particularly in compressible flows.

The literature survey presented herein, while not exhaustive, clearly points to the need to assess the class of immersed boundary methods for hypersonic laminar flows. This motivates our studies detailed in this chapter where we focus on the development of a sharp-interface immersed boundary method in the finite volume framework and discuss its ability to accurately compute hypersonic inviscid and laminar flows. We specifically discuss the aspects of discrete conservation as well as the efficacy of the IB approach for computing heat flux and skin friction distribution in viscous flows past canonical configurations. The remainder of the chapter is organised as follows. Sections 9.2 and 9.3 describe the numerical framework in details. The investigations pertaining to conservation errors, Euler flows as well as viscous flow computations form the subject matter of Sect. 9.4. We summarise the salient findings from the present study in Sect. 9.5, where a few recommendations for future research are also outlined.

2 Finite Volume Solver for Compressible Flows

In this section, we describe the details of the finite volume flow solver which forms the basic workhorse of the numerical investigations detailed later in this chapter. The immersed boundary method, to be discussed in the following section, is integrated with this flow solver. Based on an unstructured data framework, the flow solver solves the Navier–Stokes equations for a perfect gas which in the conservative form (in two dimensions) reads,

$$ \frac{\partial \varvec{U}}{\partial t} + \frac{\partial \varvec{F_I}}{\partial x} + \frac{\partial \varvec{G_I}}{\partial y} + \frac{\partial \varvec{F_V}}{\partial x} + \frac{\partial \varvec{G_V}}{\partial y} + \alpha (\varvec{S_I}-\varvec{S_V}) = 0 $$

$$ \varvec{U} = \begin{bmatrix} \rho \\ \rho u \\ \rho v \\ \rho E \end{bmatrix} ; \quad \varvec{F_I} = \begin{bmatrix} \rho u\\ \rho u^2+p \\ \rho uv \\ \rho u\Big (E + \frac{p}{\rho }\Big ) \end{bmatrix} ; \quad \varvec{G_I} = \begin{bmatrix} \rho v\\ \rho uv \\ \rho v^2+p \\ \rho v\Big (E + \frac{p}{\rho }\Big ) \end{bmatrix} $$

$$ \varvec{F_V} = \begin{bmatrix} 0\\ \tau _{xx} \\ \tau _{xy} \\ u\tau _{xx} + v\tau _{xy} - q_x \end{bmatrix} ; \quad \varvec{G_V} = \begin{bmatrix} 0\\ \tau _{xy} \\ \tau _{yy} \\ u\tau _{xy} + v\tau _{yy} - q_y \end{bmatrix} $$

where the vectors $\mathbf {S_I}$ and $\mathbf {S_V}$ are the inviscid and viscous source terms, respectively, and are relevant only for axisymmetric flows. These may be expressed as,

$$ \varvec{S_I} = \frac{1}{y}\begin{bmatrix} \rho v\\ \rho uv \\ \rho v^2 \\ \rho v (E +\frac{p}{\rho }) \end{bmatrix} $$

$$ \varvec{S_V} = \frac{1}{y}\begin{bmatrix} 0 \\ \tau _{xy} -\frac{2}{3}y\frac{\partial }{\partial x}(\mu v/y) \\ \tau _{yy} - \tau _{\theta \theta } - \frac{2v}{3y}\mu - \frac{2}{3}y\frac{\partial }{\partial y}(\mu v/y) \\ u\tau _{xy} + v\tau _{yy} - q_y - \frac{2\mu v^2}{3y} - \frac{2y}{3}\frac{\partial }{\partial y}(\mu v^2/y) - \frac{2y}{3}\frac{\partial }{\partial x}(\mu u v/y) \end{bmatrix} $$

where,

$$\begin{aligned} \tau _{\theta \theta } = \mu \Big (-\frac{2}{3}\Big ( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \Big ) + \frac{4v}{3y} \Big ) \end{aligned}$$

We set $\alpha =1$ for axisymmetric simulations while for planar two-dimensional studies $\alpha =0$. Here, U represents the vector of conserved variables (mass, momentum and energy) and $F_I$ and $G_I$ represent the inviscid fluxes while $F_V$ and $G_V$ represent the viscous fluxes. The components of heat flux are represented by $q_x$ and $q_y$ while $\tau _{xx},\tau _{yy}$ and $\tau _{xy}$ are the components of the symmetric viscous stress tensor. Integrating these vector conservation laws over an arbitrary control volume and applying the Gauss divergence theorem yield the semi-discrete form of the governing equations. The semi-discrete form of the conservation laws in a compact form reads,

$$ \mathrm {\frac{d \varvec{U}_i}{dt}} = -\frac{1}{\Omega _i} \sum \limits _{J \epsilon i} \varvec{H}_{\perp _J}\Delta S_J - \alpha \overline{\varvec{S}}_i = \varvec{R}(\overline{U}_i) $$

$$ \varvec{H}_{\perp } = \begin{bmatrix} \rho u_{\perp } \\ \rho uu_{\perp } + pn_x \\ \rho vu_{\perp } + pn_y \\ (\rho e + p)u_{\perp } \end{bmatrix} - \begin{bmatrix} 0 \\ n_x\tau _{xx} + n_y\tau _{xy} \\ n_x\tau _{yx} + n_y\tau _{yy} \\ n_x\theta _x + n_y\theta _y \end{bmatrix} ; \quad \varvec{\overline{S}} = \varvec{\overline{S}_I} - \varvec{\overline{S}_V} $$

where $u_{\perp } = u n_x + v n_y$, $\theta _x = u\tau _{xx} + v\tau _{xy} - q_x$, $\theta _y = u\tau _{yx} + v\tau _{yy} - q_y$.

The quantity $\Omega _i$ is the volume of the ith cell, $\Delta S$ is the face area and $n_x$ and $n_y$ are the components of the outward unit normal to the face. The summation is over all faces J of a cell i, and the convective and viscous fluxes at a face are evaluated at the face mid-points using a single-point Gauss quadrature. A second-order accurate linear reconstruction proposed by Barth and Jesperson (2001) is employed to determine the states required for convective flux computations. The convective fluxes are determined using AUSM scheme (Liuo and Steffen 1993), unless otherwise specified and the Venkatakrishnan limiter (Blazek 2001) is used to ensure monotonicity of the solution. Green–Gauss reconstruction (Blazek 2001) is employed to determine the gradients required for viscous flux computations. Time advancement is realised using a five-stage Runge–Kutta scheme (Blazek 2001), although a single-stage RK scheme (equivalent to explicit Euler) is employed for steady flow computations where temporal accuracy is unimportant. This finite volume (FV) solver has been extensively validated in previous work on several problems involving inviscid and viscous compressible flows (John and Kulkarni 2014). The flow solver, being based on unstructured data, is also capable of handling adaptive grids which are constructed by an isotropic refinement strategy (Natarajan 2009) that divides each “parent” cell into four “children” with the regions where adaptation is effected identified by the user apriori.

3 Hybrid Cartesian Immersed Boundary Method

The details and implementation of the sharp-interface hybrid Cartesian immersed boundary (HCIB) method are discussed in this section. The HCIB approach was first proposed by Gilmanov and Sotiropoulos (2005) for incompressible fluid flows. The present work is an extension of their methodology to compressible inviscid and viscous flows. In the technique, the solid body is immersed into an underlying Cartesian mesh. The solid boundary is discretised using linear line segments in two dimensions (or surface triangulated in three dimensions). Unlike traditional body-conformal CFD solvers, the mesh does not conform to the geometry, and therefore, the accurate calculation of the near-wall numerical solution is critical. The HCIB approach has been implemented in the finite volume framework described previously in Sect. 9.2 and constitutes two distinct stages that are described below.

3.1 Cell Classification

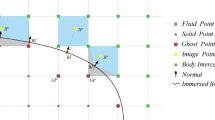
The first stage in the HCIB approach is the classification of the cells (or control volumes) of the underlying Cartesian mesh into three categories. Cells whose cell centres lie inside the solid are classified as solid cells (denoted as S) while the remaining cells are termed as fluid cells (denoted as F). This is effected using a ray-casting algorithm. All F cells which share at least one face with a S cell are then termed as immersed cells (denoted by I cells). The procedure behind this classification step is shown in Fig. 9.1 and distinguishes the regions where the solution is sought (F and I cells) from those where the solution is not necessary (S cells). For stationary cases, it is easy to see that the classification is a one-time affair whereas for moving body problems, it must be repeated at every time step.

Fig. 9.1

Classification of cells

3.2 Solution Reconstruction

The second stage in the HCIB approach involves solution reconstruction where the numerical solution in the near vicinity of the solid body is obtained by enforcing the boundary conditions while preserving the sharp interface of the geometry. The numerical solution needs to be only computed in the F and I cells with those in the F cells obtained by solving the Navier–Stokes equations. The solution in I cells is however obtained using some form of algebraic reconstruction as detailed in this section.

Fig. 9.2

Reconstruction for obtaining $\phi$ at immersed cells

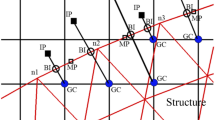
We now describe the solution reconstruction for viscous compressible flows for geometries with adiabatic as well as isothermal walls. The solution reconstruction is an interpolation along the direction locally normal to the interface as shown in Fig. 9.2. The boundary conditions are enforced directly at the sharp interface in this study. To do so, we first identify the nearest face on the solid boundary for each I cell. Following this, we identify points b and f on the body surface and in the fluid domain, respectively, which lie along the normal $\hat{n}$ to the nearest face and also contain the centroid of the I cell. The point b is the intersection point of the local normal with the geometric boundary while point f is the closest point on this line that cuts a connector joining two F cells (see Fig. 9.2). The boundary condition on the body surface is used to determine the primitive variables at b while we adopt linear interpolation of the solutions at $F_1$ and $F_2$ to evaluate the fluid properties at f.

$$\begin{aligned} \phi _f = \frac{\phi _{F1}{d_2} + \phi _{F2}{d_1}}{{d_1}+{d_2}} \end{aligned}$$

(9.1)

where $d_1$ and $d_2$ refer to distances of the point f from the centroid of cells $F_1$ and $F_2$. The primitive variables at the I cells are then obtained by a suitable interpolation at b and f points. The choice of this reconstruction can be either a polynomial or non-polynomial interpolation, and it need not necessarily be identical for all primitive variables. The specific details of this reconstruction strategy when both isothermal and adiabatic surfaces are involved are now discussed.

Assuming that the solution varies linearly and denoting the variable of interest as $\phi$, one can write its variation along the normal direction as,

$$\begin{aligned} \phi = C_1 r + C_2 \end{aligned}$$

(9.2)

where r is the distance measured from the b point on the sharp interface along the direction of the outward local normal. Subsequently, if the unknowns $C_1$ and $C_2$ can be uniquely determined from two independent conditions then the value at the I cell may be computed as,

$$\begin{aligned} \phi _{I}= C_1 r_{bI} + C_2 \end{aligned}$$

(9.3)

The constants $C_1$ and $C_2$ are typically evaluated using the boundary conditions at “b” and the interpolated solution at “f”.

3.3 Reconstruction for Velocities

For viscous flows, the solid wall satisfies both the no-slip as well as the impermeable wall boundary condition, i.e. $u_{||b}$ = 0 and $u_{\perp b}$ = 0, respectively. The quantities $u_{||}$ and $u_{\perp }$ denote the components of velocity vector along the local tangential and local normal directions, respectively, and may be determined as,

$$\begin{aligned} u_{||} = u_f n_y - v_f n_x \end{aligned}$$

(9.4)

$$\begin{aligned} u_{\perp } = u_f n_x + v_f n_y \end{aligned}$$

(9.5)

where $n_x$ and $n_y$ now refer to the components of the normal to the interface along which the one-dimensional solution reconstruction is effected. The values of these velocity components at the f point may be computed using Eq. (9.1) where $\phi$ is chosen as $u_{||}$ or $u_{\perp }$. The use of the known values at b and f points helps to compute the values of $u_{||}$ and $u_{\perp }$ at the I cells using Eq. (9.3) and one can obtain the Cartesian velocity components at the cell centres using the reverse transformation that reads,

$$\begin{aligned} u_I = (u_{||I} \ n_y) - (u_{{\perp I}} \ n_x) \end{aligned}$$

(9.6)

$$\begin{aligned} v_I = (-u_{||I} \ n_x) - (u_{{\perp I}} \ n_y) \end{aligned}$$

(9.7)

For moving bodies whose motion is induced by the flow, the velocity components of the body are nonzero and are evaluated by solving the second-order ODEs describing Newton’s second law of motion. This gives,

$$\begin{aligned} {\begin{matrix} u_b^{k+1} = u_b^k + \frac{\Delta t}{M_b} F_x^k \\ v_b^{k+1} = v_b^k + \frac{\Delta t}{M_b} F_y^k \end{matrix}} \end{aligned}$$

(9.8)

where k and $k+1$ represent the present and next time step, respectively, and $M_b$ is the mass of the body. The terms $(F_x,F_y)$ represent the force components and are determined from the wall pressure and wall shear stresses. We choose the contour of integration for this purpose as the approximated immersed boundary as highlighted in Fig. 9.1, which leads to an approximated domain stair-step representation as also in Mizuno et al. (2015).

3.4 Reconstruction for Pressure

The pressure at the cell I is obtained by invoking the boundary layer approximation that strictly holds for non-separated flows. This gives $\frac{\partial p}{\partial r}$ = 0, and as a result, one can impose the pressure outside the boundary layer on the surface. We thus have $p_b = p_I = p_f$, with $p_f$ obtained using Eq. (9.1). While this condition would be strictly valid only for thin layers and unseparated flows, they have been used for inviscid flows (Brahmachary et al. 2018) and appear to work even in scenarios with flow separation (as shall be shown in studies in Sect. 9.4.6).

3.5 Reconstruction for Temperature

The value of temperature at the point b depends on whether the wall boundary is adiabatic or isothermal. For isothermal walls, the wall temperature $T_w$ is known and is constant which results in $T_b = T_{w}$. The temperature at the immersed cell $T_I$ can then be obtained using Eq. 9.3. It is also possible to employ nonlinear and non-polynomial interpolation (Ghosh et al. 2010) although this has not been considered in the present study.

3.6 Reconstruction for Density

The density at I cells follows from the equation of state (EOS) for a perfect gas and is computed as,

$$\begin{aligned} \rho _I = \displaystyle \frac{p_I}{R T_I} \end{aligned}$$

(9.9)

where R is the gas constant and $p_I$ as well as $T_I$ follow from suitable reconstruction approaches as described in Sects. 9.3.4 and 9.3.5. This methodology of one-dimensional solution reconstruction along the local normal direction closely resembles the extended extrapolation technique in Zhao et al. (2010) except that the normal velocity varies linearly in our approach as opposed to the quadratic variation in the extended extrapolation method.

3.7 Calculation of Wall Pressure, Shear Stress and Heat Flux

For viscous computations, the major quantities of interest are the surface distribution of pressure, heat transfer and viscous stresses. We provide a concise description of the computation of these parameters in the IB-FV solver to enable reproducibility of results in the following sections.

The pressure at the wall, by virtue of the homogeneous Neumann BC, is $p_w = p_I = p_f$ and may also be quantified using the coefficient of pressure defined by,

$$\begin{aligned} C_p = (p_w - p_{\infty })/(0.5\rho _{\infty }V_{\infty }^2) \end{aligned}$$

The wall heat flux is related to the temperature gradients at the wall and is defined as,

$$\begin{aligned} q_w = k_w \displaystyle \frac{\partial T}{\partial r}\Big |_w \end{aligned}$$

where $k_w$ is the fluid thermal conductivity at the wall and is a function of the wall temperature $T_b$ (obtained from Sutherland’s law). Simple finite differencing may be employed for linear solution variation of temperature gradient in the near-wall region. The heat flux on the surface then follows as,

$$\begin{aligned} q_w = k_w \displaystyle \frac{T_I - T_w}{r_{bI}} \end{aligned}$$

A non-dimensional wall heat flux may also be defined in terms of Stanton number (St),

$$\begin{aligned} St = q_w /(0.5 \rho _{\infty } V_{\infty } c_p (T_o- T_w)) \end{aligned}$$

where $T_o$ is the total temperature of the freestream and $c_p$ is the constant pressure specific heat capacity.

Like the wall heat flux, the wall shear stress is a scalar quantity whose distribution over the surface is estimated to obtain the viscous drag acting on the body. The wall shear stress is obtained by adding up all components of the viscous force along the local tangential direction as,

$$\begin{aligned} \tau _w = (\tau _{xx} n_x + \tau _{xy}n_y) t_x + (\tau _{xy} n_x + \tau _{yy} n_y) t_y \end{aligned}$$

where $t_x = n_y$ and $t_y = -n_x$ denote the components of the local tangent vector and $n_x$ and $n_y$ are the components of the local normal to the surface. The conventional representation is to use the non-dimensional wall shear stress, which is referred to as the skin friction coefficient (or simply skin friction), $C_f$ defined as,

$$\begin{aligned} C_f = \tau _w /(0.5 \rho _{\infty } V_{\infty }^2) \end{aligned}$$

The computation of $C_f$ warrants the estimation of viscous stress components at the body faces. These may be obtained by first identifying a neighbourhood of F cells associated with each b point (and therefore a unique I cell) and then using an inverse distance weighted averaging of the velocity gradients in these F cells to obtain an estimate at the b point [for further details refer to Brahmachary et al. (2018)]. These estimates are consequently employed to calculate the viscous stresses.

3.8 Reconstruction for Euler Flows

It is important to highlight the differences and/or simplifications in the reconstruction approach discussed herein for compressible inviscid flows. In case of Euler flows, the only boundary condition available at b is $u_{\perp b}$ = 0 while the values for all remaining quantities ($u_{||}$, $p_b$ and $\rho _b$) and their gradients are obtained using inverse distance weighting (IDW) as described in Eqs. (9.10) and (9.11),

$$\begin{aligned} \phi _{b}= \frac{\sum _{i=1}^{i=n}w_i\phi _i}{\sum _{i=1}^{i=n}w_i} \end{aligned}$$

(9.10)

$$\begin{aligned} \nabla \phi _{b}= \frac{\sum _{i=1}^{i=n}w_i\nabla \phi _i}{\sum _{i=1}^{i=n}w_i} \end{aligned}$$

(9.11)

where $w_i=1/|d_i|$, $|d_i|$ being the distance between the centroids of the ith neighbour (which is a F cell) and b. Here, n represents the total number of node-sharing cells in the neighbourhood of the immersed cell.

In the following section, we shall explore the efficacy and versatility of the IB-FV solver that employs this HCIB strategy in an unstructured finite volume framework to estimate aerodynamic forces and heat loads in high-speed flows.

4 Numerical Investigations

This section is devoted to the numerical studies using the IB-FV solver for compressible inviscid and viscous flows. The importance of the interpolation strategy on the accuracy of the solution is investigated through a number of test cases involving simple moving bodies and complex stationary geometries on canonical problems in inviscid and laminar hypersonic regimes. We discuss the role of solution reconstruction on conservation errors in compressible flows. One of the critical issues related to non-conformal approaches is that of discrete conservation. Due to the non-conservative nature of the solution reconstruction performed in the I cells (as opposed to the solutions obtained at F cells by solving discrete form of the conservation laws), there is an inherent lack of conservation in IB approaches. This issue has not been addressed at length in the compressible flow regime, and we probe this aspect using two different test problems.

4.1 Transonic Flow Past Bump

The first test case is the transonic flow past a 10% thick bump. The computational domain is 3 $\times$ 1, and the associated boundary conditions are shown in Fig. 9.3. The inflow is at a freestream Mach number $M_{\infty }=0.675$ while the pressure at the outlet is fixed, $P_{out}=0.737$. This test case Ni (1982) leads to a normal standing shock nearly three quarters from the leading edge of the bump. We carry out simulations on four meshes, viz. 150 $\times$ 50, 225 $\times$ 75, 300 $\times$ 100 and 450 $\times$ 150 using the IB-FV solver. Computations have also been performed using a FV solver on body-fitted meshes of equivalent grid resolution. In Fig. 9.4a–d, we show the comparison of the solutions obtained using the non-conformal IB-FV solver along with the body-conformal FV solver. One can clearly observe that not only is the shock diffused in the coarsest grid, its location has also been inaccurately estimated with the IB-FV solver. With grid refinement, the shock location approaches that estimated using the FV solver, which is indeed conservative. One can notice that the shock location from all FV solutions is same (except the shock is diffused on coarser grids). We also see the differences between the two solvers from the pressure distributions in Fig. 9.5a and b where the average shock location using IB-FV approach depends on the grid resolution and agrees with those estimated by the FV solver only on the finest mesh and the computed results from Luo et al. (2006).

Fig. 9.3

Computational domain for transonic flow past bump along with boundary conditions

Fig. 9.4

Mach contours depicting normal standing shock for different mesh resolutions a 150 $\times$ 50, b 225 $\times$ 75, c 300 $\times$ 100 and d 450 $\times$ 150 (Min: 0.1, $\Delta$: 0.1, Max: 1.5) (Top: IB-FV solver; Bottom: FV solver on body-fitted mesh)

Fig. 9.5

Pressure distribution on the surface of the body from a FV solver on conformal grid and b IB-FV solver on non-conformal grid and its comparison with Luo et al. (2006)

These observations confirm that the solutions obtained using the IB-FV solver are not discretely conservative but the conservation errors diminish with grid refinement. We further investigate these discrete conservation errors by considering the supersonic flow past a wedge.

4.2 Supersonic Flow Past Wedge

We numerically simulate the supersonic flow past a wedge with a semi-vertex angle of 20$^{\circ }$ and a freestream Mach number $M_{\infty }=2$. This configuration is however not aligned with the underlying Cartesian mesh nor is the oblique shock that is the flow feature of interest. For this test problem as well, we simulate the flow on four different meshes in a domain of size 0.1 $\times$ 0.15. The details of the mesh are provided in Table 9.1. We compute the mass defect on every mesh as,

$$\begin{aligned} \Delta m = \sum \rho _f \ U_{\perp ,f} \ \Delta S_f \end{aligned}$$

(9.12)

Table 9.1 Mass defect $\Delta$m on different grids

Fig. 9.6

Variation of mass defect $\Delta$m with grid refinement

where the summation is over all the boundary faces of the domain as well as the interior faces shared by S and I cells, i.e. the summation is performed along the stair-step representation in Fig. 9.1. For the FV solver on body-fitted meshes, the mass defect would be of the order of the steady-state residuals, which is a result of the discrete mass conservation. Since the IB-FV framework has been shown to be not discretely conservative, we expect a finite mass defect larger than the steady-state residuals on every mesh. This is confirmed in Table 9.1 which shows the mass defect on the four different meshes. The errors are three orders of magnitude higher than the residuals, but decrease as the grid is refined. From Fig. 9.6, one can see that the mass error falls at a rate close to unity i.e. mass defect fall linearly with grid refinement. Thus, one can remark that there is a finite $\mathbf{O}(h)$ conservation error for the IB-FV approach similar to the observations made for a class of mesh-free methods (Sridar and Balakrishnan 2003) and the framework is strictly conservative only in the limit as grid spacing tends to zero.

4.3 Hypersonic Flow Past Double Ellipse

To demonstrate the ability of the IB-FV solver in handling hypersonic Euler flows past complex configuration, we study the high-speed high angle-of-attack flow past a double-ellipse configuration (Gustaffson et al. 1991). The freestream Mach number is $M_{\infty }=8.15$ and the angle of attack of 30$^{\circ }$ makes it challenging to accurately simulate the flow as well as estimate the surface pressure distribution. The double ellipse is immersed into two different Cartesian meshes with a total number of cells $n_c$ = 36,000 in a computational domain of $[-0.1,0.1] \times [-0.1,0.1]$—while one employs a uniform grid (see Fig. 9.7a) with equal grid spacing the other utilises a non-uniform spacing (see Fig. 9.7b) which is finer near the canopy region.

Fig. 9.7

a Uniform, b non-uniform Cartesian grid employed in IB-FV solver for flow over double ellipse

Fig. 9.8

a Pressure distribution and b Mach contours for hypersonic flow past double ellipse (Min: 0, $\Delta$: 0.5, Max: 8.15)

The significance of the mesh in the context of non-conformal IB-FV solver can be understood from Fig. 9.8a where the surface distribution of pressure coefficient $C_p$ is shown for both the uniform and non-uniform meshes. It can be observed that while results computed on both these meshes yield an overall fair agreement with the numerical data of Gustafsson et al. (1991), the uniform mesh is not very accurate in resolving the pressure jump across the weak canopy shock. The non-uniform mesh clustering however accurately captures the weak canopy shock and hints towards the need for selective mesh refinement in regions where sharp gradients in flow are likely. Figure 9.8b depicts the Mach contours that show the strong detached bow shock as well as the weak canopy shock. We can, therefore, remark that the IB-FV solver is capable of accurately computing flows with sharp flow gradients but necessitates sufficient local mesh resolution to also resolve the complex geometries.

Fig. 9.9

Location of body and shock at time $t=0$ s

Table 9.2 Position of centre of mass of cylinder (in m) at time $t \sim 0.3$s

4.4 Cylinder Lift-Off

To highlight the applicability of the IB-FV solver for moving body problems, we simulate the supersonic flow past a cylinder initially at rest but “lifts-off” due to the aerodynamic forces. The test case consists of a rectangular domain of size $0.1 \times 0.2$ with a cylinder of radius 0.05 m and density $\rho _c$ = 10.77 kg/m$^3$ placed at the bottom wall (0.15, 0.05), as shown in Fig. 9.9. The pre-shock condition is maintained as $\rho$=1.4 kg/m$^3$ and $p=1$ Pa, whereas the left boundary is assigned as post-shock state. The cylinder is considered rigid and the influence of gravity is neglected and we compare our solutions with available numerical results in the literature that make the same assumptions. Studies were conducted on uniform Cartesian grids whose details are provided in Table 9.2 which also contains the position of the centre of mass of the cylinder at a final time of $t \sim$ 0.3s. It can be observed that while there are differences in the position of the cylinder when compared with the results in Arienti et al. (2003), these differences tend to diminish with increasing mesh resolution. These differences can also be attributed to the fact that the reconstruction strategy in the I cells in the present work are different from those in Arienti et al. (2003). Figure 9.10 shows the pressure contours at two different time instances which clearly depict the complex unsteady flow phenomena. We also compare the time history of the trajectory of the cylinder with those computed by Sambasivan and UdayKumar (2009) in Fig. 9.11 and a good agreement in the results is further proof of the ability of the proposed IB-FV framework in computing high-speed Euler flows accurately.

Fig. 9.10

Pressure contours at a $t=0.16$ s (Min: 0, $\Delta$: 0.4, Max: 19.22), b $t=0.3$ s (Min: 0, $\Delta$: 0.4, Max: 19.22) on 1000 $\times$ 200 grid

Fig. 9.11

Trajectory of the centre of mass of the cylinder on 1000 $\times$ 200 grid

In the test case to follow, we shall investigate the efficacy of the present IB-FV flow solver for scenarios involving laminar hypersonic flows with an emphasis on the accurate prediction of wall heat flux and skin friction.

4.5 Hypersonic Flow Past a Flat Plate

We first numerically simulate the viscous compressible flow past a flat plate of length $L=0.5334$ m at a freestream Mach number $M_{\infty }=6$. Although the geometry is simple, the high freestream Reynolds number $Re_{\infty }=1.4 \times 10^{7}$ makes it an interesting test case to test the ability of the IB-FV solver in accurately predicting the wall property distributions. The freestream pressure and temperature are $P_{\infty }=2211.56$ Pa and $T_{\infty }=65$ K, respectively, and the surface of the flat plate is maintained at a constant temperature $T_{w}=100$ K. We consider a computational domain of size 0.1 $\times$ 0.5334 which is divided into a total number of control volumes $n_c$ = 50,000, with 250 grid points along the length of the body and 200 grid points normal to it. The grid is non-uniform with clustering near the wall surface and a minimum grid spacing of $\Delta y_{min}=4 \times 10^{-6}$ m is chosen to ensure that the boundary layers are well-resolved. The computations have also been performed using the FV solver as well for the sake of comparison.

Fig. 9.12

Distribution along the surface of the wall for a wall pressure and b Stanton number with numerical data of Lillard and Dries (2005)

Figure 9.12a shows the comparison of the pressure distribution along the surface of the flat plate obtained from the IB-FV and the FV solvers. The pressure distributions from both the solvers are in excellent agreement as is also the distribution of wall Stanton number in Fig. 9.12b. It is also interesting to note that the heat flux distribution computed suing the IB-FV solver also agrees well with the numerical data of Lillard and Dries (2005). Although the flat plate geometry conforms to the Cartesian grid, the IB-FV solver computes the near-wall quantities using a linear reconstruction as opposed to the FV solver which solves the conservation laws. The excellent comparison of wall pressure and Stanton number distributions is a testimony to the fact that the linear reconstruction suffices to accurately estimate the wall heat fluxes on simple geometries even at high Reynolds numbers.

Fig. 9.13

a Ramp geometry (schematic, not to scale), b locally adapted grid and c pressure contour for flow past compression ramp (Min: 0, $\Delta$: 51.66, Max: 620)

Fig. 9.14

Comparison of a pressure coefficient $C_p$, b skin friction coefficient $C_f$, c Stanton number St with experimental data Holden 1978

4.6 Hypersonic Flow Past a Compression Ramp

In order to consider non-aligned geometries, we numerically investigate the flow past a compression ramp which has been studied in the past both numerically as well as experimentally (Holden 1978). Figure 9.13a describes the configuration consisting of a straight ramp of length $L=0.4394$ m and a semi-vertex angle of 15$^{\circ }$. The freestream conditions are taken the same as that of the experimental study with $M_{\infty }=11.63$ and $Re_{\infty }$ = 552,216/m. The freestream temperature is $T_{\infty }$ = 67.05 K with the ramp surface kept at a constant temperature of $T_{w}$ = 294.38 K. The computational domain is initially divided into $n_c$ = 67,500 volumes with a minimum grid spacing of $\Delta y$ = 3.2 $\times$10$^{-4}$ m. This initial resolution was improved to properly capture the boundary layer by selective adaptation and the final adapted mesh shown in Fig. 9.13b had 229,338 control volumes with a minimum grid spacing of $\Delta y$ = 2$\times 10^{-5}$ m. This corresponds to a cell Reynolds number (based on freestream conditions and local grid resolution) around 11 and is shown to be sufficient to resolve the boundary layer.

Figure 9.13c shows the pressure contours where the leading edge shock emanating near the compression corner strikes the ramp and this region corresponds to the maximum pressure on the ramp surface. Figure 9.14a compares the surface distribution of coefficient of pressure $C_p$ which shows an excellent agreement with experimental data. The comparison of wall skin friction and Stanton number in Fig. 9.14b and c also agrees quite well with the experimental observations. These results demonstrate that the IB-FV solver is fairly accurate even when the geometries are not conforming to the underlying mesh, provided the mesh resolution near the boundary is sufficient enough. This demands a low value for the cell Reynolds number and can be achieved using selective adaptive refinement as in this study.

4.7 Hypersonic Flow Past a Cylinder

As a final test case, we consider the laminar hypersonic flow past a blunt configuration that has been studied experimentally in the past. This is a canonical configuration representative of the nose cone of re-entry geometries, and the test case is an ideal one to assess the IB-FV framework for high Reynolds number compressible flows past blunt geometries. The configuration is a circular cylinder of radius 0.0381 m (see Fig. 9.15a) in a hypersonic flow with freestream Mach number of $M_{\infty }$ = 8.03 and freestream Reynolds number of $Re_{\infty }$ = 1.835$\times$10$^5$. The cylinder walls are maintained at $T_{w}$ = 294.44 K while the freestream temperature is $T_{\infty }$ =124.94 K, following the experimental study by Wieting (1987). The computational domain of size 0.07 m $\times$ 0.14 m is initially discretised by a uniform Cartesian mesh with a grid spacing of 2.3$\times 10^{-4}$ m, into which the cylinder is immersed. This grid resolution is improved significantly by four levels of local mesh refinement resulting in a final grid of 244,433 control volumes that have a near-wall resolution of 1.43$\times 10^{-5}$ m.

Fig. 9.15

a Cylinder geometry and b pressure contour for flow past cylinder (Min: 0, $\Delta$: 5087, Max: 71,220)

Fig. 9.16

Pressure distribution along the cylinder and its comparison with experimental data (Wieting 1987)

Table 9.3 Comparison of stagnation point heat flux $q_o$

Figure 9.15b shows the pressure contours from the steady-state solution where the detached bow shock is clearly visible. The surface pressure distribution in Fig. 9.16 is in excellent agreement with the experimental data of Wieting (1987) (for both initial and final grids), indicating that the grid resolution is not critical in predicting the wall pressures. However, one can observe from Table 9.3 that this is not the case for stagnation point heat flux, which is severely under-predicted when compared to the experimental data. Surprisingly, the estimates of stagnation point wall heat flux showed little improvement with local adaptation. This is in stark contrast to the performance of the solver for the test case in Sect. 9.4.6 where the Stanton number distribution on the ramp surface was quite accurately predicted. The inaccurate predictions of the wall heat flux raise concerns regarding the reconstruction strategy and recent studies in Brahmachary (2019) point to the need to evolve physics-driven reconstruction with possibly non-linear/non-polynomial interpolants for velocities and temperature.

5 Conclusions

The present work is directed towards the development and assessment of a sharp-interface immersed boundary/finite volume approach for high-speed compressible flows in an unstructured Cartesian mesh framework. The methodology adopts a one-dimensional linear reconstruction that preserves the sharp geometric interface and the framework is rigorously tested for both inviscid and viscous flows. We show that the framework is not discretely conservative but the conservation errors are found to decrease with grid refinement, pointing to the consistency of the approach. Numerical investigations on inviscid test problems with stationary and moving bodies show that the IB-FV solver can quite accurately predict the wall pressures and aerodynamic forces. However, the numerical framework was not entirely accurate for laminar hypersonic flow problems. While the IB-FV solver could compute the wall pressures accurately for the three geometric configurations studied herein at high Reynolds number, it could compute the surface heat fluxes accurately only for non-blunt geometries. On blunt configurations, the IB-FV solver significantly underestimated the stagnation point heat flux and these estimates were largely unaffected by increasing grid resolution. The source of these errors in heat flux predictions clearly lies in the reconstruction accuracy and conservation errors, and a thorough diagnostic analysis (Brahmachary 2019) needs to be undertaken to uncover the deficiencies of the sharp-interface IB-FV solver and improve its performance for high Reynolds number hypersonic flows.