Coupling the Curvilinear Immersed Boundary Method with Rotation-Free Finite Elements for Simulating Fluid–Structure Interaction: Concepts and Applications

Abstract

The sharp interface curvilinear immersed boundary (CURVIB) method coupled with a rotation-free finite element (FE) method for thin shells provides a powerful framework for simulating fluid–structure interaction (FSI) problems for geometrically complex, arbitrarily deformable structures. The CURVIB and FE solvers are coupled together on the flexible solid–fluid interfaces, which contain the structural nodal positions, displacements, velocities, and loads calculated at each time level and exchanged between the flow and structural solvers. Loose and strong coupling FSI schemes are employed, enhanced by the Aitken acceleration technique to ensure robust coupling and fast convergence, especially for low mass ratio problems. Large-eddy simulation (LES) of turbulent flow FSI problems employ the dynamic Smagorinsky subgrid scale model with a wall model for reconstructing velocity boundary conditions near the immersed boundaries. In this chapter, the CURVIB-FE FSI algorithm is reviewed and its capabilities are demonstrated via a series of examples involving thin flexible structures undergoing very large deformations. The inverted flag problem is employed to validate the method, and the problem of a tri-leaflet aortic valve in an anatomic aorta is employed to demonstrate its potential in complex cardiovascular flow applications.

1 Introduction

Unsteady fluid–structure interaction (FSI) problems taking place in geometrically complex domains and involving large deformations of three-dimensional, thin structures are encountered in a broad range of engineering and biological problems across a range of Reynolds numbers and flow regimes. Examples range from inflating parachutes and flow-activated energy harvesting devices, to swimming aquatic organisms, to native as well as prosthetic heart valves, to name a few. The inherent complexity of such problems along with the highly nonlinear nature of the ensuing FSI, which is associated primarily with the large deformations of the solid, present unique challenges to numerical methods. Such challenges arise from, among others: (i) the need to model geometric and constitutive nonlinearities of the solid bodies; (ii) the often arbitrary complexity of the dynamically evolving flow domains, due to the arbitrarily large amplitude of the deformation thin flexible structures may undergo; and (iii) the challenges in obtaining robust and efficient FSI algorithms, especially in problems with low mass ratios (Sotiropoulos and Yang 2014; Baek and Karniadakis 2012) which are commonly encountered in cardiovascular flow simulations. These challenges along with recently developed approaches for tackling them constitute the main focus of this chapter.

There are two general approaches typically used for simulating complex flows with deformable boundaries: (1) the boundary conforming arbitrary Lagrangian Eulerian (ALE) approach; and (2) immersed boundary (IB) methods. The ALE approach (Hirt et al. 1974; Donea et al. 1982) is well suited for resolving near-wall viscous regions in high Reynolds number flows due to its inherent body-fitted mesh structure that conforms to boundaries at all times. However, for significant movement of the boundaries, ALE methods are cumbersome to apply to problems with large deformations since they require frequent remeshing in order to prevent the mesh from becoming severely distorted. The remeshing procedure is computationally expensive making ALE methods inefficient in complex three-dimensional problems. Fixed, non-boundary conforming, grid methods provide another alternative to solving problems with deformable boundaries and complex geometry. Such methods are generally referred to as immersed boundary (IB) methods and are especially attractive for simulations of complex flows in engineering and biology because they do not require remeshing and can readily handle arbitrarily large deformations of the structures. The various types of IB methods have been recently reviewed by Sotiropoulos and Yang (2014). The interested reader is referred to this paper as well as the earlier review by Mittal and Iaccarino (2005) for details. Promising approaches that enhance the capabilities of IB methods in the simulation of fluid flow interacting with moving/deformable bodies at high Re numbers are methods involving adaptive mesh refinements (Vanella et al. 2010; Angelidis et al. 2016).

In this chapter, we focus our review of the literature exclusively on IB numerical approaches proposed for handling FSI of flexible structures in complex domains. We pay special attention to the distinction between discretization techniques used to handle the flow and those applied to structural governing equations, since a range of formulations have been proposed in the past. These include pure finite-difference (FD) (Griffith et al. 2009; Wiens and Stockie 2015; Zhu and Peskin 2002; Le et al. 2009; Luo et al. 2008) or finite element (FE) (Dettmer and Períc 2006; Barker and Cai 2010; Bazilevs et al. 2012) methods for both the flow and structural equations as well as mixed formulations combining FD (or finite volume) discretization for the flow with FE for the structural equations (Zheng et al. 2010; Farhat and Lakshminarayan 2014).

Diffused interface IB methods use FD for both the fluid and structural solvers (Griffith et al. 2009). In this approach, the loading on the structural surface, due to interaction with the fluid, is introduced by appropriately defined body forces in the momentum fluid equations. A number of successful applications of such methods, which we shall refer to herein as IB-FD-FD methods for their use of FD discretization for both the fluid and solid equations, have been reported over the years (Wiens and Stockie 2015; Zhu and Peskin 2002; Le et al. 2009). The accuracy of such methods can be improved by incorporating local mesh refinement as was done in Griffith et al. (2009). One potential difficulty with this class of methods, however, arises from treating the solid surface as diffused interface, which complicates the accurate calculation of the wall shear stress field on the surface. Yet, such detailed calculations may be required in cardiovascular flow problems, such as heart valve flow simulations, in which complex wall shear stress patterns on the valve leaflets have been linked with increased potential for aortic valve diseases and other aortopathies (Ge and Sotiropoulos 2010).

A sharp interface IB method using FD formulations for both the flow and structural equations was proposed by Luo et al. (2008). This method was formulated for linear viscoelastic solids and applied to simulate two-dimensional FSI in laryngeal aerodynamics. The same formulation was later modified to incorporate a FE formulation for the structural equations and applied to simulate FSI of a high mass ratio 3D flapping wing at very low Reynolds number (Re = 50) (Luo et al. 2010). Tian et al. (2014) further extended this method to simulate several complex FSI problems at low Reynolds numbers (Re ∼ 102). An ALE formulation utilizing the so-called embedded boundary approach was proposed by Farhat and Lakshminarayan (2014) for solving compressible FSI problems for external aerodynamics applications at high Reynolds numbers. This approach employs finite volume discretization for the fluid equations with finite elements for the structural equations. While this approach can work well for structures in unbounded domains, remeshing difficulties may arise when the structure is embedded within a complex confined domain. A pure finite-element-based formulation, for both the flow and the structural equations, was recently proposed by Kamensky et al. (2015). This method employs the immersogeometric FSI approach and was applied to simulate FSI of a bioprosthetic heart valve in a straight aorta.

In FSI simulations of biological tissues, e.g., heart valve leaflet interaction with blood flow, it is critical to use a relevant and efficient structural model that is able to realistically represent the deformation of the tissue under loads imposed by the pulsatile blood flow. Such undertaking, however, is not a trivial task since the large deformations of the tissue and its concomitant geometric nonlinearity pose major modeling challenges. To circumvent these challenges recent studies attempting to simulate FSI of tissue valves chose to either use simplified membrane-like materials (Borazjani 2013) or treat the valve leaflets as thick bodies (Tian et al. 2014). However, biological tissues of leaflets are normally thin and they exhibit significant bending. Therefore, a shell model for the solid body is a more appropriate choice (Kamensky et al. 2015; Sacks et al. 2009). Most finite element (FE) methodologies for handling shells, however, are computationally very demanding as they employ two or three nodal rotations alongside with three nodal translations, i.e., 5 or 6 degree of freedom per node. An exhaustive review of this large body of literature is beyond the scope of this chapter, but the reader is referred to a number of recent review papers on the topic (Stolarski et al. 1995; Gal and Levy 2006). Note that the efficiency of the FE shell model becomes of paramount concern in FSI simulations of complex problems where the need to couple the fluid and structural solvers together can dramatically increase the computational cost per time step. For that, in our work we have selected to adapt and incorporate in the FSI methodology a previously developed nonlinear, rotation-free triangular shell element formulation (Stolarski et al. 2013), which has already been shown to provide accurate and robust solutions of various thin shell FE problems. We have successfully coupled such an approach with the sharp interface curvilinear IB (CURVIB) method, previously developed by our group (Ge and Sotiropoulos 2007) to simulate FSI problems (Gilmanov et al. 2015, 2018). In this chapter, we review the basic features of this novel CURVIB-FE-FSI formulation.

The CURVIB method employs second-order accurate, central finite differencing discretization for the flow equations along with an efficient fractional step approach for satisfying the discrete continuity equation to machine zero in curvilinear grids. This method has also been extended to carry out large-eddy simulation (LES) of turbulent flows using wall models for reconstructing boundary conditions at the immersed boundary nodes (Kang et al. 2011). The LES version of the CURVIB method has been validated extensively for a broad range of complex turbulent flows. Some recent examples include: turbulent flow past an axial flow turbine in an open channel (Kang et al. 2014); open-channel turbulence interacting with a mobile sediment bed (Khosronejad and Sotiropoulos 2014), and complex rigid structures interacting with a free surface (Calderer et al. 2014). As such the CURVIB method provides an efficient and accurate approach for simulating geometrically complex flows across a range of Reynolds numbers. Furthermore, since the CURVIB method employs unstructured triangular meshes to discretize immersed boundaries, the method is ideally suited for coupling it with our efficient rotation-free FE shell model (Stolarski et al. 2013), which is ideally suited for handling FSI problems involving arbitrarily large deformations. To enable this coupling, we report herein on a number of algorithmic advances and significant improvements of our previously developed methodology. Our FE solver is highly efficient and versatile for thin bodies—it can be applied in analysis of a variety of structures including engineering structures such as shells, plates, beams and may incorporate various material properties, including those characterizing biological tissues such as heart valves and arterial walls.

In this chapter, we present the recently developed methodology and demonstrate its ability to simulate very challenging FSI problems involving large amplitude oscillations. The first problem is that of an inverted elastic flag, recently studied experimentally by Kim et al. (2013), which is especially challenging because: (1) the flow occurs at high Reynolds number and requires implementing the resulting CURVIB-FE-FSI formulation in conjunction with LES; and (2) depending on the elasticity of the flag the FSI problem exhibits dynamically rich variety of solutions (Kim et al. 2013). To the best of our knowledge, the first numerical solution of that problem was reported in Gilmanov et al. (2015). Here, we report simulations for a set of parameters under which the flag undergoes periodic oscillations and show that the computed motion of the flag is in excellent agreement with the measurements. In the second application problem, we demonstrate the ability of the coupled CURVIB-FE-FSI method to simulate the FSI of a tri-leaflet valve in an anatomic aorta. Our simulations capture the rich 3D vorticity dynamics during the opening and closing of the valve leaflets.

The chapter is organized as follows. In Sect. 4.2, we describe the governing equations for both fluid and solid structures. In Sect. 4.3, we present the numerical approach used to solve the coupled system of fluid and solid equations with appropriate boundary conditions. In Sect. 4.4, the flapping of an inverted flag is presented. In this section, we also demonstrate the applicability of the proposed FSI approach to simulate pulsatile blood flow in an anatomic aorta with a tri-leaflet heart valve using both isotropic and nonlinear anisotropic materials (Gilmanov et al. 2018). Finally, in the Sect. 4.5, we summarize the major features of he presented approach.

2 Governing Equations

We consider FSI of a deformable body ${\Omega }_{\text{s}}$ submerged in an incompressible fluid occupying a volume ${\Omega }_{\text{f}}$ bounded by $\partial {\Omega }_{\text{f}}$, the method is applicable to multiple deformable thin bodies but for the ease of presentation and without loss of generality we present the method for a single body.

In what follows, we use bold symbols for vectors and bold underlined symbols for tensors and matrices. The regular and italic symbols are reserved for scalar and tensor components, respectively. The overbar notation indicates known and/or prescribed values.

2.1 The Equations for the Fluid Domain

In general, fluid boundaries can be presented as consisting of three non-overlapping parts: $\partial {\Omega }_{\text{f}} = {\Gamma }_{\text{f}}^{\text{N}} \cup {\Gamma }_{\text{f}}^{\text{D}} \cup {\Gamma }^{\text{fsi}}$. Here, ${\Gamma }_{\text{f}}^{\text{D}}$ and ${\Gamma }_{\text{f}}^{\text{N}}$ are the stationary boundaries in which Dirichlet and/or Neumann boundary conditions are specified. ${\Gamma }^{\text{fsi}}$ is the interface between the fluid domain and the solid domain, i.e., the moving interface the configuration of which needs to be determined by solving the FSI problem.

The equations governing the motion of Newtonian incompressible fluid in a domain ${\Omega}_{\text{f}}$ the Navier–Stokes and continuity equations, which read in vector/tensor notation as follows:

$$\begin{aligned} & \rho_{\text{f}} \frac{{{\text{d}}\varvec{v}}}{\text{d}t} = {\nabla} \cdot {\underline{\varvec{\sigma}}}_{\text{f}} \,{\text{in}}\,\Omega_{\text{f}} , \\ & \nabla \cdot \varvec{v} = 0\,{\text{in}}\,\Omega_{\text{f}} . \\ \end{aligned}$$

(4.1)

In the above equations, $\rho_{\text{f}}$ is the mass density of the fluid, d/dt is the material or Lagrangian time derivative, v is the fluid velocity vector, and ${\underline{\varvec{\sigma}}}_{\text{f}}$ is the fluid stress tensor. The above equations are subjected to various boundary conditions for the velocity v on the various segments comprising the fluid boundary. For example, on the Dirichlet portion of the boundary ${\Gamma }_{\text{f}}^{\text{D}}$ Dirichlet boundary conditions and on the Neumann segment of the boundary ${\Gamma }_{\text{f}}^{\text{N}}$, a stress boundary condition of the following form may be applied:

$$\varvec{v} = \bar{\varvec{v}}\,{\text{on}}\,{\Gamma }_{\text{f}}^{\text{D}} \quad {\underline{\varvec{\sigma}}}_{\text{f}} \cdot \varvec{n}_{\text{f}} = \bar{\varvec{t}}_{\text{f}} \,{\text{on}}\,{\Gamma }_{\text{f}}^{\text{N}}$$

(4.2)

where $\bar{\varvec{v}}$ and $\bar{\varvec{t}}_{\text{f}}$ are known functions, $\varvec{n}_{\text{f}}$ is the normal unit vector to the ${\Gamma }_{\text{f}}^{\text{N}}$ boundary. For FSI problems, the immersed deformable body has its own displacement field u, velocity field $\dot{\varvec{u}}$, and stress field ${\underline{\varvec{\sigma}}}_{\text{s}}$. On ${\Gamma }^{\text{fsi}}$ the velocity field and the normal stress field must be continuous. This physical requirement gives rise to the following set of boundary conditions on the FSI segment of the fluid boundary:

$$\varvec{v} = \dot{\varvec{u}},\quad {\underline{\varvec{\sigma}}}_{\text{f}} \cdot \varvec{n}_{\text{f}} = {\underline{\varvec{\sigma}}}_{\text{s}} \cdot \varvec{n}_{\text{s}} \,{\text{on}}\,{\Gamma }^{\text{fsi}}$$

(4.3)

Here, $\varvec{n}_{\text{f}}$ and $\varvec{n}_{\text{s}}$ are the local normal unit vectors on the fluid and solid interfaces, respectively. Note, therefore, that on the ${\Gamma }^{\text{fsi}}$ segment of the boundary both Dirichlet and Neumann conditions must be satisfied (given by Eq. 4.3) so that the problem is well posed and the Navier–Stokes Eqs. (4.1) supplied with boundary conditions (4.2) on ${\Gamma }_{\text{f}}^{\text{D}}$ and ${\Gamma }_{\text{f}}^{\text{N}}$ can be solved.

To facilitate the subsequent presentation of the FSI algorithm, we denote the governing equations for the fluid domain as an operator ${\boldsymbol{\mathcal{F}}}$, which receives the input information from the boundary conditions and yields the pressure p and velocity field v inside the fluid domain ${\Omega}_{\text{f}}$ as follows:

$$\left( {p,\varvec{v}} \right) = {\boldsymbol{\mathcal{F}}}\left( {\bar{\varvec{v}},\overline{{\varvec{t}_{\text{f}} }} ,\dot{\varvec{u}},{\underline{\varvec{\sigma}}}_{\text{s}} } \right)\,{\text{in}}\,{\Omega}_{\text{f}}$$

(4.4)

here $\dot{\varvec{u}}$ and ${\underline{\varvec{\sigma}}}_{\text{s}}$ are applied at the boundary ${\Gamma }^{\text{fsi}}$. Equation (4.4), therefore, should be viewed as the operator notation for Eqs. (4.1–4.3).

2.2 The Equations for the Solid Domain

In the solid domain, we use the Lagrangian viewpoint to describe the motion of the solid undergoing large deformations. In this approach, the current position r of a material point at time t is related to its position R at the reference configuration by the mapping ${\varvec{\Phi}}{:}\varvec{r} =\varvec{\varPhi}(\varvec{R})$. The gradient of that transformation (the so-called deformation gradient) is therefore: $\varvec{F} = \partial\varvec{\varPhi}/\partial \varvec{R}.$ The displacement and velocity of a material point are defined as:

$$\varvec{u} = \varvec{r} - \varvec{R},\quad \dot{\varvec{u}} = {\text{d}}\varvec{u}/{\text{d}}t$$

(4.5)

The momentum equations for the solid part, formulated in the current configuration, have the following form (Kang et al. 2011):

$$\rho_{\text{s}} \frac{{{\text{d}}\dot{\varvec{u}}}}{{{\text{d}}t}} = \nabla \cdot {\underline{\varvec{\sigma}}}_{\text{s}} \,{\text{in}}\,{\Omega}_{\text{s}} ,$$

(4.6)

where $\rho_{\text{s}}$ is the current mass density of the material. Here, ${\underline{\varvec{\sigma}}}_{\text{s}}$ is the Cauchy stress tensor for the solid structure, with the symbol $\nabla$ representing the gradient operator in the current configuration. The boundary of the solid structure can be represented as sum of non-overlapping parts $\partial {\Omega}_{\text{s}} = {\Gamma }_{\text{s}}^{\text{N}} \cup {\Gamma }_{\text{s}}^{\text{D}} \cup {\Gamma }^{\text{fsi}}$, where the indices D and N denote boundaries with Dirichlet and Neumann conditions, respectively:

$$\dot{\varvec{u}} = \varvec{\bar{\dot{u}}}\quad {\text{on}}\quad {\Gamma }_{\text{s}}^{\text{D}} ,\quad {\underline{\varvec{\sigma}}}_{\text{s}} \cdot \varvec{n}_{\text{s}} = \bar{\varvec{t}}_{\text{s}} \quad {\text{on}}\quad {\Gamma }_{\text{s}}^{\text{N}}$$

(4.7)

where ${\Gamma }_{\text{s}}^{\text{D}}$ and ${\Gamma }_{\text{s}}^{\text{N}}$ represents the portions of the surface of the body in its current configuration where Dirichlet and Neumann conditions are applied, respectively, $\bar{\varvec{t}}_{\text{s}}$ is a traction vector acting on the surface, $\varvec{n}_{\text{s}}$ is a unit normal to the boundary and $\varvec{\bar{\dot{u}}}$ is the velocity prescribed on the surface.

For FSI problems, additional boundary conditions must be implemented on the ${\Gamma }^{\text{fsi}}$:

$$\dot{\varvec{u}} = \varvec{v}\,{\text{on}}\,{\Gamma }^{\text{fsi}} ,\quad {\underline{\varvec{\sigma}}}_{\text{s}} \cdot \varvec{n}_{\text{s}} = \varvec{t}_{\text{f}} \,{\text{on}}\,{\Gamma }^{\text{fsi}}$$

(4.8)

here ${\Gamma }^{\text{fsi}}$ is part of the moving structure surface the configuration of which needs to be determined by solving the FSI problem, $\varvec{t}_{\text{f}} = {\underline{\varvec{\sigma}}}_{\text{f}} \cdot \varvec{n}_{\text{f}}$ is a traction vector which acts on this part of surface from the fluid, ${\underline{\varvec{\sigma}}}_{\text{f}}$ and $\varvec{n}_{\text{f}}$ are the stress tensor and surface normal unit vector from the fluid. We will discuss later how to define the traction vector for thin surfaces.

The solid momentum equations and the boundary conditions can be recast in terms of an operator ${\boldsymbol{\mathfrak{H}}}$, which incorporates both the (kinematic and dynamic) boundary conditions and constitutive equations to yield the velocity $\dot{\varvec{u}}$ and displacement field u

$$\left( {\varvec{u},\dot{\varvec{u}}} \right) = {\boldsymbol{\mathfrak{H}}}\left( {\bar{\varvec{v}},\bar{\varvec{t}},\varvec{v},\varvec{t}_{\text{f}} } \right)\,{\text{in}}\,{\Omega}_{\text{s}} ,$$

(4.9)

here v and $\varvec{t}_{\text{f}}$ are applied at the boundary ${\Gamma }^{\text{fsi}}$ .

3 Numerical Algorithms for Fluid–Structure Interaction

A sharp interface IB algorithm for solving FSI problems with thin deformable structures embedded in a fluid domain requires developing and integrating the following algorithmic components: (1) an algorithm for solving the fluid flow equations (Sect. 4.3.1); (2) an algorithm for solving the thin shell structural equations (Sect. 4.3.2); (3) an approach for defining the action from the thin shell onto the surrounding fluid by identifying the IB nodes in the vicinity of the body where boundary conditions need to reconstructed (Sect. 4.3.3); (4) an approach for calculating the action from the fluid to the thin shell body computing the forces due to pressure and shear (Sect. 4.3.4); and (5) an algorithm that integrates the fluid and solid solvers into a coupled FSI formulation. In this section, we discuss the approaches we adopt in this work to develop these algorithmic components (Sect. 4.3.5).

3.1 The Fluid Solver ${\boldsymbol{\mathcal{F}}}$

The fluid solver is based on the CURVIB approach (Ge and Sotiropoulos 2007) which uses the hybrid stagger/non-staggered approach originally proposed by Gilmanov and Sotiropoulos (2005) to solve the governing equations in generalized curvilinear grids (Ge and Sotiropoulos 2007). The Navier–Stokes and continuity equations (4.1) are partially transformed in generalized curvilinear coordinates and read in tensor form (repeated indices $j = 1, 3$ assumes summation) as follows:

$$\frac{\partial }{{\partial \xi^{j} }}\left( {\frac{{V^{j} }}{J}} \right) = 0,\quad \frac{{\partial v_{q} }}{\partial t} + C\left( {v_{q} } \right) + G_{q} \left( p \right) - \frac{1}{\text{Re}}D\left( {v_{q} } \right) = 0, \quad q = 1,2,3,$$

(4.10)

where the Cartesian velocity vector is denoted as $\varvec{v}\left( {v_{1} , v_{2} , v_{3} } \right)$, p, the pressure divided by the density $\rho_{\text{f}} ,V^{j} = v_{r} \xi_{{x_{r} }}^{j}$ is the jth contravariant velocity component in the general curvilinear coordinate system $\xi \left( {\xi_{1} , \xi_{2} , \xi_{3} } \right)$, J is the Jacobian of the geometric transformation $J = \partial \left( {\xi_{1} , \xi_{2} , \xi_{3} } \right)/\partial \left( {x_{1} , x_{2} , x_{3} } \right)$, and $g^{rm} = \xi_{{x_{q} }}^{r} \xi_{{x_{q} }}^{m}$ is the contravariant metric tensor. The convective $C\left( {v_{q} } \right)$, gradient $G_{q} (p)$, and viscous $D\left( {v_{q} } \right)$ operators in Eq. (4.10) are defined in curvilinear coordinates as (the repeated indexes r, m imply summation over the values 1, 2, 3):

$$\begin{aligned} C\left( {v_{q} } \right) & = J\frac{ \partial }{{ \partial \xi^{r} }} \left( {\frac{{V^{r} }}{J}v_{q} } \right),\quad q = 1, 2, 3, \\ D\left( {v_{q} } \right) & = J\frac{ \partial }{{ \partial \xi^{r} }} \left( {\frac{{g^{rm} }}{J}\frac{{\partial v_{q} }}{{\partial \xi^{m} }}} \right), \\ G_{q} (p) & = J \frac{ \partial }{{ \partial \xi^{r} }}\left( {\frac{{\xi_{{x_{q} }}^{r} }}{J}p} \right). \\ \end{aligned}$$

(4.11)

The above equations are discretized via a hybrid staggered/non-staggered approach using three-point central differencing for all spatial derivatives and integrated in time via a second-order accurate fractional step, pressure projection method. The momentum equations are solved with a Jacobian-free solver, while flexible generalized minimal residual (FGMRES) method with multigrid pre-conditioner is used to solve the Poisson equation to satisfy the discrete continuity equation to machine zero (see Ge and Sotiropoulos 2007 for details).

Complex immersed boundaries are handled using a sharp interface IB method with velocity reconstruction along the local normal to the body (Ge and Sotiropoulos 2007; Gilmanov and Sotiropoulos 2005; Borazjani et al. 2008). Some details concerning the reconstruction method for thin flexible boundaries will be provided in a subsequent section of this chapter.

The CURVIB method has been recently extended to carry out LES of turbulent flows in geometrically complex domains. The details of the LES version of our flow solver can be found in Kang et al. (2011, 2014). Here, it suffices to mention that the dynamic Smagorinsky model (Germano et al. 1991) is used for subgrid-scale closure with three-point central, second-order accurate finite differencing for the convective terms. Boundary conditions at IB nodes in the vicinity of complex immersed boundaries are reconstructed using a wall model approach adapted for the CURVIB method by Kang et al. (2011). In this chapter, we will report the first application of the LES version of method to simulate FSI of a flexible structure at high Reynolds number.

3.2 The Solid Solver ${\boldsymbol{\mathfrak{H}}}$: Finite Element Model for Thin Shells

The momentum equations for the solid (Eq. 4.6) can be expressed in various weak formulations using the principle of virtual work. In this work, we select the Lagrangian version of the weak form, which is related to the initial configuration, uses the second Piola–Kirchhoff stress tensor $\underline{\varvec{S}}$ and the variation of the Green–Lagrange strain tensor $\underline{\varvec{E}}$. By virtue of how they appear in the principle of virtual work given below, these two tensors constitute a dual set in the reference configuration representing volume $V_{0}$ bounded by the surface boundary $A_{0}$. This version of the weak form reads as follows:

$$\iiint\limits_{{V_{0} }} {\left( {\delta \underline{\varvec{E}}^{\text{T}} \underline{\varvec{S}} + \delta \varvec{u}^{\text{T}} \rho_{\text{s}} \varvec{\ddot{u}}} \right){\text{d}}V_{0} } - \iint\limits_{{A_{0} }} {\delta \varvec{u}^{\text{T}} \varvec{t}_{0} {\text{d}}A_{0} } = 0.$$

(4.12)

In the above equation, $\rho_{\text{s}}$ is the constant density of the solid in the original configuration, $\varvec{t}_{0}$ represent the surface loads in that configuration, and $\varvec{\ddot{u}}$ is the acceleration. To focus on the essential features of the algorithm in the illustrative examples presented in this chapter the Neo–Hookean (Macosko 1994) constitutive equation is used. Thus, in any fixed, local coordinate system the stress and strain tensors are related as follows:

$$\underline{\varvec{S}}^{\text{loc}} = \underline{\varvec{D}}^{\text{loc}} \underline{\varvec{E}}^{\text{loc}}$$

(4.13)

with

$$\underline{\varvec{D}}^{\text{loc}} = \frac{Y}{{1 - \nu^{2} }}\left[ {\begin{array}{*{20}c} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & {\frac{1 - \nu }{2}} \\ \end{array} } \right],$$

(4.14)

where Y is the Young’s modulus and $\nu$ is the Poisson’s ratio, index loc indicates that constitutive equation is described in a local Cartesian system. Having the stresses defined in that specific system, they can be transformed to any other system by the usual transformation roles for tensors.

Although, to simplify our exposition of the concepts, in the examples presented here the constitutive equations defined above are used, the overall methodology described here has been recently combined with complex material behavior, more appropriate for biological applications. Gilmanov et al. (2016) incorporated a general, hypereleastic constitutive model in the rotation-free, large deformation, shell finite element (FE) formulation and applied it to dynamic simulations of an aortic heart valve. In a forthcoming paper (Gilmanov et al. 2018), we incorporate the rotation-free thin shell FE method for nonlinear, anisotropic, hyperplastic tissues (Gilmanov et al. 2016) in the CURVIB-FE-FSI framework (Gilmanov et al. 2015). The main goal of that paper was to provide quantitative illustrations of the significant effects that the material properties of the heart valve leaflets have on hemodynamics.

We consider only thin shell models for the solid domain. In the Kirchhoff–Love model of thin shells (Timoshenko and Woinowsky-Krieger 1959) the position vector R of any point within the volume of the shell in the reference configuration is defined in terms of the surface curvilinear coordinates and the local normal distance $\zeta$ to the middle surface, with $- h_{0} /2 \le \zeta \le h_{0} /2$, and $h_{0}$ being the thickness of the shell. The position of the points in the current configuration of the shell r is defined in the same way and can be mapped back to the reference configuration using the same local normal distance to the middle surface $\zeta$. For the Kirchhoff–Love model of thin shells the components of the Green–Lagrange strain tensor in the entire volume of the shell can be expressed via the deformation of the shell’s middle surface as follows (Stolarski et al. 2013):

$$E_{ij} = E_{ij}^{\text{m}} + \zeta E_{ij}^{\text{b}}.$$

(4.15)

Here $E_{ij}^{\text{m}}$ are the membrane and $E_{ij}^{\text{b}}$ the bending components of the strain tensor.

We adopt here the model developed by Stolarski et al. (2013), which employs triangular finite elements and approximates the shell curvature tensor without using the rotational degrees of freedom. To accomplish that the curvature of a given element is associated with nodal displacements of that element as well as with nodal displacements of the three surrounding elements, this permits definition of a complete quadratic polynomial, representing configuration of that group of four elements (called “the patch”) in a moving with the shell rectilinear coordinate system. This polynomial, simply by its differentiation, permits for simple, and accurate, approximations of the element curvature tensor at any stage of the large deformation process. Most importantly, since the above approach is used only to compute the bending strains within the element and the computation of the membrane strains is based on the flat geometry of the element, the non-physical membrane locking is automatically avoided. For the derivation and the details of the method the reader is referred to Stolarski et al. (2013).

The outlined approach leads to the discretized FE version of the governing equations for the structure. By virtue of Eq. (4.15), the weak formulation of Eq. (4.6) can be written in the following form, containing the sum over all elements $e = 1, \ldots ,\overline{E}$ of the triangulated domain:

$$\mathop \sum \limits_{e = 1}^{{\overline{E} }} \left( {\iiint\limits_{{\_V_{0} }} {\left( {\delta \varvec{u}_{e}^{\text{T}} \left( {\underline{\varvec{B}}^{\text{m}} + \zeta \underline{\varvec{B}}^{\text{b}} } \right)^{\text{T}} \underline{\varvec{S}} - \delta \varvec{u}_{e}^{\text{T}} \rho_{\text{s}} \varvec{b} + \delta \varvec{u}_{e}^{\text{T}} \rho_{\text{s}} \varvec{\ddot{u}}_{\varvec{e}} } \right)} {\text{d}}V_{0} - \iint\limits_{{A_{0} }} {\delta \varvec{u}_{e}^{\text{T}} \varvec{t} {\text{d}}A_{0} }} \right) = 0,$$

(4.16)

where $\varvec{u}_{e}$, $\varvec{\ddot{u}}_{e}$ are the displacement and acceleration within the element e, $\underline{\varvec{B}}^{\text{m}}$ and $\underline{\varvec{B}}^{\text{b} }$ are membrane and bending strain-displacement matrices, respectively. Thus, the vector of internal forces is

$$\varvec{f}_{e}^{\text{int}} = \iiint\limits_{{V_{0e} }} {}\left[ {\left( {\underline{\varvec{B}}^{\text{m}} } \right)^{\text{T}} \underline{\varvec{T}}^{\text{T}} \underline{\varvec{D}}^{\text{loc}} \varvec{T}\underline{\varvec{E}}^{\text{m}} + \zeta^{2} \left( {\underline{\varvec{B}}^{\text{b}} } \right)^{\text{T}} \underline{\varvec{T}}^{\text{T}} \underline{\varvec{D}}^{\text{loc}} \underline{\varvec{T}} \underline{\varvec{E}}^{\text{b}} } \right]{\text{d}}V_{0} ,$$

(4.17)

where superscript indices (m) and (b) indicate membrane and bending-related matrices in the curvilinear coordinate system on the surface (Stolarski et al. 2013), while matrix $\underline{\varvec{T}}$ represents the necessary transformation of tensors to make the representation of the stresses and strains in the correctly related coordinate systems. Because of the space restrictions, the detailed formulation of all matrices we employ is not given here. Instead, we refer the Readers to the recently published paper (Stolarski et al. 2013), where all such details of the formulation are presented.

The element vector of the nodal external forces $\varvec{f}_{e}^{\text{ext}}$ and the element mass matrix $\varvec{M}_{e}$ resulting from the presented formulation take the following form

$$\varvec{f}_{e}^{\text{ext}} = \iint\limits_{{A_{0e} }} {\varvec{N}^{\text{T}} \varvec{t }{\text{d}}A_{0} },\quad \underline{\varvec{M}}_{e} = \iiint\limits_{{V_{0e} }} {\rho_{\text{s}} \varvec{N}^{\text{T}} \varvec{N}{\text{d}}V_{0} },$$

(4.18)

where t is a traction vector, and N is a vector of linear basis functions (Stolarski et al. 2013). Here, the external forces $\varvec{f}_{e}^{\text{ext}} (\varvec{u},\varvec{t})$ depend both on structure displacements u and the applied fluid traction t. Assembly of the above vectors and matrices leads to the following final form of the structural domain equations:

$$\varvec{f}^{\text{int}} (\varvec{u}) + \underline{\varvec{M}} \varvec{\ddot{u}} = \varvec{f}^{\text{ext}} (\varvec{u}, \varvec{t}).$$

(4.19)

In this chapter, three types of boundary conditions for the shell are used: free, hinged, and fixed boundary conditions. Detailed description and implementation of these boundary conditions one can find in Stolarski et al. (2013).

In the numerical integration of some dynamic, nonlinear problems with high frequency modes, a dissipative mechanism is needed in Eq. (4.19) to dump spurious oscillations and help get converged solutions (Smith and Griffith 2004). If dissipation is to be included in the system, a term related to the velocities has to be added in Eq. (4.19) as follows:

$$\varvec{f}^{\text{int}} (\varvec{u}) + \underline{\varvec{M}} \varvec{\ddot{u}} + \underline{\varvec{D}} \dot{\varvec{u}} = \varvec{f}^{\text{ext}} (\varvec{u}, \varvec{t}),$$

(4.20)

where the matrix $\underline{\varvec{D}}$ defines the dissipation term.

The detailed description of the solid solver algorithm with all matrices can be found in Stolarski et al. (2013). A short description of this algorithm is presented below.

We employ the Newmark time integration algorithm (Newmark 1959) to solve solid structure Eq. (4.20), which is formulated as follows:

$$\begin{aligned} \dot{\varvec{u}}^{n + 1} & = \dot{\varvec{u}}^{n} + {{{\Delta}}} t\left( {1 - \gamma } \right)\varvec{\ddot{u}}^{n} + {{{\Delta}}} t\gamma \varvec{\ddot{u}}^{n + 1} , \\ \varvec{u}^{n + 1} & = \varvec{u}^{n} + {{{\Delta}}} t\varvec{u}^{n} + {{{\Delta}}} t^{2} \left( {\frac{1}{2} - \omega } \right)\varvec{\ddot{u}}^{n} + {{{\Delta}}} t^{2} \omega \varvec{\ddot{u}}^{n + 1} , \\ \end{aligned}$$

(4.21)

where ${{{\Delta}}} t$ is the time step, subscript $n, n + 1$ indicates time level $t^{n + 1} = t^{n} + {{{\Delta}}} t$, and $\gamma , \omega$ are parameters that determine the stability and accuracy of the scheme. Implicit schemes are unconditionally stable for $2\omega \ge \gamma \ge 0.5$. The Newmark scheme has second-order accuracy for $\gamma = 0.5, \omega = 0.25$ (Smith and Griffith 2004). From Eq. (4.21), one gets the following formulas for the velocity and acceleration vectors

$$\begin{aligned} \varvec{\ddot{u}}^{n + 1} & = \frac{1}{{\omega {{{\Delta}}} t^{2} }}\left( {\varvec{u}^{n + 1} - \varvec{u}^{n} } \right) - \frac{1}{{ \omega {{{\Delta}}} t}}\dot{\varvec{u}}^{n} - \left( {\frac{1}{2\omega } - 1} \right)\varvec{\ddot{u}}^{n} , \\ \dot{\varvec{u}}^{n + 1} & = \frac{\gamma }{{\omega {{{\Delta}}} t}}\left( {\varvec{u}^{n + 1} - \varvec{u}^{n} } \right) - \left( {\frac{\gamma }{\omega } - 1} \right)\dot{\varvec{u}}^{n} - {{{\Delta}}} t\left( {\frac{\gamma }{2\omega } - 1} \right)\varvec{\ddot{u}}^{n} , \\ \end{aligned}$$

(4.22)

which, when inserted in Eq. (4.20), yield

$$\begin{aligned} & \varvec{f}^{\text{int}} \left( {\varvec{u}^{n + 1} } \right) + \underline{\varvec{M}} \left[ {\frac{1}{{\omega {{{\Delta}}} t^{2} }}\left( {\varvec{u}^{n + 1} - \varvec{u}^{n} } \right) - \frac{1}{{\omega {{{\Delta}}} t}}\dot{\varvec{u}}^{n} - \left( {\frac{1}{2\omega } - 1 } \right)\varvec{\ddot{u}}^{n} } \right] \\ & \quad + \underline{\varvec{D}} \left[ {\frac{\gamma }{{\omega {{{\Delta}}} t}}\left( {\varvec{u}^{n + 1} - \varvec{u}^{n} } \right) - \left( {\frac{\gamma }{\omega } - 1} \right)\dot{\varvec{u}}^{n} - \left( {\frac{\gamma }{2\omega } - 1 } \right)\varvec{\ddot{u}}^{n} } \right] = \varvec{f}^{\text{ext}} . \\ \end{aligned}$$

(4.23)

When the unknown $\varvec{u}^{n + 1}$ is retained in the left-hand side of the equation and the known variables are gathered in the right-hand side, the following discrete equation is obtained

$$\begin{aligned} & \varvec{f}^{\text{int}} \left( {\varvec{u}^{n + 1} } \right) + \frac{1}{{\omega {{{\Delta}}} t^{2} }}\underline{\varvec{M}} \varvec{u}^{n + 1} + \frac{\gamma }{{\omega {{{\Delta}}} t}}\underline{\varvec{D}} \varvec{u}^{n + 1} \\ & = \underline{\varvec{M}} \left[ {\frac{1}{{\omega {{{\Delta}}} t^{2} }} \varvec{u}^{n} + \frac{1}{{\omega {{{\Delta}}} t}} \dot{\varvec{u}}^{n} + \left( {\frac{1}{2\omega } - 1} \right)\varvec{\ddot{u}}^{n} } \right] \\ & \quad + \underline{\varvec{D}} \left[ {\frac{\gamma }{{\omega {{{\Delta}}} t}}\varvec{u}^{n} + \left( {\frac{\gamma }{\omega } - 1} \right)\dot{\varvec{u}}^{n} + {{{\Delta}}} t\left( {\frac{\gamma }{2\omega } - 1} \right)\varvec{\ddot{u}}^{n} } \right] + \varvec{f}^{\text{ext}} . \\ \end{aligned}$$

(4.24)

The last equation constitutes a nonlinear system of algebraic equations that has to be solved at each time step. This system is solved using the Newton linearization approach. Denoting by $\varvec{u}_{i}^{n + 1}$ the value of $\varvec{u}^{n + 1}$ at iteration i, the following equation is obtained by linearizing $\varvec{f}^{\text{int}} \left( {\varvec{u}_{i}^{n + 1} } \right) = \varvec{f}^{\text{int}} \left( {\varvec{u}_{i - 1}^{n + 1} + {{{\Delta}}} \varvec{u}_{i}^{n + 1} } \right)$:

$$\varvec{f}^{\text{int}} \left( {\varvec{u}_{i}^{n + 1} } \right) \approx \varvec{f}^{\text{int}} \left( {\varvec{u}_{i - 1}^{n + 1} } \right) + \underline{\varvec{K}}_{i - 1}^{n + 1} {{{\Delta}}} \varvec{u}_{i}^{n + 1} = 0,$$

(4.25)

where K is the tangent stiffness matrix. The increment ${{{\Delta}}} \varvec{u}_{i}^{n + 1}$ between the iteration $i - 1$ and i is the solution of the following system of linear algebraic equations, resulting from Eq. (4.24).

$$\left( {\underline{\varvec{K}} + \frac{1}{{\omega {\Delta} t^{2} }}\underline{\varvec{M}} + \frac{\gamma }{{\omega {\Delta} t}}\underline{\varvec{D}} } \right)_{i - 1}^{n + 1} {\Delta} \varvec{u}_{i}^{n + 1} = \varvec{R}_{i - 1}^{n + 1} ,$$

(4.26)

with the residual

$$\begin{aligned} \varvec{R}_{i - 1}^{n + 1} & = - \varvec{f}^{\text{int}} \left( {\varvec{u}_{i - 1}^{n + 1} } \right) - \left[ {\frac{1}{{\omega {\Delta} t^{2} }}\underline{\varvec{M}} + \frac{\gamma }{{\omega {\Delta} t}}\underline{\varvec{D}} } \right]\varvec{u}_{i - 1}^{n + 1} \\ & \quad + \underline{\varvec{M}}_{i - 1}^{n + 1} \left[ {\frac{1}{{\omega {\Delta} t^{2} }}\varvec{u}_{i - 1}^{n} + \frac{1}{{\omega {\Delta} t}}\dot{\varvec{u}}_{i - 1}^{n} + \left( {\frac{1}{2\omega } - 1} \right)\varvec{\ddot{u}}_{i - 1}^{n} } \right] \\ & \quad + \underline{\varvec{D}}_{i - 1}^{n + 1} \left[ {\frac{\gamma }{{\omega {\Delta} t}}\varvec{u}_{i - 1}^{n} + \left( {\frac{\gamma }{\omega } - 1} \right)\dot{\varvec{u}}_{i - 1}^{n} + {\Delta} t\left( {\frac{\gamma }{2\omega } - 1} \right)\varvec{\ddot{u}}_{i - 1}^{n} } \right] + \varvec{f}^{\text{ext}} , \\ \end{aligned}$$

(4.27)

in which the forces $\varvec{f}^{\text{ext}} \left( {\varvec{u}^{n} ,t^{n} } \right), \varvec{f}^{\text{int}} \left( {\varvec{u}^{n} } \right)$ are computed according to the explicit formulas presented in the preceding sections. The matrix D presented in Eq. (4.20) can be independently defined as linear combination of mass and stiffness matrices $\underline{\varvec{M}} ,\underline{\varvec{K}}$ (the so-called proportional damping)

$$\underline{\varvec{D}} = f_{m} \underline{\varvec{M}} + f_{k} \underline{\varvec{K}} ,$$

(4.28)

where $f_{m}$ and $f_{k}$ are constants and are called “Rayleigh” damping coefficients (Smith and Griffith 2004).

The solution of the above linear equations, ${\Delta} \varvec{u}_{i}^{n + 1}$, is used to update displacements, velocities, and accelerations as follows:

$$\begin{aligned} \varvec{u}_{i}^{n + 1} & = \varvec{u}_{i - 1}^{n + 1} + {\Delta} \varvec{u}_{i}^{n + 1} , \\ \dot{\varvec{u}}_{i}^{n + 1} & = \frac{\gamma }{{\omega {\Delta} t}}\left( {\varvec{u}_{i}^{n + 1} - \varvec{u}_{i}^{n} } \right) - \left( {\frac{\gamma }{\omega } - 1} \right)\dot{\varvec{u}}_{i}^{n} - {\Delta} t\left( {\frac{\gamma }{2\omega } - 1} \right)\varvec{\ddot{u}}_{i}^{n} , \\ \varvec{\ddot{u}}_{i}^{n + 1} & = \frac{1}{{\omega {\Delta} t^{2} }}\left( {\varvec{u}_{i}^{n + 1} - \varvec{u}_{i}^{n} } \right) - \frac{1}{{\omega {\Delta} t}}\dot{\varvec{u}}_{i}^{n} - \left( {\frac{1}{2\omega } - 1} \right)\varvec{\ddot{u}}_{i}^{n} . \\ \end{aligned}$$

(4.29)

The iterative process is declared converged when a specified tolerance of the iterative process is met, and the algorithm is advanced to the next time level.

The conjugate gradient (CG) method (Smith and Griffith 2004) is used to solve the linear system of Eq. (4.26). Overall, the cost of using CG is relatively low. The overall computational cost, however, depends on the number of Newton iterations to update the displacement, velocity, and acceleration of the nodal points of the structural mesh.

3.3 Representation of Immersed Thin Structures in the Fluid Domain

Α key feature of our method is that it employs a FE formulation for thin shells in which the structural equations are formulated in terms of variables defined on its mid-surface (see Sect. 4.3.2). This approach is accurate and, thus, appropriate for analysis of thin structures, but it also augments the efficiency of the overall FSI methodology.

Whether or not the thickness of the structures is accounted for in the FSI analysis presents important algorithmic challenges for the CURVIB method. This is because the CURVIB method is designed to use normal vectors to the immersed surface to: (i) identify the position of background grid nodes relative to the fluid/structure interface by finding fluid nodes (IB nodes) in the immediate proximity of the interface as illustrated in Fig. 4.1; (ii) reconstruct velocity boundary conditions at immersed boundary (IB) nodes along the local normal to the boundary; and (iii) calculate the loads on the structure imparted by fluid stresses for FSI problems (see Sect. 4.3.4). Bodies with nonzero thickness, which have been handled in all previous applications of the CURVIB method, are closed surfaces (i.e., the topologically equivalent to a sphere). This implies that at every point on the surface of the body there is a unique normal vector that points toward the fluid side of the interface, namely the positive wall normal vector (see Fig. 4.2a). On the other hand, when the structure is represented only by its mid-plane, as in the present FE thin shell model, the resulting surface is what is referred to in topological terms as a surface with boundary (i.e., the topological equivalent of a disk). For such a case, it is readily apparent from Fig. 4.2b that at each point on the surface both the positive and negative wall normal vectors point toward the fluid side of the interface. Consequently, the standard node classification and boundary condition reconstruction algorithms used in the CURVIB method (Borazjani et al. 2008) cannot be readily applied and need to be modified. In this section, we describe the algorithmic changes we have implemented to the CURVIB method to enable its coupling with the thin shell FE formulation.

Fig. 4.1

Figure reprinted with permission from Gilmanov et al., Journal of Computational Physics, 300, 814–843 (2015). Copyright 2015, American Institute of Physics

The background grid where the governing equations for the fluid are solved along with the thin body immersed and associated IB nodes. Solid circles and solid line are vertices and elements of the solid structure, respectively. Open circles are IB nodes from positive side and open circles with small primes are IB nodes from negative side of the surface. The red line marks the interface between the fluid domain and the layer of IB nodes surrounding the thin structure.

Fig. 4.2

Figures reprinted with permission from Gilmanov et al., Journal of Computational Physics, 300, 814–843 (2015). Copyright 2015, American Institute of Physics

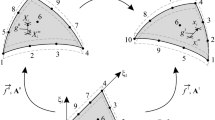
Two different approaches for considering thin immersed body in the fluid. a A closed body for which only the outward normal vector points toward the fluid side of the interface. The standard CURVIB formulation has been developed for such bodies. b A surface with boundary (the mid-surface of the thin structure). A two-side surface for which both the positive and negative surface normal vectors point toward the fluid side of the interface. In both sketches open circles denote background grid nodes (IB marks the immersed boundary nodes where boundary conditions are reconstructed), closed circles are Lagrangian points discretizing the body, and e is the center of a structure shell element. Dashed lines indicate the direction of the searching algorithm from the background (fluid) grid node $A\left( {i, j, k} \right)$ to the adjacent points $B\left( {i \pm 1, j \pm 1, k \pm 1} \right)$. The points ${\text{IB}}^{ + }$ and ${\text{IB}}^{ - }$ in (b) indicate IB nodes from positive and negative side of the surface, respectively.

At each triangular element e on the mid-surface of the thin structure, we calculate the positive $\varvec{n}_{e}^{ + }$ and negative $\varvec{n}_{e}^{ - }$ surface normal vectors to identify the positive and negative, respectively, sides of the surface. The normal vectors are calculated at the center of the element e, and the positive normal is defined as the outward normal of the triangle with clockwise nodal numbering. It is thus evident that $\varvec{n}_{e}^{ + } = - \varvec{n}_{e}^{ - }$. The triangulated surface is tracked with a set of Lagrangian points (the nodes of the triangles), which are used to define the boundary conditions (position and velocity of each Lagrangian node) for the fluid solver.

To find the IB nodes for a given configuration of the thin structure mid-surface we begin by checking the intersection between the lines connecting the centers of fluid cells in the vicinity of the body (dashed lines) and the surface (solid lines) as shown in Fig. 4.2b. In three dimensions, the intersection is found by checking six surrounding grid lines from the local grid point $A\left( {i, j, k} \right)$ and the adjacent points $B\left( {i \pm 1, j \pm 1, k \pm 1} \right)$ (Fig. 4.2b). A fluid node is also considered as an IB node if the distance between the point and the center of an element e is less than one grid cell size ${\Delta} h$, i.e., $\left| {{\Delta} \varvec{r}_{ib,e} } \right| < \min\,{\Delta} h$, where ${\Delta} \varvec{r}_{ib,e} = \left( {{\mathbf{r}}_{\text{ib}} - {\mathbf{r}}_{e} } \right)$, $\varvec{r}_{\text{ib}}$ is the position of the IB node and $\varvec{r}_{e}$ is the position vector of the center of the triangular element (see Fig. 4.2b). The IB node is assigned to correspond to the surface element e on the solid surface.

To implement this algorithm in parallel computing, we utilize the bounding box search approach (Borazjani et al. 2008) in order to reduce the involvement of unnecessary surface triangles in the searching algorithm. We cover the entire structure with a volume of size $\left[ {x_{\min} - x_{\max} ; y_{\min} - y_{\max} ; z_{\min} - z_{\max} } \right]$. This volume is further divided into $N_{i} \times N_{j} \times N_{k}$ smaller bounding boxes uniformly. The choice of $N_{i} , N_{j} , N_{k}$ depends on the number of triangulated elements and the number of grid points per processors. In our simulations, $N_{i} , N_{j} , N_{k}$ are typically chosen to be less than 50. Our line intersection strategy above is applied only for fluid points and triangulated elements that belong to the same bounding box or adjacent ones.

To handle the aforementioned difficulty arising in our thin body approach, due to the fact that both positive and negative wall normal vectors at every element point toward the fluid, we separate the IB nodes in two categories: (i) positive ${\text{IB}}^{ + }$ and (ii) negative ${\text{IB}}^{ - }$ nodes. Note that this type of separation is crucial for the load calculation discussed in Sect. 4.3.4. To determine whether an IB node is on the positive (+) or negative (−) side of the surface, we compute the dot product of the positive local normal vector with the vector connecting the center of the triangular surface element with the closest IB node: if $\left( {\varvec{n}_{e}^{ + } \cdot{\Delta} \varvec{r}_{ib,e} } \right) > 0$ then the IB node is located on the positive side, otherwise it is on the negative side (see Fig. 4.2b). We also note that the relationship between an IB node and the corresponding surface element e is not unique as there could be several IB nodes that correspond to the same solid surface element. This is particularly true when the background fluid grid size is much smaller than the triangulated cell of the solid surface. In the subsequent section, we discuss how we handle surface elements that do not have a unique IB node associated with them insofar as the calculation of the forces acting on that element is concerned.

For Reynolds numbers for which the grid spacing is sufficiently fine to resolve the near wall flow, velocity boundary conditions are reconstructed at the IB nodes using linear interpolation along the local normal of the solid surface (Gilmanov et al. 2003). In our fractional step method for solving Eq. (4.1) (Ge and Sotiropoulos 2007), this relationship is implicitly incorporated into the nonlinear momentum equation and is enforced at all times. For high Reynolds number simulations a wall model is used to reconstruct boundary conditions at the IB nodes as described in Kang et al. (2014).

3.4 Calculation of Loads on the Interface ${\varvec{\Gamma}}^{{{\mathbf{fsi}}}}$

To enable the coupling of the fluid and structural domains in our FSI algorithm, the flow imparted loads must be calculated on the solid surface in order to properly define the problem for the structural solver.

A major challenge in load calculation is the need to efficiently calculate the traction vector $\varvec{t}_{\text{f}}$ on the fluid–solid interface in parallel environment since the solid body can span across partitioned computational domains, which are assigned to different processors. It is thus necessary to develop a scalable algorithm to collectively compute the local loading at each processor and assemble all the information to have a complete loading distribution $\varvec{t}_{\text{f}}$ on the interface ${\Gamma }^{\text{fsi}}$. Here, we utilize the layer of the IB nodes discussed in Sect. 4.3.3 above and illustrated in Fig. 4.1. We calculate separately the pressure and viscous forces on this layer of IB nodes for each processor and the final loading condition on the IB nodes is assembled from all portions of all processors.

Since the fractional step method we employ only requires velocity boundary conditions at the IB nodes (Ge and Sotiropoulos 2007), the pressure p at these nodes is not available. For that we calculate pressure at the IB nodes using interpolation along the normal direction in the similar fashion for the velocity components as reported in Gilmanov and Sotiropoulos (2005).

We note that we fully retain the sharp interface nature of our method in the calculation of the traction vectors even though the thin body is represented by its mid-surface. This is accomplished by using the previously discussed positive and negative wall normal vectors to independently calculate and store the forces acting on the (+) and (−) sides of each element on the interface using one-sided interpolation directed from the element toward the respective (+) or (−) side of the fluid nodes. Consequently, the so-calculated + and − traction vectors at each surface element exhibit a discontinuity across the thin body, which is an important physical feature of the problem preserved by this approach. The shear stress tensor components $\tau_{f,ij}$ are evaluated locally at every fluid node using the second-order differencing to compute the velocity gradients:

$$\tau_{f,i j} = \mu \left( {\frac{{\partial v_{i} }}{{\partial x_{j} }} + \frac{{\partial v_{j} }}{{\partial x_{i} }}} \right).$$

(4.30)

Depending on the grid resolution, the components of the shear stress tensor $\varvec{\tau}_{\text{f}}$ are interpolated along the normal direction $\varvec{n}^{ \pm }$ in similar fashion as the pressure (Gilmanov and Sotiropoulos 2005) or reconstructed using a wall model (Kang et al. 2012) to obtain values at the ${\text{IB}}^{ \pm }$ nodes $\varvec{\tau}_{\text{ib}}^{ \pm }$. Finally, the fluid stress tensor $\varvec{\sigma}_{\text{ib}}^{ \pm }$ at the ${\text{IB}}^{ \pm }$ nodes is evaluated as follows:

$${\underline{\varvec{\sigma}}}_{\text{ib}}^{ \pm } = - p_{\text{ib}}^{ \pm } \underline{\varvec{I}} + \underline{\varvec{\tau}}_{\text{ib}}^{ \pm } ,$$

(4.31)

where $\underline{\varvec{I}}$ is the unit tensor. After the fluid stress tensor ${\underline{\varvec{\sigma}}}_{\text{ib}}^{ \pm }$ has been obtained, a one-sided projection procedure, from the corresponding + or − IB nodes to the actual solid surface is required to find the stress tensor on ${\Gamma }^{\text{fsi}}$. This procedure is described as follows. We already mentioned above in the Sect. 4.3.3 that the relationship between IB nodes and a surface element e is not unique as there could be several IB nodes (say $\overline{N}_{e}^{ \pm }$ such nodes exist) that are associated with the same surface element e. Note that only either positive or negative IB nodes are involved in the load calculation process of positive or negative stresses, correspondingly. Therefore, for such cases and in order to calculate the fluid stress tensor ${\underline{\varvec{\sigma}}}_{e}^{ \pm }$ on the surface of the body ${\Gamma }^{\text{fsi}}$ an interpolation procedure is implemented from the surrounding ${\text{IB}}^{ \pm }$ nodes to the solid surface element as follows:

$${\underline{\varvec{\sigma}}}_{e}^{ \pm } = \mathop \sum \limits_{{\text{ib}} = 1}^{{\overline{N}_{e}^{ \pm } }} {\underline{\varvec{\sigma}}}_{\text{ib}}^{ \pm } /\left| {{\Delta} \varvec{r}_{ib,e}^{ \pm } } \right|/\mathop \sum \limits_{{\text{ib}} = 1}^{{\overline{N}_{e}^{ \pm } }} 1/\left| {{\Delta} \varvec{r}_{{\text{ib}},e}^{ \pm } } \right|.$$

(4.32)

Finally, the net loading at each triangular element on the thin structure mid-surface is defined as the sum of loads from both sides of the middle surface $\varvec{t}_{e} = \varvec{t}_{e}^{ + } + \varvec{t}_{e}^{ - }$, where $\varvec{t}_{e}^{ \pm } = {\underline{\varvec{\sigma}}}_{e}^{ \pm } \cdot \varvec{n}_{e}^{ \pm }$ (see Fig. 4.3). Note that the total traction vector of the load $\varvec{t}_{e}$ is calculated using all (positive and negative) IB nodes associated with the center of the triangular element e. In our FE solver, however, the traction vector is required at the vertices of the triangular elements $\varvec{t}_{v}$. Thus, an interpolation procedure is implemented to transfer the traction vector from the elements to the nodes using distance weighted average: $\varvec{t}_{v} = \varvec{I}\left( {\varvec{t}_{e} } \right) = \mathop \sum \nolimits_{e = 1}^{{\bar{e}}} \left( {\varvec{t}_{e} /\left| {{\Delta} \varvec{r}_{v,e} } \right|} \right)/\mathop \sum \nolimits_{e = 1}^{{\bar{e}}} \left( {1/\left| {{\Delta} \varvec{r}_{v,e} } \right|} \right)$, where the summation is implemented over all elements e adjacent to the vertex v and $\left| {{\Delta} \varvec{r}_{v,e} } \right|$ is a distance from the vertex v to the center of the element e.

Fig. 4.3

Figure reprinted with permission from Gilmanov et al., Journal of Computational Physics, 300, 814–843 (2015). Copyright 2015, American Institute of Physics

The thin structure in our formulation is treated as a sharp interface. The schematic illustrates that at each element e on the surface, two traction vectors are computed from the positive $\varvec{t}_{e}^{ + }$ and negative $\varvec{t}_{e}^{ - }$ sides of the interface. The total traction vector $\varvec{t}_{e} = \varvec{t}_{e}^{ + } + \varvec{t}_{e}^{ - }$ is used to compute the local load imparted by the flow on the structure on each surface element.

3.5 The Algorithm for Coupling the Fluid ${\boldsymbol{\mathcal{F}}}$ and Solid ${\boldsymbol{\mathfrak{H}}}$ Solvers

The governing equations of the fluid (Eq. 4.1) and solid (Eq. 4.6) domains as well as the continuity conditions on the interface constitute a modularly partitioned fluid–structure interaction problem, which can be solved by coupling together two independent solvers: the fluid solver ${\boldsymbol{\mathcal{F}}}$ and the solid solver ${\boldsymbol{\mathfrak{H}}}$. We use the conventional Dirichlet–Neumann partition (Felippa et al. 2001) to couple the system of fluid–solid equations. This means that the fluid equations are solved by enforcing Dirichlet boundary condition, while the solid equations are solved by prescribing the load on the interface ${\Gamma }^{\text{fsi}}$ (Fernandez et al. 2007). The need to enforce the continuity of the velocity and the normal stresses on the interface ${\Gamma }^{\text{fsi}}$ requires that both the displacement and velocity of the solid body u and $\dot{\varvec{u}}$ must be tracked. We define Q as the solution of solid solver ${\boldsymbol{\mathfrak{H}}}$ (Eq. 4.9):

$$\varvec{Q } = \left( {\varvec{u}, \dot{\varvec{u}}} \right)$$

(4.33)

From Eq. (4.4) and (4.9), the FSI coupling can be formulated as a fixed-point operator for Q:

$$\varvec{Q } = {\boldsymbol{\mathfrak{H}}} \circ {\boldsymbol{\mathcal{F}}}(\varvec{Q})$$

(4.34)

To facilitate the description of the FSI algorithm, let us assume, without loss of generality, that the pressure and velocity fields $\varvec{v}^{n}$, $p^{n}$ for the fluid alongside with the displacements and velocities of the solid structure $\varvec{u}^{n}$, $\dot{\varvec{u}}^{n}$ are known at time step n. The fluid and structural equations, Eqs. (4.35–4.36), are solved to obtain the structural displacement and velocity as well as the fluid pressure and velocity fields at time step $t^{n + 1}$ with the current boundary conditions on ${\Gamma }_{\text{f}}^{N} \cup {\Gamma }_{\text{f}}^{D} \cup {\Gamma }^{\text{fsi}}$ via a series of subiterations $(l)$ to satisfy Eq. (4.34). We seek the solution of the discrete fluid operator ${\boldsymbol{\mathcal{F}}}$ at time step $t^{n + 1}$ as:

$${\boldsymbol{\mathcal{F}}}\left( {\varvec{v}^{n + 1} , p^{n + 1} ,\varvec{u}^{n + 1} ,\dot{\varvec{u}}^{n + 1} } \right) = 0, \,\, {\text{in}}\,{\Omega }_{\text{f}} ,$$

(4.35)

and the solution of the discrete solid operator ${\boldsymbol{\mathfrak{H}}}$ as follows:

$${\boldsymbol{\mathfrak{H}}}\left( {\varvec{u}^{n + 1} ,\dot{\varvec{u}}^{n + 1} , \varvec{t}^{n + 1} } \right) = 0, \,\, {\text{in}}\,{\Omega }_{\text{s}} ,$$

(4.36)

where $\varvec{t}^{n + 1} = {\boldsymbol{\mathcal{L}}}\left( {\varvec{v}^{n + 1} , p^{n + 1} } \right)$ is the traction vector imparted by the fluid on the body surface ${\Gamma }^{\text{fsi}}$. The function ${\boldsymbol{\mathcal{L}}}\left( {\varvec{v}^{n + 1} , p^{n + 1} } \right)$ represents the loading on the structure surface from the pressure and velocity fields in fluid. The approach we employ to calculate ${\boldsymbol{\mathcal{L}}}$ in the discrete space is described in Sect. 4.3.4, Eqs. (4.30–4.32). The fixed-point subiteration procedure to find Q at time steps n + 1 can thus be written as follows:

$$\varvec{Q}_{l + 1}^{n + 1} = {\boldsymbol{\mathfrak{H}}}^{n + 1} \circ {\boldsymbol{\mathcal{F}}}^{n + 1} \left( {\varvec{Q}_{l}^{n + 1} } \right),$$

(4.37)

where l + 1 is the new iterate of $\varvec{Q}^{n + 1}$. In our fixed-point iteration, the fluid solver ${\boldsymbol{\mathcal{F}}}$ uses displacements and velocity of the solid structure $\varvec{u}_{l}^{n + 1} ,\dot{\varvec{u}}_{l}^{n + 1}$ and gives new fluid velocity $\varvec{v}_{l + 1}^{n + 1}$ and pressure field $p_{l + 1}^{n + 1}$ by solving Eq. (4.35). The solid solver ${\boldsymbol{\mathfrak{H}}}$ in turn uses the so updated fluid velocities, and pressure field to advance the solution of displacements and velocity of the solid structure $\varvec{u}_{l + 1}^{n + 1} ,\dot{\varvec{u}}_{l + 1}^{n + 1}$. Subiterations (l) are implemented every time step to satisfy the coupled system of equations and advance the solution to time step $n + 1$:

$$\begin{aligned} & \left( {\varvec{v}_{l + 1}^{n + 1} , p_{l + 1}^{n + 1} } \right) = {\boldsymbol{\mathcal{F}}}\left( {\varvec{v}_{l}^{n + 1} , p_{l}^{n + 1} ,\varvec{u}_{l}^{n + 1} ,\dot{\varvec{u}}_{l}^{n + 1} } \right), \\ & \left( {\varvec{u}_{i + 1}^{n + 1} ,\dot{\varvec{u}}_{i + 1}^{n + 1} } \right)_{l + 1} = {\boldsymbol{\mathfrak{H}}}\left( {\left( {\varvec{u}_{i}^{n + 1} ,\dot{\varvec{u}}_{i}^{n + 1} } \right)_{l} , \varvec{t}_{l}^{n + 1} } \right), \quad l = 0, 1, 2, \ldots ; i = 1, 2, 3 \ldots \\ \end{aligned}$$

(4.38)

where index l is the number of fixed-point iteration and all variables at level $l = 0$ are at the previous time step n, index i is the number of Newton iteration for structural equations. The subiterations continue until an appropriate norm of the error of the flow and structural variables between levels l + 1 and l has been reduced to a desired tolerance and the above equations have been satisfied at level n + 1. The above procedure is generally described as a strongly coupled FSI algorithm and ensures that the continuity of the stress at the fluid–structure interface is satisfied within the desired convergence threshold. If we just apply the above algorithm for one subiteration (l = 0), the requirement for the continuity of the stress is enforced only within an error that depends on the accuracy of the temporal discretization scheme. Such an algorithm is generally far more efficient than the strongly coupled approach and is referred to as loosely coupled iteration. Generally, loosely coupled FSI schemes are robust for problems involving large mass ratio (structural density considerably larger than the fluid density) while strongly coupled iterations are required to enhance robustness for problems with mass ratios of order one or lower (Sotiropoulos and Yang 2014; Baek and Karniadakis 2012).

For mass ratio problems of order one $\left( {\rho_{\text{f}} /\rho_{\text{s}} \approx 1} \right)$, which arise in simulations of heart valves, the Aitken nonlinear relaxation technique is also implemented to accelerate the convergence of the strongly coupled FSI algorithm (Borazjani et al. 2008; Küttler and Wall 2008). The convergence tolerance for the structural and strongly coupled FSI solvers is of order $10^{ - 8}$ in terms of the $L_{\infty }$ norm.

We note that for all the cases we simulate in this work, although the underlying FSI dynamics is complex, the degrees of freedom (DOF) for the structural mesh are quite low (in the order of thousands) compared to the fluid DOFs (in the order of millions) since the structures are relatively small and simple. Thus, the cost for solving the solid equations is small in comparison with the fluid equations. For that the solid solver is implemented as a serial code possessed by the root processor. All processors involved in the solution of the fluid equations receive the same image Q of the structure from the root processor.

Our code is parallelized and uses the Petsc Library. The simulations we report herein have been carried out on a cluster with dual 8-core AMD 6112. To estimate the efficiency of the code, we report the CPU time per node of the computational grid, per processor, and per time step. For the inverted flag problem we report in Sect. 4.4.2 below this quantity is equal to $t_{\text{CPU}} /\left( {{\text{Nodes}} \cdot {\text{Procs}} \cdot n\,{\text{time}}} \right) \approx 3 \times 10^{ - 2} \,{\upmu}{\text{s}}$.

4 Application to Complex FSI Problems

In this section, we demonstrate the predictive capabilities of the proposed CURVIB-FE-FSI algorithm by applying it to simulate two quite challenging both involving FSI with thin flexible structures. The first is the large amplitude vibrations of an inverted flexible flag, which has been studied experimentally by Kim et al. (2013). In the second example, we demonstrate the ability of the CURVIB-FE-FSI algorithm to simulate pulsatile, physiologic flow through a tri-leaflet aortic valve placed in an anatomic aorta. This second problem is more challenging because it is geometrically more complex, is characterized by low mass ratio $\left( {\rho_{\text{s}} /\rho_{\text{f}} \sim 1} \right)$ and imposes a more stringent overall test for the stability and robustness of the FSI solver. Note that both of these problems were first presented in Gilmanov et al. (2015).

4.1 Oscillations of a Flapping Inverted Flag

The computational challenges in this problem are related to the large amplitude oscillations of the flag as well as to high Reynolds number of the flow. This problem was also investigated in recently published laboratory experiment (Kim et al. 2013). The problem is referred to as the inverted flag because the flag, a thin flexible sheet of length L, is mounted on its trailing edge with its leading edge free to move in response to a uniform incoming flow $u_{\infty }$ (see Fig. 4.4a). Kim et al. (2013) carried out a series of experiments by varying $u_{\infty }$ and/or the structural properties of the flag and identified a dynamically rich phase space of flag responses. They showed that the non-dimensional parameter that governs the dynamics of the FSI problem is the nondimensional bending stiffness $\beta = B/\rho_{\text{f}} u_{\infty }^{2} L^{3} ,$ where B is a flexural rigidity $B = Yh_{0}^{3} /12\left( {1 - \nu^{2} } \right)$ of the flag, $\rho_{\text{f}}$ is the fluid density, Y is the Young’s modulus, $\nu$ is the Poisson’s ratio, and $h_{0}$ is the thickness of the plate. Kim et al. (2013) identified three regimes of flag response as a function of $\beta$: (1) the straight mode, where the flag is too rigid to be deflected by the flow and remains straight (large values of $\beta$); (2) the flapping mode, where the flag undergoes large amplitude flapping oscillations (intermediate values of $\beta$); and (3) the deflected mode, where the flag is so flexible that it is deflected by the flow toward one side and remains fixed at this position at all times (small $\beta$ values). Here, we report simulations for $\beta = 0.1$, which is in the flapping regime. This regime is quite challenging from the FSI simulation standpoint as it involves very large amplitude oscillations. The specific $\beta$ value is selected because for this value the experiment of Kim et al. (2013) revealed a complex dynamic response of the flag characterized by rich flapping dynamics including several local minima and maxima of the flag leading edge position during the cycle of flapping motion. We carry out simulations for the following values of the various governing parameters for this problem: $Y = 2.38 \times 10^{9}$ Pa, $\nu = 0.38$, $\rho_{\text{s}} = 1.2 \times 10^{3}$ kg/m³, $h_{0} = 8 \times 10^{ - 4}$ m, $H = L = 0.3$ m, $u_{\infty } = 6.7$ m/s, $\mu = 1.92 \times 10^{ - 5}$ Pa s, $\rho_{\text{f}} = 0.98$ kg/m³, hence $B = 0.118$ N m and $\beta = 0.1$. The corresponding Reynolds number, based on the inflow velocity and flag length, is $Re = u_{\infty } \rho_{\text{f}} L/\mu$ = 99,505, and, therefore, the massively separated flow in the wake of the flapping flag is expected to be turbulent. For that we employ the CURVIB-FE-FSI method in LES mode with three-point central differencing for the convective terms in the flow equations, the dynamic Smagorinsky subgrid-scale model (Germano et al. 1991) for closure, and the wall model of (Wang and Moin 2002) to reconstruct boundary conditions on the flag as adapted for the CURVIB method by Calderer et al. (2014). The plate surface is discretized with 206 triangle elements and the background fluid grid is discretized with a uniform Cartesian mesh with $561 \times 201 \times 201$ in the stream wise (x), vertical (y), and transverse (z) directions, respectively. The non-dimensional time step is equal to $\widetilde{{{\Delta} t}} = 0.01$.

Fig. 4.4

Figures reprinted with permission from Gilmanov et al., Journal of Computational Physics, 300, 814–843 (2015). Copyright 2015, American Institute of Physics

a Computational domain used to simulate the inverted flag problem. The side $x_{\min}$ and all four sides $y_{\min} , y_{\max} , z_{\min} , z_{\max}$ are Dirichlet boundaries with inflow $u = u_{\infty }$ and no-slip boundary conditions $\varvec{v} = 0$, respectively. On the boundary $x_{\max}$ Neumann condition $\partial \varvec{v}/\partial n = 0$ is implemented; b Comparison of calculated (solid line) and measured (Khosronejad and Sotiropoulos 2014) time histories of the flag leading edge displacements for flapping mode with β = 0.1. Open circles are experimental data.

Figure 4.4b compares the measured (Kim et al. 2013) and computed time histories of the flag leading edge deflection. It is seen that the computed results are in excellent agreement with the experimental measurements. The simulations not only capture the amplitude and period of oscillations with good accuracy but also resolve the two local deflection maxima (minima) that occur in the vicinity of maximum $\left( {y_{\min} \,{\text{or}}\,y_{\max} } \right)$ flag deflection. A more quantitative comparison with the measurements reveals that the maximum discrepancy between experiments and simulations, which occurs around maximum and minimum tip deflection, does not exceed 7% of the measured values.

Figure 4.5 depicts the calculated instantaneous out of plane vorticity field at various instants during the flapping cycle. These snapshots as well as video animations of the vorticity field (not shown herein) clearly show that the flapping dynamics is correlated with the formation of a large leading edge vortex as the flag tip approaches maximum deflections. The vortex begins to form as the flag moves upward as a result of shear-layer roll-up and leads to massive separation and shedding of vorticity in the wake at maximum deflections. The resulting wake is very complex and exhibits a large-scale meandering motion as a result of the continuous flapping motion of the flag. The computed results shown in Fig. 4.5 are in good overall qualitative agreement with the flow visualizations reported by Kim et al. (2013) and their overall description of the underlying wake dynamics as obtained in their experiments.

Fig. 4.5

Figures reprinted with permission from Gilmanov et al., Journal of Computational Physics, 300, 814–843 (2015). Copyright 2015, American Institute of Physics

Snapshots of the simulated inverted flag flow fields during a half period of oscillation. Contours are the out-of-plane vorticity component (z-vorticity) are plotted at various instants in time. The corresponding flag shape is also shown and the corresponding time instant is marked with a red dot in the inset. Light blue circle indicates the fixed trailing edge and the arrow indicates direction of moving leading edge.

To elucidate the three-dimensional structure of this highly unsteady and massively separated wake, we plot in Fig. 4.6 several snapshots of the Q-criterion (Hunt et al. 1988). It is evident from this figure that the flow is dominated by shear-layer roll-up off the sharp edges of the flag, which leads to the formation of an arch vortex along the leading edge and intertwined spiral vortex tubes shed off the two sides of the flag. These structures separate from the flag and break up into small-scale turbulence in the wake.

Fig. 4.6

Figures reprinted with permission from Gilmanov et al., Journal of Computational Physics, 300, 814–843 (2015). Copyright 2015, American Institute of Physics

Snapshots of Q-criterion iso-surfaces (Hunt et al. 1988) at three time instants showing the inverted flag near the maximum $\left( {y_{\max} } \right)$ deflection. These snapshots elucidate the 3D coherent structures in the wake of the flapping flag. The red dot in the inset of each figure identifies the corresponding instant.

To our knowledge the results reviewed herein Gilmanov et al. (2015) elucidated for the first time the three-dimensional structure of the wake of a flapping inverted flag and clearly illustrated the ability of our CURVIB-FE-FSI method to solve a very complex, high Reynolds number problem involving complex large amplitude vibrations of a thin structure. Even though not shown herein, we have carried out simulations for values of $\beta$ in all three experimentally identified flag response regions and our results are in very good agreement with the experiments of Kim et al. (2013).

4.2 FSI Simulation of Tri-leaflet Aortic Valve

In this section, we demonstrate the ability of the method to simulate physiologic flow through a tri-leaflet aortic valve located in an anatomically realistic aorta. The flow through the aorta is driven by a prescribed physiologic flow wave form at the aorta inlet, the response of the valve leaflets and associated flow field are simulated by the new CURVIB-FE-FSI algorithm.

We consider a tri-leaflet aortic heart valve and model it as a thin shell using the rotational free FE formulation of Stolarski et al. (2013) as described in Sect. 4.3.2 above. We use in these simulations a model suitable for a prosthetic polymeric aortic valve with isotropic material and the Neo–Hookean constitutive equation. The geometric and material characteristics of the valve are specified from values available in the literature to correspond to a prosthetic polymeric valve (Carmody et al. 2006) and are as follows: valve diameter $d_{0} = 0.0254$ m, leaflet thickness $h_{0} = 6.0 \times 10^{ - 4}$ m, Young modulus $Y = 1$ MPa, Poisson coefficient $\nu = 0.35$, and density $\rho_{\text{s}} = 1.2 \times 10^{3}$ kg/m³. As shown in Fig. 4.7a the valve is placed in an anatomic aorta, which has been reconstructed from patient-specific MRI data.

Fig. 4.7

Figures reprinted with permission from Gilmanov et al., Journal of Computational Physics, 300, 814–843 (2015). Copyright 2015, American Institute of Physics

a Computational domain for the FSI simulations of a tri-leaflet heart valve in an anatomic aorta. At inflow pulsatile physiological flow shown in (a) is simulated; at outflow Neumann boundary condition $\partial \varvec{v}/\partial n = 0$ is implemented; on the aorta wall no-slip boundary condition is implemented; b physiological incoming flow wave form specified at the inlet of the aorta.

The pulsatile flow wave form we prescribe as inflow boundary condition at the inlet of the aorta domain is shown in Fig. 4.7a. The corresponding heart beat is equal to 70 bpm, which gives a period of the cardiovascular cycle $T = 0.857$ s. The valve diameter $d_{0}$ is used as the characteristic length scale and the peak systolic velocity of $U_{0} = 0.8$ m/s is used as the velocity scale. Using the viscosity of blood $\mu = 3.52 \times 10^{ - 3}$ Pa s, and blood density $\rho_{\text{f}} = 1050$ kg/m³, gives a peak systolic Reynolds number ${\text{Re}} = 6000$, which well within the physiologic range (Carmody et al. 2006). The characteristic time scale is equal to $T_{0} = d_{0} /U_{0} = 3.1 \times 10^{ - 2}$ s and thus the non-dimensional period of cardiac cycle is $\widetilde{T} = T/T_{0} = 0.857/3.1 \times 10^{ - 2} = 27.6$ non-dimensional time units. The non-dimensional time step for the simulations is set equal to  $\tilde{t} = 0.01$, which corresponds to discretizing the cardiac cycle with $N_{\text{time}} = \widetilde{T}/\tilde{t} = 2760$ computational time steps. Since the density ratio for this problem is of order one, the strong coupling FSI iteration is required for stable and robust simulations. In all subsequently presented simulations 4–10 strong coupling iterations are sufficient to reduce the residuals by 8 orders of magnitude.

The overall computational setup is shown in Fig. 4.7a and consists of (a) the anatomic aorta, (b) the flexible tri-leaflet prosthetic heart valve, (c) the rigid valve support structure, and (d) housing. A curvilinear boundary-fitted grid is used to discretize aorta domain with $101 \times 101 \times 601$, in the two transverse and stream wise directions, respectively. The valve leaflets are discretized with 476 triangle elements.

The flow wave form shown in Fig. 4.7b, which corresponds to the systolic phase of the cardiac cycle during which the aortic valve opens and closes, is used to specify time-dependent Dirichlet conditions for the velocity at the inlet. At the outlet of the aorta zero-gradient Neumann condition $\partial \varvec{v}/\partial n = 0$ is applied for all three velocity components along with a correction of the so-resulting velocity field to enforce global mass conservation. No-slip and no-flux boundary conditions are applied on all solid surfaces.

We note that in our numerical method the discrete continuity equation is satisfied to machine zero at each time step, thus preserving the incompressible nature of the flow locally and globally. This is accomplished by solving the Poisson equation in the projection step of the fractional step method with the residual reaching machine zero at every physical time step. For more details, we refer the reader to Kang et al. (2011).

The calculated flow fields for one simulated systolic cardiac cycle are shown in Fig. 4.8. Contours of instantaneous vorticity magnitude are plotted in this figure on a plane passing through the center of the aorta. As seen in this figure, a well-defined vortex ring forms as soon as the valve opens at early systole (Fig. 4.8a). Shear layers connecting the aortic valve vortex ring with the valve leaflets are also evident in Fig. 4.8a. As the valve leaflets continue to open, the vortex ring advances and impinges on the curved aorta wall and breaks up. The valve leaflet shear layers intensify as the flow rate through the valve increases and the flow in the wake of the valve leaflets is seen to break up into small-scale turbulence at approximately halfway within the accelerating phase of the cardiac cycle (Fig. 4.8c). By the time the peak systolic flow is reached and the valve has opened fully, the flow in the aorta is seen to have transitioned to a fully turbulent state downstream of the valve leaflets (Fig. 4.8d). This state persists even after the valve closes and the flow structures in the aorta gradually decay (Fig. 4.8f).

Fig. 4.8

Figures reprinted with permission from Gilmanov et al., Journal of Computational Physics, 300, 814–843 (2015). Copyright 2015, American Institute of Physics

Instantaneous contours of vorticity magnitude on a plane through the aorta plane of symmetry during systolic phase showing the opening and closing process of the aortic heart valve. The red dot in the inset of each figure identifies the corresponding instant during the cardiac cycle.

The results shown in Fig. 4.8 reveal significant differences between the simulated flow patterns reported in Le and Sotiropoulos (2013) for a mechanical bi-leaflet heart valve (MBHV) in the same anatomic aorta. More specifically, when a MBHV is implanted in the aortic position the turbulent state downstream of the valve leaflets does not emerge until shortly after peak systole. For the tri-leaflet valve, however, Fig. 4.8 clearly shows that the flow transitions to turbulence well before peak systole is reached. This finding should be attributed to the complex vortex dynamics induced by the shape of the tri-leaflet valve orifice as it opens and the interaction of the aortic valve vortex ring with the aorta wall.

To illustrate the three-dimensional dynamics of coherent structures as the valve opens, we plot in Fig. 4.9 instantaneous snapshots of the Q iso-surface (Hunt et al. 1988). As seen in Fig. 4.9a, as the valve opens the shear layer from the valve leaflets rolls up to form a three-lobed vortex ring that follows the shape of the valve orifice. As the valve continues to open, this vortex ring becomes distorted as each one of its three lobes, forming at the valve commissures, bends forward and propagates at faster speed than the rest of the ring. This complex deformation of the aortic valve ring is clearly evident in Fig. 4.9c where three distinct vortex loops are seen to have formed. Each loop forms because of the faster propagation and associated stretching of the corresponding lobe of the initial ring. Essentially the vortex interactions and instabilities revealed by our simulations are similar to those observed in pulsatile flow through corrugated nozzles (New and Tsovolos 2012). These instabilities along with the subsequent impingement of the three-lobed aortic valve ring on the aorta wall are ultimately responsible for the relatively early transition to turbulence of the flow in the wake of a tri-leaflet valve.

Fig. 4.9

Instantaneous iso-surfaces of the Q-criterion (Hunt et al. 1988) at various instant in time during valve opening. The red dot in the inset of each figure identifies the corresponding instant during the cardiac cycle. Figures reprinted with permission from Gilmanov et al., Journal of Computational Physics, 300, 814–843 (2015). Copyright 2015, American Institute of Physics

As mentioned earlier, in all of the above simulations, a linear, isotropic Saint-Venant (StV) material model was used, which has been also employed in the past, e.g., in Tepole et al. (2015) and may be applicable only to a certain type of prosthetic valves. Recently, the May-Newman and Yin (MNY) model (May-Newman and Yin 1998) and its applicability to heart valve has been discussed in Gilmanov et al. (2016) to simulate natural heart valves. However, the analysis presented in that paper did not involve fluid flow and, consequently, no FSI algorithm was used. Instead, the dynamic behavior of leaflets was investigated by prescribing time-varying pressure loading taken from experiments. For the set of parameters used, we found in Gilmanov et al. (2016) that heart valve with the StV material model is more obstructive to the blood flow in comparison with the heart valve with the MNY material model. The complete FSI simulations (Gilmanov et al. 2018) led to the same conclusion that the StV heart valve is more obstructive to the blood flow and creates more complex blood flow patterns. To qualitatively compare the opening kinematics of StV and MNY heart valves and the associated differences in hemodynamic patterns, in Fig. 4.10 the results of FSI simulations with StV and MNW heart valves are shown. The instantaneous vorticity contours for the two considered cases (StV and MNY) are shown in the first and second columns of Fig. 4.10. To illustrate the three-dimensional dynamics of the coherent structures as the valve opens, we plot in Fig. 4.10 (third and fourth columns) the instantaneous Q iso-surfaces (Hunt et al. 1988). Figure 4.10a shows that for the time interval shown, the StV heart valve opens only partially and obstructs the blood flow, causing significant vorticity generation downstream of the valve leaflets. At exactly the same time, the MNY heart valve is fully open and vortices are shed from the fully formed valve orifice (Fig. 4.10a–c). One can see that with the StV material, the jet spreads into the aorta faster than that for the MNY valve. Starting at $t \approx 0.12 \, {\text{s}}$, the large-scale coherent structures arising in the StV valve material disintegrate into small turbulent structures (Fig. 4.10a). For the MNY material on the other hand, the vortices remain coherent, which indicates that the MNY valve flow remains laminar for a longer period of the cardiac cycle than the StV valve flow. In fact, only starting at approximately $t \approx 0.192 \, {\text{s}}$ (Fig. 4.10c), the large-scale vortex structure arising in the MNY valve disintegrates as it begins to interact with the aortic wall.

Fig. 4.10

Figures reprinted with permission from Gilmanov et al., Journal of Biomechanical Engineering, 140 (2018). Copyright 2018, American Institute of Physics

Comparison of instantaneous contours of vorticity on a plane through the aorta during systolic phase showing the opening process of the StV aortic valve (first column) and MNY aortic valve (second column). The third and fourth columns are the instantaneous iso-surfaces of the Q-criterion (Hunt et al. 1988) for StV and MNY models, respectively. The dot in the inset of each figure identifies the corresponding instant during the cardiac cycle: a $t_{a} = 0.128 \, {\text{s}}$, b $t_{b} = 0.16 \, {\text{s}}$, and c $t_{c} = 0.192\, {\text{s}}$.

Helical flow patterns have been observed in the aortic arch, which are clearly seen from the movies (not shown here) of Q-structures spreading into the aorta. As mentioned earlier, these flow patterns are dependent on the kinematics of the valve which, in the coupled FSI analysis, is dependent on the properties of the leaflet material. We have shown that as the StV valve opens, the shear layer induced by the valve leaflets rolls up to form a three-lobed vortex ring (Fig. 4.9), which corresponds to the shape of the valve orifice. For the MNY valve, however, the opening process is faster and the resistance to the blood flow is reduced, which leads to a toroidal shape of the vortex. As the valve continues to open (Fig. 4.10b and c), the vortex ring for the StV valve becomes distorted but for the MNY valve remains toroidal and coherent. As discussed above, for the MNY valve, the coherent vortex ring begins to get disorganized only later due to its interaction with aortic wall (Fig. 4.10c). It is clearly seen that this large coherent structure produced by the MNY valve propagates into the aorta along a helical path (Fig. 4.10).

To our knowledge the results we have presented herein [originally reported in Gilmanov et al. (2018)] represent the first FSI simulation of a tri-leaflet heart valve whose material is nonlinear and anisotropic and which is interacting with an anatomic aorta at physiologic conditions. The ability of the method to resolve the very complex flow patterns and associated vorticity dynamics as the valve leaflets open and close illustrates its potential as a powerful tool for patient-specific simulations of native and prosthetic heart valves.

5 Conclusions

We have presented a recently developed computational approach for simulating fluid–structure interaction (FSI) problems in complex domains with thin flexible solid structures. It is based on integrating the sharp interface CURVIB solver, previously developed for FSI problems with rigid structures (Borazjani et al. 2008), with an accurate and efficient rotation-free FE formulation for thin shells (Stolarski et al. 2013) into a coupled FSI framework that is able to handle very large deformations/displacements of thin shell structures. The inverted flag case in particular, which to the best of our knowledge we simulated numerically for the first time (Gilmanov et al. 2015), illustrates the ability of our method to simulate with LES a dynamically rich, high-Reynolds number FSI problem. Comparisons with the measurements of Kim et al. (2013) for this case revealed the ability of the method to capture even subtle features of the flag kinematics, such as the existence of multiple local extrema near the location of maximum deflection, and reproduce wake structures similar to those visualized in the laboratory. We subsequently reviewed results from recent application of our method (Gilmanov et al. 2015, 2018) to simulate the dynamics of a tri-leaflet aortic heart valve placed in an anatomic aorta to demonstrate the capability of the method to solve complex FSI problems in realistic cardiovascular anatomies and at physiologic conditions. Our simulations elucidated the rich vorticity dynamics during the opening of the valve leaflets. The differences for StV and MNY valves’ motion and their deformation were shown to give rise to significantly different hemodynamics both near the valve and in the ascending aorta. For the StV valve, the vortex ring is seen to grow in complexity rapidly and ultimately break into turbulence much sooner during the accelerating phase of systole than for the MNY valve. Our simulations show that the heart valve with the StV material model is more obstructive to the blood flow in comparison with the heart valve with the MNY material model.