A Higher-Order Cut-Cell Methodology for Large Eddy Simulation of Compressible Viscous Flow Problems with Embedded Boundaries

Abstract

We have developed a finite volume-based conservative cut-cell method that is up to third-order accurate for simulation of compressible viscous flow problems. A sharp representation of the embedded boundaries, described using a signed distance function, is facilitated by use of block-structured adaptive mesh refinement. A high-order reconstruction is performed by using a cell-centered piecewise polynomial approximation of flow quantities. To ensure the stability of the scheme in the presence of very low volume cut-cells, a novel cell clustering approach that preserves the design order of accuracy even locally has been developed. It is shown through numerical examples that using the proposed approach, smooth representation of flow-field quantities and their derivatives can be achieved on embedded boundaries. Smooth reconstruction of wall shear stress and a high-order accuracy makes this approach a good candidate for large eddy simulation (LES). A multi-level extension of the one-equation kinetic subgrid energy-based closure to perform LES with local refinement and embedded boundaries is presented. Results are shown for various canonical cases to demonstrate the accuracy of the approach.

1 Introduction

The advantages of using embedded boundary (EB) methods for computational fluid dynamics (CFD) applications are well known. The foremost being ease of grid generation for complex geometries and moving boundaries. In EB approaches, the domain boundaries are not resolved by the numerical grid, rather the numerical schemes used to solve the flow governing equations are modified appropriately to account for the presence of physical boundaries. It is in this numerical treatment of the embedded boundary the various EB approaches vary. An excellent overview of the existing methods to represent embedded boundaries within the background mesh is provided by Mittal and Iaccarino (2005). For the purposes of this study, we only consider the cut-cell-based EB method in which regular mesh elements cut by the intersection of the solid boundary are reshaped to conform to the shape of the interface. The cut-cell approach is designed to satisfy the underlying conservation laws for the cells near the interface. Strict global and local conservation of mass, momentum, and energy is guaranteed by resorting to a finite volume discretization even for the cut-cells. The Cartesian cut-cell finite volume methods (Clarke et al. 1986; Udaykumar et al. 1996; Hartmann et al. 2011; Muralidharan and Menon 2016) are, therefore, in comparison to finite difference ghost cell methods (Kim 2001; Majumdar 2001), attractive as they enforce strict conservation and also can avoid the generation of spurious pressure fluctuations that are observed typically with ghost fluid methods (Cecere and Giacomazzi 2014; Mittal and Iaccarino 2005; Merlin et al. 2012).

One of the motivations of developing EB methods is to apply them to solve realistic flow problems involving complex geometries. Due to highly turbulent nature of most of the practical flows, resolving all scales of motion, as is done in a Direct Numerical Simulation (DNS), is not possible due to the high computational costs involved. The alternative is to employ large eddy simulation (LES) in which only the most energy-containing eddies are resolved by the numerical grid and effect of small scales of motion on the larger scales is modeled. Adaptive mesh refinement (AMR) is another popular strategy for reducing computational cost by providing higher grid resolution only in the regions of interest. AMR was originally proposed for shock hydrodynamics (Berger and Colella 1989) and has been traditionally applied to mainly inviscid flows to capture features such as shocks, contact discontinuities, and expansions.

The introduction of unconventional numerical techniques such as embedded boundary methods and AMR can complicate the closure problem for LES. The majority of subgrid closures for LES have been developed for body-conformal, uniform grids without local refinement. The behavior of the closure models for unconventional methodologies such as dynamic mesh refinement (Berger and Colella 1989) and embedded boundary techniques (Mittal and Iaccarino 2005) is not completely understood. Additionally, a common problem with most EB methods is that they are of lower-order accuracy near boundary. Besides, these methods also suffer from issues such as mass loss and noisy reconstruction of flow solution quantities such as wall shear stress and heat flux (Coirier and Powell 1996). In the context of turbulence modeling using LES technique, the numerical errors at the boundary can strongly interact with the subgrid closure models introducing a significant uncertainty in the simulation results (Kravchenko and Moin 1997). Therefore, use of high-order EB schemes with smooth behavior of flow quantities and their derivatives at the boundary becomes particularly relevant for LES as the truncation errors from lower-order schemes can exceed the magnitude of the subgrid-scale term (Kravchenko and Moin 1997).

To date, there have been only a few reported works on modeling turbulence using the cut-cell-based EB methods. Meyer et al. (2010) developed a conservative second-order accurate immersed interface method suitable for LES of high Reynolds number incompressible flows. However, an implicit LES approach in the capacity of ALDM approach was employed for the turbulence closure. Essentially, the numerical dissipation of the scheme was assumed to mimic the physical dissipation due to action of small-scale unresolved turbulence. In a recent article, Berger and Aftosmis (2012) extensively analyzed modeling of steady viscous compressible flows using Cartesian cut-cell finite volume method. They explored the use of wall models for laminar and turbulent flows to suppress numerical oscillations in the second derivatives used for viscous flux computations. To the best of the author’s knowledge, there have not been many studies in the area of LES with embedded boundary methods and dynamic refinement for turbulent flow problems.

A high-order accurate adaptive Cartesian cut-cell method has been recently developed by Muralidharan and Menon (2016, 2018) that addresses most of the shortcomings of the previous approaches. A high-order solution was achieved by using a k-exact reconstruction based on a piecewise polynomial approximation of the flow solution locally near the embedded boundary. A novel cell clustering approach was employed that was based on previously established cell-linking approaches for dealing with the ‘small cell’ problem afflicting all the cut-cell methods. One of the key strengths of the cell clustering approach is that it preserves the order of accuracy of the underlying numerical scheme both locally and globally. Additionally, the approach ensured smooth reconstruction of quantities involving flow gradient such as the skin friction coefficient. These features make this approach very suitable for LES of turbulent flow problems. In an another recent study by the authors, a multi-level subgrid closure for LES of compressible flow problem with local adaptive mesh refinement was developed (Muralidharan and Menon 2019) (henceforth called as AMRLES). Consistent and conservative behavior of the subgrid kinetic energy across the multiple levels was demonstrated using the AMRLES approach. The goal of this study is to extend the multi-level closure for LES to problems with embedded boundaries. Appropriate closure model corrections to AMRLES framework suited to the cut-cell EB method are proposed. The cut-cell-AMRLES strategy is then assessed for canonical flow problems. Detailed evaluation of the closure model coefficients is performed and reported.

The organization of the paper is as follows. In the first section, the mathematical formulation and the numerical approach are described. The details of the closure of the subgrid-scale turbulence in the presence of a locally refined grid and embedded boundary are also detailed in this section. The results for canonical turbulent flow problems with the proposed cut-cell-AMRLES framework are reported in the next section. Finally, summary of the work is presented along with future directions in the conclusion section.

2 Mathematical Formulation and Numerical Approach

2.1 Governing Equations for Multi-level AMRLES

In the current study, block-structured adaptive mesh refinement is performed near embedded boundaries to better resolve the near-wall flow features. To perform block-based refinement, the flow solver is interfaced with BoxLib AMR library developed at LBNL. Accordingly, the Favre-filtered compressible LES governing equations for a multi-level AMR grid with $l= 1,2, \ldots ,N$ levels of refinement as detailed in a previous work (Muralidharan and Menon 2019) are given by:

$$\begin{aligned} \frac{\partial }{\partial t} \left( \begin{array} {c} \overline{\overline{\rho }}^{l} \\ \overline{\overline{\rho }}^{l} \widetilde{\widetilde{u}_j}^{l} \\ \overline{\overline{\rho }}^{l} \widetilde{\widetilde{E}}^{l} \end{array} \right) + \frac{\partial }{\partial x_j} \left( \begin{array}{c} \overline{\overline{\rho }}^{l} \widetilde{\widetilde{u}}^{l}_i \\ \overline{\overline{\rho }}^{l} \widetilde{\widetilde{u}}^{l}_i \widetilde{\widetilde{u}}^{l}_j +\overline{\overline{p}}^{l} \delta _{ij} - \widetilde{\widetilde{\tau }}^{l}_{ij} + \tau _{ij}^{{\text {sgs}},l} \\ (\overline{\overline{\rho }}^{l} \widetilde{\widetilde{E}}^{l} + \overline{\overline{p}}^{l}) \widetilde{\widetilde{u}}^{l}_j - \widetilde{\widetilde{u}}^{l}_i \widetilde{\widetilde{\tau }}^{l}_{ij} + \overline{\overline{q}}^{l}_j + H_j^{{\text {sgs}},l} + \sigma _j^{{\text {sgs}},l} \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right) \end{aligned}$$

(10.1)

where $\rho ,u_i, E, and p$ are the density, velocity components, total energy, and pressure, respectively. $\tau _{ij}$ is the viscous stress tensor, and $q_i$ is the thermal conductivity flux in the ith direction. In the above equations, all the subgrid-scale terms, indicated with a sgs superscript, are unclosed, and therefore, require modeling. The multi-level filtering operation, denoted by $\overline{\overline{~}}^l$, can be defined as:

$$\begin{aligned} \overline{\overline{\phi }}^{l} = \mathcal {G}_{l} * \mathcal {G}_{l+1} * \cdots *\mathcal {G}_N \phi . \end{aligned}$$

(10.2)

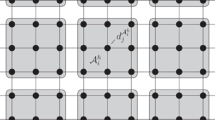
for any flow quantity $\phi$. $\mathcal {G}_l$ is the filtering operator associated with level l which can vary from $l = 1, 2, \ldots , N$ with N being the maximum level of refinement. The representation of the filtered quantity on a multi-level AMR grid is shown both in the wavenumber space and in the physical hierarchical grid system in Fig. 10.1. The wavenumber corresponding to each AMR level and the corresponding filtered quantity at that level is indicated in the figure.

Fig. 10.1

Reprinted with permissions from Muralidharan and Menon (2019)

Schematic of turbulent kinetic energy spectra in a physical space and b wavenumber space. The multi-level filtering of a flow quantity $\phi$ and the associated wave number are also indicated.

The closure models for each of the sgs, l terms are summarized below:

$$\begin{aligned} \tau _{ij}^{{\text {sgs}},l}= & {} -2\overline{\overline{\rho }}^l~ \nu _t^l \left( \widetilde{\widetilde{S}}^{l}_{ij} - \frac{1}{3} \widetilde{\widetilde{S}}^l_{kk} \delta _{ij} \right) + 2/3\overline{\overline{\rho }}^l \overline{\overline{k}}^{{\text {sgs}},l}\delta _{ij}, \end{aligned}$$

(10.3)

$$\begin{aligned} \nu ^l_t= & {} C_\nu ^l \sqrt{k^{{\text {sgs}}, l}} \Delta ^l, \end{aligned}$$

(10.4)

and

$$\begin{aligned} H_i^{{\text {sgs}},l} + \sigma _i^{{\text {sgs}},l} = -\left( \overline{\overline{\rho }}^l \nu ^l_t + \mu ^l \right) \frac{\partial \overline{\overline{k}}^{{\text {sgs}},l}}{\partial x_i} - \frac{\overline{\overline{\rho }}^l \nu ^l_t c_p^l}{Pr_t^l} \frac{\partial \widetilde{\widetilde{T}}^l}{\partial x_i} + \widetilde{\widetilde{u}^l}_j \tau _{ij}^{{\text {sgs}},l}. \end{aligned}$$

(10.5)

The transport equation for the subgrid kinetic energy for a multi-level AMR grid system is given by:

$$\begin{aligned} \frac{\partial \overline{\overline{\rho }} {k}^{{\text {sgs}},l}}{\partial t} + \frac{\partial }{\partial x_{i}} \left( \overline{\overline{\rho }}^l \widetilde{\widetilde{u}}^l_{i} {k}^{{\text {sgs}},l} \right)= & {} \mathcal T_{k^{{\text {sgs}},l}} + pd_{k^{{\text {sgs}},l}} + P_{k^{{\text {sgs}},l}} - D_{k^{{\text {sgs}},l}}, \end{aligned}$$

(10.6)

with the different closure terms in the $k^{{\text {sgs}}}$ equation taking the following form:

$$\begin{aligned} \mathcal T_{k^{{\text {sgs}},l}}= & {} \frac{\partial }{\partial x_i} \left[ (\overline{\overline{\rho }}^l \nu ^l_t + \mu ) \frac{\partial {k}^{{\text {sgs}},l}}{\partial x_i} + \frac{\overline{\overline{\rho }}^l \nu ^l_t \widetilde{\widetilde{R}}^l}{Pr^l_t} \frac{\partial \widetilde{\widetilde{T}}^l}{\partial x_i} \right] , \end{aligned}$$

(10.7)

$$\begin{aligned} pd_{k^{{\text {sgs}},l}}= & {} \alpha _{pd}^l {M_t^{{\text {sgs}},l}}^2 \left( \frac{\overline{\overline{\rho }}^l\widetilde{\widetilde{S}}^l {k}^{{\text {sgs}},l}}{D^{{\text {sgs}},l}} \right) ^2 \left( P_{k^{{\text {sgs}},l}} - D_{k^{{\text {sgs}},l}} \right) , \end{aligned}$$

(10.8)

$$\begin{aligned} P_{k^{{\text {sgs}},l}}= & {} -\tau _{ij}^{{\text {sgs}},l} \widetilde{\widetilde{S}}^l_{ij}, \end{aligned}$$

(10.9)

$$\begin{aligned} D_{k^{{\text {sgs}},l}}= & {} \overline{\overline{\rho }}^l C_\epsilon ^l \left( {{k}^{{\text {sgs}},l}} \right) ^{3/2} / {\Delta ^l}. \end{aligned}$$

(10.10)

Equations (10.3–10.10) are in fact exact equivalents of a single-level $k^{{\text {sgs}}}$ transport equation with single-level flow variables now replaced with their multi-level representation. The coefficients, $C_\nu ^l$ , $C_\epsilon ^l$, $\alpha _{pd}^l$, and ${\text {Pr}}_t^l$, are computed still computed dynamically for each level after employing a test filter with twice the local grid size and using a least square approach (Génin and Menon 2010).

As detailed in the previous study (Muralidharan and Menon 2019), the sgs terms in Eq. (10.1) are closed using the standard single-level closures for each level independently. The only difference is in the treatment of the subgrid turbulent kinetic energy $k^{{\text {sgs}},l}$ for which an additional correction is performed as given by:

$$\begin{aligned} \overline{\overline{\rho }} k^{{\text {sgs}},l}= & {} \overline{\overline{\rho k^{{\text {sgs}}}}}^l + \overline{\overline{\rho \delta }}^{{\text {sgs}},l}, \end{aligned}$$

(10.11)

$$\begin{aligned} \overline{\overline{\rho \delta }}^{{\text {sgs}},l}= & {} \overline{\overline{\rho u_iu_i}}^l - \frac{\overline{\overline{\rho u_i}}^l \overline{\overline{\rho u_i}}^l}{\overline{\overline{\rho }}^l}. \end{aligned}$$

(10.12)

The multi-level correction procedure is illustrated in Fig. 10.2. For unrefined regions, the single-level transport equation-based closure is employed. But for the refined regions indicated by yellow and blue colors, the correction described by Eq. (10.12) is applied. The multi-level formulation can be seen as a mixed model that employs, the transport equation-based sgs model at the finest resolution and adding a correction based on the explicit filtering of represented turbulent kinetic energy on the grid resolution finer than the current level.

2.2 Extension of the Multi-level AMRLES to Embedded Boundaries

While in theory the multi-level formulation can be naturally extended for wall bounded flows with embedded boundary representation, the procedure for dynamically computing the coefficients becomes more complicated as test-level filtering is not clearly defined at the embedded boundary. To overcome this problem, a two-layer approach to the closure model is suggested. On the finest level comprising the wall boundary, the flow is solved without any closure model (in a DNS mode) and away from the boundary on the coarser underlying grids, the multi-level sgs closure is employed. The multi-level correction from the finest (N) to the coarser grid ($N-1$) injects the filtered subgrid turbulent kinetic energy ($k^{{\text {sgs}},N-1}$) which is then transported on the coarser grid levels. The two-layer sgs closure with EB is illustrated in Fig. 10.2.

Fig. 10.2

Schematic of the multi-level correction for $k^{{\text {sgs}}}$ on a AMR mesh with EB

2.3 Formulation and Implementation of Cut-Cell Method

A Cartesian-based strictly conservative cut-cell method that is upto third-order accurate for viscous problems with embedded boundaries has been developed in the past. Readers are referred to a previously published work of the authors (Muralidharan and Menon 2016) for the detailed formulation and validation of the high-order cut-cell method. A summary of the high-order cut-cell method is provided below.

Cut-cell method (Hartmann et al. 2008; Yang et al. 2000) is used in this work to represent embedded boundaries on a Cartesian grid. Information for defining the cut-cells at the embedded boundary is extracted from a levelset field description. Levelset, as defined by Osher and Sethian (1988), Osher and Fedkiw (2003), is a continuous scalar field having values $\phi > 0$ in the fluid region, $\phi <0$ in the solid region and $\phi =0$ at the interface. Once the levelset field is described completely, all the cut-cell metrics can be computed.

To create a cut-cell, the levelset field is assumed to be piecewise linear in a cell and is given as:

$$\begin{aligned} \phi (x,y,z)&= \sum \limits _{p1=0}^1 \sum \limits _{p2=0}^1 \sum \limits _{p3=0}^1 x^{p1} y^{p2} z^{p2} a_{p1,p2,p3} , \\&(p1+p2+p3) \le 1 \nonumber \end{aligned}$$

(10.13)

in which the coefficients, $a_{p1,p2,p3}$, are determined based on the nodal values, $\phi _i,~i=1,8$ for a given computational cell. The embedded boundary surface is defined by the function $\phi (x,y,z)=0$. The boundary equation along with the linear system of equations representing the cut-cell edges is solved simultaneously to provide the points of intersection of the boundary with the edges. The process of finding the cut surface is illustrated in Fig. 10.3a. As shown, the embedded surface is approximated by a planar cut in a given computation cell (i, j, k).

Fig. 10.3

Reprinted with permissions from Muralidharan and Menon (2016)

Schematic of a three-dimensional cut-cell: a creation from levelset description $\phi$ with cut surface described by $\phi (x,y,z)=0$. b Various geometric variables for defining a cut-cell to represent an embedded boundary.

The main idea behind achieving a higher-order accuracy at the embedded boundaries is use of a piecewise high-order polynomial approximation of cell-centered flow quantities as proposed by Ivan and Groth (2014). Accordingly, the following reconstruction polynomial of order k for any conservative or primitive flow quantity u in a given cell i is defined as follows:

$$\begin{aligned} u_i^k(x,y,z)&= \sum _{{p_1}=0}^{k} \sum _{{p_2}=0}^k \sum _{{p_3}=0}^k (x-x_{c,i})^{p_1} (y-y_{c,i})^{p_2}(z-z_{c,i})^{p_3} D^k_{p_1,p_2,p_3}, \nonumber \\&p_1 + p_2 + p_3 \le k \end{aligned}$$

(10.14)

where ($x_{c,i}, y_{c,i}, z_{c,i}$) are the cell center coordinates and $D^k_{p_1,p_2,p_3}$ are coefficients of kth-order approximation of u, which can be proved to be scalar multiples of derivatives of u using Taylor series expansion. Once these coefficients are determined, the above polynomial approximation in Eq. (10.14) can be employed to reconstruct, anywhere within the cell i, the quantity u and its pth derivative with the order of accuracy $(k+1)$ and $(k-p+1)$, respectively. Using the volume-averaged values of the current cell $\overline{u_i}$,

$$\begin{aligned} \overline{u_i} = \frac{1}{V} \int _v \sum _{{p_1}=0}^{k} \sum _{{p_2}=0}^k \sum _{{p_3}=0}^k (x-x_{c,i})^{p_1} (y-y_{c,i})^{p_2}(z-z_{c,i})^{p_3} D^k_{p_1,p_2,p_3}dv, \end{aligned}$$

(10.15)

and the neighboring cell $\overline{u_j}$, the coefficients $D^k_{p_1,p_2,p_3}$ can be found by solving a system of linear equations defined as follows:

$$\begin{aligned} \overline{u}_j-\overline{u}_i&= \sum _{{p_1}=0}^{k} \sum _{{p_2}=0}^k \sum _{{p_3}=0}^k (\widehat{x^{p_1} y^{p_2} z^{p_3}})_{ij} D^k_{p_1,p_2,p_3} ~|~ j = 1, \ldots , n_p , \nonumber \\&p_1 + p_2 + p_3 \le k \end{aligned}$$

(10.16)

where $n_p$ represents the number of neighbors that are required to solve the ith cell-centered quantity and depends on the order of reconstruction. In Eq. (10.16), $\widehat{x^{p_1} y^{p_2} z^{p_3}}$ is the geometric moment of jth cell about ith cell center given by:

$$\begin{aligned} (\widehat{x^{p_1} y^{p_2} z^{p_3}})_{ij} = \int _{v_j} (x-x_{c,i})^{p_1}(y-y_{c,i})^{p_2}(z-z_{c,i})^{p_3}dv. \end{aligned}$$

(10.17)

More details on solving Eq. (10.17) can be found in a previous work by the authors (Muralidharan and Menon 2016).

2.4 Numerical Approach

The fluid solver is a finite volume, compressible, time-accurate LES code capable of solving multi-phase, reacting, turbulent flows in both simple and complex geometries using a structured, parallel multi-block scheme with second- and/or fourth-order accuracy (Chakravarthy and Menon 2001; Génin and Menon 2010). Unless stated otherwise, to evaluate the inviscid and viscous fluxes away from the embedded boundary, Mac-Cormack’s predictor–corrector (MacCormack 2003) method is employed on the full cells. The finite volume version of the Mac-Cormack’s method couples the time and spatial integration schemes. First-order or second-order extrapolation of cell-averaged values that alternates between the downwind and the upwind directions at each step is performed to compute the fluxes on the cell faces. This results in a second-order accurate scheme in both time and space. A higher-order extrapolation can increase the accuracy of the scheme to fourth order.

At the embedded boundary, the Central Essentially Non-Oscillating (CENO) scheme using the k-exact reconstruction is used. The viscous fluxes are computed using central finite difference, and the inviscid fluxes are evaluated by solving the Riemann problem at the cell interfaces using the Hartmann-Lax-van Leer family of approximate Riemann solvers (HLL and HLLC) (Toro 2009).

3 Results and Discussion

The goal of the following numerical case studies is to assess the multi-level cut-cell-AMRLES subgrid closure for performing LES of flows with embedded boundaries. To demonstrate the accuracy of the scheme, order of accuracy analysis for a Laplace problem on a domain with embedded boundaries is reported. Results are then presented for LES of transitional flow past a cylinder and sphere.

3.1 Order of Accuracy Analysis for the Cut-Cell EB Method

To demonstrate the accuracy of the cut-cell finite volume scheme, the following Laplace’s problem:

$$\begin{aligned} \frac{\partial ^2 \psi }{\partial x^2} + \frac{\partial ^2 \psi }{\partial y^2} = 0 , \end{aligned}$$

(10.18)

is solved on a series of successively refined grids and with two different orders of reconstruction: $k=2$ and $k=3$. The exact solution of Eq. (10.18) is: $\psi _{\text {exact}} = \sin x \exp y$. Although a high-order accurate reconstruction of the flow-field quantities and their derivatives iss obtained using the k-exact approach, the solution accuracy degrades due to the aforementioned cell-mixing process. Particularly for viscous flow problems, the classical cell-mixing method achieves numerical stability in computations but causes significant noise in the reconstruction of the derivative quantities, e.g., shear stress and heat flux (Muralidharan and Menon 2016).

The cell clustering scheme is now assessed for this Laplace’s problem on a domain, D with a embedded boundary, $\Gamma$. The boundary is defined by a levelset description $\phi$ on a 1 $\times$ 1 unit domain given by:

$$\begin{aligned} \phi _1(x,y)= & {} 1 - \sqrt{\frac{(x-x_c)^2}{r_1^2} + \frac{(y-y_c)^2}{r{_2}^2}}, \end{aligned}$$

(10.19)

$$\begin{aligned} \phi _2(x,y)= & {} 1 - \sqrt{\frac{(x-x_c)^2}{r_2^2} + \frac{(y-y_c)^2}{r{_1}^2}}, \end{aligned}$$

(10.20)

$$\begin{aligned} \phi (x,y)= & {} \min (\phi _1,\phi _2) \end{aligned}$$

(10.21)

where $(x_c,y_c)$ is set at (0.5, 0.5) and $r_1= 0.3, r_2 = 0.5$. The boundary represented by the above levelset description is shown in the following Fig. 10.4.

Fig. 10.4

Reprinted with permissions from Muralidharan and Menon (2016)

a Immersed domain for the Laplace’s problem represented using cut-cells. b Exact solution to Laplace’s problem, $\psi _{\text {exact}}=\sin x \exp y$.

Equation (10.18) is solved using the finite volume approach described in Sect. 10.2. All the conserved quantities are frozen, and an additional scalar equation is solved for $\psi$ with a Dirichlet boundary condition $\psi (x_\Gamma ,y_\Gamma ) = \psi _{\text {exact}}$ imposed at the immersed boundaries. The $L^1$, $L^2$, and $L^{\infty }$ norm of the errors are computed as $L^p(e_{\psi }) = \left( \frac{1}{\sum _i v_i} \sum _i v_i \vert e_{\psi } \vert ^p \right) ^\frac{1}{p}$ with $v_i$ being the volume of cell, p is error norm, and $\vert e_\psi \vert = \vert \psi - \psi _{\text {exact}} \vert$. The error norms are reported for different mesh sizes and for $k=2$ and $k=3$ in Table 10.1. The plot of the error norms along with the design order of accuracy is shown in Fig. 10.5. To maintain consistency of the error analysis, the k-exact-based CENO reconstruction is used for both the full and cut-cells to evaluate the viscous fluxes.

Table 10.1 Error norms for solution to Laplace equation for different orders of k-exact reconstruction [Reprinted with permissions from Muralidharan and Menon (2016)]

Fig. 10.5

[Reprinted with permissions from Muralidharan and Menon (2016)]

Error norms of $\psi$ for the solution to the Laplace’s problem at different grid resolutions for the Laplace’s problem with different orders of k-exact reconstruction

The error in the solution includes the effects of small cell clustering and mixing. With the cell clustering algorithm, the design order of accuracy is achieved for both $k=2$ and $k=3$. Previous studies employing cut-cell (Hartmann et al. 2011; Cecere and Giacomazzi 2014) have only reported the reconstruction error which does not account for the small cell effects. It is noted that in the current approach, the design order of accuracy is achieved both locally and globally. This clearly indicates the robustness of the proposed cell clustering approach in handling complex surface topologies and still achieves higher order. The Laplace’s problem is representative of the class of viscous flow problems since it involves elliptic, diffusion like term, and therefore, the inferences made on order of accuracy for this simple problem should be applicable to compressible viscous flow problems in general.

Fig. 10.6

Snapshot of local mesh refinement near cylinder surface for ${\text {Re}}_d$ = 3900 flow past a cylinder

3.2 LES of $Re_d$ = 3900 Flow Past a Cylinder

In this study, LES is employed to simulate the turbulent flow of $Re_d$ = 3900 over a cylinder of diameter, d. The simulations are performed in a large rectangular domain of size (30d $\times$ 30d $\times$  $\pi$d) with a base resolution of (150$\,\times \,$150$\,\times \,$20). As shown in Fig. 10.6, six AMR levels are employed such that the effective resolution at the cylinder surface is 0.003125d, which falls in at around $y^{+}=4$, where ${+}$ indicates non-dimensionalization by the viscous length scale. The first point of the wall is located at $y^{+} = 2$. The grid resolution is comparable to a previous study of the same problem (Ranjan and Menon 2015). This problem has been extensively studied using both body conformal and immersed boundary approaches in the past and therefore is an ideal reference case for evaluating the current AMRLES closure with embedded boundaries. Characteristic-based subsonic inflow is used in the left boundary, while subsonic outflow condition is prescribed to the top, bottom, and right boundaries. Front and back surfaces are prescribed with periodic boundary condition.

The stringent wall resolution requirement is due to lack of use of any wall modeling for performing AMRLES which makes this a wall-resolved LES. The coefficients for the subgrid closure models are evaluated dynamically using the LDKM approach (Génin and Menon 2010). The flow Mach number is set at $M = 0.2$ which is low enough to avoid any compressibility effects. The time history of the drag and lift coefficient plots is shown in Fig. 10.7.

Fig. 10.7

Time history of drag ($C_d$) and lift ($C_l$) coefficient of ${\text {Re}}_d$ = 3900 flow past a cylinder

The average drag coefficient of $\overline{C_d} \approx 1$ matches with the data from past studies (Son and Hanratty 1969; Ranjan and Menon 2015). The amplitude changes in the lift coefficient are due to vortex shedding events occurring downstream of the cylinder. The vortex structures in the wake of the cylinder are identified by the iso-surface of Q-criterion colored with streamwise velocity and are shown in Fig. 10.8. It can be observed that the boundary layer separates around the top and bottom of cylinder and forms shear layers which breaks up into coherent structures and eventually into small-scale turbulence within a couple of diameters downstream of the cylinder.

Fig. 10.8

Vortex structures’ visualization by iso-surface of Q-criterion colored with streamwise velocity

The instantaneous snapshots of vorticity magnitude, subgrid kinetic energy, and eddy viscosity ratio are shown in Fig. 10.9. An important observation from the subgrid kinetic energy plot is that the $k^{{\text {sgs}}}$ is generated in shear layer following the coarsening of the finest AMR mesh covering the cylinder surface. As noted in the grid turbulence case study discussed in a previous study (Muralidharan and Menon 2019), the generation of $k^{{\text {sgs}}}$ from a fine/coarse AMR interface occurs solely due to the multi-level subgrid closure. The inflow is laminar and therefore in the free-stream $k^{{\text {sgs}}} = 0$. Without the correction, $k^{{\text {sgs}}}$ will remain zero in the wake resulting in insufficient dissipation at small scales.

Fig. 10.9

Instantaneous snapshot of a vorticity magnitude, b subgrid kinetic energy, and c eddy viscosity ratio in the center x-y plane

Statistics are collected for 100 non-dimensionalized time units, $t = d/ u_\infty$ . In Fig. 10.10, the average pressure coefficient $\overline{C_p}$ and the skin friction coefficient $\overline{C_f}$ are plotted over the surface of the cylinder. The data was averaged in space and also along the z-direction. Excellent agreement is obtained for the point of separation and pressure coefficient data. The skin friction coefficient is also matching well with the past data. Also, note the smoothness in the pressure and skin friction coefficient. To the best of the author’s knowledge, such a smooth reconstruction, especially in the skin friction coefficient has never been shown in any of the past IB studies. Overall, the Cut-cell-AMRLES approach captures the near-wall solution very well. There are some oscillations in the skin friction coefficient plot around 50$^\circ$. These oscillations indicate that the flux reconstruction in the cell present in these regions is not accurate. More investigation is needed to ascertain the source of these numerical artifacts, but the current hypothesis is that the cell clustering and thus the polynomial reconstruction are affected because of some degenerated small cells. Nevertheless, in other regions, the skin friction coefficient distribution is smooth.

Fig. 10.10

Time and spatially averaged (in homogeneous direction) data of a pressure coefficient $\overline{C_p}$ and b skin friction coefficient for ${\text {Re}}_d$ = 3900 flow past cylinder. Block dots in a represent data from a past experimental study (Norberg 1987) and b represent data from a body-fitted LES (Ranjan and Menon 2015)

To further assess the performance of the subgrid closure, the time-averaged plots of various flow- and closure-related quantities are presented in Fig. 10.11. The streamline plots along with the streamwise velocity contours clearly show two recirculation bubbles in the back of the cylinder which are close to symmetric with respect to the streamwise direction. The reattachment length from for bubble is around two diameters which matches with observations from past experimental studies. From the figure, the generation of $k^{{\text {sgs}}}$ in the free shear layer formed from the boundary layer separation is clearly seen in the mean sense. The closure model parameters $C_{\nu }$, $C_{\epsilon }$ that are computed dynamically show a wide variation, especially in the wake region. As expected there is a significant increase in the value of parameter $\overline{C_\nu }$ in the wake region where the large-scale vortex structures breakdown and flow become turbulent. The increase in $C_\nu$ in turn increases the contribution of the subgrid stress to the momentum equation through Eq. (10.4). The plot of the time-averaged $C_\epsilon$ shows high values near the boundary and the shear layer. Downstream of the cylinder in the turbulent wake, the value of the $C\epsilon$ drops. Since this parameter is a scaling coefficient for the model of dissipation of subgrid turbulent kinetic energy, a high value of $C\epsilon$ implies increased subgrid dissipation in the near-wall region and shear layer.

Fig. 10.11

Time-averaged plots of a streamwise velocity, b subgrid kinetic energy, c LDKM parameter $C_\nu$, and d LDKM parameter $C_\epsilon$ in center x-y plane

The quality of the wake predictions by the Cut-cell-AMRLES approach is assessed by comparing the mean streamwise velocity along the centerline of the cylinder with previous data in Fig. 10.12. Overall, the velocity deficit and recovery post reattachment is captured well in the current simulation. But it appears that the length of the recirculation bubble is over-predicted which is causing a delayed reattachment. Since the near-wall predictions are in excellent agreement with past data, the reason for this discrepancy is suspected to be mainly because of lack of convergence of the temporal statistics. A previous study (Ranjan and Menon 2015) performed time averaging after 700 non-dimensionalized time units for an interval of 250 time units, whereas in the current study, time statistics were collected after 150 time units for only an additional 100 time units. The wake predictions are expected to improve with collection of more time-averaged data.

Fig. 10.12

Time-averaged streamwise velocity along the cylinder centerline. Blue solid line—Cut-cell-AMRLES, black dotted line—body-fitted LES (Ranjan and Menon 2015), black filled dots—experimental (Shih et al. 1993), black filled triangles—experimental (Ong and Wallace 1996)

3.3 LES of ${\text {Re}}_d$ = 3700 Flow Past a Sphere

Simulations of flow past spheres can be quite challenging with traditional body-conformal structured grid methods mainly because of the complexity involved in generating a good quality mesh especially near the wake region. Here, the Cut-cell-AMRLES approach is employed to simulate the turbulent flow of ${\text {Re}}_d$ = 3700 over a sphere of diameter, d. The simulations are performed in a rectangular domain of size 30d $\times$ 30d$\times$ 30d with a base resolution of (150$\,\times \,$150 $\times$ 150). The AMR levels and grid resolution are kept same as the previous ${\text {Re}}_d=3900$ study as the Reynolds numbers are comparable. The plot of the AMR refinement for the sphere is shown in Fig. 10.13. Characteristic-based subsonic inflow is used in the left boundary, while subsonic outflow condition is prescribed to all the other boundaries. DNS simulation of the same Reynolds number has been performed in the past (Rodriguez et al. 2011) using an body-conformal unstructured approach.

Fig. 10.13

Snapshot of local mesh refinement near surface for ${\text {Re}}_d$ = 3700 flow past a sphere

The time history of the drag and lift coefficient plots is shown in Fig. 10.14. The average value of the drag coefficient is found to be $\overline{C_d}$ = 0.38. This is close to the value of $\overline{C_{d,{\text {DNS}}}}$ = 0.39 predicted by the DNS study. To visualize the vortex structures in the wake of the sphere, the iso-surface of Q-criterion colored with streamwise velocity is shown in Fig. 10.15. Similar to the cylinder case, the boundary separates from the sphere surface and forms shear layer envelope which breaks down rapidly into small-scale turbulence within a couple of diameters downstream. Due to the three-dimensional nature of the free shear layer, the break down to small-scale turbulence is much faster compared to flow past a cylinder.

Fig. 10.14

Time history of drag ($C_d$) and lift ($C_l$) coefficient of ${\text {Re}}_d=3700$ flow past a sphere

Fig. 10.15

Vortex structures visualization by iso-surface of Q-criterion colored with streamwise velocity

The instantaneous snapshots of subgrid kinetic energy and eddy viscosity ratio are shown in Fig. 10.16. It can be seen from the figure that the behavior of the various flow-field quantities is similar to the previous case of flow past cylinder. The multi-level closure injects $k^{{\text {sgs}}}$ when near-wall refinement ends into the shear layer. A jump in the subgrid kinetic energy and the eddy viscosity is observed after a fine/coarse AMR interface.

Fig. 10.16

Instantaneous snapshot of a subgrid kinetic energy and b eddy viscosity ratio in the center x-y plane

The data is time averaged over 100 non-dimensionalized time units. The plots of the average pressure coefficient $\overline{C_p}$ and the skin friction coefficient $\overline{C_f}$ extracted along the midplane of the sphere are presented in Fig. 10.17. The current results show excellent agreement with the data from DNS and an experimental study for the $C_p$, $C_f$, the back pressure and the point of separation. Again it has to be reiterated that to the best of the author’s knowledge, such a good match has never been reported in addition to smooth reconstruction of pressure and especially skin friction coefficient, in any of the past studies employing an embedded boundary technique. The contour plot of the pressure distribution on the sphere surface is shown in Fig. 10.18.

Fig. 10.17

Time-averaged data of a pressure coefficient $\overline{C_p}$ and b skin friction coefficient for ${\text {Re}}_d$ = 3700 flow past cylinder. Solid blue line- Cut-cell-AMRLES Block dots in a represent data from a past experimental study (Norberg 1987) and b represent data from a body-fitted LES (Ranjan and Menon 2015)

Fig. 10.18

Smooth distribution of pressure on the sphere surface for ${\text {Re}}_d = 3700$ flow past a sphere

The wake predictions are assessed by comparing the mean streamwise velocity and the RMS of streamwise velocity along the centerline with previous DNS results in Fig. 10.19. The velocity deficit and recovery post reattachment are captured well in the current simulation. The magnitude of the RMS of streamwise velocity is slightly over-predicted, but the peak locations match well with the DNS data. As for the cylinder study, the wake predictions are expected to improve with collection of more time-averaged data.

Fig. 10.19

Time-averaged streamwise velocity along the cylinder centerline. Blue—Cut-cell-AMRLES, Black dots—Body-fitted unstructured DNS (Rodriguez et al. 2011)

4 Conclusions

We have presented a multi-level subgrid closure model suited to a cut-cell-based EB approach for LES of compressible flow problems. In the proposed framework, the multi-level formalism of the block-structured refinement is exploited to build a two-layer closure model. At the finest level comprising of the cut-cells used to represent the embedded boundary, all the turbulence length scales are resolved and therefore no subgrid closure is employed. The multi-level correction recently developed for AMRLES is then applied to provide the filtered subgrid kinetic energy to the underlying coarser grids. A key advantage of the approach is that the multi-level correction of the subgrid kinetic energy ($k^{{\text {sgs}}}$) naturally introduces subgrid turbulence into the coarser grids thus facilitating essentially a multi-level boundary condition for $k^{{\text {sgs}}}$ at the embedded boundaries. The cut-cell-AMRLES framework thus builds on the earlier works of the authors (Muralidharan and Menon 2016, 2019) combining a high-order cut-cell EB approach with the AMRLES subgrid closure.

To demonstrate the accuracy of the cut-cell method, grid convergence studies are presented for a 2D elliptic problem. The error analysis performed indicates that the method achieves the design order of accuracy both locally and globally. The cut-cell-AMRLES approach is then applied to study transitional turbulent flow past a cylinder and sphere. Results show that there is a good agreement of the pressure and skin friction coefficient data with past studies. The streamwise velocity and its fluctuation are also compared well with the past data. The detailed analysis of the various turbulent model parameters presented indicates that the proposed model behavior is consistent and addresses some of the problems faced in the past related to LES of AMR with embedded boundaries. For high Reynolds number fully turbulent flow problems, resolving the near-wall turbulent can become considerably more expensive since the adaptive refinement is isotropic. To handle such high Reynolds number flow regimes, integration of the cut-cell-AMRLES approach with wall-modeled LES (WMLES) (Kawai and Larsson 2012) can be attempted is a part of the future work.