Keywords

16.1 Introduction

The solution to the problem of stress distribution in an infinite plate with circular hole subjected to uniaxial loading was first obtained by Kirsch [1]. The details of the analytical solution are found in Timoshenko [2] and Wang [3]. Complex variables approach was first introduced into plane elastic problems in 1909 by Kolosov [4, 5], which was further utilised in solving various problems in elastostatics by Muskhelishvili [6] and others. With improvements in computer performance, numerical techniques like finite element method (FEM) and boundary element method (BEM) became popular methods of solving various engineering problems. However, FEM and BEM have the limitation of increased computing cost and accuracy when discontinuities like holes and cracks are present in the material. Body force method (BFM) originally proposed by Nisitani [7, 8] is a boundary type technique for stress analysis. The software program named BFM2D, developed by Nisitani [8] and based on BFM is reported to provide accurate results even with coarse mesh. More recently, Manjunath and Ramakrishna have applied BFM and solved various problems including Flamant and Melan problem [9,10,11].

16.2 Body Force Method

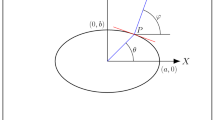
Body force method is a boundary type technique based on the principle of superposition. For a plate with circular hole subjected to uniform tension as shown in Fig. 16.1a, the circular hole is considered as imaginary hole, which is divided into a number of divisions (imaginary hole is divided into four divisions in Fig. 16.1b), at the mid-point of each division, body forces \(\rho_{xi}\), \(\rho_{yi}\) are applied in x- and y-directions, the magnitudes of which are unknown to begin with. Applying equilibrium condition to each division in x- and y-directions due to the body forces and external applied load, we obtain a set of linear equations which can be expressed in the form, \(\varvec{Ax} = \varvec{b}\) where A is influence coefficient matrix obtained from Kelvin’s problem (point load in an infinite plane) where unit loads are applied in x- and y-directions, x is the unknown body force vector and b is a vector consisting of forces on each division in x- and y-directions due to external applied load. The stress at an arbitrary point \({\mathbf{P}}\left( {x,y} \right)\) (Fig. 16.1a) is obtained by the summation of stresses at point \({\mathbf{P}}\left( {x,y} \right)\) due to body forces \(\rho_{xi}\), \(\rho_{yi}\) and stresses due to the applied uniform load as shown in Fig. 16.1b.

Fig. 16.1
figure 1

Plate with a circular hole subjected to uniform tension and its equivalence in BFM

Full size image

16.3 Modified Body Force Method

Body forces \(\rho_{xi}\), \(\rho_{yi}\) can also be computed from complex potential functions which describe the given loading and boundary conditions. The complex potential functions for an infinite plate subjected to uniform tensile stress in x-direction are well known [10]. In this study, body forces are obtained from complex potential function given by Honein [10]. These body forces are applied at the mid-point of each division. The stress at an arbitrary point \({\mathbf{P}}\left( {x,y} \right)\) is obtained by the summation of stresses due to the computed body forces and stresses due to the applied load.

Stresses are related to complex potential functions \(\varphi \left( z \right)\) and \(\psi \left( z \right)\) [2, 3, 5, 6] by the following relations:

$$\sigma_{x} + \sigma_{y} = 2\left( {\varphi^{{\prime }} \left( z \right) + \overline{{\varphi^{{\prime }} \left( z \right)}} } \right) = 4{\Re }\left\{ {\varphi^{{\prime }} \left( z \right)} \right\}$$
(16.1)
$$\sigma_{y} - \sigma_{x} + 2i\tau_{xy} = 2\left( {\bar{z}\varphi^{{\prime \prime }} \left( z \right) + \psi^{{\prime }} \left( z \right)} \right)$$
(16.2)

Forces acting on an arc from A to B are related to complex potential functions by the following relations [12]:

$$P_{x} + P_{y} = - i \left[ {\varphi \left( z \right) + z \cdot \overline{{\varphi^{{\prime }} \left( z \right)}} + \overline{\psi \left( z \right)} } \right]_{A}^{B}$$
(16.3)

Complex potential functions for an infinite plate subjected to uniform tensile stress in x-direction are as follows [10]:

$$\varphi \left( z \right) = \frac{z}{4} \cdot \sigma_{x}^{\infty }$$
(16.4)
$$\psi \left( z \right) = - \frac{z}{2} \cdot \sigma_{x}^{\infty }$$
(16.5)

Complex potential functions \(\varphi \left( z \right)\) and \(\psi \left( z \right)\) from Eqs. (16.4) and (16.5) when substituted in Eqs. (16.1) and (16.2), the following stresses are obtained:

$$\sigma_{x} = \sigma_{x}^{\infty }$$
(16.6)
$$\sigma_{y} = 0$$
(16.7)
$$\tau_{xy} = 0$$
(16.8)

Equations (16.6), (16.7) and (16.8) accurately describe the state of stress at arbitrary point \({\mathbf{P}}\left( {x,y} \right)\) in an infinite plate without any discontinuity.

Complex potential functions from Eqs. (16.4) and (16.5) when substituted in Eq. (16.3), the following forces are obtained:

$$P_{x} = \sigma_{x}^{\infty } \cdot \left[ {y_{B} - y_{A} } \right]$$
(16.9)
$$P_{y} = 0$$
(16.10)

Body forces are computed for an infinite plate with unit thickness having a circular hole of 5 mm radius subjected to uniform tensile stress of 100 MPa. Table 16.1 shows numeric values of the body forces obtained from Eqs. (16.9) and (16.10), for four divisions of the imaginary circle.

Table 16.1 Body force values for four divisions of the imaginary circle
Full size table

16.4 Theoretical Results

In an infinite plane with thickness h, the stress in polar coordinates at an arbitrary point \(z = x + i \cdot y\) due to concentrated load \(P_{x} + i \cdot P_{y}\) acting at location \(z = x_{0} + i \cdot y_{0}\) is reproduced from Wang [13].

$$\sigma_{r} = - \frac{{\left( {3 + \nu } \right)}}{4\pi h}\left( {\frac{{P_{x} \cos \theta + P_{y} \sin \theta }}{r}} \right)$$
(16.11)
$$\sigma_{\theta } = \frac{{\left( {1 - \nu } \right)}}{4\pi h}\left( {\frac{{P_{x} \cos \theta + P_{y} \sin \theta }}{r}} \right)$$
(16.12)
$$\tau_{r\theta } = \frac{{\left( {1 - \nu } \right)}}{4\pi h}\left( {\frac{{P_{x} \sin \theta - P_{y} \cos \theta }}{r}} \right)$$
(16.13)

Stress at arbitrary point \({\mathbf{P}}\left( {x,y} \right)\) is obtained by summing stresses (Eqs. 16.11–16.13) due to body forces obtained for Eqs. (16.9) and (16.10) and stresses due to applied load.

The expression for stresses in polar coordinates for an infinite plate with circular hole (Fig. 16.1a) is available in Timoshenko [12]. These equations are reproduced here from [12].

$$\sigma_{r} = \frac{{\sigma_{x}^{\infty } }}{2}\left( {1 - \frac{{a^{2} }}{{r^{2} }}} \right) + \frac{{\sigma_{x}^{\infty } }}{2}\left( {1 + \frac{{3a^{4} }}{{r^{4} }} - \frac{{4a^{2} }}{{r^{2} }}} \right)\cos 2\theta$$
(16.14)
$$\sigma_{\theta } = \frac{{\sigma_{x}^{\infty } }}{2}\left( {1 + \frac{{a^{2} }}{{r^{2} }}} \right) - \frac{{\sigma_{x}^{\infty } }}{2}\left( {1 + \frac{{3a^{4} }}{{r^{4} }}} \right)\cos 2\theta$$
(16.15)
$$\tau_{r\theta } = - \frac{{\sigma_{x}^{\infty } }}{2}\left( {1 - \frac{{3a^{4} }}{{r^{4} }} + \frac{{2a^{2} }}{{r^{2} }}} \right)\sin 2\theta$$
(16.16)

16.5 Numerical Results

A plate with unit thickness having a circular hole of 5 mm radius is considered with an applied uniform tensile stress of 100 MPa. The radial, hoop and shear stresses along radial direction at angles 0°, 45° and 90° are computed using body force Eqs. (16.9) and (16.10) (legend BFM) and are compared with analytical results (Eqs. 16.14–16.16).

Figures 16.2, 16.3 and 16.4 show stresses along 0° radial line. Radial and hoop stresses show trends in line with the theoretical results.

Fig. 16.2
figure 2

Radial stress (\(\sigma_{r}\)) along radial line making 0° with x-axis, and circle is divided into 1024 divisions

Full size image
Fig. 16.3
figure 3

Hoop stress (\(\sigma_{\theta }\)) along radial line making 0° with x-axis, and circle is divided into 1024 divisions

Full size image
Fig. 16.4
figure 4

Shear stress (\(\tau_{r\theta }\)) along radial line making 0° with x-axis, and circle is divided into 1024 divisions

Full size image

Figures 16.5, 16.6 and 16.7 show stresses along 45° radial line. Radial, hoop and shear stresses show trends in line with the theoretical results. However, it is observed that the magnitudes of these stresses in the proximity of the circular hole deviate from theoretical values.

Fig. 16.5
figure 5

Radial stress (\(\sigma_{r}\)) along radial line making 45° with x-axis, and circle is divided into 1024 divisions

Full size image
Fig. 16.6
figure 6

Hoop stress (\(\sigma_{\theta }\)) along radial line making 45° with x-axis, and circle is divided into 1024 divisions

Full size image
Fig. 16.7
figure 7

Shear stress (\(\tau_{r\theta }\)) along radial line making 45° with x-axis, and circle is divided into 1024 divisions

Full size image

Figures 16.8, 16.9 and 16.10 show stresses along 90° radial line. Radial and hoop stresses show trends in line with the theoretical results.

Fig. 16.8
figure 8

Radial stress (\(\sigma_{r}\)) along radial line making 90° with x-axis, and circle is divided into 1024 divisions

Full size image
Fig. 16.9
figure 9

Hoop stress (\(\sigma_{\theta }\)) along radial line making 90° with x-axis, and circle is divided into 1024 divisions

Full size image
Fig. 16.10
figure 10

Shear stress (\(\tau_{r\theta }\)) along radial line making 90° with x-axis, and circle is divided into 1024 divisions

Full size image

Figures 16.11, 16.12 and 16.13 show radial, hoop and shear stresses along 0° radial line. Here, circle is divided into 1024 divisions, with Poisson’s ratio (a) ν = 0, (b) ν = 0.32. It is observed that taking Poisson’s ratio as zero has little effect on the radial and shear stresses. With nonzero Poisson’s ratio, hoop stress shows little improvement in its trend towards theoretical results.

Fig. 16.11
figure 11

Radial stress along radial line making 0° with x-axis, circle is divided into 1024 divisions, a ν = 0, b ν = 0.32

Full size image
Fig. 16.12
figure 12

Hoop stress along radial line making 0° with x-axis, circle is divided into 1024 divisions, a ν = 0, b ν = 0.32

Full size image
Fig. 16.13
figure 13

Shear stress along radial line making 0° with x-axis, circle is divided into 1024 divisions, a ν = 0, b ν = 0.32

Full size image

16.6 Conclusion

In this study, stress distribution is obtained by summation of stresses due to body forces derived from complex potential functions for a plate with uniform load in x-direction and stresses due to applied load (modified body force method). Results obtained from this method show trends in line with theoretical solution. However, numerical values obtained deviate from the theoretical solution. One of the possible reasons for this deviation in numerical values is that the boundary of the imaginary circle being stress-free may not be completely satisfied. Better results can be obtained when accurate estimates of the body forces on the boundary of the imaginary circle are made. Alternately, body forces obtained from a set of linear equations \(\varvec{Ax} = \varvec{b}\) (body force method) can be used to obtain the stress distribution.

Modified body force method may be useful in the instances where theoretical results are unavailable and this method can give values of stresses approaching actual stresses.

As suggested by Nisitani [14], it is acceptable to take Poisson’s ratio ν = 0 since the marginal improvement in computed stresses is observed when nonzero Poisson’s ratio is used.