Keywords

1 Introduction

In contrast to digital circuits which use mainly active devices, on-chip passive components are imperative adjuncts to most RF circuits [1, 2]. These components which include inductors, capacitors, resistors, etc. are well known to be cost-limiting elements in RF-integrated circuits (ICs). While these components can be realized using CMOS technology, their specific designs necessitate special consideration due to the requirement of high quality factor at relatively higher frequencies.

For low-frequency applications, passive devices can be connected externally, but as the frequency level increases, the characteristics of the passive devices would get overwhelmed by parasitic effects [3]. Consequently, on-chip passive components are preferred for RF applications. On-chip planar loop inductors in RFICs are pivotal for filtering and tuning purposes. It is due to the following reasons; planar loop inductors are the most widely used type of on-chip inductors: (i) better immunity to conduction losses due to minimized substrate coupling, (ii) superior shielding to substrate effects, (iii) known current return path, etc.

However, the parasitic affected planar loop inductor design space is packed with trade-offs and the existing 3-D field solver-based stochastic optimization process [4] is computationally inefficient, and hence not ideally suited for practical inductor design.

Thus, a prompt and efficient semi-empirical approach is presented herein to design on-chip planar loop inductors for use in various RFICs. This approach is based on a lucid and widely accepted inductor model [5], where expressions are in line with the proposed semi-empirical method.

After casting primary information on the semi-empirical optimization technique in Sect. 2, design of planar loop inductor-based differential resonator is formulated in Sect. 3. Interpretation of optimum performance metrics is carried out in Sect. 4. Finally, inferences based on envisaged results are arbitrated in Sect. 5.

2 Semi-empirical Optimization

The semi-empirical technique used here to carry out the optimization of on-chip planar loop inductor is orthogonal convex optimization [6]. This method, unlike classical or knowledge based or other global optimization techniques, can determine the veritable best design solution for a given set of mutually congruent design specifications. Due to the inherent nature of convex functions, this method is prompt and capable of catering vital information on sensitivity and design trade-offs, with least oversight from RFIC designers.

Orthogonal convex optimization technique is a special bracket of semi-empirical optimization, where the basic idea of modeling any practical problem starts with the formulation of design objective and constraints. Although successful formulation of each and every design aspect is not guaranteed, any duly modeled practical problem can be solved with unmatched efficiency.

Objective and constraint functions can be monomial or posynomial or positive fractional power or pointwise maximum of posynomials [6]. Standard form of such a semi-empirical optimization problem is given by

$$ \begin{array}{*{20}l} {\text{optimize}} \hfill & {f_{0} (x)} \hfill & {} \hfill \\ {\text{subject to}} \hfill & {g_{i} (x) = 1,} \hfill & {i = \left( {1, \ldots ,p} \right)} \hfill \\ {} \hfill & {f_{i} (x) \le 1,} \hfill & {i = \left( {1, \ldots ,m} \right)} \hfill \\ {} \hfill & {x_{i} > 0,} \hfill & {i = \left( {1, \ldots ,n} \right)} \hfill \\ \end{array} $$
(1)

where g1, …, gp are monomial and f1, …, fm are posynomial constraints of vector x comprising of n real positive variables. Objective function f0 is either a posynomial to minimize or a monomial to maximize/minimize.

g(x): Rn → R is said to be a monomial function or simply a monomial [6] if its domain is the set of vectors with positive components and its values are given by the following power law expression:

$$ g(x) = cx_{1}^{{a_{1} }} \ldots x_{n}^{{a_{n} }} $$
(2)

where c > 0 is the coefficient and a = a1, …, an is the exponent of the monomial.

f(x): Rn → R is said to be a posynomial function or simply a posynomial [6] if its domain is the set of vectors with positive components and its values take the form of nonnegative sum of monomials

$$ f(x) = \sum\limits_{k = 1}^{K} {c_{k} g_{k} (x)} $$
(3)

where gk(x) are monomials and ck ≥ 0 for k = 1, …, K.

To overcome the non-convexity of monomial and posynomial functions, they are transformed into affine and convex functions, respectively, by introducing a new set of variables yi = log xi, in lieu of xi. Thus, Eq. (1) can be reiterated as

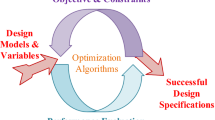
$$ \begin{array}{*{20}l} {\text{optimize}} \hfill & {f_{0} (y) = \log \left( {\sum\limits_{k = 1}^{{K_{0} }} {e^{{a_{0k}^{T} y + b_{0k} }} } } \right)} \hfill & {} \hfill \\ {\text{subject to}} \hfill & {g_{i} (y) = a_{i}^{T} y + b_{i} = 0,} \hfill & {i = \left( {1, \ldots ,p} \right)} \hfill \\ {} \hfill & {f_{i} (y) = \log \left( {\sum\limits_{k = 1}^{{K_{0} }} {e^{{a_{ik}^{T} y + b_{ik} }} } } \right) \le 0,} \hfill & {i = \left( {1, \ldots ,m} \right)} \hfill \\ \end{array} $$
(4)

From the parlance of electronic device and circuit optimization, this semi-empirical technique conforms to the generic flowchart depicted in Fig. 1.

Fig. 1
figure 1

Generic flowchart of the semi-empirical optimization technique

Full size image

According to Fig. 1, a set of device and circuit equations describing the electronic system are considered at the onset. Then a group of operational scenarios describing the thresholds or ranges over which these device and circuit equations remain valid are imposed on these equations as scenario-specific constraints. Based on the type of semiconductor and technology node, some scenario-independent variables related to the device physics are also introduced.

The aforesaid formulations are followed by a concurrent evaluation of the available set of equations over the entire range of user-defined constraints to determine the globally optimum solution (if any) for the design problem; otherwise, infeasibility is reported unambiguously.

3 Design Formulation

Due to the absence of ground reference, resonators with differential inputs are more immune to background electrical noise compared to single-ended input operations. The planar loop inductor shunted with a load capacitance CL and a load resistance RL forms the resonator circuit for floating (differential) mode operation, designed to resonate at operating frequency f. Schematic of the resonator is illustrated in Fig. 2.

Fig. 2
figure 2

Schematic of planar loop inductor-based resonator

Full size image

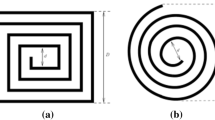
Using the concepts of semi-empirical model parameter estimation [7] and simple expression for planar inductances [8, 9], compatible expressions for the lumped model of the planar loop inductor with a centerline diameter d and breadth b can be obtained with typical errors not exceeding 3%.

$$ \begin{array}{*{20}l} {L_{i} = 2.1 \times 10^{ - 6} d^{1.28} b^{ - 0.25} f^{ - 0.01} } \hfill \\ {R_{s} = 0.1\frac{d}{b} + 3 \times 10^{ - 6} db^{ - 0.84} f^{0.5} + 5 \times 10^{ - 9} db^{ - 0.76} f^{0.75} + 0.02dbf} \hfill \\ {C_{e} = 1 \times 10^{ - 11} d + 5 \times 10^{ - 6} db} \hfill \\ \end{array} $$
(5)

where Li is inductance, Rs is series resistance, and Ce is effective capacitance of the inductor lumped model. Loss incurred from substrate capacitance is included in Rs and Ce. The planar loop inductor and its lumped model are shown in Fig. 3.

Fig. 3
figure 3

Planar loop inductor and its lumped model

Full size image

Area of the planar loop inductor Apli can be formulated as

$$ A_{pli} = (d + b)^{2} $$
(6)

Total capacitance CT of the resonator circuit is given by

$$ C_{T} = C_{e} + C_{L} $$
(7)

Resonance condition for the resonator circuit is as follows:

$$ 4\pi^{2} f^{2} L_{i} C_{T} = 1 $$
(8)

Resulting RLC tank conductance gt of the lumped model is

$$ g_{t} = \frac{{R_{s} }}{{4\pi^{2} f^{2} L_{i}^{2} }} + \frac{1}{{R_{L} }} $$
(9)

Formally, the ratio of energy stored in the magnetic field to energy dissipated in one oscillation cycle is coined as the quality factor Qt, which in turn is an important figure of merit for any inductor.

In case of real inductors, energy stored in the electric field due to parasitic capacitances is a loss. Hence, Qt is proportional to the difference between the peak magnetic and electric energy. Qt is zero at self-resonance frequency, when the peak magnetic and electric energies are equal. Also, no net magnetic energy from the inductor is available above self-resonance.

Inverse of quality factor of the RLC tank Qt-inv is formulated as

$$ Q_{{t{ - }inv}} = \frac{{R_{S} }}{{2\pi fL_{i} }} + \frac{{2\pi fL_{i} }}{{R_{L} }} $$
(10)

Using Eqs. (5)–(10) for the objective and constraint formulations of the semi-empirical design problem of planar loop inductor-based differential resonator circuit optimization is summarized as follows:

$$ \begin{array}{*{20}l} {\text{minimize}} \hfill & {g_{t} } \hfill \\ {\text{subject to}} \hfill & {Q_{{t{ - }inv}} \le \frac{1}{{Q_{{t{ - }inv_{min} }} }},\quad \left( {\frac{d}{b}} \right)_{min} \le \frac{d}{b} \le \left( {\frac{d}{b}} \right)_{max} ,} \hfill \\ {} \hfill & {d_{min} \le d \le d_{max} ,\quad b_{min} \le b \le b_{max} ,\quad A_{pli} \le A_{{pli{ - }max}} ,} \hfill \\ {} \hfill & {4\pi^{2} f^{2} L_{i} C_{T} = 1,\quad f_{\hbox{min} } \le f \le f_{\hbox{max} } } \hfill \\ \end{array} $$
(11)

4 Result Interpretation

The optimization problem is formulated and implemented on MATLAB using ggplab toolbox. Specifications and constraints are listed in Table 1.

Table 1 Constraint and specification for planar loop inductor-based resonator
Full size table

Optimal solution for the design instance in Eq. (11) is outlined in Table 2.

Table 2 Optimal solution for planar loop inductor-based resonator
Full size table

Optimum values for the lumped model of the planar loop inductor are computed from Eq. (5) by using the optimal design parameters from Table 2. Respective lumped model parameters are enlisted in Table 3.

Table 3 Optimum values for planar loop inductor lumped model
Full size table

Sensitivity of the normalized values of the area of planar loop inductor with respect to the normalized operating frequency is plotted in Fig. 4. Since the objective of this graph is to showcase the interdependence between design variables, the axes are interchangeable.

Fig. 4
figure 4

Interdependence between inductor area and operating frequency

Full size image

Due to compelling reasons in practical optimization instances, design variables or constraints are not really set in stone. Therefore, in order to interpret the effect of change of constraints on optimal values of design objectives, the need for trade-off analyses becomes inevitable.

In line with that, the consequences of variations in operating frequency and inductor area on normalized values of quality factor and impedance of the differential resonator are illustrated in Figs. 5, 6, 7, and 8.

Fig. 5
figure 5

Quality factor versus operating frequency trade-off

Full size image
Fig. 6
figure 6

Impedance versus operating frequency trade-off

Full size image
Fig. 7
figure 7

Quality factor versus inductor area trade-off

Full size image
Fig. 8
figure 8

Impedance versus inductor area trade-off

Full size image

These graphs are imperative measures in analyzing the effect of variation of these parameters, viz., inductor area, operating frequency on the overall performance of the resonator circuit for a trade-off packed design space bound by user-defined objective and constraints.

Figure 9 shows absolute error distribution for the lumped model of planar spiral inductor, when compared to the analytical expression of inductances computed using 3-D field solver. The graph shows that the typical errors are smaller than 3% over the entire range, which ascertains adequate level of fidelity propounded.

Fig. 9
figure 9

Semi-empirical expression versus 3-D field solver simulation

Full size image

5 Inference

In this discourse, a simple yet highly efficient semi-empirical optimization technique is devised to formulate and compute globally optimal design solution for an on-chip passive component (planar loop inductor)-based resonator circuit for floating mode RF applications. In connection with previous literature [7], transformation of relevant design attributes into monomial or posynomial expressions through parameter fitting is also exercised in this work.

Apart from meeting the primary objective of determining the globally optimal design solution, prompt exploration of the design space through sensitivity and trade-off analyses is also exhibited in this discourse. Fidelity assessment of the semi-empirical lumped model of the on-chip planar spiral inductor against the inductor analytical expression reflects proximal conformity.

Based on the results obtained, it can be inferred straightaway that the proposed semi-empirical technique is capacious of optimizing on-chip passive components for RF applications with industry acceptable standard of accuracy. Exploration of more complicated RFIC design problems pertaining to the present context remains as the objective for subsequent endeavors.