1 Introduction

The study of thermal convection has attracted the attention of the researchers for many years due to its widespread appearance in many natural as well as industrial systems. Examples of systems where convection plays a significant role in the dynamics are atmosphere, interiors of stars and planets, crystal growth industry, liquid metal blanket etc. (Hartmann et al. 2001; Busse 1989; Miesch 2000; Hurle and Series 1994; Kirillov et al. 1995; Glatzmaier et al. 1999). Investigating thermal convection in these real systems is often very complicated, as it may occur under arbitrary geometry in presence of additional factors like magnetic field, rotation etc. However, to understand the basic physics of convection, researchers consider a simplified model of convection called Rayleigh-Bénard convection.

In this chapter, we consider RBC under rectangular geometry, which consists of a thin layer of fluid, infinitely extended in horizontal directions, kept between two horizontal conducting plates and the system is heated from below. The study of thermal convection under this simplified model, has not only contributed significantly to the understanding of basic physics of convection but also played crucial role in the developments of the subjects like hydrodynamic instabilities (Chandrasekhar 1961; Drazin and Reid 1981; Verma 2018), pattern formation (Cross and Hohenberg 1993; Croquette 1989a, b) and nonlinear dynamics (Manneville 1990; Getling 1998; Busse 1978).

In spite of its simplicity, RBC exhibits a plethora of interesting convective phenomena including instabilities, patterns, chaos and turbulence etc. The study of these instabilities, patterns, chaos and turbulence for different fluids are important topics of research in RBC for many years and still an active area of research (Chandrasekhar 1961; Ahlers et al. 2009; Bodenschatz et al. 2000; Lohse and Xia 2010; Busse 1985; Pal and Kumar 2002; Nandukumar and Pal 2016; Dan et al. 2015, 2014; Pal et al. 2013; Dan et al. 2017).

In this chapter, we discuss low dimensional modeling technique for investigating convective instabilities and the associated pattern dynamics near the onset of convection under rectangular Rayleigh-Bénard geometry. This technique can be used for investigating instabilities in a variety of extended dissipative systems including rotating convection (Veronis 1966, 1959; Maity et al. 2013; Maity and Kumar 2014; Pharasi and Kumar 2013), binary mixture (Kumar 1990), magnetoconvection (Pal and Kumar 2012; Basak and Kumar 2015; Nandukumar and Pal 2015), and rotating magnetoconvection (Ghosh and Pal 2017).

2 Physical System

We consider RBC system consisting of a thin horizontal layer of fluid of thickness d, thermal expansion coefficient \(\alpha \), kinematic viscosity \(\nu \) and thermal diffusivity \(\kappa \) confined between two conducting plates. The system is heated from below. A schematic diagram showing a cross sectional view of the RBC set up has been shown in Fig. 17.1. The temperatures of the lower and upper plates are fixed at \(\mathrm {T_l}\) and \(\mathrm {T_u}\) respectively so that an adverse temperature gradient \(\beta = \frac{\mathrm {T_l} - \mathrm {T_u}}{d}\) is maintained.

Fig. 17.1
figure 1

Sectional view of a Rayleigh-Bénard convection set up on a plane perpendicular to y-axis

Full size image

The above physical system is governed by the following set of equations (Chandrasekhar 1961):

  1. 1.

    Equation of continuity:

    $$\begin{aligned} \frac{\partial \rho }{\partial t} + {\nabla }\cdot (\rho \mathbf{v}) = 0, \end{aligned}$$
    (17.1)

    where the symbols \(\rho \), \(\mathbf{v}\) and t respectively denote fluid density, velocity and time.

  2. 2.

    Energy balance equation:

    $$\begin{aligned} \rho \left[ \frac{\partial }{\partial t}(C_V \mathrm {T}) + (\mathbf{v}\cdot {\nabla })(C_V \mathrm {T})\right] = {\nabla }\cdot (k {\nabla } \mathrm {T}) + \Phi - P({\nabla }\cdot \mathbf{v}), \end{aligned}$$
    (17.2)

    where \(C_V\), \(\mathrm {T}\), \(\mathrm {P}\), k and \(\Phi \) represent specific heat at constant volume, temperature, pressure, co-efficient of heat conduction and heat dissipation term respectively.

  3. 3.

    Equation of motion:

    $$\begin{aligned} \rho \left[ \frac{\partial \mathbf{v}}{\partial t} + (\mathbf{v}\cdot {\nabla })\mathbf{v}\right] = \rho g {\hat{\mathbf {e_3}}}-{\nabla } P+\mu \nabla ^2 \mathbf{v}+ \frac{\mu }{3}{\nabla }({\nabla }\cdot \mathbf{v}), \end{aligned}$$
    (17.3)

    where g is the acceleration due to gravity, \({\hat{\mathbf{e}}_{3}}\) is the unit vector along vertically upward direction and \(\mu \) is the dynamic viscosity of the fluid.

Equations (17.1)–(17.3) are the basic hydrodynamic equations of RBC. Now Eqs. (17.1)–(17.3) are supplemented by the equation of state

$$\begin{aligned} \rho =\rho _0[1-\alpha (\mathrm {T}-\mathrm {T_l})], \end{aligned}$$
(17.4)

where \(\alpha \) is the coefficient of volume expansion of the fluid and \(\rho _0\) is the reference density of the fluid.

3 Boussinesq Approximation

Boussinesq approximation is widely used by the scientists for studying RBC (Chandrasekhar 1961; Boussinesq 1903; Verma 2018). Under this approximation, density is considered to be constant in all terms of the governing equations except in the buoyancy term of the equation of motion where the variation of density due to temperature change is taken into account. Moreover, fluid properties like kinematic viscosity, thermal diffusivity are assumed to be constant. Under this approximation, Eq. (17.1) becomes,

$$\begin{aligned} {\nabla }\cdot \mathbf{{v}}=0, \end{aligned}$$
(17.5)

and Eqs. (17.2) and  (17.3) respectively change to

$$\begin{aligned} \frac{\partial \mathrm {T}}{\partial t}+ (\mathbf {v}\cdot {\nabla }) \mathrm {T}= & {} \kappa {\nabla }^2 \mathrm {T},\end{aligned}$$
(17.6)
$$\begin{aligned} \frac{\partial \mathbf {v}}{\partial t}+(\mathbf {v}\cdot {\nabla })\mathbf {v}= & {} (1+\frac{\delta \rho }{\rho _0})g\hat{e}_{3}-\frac{1}{\rho _0}{\nabla }P+\nu {\nabla }^2\mathbf {v}, \end{aligned}$$
(17.7)

where \(\delta \rho \) is the change in density, \(\nu \) = \(\frac{\mu }{\rho _0}\) is kinematic viscosity and \(\kappa =\frac{k}{\rho _0 C_V}\) is the thermal diffusivity of the fluid.

4 Perturbation Equations

To study convective flow, we derive perturbation equations for the convective states using the equations of the basic (conduction) state. In the following subsection basic state equations are derived.

4.1 Basic State

In conduction state, the fluid is motionless. Therefore, we have

$$\begin{aligned} {\mathbf{v}_b}=(\mathrm {v_1}, \mathrm {v_2}, \mathrm {v_3}) \equiv (0, 0, 0) , ~\mathrm {T_b} \equiv ~\mathrm {T(z)}, \end{aligned}$$
(17.8)

where \({\mathbf{v}_b}\) and \(\mathrm {T_b}\) are the velocity and temperature at the basic state. Now, temperature \(\mathrm {T_b}\) of the fluid in basic state is deduced from Eq. (17.6) which is given by

$$\begin{aligned} \mathrm {T_b}(z) = \mathrm {T_l}-\beta z, \end{aligned}$$
(17.9)

where \(\mathrm {T_l}\) is the temperature at the bottom layer, d is the thickness of the fluid layer and \(\beta d~~(= \triangle \mathrm {T} = \mathrm {T_l}-\mathrm {T_u})\) is the temperature difference of the lower and upper plates.

The density distribution is then given by,

$$\begin{aligned} \rho _b (z) =\rho _0(1-\alpha \beta z), \end{aligned}$$
(17.10)

where \(\rho _0\) is the reference fluid density and \(\alpha \) is the coefficient of volume expansion of the fluid.

Hence the pressure distribution for this basic state is obtained by using Eqs. (17.8), (17.9) and (17.10) in Eq. (17.7) which is given by

$$\begin{aligned} P_b(z) = P_0-g\rho _0(z+\frac{1}{2}\alpha \beta z^2), \end{aligned}$$
(17.11)

where \(P_b(z)\) is pressure distribution of the fluid in basic state and \(P_0\) is the reference pressure of the fluid.

4.2 Convective State

As convection sets in, the basic fields given by Eqs. (17.8), (17.9),  (17.10) and (17.11) are perturbed and let they are described by,

$$\begin{aligned} \mathrm {T_b(z)}\rightarrow \mathrm {T(x,y,z,t)}= & {} \mathrm {T_b(z)} + \theta (x,y,z,t),\\ \mathrm {P_b(z)}\rightarrow \mathrm {P(x,y,z,t)}= & {} \mathrm {P_b(z)} + p(x,y,z,t),\\ \mathrm {\mathbf{{v}}_b(x,y,z,t)}\rightarrow \mathrm {\mathrm {\mathbf{v}}(x,y,z,t)}= & {} {\mathbf{{v}}_b(x,y,z,t)} + {\mathbf{{v}}(x,y,z,t)},\\ \mathrm {\rho _b(z)} \rightarrow \mathrm {\rho (x,y,z,t)}= & {} \mathrm {\rho _b(z)} + \delta \mathrm {\rho }=\mathrm {\rho _b(z)} - \mathrm {\rho _0}\alpha \theta , \end{aligned}$$

where T(x, y, z, t), P(x, y, z, t), \({{\mathbf{v}}(x,y,z,t)} = (v_1, v_2, v_3)\) and \({\rho (x,y,z,t)}\) are convective temperature, pressure, velocity and density fields respectively. The fields \(\theta \), p, \(\mathbf{{v}}\) and \(\delta \mathrm {\rho }\) are the perturbations over the basic conduction state. Now, the equations of motion, the energy equation and equation of continuity, for perturbed fields change to

$$\begin{aligned} \frac{\partial \mathbf{{v}}}{\partial t}+(\mathbf{{v}}\cdot {\nabla })\mathbf{{v}}= & {} -\frac{{\nabla }p}{\rho _0} + g \alpha {{\hat{\mathbf{e}}_3}} \theta + \nu {\nabla }^2 \mathbf{{v}},\end{aligned}$$
(17.12)
$$\begin{aligned} \frac{\partial \theta }{\partial t} + (\mathbf{{v}}\cdot {\nabla }) \theta= & {} \beta {{\hat{\mathbf{e}}_3}}\cdot \mathbf{{v}} + \kappa {{\nabla }^2}\theta , \end{aligned}$$
(17.13)
$$\begin{aligned} {\nabla }\cdot \mathbf{{v}}= & {} 0. \end{aligned}$$
(17.14)

5 Boundary Conditions

Mathematical description of a physical system should include proper boundary conditions along with the governing equations. In this section we discuss about the boundary conditions we have used to demonstrate the low dimensional modeling technique. Now, irrespective of the nature of bounding surfaces, we must have \(v_3=0\) at the horizontal bounding surfaces. The top and bottom plates are maintained at constant temperatures, which imply \(\theta = 0\). In this chapter, we consider free-slip boundaries which mean the tangential stresses at the bounding plates vanish. Therefore, one gets

$$\begin{aligned} \frac{\partial v_1}{\partial z} = \frac{\partial v_2}{\partial z} = 0 \text{ at } \text{ the } \text{ boundaries. } \end{aligned}$$
(17.15)

Now differentiating the equation of continuity (17.14) with respect to z and using (17.15), we get

$$\begin{aligned} \frac{\partial ^2 v_3}{\partial z^2} = 0, \text{ on } \text{ free-slip } \text{ boundaries. } \end{aligned}$$
(17.16)

The vertical component of vorticity will satisfy

$$\begin{aligned} \frac{\partial \omega _3}{\partial z} = 0, \text{ on } \text{ free-slip } \text{ surfaces. } \end{aligned}$$
(17.17)

6 Nondimensionalization

To reduce the number of free parameters and the problems due to the large variation of the values of the parameters, Eqs. (17.12)–(17.14) are made dimensionless. In this chapter, we study convection in two different kinds of fluids namely high Prandtl-number (\(\mathrm {Pr} > 1\)) and low Prandtl-number (\(\mathrm {Pr} < 1\)) fluids.

For low Prandtl-number fluid convection, we nondimensionalize the governing equations using the units d for length, viscous diffusion time \(\frac{d^2}{\nu }\) for time and \(\frac{\nu \beta d}{\kappa }\) for temperature. Now if the primed quantities \(x'\), \(y'\), \(z'\), \(t'\) and \(\theta '\) denote the dimensionless quantities then the dimensional variables can be written as

$$ x=dx', y=dy', z=dz', t=\frac{d^2}{\nu } t'\, \text {and}\, \theta =\frac{\nu \beta d}{\kappa } \theta '. $$

Using these quantities, Eqs. (17.12)–(17.14) can be written in the dimensionless form as

$$\begin{aligned} \frac{\partial \mathbf{{v}}'}{\partial t'}+(\mathbf{{v}}' \cdot \nabla ')\mathbf{{v}}'= & {} - \nabla ' p' + {{\nabla }'}^2{\mathbf{v}'}+\mathrm {Ra} \theta ' \hat{e}_{3},\end{aligned}$$
(17.18)
$$\begin{aligned} \mathrm {Pr}\left[ \frac{\partial \theta '}{\partial t'}+(\mathbf{v}' \cdot \nabla ')\theta '\right]= & {} {{\nabla }'}^2 \theta ' + {v_3}',\end{aligned}$$
(17.19)
$$\begin{aligned} \nabla ' \cdot \mathbf{v'}= & {} 0, \end{aligned}$$
(17.20)

where \(\mathrm {Ra}=\frac{\alpha \beta g d^4}{\nu \kappa }\) and \(\mathrm {Pr}=\frac{\nu }{\kappa }\) are two nondimensional numbers namely the Rayleigh number, which is the ratio of buoyancy and dissipative forces and the Prandtl number, which is the ratio of kinematic viscosity and thermal diffusivity respectively.

On the other hand, for high Prandtl number fluids, we use the scales \(\frac{\beta d}{\mathrm {Ra}}\) for temperature, thermal diffusion time scale \(\frac{d^2}{\kappa }\) for time and other scales same as the low Prandtl-number fluids to nondimensionalize the governing equations. The dimensionless equations in this case become

$$\begin{aligned} \frac{\partial \mathbf{{v}}'}{\partial t'}+(\mathbf{{v}}' \cdot \nabla ')\mathbf{{v}}'= & {} - \nabla ' p' + \mathrm {Pr}{{\nabla }'}^2{\mathbf{v}'}+\mathrm {Pr} \theta ' \hat{e}_{3},\end{aligned}$$
(17.21)
$$\begin{aligned} \frac{\partial \theta '}{\partial t'}+(\mathbf{v}' \cdot \nabla ')\theta '= & {} {{\nabla }'}^2 \theta ' + \mathrm {Ra}{v_3}',\end{aligned}$$
(17.22)
$$\begin{aligned} \nabla ' \cdot \mathbf{v}'= & {} 0. \end{aligned}$$
(17.23)

In the subsequent sections we use the above dimensionless set of equations by dropping the primes from all the variables and operators.

7 Linear Theory

We now determine the critical Rayleigh number (\({\mathrm {Ra}_c}\)) and critical wave number (\(k_c\)) at the onset of convection using the linear theory (Chandrasekhar 1961). The linearized version of Eqs. (17.18)–(17.20) are given by

$$\begin{aligned} \frac{\partial \mathbf {v}}{\partial t}= & {} -\nabla {p} + \nabla ^2\mathbf{{v}} + \mathrm {Ra} \theta {{\hat{\mathbf{e}}_3}}, \end{aligned}$$
(17.24)
$$\begin{aligned} \mathrm {Pr}\frac{\partial \theta }{\partial t}= & {} v_3+\nabla ^2\theta , \end{aligned}$$
(17.25)
$$\begin{aligned} \nabla \cdot \mathbf{v}= & {} 0. \end{aligned}$$
(17.26)

Taking twice curl of Eq. (17.24) we get the following equation

$$\begin{aligned} \frac{\partial }{\partial t} \nabla ^2 v_3 = \nabla ^4 v_3 + \mathrm {Ra} \nabla _H^2 \theta , \end{aligned}$$
(17.27)

for the vertical velocity, where \(\nabla _H^2 = \frac{\partial ^2}{{\partial x}^2}+\frac{\partial ^2}{{\partial y}^2}\) is the horizontal Laplacian. Eliminating \(\theta \) from (17.27) using (17.25) we get

$$\begin{aligned}{}[\nabla ^2(\mathrm {Pr}\partial _t - \nabla ^2)(\partial _t - \nabla ^2) - \mathrm {Ra} \nabla _H^2]v_3 = 0. \end{aligned}$$
(17.28)

We consider the expansion of vertical velocity in normal modes as

$$\begin{aligned} v_3(x,y,z,t) = W(z)exp[i(k_{x}x + k_{y}y) + \sigma t], \end{aligned}$$
(17.29)

where, \(k_x\) and \(k_y\) are the wave numbers along x and y direction respectively and \(k = \sqrt{k_x^2 + k_y^2}\) is the horizontal wave number. Inserting Eq. (17.29) in Eq. (17.28), and choosing a trial solution \(W(z) = Asin(n\pi z)\), which is compatible with the boundary conditions, we arrive at the stability condition

$$\begin{aligned} (n^2\pi ^2 + k^2)(n^2\pi ^2 + k^2 + \mathrm {Pr}\sigma )(n^2\pi ^2 + k^2 + \sigma ) = \mathrm {Ra} k^2. \end{aligned}$$
(17.30)

Since we are interested in stationary convection we set \(\sigma = 0\) in Eq. (17.30) to get

$$\begin{aligned} (n^2\pi ^2 + k^2)^3 = \mathrm {Ra} k^2. \end{aligned}$$
(17.31)

Therefore, the Rayleigh number \(\mathrm {Ra}\) is given by

$$\begin{aligned} \mathrm {Ra} = \frac{(n^2\pi ^2 + k^2)^3}{k^2}. \end{aligned}$$
(17.32)

We now find the minimum value of \(\mathrm {Ra}\) which is the critical Rayleigh number (\(\mathrm {Ra}_{c}\)) for the onset of convection together with the corresponding critical wave number \(k_c\). From Eq. (17.32) we observe that the minimum value of \(\mathrm {Ra}\) occurs for a given \(k^2\) when \(n = 1\). Therefore we have

$$\begin{aligned} \mathrm {Ra} = \frac{(\pi ^2 + k^2)^3}{k^2}. \end{aligned}$$
(17.33)

The above equation imply that for all values of \(\mathrm {Ra}\) less than that are given by Eq. (17.33), disturbances associated with wave number k decay, while the same disturbances grow when \(\mathrm {Ra}\) exceeds the value given by (17.33). When the value of \(\mathrm {Ra}\) equals the value given by Eq. (17.33), the disturbances with wave number k become marginally stable. Therefore, the \(\mathrm {Ra}_{c}\) is determined by the condition

$$\begin{aligned} \frac{\partial \mathrm {Ra}}{\partial k^2} = \frac{(\pi ^2 + k^2)^2(2k^2 - \pi ^2)}{k^4} = 0. \end{aligned}$$
(17.34)

Which gives us \(k^2 = \frac{\pi ^2}{2}\) and the corresponding value of \(\mathrm {Ra}_{c}\) as

$$\begin{aligned} \mathrm {Ra}_{c} = \frac{27}{4}{\pi ^4} \sim 657.5114. \end{aligned}$$
(17.35)

Note that we get same critical values of the Rayleigh number (\(\mathrm {Ra}_{c}\)) and critical wave number (\(\mathrm {k}_{c}\)) even if we consider Eqs. (17.21)–(17.23) at the outset. In the following discussion, we use another parameter called reduced Rayleigh number defined by \(r = \frac{\mathrm {Ra}}{\mathrm {Ra}_{c}}\).

8 Direct Numerical Simulations

For low dimensional modeling, the performance of direct numerical simulations for some set of parameter values and the data obtained from there can be of great help. Therefore, before going for low dimensional modeling, we perform DNS of the system using a pseudo spectral code Tarang (Verma et al. 2013). In the simulation, vertical velocity \((v_3)\), vertical vorticity \((\omega _3)\) and temperature \((\theta )\) fields are expanded using the set of orthogonal basis functions either with respect to \(\{e^{i(lk_x x+mk_y y)} \sin (n\pi z) : l, m, n = 0, 1, 2,\ldots \}\) or with respect to \(\{e^{i(lk_x x+mk_y y)} \cos (n\pi z) : l, m, n = 0, 1, 2,\ldots \}\) whichever is compatible with the free-slip boundary conditions, where \(k_x\), \(k_y\) are the wave numbers along x and y directions respectively. Therefore, the expressions of vertical velocity, vertical vorticity and temperature fields are given by

$$\begin{aligned} \mathrm {v}_{3} (x,y,z,t)= & {} \sum _{l,m,n} W_{lmn}(t)e^{i(lk_xx+mk_yy)}\sin {(n\pi z)},\end{aligned}$$
(17.36)
$$\begin{aligned} \omega _3 (x,y,z,t)= & {} \sum _{l,m,n} Z_{lmn}(t)e^{i(lk_xx+mk_yy)}\cos {(n\pi z)},\end{aligned}$$
(17.37)
$$\begin{aligned} {\mathrm {~and~}} \theta (x,y,z,t)= & {} \sum _{l,m,n} T_{lmn}(t)e^{i(lk_xx+mk_yy)}\sin {(n\pi z)}. \end{aligned}$$
(17.38)

In the simulation, we set \(k_x=k_y=k_c=\frac{\pi }{\sqrt{2}}\), the critical wave number. The aspect ratio of the simulations is \(\frac{2 \pi }{k_c}:\frac{2 \pi }{k_c}:1 \equiv 2\sqrt{2}:2\sqrt{2}:1\). An open source software called Fastest Fourier transform in the west (FFTW)  (Frigo and Johnson 2005) is used for computations in the Fourier space. Inverse Fourier transform routines of the same package are used for mapping to the real space. For time advancement, fourth order Runge-Kutta scheme with Courant-Friedrichs-Lewy (CFL) condition is used in the code. Mostly \({32}^3\) grid resolution is considered for the simulations. Note that, \(32^3\) grid resolution means the values of l, m and n in the above expansions are run over the integers set \(\{0, 1, 2,\ldots , 31\}\). In the following we present some results of DNS for illustrating low dimensional modeling technique.

8.1 Onset of Convection for \(\mathrm {Pr} = 10\)

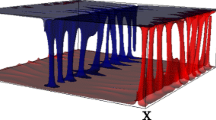
We perform DNS of the system for \(\mathrm {Pr} = 10\) to investigate the flow patterns close to the onset of convection. Note that Eqs. (17.21)–(17.23) are used for the simulation. Figure 17.2 shows the time series of \(W_{101}\) and \(W_{011}\) as well as flow pattern as observed in DNS at \(r = 5\). The flow pattern in this case is found to be two dimensional (2D) rolls. This type of flow patterns are reported for high Prandtl number fluid convection in Krishnamurti (1970), Busse and Whitehead (1971). In Sect. 17.9.1 we’ll show the derivation of famous Lorenz model (1963) by using low dimensional modeling technique and describe the origin of 2D rolls pattern at the onset of convection.

Fig. 17.2
figure 2

Time series of the Fourier modes \(W_{101}\) and \(W_{011}\) and flow patterns corresponding to 2D rolls solutions as obtained from DNS for \(r = 5\) and \(\mathrm {Pr} = 10\). Isotherms computed at the mid plane \(z = 0.5\) generate the pattern. Brown and blue regimes on the patterns represent hotter and colder regions

Full size image

8.2 Onset of Convection for Low Prandtl Number Fluids in the Limit \(\mathrm {Pr}\rightarrow 0\).

It has been shown earlier that the low Prandtl number fluid convection can be approximated by considering the limit \(\mathrm {Pr} \rightarrow 0\) (Thual 1992; Busse 1972; Pal et al. 2009, 2013). In this limit, the temperature Eq. (17.19) reduces to

$$\begin{aligned} \nabla ^2\theta = -v_3. \end{aligned}$$
(17.39)
Fig. 17.3
figure 3

Time series of the Fourier modes \(W_{101}\) and \(W_{011}\) (first row) and flow patterns corresponding to OCR-I solutions as obtained from DNS (second and third rows) for \(r = 1.04\). The flow patterns (a–h) correspond to the instants shown on the time series of the top panel. The flow patters are isotherms computed at the mid plane \(z = 0.5\)

Full size image

We now simulate Eqs. (17.18),  (17.20) and (17.39) to get an idea about the pattern dynamics and bifurcation structure near the onset of convection. Figure 17.3 shows the time evolution of the significant Fourier modes and associated pattern dynamics as obtained from DNS for \(r = 1.04\). From the figure, it is clear that 2D rolls flow patterns oriented along y and x axes are periodically evolved with intermediate square patterns. This flow regime is called oscillatory cross rolls of type-I (OCR-I). Interestingly, for a higher r stationary solution is observed in DNS. Figure 17.4 shows the time series as well as flow pattern corresponding to this stationary solution. From the time series we observe that the solution is stationary with \(W_{101} = W_{011}\) and pattern is of stationary square (SQ) type. These DNS results are intriguing, investigation of the origin of these flow patterns and the associated bifurcation structure follow naturally. However, this is difficult to achieve in DNS, because, on one hand it is costly in terms of computer time and on the other hand, DNS only capture the stable solutions of the system and can not identify the unstable solutions. Due to this reason, low dimensional models can be very useful. In the next section, we discuss how a low dimensional model can be derived from the DNS data and successfully explains the origin of different flow patterns to unfold a very rich bifurcation.

Fig. 17.4
figure 4

Time series of the Fourier modes \(W_{101}\) and \(W_{011}\) (left) and flow patterns corresponding to SQ solutions as obtained from DNS (right) for \(r = 1.28\). The flow patterns are isotherms computed at the mid plane \(z = 0.5\). Brown regimes are hotter and blue regimes are colder

Full size image

9 Low Dimensional Modeling

We use standard Galerkin technique (Galerkin 1915) to construct the low dimensional models. To start with, large scale modes in the vertical velocity, vertical vorticity and temperature are selected from the DNS data by computing the energy contained in the modes relative to the total energy. Then we retain only those modes in the expansions of the vertical velocity (\(\mathrm {v}_{3}\)), vertical vorticity (\(\omega _3\)) and temperature (\(\theta \)) and write truncated series for these independent variables.

The horizontal components of velocity field are then determined by using the solenoidal property of the velocity and vorticity fields which leads to the expressions:

$$\begin{aligned} \nabla _H^2 {\mathrm {v}_{1}}= & {} -\frac{\partial \omega _3}{\partial y} -\frac{\partial ^2 \mathrm {v}_{3}}{\partial x \partial z},\end{aligned}$$
(17.40)
$$\begin{aligned} \nabla _H^2 {\mathrm {v}_{2}}= & {} \frac{\partial \omega _3}{\partial x} -\frac{\partial ^2 \mathrm {v}_{3}}{\partial y \partial z}. \end{aligned}$$
(17.41)

where \(\nabla _H^2 \equiv \frac{\partial ^2}{\partial x^2} + \frac{\partial ^2}{\partial y^2}\) is the horizontal Laplacian. The expressions for \(\omega _1\) and \(\omega _2\) are now obtained by taking the curl of the velocity vector \(\mathbf{v} \equiv (\mathrm {v}_{1}, \mathrm {v}_{2}, \mathrm {v}_{3})\). Once the components of velocity, vorticity and temperature are calculated, for low Prandtl number fluids we take curl twice of Eq. (17.18) and determine the following two equations for vertical velocity and vorticity:

$$\begin{aligned} \partial _t(\nabla ^2 \mathrm {v}_{3})= & {} \nabla ^4 {\mathrm {v}_{3}} + \mathrm {Ra} \nabla ^2_H \theta \nonumber \\- & {} \hat{\mathbf{e}}_3\cdot \nabla \times \left[ ({\varvec{\omega }}{\cdot }\nabla )\mathbf{v} -( \mathbf{v}{\cdot }\nabla ){\varvec{\omega }} \right] ,\end{aligned}$$
(17.42)
$$\begin{aligned} \partial _t \omega _3= & {} \nabla ^2 \omega _3+\left[ ({\varvec{\omega }}{\cdot }\nabla ) {\mathrm {v}_{3}} -(\mathbf{v}{\cdot }\nabla )\omega _3\right] . \end{aligned}$$
(17.43)

On the other hand, for high Prandtl number fluids, we take curl of Eq. (17.21) twice and get

$$\begin{aligned} \partial _t(\nabla ^2 \mathrm {v}_{3})= & {} \mathrm {Pr}\nabla ^4 {\mathrm {v}_{3}} + \mathrm {Pr} \nabla ^2_H \theta \nonumber \\- & {} \hat{\mathbf{e}}_3\cdot \nabla \times \left[ ({\varvec{\omega }}{\cdot }\nabla )\mathbf{v} -( \mathbf{v}{\cdot }\nabla ){\varvec{\omega }} \right] ,\end{aligned}$$
(17.44)
$$\begin{aligned} \partial _t \omega _3= & {} \mathrm {Pr}\nabla ^2 \omega _3+\left[ ({\varvec{\omega }}{\cdot }\nabla ) {\mathrm {v}_{3}} -(\mathbf{v}{\cdot }\nabla )\omega _3\right] . \end{aligned}$$
(17.45)

Then we substitute the expressions of \(\mathrm {v}_{1}\), \(\mathrm {v}_{2}\), \(\mathrm {v}_{3}\), \(\omega _1\), \(\omega _2\), \(\omega _3\) and \(\theta \) in Eqs. (17.42), (17.43) and (17.19) for low Prandtl-number fluids, while for high Prandtl number fluids we substitute the same in Eqs. (17.44), (17.45) and (17.22) and use the orthogonality property of the functions \(\{e^{i(lk_xx+mk_yy)}\sin {(n\pi z)}: l, m, n = 0,1, 2, \ldots \}\) and \(\{e^{i(lk_xx+mk_yy)}\cos {(n\pi z)}: l, m, n = 0,1, 2, \ldots \}\) over the intervals \([0, \frac{2\pi }{k_x}]\), \([0, \frac{2\pi }{k_y}]\) and [0, 1] along x-, y- and z- axis respectively to obtain a set of coupled nonlinear ordinary differential equations of the large-scale amplitudes of the large scale modes of \(\mathrm {v}_{3}\), \(\omega _3\) and \(\theta \) which is our low-dimensional model. These low dimensional models are then analyzed using the theory of nonlinear dynamics (Strogatz 2001) and continuation software like MATCONT (Dhooge et al. 2003).

9.1 The Lorenz Model

AS mentioned above, to study the onset of convection in high Prandtl number fluids using low dimensional modeling we identify the large scale modes from the DNS data by calculating the contribution of a mode to the total energy. We find from the DNS data that near the onset of convection for \(\mathrm {Pr} = 10\), the mode \(W_{101}\cos {k_cx}\sin {\pi z}\) in \(v_3\) contributes most to the energy and vertical vorticity is not developed. Therefore, we choose

$$\begin{aligned} \mathrm {v}_{3} = W_{101}(t)\cos {k_c x}\sin {\pi z}~\mathrm {and}~\omega _3 = 0. \end{aligned}$$

The horizontal components of the velocity computed using Eqs. (17.40) and (17.41) are given by

$$\begin{aligned} \mathrm {v}_{1}= & {} -\frac{\pi }{k_c}W_{101}(t)\sin {k_c x}\cos {\pi z}~\mathrm {and}~\mathrm {v}_{2}=0. \end{aligned}$$
(17.46)

Now from Eq. (17.22) we observe that \(\theta \) linearly couples with \(v_3\). Therefore, we take

$$\begin{aligned} \theta = T_{101}(t)\cos {k_c x}\sin {\pi z}. \end{aligned}$$
(17.47)

As the linear growth rate of the mode \(W_{101}\) is positive above the onset of convection, for saturation, Lorenz (1963) considered least nonlinear correction in \(\theta \) in terms of the mode \(T_{002}(t)\sin {2\pi z}\) and the expression for \(\theta \) becomes

$$\begin{aligned} \theta = T_{101}(t)\cos {k_c x}\sin {\pi z} + T_{002}(t)\sin {2\pi z}. \end{aligned}$$
(17.48)

Horizontal components of vorticity then become

$$\begin{aligned} \omega _1&= 0&\end{aligned}$$
(17.49)
$$\begin{aligned} \mathrm {and}~\omega _2= & {} \frac{\pi ^2}{k_c}W_{101}(t)\sin {k_c x}\sin {\pi z}. \end{aligned}$$
(17.50)

Substituting the expressions of \(\mathrm {v}_{1}\), \(\mathrm {v}_{2}\), \(\mathrm {v}_{3}\), \(\mathrm {\omega }_{1}\), \(\mathrm {\omega }_{2}\), \(\mathrm {\omega }_{3}\) and \(\mathrm {\theta }\) in Eqs. (17.44) and  (17.22) and using the orthogonality property of the basis functions we get,

$$\begin{aligned} \dot{W_{101}}= & {} \frac{\mathrm {Pr}k_c^2}{k_c^2 + \pi ^2} T_{101} -\mathrm {Pr}(k_c^2 + \pi ^2) W_{101},\end{aligned}$$
(17.51)
$$\begin{aligned} \dot{T_{101}}= & {} -(k_c^2 + \pi ^2)T_{101} + \mathrm {Ra}W_{101} + \pi T_{002}W_{101},\end{aligned}$$
(17.52)
$$\begin{aligned} \dot{T_{002}}= & {} -4\pi ^2 T_{002}-\frac{\pi }{2}W_{101}T_{101}. \end{aligned}$$
(17.53)

The method described above for deriving this model is called Galerkin projection (1915). Now using the transformation \(\tau = (k_c^2+\pi ^2)t\), \(X=\frac{k_c}{k_c^2+\pi ^2}W_{101}\), \(Y = \frac{k_c^3}{(k_c^2 + \pi ^2)^3}T_{101}\) and \(Z = -\frac{\pi k_c^2}{(k_c^2 + \pi ^2)^3}T_{002}\), the above set of ordinary differential equations transforms to the following Lorenz model (1963)

$$\begin{aligned} \dot{X}= & {} \mathrm {Pr} (Y - X),\end{aligned}$$
(17.54)
$$\begin{aligned} \dot{Y}= & {} X(r - Z) - Y,\end{aligned}$$
(17.55)
$$\begin{aligned} \dot{Z}= & {} XY - \beta Z, \end{aligned}$$
(17.56)

where \(\beta = \frac{4\pi ^2}{k_c^2 + \pi ^2}\).

Fig. 17.5
figure 5

Bifurcation diagram constructed from the Lorenz model for \(\mathrm {Pr} = 10\) and \(0<r\le 10\). Values of X corresponding to different stationary solutions are shown with different colors. Solid and dashed orange curves represent the stable and unstable conduction state respectively. Blue and black curves represent two 2D rolls branches connected by the symmetry of the Lorenz model (\(X\rightarrow -X\), \(Y\rightarrow -Y\) and \(Z\rightarrow Z\)). Streamlines, flow patterns and time series associated with these branches are also shown

Full size image

We now construct a bifurcation diagram of the Lorenz model using the MATCONT software (Dhooge et al. 2003) for \(\mathrm {Pr} = 10\) and r is varied in the range \(0 < r \le 10\) (see Fig. 17.5). The conduction state is stable for \(r < 1\) and at \(r = 1\) it becomes unstable via a supercritical pitchfork bifurcation. Two stable 2D rolls branches (solid blue and black curves) are originated from there. The stream lines corresponding to these solution branches are shown inside Fig. 17.5 and are found to be counter rotating. Flow pattern for these solutions and time series of X are also shown in the figure. In spite of drastic simplification, these results of Lorenz model are found to match closely with the DNS results. However, the results of Lorenz model starts deviating for large values of r and in that case one has to go for higher nonlinear corrections to get the satisfactory results.

9.2 A Four Dimensional Model for Zero-Prandtl Number Convection

In this subsection, we discuss the derivation of another low dimensional model to investigate instabilities and bifurcation structure near the onset of convection of low Prandtl-number fluids in the vanishing Prandtl number limit (\(\mathrm {Pr}\rightarrow 0\)). Here also we select the large scale modes from DNS data by calculating contributions of each selected mode to the total energy. In this process, we select the following expressions of \(\mathrm {v}_{3}\) and \(\mathrm {\omega }_{3}\):

$$\begin{aligned} \mathrm {v}_{3}= & {} W_{101}(t)\cos {k_c x}\sin {\pi z} + W_{011}(t)\cos {k_c y}\sin {\pi z} \nonumber \\+ & {} W_{112}(t)\cos {k_c x}\cos {k_c y}\sin {2\pi z} + W_{121}(t)\cos {k_c x}\cos {2k_c y}\sin {\pi z}\nonumber \\+ & {} W_{211}(t)\cos {2k_c x}\cos {k_c y}\sin {\pi z},\end{aligned}$$
(17.57)
$$\begin{aligned} \mathrm {\omega }_{3}= & {} Z_{110}(t)\sin {k_c x}\sin {k_c y} + Z_{112}(t)\sin {k_c x}\sin {k_c y}\cos {2\pi z}. \end{aligned}$$
(17.58)

The expression for \(\theta \) in this case (\(\mathrm {Pr}\rightarrow 0\)) is determined from Eq. (17.39) and is given by

$$\begin{aligned} \theta= & {} \frac{1}{k_c^2 + \pi ^2}W_{101}(t)\cos {k_c x}\sin {\pi z} + \frac{1}{k_c^2 + \pi ^2}W_{011}(t)\cos {k_c y}\sin {\pi z} \nonumber \\+ & {} \frac{1}{2k_c^2 + \pi ^2}W_{112}(t)\cos {k_c x}\cos {k_c y}\sin {2\pi z} \nonumber \\+ & {} \frac{1}{5k_c^2 + \pi ^2}W_{121}(t)\cos {k_c x}\cos {2k_c y}\sin {\pi z}\nonumber \\+ & {} \frac{1}{5k_c^2 + \pi ^2}W_{211}(t)\cos {2k_c x}\cos {k_c y}\sin {\pi z}. \end{aligned}$$
(17.59)

Using Eqs. (17.40) and (17.41) we then find

$$\begin{aligned} \mathrm {v}_{1}= & {} -\frac{\pi }{k_c}W_{101}(t)\sin {k_c x}\cos {\pi z} -\frac{\pi }{k_c}W_{112}(t)\sin {k_c x}\cos {k_c y}\cos {2\pi z}\nonumber \\- & {} \frac{2\pi }{5k_c}W_{211}(t)\sin {2k_c x}\cos {k_c y}\cos {\pi z} -\frac{\pi }{5k_c}W_{121}(t)\sin {k_c x}\cos {2k_c y}\cos {\pi z}\nonumber \\+ & {} \frac{1}{2k_c}Z_{110}(t)\sin {k_c x}\cos {k_c y} +\frac{1}{2k_c}Z_{112}(t)\sin {k_c x}\cos {k_c y}\cos {2\pi z},\end{aligned}$$
(17.60)
$$\begin{aligned} \mathrm {v}_{2}= & {} -\frac{\pi }{k_c}W_{011}(t)\sin {k_c y}\cos {\pi z} -\frac{\pi }{k_c}W_{112}(t)\cos {k_c x}\sin {k_c y}\cos {2\pi z}\nonumber \\- & {} \frac{\pi }{5k_c}W_{211}(t)\cos {2k_c x}\sin {k_c y}\cos {\pi z} -\frac{2\pi }{5k_c}W_{121}(t)\cos {k_c x}\sin {2k_c y}\cos {\pi z}\nonumber \\- & {} \frac{1}{2k_c}Z_{110}(t)\cos {k_c x}\sin {k_c y} -\frac{1}{2k_c}Z_{112}(t)\cos {k_c x}\sin {k_c y}\cos {2\pi z}. \end{aligned}$$
(17.61)

After calculating all the velocity components, horizontal components of vorticity are determined by taking curl of the velocity vector. The expression for horizontal components of vorticity are given by

$$\begin{aligned} \mathrm {\omega }_{1}= & {} -\left( k_c + \frac{\pi ^2}{k_c}\right) W_{011}(t)\sin {k_c y}\sin {\pi z} -\left( k_c + \frac{2\pi ^2}{k_c}\right) W_{112}(t)\cos {k_c x}\sin {k_c y}\sin {2\pi z}\nonumber \\- & {} \left( k_c + \frac{\pi ^2}{5k_c}\right) W_{211}(t)\cos {2k_c x}\sin {k_c y}\sin {\pi z} - \frac{\pi }{k_c}Z_{112}(t)\cos {k_c x}\sin {k_c y}\sin {2\pi z}\nonumber \\- & {} 2\left( k_c + \frac{\pi ^2}{5k_c}\right) W_{121}(t)\cos {k_c x}\sin {2k_c y}\sin {\pi z},\end{aligned}$$
(17.62)
$$\begin{aligned} \mathrm {\omega }_{2}= & {} \left( k_c + \frac{\pi ^2}{k_c}\right) W_{101}(t)\sin {k_c x}\sin {\pi z} + \left( k_c + \frac{2\pi ^2}{k_c}\right) W_{112}(t)\sin {k_c x}\cos {k_c y}\sin {2\pi z}\nonumber \\- & {} \frac{\pi }{k_c}Z_{112}(t)\sin {k_c x}\cos {k_c y}\sin {2\pi z} + \left( k_c + \frac{\pi ^2}{5k_c}\right) W_{121}(t)\sin {k_c x}\cos {2k_c y}\sin {\pi z}\nonumber \\+ & {} 2\left( k_c + \frac{\pi ^2}{5k_c}\right) W_{211}(t)\sin {2k_c x}\cos {k_c y}\sin {\pi z}. \end{aligned}$$
(17.63)

Substituting the expressions of \(\mathrm {v}_{1}\), \(\mathrm {v_2}\), \(\mathrm {v}_{3}\), \(\mathrm {\omega }_{1}\), \(\mathrm {\omega }_{2}\), \(\mathrm {\omega _3}\) and \(\mathrm {\theta }\) in Eqs. (17.42) and  (17.43) and using the orthogonality of the basis functions we get a set of seven equations for the Fourier amplitudes. This 7-mode model and the MAPLE code for deriving it are given in the Appendix.

Now from the equations of \(W_{112}\), \(Z_{110}\) and \(Z_{112}\), we observe that near the onset of convection, linear decay rate of these modes are quite high. Therefore, we adiabatically eliminate (Manneville 1990) these modes to get the following set of four coupled nonlinear ordinary differential equations (Pal et al. 2013):

$$\begin{aligned} \dot{W_{101}}= & {} \frac{3\pi ^2}{2}(r-1)W_{101}+a_1W_{101}W_{011}^2+a_2W_{101}W_{011}W_{211}+a_3W_{011}W_{121}W_{211}\nonumber \\+ & {} a_4W_{121}W_{211}^2+a_5W_{011}^2W_{121}+a_6W_{101}W_{211}^2,\end{aligned}$$
(17.64)
$$\begin{aligned} \dot{W_{011}}= & {} \frac{3\pi ^2}{2}(r-1)W_{011}+a_1W_{101}^2W_{011}+a_2W_{101}W_{011}W_{121}+a_3W_{101}W_{121}W_{211}\nonumber \\+ & {} a_4W_{121}^2W_{211}+a_5W_{101}^2W_{211}+a_6W_{011}W_{121}^2,\end{aligned}$$
(17.65)
$$\begin{aligned} \dot{W_{121}}= & {} \frac{\pi ^2}{98}(135r-343)W_{121}+b_1W_{101}W_{011}^2+b_2W_{101}W_{011}W_{211}+b_3W_{011}W_{121}W_{211}\nonumber \\+ & {} b_4W_{121}W_{211}^2+b_5W_{011}^2W_{121}+b_6W_{101}W_{211}^2,\end{aligned}$$
(17.66)
$$\begin{aligned} \dot{W_{211}}= & {} \frac{\pi ^2}{98}(135r-343)W_{211}+b_1W_{101}^2W_{011}+b_2W_{101}W_{011}W_{121}+b_3W_{101}W_{121}W_{211}\nonumber \\+ & {} b_4W_{121}^2W_{211}+b_5W_{101}^2W_{211}+b_6W_{011}W_{121}^2. \end{aligned}$$
(17.67)

The coefficients present in the above equations are \(a_1 = \frac{3}{100}\), \(a_2 = \frac{31}{3000}\), \(a_3 = -\frac{209}{30000}\), \(a_4 = \frac{63}{60000}\), \(a_5 = -\frac{47}{1500}\), \(a_6 = \frac{1}{200}\), \(b_1 = -\frac{93}{700}\), \(b_2 = -\frac{67}{7000}\), \(b_3 = -\frac{7407}{70000}\), \(b_4 = \frac{3969}{700000}\), \(b_5 = -\frac{928}{7000}\) and \(b_6 = \frac{3816}{70000}\) with r as the reduced Rayleigh number.

Now introducing the notations \(\mathbf{X} = [X_1, X_2]^T \equiv [W_{101}, W_{011}]^T\), \(\mathbf{Y} = [Y_1, Y_2]^T \equiv [W_{121}, W_{211}]^T\), \(\mathbb {A} = [0~1; 1~0]\), \(\mu _1 = \frac{3\pi ^2}{2}(r-1)\) and \(\mu _2 = \frac{\pi ^2}{98}(135r-343)\) we can write the above set of four equations as

$$\begin{aligned} \dot{\mathbf{X}}= & {} \mu _1 \mathbf{X} + X_1 X_2 \mathbb {A}(a_1 \mathbf{X} + a_2 \mathbf{Y}) + Y_1 Y_2 \mathbb {A}(a_3\mathbf{X} + a_4\mathbf{Y})\nonumber \\+ & {} a_5[X_2^2 Y_1, X_1^2 Y_2]^T + a_6[X_1 Y_2^2, X_2 Y_1^2]^T,\end{aligned}$$
(17.68)
$$\begin{aligned} \dot{\mathbf{Y}}= & {} \mu _2 \mathbf{Y} + X_1 X_2 \mathbb {A}(b_1 \mathbf{X} + b_2 \mathbf{Y}) + Y_1 Y_2 \mathbb {A}(b_3\mathbf{X} + b_4\mathbf{Y})\nonumber \\+ & {} b_5[X_2^2 Y_1, X_1^2 Y_2]^T + b_6[X_1 Y_2^2, X_2 Y_1^2]^T. \end{aligned}$$
(17.69)

(Equations  (17.68) and  (17.69) are reused from Pal et al. (2013) with the permission from American Physical Society.)

Fig. 17.6
figure 6

Bifurcation diagram constructed from the 4-mode model. Horizontal axis shows the variation of the parameter r in the region \(1.01 \le r \le 1.3\). Along vertical axis the extrema corresponding to different solutions are shown with different colors. The solid and dashed curves represent the stable and unstable solutions respectively. The orange, green, red, pink, blue, black and cyan respectively represent conduction state, OCR-I, OCR-II, OCR-II\('\), CR, CR\('\) and SQ solutions respectively. Stationary and time periodic flow patterns corresponding to different solutions are also shown. PB and HB respectively represent pitchfork and Hopf bifurcation points

Full size image

This minimal set of equations are found to capture the bifurcation structure near the onset of convection of zero-Prandtl number (Pal et al. 2009, 2013) fluids quite satisfactorily. Figure 17.6 shows the bifurcation diagram constructed from the above 4-mode model using the MATLAB based continuation software MATCONT (Dhooge et al. 2003). The bifurcation diagram unfolds a very rich bifurcation structure near the onset of convection. This is found to be consistent with the DNS results (Pal et al. 2013). In fact the 4-mode model tracked six different solutions namely OCR-I, OCR-II, OCR-II\('\), CR, CR\('\) and SQ out of which only OCR-I and SQ were reported in DNS (Thual 1992). Later the existence of other solutions are also verified in DNS (Pal et al. 2013). The pattern dynamics corresponding to the OCR-I and SQ solutions have already been discussed in Sect. 17.8.2. Oscillatory cross rolls patterns of type-II are either oriented along y-axis (OCR-II) or along x-axis (OCR-II\('\)). These are periodic patterns with varying wavyness. CR and CR\('\) are stationary flow patterns oriented along y-axis and x-axis respectively. All these flow patterns are shown inside the bifurcation diagram.

10 Conclusions

In this chapter, we have discussed low dimensional modeling technique for investigating instabilities near the onset of Rayleigh-Bénard convection. The technique is illustrated using two examples. In these examples, convective instabilities near the onset of convection of high Prandtl number and zero Prandtl number fluids are investigated by simultaneous performance of DNS and low dimensional modeling. It is found that low dimensional models derived by the method described in this chapter can produce faithful results close to the onset of convective instability. Based on the discussions in this chapter, we emphasize that simultaneous performance of DNS and low dimensional modeling is a powerful technique for the investigation of different instabilities in dissipative systems where boundary conditions of the associated boundary value problem allow expansion of the independent fields in terms of suitable set of orthogonal basis functions. Moreover, this technique is expected to work for investigating instabilities in systems with spherical and cylindrical geometries.