Approximate Solution of Higher Order Two Point Boundary Value Problems Using Uniform Haar Wavelet Collocation Method

Abstract

An efficient collocation method is proposed for the numerical solution of second and fourth order two-point boundary value problems (B.V.P.) based on uniform Haar wavelet. We have converted higher order differential equations into a system of differential equations of lower order and then solve it by uniform Haar wavelet, which reduces the time and complexity of the system. The technique introduced here is easy to apply. The performance of the present method yield more accurate results on increasing the resolution level. To demonstrate the robustness and accuracy of the Haar wavelet collocation method, five problems have been solved and compared with the existing methods present in the literature [1,2,3,4,5,6].

1 Introduction

Wavelet Analysis is a new development in the field of Mathematics. Wavelets were introduced in seismology to provide a time localisation to seismic analysis. Wavelet theory involves representing square integrable functions in terms of simple wavelet functions at different scale and positions. The fundamental idea of wavelet is translation and scaling according to the need [7,8,9,10]. The best property of wavelet is compact support, which is boom for the numerical solution of differential equations. Meanwhile in numerical analysis, wavelet methods have become an important tool for solution of differential and integral equations that has been discussed in many research papers with different approaches such as Galerkin method, finite element method, finite difference method, filter-bank method, adaptive method etc. [7, 8, 11,12,13,14,15]. One of the best and easiest wavelet in wavelet theory is Haar wavelet. Gaussian and Legendre wavelet is also applied in treatment of Numerical solutions of differential equations but lots of numerical difficulties appeared on using these wavelets. The detection of singularities, local high frequencies, irregular structures and transient phenomena exhibited by analyzed function is possible on using wavelets. Use of orthogonal functions to construct the solution of differential equations was initially established in 1995 by Chen and Hsiao [14]. During the last two decades different types of functions have been applied to find the approximate solution of differential equations. But Haar wavelet gives the desirable results for such types of problems due to its simplicity, orthogonality and compact support.

2 Multiresolution Analysis and Haar Wavelet

Definition: A multiresolution analysis consists of a sequence $\{ V_{j}:j \in Z \}$ of embedded closed subspace of $L^{2}(R)$ that satisfy the following properties:

• 1. Increasing: $V_{j}\subset V_{j+1}:j\in Z$

• 2. Density: $\overline{\bigcup _{j \in Z} V_{j}}=L^{2}(R)$

• 3. Separation: $\bigcap _{j\in Z}V_{j}=\{0\}$

• 4. Scaling: $f(t)\in V_{j}$ if and only if $f(2t)\in V_{j+1}$

• 5. Orthonormal basis: $\exists$ a scaling function $\phi \in V_{0}$ such that $\{\phi _{0,k}(t)=\phi (t-k):k \in Z\}$ is an orthonormal basis for $V_{0}.$

Haar Wavelet: Haar function was discovered long before the wavelet was introduced by Hungarian Mathematician Alfred Haar in 1909. Haar is the simplest orthonormal wavelet with compact support [16].

The Haar wavelet family for $t\in [0,1]$ is defined as follows:

$$\begin{aligned} h_{u}(t)= {\left\{ \begin{array}{ll} 1, \quad \xi _{1}(u) \le t< \ \xi _{2}(u)\\ -1, \ \xi _{2}(u) \le t < \xi _{3}(u)\\ 0, \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(2.1)

where u indicates the wavelet number and

$\xi _{1}(u)=\frac{k}{m} \quad ,\xi _{2}(u)=\frac{k+0.5}{m} ,\quad \xi _{3}(u)=\frac{k+1}{m}$

$m=2^j,j=0,1,2...,J,$ and integer $k=0,1...,m-1.$

Also J indicates the level of resolution and k represents the translation parameter. Index u is calculated as $u=m+k+1$ which is true for $u\ge 2.$

For $u=1$ the Haar wavelet is given by

$$\begin{aligned} h_{1}(t)= {\left\{ \begin{array}{ll} 1, \quad 0 \le t < 1 \\ 0, \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(2.2)

Because of constant and piecewise nature of Haar wavelet, derivative vanishes. Due to lack of differentiability authors move towards integration approach instead of differentiation [14].

The integration of Haar wavelet has been obtained from [13] and given as follows:

$$\begin{aligned} I_{1}h_{u}(t)= {\left\{ \begin{array}{ll} t-\xi _{1}(u), \quad \xi _{1}(u) \le t< \ \xi _{2}(u)\\ \xi _{3}(u)-t,\quad \ \xi _{2}(u) \le t < \xi _{3}(u)\\ 0, \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(2.3)

The double integration of Haar wavelet can be given as follows:

(2.4)

Proceeding in similar manner the nth integration of Haar wavelet can be written as:

$$\begin{aligned} I_{n}h_{u}(t)= {\left\{ \begin{array}{ll} 0, if \quad t< \xi _{1}(u) \\ \frac{1}{n!}[t-\xi _{1}(u)]^n, \quad \xi _{1}(u) \le t< \ \xi _{2}(u)\\ \frac{1}{n!}[(t-\xi _{1}(u))^n-2(t-\xi _{2}(u))^n], \quad \xi _{2}(u) \le t < \xi _{3}(u)\\ \frac{1}{n!}[(t-\xi _{1}(u))^n-2(t-\xi _{2}(u))^n+(t-\xi _{3}(u))^n],\quad \xi _{3}(u) \le t \end{array}\right. } \end{aligned}$$

(2.5)

Now consider, any square integrable function $f(t)\in L^2[0,1]$, can be approximated by the dialation and translation of Haar wavelet [12, 13]

$$\begin{aligned} f(t)=\sum _{u=1}^{N}a_{u}h_{u}(t) \end{aligned}$$

(2.6)

The Haar wavelet coefficients $a_{u}$ are calculated as

$$\begin{aligned} a_{u} =< y(t),h_{u}(t) >= \int \limits _{0}^{1}y(t) \cdot \overline{h_{u}(t)}dt. \end{aligned}$$

(2.7)

The collocation points are given as

$$\begin{aligned} X(u)=\frac{2u-1}{m}, u=1,2,...,m. \end{aligned}$$

(2.8)

The matrix of Haar wavelet with respect to the collocation points is given as

$$\begin{aligned} H=\left( \begin{array}{cccccccc} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} -1 &{} -1 &{} -1 &{} -1 \\ 1 &{} 1 &{} -1 &{} -1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} -1 &{} -1 \\ 1 &{} -1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} -1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} -1 \\ \end{array} \right) \end{aligned}$$

The matrix of integral and double integral of Haar wavelet with respect to the collocation points are given as:

$$\begin{aligned} I_{1}H=\frac{1}{16}\left( \begin{array}{cccccccc} 1 &{} 3 &{} 5 &{} 7 &{} 9 &{} 11 &{} 13 &{} 15 \\ 1 &{} 3 &{} 5 &{} 7 &{} 7 &{} 5 &{} 3 &{} 1 \\ 1 &{} 3 &{} 3 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 3 &{} 3 &{} 1 \\ 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 \\ \end{array} \right) , I_{2}H=\frac{1}{512} \left( \begin{array}{cccccccc} 1 &{} 9 &{} 25 &{} 49 &{} 81 &{} 121 &{} 169 &{} 225 \\ 1 &{} 9 &{} 25 &{} 49 &{} 79 &{} 103 &{} 119 &{} 127 \\ 1 &{} 9 &{} 23 &{} 31 &{} 32 &{} 32 &{} 32 &{} 32 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 9 &{} 23 &{} 31 \\ 1 &{} 7 &{} 8 &{} 8 &{} 8 &{} 8 &{} 8 &{} 8 \\ 0 &{} 0 &{} 1 &{} 7 &{} 8 &{} 8 &{} 8 &{} 8 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 7 &{} 8 &{} 8 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 7 \\ \end{array} \right) \end{aligned}$$

3 Methods of Solution

3.1 Method for Solving Second Order Differential Equations

Consider a second order differential equation

$$\begin{aligned} y^{\prime \prime }=\phi (t,y,y^{\prime }) \end{aligned}$$

(3.1)

with boundary conditions

$$\begin{aligned} y(0)=\alpha ,y(1)=\beta . \end{aligned}$$

(3.2)

Let us suppose that

$$\begin{aligned} y^{\prime }(t)=z(t)\Rightarrow y^{\prime \prime }(t)=z^{\prime }(t) \end{aligned}$$

(3.3)

$$\begin{aligned} y^{\prime }(t)= \sum _{u=1}^{N}a_{u}h_{u}(t) \end{aligned}$$

(3.4)

$$\begin{aligned} z^{\prime }(t)= \sum _{u=1}^{N}b_{u}h_{u}(t). \end{aligned}$$

(3.5)

Now integrating Eqs. (3.4) and (3.5) with respect to t from 0 to t we get

$$\begin{aligned} y(t)=\sum _{u=1}^{N}a_{u}I_{1}h_{u}(t)+y(0) \end{aligned}$$

(3.6)

and

$$\begin{aligned} z(t)=\sum _{u=1}^{N}b_{u}I_{1}h_{u}(t)+z(0). \end{aligned}$$

(3.7)

Substituting the values from Eqs. (3.3–3.7) in (3.1), we get the following system of equations

$$\begin{aligned} \sum _{u=1}^{N}b_{u}h_{u}(t)= \phi (t,\sum _{u=1}^{N}a_{u}I_{1}h_{u}(t)+y(0),\sum _{u=1}^{N}b_{u}I_{1}h_{u}(t)+z(0)) \end{aligned}$$

(3.8)

Solving the above system of equation and find out the unknown Haar wavelet coefficient $a_{u}$ and $b_{u}$ with the help of Eq. (3.3) and then put in Eq. (3.6) to get the approximate solution of the differential equation.

3.2 Method for Solving Fourth Order Differential Equations

Consider the fourth order ordinary linear differential equation of the form.

$$\begin{aligned} y^{\prime \prime \prime \prime }=\phi (t,y,y^{\prime },y^{\prime \prime },y^{\prime \prime \prime }) \end{aligned}$$

(3.9)

with boundary conditions

$$\begin{aligned} y(0)=a,y(1)=b,y^{\prime \prime }(0)=c,y^{\prime \prime }(1)=d. \end{aligned}$$

Let us suppose that

$$\begin{aligned} y^{\prime \prime }(t)=z(t), \end{aligned}$$

(3.10)

$$\begin{aligned} y^{\prime \prime \prime }(t)=z^{\prime }(t), \end{aligned}$$

(3.11)

$$\begin{aligned} y^{\prime \prime \prime \prime }(t)=z^{\prime \prime }(t). \end{aligned}$$

(3.12)

$$\begin{aligned} \quad \text {and} \quad \quad y^{\prime \prime }(t)=\sum _{u=1}^{N}a_{u}h_{u}(t). \end{aligned}$$

(3.13)

On integrating Eq. (3.13) from 0 to t with respect to t we get

$$\begin{aligned} y^{\prime }(t)=\sum _{u=1}^{N}a_{u}P_{u,1}(t)+y^{\prime }(0) \end{aligned}$$

(3.14)

Again integrating Eq. (3.14) from 0 to t, with respect to t we get

$$\begin{aligned} y(t)=\sum _{u=1}^{N}a_{u}P_{u,2}(t)+ty^{\prime }(0)+y(0) \end{aligned}$$

(3.15)

Also we assume that

$$\begin{aligned} z^{\prime \prime }=\sum _{u=1}^{N}b_{u}h_{u}(t) \end{aligned}$$

(3.16)

On integrating Eq. (3.16) from 0 to t we get,

$$\begin{aligned} z^{\prime }(t)=\sum _{u=1}^{N}b_{u}P_{u,1}(t)+z^{\prime }(0) \end{aligned}$$

(3.17)

Again integrating Eq. (3.17) from 0 to t we get

$$\begin{aligned} z(t)=\sum _{u=1}^{N}b_{u}P_{u,2}(t)+tz^{\prime }(0)+z(0) \end{aligned}$$

(3.18)

We can find the values of $y^{\prime }(0),y^{\prime \prime }(0),y^{\prime \prime \prime }(0) \quad \text {and} \quad y^{\prime \prime \prime \prime }(0)$ from the boundary conditions. Now put Eqs. (3.10–3.18) in (3.9), we get the following system of equation

$$\begin{aligned} \sum _{u=1}^{N}b_{u}h_{u}(t)=\phi (t,\sum _{u=1}^{N}a_{u}P_{u,2}(t)+t.y^{\prime }(0)+y(0), \sum _{u=1}^{N}a_{u}P_{u,1}(t)+y^{\prime }(0),\nonumber \\ \sum _{u=1}^{N}b_{u}P_{u,2}(t)+t.z^{\prime }(0)+z(0),\sum _{u=1}^{N}b_{u}P_{u,1}(t)+z^{\prime }(0)) \nonumber \\ \end{aligned}$$

(3.19)

Find the value of the vector $a_{u}$ and then put these values in the Eq. (3.15) to get the Haar approximate solution of the required differential equation.

4 Numerical Examples

In this section we have tested five problems to demonstrate the accuracy and effectiveness of proposed method.

Problem 1

Consider the second order differential equations [1]        

$$\begin{aligned} y^{\prime \prime }=100y , \end{aligned}$$

(4.1)

with boundary conditions

$$\begin{aligned} y(0)=y(1)=1. \end{aligned}$$

(4.2)

Exact solution of the problem is

$$\begin{aligned} y=\frac{\cos h(10t-5)}{\cos h5} \end{aligned}$$

(4.3)

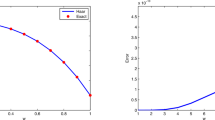
Obtained maximum absolute errors for different resolutions are given in Table 1 and graph for J $=$ 4 is given in Fig. 1.

Table 1 Maximum absolute error for Problem 1

Fig. 1

Exact and Haar solution of Problem 1 for J $=$ 4

Problem 2

Consider Dirichlet problem given in [4]:

$$\begin{aligned} -y^{\prime \prime }=(\frac{537}{10} \pi )^{2}\sin (\frac{537}{10}\pi t)+(\frac{23}{10} \pi )^{2}\sin (\frac{23}{10} \pi t) , \end{aligned}$$

(4.4)

with boundary conditions

$$\begin{aligned} y(0)=0, \quad y(1)=0, t\in [0,1]. \end{aligned}$$

(4.5)

Exact solution is

$$\begin{aligned} y=(\frac{537}{10} \pi )\sin (\frac{537}{10} \pi t)+(\frac{23}{10} \pi )\sin (\frac{23}{10} \pi t). \end{aligned}$$

(4.6)

Obtained maximum absolute errors for different resolutions are given in Table 2 and graph for $J=6$ is given in Fig. 2.

Table 2 Maximum absolute error for Problem 2

Fig. 2

Exact and Haar solution of Problem 2

Problem 3

Consider Dirichlet problem given in [4]:       

$$\begin{aligned} -y^{\prime \prime }+y=[1+(\frac{537}{10} \pi )^{2}]\sin (\frac{537}{10} \pi t)+[1+(\frac{23}{10} \pi )^{2}]\sin (\frac{23}{10} \pi t) ,\end{aligned}$$

(4.7)

with boundary conditions

$$\begin{aligned} y(0)=0,\quad y(1)=0. \quad t\in [0,1] \end{aligned}$$

(4.8)

Exact solution is

$$\begin{aligned} y=(\frac{537}{10} \pi )\sin (\frac{537}{10} \pi t)+(\frac{23}{10}\pi )\sin (\frac{23}{10} \pi t) . \end{aligned}$$

(4.9)

Obtained maximum absolute errors for different resolutions are given in Table 3 and graph is given in Fig. 3.

Table 3 Maximum absolute error for Problem 3

Fig. 3

Exact and Haar solution of Problem 3 for J $=$ 9

Problem 4

Let us assume the fourth order B.V.P. given in [3]       

$$\begin{aligned} y^{\prime \prime \prime \prime }+ty=-(t^3+7t+8)e^t,\quad t\in [0,1] \end{aligned}$$

(4.10)

with boundary conditions

$$\begin{aligned} y(0)=y(1)=0, \end{aligned}$$

(4.11)

$$\begin{aligned} \quad y^{\prime \prime }(t)=1 \quad when \quad t=0, \end{aligned}$$

(4.12)

$$\begin{aligned} \quad y^{\prime \prime }(t)=-4e. \quad when \quad t=1 \end{aligned}$$

(4.13)

Exact solution of the problem is

$$\begin{aligned} y(t)=t(1-t)e^t. \end{aligned}$$

(4.14)

Obtained maximum absolute errors for different resolutions are given in Table 4 and graph is given in Fig. 4.

Table 4 Maximum absolute errors for Problem 4

Fig. 4

Exact and Haar solution of Problem 4 for J $=$ 4

Problem 5

Let us assume the fourth order B.V.P. given in [3]        

$$\begin{aligned} y^{\prime \prime \prime \prime }-y=-4(2 t \cos t+3 \sin t),\quad t\in [0,1] \end{aligned}$$

(4.15)

with boundary conditions

$$\begin{aligned} y(0)=y(1)=0, \quad y^{\prime \prime }(t)=0,\quad when \quad t=0,y^{\prime \prime }(1)=4\cos 1+2\sin 1.\nonumber \\ \end{aligned}$$

(4.16)

Exact solution of the problem is

$$\begin{aligned} y(t)=(t^2-1)\sin t. \end{aligned}$$

(4.17)

Obtained maximum absolute errors for different resolutions are given in Table 5 and graph is given in Fig. 5.

Table 5 Maximum absolute errors for Problem 5

Fig. 5

Exact and Haar solution of Problem 5 for J $=$ 4

5 Conclusion

We have converted second order differential equation into system of first order and fourth order differential equations into system of second order of differential equation, which is easy to solve to get the approximations of higher order two point boundary value problems. Haar wavelet collocation method has been applied on second and fourth order two point B.V.P. We have compared our results with the existing method given in [1, 3,4,5,6] which shows that our results are better.