Keywords

1 Introduction

Dengue disease is a common arboviral disease in tropical regions of the world. It is transferral to humans by the bite of Aedes mosquitoes. There are four types of virus which is denoted by one, two, three, and four. The bites of the Aedes mosquitoes is the reason of the viruses that transferral to humans. If a person infected once in the life by these one of the four serotypes of viruses will never get infected by that serotype again but loses immunity to other three stereotypes of the viruses [8]. There are lots of Bio-mathematical models have been proposed to recognize the transferral dynamics of these type of infectious diseases. In recent years, modeling has become a valuable tool in the analysis of dengue disease transferral dynamics and to determine the factors that influence the spread of disease to support control measures. Many researchers have proposed [5,6,7,8, 13, 14, 16, 18] epidemic model [10] to study the transferral dynamics of dengue disease.

There is no specific medicine to cure dengue disease. Awareness programs can be helpful in reducing the prevalence of the disease. Different Bio-mathematical models have been proposed to study the impact of awareness in controlling dengue and these type diseases. Prevention of mosquitoes bites is one of the ways to prevent dengue disease. The mosquitoes bite humans during day and night when lights are on. So, to get rid of mosquitoes bite, people can use mosquito repellents and nets. If infected hosts feel they have symptoms of the disease and approach the doctor in time for the supportive treatment, they can recover fast. This type of awareness can help controlling the disease. Another way of controlling dengue is destroying larval breeding sites of mosquitoes and killing them. Spray of insecticides may be applied to control larvae or adult mosquitoes which can transmit dengue viruses. This type of biological model have two properties as we observed Markovian and Non-Markovian. In dengue spread model does not really follow the Markovian process therefore does have memory effect, thus can well be described using the concept of nonlocal differential operators with non local and non singular kernel as these operators have a crossover from exponential decay law to power law as waiting time distribution.

Fc is applied in various directions of Bio-mathematics, physics, signal-processing, fluid-mechanics, visco-elasticity, finance, electro-chemistry and in many more. In the branch of fc, we study fractional integral and fractional derivative as an important aspects. Recently, many researcher and scientists have studied various type of issues in this special branch [1,2,3, 9]. The Caputo-Fabrizo derivative brought new weapons into applied mathematics to model complex real-world problems more accurately. Caputo-Fabrizio derivative is give the result of non-Markovian process. In the RL derivative the kernal inside it is gives the result for power law but Caputo-Fabrizio shows the result for exponential decay.

The main objective of this chapter is to discuss fractional Caputo-Fabrizio derivative for the mathematical system to finding the crossover effects and memory effect Also by using fixed point theorem we are finding the details of the uniqueness and exactness and of the solution. The development of this article is as follows. In Sect. 2, we discuss the Caputo-Fabrizio and AB derivative. In Sect. 3, the mathematical portion of fractional dengue spread model and also by applying CF derivative we find the approximate solution. In Sect. 4, by using fixed point theorem, we proved the uniqueness and existence of system of solutions in Sect. 6, Numerical Solution are discuss and in the last Sect. 7 we presented concluding remarks.

2 Preliminaries

Some definitions and properties of the fractional derivative are presented here.

Definition 2.1

Let f be a function not necessarily differentiable, and \(\kappa \) be a real number such that \(0<\kappa \le 1\), then the Riemann-Liouville derivative with \(\kappa \) order with power law is given as [15]

$$\begin{aligned} ^{RL}D_t^\kappa [f(t)]=\frac{1}{\Gamma (1-\kappa )}\frac{d}{dt}\int \limits _{0}^{t}(t-y)^{-\kappa }f(y)dy. \end{aligned}$$
(2.1)

Definition 2.2

Let \(f\in H^1(a,b), b>a, \kappa \in [0,1]\) then the new Caputo derivative of fractional order is given by:

$$\begin{aligned} D^\kappa _t(f(t))=\frac{M(\kappa )}{(1-\kappa )}\int \limits _{a}^{t}f^{'}(x)\exp \left[ -\kappa \frac{t-x}{1-\kappa } \right] dx. \end{aligned}$$
(2.2)

where \(M(\kappa )\) is a normalization function such that \(M(0)=M(1)=1\) [4]. But, if the function does not belong to \(H_1(a,b)\) then, the derivative can be reformulated as

$$\begin{aligned} D^\kappa _t(\!f(t))=\frac{ M(\kappa )}{(1-\kappa )}\int \limits _{a}^{t}(f(t)-f(x))\exp \left[ -\kappa \frac{t-x}{1-\kappa } \right] dx. \end{aligned}$$
(2.3)

Remark 2.1

The authors remarked that, if \(\sigma =\frac{1-\kappa }{\kappa }\in [0,\infty ),\) \(\kappa =\frac{1}{1+\kappa }\in [0,1]\), then Eq. (2.1) assumes the form

$$\begin{aligned} D^\kappa _t(f(t))=\frac{N(\sigma )}{(\sigma )}\int \limits _{a}^{t}f^{'}(x)\exp \left[ -\frac{t-x}{\sigma } \right] dx,\;\;N(0)=N(\infty )=1 \end{aligned}$$
(2.4)

In Addition,

$$\begin{aligned} \lim \limits _{\sigma \rightarrow 0}\frac{1}{\sigma }\exp \left[ -\frac{t-x}{\sigma } \right] =\delta (x-t) \end{aligned}$$
(2.5)

Now after the introduction of a new derivative, the associate anti-derivative becomes important, the associated integral of the new Caputo derivative with fractional order was proposed by Losada and Nieto [11].

Definition 2.3

[11] Let \(0<\kappa <1\). The fractional integral of order \(\kappa \) of a function f is defined by

$$\begin{aligned} I^t_\kappa (f(t))=\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}f(t)+\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}f(s)ds, t\ge 0. \end{aligned}$$
(2.6)

Remark 2.2

Note that, according to above definition, the fractional integral of Caputo type of function of order \(0<\kappa <1\) is an average between function f and its integral of order one. This therefore imposes

$$\begin{aligned} \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}f(t)+\frac{2\kappa }{(2-\kappa )M(\kappa )}=1 \end{aligned}$$
(2.7)

The above expression yields an explicit formula for

$$\begin{aligned} M(\kappa )=\frac{2}{2-\kappa }, 0\le \kappa \le 1 \end{aligned}$$
(2.8)

Because of the above, Losada and Nieto proposed that the new Caputo derivative of order \(0<\kappa <1\) can be reformulated as

$$\begin{aligned} D^\kappa _t(f(t))=\frac{1}{1-\kappa }\int \limits _{a}^{t}f^{'}(x)\exp \left[ -\kappa \frac{t-x}{1-\kappa } \right] dx. \end{aligned}$$
(2.9)

3 Model Description

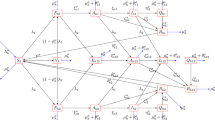
In the given model, total host human population, \(N_h\). We divided this human population into four parts: \(R_h\)(recovered), \(I_h\)(infectious), \(E_h\)(exposed), \(S_h\)(susceptible) and total vector (mosquito) population, also we divide \(N_v\) into three parts: \(I_v\) (infectious), \(E_v\) (exposed), \(S_v\) (susceptible). We assume that the fraction \(u_1\) of susceptible hosts use mosquito repellents to avoid mosquitoes bite. So, the fraction \((1-u_1)\) of susceptible hosts interact with infectious mosquitoes. The fraction \(u_2\) of infectious hosts seek for the timely supportive treatment and recover fast by the rate \(r_h(r>1)\). The fraction \(r_1u_2\) (\(r_1\) is the proportionality constant) of infectious hosts use mosquito repellents to avoid mosquitoes bite. \(u_3\) is a control variable that represents the eradication effort of insecticide spraying. That follows that morality rate of mosquito population increases at a rate \(r_2u_3\) (\(r_2\) is the proportionality constant) and also it is assume that recruitment rate of this is reduced by a factor of \(1-u_3\).

In this section, we describes the geometry of dengue disease together with control measures. The system of differential equations which shows the present SEIR-SEI vector host model is given in [13].

$$\begin{aligned} \begin{aligned}&\frac{dS_h}{dt}=\mu _hN_h-(1-u_1)\frac{b\beta _h}{N_h}S_hI_\nu -\mu _hS_h\\&\frac{dE_h}{dt}=(1-u_1)\frac{b\beta _h}{N_h}S_hI_\nu -(\nu _h+\mu _h)E_h\\&\frac{dI_h}{dt}= \nu _hE_h-[ru_2\gamma h + (1-u_2)\gamma h+\mu _h]I_h\\&\frac{dR_h}{dt}=[ru_2\gamma _h+(1-u_2)\gamma _h]I_h-\mu _hR_h\\&\frac{dS_v}{dt}=(1-u_3)\pi _\nu -(1-r_1u_2)\frac{b\beta _h\nu }{N_h} S_\nu I_h-(r_2u_3+\mu _h\nu )S_\nu \\&\frac{dE_\nu }{dt}=(1-r_1u_2)\frac{b\beta _h\nu }{N_h}S_\nu I_h-(r_2u_3+\nu _\nu +\mu _h\nu )E_\nu \\&\frac{dI_\nu }{dt}=\nu _\nu E_\nu -(r_2u_3+\mu \nu )I_\nu \end{aligned} \end{aligned}$$
(3.1)

The parameters of the model are given in the following table.

Symbols

Description

\(\mu _h\)

Death rate of host population

\(\nu _h\)

Host’s incubation rate

\(\gamma _h\)

Recovery rate of host population

\(\beta _h\)

Transmission probability from vector to host

\(\pi _\nu \)

Vector population recruitment rate

\(\mu _\nu \)

Vector population death rate

\(\nu _\nu \)

Vector’s incubation rate

\(\beta _\nu \)

Host to vector the transmission probability

b

Rate (biting) of vector

Total host population, \(N_h=R_h+I_h+E_h+S_h\), total vector population, \(N_\nu =I_\nu +E_\nu +S_\nu \).

$$\begin{aligned} \frac{dN_h}{dt}=0\;\;\text {and} \;\;\frac{dN_\nu }{dt}=(1-u_3)\pi _\nu -(r_2u_3+\mu _\nu )N_\nu . \end{aligned}$$

So, \(N_h\) remains constant and \(N_\nu \) approaches the equilibrium \((1-u_3)\pi _\nu (r_2u_3+\mu _\nu \nu )\) as \(t\rightarrow \infty \). Introducing the proportions

$$\begin{aligned} \begin{aligned}&s_\nu =\frac{S_\nu }{(1-u_3)\pi \nu /(r_2u_3+\mu _\nu )}, s_h=\frac{S_h}{N_h},\;\;e_h=\frac{E_h}{N_h},\;\;i_h=\frac{I_h}{N_h},\;\;r_h=\frac{R_h}{N_h},\\&e_\nu =\frac{E_\nu }{(1-u_3)\pi _\nu \nu /(r_2u_3+\mu _\nu \nu )},\;\; i_\nu =\frac{I_\nu }{(1-u_3)\pi _\nu /(r_2u_3+\mu _\nu \nu )} \end{aligned} \end{aligned}$$

Since \(s_\nu =1-e_\nu -i_\nu \) and \(r_h=1-s_h-e_h-i_h\) the system of Eq. (3.1) is the equivalent written by five dimensional non-linear system of ODEs:

$$\begin{aligned} \begin{aligned}&\frac{ds_h}{dt}=\mu _h(1-s_h)-\alpha s_hi_\nu \\&\frac{de_h}{dt}=\alpha s_hi_\nu -\beta e_h\\&\frac{di_h}{dt}=\nu _he_h-\gamma i_h\\&\frac{de_\nu }{dt}=\delta s_\nu i_h-(\epsilon +\nu _\nu )e_\nu \\&\frac{di_\nu }{dt}=\nu _\nu e_\nu -\epsilon i_\nu \end{aligned} \end{aligned}$$
(3.2)

Here,

$$\begin{aligned} \begin{aligned}&\alpha =\frac{b\beta _h\pi _\nu (1-u_1)(1-u_3)}{N_h(r_2u_3+\mu \nu )},\;\;\beta =\nu _h+\mu _h,\;\;\gamma =ru_2\gamma _h+(1-u_2)\gamma _h+\mu _h,\\&\delta =(1-r_1u_2)b\beta _\nu ,\;\;\epsilon =r_2u_3+\mu _\nu . \end{aligned} \end{aligned}$$

Due to Markovian process, this system is exponentially stable with no memory. Thus, to include the memory effect into this bio-mathematical model, we introduced Caputo-Fabrizio arbitrarily ordered derivative to moderate this system by non Markovian process as given by

$$\begin{aligned} \begin{aligned}&^{CF}_0D^\kappa _ts_h=\mu _h(1-s_h)-\alpha s_hi_\nu \\&^{CF}_0D^\kappa _te_h=\alpha s_hi_\nu -\beta e_h\\&^{CF}_0D^\kappa _ti_h=\nu _he_h-\gamma i_h\\&^{CF}_0D^\kappa _te_\nu =\delta s_\nu i_h-(\epsilon +\nu _\nu )e_\nu \\&^{CF}_0D^\kappa _ti_\nu =\nu _\nu e_\nu -\epsilon i_\nu \end{aligned} \end{aligned}$$
(3.3)

These come with the initial conditions

$$\begin{aligned} i_\nu (0)=\delta _5,\;\;e_\nu (0)=\delta _4,\;\;\;\;i_h(0)=\delta _3,\;\;e_h(0)=\delta _2,\;\;s_h(0)=\delta _1. \end{aligned}$$
(3.4)

4 Uniqueness and Existence of a System of Solutions of Dengue Models with Non-Markovian Properties

In this section investigate numerical result of fractional model based on CF derivative. We discuss the uniqueness and existence of the solutions by fixed point theorem. For this we apply the fractional integral operator due to Nieto and Losada [11] on Eq. (3.3), to examine the existence of the system of solutions. We obtain

$$\begin{aligned} \begin{aligned}&s_h(t)-s_h(0)=\,^{CF}_0I^\kappa _t\left\{ \mu _h(1-s_h)-\alpha s_hi_\nu \right\} \\&e_h(t)-e_h(0)=\,^{CF}_0I^\kappa _t\left\{ \alpha s_hi_\nu -\beta e_h\right\} \\&i_h(t)-i_h(0)=\,^{CF}_0I^\kappa _t\left\{ \nu _he_h-\gamma i_h\right\} \\&e_\nu (t)-e_\nu (0)=\,^{CF}_0I^\kappa _t\left\{ \delta s_\nu i_h-(\epsilon +\nu _\nu )e_\nu \right\} \\&i_\nu (t)-i_\nu (0)=\,^{CF}_0I^\kappa _t\left\{ \nu _\nu e_\nu -\epsilon i_\nu \right\} \end{aligned} \end{aligned}$$
(4.1)

By using the equation discussed by Nieto and Losada [11], we have

$$\begin{aligned} \begin{aligned} i_\nu (t)-i_\nu (0)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left\{ \nu _\nu (y)e_\nu (y)-\epsilon i_\nu (y)\right\} dy\\ {}&\quad \,+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left\{ \nu _\nu (t) e_\nu (t)-\epsilon i_\nu (t)\right\} \\ e_\nu (t)-e_\nu (0)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left\{ \delta s_\nu (y)i_h(y)-(\epsilon +\nu _\nu (y))e_\nu (y)\right\} dy \\&\quad \,+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left\{ \delta s_\nu (t) i_h(t)-(\epsilon +\nu _\nu (t))e_\nu (t)\right\} \\ i_h(t)-i_h(0)&= +\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left\{ \nu _h(y)e_h(y)-\gamma i_h(y)\right\} dy\\ {}&\quad \;+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left\{ \nu _h(t)e_h(t)-\gamma i_h(t)\right\} \\ e_h(t)-e_h(0)&= \frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left\{ \alpha s_h(y)i_\nu (y)-\beta e_h(y)\right\} dy\\ {}&\quad \,+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left\{ \alpha s_h(t)i_\nu (t)-\beta e_h(t)\right\} \\ s_h(t)-s_h(0)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left\{ \mu _h(1-s_h(y))-\alpha s_h(y)i_\nu (y)\right\} dy\\&\quad \,+ \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left\{ \mu _h(1-s_h(t))-\alpha s_h(t)i_\nu (t)\right\} \end{aligned} \end{aligned}$$
(4.2)

So we can write for clarity

$$\begin{aligned}&Z_1(t,s_h)=\mu _h(1-s_h(t))-\alpha s_h(t)i_\nu (t), \nonumber \\&Z_2(t,e_h)=\mu _h(1-s_h(y))-\alpha s_h(y)i_\nu (y) \nonumber \\&Z_3(t,i_h)=\nu _h(t)e_h(t)-\gamma i_h(t) \nonumber \\&Z_4(t,e_\nu )=\delta s_\nu (t) i_h(t)-(\epsilon +\nu _\nu (t))e_\nu (t) \nonumber \\&Z_5(t,i_\nu )= \nu _\nu (t) e_\nu (t)-\epsilon i_\nu (t) \end{aligned}$$
(4.3)

Theorem 4.1

If the following inequality holds then The kernels \(Z_1, Z_2, Z_3, Z_4\) and \(Z_5\) satisfy the Lipschitz condition and contraction.

$$0<a_1+\beta b_1\le 1.$$

Proof

Starting with the kernel \(Z_1\). Let two function is \(s_{h_1}\) and \(s_{h_2}\) then we get the following:

$$\begin{aligned} \Vert Z_1(t,s_h)-Z_1(t,s_{h_1})\Vert =\Vert -\mu _h\left\{ s_h(t)-s_{h_1}(t)\right\} -\alpha \left\{ s_h(t)-s_{h_1}(t)\right\} i_\nu (t) \Vert . \end{aligned}$$
(4.4)

Now using the triangular inequality (4.4), we have

$$\begin{aligned} \begin{aligned} \Vert Z_1(t,s_h)-Z_1(t,s_{h_1})\Vert&\le \Vert \alpha \left\{ s_h(t)-s_{h_1}(t)\right\} i_\nu (t)\Vert +\Vert \mu _h\left\{ s_h(t)-s_{h_1}(t)\right\} \Vert \\&\le \Vert s_h(t)-s_{h_1}(t)\Vert \left\{ a_1+b_1\Vert i_\nu (t)\Vert \right\} \\&\le \left\{ a_1+b_1\beta \right\} \Vert s_h(t)-s_{h_1}(t)\Vert \le \gamma _1\Vert s_h(t)-s_{h_1}(t)\Vert \end{aligned} \end{aligned}$$
(4.5)

Taking \(\gamma _1=a_1+\beta b_1\) here the \(\beta =i_\nu (t)\) are bounded functions, then we have

$$\begin{aligned} \Vert Z_5(t,i_\nu )-Z_1(t,i_{\nu _1})\Vert =\gamma _5\Vert i_\nu (t)-i_{\nu _1}(t)\Vert \end{aligned}$$
(4.6)

Hence, the Lipschitz condition is satisfied for \(Z_1\), and if additionally \(0<(a_1+\beta b_1\le 1)\), this condition is satisfy then it gives us a contraction for \(Z_1\).

Similarly all the cases II, II, III and IV satisfy the Lipschitz condition as follows:

$$\begin{aligned} \begin{aligned}&\Vert Z_4(t,e_\nu )-Z_1(t,e_{\nu _1})\Vert =\gamma _4\Vert e_\nu (t)-e_{\nu _1}(t)\Vert ,\\&\Vert Z_3(t,i_h)-Z_1(t,i_{h_1})\Vert =\gamma _3\Vert i_h(t)-i_{h_1}(t)\Vert ,\\&\Vert Z_2(t,e_h)-Z_1(t,e_{h_1})\Vert =\gamma _2\Vert e_h(t)-e_{h_1}(t)\Vert ,\\&\Vert Z_1(t,s_h)-Z_1(t,s_{h_1})\Vert =\gamma _1\Vert s_h(t)-s_{h_1}(t)\Vert . \end{aligned} \end{aligned}$$
(4.7)

when we consider the kernels, the Eq. (4.2) becomes

$$\begin{aligned} i_\nu (t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_5(y,i_\nu ) \right) dy+i_\nu (0)+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}Z_5(t,i_\nu ) \nonumber \\ e_\nu (t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_4(y,e_\nu )\right) dy+e_\nu (0)+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}Z_4(t,e_\nu ), \nonumber \\ i_h(t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_3(y,i_h)\right) dy+i_h(0)+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}Z_3(t,i_h), \nonumber \\ e_h(t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_2(y,e_h)\right) dy+e_h(0)+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}Z_2(t,e_h), \nonumber \\ s_h(t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_1(y,s_h) \right) dy+s_h(0)+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}Z_1(t,s_h). \end{aligned}$$
(4.8)

Now, presenting the following recursive formula:

$$\begin{aligned} \begin{aligned} i_{\nu _n}(t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_5(y,i_{\nu _{n-1}}) \right) dy+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}Z_5(t,i_{\nu _{n-1}})\\ e_{\nu _n}(t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_4(y,e_{\nu _{n-1}})\right) dy,+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}Z_4(t,e_{\nu _{n-1}}) \\ i_{h_n}(t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_3(y,i_{h_{n-1}})\right) dy+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}Z_3(t,i_{h_{n-1}}) ,\\ e_{h_n}(t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_2(y,e_{h_{n-1}})\right) dy+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}Z_2(t,e_{h_{n-1}}), \\ s_{h_n}(t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_1(y,s_{h_{n-1}}) \right) dy+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}Z_1(t,s_{h_{n-1}}), \\ \end{aligned} \end{aligned}$$
(4.9)

and the initial conditions are gives as below:

$$\begin{aligned} \begin{aligned}&i_{\nu _0}(t)=i_{\nu }(0), \;\;e_{\nu _0}(t)=e_{\nu }(0),\;\;i_{h_0}(t)=i_{h}(0),\;\;e_{h_0}(t)=e_{h}(0),\;\; s_{h_0}(t)=s_{h}(0). \end{aligned} \end{aligned}$$
(4.10)

Now, difference between the successive terms are presented as follow:

$$\begin{aligned} \varsigma _n(t)=i_{\nu _n}(t)-i_{\nu _{n-1}}(t)&= \frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_5(y,i_{\nu _{n-1}}) -Z_5(y,i_{\nu _{n-2}})\right) dy \nonumber \\&\quad \,+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left( Z_5(t,i_{\nu _{n-1}}) -Z_5(t,i_{\nu _{n-2}})\right) \nonumber \\ \chi _n(t)= e_{\nu _n}(t)-e_{\nu _{n-1}}(t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_4(y,e_{\nu _{n-1}})-Z_4(y,e_{\nu _{n-2}})\right) dy \nonumber \\&\quad \,+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left( Z_4(t,e_{\nu _{n-1}})-Z_4(t,e_{\nu _{n-2}})\right) , \nonumber \\ \xi _n(t)=i_{h_n}(t)-i_{h_{n-1}}(t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_3(y,i_{h_{n-1}})-Z_3(y,i_{h_{n-2}})\right) dy \nonumber \\&\quad \,+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left( Z_3(t,i_{h_{n-1}})-Z_3(t,i_{h_{n-2}})\right) , \nonumber \\ \psi _n(t)=e_{h_n}(t)-e_{h_{n-1}}(t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_2(y,e_{h_{n-1}})-Z_2(y,e_{h_{n-2}})\right) dy \nonumber \\&\quad \,+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left( Z_2(t,e_{h_{n-1}})-Z_2(t,e_{h_{n-2}})\right) \nonumber \\ \phi _n(t)=s_{h_n}(t)-s_{h_{n-1}}(t)&=\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_1(y,s_{h_{n-1}})-Z_1(y,s_{h_{n-2}})\right) dy \nonumber \\&\quad \,+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left( Z_1(t,s_{h_{n-1}})-Z_1(t,s_{h_{n-2}})\right) \end{aligned}$$
(4.11)

Noticing that

$$\begin{aligned} \begin{aligned}&s_{h_n}(t)=\sum _{i=0}^{n}\phi _i(t),\\&e_{h_n}(t)=\sum _{i=0}^{n}\psi _i(t),\\&i_{h_n}(t)=\sum _{i=0}^{n}\xi _i(t),\\&e_{\nu _n}(t)=\sum _{i=0}^{n}\chi _i(t),\\&i_{\nu _n}(t)=\sum _{i=0}^{n}\varsigma _n(t). \end{aligned} \end{aligned}$$
(4.12)

Step by step we get

$$\begin{aligned} \Vert \phi _n(t)\Vert&=\Vert s_{h_n}(t)-s_{h_{n-1}}(t)\Vert \nonumber \\&=\left\| \frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}\left( Z_1(y,s_{h_{n-1}})-Z_1(y,s_{h_{n-2}})\right) dy\right. \nonumber \\&\quad \,+ \left. \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left( Z_1(t,s_{h_{n-1}})-Z_1(t,s_{h_{n-2}})\right) \right\| \end{aligned}$$
(4.13)

Employing the triangular inequality, Eq. (4.13) reduces to

$$\begin{aligned} \begin{aligned} \Vert s_{h_n}(t)-s_{h_{n-1}}(t)\Vert&\le \frac{2\kappa }{(2-\kappa )M(\kappa )}\left\| \int \limits _{0}^{t}\left( Z_1(y,s_{h_{n-1}})-Z_1(y,s_{h_{n-2}})\right) dy\right\| \\ {}&\quad \,+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left\| \left( Z_1(t,s_{h_{n-1}})-Z_1(t,s_{h_{n-2}})\right) \right\| . \end{aligned} \end{aligned}$$
(4.14)

The Lipschitz condition is satisfy with the kernel, we have

$$\begin{aligned} \begin{aligned} \Vert s_{h_n}(t)-s_{h_{n-1}}(t)\Vert&\le \frac{2\kappa }{(2-\kappa )M(\kappa )} \gamma _1\int \limits _{0}^{t}\left\| s_{h_{n-1}}-s_{h_{n-2}} dy\right\| \\ {}&\quad \,+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _1\left\| s_{h_{n-1}}-s_{h_{n-2}}\right\| , \end{aligned} \end{aligned}$$
(4.15)

then we get

$$\begin{aligned} \Vert \phi _n(t)\Vert \le \frac{2\kappa }{(2-\kappa )M(\kappa )} \gamma _1\int \limits _{0}^{t}\left\| \phi _{n-1}(y) \right\| dy+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _1\left\| \phi _{n-1}(t)\right\| . \end{aligned}$$
(4.16)

Similarly, the following results are obtained by us:

$$\begin{aligned} \begin{aligned} \left\| \varsigma _n(t)\right\|&\le \frac{2\kappa }{(2-\kappa )M(\kappa )}\gamma _5\int \limits _{0}^{t}\left\| \varsigma _{n-1}(y)\right\| dy+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _5\left\| \varsigma _{n-1}(t)\right\| ,\\ \left\| \chi _n(t)\right\|&\le \frac{2\kappa }{(2-\kappa )M(\kappa )}\gamma _4\int \limits _{0}^{t}\left\| \chi _{n-1}(y)\right\| dy+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _4\left\| \chi _{n-1}(t)\right\| , \\ \left\| \xi _n(t)\right\|&\le \frac{2\kappa }{(2-\kappa )M(\kappa )}\gamma _3\int \limits _{0}^{t} \left\| \xi _{n-1}(y)\right\| dy+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _3\left\| \xi _{n-1}(t)\right\| ,\\ \left\| \psi _n(t)\right\|&\le \frac{2\kappa }{(2-\kappa )M(\kappa )}\gamma _2\int \limits _{0}^{t}\left\| \psi _{n-1}(y) \right\| dy+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _2\left\| \psi _{n-1}(t) \right\| . \end{aligned} \end{aligned}$$
(4.17)

Now we are presenting the subsequent theorem by consideration of the above results, \(\square \)

Theorem 4.2

The fractional dengue Models (3.3) with Non-Markovian Properties has a system of solutions under the conditions that we can find \(t_0\) such that

$$\begin{aligned} \frac{2\kappa }{(2-\kappa )M(\kappa )} \gamma _1t_0+\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _1\le 1 \end{aligned}$$

Proof

Here first we considered that the functions \(i_{\nu }(t), e_{\nu }(t), i_{h}(t), e_{h}(t), s_{h}(t)\) are bounded and Also, we prove that Lipschitz condition is satisfy with the kernels and hence on consideration of the results of Eqs. (4.16) and (4.17) and by employing the recursive method, we derive the relation as follows:

$$\begin{aligned} \begin{aligned}&\Vert \phi _n(t)\Vert \le \left\| s_{h}(0) \right\| \left[ \left( \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _1\right) +\left( \frac{2\kappa }{(2-\kappa )M(\kappa )} \gamma _1t\right) \right] ^n,\\&\left\| \psi _n(t)\right\| \le \left\| e_{h}(0)\right\| \left[ \left( \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _2\right) +\left( \frac{2\kappa }{(2-\kappa )M(\kappa )} \gamma _2t\right) \right] ^n,\\&\left\| \xi _n(t)\right\| \le \left\| i_{h}(0)\right\| \left[ \left( \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _3\right) +\left( \frac{2\kappa }{(2-\kappa )M(\kappa )} \gamma _3t\right) \right] ^n,\\&\left\| \chi _n(t)\right\| \le \left\| e_{\nu }(0)\right\| \left[ \left( \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _4\right) +\left( \frac{2\kappa }{(2-\kappa )M(\kappa )} \gamma _4t\right) \right] ^n,\\&\left\| \varsigma _n(t)\right\| \le \left\| i_{\nu }(0)\right\| \left[ \left( \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _5\right) +\left( \frac{2\kappa }{(2-\kappa )M(\kappa )} \gamma _5t\right) \right] ^n.\\ \end{aligned} \end{aligned}$$
(4.18)

Therefore, the system of functions (4.12) is smooth and exists. However, to show that the above functions are the system of solutions of the given system of Eq. (3.3), we assume that

$$\begin{aligned} \begin{aligned}&i_{\nu }(t)-i_{\nu }(0)=i_{\nu }(t)-F_{\nu _n}(t)\\&e_{\nu }(t)-e_{\nu }(0)=e_{\nu _n}(t)-E_{\nu _n}(t),\\&i_{h}(t)-i_{h}(0)=i_{h_n}(t)-D_{h_n}(t),\\&e_{h}(t)-e_{h}(0)=e_{h_n}(t)-C_{h_n}(t),\\&s_{h}(t)-s_{h}(0)=s_{h_n}(t)-B_{h_n}(t). \end{aligned} \end{aligned}$$
(4.19)

So, we have

$$\begin{aligned} \left\| B_{h_n}(t)\right\|&=\left\| \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left( Z(t,s_{h})-Z(t,s_{h_{n-1}})\right) \right. \nonumber \\&\left. \quad \,+ \frac{2\kappa }{(2-\kappa )M(\kappa )} \int \limits _{0}^{t}\left( Z(y,s_{h})-Z(y,s_{h_{n-1}})\right) dy\right\| \nonumber \\&\le \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left\| \left( Z(t,s_{h})-Z(t,s_{h_{n-1}})\right) \right\| \nonumber \\&\quad \,+ \frac{2\kappa }{(2-\kappa )M(\kappa )} \int \limits _{0}^{t}\left\| \left( Z(y,s_{h})-Z(y,s_{h_{n-1}})\right) \right\| dy \nonumber \\&\le \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _1\left\| s_{h}-s_{h_{n-1}}\right\| \nonumber \\&\quad \,+ \frac{2\kappa }{(2-\kappa )M(\kappa )} \int \limits _{0}^{t}\gamma _1\left\| s_{h}-s_{h_{n-1}}\right\| t. \end{aligned}$$
(4.20)

On using this process recursively, it yields

$$\begin{aligned} \left\| B_{h_n}(t)\right\| \le \left( \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )} + \frac{2\kappa }{(2-\kappa )M(\kappa )}t \right) ^{n+1}\gamma _1^{n+1}\alpha . \end{aligned}$$
(4.21)

On taking the limit on Eq. (4.21) as \(n\rightarrow \infty \), we get

$$\left\| B_{h_n}(t)\right\| \rightarrow 0.$$

Similarly, we get

\(\left\| F_{\nu _n}(t)\rightarrow 0\right\| \), \(\left\| E_{\nu _n}(t)\rightarrow 0\right\| \), \(\left\| D_{h_n}(t)\rightarrow 0\right\| ,\) and \( \left\| C_{h_n}(t)\right\| \rightarrow 0\).

Hence existence is verified.\(\square \)

Now, On proving the uniqueness of a system of solutions of Eq. (3.3)

Let there exist another system of solutions of (3.3) \(s_{h_1}(t), e_{h_1}(t), i_{h_1}(t), e_{\nu _1}(t)\) and \(i_{\nu _1}(t)\) then

$$\begin{aligned} \begin{aligned} s_{h}(t)-s_{h_1}(t)&=\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left( Z_1(t,s_{h})-Z_1(t,s_{h_1})\right) \\&\quad \,+ \frac{2\kappa }{(2-\kappa )M(\kappa )} \int \limits _{0}^{t}\left( Z_1(y,s_{h})-Z_1(y,s_{h_1})\right) dy. \end{aligned} \end{aligned}$$
(4.22)

On Eq. (4.22), if we applying norm then we get,

$$\begin{aligned} \begin{aligned} \left\| s_{h}(t)-s_{h_1}(t)\right\|&\le \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left\| \left( Z_1(t,s_{h})-Z_1(t,s_{h_1})\right) \right\| \\&\quad \,+ \frac{2\kappa }{(2-\kappa )M(\kappa )} \int \limits _{0}^{t}\left\| \left( Z_1(y,s_{h})-Z_1(y,s_{h_1})\right) \right\| dy. \end{aligned} \end{aligned}$$
(4.23)

From employing the Lipschitz conditions of the kernel, we have

$$\begin{aligned} \begin{aligned} \left\| s_{h}(t)-s_{h_1}(t)\right\|&\le \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _1\left\| s_{h}-s_{h_1}\right\| + \frac{2\kappa }{(2-\kappa )M(\kappa )}\gamma _1t \left\| \left( s_{h}-s_{h_1}\right) \right\| . \end{aligned} \end{aligned}$$
(4.24)

It gives

$$\begin{aligned} \begin{aligned} \left\| s_{h}(t)-s_{h_1}(t)\right\| \left( 1- \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _1 - \frac{2\kappa }{(2-\kappa )M(\kappa )}\gamma _1t \right) \le 0 . \end{aligned} \end{aligned}$$
(4.25)

Theorem 4.3

The system of Eq. (3.3) has a unique system of solutions if the following condition holds:

$$\begin{aligned} \left\| s_{h}(t)-s_{h_1}(t)\right\| \left( 1- \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _1 - \frac{2\kappa }{(2-\kappa )M(\kappa )}\gamma _1t \right) \ge 0 . \end{aligned}$$
(4.26)

Proof

If the condition holds (4.26), then

$$\begin{aligned} \begin{aligned} \left\| s_{h}(t)-s_{h_1}(t)\right\| \left( 1- \frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\gamma _1 - \frac{2\kappa }{(2-\kappa )M(\kappa )}\gamma _1t \right) \le 0, \end{aligned} \end{aligned}$$
(4.27)

then we have

$$\left\| s_{h}(t)-s_{h_1}(t)\right\| =0.$$

Then we get

$$\begin{aligned} s_{h}(t)=s_{h_1}(t) \end{aligned}$$
(4.28)

Similarly, we have

$$\begin{aligned} \begin{aligned}&i_{\nu }(t)=i_{\nu _1}(t),\\&e_{\nu }(t)= e_{\nu _1}(t),\\&i_{h}(t)=i_{h_1}(t),\\&e_{h_1}(t)=e_{h_1}(t). \end{aligned} \end{aligned}$$
(4.29)

Therefore, this verified the uniqueness of the system of solutions of Eq. (3.3).\(\square \)

5 Numerical Solution

In this section, we construct a numerical scheme for fractional model based on the CF derivative. On applying this scheme we first consider the following non-linear fractional ODE:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}^{CF}_0D^\kappa _tu(t)=f(t,u(t))\\ &{}u(0)=u_0 \end{array}\right. } \end{aligned}$$
(5.1)

On applying the fundamental theorem of fc The above eq can be converted to a fractional integral equation:

$$\begin{aligned} \begin{aligned} u(t)-u(0)=\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}f(t,u(t))+\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{0}^{t}f(\tau ,u(\tau ))d\tau , \end{aligned} \end{aligned}$$
(5.2)

At a given point \(t_{n+1}\), \(n=0,1,2,\ldots \) we reformulated the above equation as

$$\begin{aligned} \begin{aligned} u(t_{n+1})-u(t_0)=\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}[f(t_{n+1})-f(t_n)]+\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{t_{n}}^{t_{n+1}}f(\tau ,u(\tau ))d\tau \end{aligned} \end{aligned}$$
(5.3)

The second step is approximation of our numerical scheme of the function f(t, u(t)). Thus we approximate f(t, u(t)) by using the well-known Lagrange interpolation polynomial to obtain following result for the interval \([t_n,t_{n+1}]\),

$$\begin{aligned} \begin{aligned}&P(\tau )(\approx f{(\tau ,u{(\tau )})})=\left\{ \frac{(\tau -t_{n-1})}{(t_n-t_{n-1})} \right\} f(t_n,u_n)+\left\{ \frac{(\tau -t_{n})}{(t_{n-1}-t_{n})} \right\} f(t_{n-1},u_{n-1}) \end{aligned} \end{aligned}$$
(5.4)
$$\begin{aligned} \begin{aligned} P(\tau )(\approx f{(\tau ,u{(\tau )})})=\left\{ \frac{(\tau -t_{n-1})}{(t_n-t_{n-1})} \right\} f_n+\left\{ \frac{(\tau -t_{n})}{(t_{n-1}-t_{n})} \right\} f_{n-1} \end{aligned} \end{aligned}$$
(5.5)

The above approximation can included in Eq. (5.3) to produce

$$\begin{aligned} \begin{aligned} u(t_{n+1})-u(t_0)&=\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}[f(t_{n+1})-f(t_n)]\\&\quad \,+\frac{2\kappa }{(2-\kappa )M(\kappa )}\int \limits _{t_{n}}^{t_{n+1}}\left[ \left\{ \frac{(\tau -t_{n-1})}{(t_n-t_{n-1})} \right\} f_n+\left\{ \frac{(\tau -t_{n})}{(t_{n-1}-t_{n})} \right\} f_{n-1}\right] d\tau \end{aligned} \end{aligned}$$
(5.6)

thus, after some simplifications and integrating, the following equation is obtained:

$$\begin{aligned} \begin{aligned} u_{n+1}-u_{n}=\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}[f_{n+1}-f_n]+\frac{2\kappa }{(2-\kappa )M(\kappa )}h\left[ \frac{3}{2}f_n-\frac{1}{2}f_{n-1} \right] \end{aligned} \end{aligned}$$
(5.7)

Now for finding the numerical solution of fractional model based on the CF derivative. For the Eq. (3.3) we get the solution

$$\begin{aligned} s_{h_{n+1}}-s_{h_{n}}&=\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left[ \mu _h(1-s_{h_{n+1}})-\alpha s_{h_{n+1}}i_{\nu _{n+1}}-\mu _h(1-s_{h_{n}})+\alpha s_{h_{n}}i_{\nu _n}\right] \nonumber \\&\quad \,+\frac{2\kappa h}{(2-\kappa )M(\kappa )}\left[ \frac{3}{2}[\mu _h(1-s_{h_n})-\alpha s_{h_n}{i_{\nu _n}}]-\frac{1}{2}[\mu _h(1-s_{h_{n-1}})-\alpha s_{h_{n-1}}i_{\nu _{n-1}}]\right] \nonumber \\ e_{h_{n+1}}-e_{h_{n}}&=\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left[ \alpha s_{h_{n+1}}i_{\nu _{n+1}}-\beta e_{h_{n+1}}-\alpha s_{h_{n}}i_{\nu _{n}}+\beta e_{h_{n}}\right] \nonumber \\&\quad \,+\frac{2\kappa h}{(2-\kappa )M(\kappa )}\left[ \frac{3}{2}\left[ \alpha s_{h_{n}}i_{\nu _{n}}-\beta e_{h_{n}}\right] -\frac{1}{2}\left[ \alpha s_{h_{n-1}}i_{\nu _{n-1}}-\beta e_{h_{n-1}}\right] \right] \nonumber \\ i_{h_{n+1}}-i_{h_{n}}&=\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left[ \nu _{h_{n+1}}e_{h_{n+1}}-\gamma i_{h_{n+1}} -\nu _{h_{n}}e_{h_{n}}+\gamma i_{h_{n}}\right] \nonumber \\&\quad \,+\frac{2\kappa h}{(2-\kappa )M(\kappa )}\left[ \frac{3}{2}\left[ \nu _{h_{n}}e_{h_{n}}-\gamma i_{h_{n}}\right] -\frac{1}{2}[\nu _{h_{n-1}}e_{h_{n-1}}-\gamma i_{h_{n-1}}\right] \nonumber \\ e_{\nu _{n+1}}-e_{\nu _n}&=\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left[ \delta s_{\nu _{n+1}} i_{h_{n+1}}-(\epsilon +\nu _{\nu _{n+1}})e_{\nu _{n+1}} -\delta s_{\nu _{n}} i_{h_{n}}+(\epsilon +\nu _{\nu _{n}})e_{\nu _{n}}\right] \nonumber \\&\quad \,+\frac{2\kappa h}{(2-\kappa )M(\kappa )}\left[ \frac{3}{2} \left[ \delta s_{\nu _{n}} i_{h_{n}}-(\epsilon +\nu _{\nu _{n}})e_{\nu _{n}} \right] -\frac{1}{2}\left[ \delta s_{\nu _{n-1}} i_{h_{n-1}}-(\epsilon +\nu _{\nu _{n-1}})e_{\nu _{n-1}}\right] \right] \nonumber \\ i_{\nu _{n+1}}-i_{\nu _n}&=\frac{2(1-\kappa )}{(2-\kappa )M(\kappa )}\left[ \nu _{\nu _{n+1}} e_{\nu _{n+1}}-\epsilon i_{\nu _{n+1}}-\nu _{\nu _{n}} e_{\nu _{n}}+\epsilon i_{\nu _{n}}\right] \nonumber \\&\quad \,+\frac{2\kappa h}{(2-\kappa )M(\kappa )}\left[ \frac{3}{2} \left[ \nu _{\nu _{n}} e_{\nu _{n}}-\epsilon i_{\nu _{n}}\right] -\frac{1}{2}\left[ \nu _{\nu _{n-1}} e_{\nu _{n-1}}-\epsilon i_{\nu _{n-1}}\right] \right] \end{aligned}$$
(5.8)

6 Numerical Simulation

In this part, By using the proposed numerical scheme of the model for different values of fractional order we present the numerical simulation. The numerical simulations are shown in Figs. 1, 2, 3, 4 and 5. Figure 1 is considered \(\kappa \) to be 1, Fig. 2 is considered \(\kappa \) to be 0.75, Fig. 3 is considered \(\kappa \) to be 0.55, in Fig. 4 is considered \(\kappa \) to be 0.35 and finally Fig. 5 is considered \(\kappa \) to be 0.15.

To achieve our numerical simulation the following initial conditions and parameters were used [17].

\(N_h =\) 5,071,126, \(\pi _\nu =\) 2,500,000, \(\nu _h =\) 0.1667, \(\mu _h = 0.0045, \mu _\nu = 0.02941, \gamma _h = 0.328833, b\beta _h = 0.75, b\beta _\nu = 0.375, \nu _\nu = 0.1428.\)

Fig. 1
figure 1

For \(\kappa \) = 1

Full size image
Fig. 2
figure 2

For \(\kappa \) = 0.75

Full size image
Fig. 3
figure 3

For \(\kappa \) = 0.55

Full size image
Fig. 4
figure 4

For \(\kappa \) = 0.35

Full size image
Fig. 5
figure 5

For \(\kappa \) = 0.15

Full size image

7 Conclusion

Although the dynamics spread of Dengue fever has in the attention of many researchers in the same field of applied mathematics in biology, it is worth noting that, still there is no attention has been given to modeling the spread with a differential operator having non-Markovian properties but the associated evolution equation having Markovian properties. If we consider the recent development in fractional differentiation and integration, a derivative with non-local kernel and non-singular was suggested by Caputo and Fabrizio and posses several properties that one observed in many problems occurring in biological modeling. We these properties, we devoted our paper to the discussion and analysis underpinning the dynamical spread of Dengue in given population. We provided a motivation to underpin why this operator is used for this model, then, we presented a detailed analysis of uniqueness and existence and the exact solution using the fixed-point theorem in Banach space. With the aim of improving the accuracy of numerical scheme, a new method was suggested by Toufit and Atangana [19] and was found to be highly accurate and very easier to implement. We used this numerical scheme to solve the new model with fading memory induces by the exponential kernel and presented numerical simulation.